A Review on Testing of Electrochemical Cells for Aging Models in BESS
Abstract
:1. Introduction
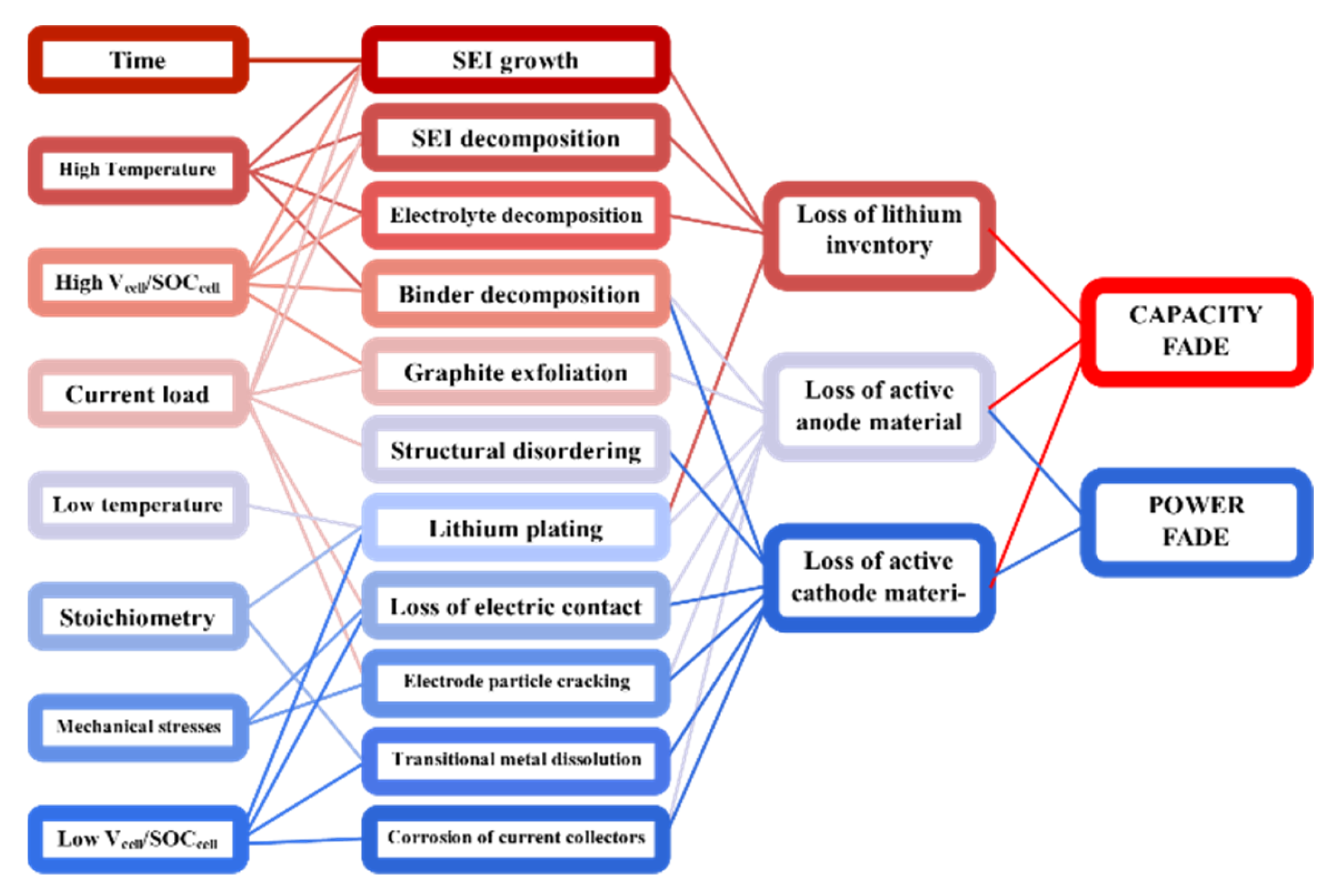
2. Short Recap on Aging Mechanisms
- Loss of lithium inventory
- Loss of active material in anode and cathode
Single-Cell Aging Models
- Electrochemical models: Based on the detail of reactions that happen inside of the battery. The main core of these models are the cell’s electrochemical models, such as P2D models, SP models, and extended SP models [20,28,29]. For example, the degradation model in [30] has been developed based on three main assumptions. First, they assumed that no overcharged or undercharged will occur. Secondly, the aging in the cathode has been neglected, and thirdly, aging caused by internal mechanical stresses has been neglected. By solving the equations for the transfer function between the aging representatives (which are capacity loss, SEI resistance, and deposited layer growth). They were able to predict the remaining capacity of the battery with a maximum error of 3%. They used EIS, X-ray diffraction and X-ray photoelectron spectroscopy, and electron microscopy to gather data. To validate the models and obtain the model parameters, they cycled the cells in a temperature chamber at 25 °C with a defined protocol at 1C, 2C, and 3C. According to various research [30,31], the side reactions at the anode are the main cause of degradation in electrochemical cells.In [32], based on the extended SP model of the battery, and with the help of cycling aging and EIS test, the correlation of the model factors and cycling of the battery has been obtained. The detail of obtaining each model identification has been explained in the paper. According to their results, it can be said that at 1C, besides three identifications, the correlation of the other identifications with the number of cycles was not that high. But, as they mentioned in their paper, this way can be a suitable approach to finding and building an electrochemical model for the aging of the battery. The same approach has been adopted in the [33]. Indeed, they used particle swarm optimization for the identification of the model parameters. The errors obtained by fitting the model for predicting the remaining capacity were between 2% and 4% based on the data fed to the model. In order to reduce the number of parameters in the electrochemical model, in [34], they used a fractional order of simplified P2D model known as SPM. By doing so, it is possible to estimate the capacity and resistance.
- Equivalent circuit-based models: Based on the understanding of the physical and chemistry of the cell, it is possible to model the battery as an equivalent circuit model (ECM). An ECM has three major parts. The thermodynamics of the battery has been shown by a static part. The kinetics aspect of the cell has been modeled with a dynamic part and, finally, a load to complete the circuit for charge and discharge [35]. A circuit was developed by [36] to see the effect of aging. The constant phase element (CPE) has been used to model nonideal impedances that occur between the anode and cathode electrodes. Also, for modeling the diffusion process, a Walburg impedance has been used. Then, with the use of the EIS test, the parameter of the ECM was achieved every 30 cycles. Therefore, the relation between every parameter of the circuit and the SOH of the battery was investigated. A more simple approach has been carried out in [37] using the cell’s Thevenin equivalent circuit. The relationship between the circuit parameters and SOC, SOH, and temperature was investigated experimentally by performing HPPC and capacity tests at different temperatures. The results were then used in a look-up table to predict the terminal voltage. In a more complex model, in [38], an ECM has been used along with a minimal electrochemical model (MEM), which is based on the loss of lithium inventory to estimate the SOC and SOH of the battery. A recursive least squares method was obtained to identify the ECM parameters online, then using an unscented Kalman filter (UKF)—which is a state estimation algorithm for nonlinear systems—the SOC(ECM) (this is SOC estimated from ECM) can be calculated. Then, the corrected current can be calculated and fed to the electrochemical model to estimate the SOC and SOH.
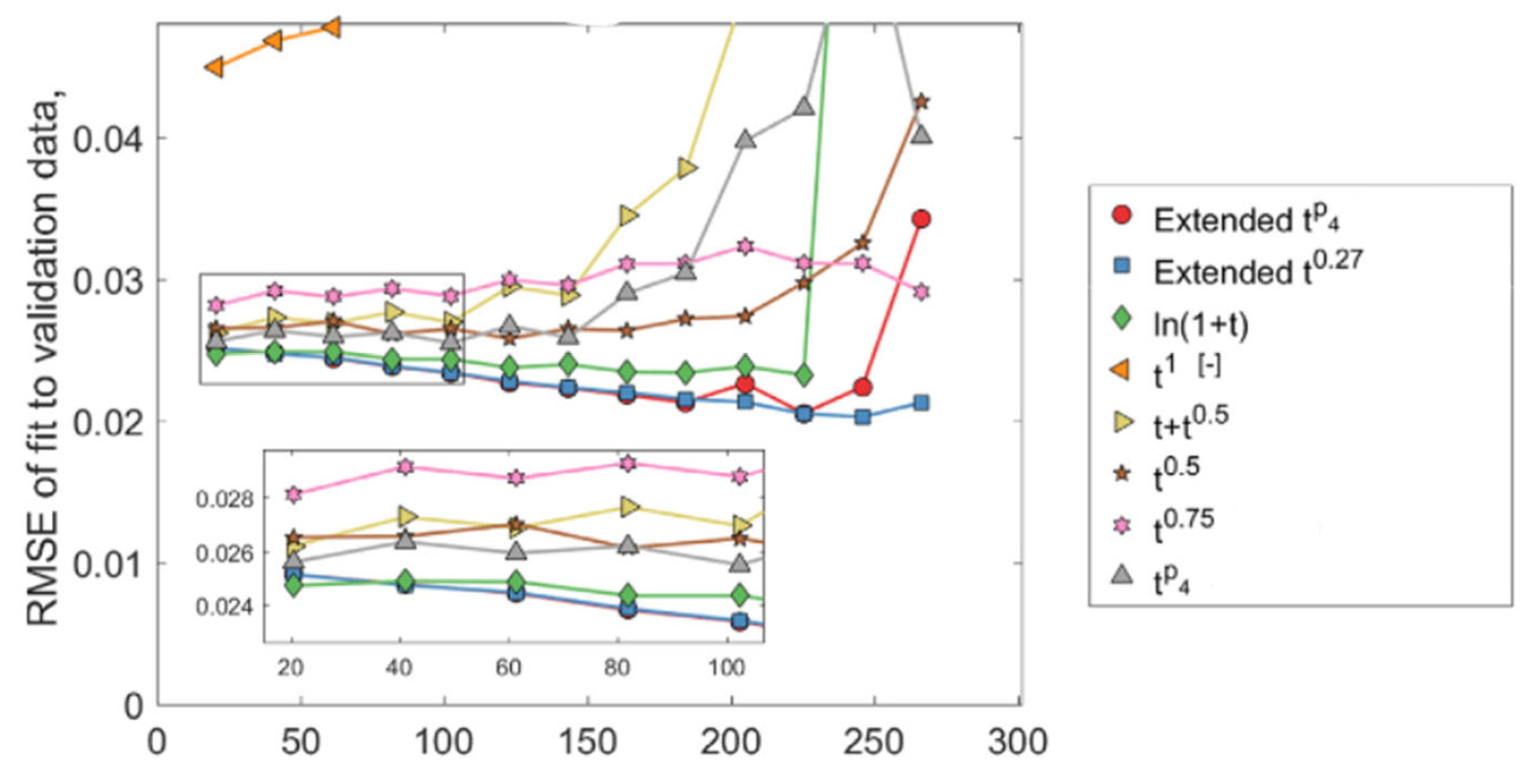
- Performance-based models: This approach is based on finding the relationship between stress factors and aging parameters of the cell, such as capacity fade or resistance increase, by doing experimental tests. It is possible to divide this method into three categories: cycle aging, calendar aging, and global aging [27]. To provide an example, one of the most famous formulas for calendar aging is to consider the relation of capacity and time as a root square. In [39], they proposed another combination, such as . Then, by fitting the data in each formula, the results were compared as shown in Figure 4. These models are the most suitable models to use in machine learning. Also, in [40], they use a deep learning architecture called an attention-based long short-term memory network (ALSTM) to model the calendar aging. The ALSTM network is designed to integrate both knowledge-based features, such as the battery chemistry and operating conditions, and data-driven features, such as the battery’s discharge profile and temperature history. Similarly, in [41], a degradation and cycle life prediction model was built based on the Arrhenius equation, which takes into account several factors that contribute to battery degradation, including temperature, state of charge, and the number of charge–discharge cycles. After proposing the model, a particle filter-based data-driven method was introduced to track the model parameters. In a more complex model, in [42], they tried to optimize a support vector regression using the data available about the temperature, SOC, and time effect on the calendar aging. The results showed that using these data improves the prediction of calendar aging by increasing the R-squared by around 0.1 with respect to a classic SVR.
- Empirical and statistical approaches: The empirical models are the ones that are trying to find the relation between stress factors and the cycle or calendar aging in the batteries, based on the data gathered from the experiments without considering deeply the physical or chemical side of the battery [27,43]. To be exact, empirical models benefit from the machine learning algorithms fitting a curve in experimental data. In [44], different neural networks have been used to fit the data obtained from the cycling and IC experiments. These models are suitable for the prediction of the RUL. For example, in [45]. A neural network (NN) was applied to establish the link between stress factors and SOH. Subsequently, a bat-based particle filter was employed to dynamically adjust the NN-derived model online, enabling the prediction of RUL while aligning with the battery’s SOH pattern. Similarly, in [46], they used the voltage, current, and capacity of the cells to predict the RUL using empirical decomposition and LSTM. A more complicated algorithm has been adopted in [47] by proposing a capacity forecast generative adversarial network-based (CFGAN) model. To obtain the best from the GAN-based network, they use a conditioner so the data that the generator builds would be more accurate. The results show that, compared to other deep learning models, the CFGAN has better accuracy in point and probabilistic forecasting of calendar aging.An important fact in using empirical models is the situation of the tests. The more the tests are in a controlled situation, the better the results. As indicated in [43], a proper dataset should use full equivalent cycles (FECs) or equivalent measures such as the number of cycles or Ah throughput. It also should determine the chemistry of the tested LIB reference and keep stress factors such as temperature, depth of discharge, mean state of charge, and charge and discharge rate constant throughout the entire static degradation test. In addition, the magnitude of these stress factors should be determined for each deployed test. After cycling the cells, the measurement tests are playing a very important role. In [48], they used incremental capacity analysis (ICA) and integrated voltage (IV). In [49], they used the low-frequency EIS measurements and Gaussian regression model to fit the data. On the other hand, it is also possible not to use any additional experiments. As in [50], they just used the remaining capacity of the battery in different temperatures and DOD to find the relation between capacity and stress factors. In [51], they combine a support vector regression model and an extreme learning machine model to extract features from the battery signal, which just consists of the cycle number and capacity of the battery.
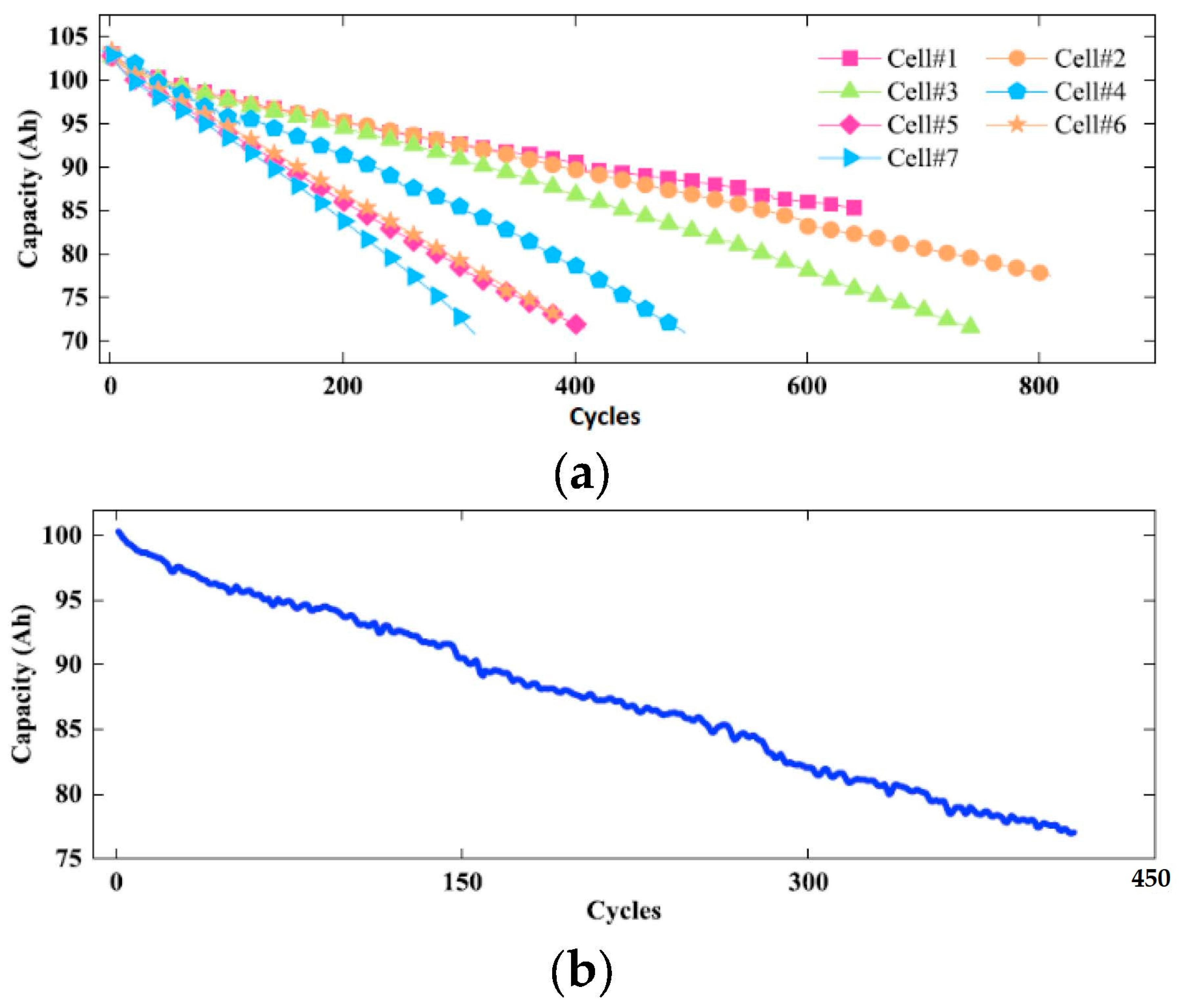
3. Tests for Single Electrochemical Cells
4. Tests for BESS Aging Models
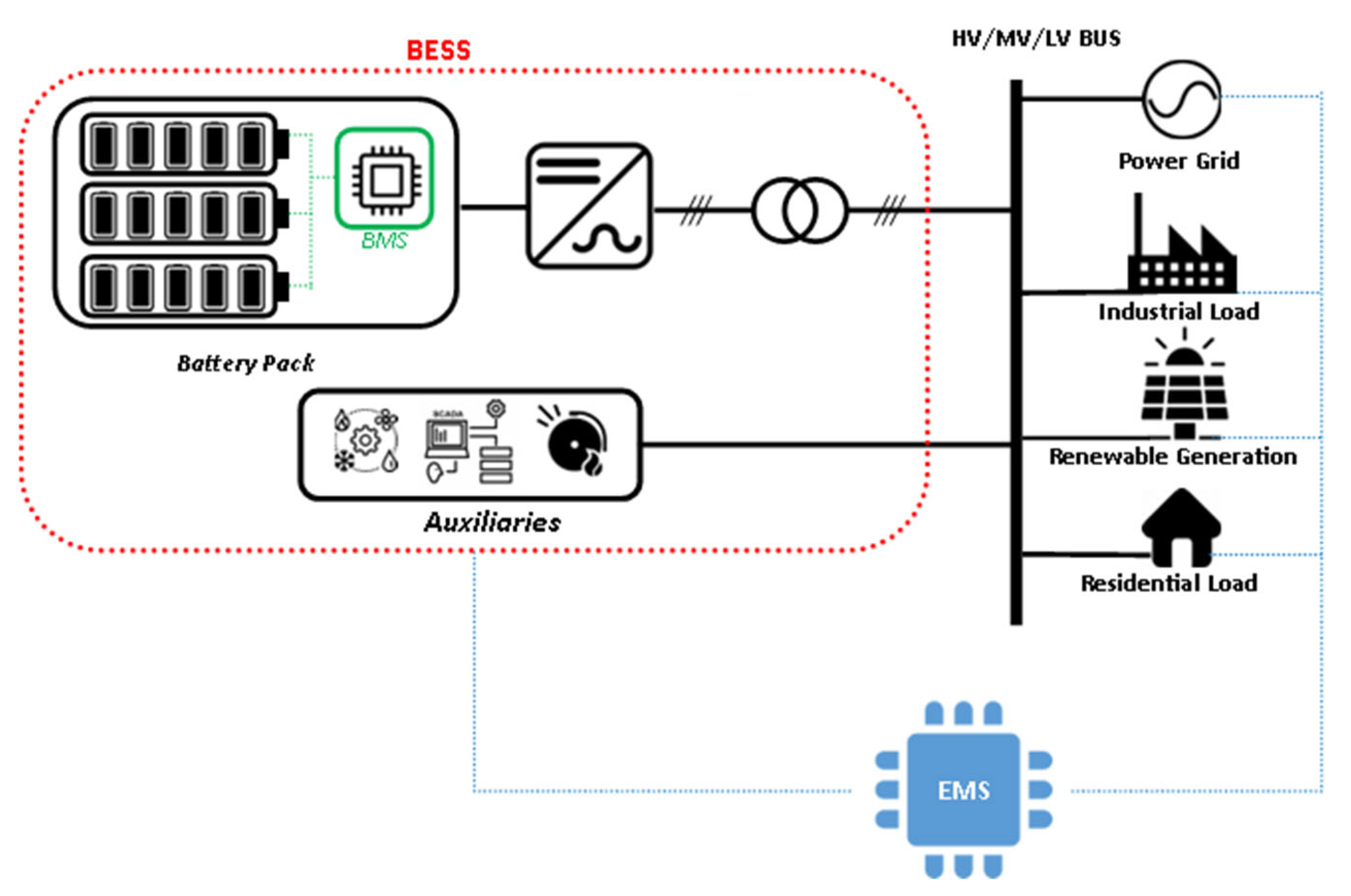
4.1. BESS Structure
4.2. Tests
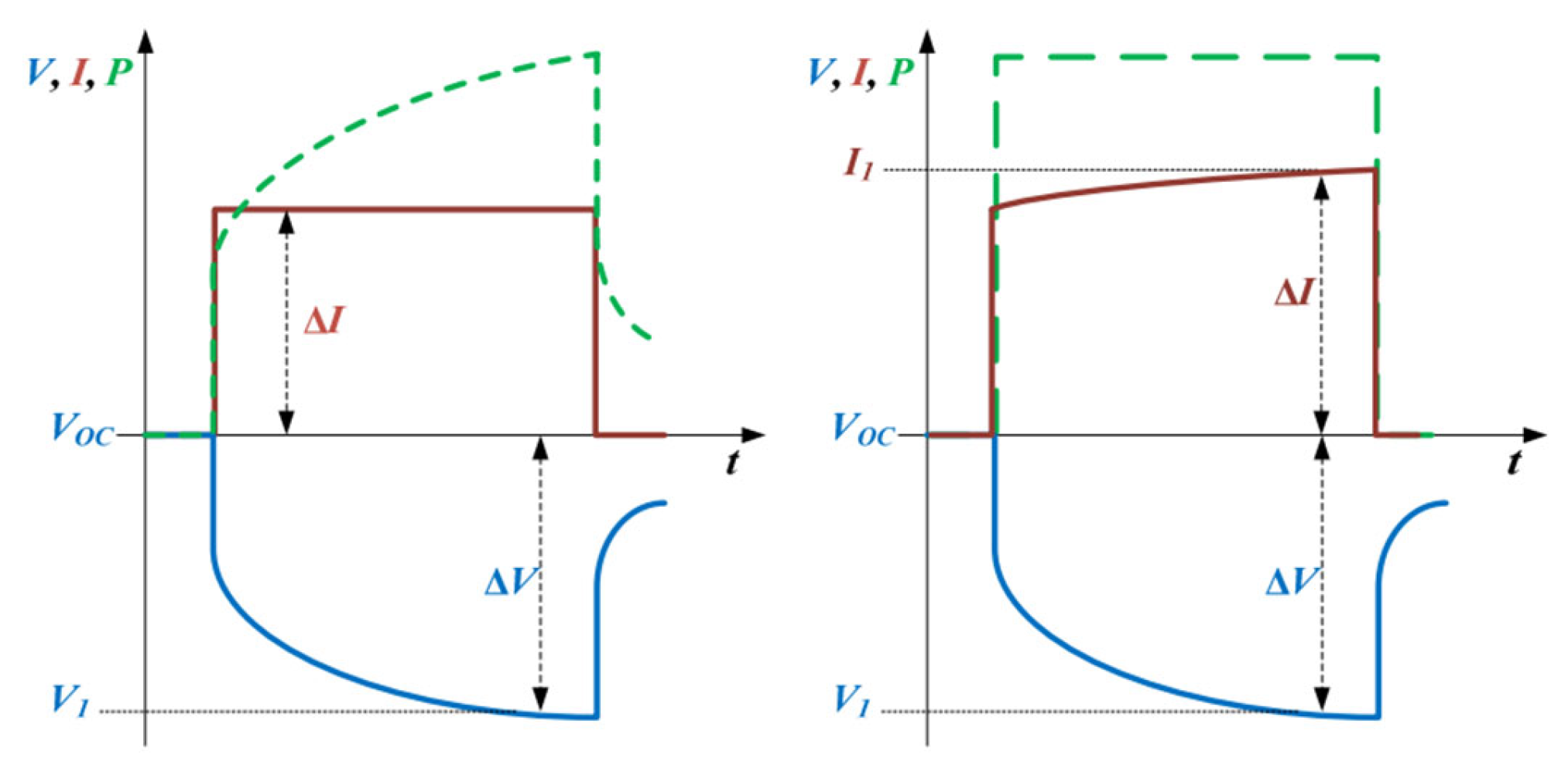
4.2.1. BESS Characterization Tests
| Ref. | System Under Test | Tests | Test Steps | Outcome of the Test | Strong Points | Weak Points |
|---|---|---|---|---|---|---|
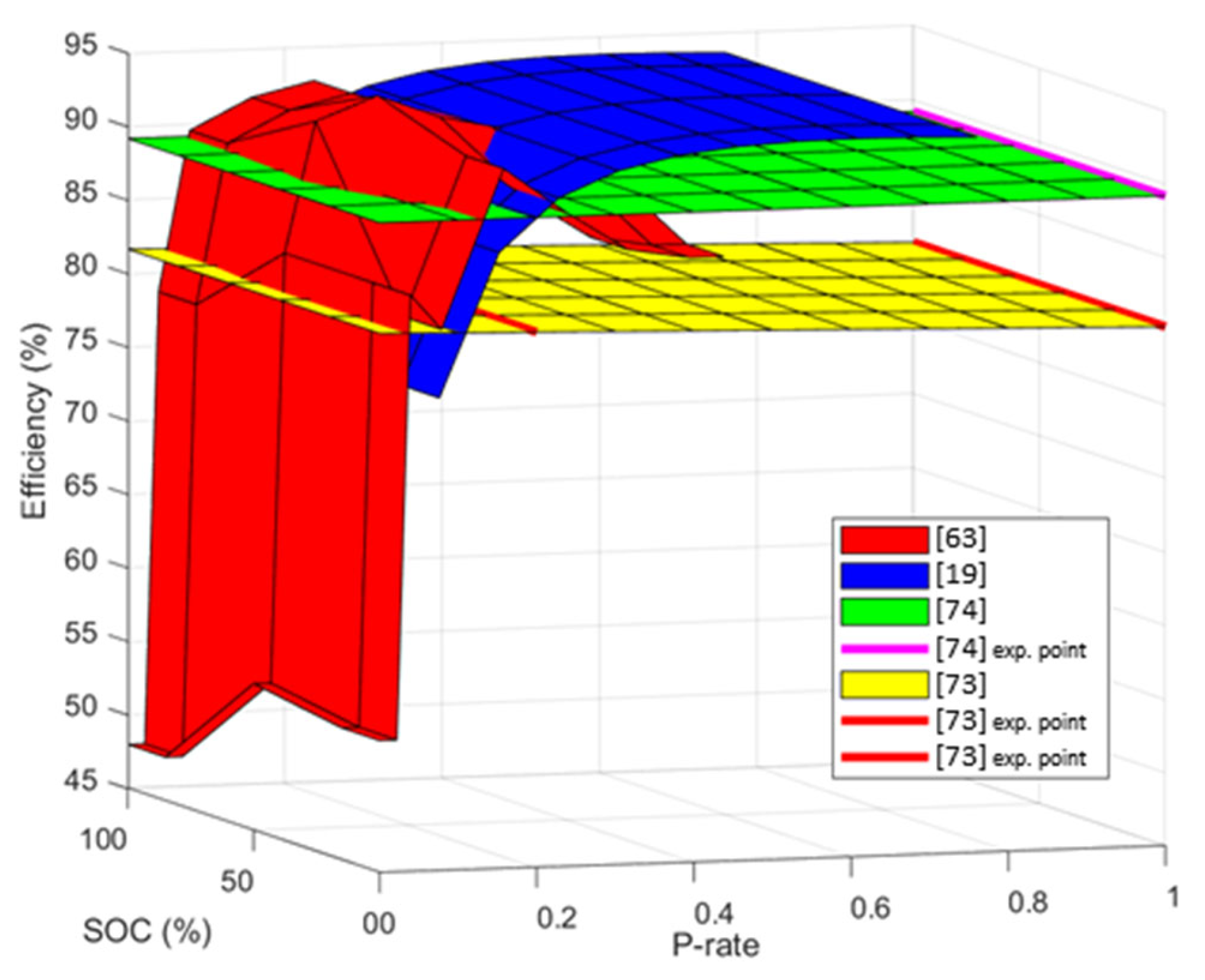
| [74] | 1. 0.4 MW 0.1 MWh (LiFePO4/C) 2. 1.2 MW 0.3 MWh (LMO2/Li4Ti5O12) | Capacity |
|
|
|
|
| DC resistance |
|
| ||||
| AC resistance |
| |||||
| [4] | 1 MW 580 MWh (Li-ion) | Efficiency |
|
|
|
|
| [73] | 1 MW 1 MWh (LTO) | Rated energy |
|
|
|
|
| Power accuracy |
|
| ||||
| Capability curve |
|
| ||||
| Efficiency |
|
| ||||
| [71] | 6.4 kW 10.6 kWh (NMC) | Efficiency |
|
|
|
|
| [70] | 48 V 200 Ah (FZSoNick) | Efficiency |
|
|
|
|
| [63] | 570 kWh 250 kW (NMC) | SOC-OCV and capability curve |
|
|
|
|
| Efficiency |
|
| ||||
| [19] | 822 MWh 500 kW (NMC) | Efficiency |
|
|
|
|
| [75] | 100 kWh 100 kW | Usable energy and efficiency |
|
|
|
|
| Response time and accuracy |
|
| ||||
| Standby losses due to battery self-discharge |
|
|
4.2.2. Alternative Methods
4.2.3. Comparison
4.3. Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | artificial intelligence |
| ALSTM | attention-based long short-term memory |
| BESSs | battery energy storage systems |
| BMS | battery management system |
| CC | constant current |
| CCCV | constant current-constant voltage |
| CPE | constant phase element |
| C-rates | charge/discharge rate |
| CV | constant voltage |
| DC-IR | dc internal resistance |
| DOD | depth of discharge |
| DV | derivative voltage |
| ECM | equivalent circuit model |
| EIS | electrochemical impedance spectroscopy |
| EOL | end of life |
| EV | electric vehicle |
| FEC | full equivalent cycles |
| GPR | Gaussian process regression |
| HPPC | hybrid pulse power characterization |
| HVAC | heating ventilation air conditioning |
| IC | incremental capacity |
| ICA | incremental capacity analysis |
| IV | integrated voltage |
| MEM | minimal electrochemical model |
| MOSFET | metal-oxide-semiconductor field-effect transistor |
| NASA | national aeronautics and space administration |
| NN | neural network |
| OCV | open circuit voltage |
| P | active power |
| PCS | power conversion system |
| P-rate | power rate |
| Q | reactive power |
| RUL | remaining useful life |
| SEI | solid electrolyte interphase |
| SOC | state of charge |
| SOH | state of health |
| TL | transfer learning |
| UKF | unscented Kalman filter |
References
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Preger, Y.; Barkholtz, H.M.; Fresquez, A.; Campbell, D.L.; Juba, B.W.; Romàn-Kustas, J.; Ferreira, S.R.; Chalamala, B.R. Degradation of Commercial Lithium-Ion Cells as a Function of Chemistry and Cycling Conditions. J. Electrochem. Soc. 2020, 167, 120532. [Google Scholar] [CrossRef]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of lithium-ion battery degradation for cell life assessment. IEEE Trans Smart Grid 2018, 9, 1131–1140. [Google Scholar] [CrossRef]
- Koller, M.; Borsche, T.; Ulbig, A.; Andersson, G. Review of grid applications with the Zurich 1 MW battery energy storage system. Electr. Power Syst. Res. 2015, 120, 128–135. [Google Scholar] [CrossRef]
- Xiong, R.; Pan, Y.; Shen, W.; Li, H.; Sun, F. Lithium-ion battery aging mechanisms and diagnosis method for automotive applications: Recent advances and perspectives. Renew. Sustain. Energy Rev. 2020, 131, 110048. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li(NiMnCo)O2 based 18650 lithium-ion batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Liu, K.; Wei, Z.; Zhang, C.; Shang, Y.; Teodorescu, R.; Han, Q.L. Towards Long Lifetime Battery: AI-Based Manufacturing and Management. IEEE/CAA J. Autom. Sin. 2022, 9, 1139–1165. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z. State of health estimation for Li-ion battery via partial incremental capacity analysis based on support vector regression. Energy 2020, 203, 117852. [Google Scholar] [CrossRef]
- Son, S.; Jeong, S.; Kwak, E.; Kim, J.H.; Oh, K.Y. Integrated framework for SOH estimation of lithium-ion batteries using multiphysics features. Energy 2022, 238, 121712. [Google Scholar] [CrossRef]
- He, Z.; Gao, M.; Ma, G.; Liu, Y.; Chen, S. Online state-of-health estimation of lithium-ion batteries using Dynamic Bayesian Networks. J Power Sources 2014, 267, 576–583. [Google Scholar] [CrossRef]
- Yang, D.; Wang, Y.; Pan, R.; Chen, R.; Chen, Z. A Neural Network Based State-of-Health Estimation of Lithium-ion Battery in Electric Vehicles. Energy Procedia 2017, 105, 2059–2064. [Google Scholar] [CrossRef]
- Wu, X.; Li, M.; Du, J.; Hu, F. SOC prediction method based on battery pack aging and consistency deviation of thermoelectric characteristics. Energy Rep. 2022, 8, 2262–2272. [Google Scholar] [CrossRef]
- Che, Y.; Stroe, D.I.; Hu, X.; Teodorescu, R. Semi-Supervised Self-Learning-Based Lifetime Prediction for Batteries. IEEE Trans Ind. Inf. 2023, 19, 6471–6481. [Google Scholar] [CrossRef]
- Liu, K.; Peng, Q.; Che, Y.; Zheng, Y.; Li, K.; Teodorescu, R.; Widanage, D.; Barai, A. Transfer learning for battery smarter state estimation and ageing prognostics: Recent progress, challenges, and prospects. Adv. Appl. Energy 2023, 9, 100117. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, K.; Liu, X.; Li, Y.; Du, L.; Gao, F. Multi-level Data-driven Battery Management: From Internal Sensing to Big Data Utilization. IEEE Trans. Transp. Electrif. 2023. early access. [Google Scholar] [CrossRef]
- Liu, K.; Tang, X.; Teodorescu, R.; Gao, F.; Meng, J. Future Ageing Trajectory Prediction for Lithium-Ion Battery Considering the Knee Point Effect. IEEE Trans. Energy Convers. 2022, 37, 1282–1291. [Google Scholar] [CrossRef]
- Che, Y.; Deng, Z.; Tang, X.; Lin, X.; Nie, X.; Hu, X. Lifetime and Aging Degradation Prognostics for Lithium-ion Battery Packs Based on a Cell to Pack Method. Chin. J. Mech. Eng. Engl. Ed. 2022, 35, 1–16. [Google Scholar] [CrossRef]
- Grimaldi, A.; Minuto, F.D.; Perol, A.; Casagrande, S.; Lanzini, A. Ageing and energy performance analysis of a utility-scale lithium-ion battery for power grid applications through a data-driven empirical modelling approach. J. Energy Storage 2023, 65, 107232. [Google Scholar] [CrossRef]
- Turković, A.; Pavlović, M.; Dubček, P.; Lučić-Lavčević, M.; Etlinger, B.; Bernstorff, S. You may also like SAXS/DSC Study of Polymer Electrolyte for Zn Rechargeable Nanostructured Galvanic Cells Nano or Microclustering as an Explanation for the Unusual Thermal Behavior of Nickel Polymer Electrolytes. J. Electrochem. Soc. 1993, 140, A554. [Google Scholar]
- Reza, M.; Hannan, M.; Ker, P.J.; Mansor, M.; Lipu, M.H.; Hossain, M.; Mahlia, T.I. Uncertainty parameters of battery energy storage integrated grid and their modeling approaches: A review and future research directions. J. Energy Storage 2023, 68, 107698. [Google Scholar] [CrossRef]
- Bazargan, D.; Filizadeh, S.; Gole, A.M. Stability analysis of converter-connected battery energy storage systems in the grid. IEEE Trans. Sustain. Energy 2014, 5, 1204–1212. [Google Scholar] [CrossRef]
- Collath, N.; Tepe, B.; Englberger, S.; Jossen, A.; Hesse, H. Aging aware operation of lithium-ion battery energy storage systems: A review. J. Energy Storage 2022, 55, 105634. [Google Scholar] [CrossRef]
- Reniers, J.M.; Mulder, G.; Howey, D.A. Review and Performance Comparison of Mechanical-Chemical Degradation Models for Lithium-Ion Batteries. J. Electrochem Soc. 2019, 166, A3189–A3200. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Wenzl, H.; Baring-Gould, I.; Kaiser, R.; Liaw, B.Y.; Lundsager, P.; Manwell, J.; Ruddell, A.; Svoboda, V. Life prediction of batteries for selecting the technically most suitable and cost effective battery. J. Power Sources 2005, 144, 373–384. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Zhou, J.; Xing, B.; Wang, C. A review of lithium ion batteries electrochemical models for electric vehicles. E3S Web Conf. 2020, 185, 04001. [Google Scholar] [CrossRef]
- Haran, B.S.; Popov, B.N.; White, R.E. Determination of the hydrogen diffusion coefficient in metal hydrides by impedance spectroscopy. J. Power Sources 1998, 75, 56–63. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Y.; Guo, B.; Zhu, C.; Zhou, X.; Wang, L.; Cao, J. A novel quantitative electrochemical aging model considering side reactions for lithium-ion batteries. Electrochim. Acta 2020, 343, 136070. [Google Scholar] [CrossRef]
- Fu, R.; Choe, S.Y.; Agubra, V.; Fergus, J. Modeling of degradation effects considering side reactions for a pouch type Li-ion polymer battery with carbon anode. J. Power Sources 2014, 261, 120–135. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.; Deng, L.; Cui, Z.; Lyu, C.; Wang, L.; Pecht, M. Aging modes analysis and physical parameter identification based on a simplified electrochemical model for lithium-ion batteries. J. Energy Storage 2020, 31, 101538. [Google Scholar] [CrossRef]
- Shao, J.; Li, J.; Yuan, W.; Dai, C.; Wang, Z.; Zhao, M.; Pecht, M. A novel method of discharge capacity prediction based on simplified electrochemical model-aging mechanism for lithium-ion batteries. J. Energy Storage 2023, 61, 106788. [Google Scholar] [CrossRef]
- Hosseininasab, S.; Lin, C.; Pischinger, S.; Stapelbroek, M.; Vagnoni, G. State-of-health estimation of lithium-ion batteries for electrified vehicles using a reduced-order electrochemical model. J. Energy Storage 2022, 52, 104684. [Google Scholar] [CrossRef]
- Liaw, B.Y.; Nagasubramanian, G.; Jungst, R.G.; Doughty, D.H. Modeling of lithium ion cells-A simple equivalent-circuit model approach. Solid State Ion. 2004, 175, 835–839. [Google Scholar] [CrossRef]
- Xia, Z.; Qahouq, J.A.A. Evaluation of Parameter Variations of Equivalent Circuit Model of Lithium-ion Battery under Different SOH Conditions. In Proceedings of the ECCE 2020-IEEE Energy Conversion Congress and Exposition, Detroit, MI, USA, 11–15 October 2020; pp. 1519–1523. [Google Scholar] [CrossRef]
- Tran, M.-K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, J.; Lund, P.D.; Zhang, Y. Co-estimating the state of charge and health of lithium batteries through combining a minimalist electrochemical model and an equivalent circuit model. Energy 2022, 240, 122815. [Google Scholar] [CrossRef]
- Hahn, S.L.; Storch, M.; Swaminathan, R.; Obry, B.; Bandlow, J.; Birke, K.P. Quantitative validation of calendar aging models for lithium-ion batteries. J. Power Sources 2018, 400, 402–414. [Google Scholar] [CrossRef]
- Hu, T.; Ma, H.; Liu, K.; Sun, H. Lithium-Ion Battery Calendar Health Prognostics Based on Knowledge-Data-Driven Attention. IEEE Trans. Ind. Electron. 2023, 70, 407–417. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Chen, Z. Degradation model and cycle life prediction for lithium-ion battery used in hybrid energy storage system. Energy 2019, 166, 796–806. [Google Scholar] [CrossRef]
- Liu, K.; Peng, Q.; Teodorescu, R.; Foley, A.M. Knowledge-Guided Data-Driven Model With Transfer Concept for Battery Calendar Ageing Trajectory Prediction. IEEE/CAA J. Autom. Sin. 2023, 10, 272–274. [Google Scholar] [CrossRef]
- Olmos, J.; Gandiaga, I.; Saez-de-Ibarra, A.; Larrea, X.; Nieva, T.; Aizpuru, I. Modelling the cycling degradation of Li-ion batteries: Chemistry influenced stress factors. J. Energy Storage 2021, 40, 102765. [Google Scholar] [CrossRef]
- Sun, H.; Yang, D.; Wang, L.; Wang, K. A method for estimating the aging state of lithium-ion batteries based on a multi-linear integrated model. Int. J. Energy Res. 2022, 46, 24091–24104. [Google Scholar] [CrossRef]
- Wu, Y.; Li, W.; Wang, Y.; Zhang, K. Remaining useful life prediction of lithium-ion batteries using neural network and bat-based particle filter. IEEE Access 2019, 7, 54843–54854. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, X.; He, Y. Remaining useful life and state of health prediction for lithium batteries based on empirical mode decomposition and a long and short memory neural network. Energy 2021, 232, 121022. [Google Scholar] [CrossRef]
- Hu, T.; Ma, H.; Sun, H.; Liu, K. Electrochemical-Theory-Guided Modeling of the Conditional Generative Adversarial Network for Battery Calendar Aging Forecast. IEEE J. Emerg Sel. Top Power Electron 2023, 11, 67–77. [Google Scholar] [CrossRef]
- Jenu, S.; Hentunen, A.; Haavisto, J.; Pihlatie, M. State of health estimation of cycle aged large format lithium-ion cells based on partial charging. J. Energy Storage 2022, 46, 103855. [Google Scholar] [CrossRef]
- Su, X.; Sun, B.; Wang, J.; Zhang, W.; Ma, S.; He, X.; Ruan, H. Fast capacity estimation for lithium-ion battery based on online identification of low-frequency electrochemical impedance spectroscopy and Gaussian process regression. Appl. Energy 2022, 322, 119516. [Google Scholar] [CrossRef]
- Liu, K.; Hu, X.; Wei, Z.; Li, Y.; Jiang, Y. Modified Gaussian Process Regression Models for Cyclic Capacity Prediction of Lithium-Ion Batteries. IEEE Trans. Transp. Electrif. 2019, 5, 1225–1236. [Google Scholar] [CrossRef]
- Yan, L.; Peng, J.; Gao, D.; Wu, Y.; Liu, Y.; Li, H.; Liu, W.; Huang, Z. A hybrid method with cascaded structure for early-stage remaining useful life prediction of lithium-ion battery. Energy 2022, 243, 123038. [Google Scholar] [CrossRef]
- Barcellona, S.; Piegari, L. Effect of current on cycle aging of lithium ion batteries. J. Energy Storage 2020, 29, 101310. [Google Scholar] [CrossRef]
- She, C.; Wang, Z.; Sun, F.; Liu, P.; Zhang, L. Battery Aging Assessment for Real-World Electric Buses Based on Incremental Capacity Analysis and Radial Basis Function Neural Network. IEEE Trans Industr. Inform. 2020, 16, 3345–3354. [Google Scholar] [CrossRef]
- Weng, C.; Feng, X.; Sun, J.; Peng, H. State-of-health monitoring of lithium-ion battery modules and packs via incremental capacity peak tracking. Appl. Energy 2016, 180, 360–368. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, M.; Pecht, M. An Online State of Health Estimation Method for Lithium-ion Batteries Based on Integrated Voltage. In Proceedings of the 2018 IEEE International Conference on Prognostics and Health Management, ICPHM 2018, Seattle, WA, USA, 11–13 August 2018. [Google Scholar] [CrossRef]
- Oudalov, A.; Chartouni, D.; Ohler, C. Optimizing a battery energy storage system for primary frequency control. IEEE Trans. Power Syst. 2007, 22, 1259–1266. [Google Scholar] [CrossRef]
- Delavari, A.; Kamwa, I.; Zabihinejad, A. A comparative study of different multilevel converter topologies for Battery Energy Storage application. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Windsor, ON, Canada, 30 April–3 May 2017. [Google Scholar] [CrossRef]
- Chatrung, N. Battery Energy Storage System (BESS) and Development of Grid Scale BESS in EGAT. In Proceedings of the 2019 IEEE PES GTD Grand International Conference and Exposition Asia, GTD Asia 2019, Bangkok, Thailand, 19–23 March 2019; pp. 589–593. [Google Scholar] [CrossRef]
- Shafique, H.; Tjernberg, L.B.; Archer, D.E.; Wingstedt, S. Energy Management System (EMS) of Battery Energy Storage System (BESS)-Providing Ancillary Services. In Proceedings of the 2021 IEEE Madrid PowerTech, PowerTech 2021-Conference Proceedings, Madrid, Spain, 28 June–2 July 2021. [Google Scholar] [CrossRef]
- Gatta, F.M.; Geri, A.; Lauria, S.; Maccioni, M.; Palone, F. Battery energy storage efficiency calculation including auxiliary losses: Technology comparison and operating strategies. In Proceedings of the 2015 IEEE Eindhoven PowerTech, PowerTech 2015, Eindhoven, Netherlands, 29 June–2 July 2015. [Google Scholar] [CrossRef]
- Bovera, F.; Spiller, M.; Zatti, M.; Rancilio, G.; Merlo, M. Development, validation, and testing of advanced mathematical models for the optimization of BESS operation. Sustain. Energy Grids Netw. 2023, 36, 101152. [Google Scholar] [CrossRef]
- Rancilio, G.; Merlo, M.; Lucas, A.; Kotsakis, E.; Delfanti, M. BESS modeling: Investigating the role of auxiliary system consumption in efficiency derating. In Proceedings of the 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, SPEEDAM 2020, Sorrento, Italy, 24–26 June 2020; pp. 189–194. [Google Scholar] [CrossRef]
- Rancilio, G.; Lucas, A.; Kotsakis, E.; Fulli, G.; Merlo, M.; Delfanti, M.; Masera, M. Modeling a Large-Scale Battery Energy Storage System for Power Grid Application Analysis. Energies 2019, 12, 3312. [Google Scholar] [CrossRef]
- Ketjoy, N.; Chamsa-ard, W.; Mensin, P. Analysis of factors affecting efficiency of inverters: Case study grid-connected PV systems in lower northern region of Thailand. Energy Rep. 2021, 7, 3857–3868. [Google Scholar] [CrossRef]
- Choi, D.; Shamim, N.; Crawford, A.; Huang, Q.; Vartanian, C.K.; Viswanathan, V.V.; Paiss, M.D.; Alam, M.J.E.; Reed, D.M.; Sprenkle, V.L. Li-ion battery technology for grid application. J. Power Sources 2021, 511, 230419. [Google Scholar] [CrossRef]
- Wei, Z.; Li, Y.; Cai, L. Electric vehicle charging scheme for a park-and-charge system considering battery degradation costs. IEEE Trans. Intell. Veh. 2018, 3, 361–373. [Google Scholar] [CrossRef]
- Zhao, C.; Li, X. Microgrid Optimal Energy Scheduling Considering Neural Network based Battery Degradation. IEEE Trans. Power Syst. 2023, 1–12. [Google Scholar] [CrossRef]
- Woody, M.; Arbabzadeh, M.; Lewis, G.M.; Keoleian, G.A.; Stefanopoulou, A. Strategies to limit degradation and maximize Li-ion battery service lifetime-Critical review and guidance for stakeholders. J. Energy Storage 2020, 28, 101231. [Google Scholar] [CrossRef]
- Reiter, A.; Lehner, S.; Bohlen, O.; Sauer, D.U. Electrical cell-to-cell variations within large-scale battery systems—A novel characterization and modeling approach. J. Energy Storage 2023, 57, 106152. [Google Scholar] [CrossRef]
- Moncecchi, M.; Borselli, A.; Falabretti, D.; Corghi, L.; Merlo, M. Numerical and Experimental Efficiency Estimation in Household Battery Energy Storage Equipment. Energies 2020, 13, 2719. [Google Scholar] [CrossRef]
- Characterisation and Efficiency Test of a Li-Ion Energy Storage System for PV Systems-Archivo Digital UPM. Available online: https://oa.upm.es/41946/ (accessed on 3 May 2023).
- IEC 61427:2005(E); Secondary Cells and Batteries for Photovoltaic Energy Systems (PVES) - General Requirements and Methods of Test. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2005.
- Palone, F.; Gemelli, G.; Rebolini, M.; Mocci, E.; Necci, A.; Pietrucci, M.; Tortora, A. Commissioning and testing of the first Lithium-Titanate BESS for the Italian transmission grid. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering, EEEIC 2015-Conference Proceedings, Rome, Italy, 10–13 June 2015; pp. 1025–1030. [Google Scholar] [CrossRef]
- Swierczynski, M.; Stroe, D.I.; Stan, A.I.; Teodorescu, R.; Laerke, R.; Kjær, P.C. Field tests experience from 1.6MW/400kWh Li-ion battery energy storage system providing primary frequency regulation service. In Proceedings of the 2013 4th IEEE/PES Innovative Smart Grid Technologies Europe, ISGT Europe 2013, Lyngby, Denmark, 6–9 October 2013. [Google Scholar] [CrossRef]
- Smith, K.; Baggu, M.; Friedl, A.; Bialek, T.; Schimpe, M.R. Performance and health test procedure for grid energy storage systems. In Proceedings of the IEEE Power and Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2018. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A.; Stein, K.; Tun, M.; Matsuura, M.; Rocheleau, R. Battery Energy Storage System battery durability and reliability under electric utility grid operations: Analysis of 3 years of real usage. J. Power Sources 2017, 338, 65–73. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A. Battery durability and reliability under electric utility grid operations: Representative usage aging and calendar aging. J. Energy Storage 2018, 18, 185–195. [Google Scholar] [CrossRef]
- Del Valle, J.A.; Ansean, D.; Viera, J.C.; Antuna, J.L.; Gonzalez, M.; Garcia, V. Analysis of Advanced Lithium-Ion Batteries for Battery Energy Storage Systems. In Proceedings of the Proceedings-2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe, EEEIC/I and CPS Europe 2018, Palermo, Italy, 12–15 June 2018. [Google Scholar] [CrossRef]
- Tang, X.; Liu, K.; Li, K.; Widanage, W.D.; Kendrick, E.; Gao, F. Recovering large-scale battery aging dataset with machine learning. Patterns 2021, 2, 100302. [Google Scholar] [CrossRef] [PubMed]
- Nebuloni, R.; Meraldi, L.; Bovo, C.; Ilea, V.; Berizzi, A.; Sinha, S.; Tamirisakandala, R.B.; Raboni, P. A hierarchical two-level MILP optimization model for the management of grid-connected BESS considering accurate physical model. Appl. Energy 2023, 334, 120697. [Google Scholar] [CrossRef]
- Collath, N.; Cornejo, M.; Engwerth, V.; Hesse, H.; Jossen, A. Increasing the lifetime profitability of battery energy storage systems through aging aware operation. Appl. Energy 2023, 348, 121531. [Google Scholar] [CrossRef]
- Parthasarathy, C.; Laaksonen, H.; Redondo-Iglesias, E.; Pelissier, S. Aging aware adaptive control of Li-ion battery energy storage system for flexibility services provision. J. Energy Storage 2023, 57, 106268. [Google Scholar] [CrossRef]
- Kumtepeli, V.; Zhao, Y.; Naumann, M.; Tripathi, A.; Wang, Y.; Jossen, A.; Hesse, H. Design and analysis of an aging-aware energy management system for islanded grids using mixed-integer quadratic programming. Int. J. Energy Res. 2019, 43, 4127–4147. [Google Scholar] [CrossRef]

| Test | Ref. | Comments | Similarities |
|---|---|---|---|
| Efficiency test | [4,19,63,70,71,72,74] |
|
|
| Rated energy | [72,73,74] |
|
| Ref. | Chemistry | Capacity (kWh)/Power (kW) | Approach/Model Specifications | |||||
|---|---|---|---|---|---|---|---|---|
| Initial SOC (%) | DOD (%) | Total Measured Points | Power Setpoints (Psetpoint/Pnominal) (p.u) | Estimated Time (min) | Repetition | |||
| [63] | NMC | 570/250 | 10, 45, 80 | 10 | 21 | 0.05, 0.09, 0.18, 0.36, 0.54, 0.72, 0.90 | 2856 | No |
| [19] | NMC | 822/500 | 10 | 80 | 11 | 0.1, 0.15, 0.2, 0.3, 0.4, 0.6, 0.7, 0.8, 0.9, 1 | 5721 | No |
| [73] | LTO | 1000/1000 | 0 | 100 | 1 | 1 | 180 | 3 times |
| [74] | -- | 100/100 | 0 | 100 | 2 | 0.2, 1 | 720 | 3 times |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pakjoo, M.; Piegari, L.; Rancilio, G.; Colnago, S.; Mengou, J.E.; Bresciani, F.; Gorni, G.; Mandelli, S.; Merlo, M. A Review on Testing of Electrochemical Cells for Aging Models in BESS. Energies 2023, 16, 6887. https://doi.org/10.3390/en16196887
Pakjoo M, Piegari L, Rancilio G, Colnago S, Mengou JE, Bresciani F, Gorni G, Mandelli S, Merlo M. A Review on Testing of Electrochemical Cells for Aging Models in BESS. Energies. 2023; 16(19):6887. https://doi.org/10.3390/en16196887
Chicago/Turabian StylePakjoo, Mehrshad, Luigi Piegari, Giuliano Rancilio, Silvia Colnago, Joseph Epoupa Mengou, Federico Bresciani, Giacomo Gorni, Stefano Mandelli, and Marco Merlo. 2023. "A Review on Testing of Electrochemical Cells for Aging Models in BESS" Energies 16, no. 19: 6887. https://doi.org/10.3390/en16196887
APA StylePakjoo, M., Piegari, L., Rancilio, G., Colnago, S., Mengou, J. E., Bresciani, F., Gorni, G., Mandelli, S., & Merlo, M. (2023). A Review on Testing of Electrochemical Cells for Aging Models in BESS. Energies, 16(19), 6887. https://doi.org/10.3390/en16196887








