Comparison between Physics-Based Approaches and Neural Networks for the Energy Consumption Optimization of an Automotive Production Industrial Process
Abstract
:1. Introduction
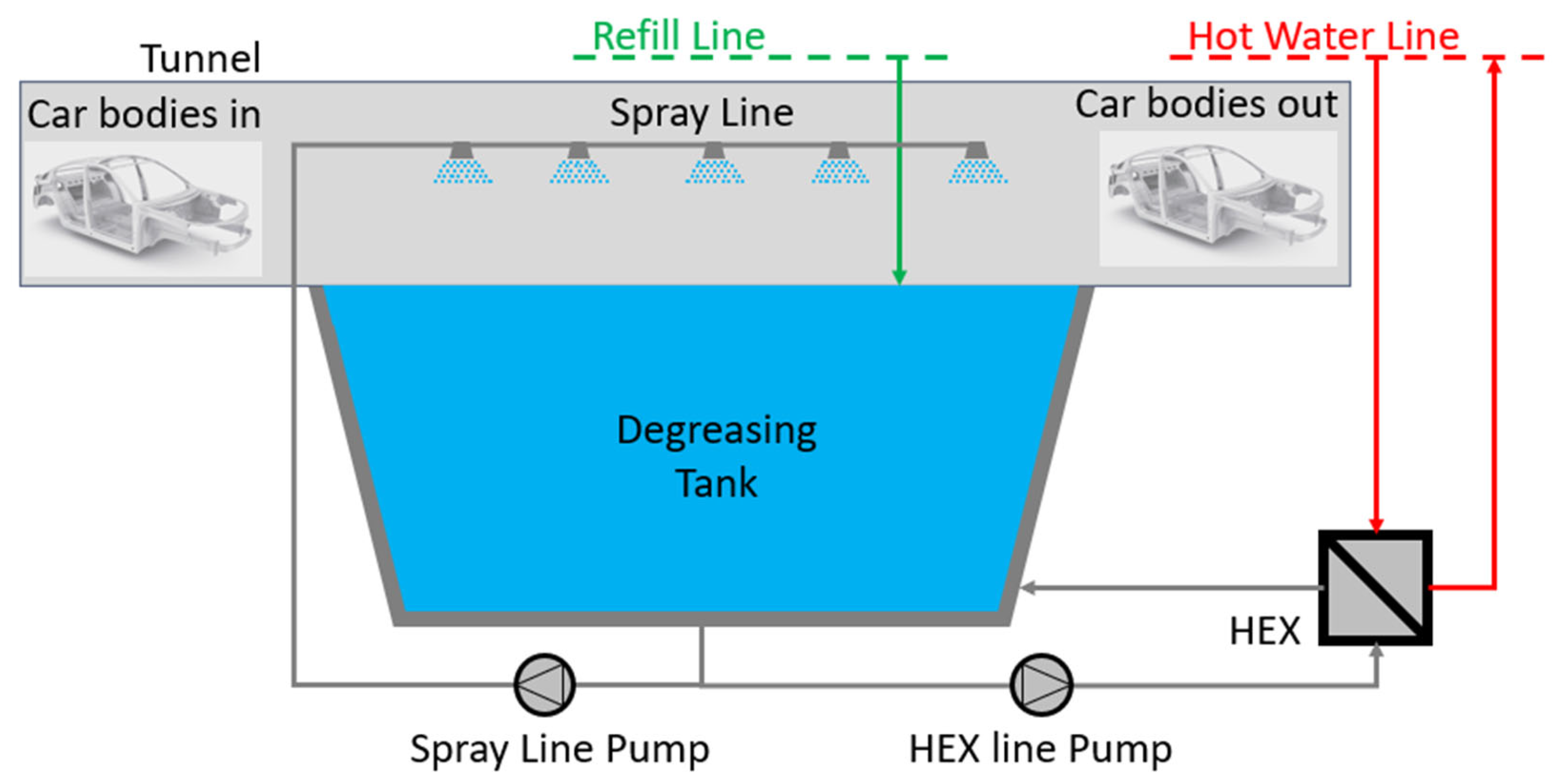
2. Case Study Description
3. Modeling Approaches
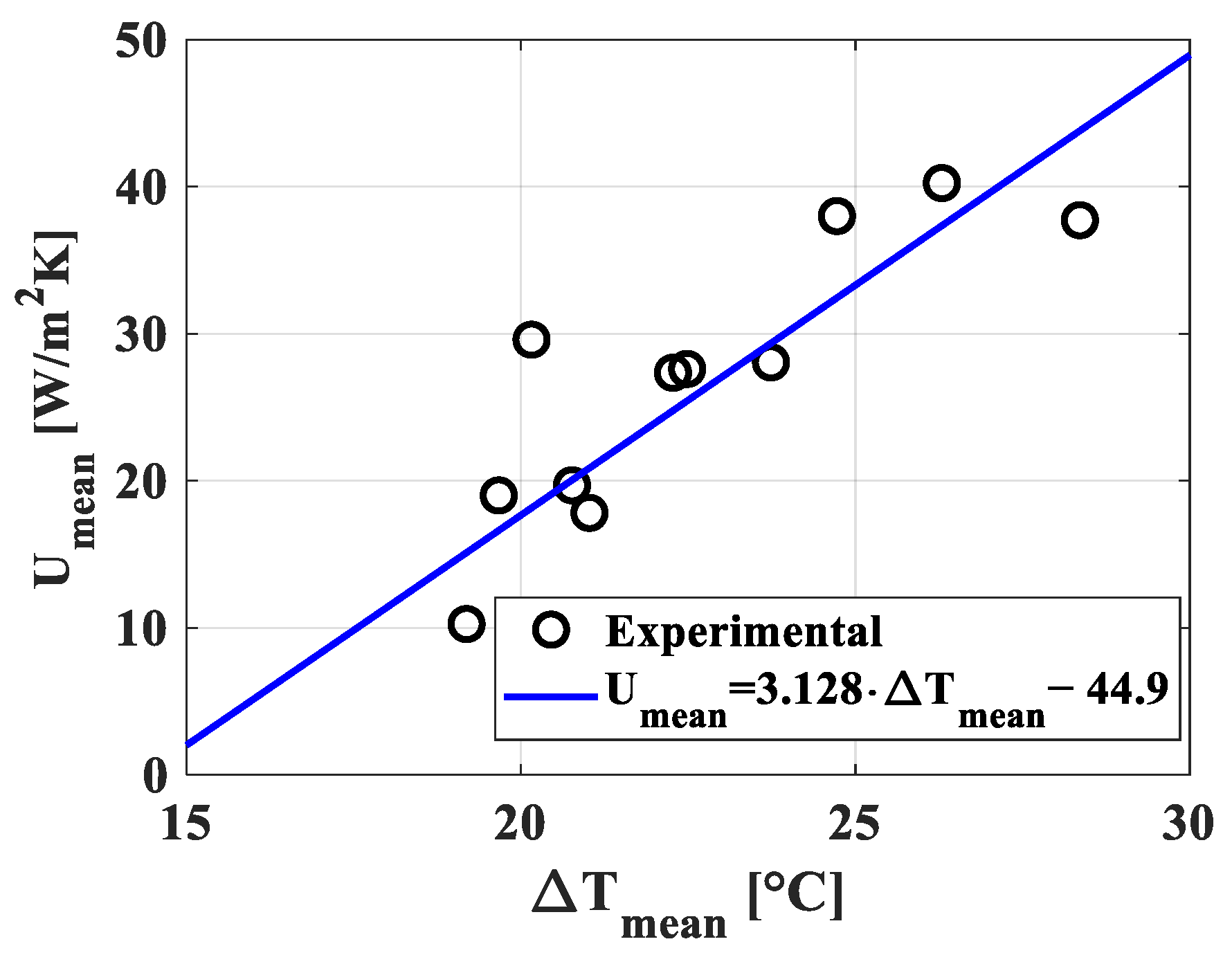
3.1. Mechanistic Physics-Based Model Approach
3.2. Artificial Neural Network (ANN) Model Approach
4. Model Calibration and Validation
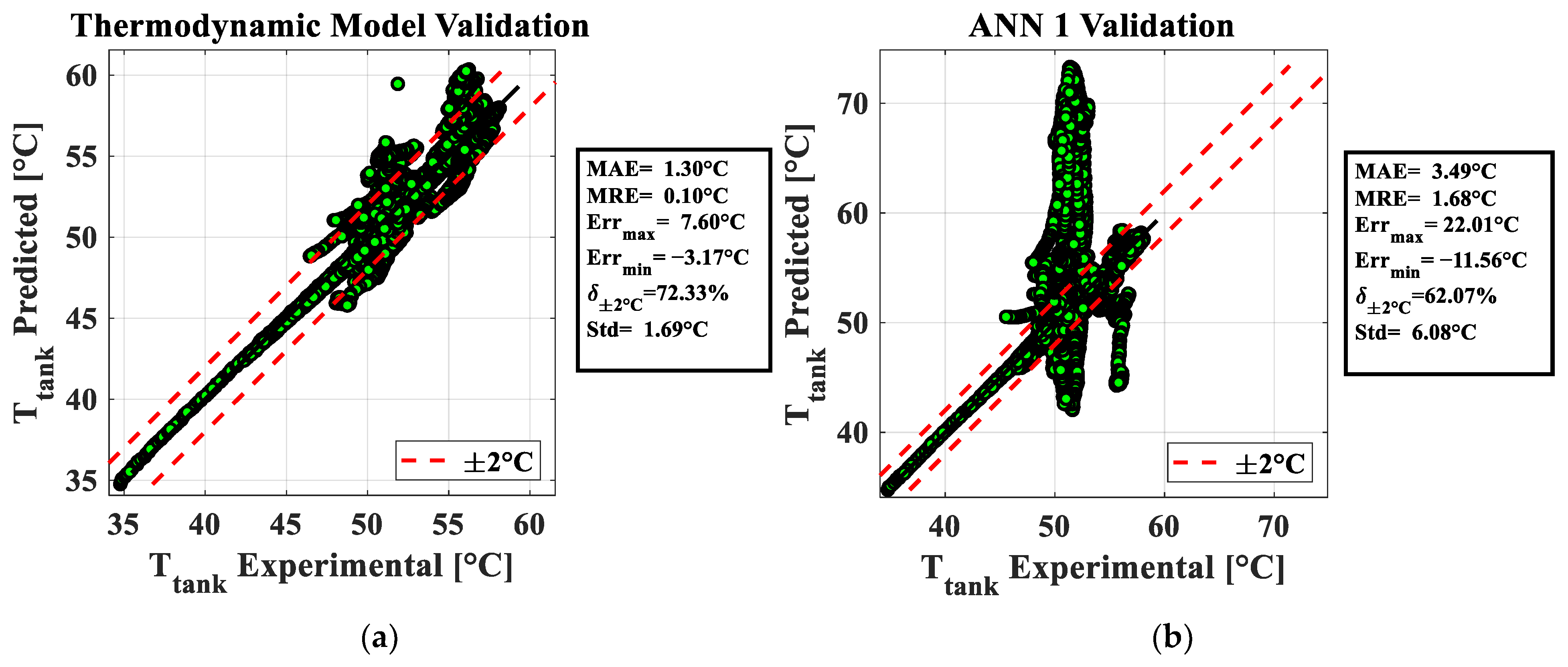
4.1. Thermodynamic Model Calibration and Validation
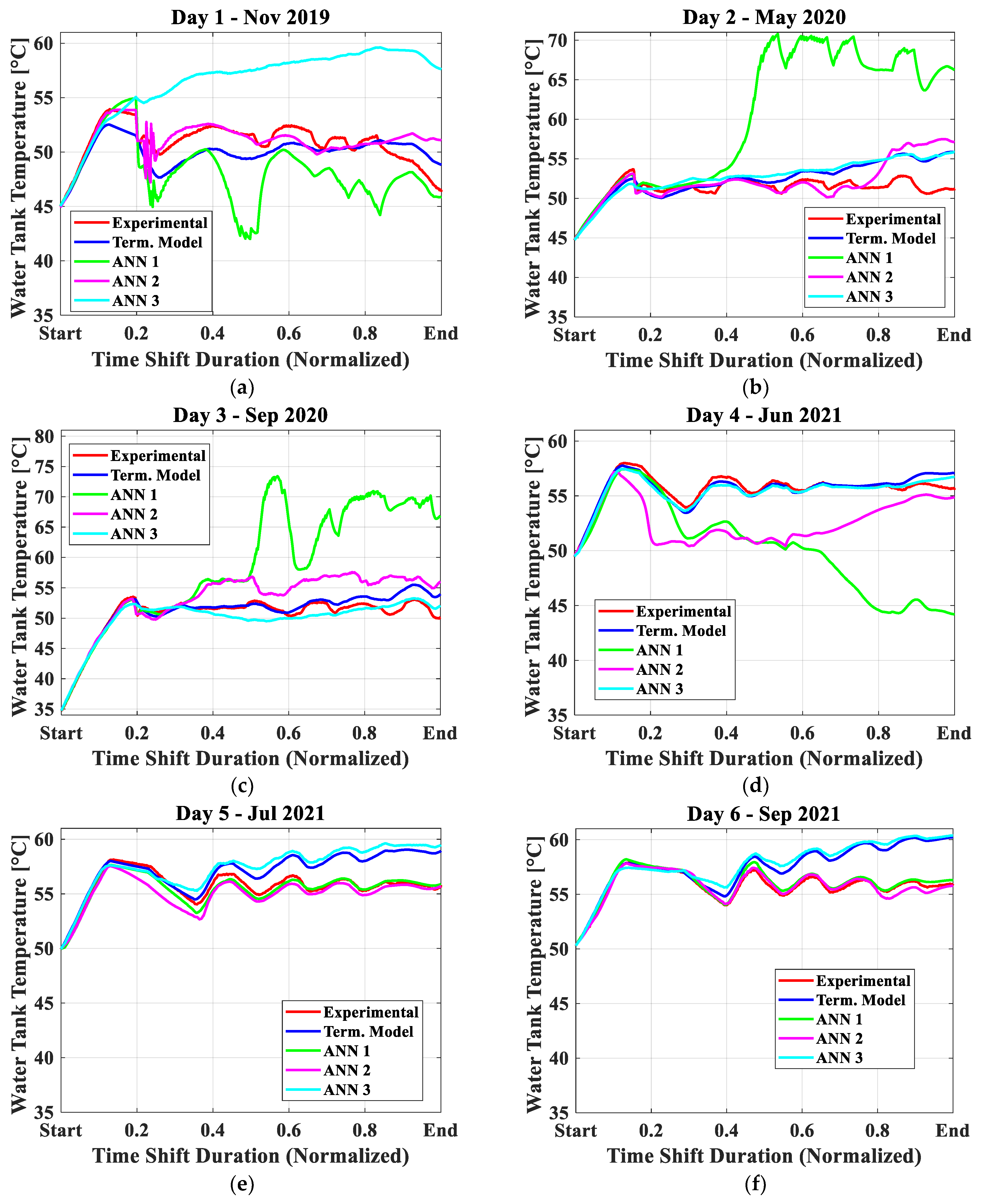
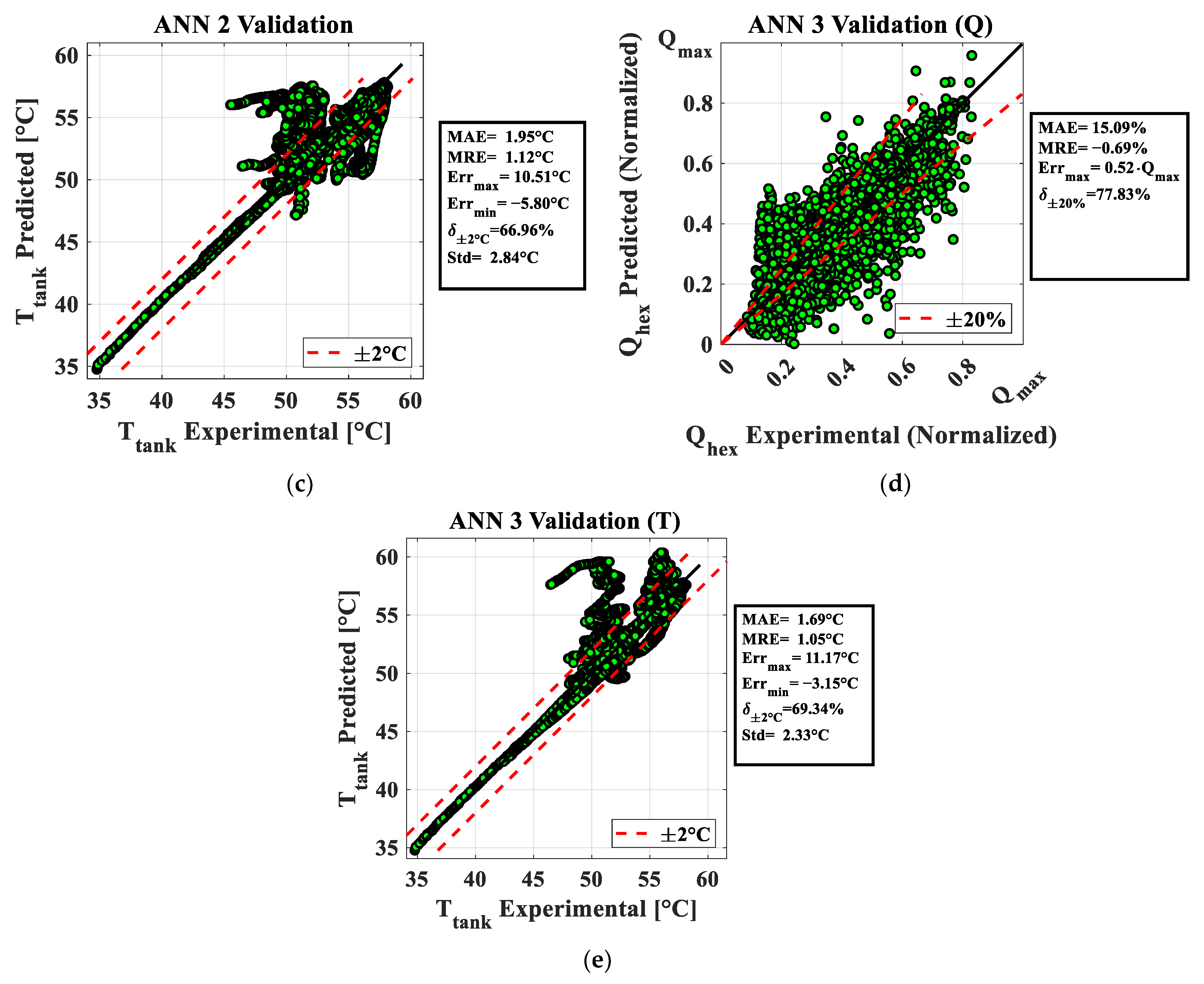
4.2. ANN Model Calibration and Validation
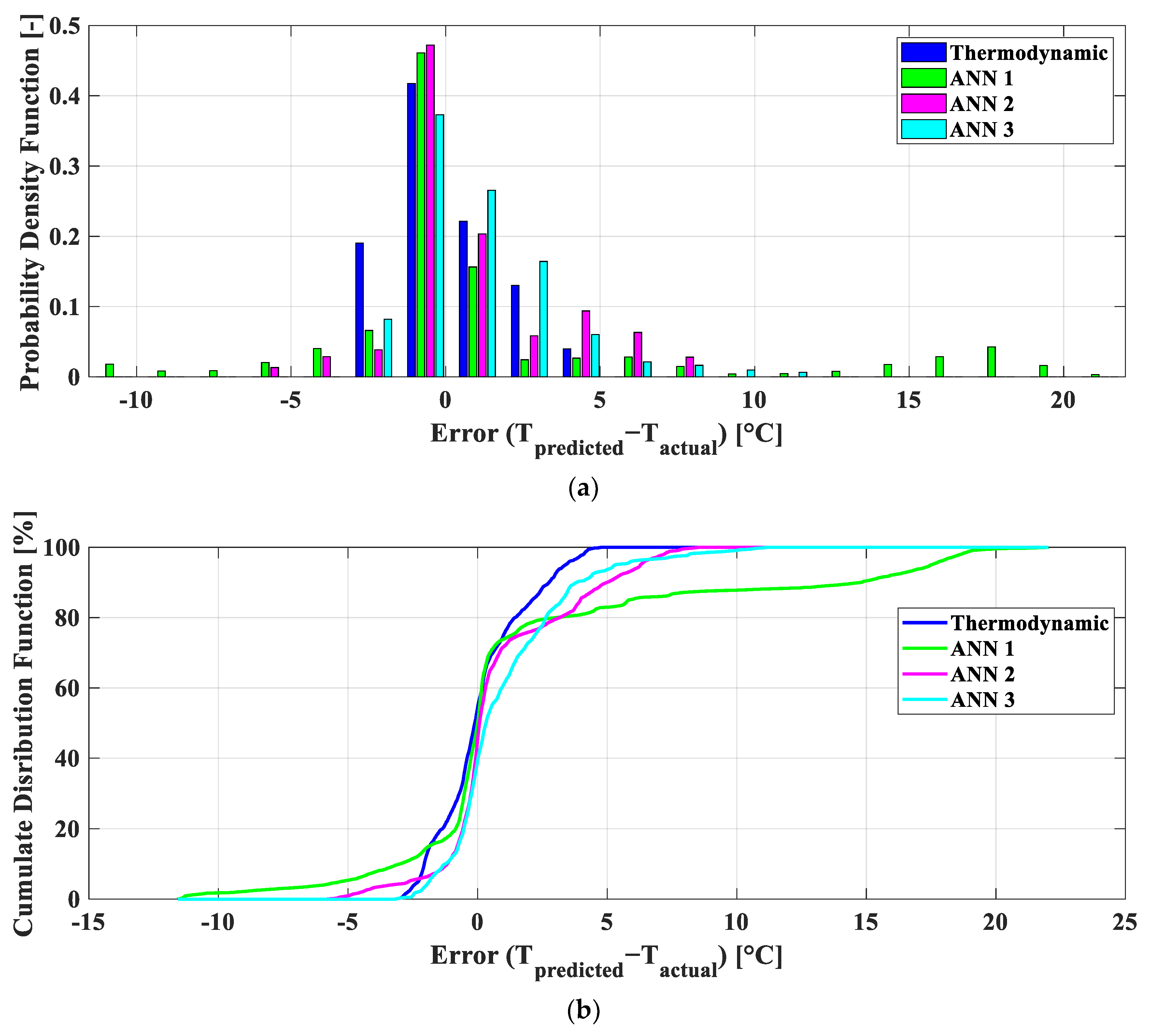
4.3. Summary of Prevision Accuracy of All the Modeling Approaches
5. Use of the Model for Optimization Strategies
5.1. Usage of the Model in Simulation Mode and Assumptions
- (1)
- A constant rated value for the spray mass flow rate was assumed 1 min before the entrance of the first car body in the process. If no car body enters in 9 min during the process, the sprays are turned off.
- (2)
- The refill mass flow rate is maintained at a constant rated value to keep the water level within a certain a priori fixed dead-band.
- (3)
- For the heat exchanger, the maximum thermal power () is imposed during a pre-heating stage to reach the desired setpoint temperature in the tank exactly when the first car body enters the process. If no car body enters in 30 min, the thermal power is turned off. The same logic is applied each time the heat exchanger is turned on.
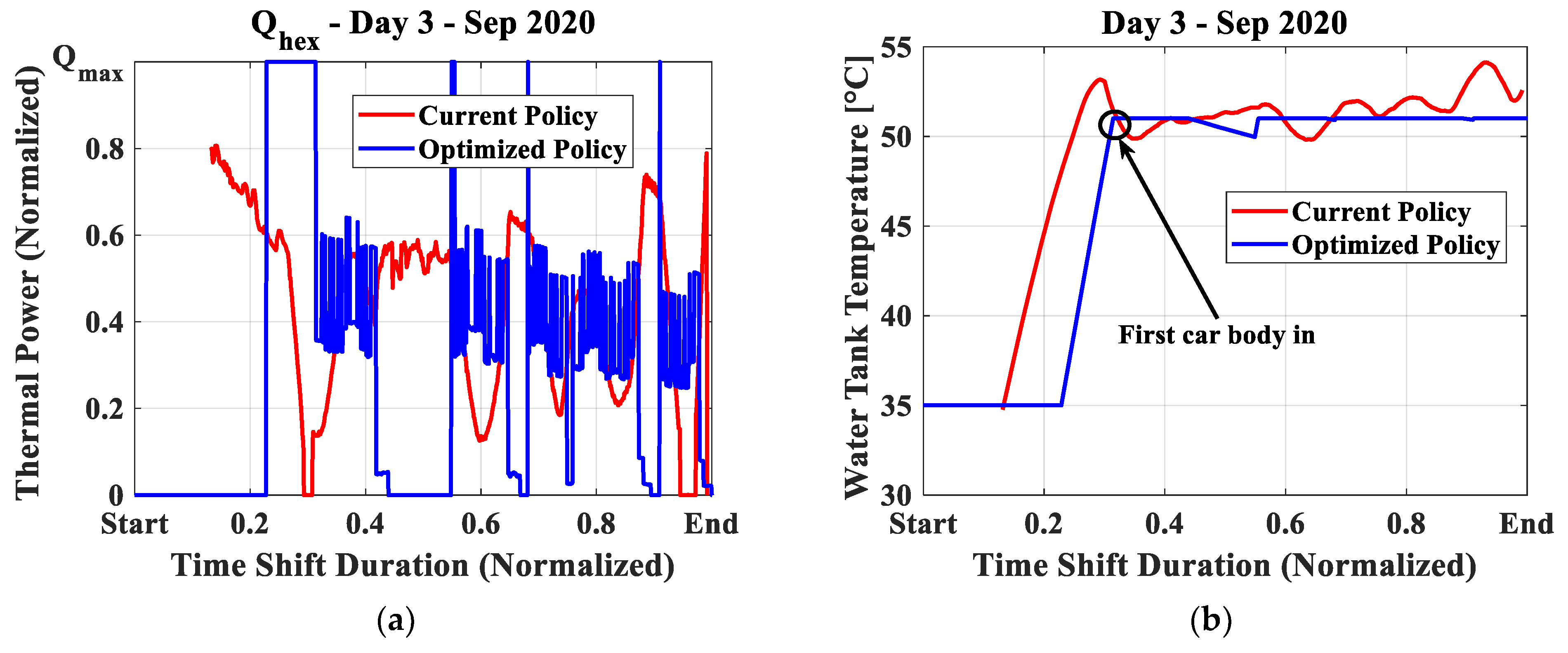
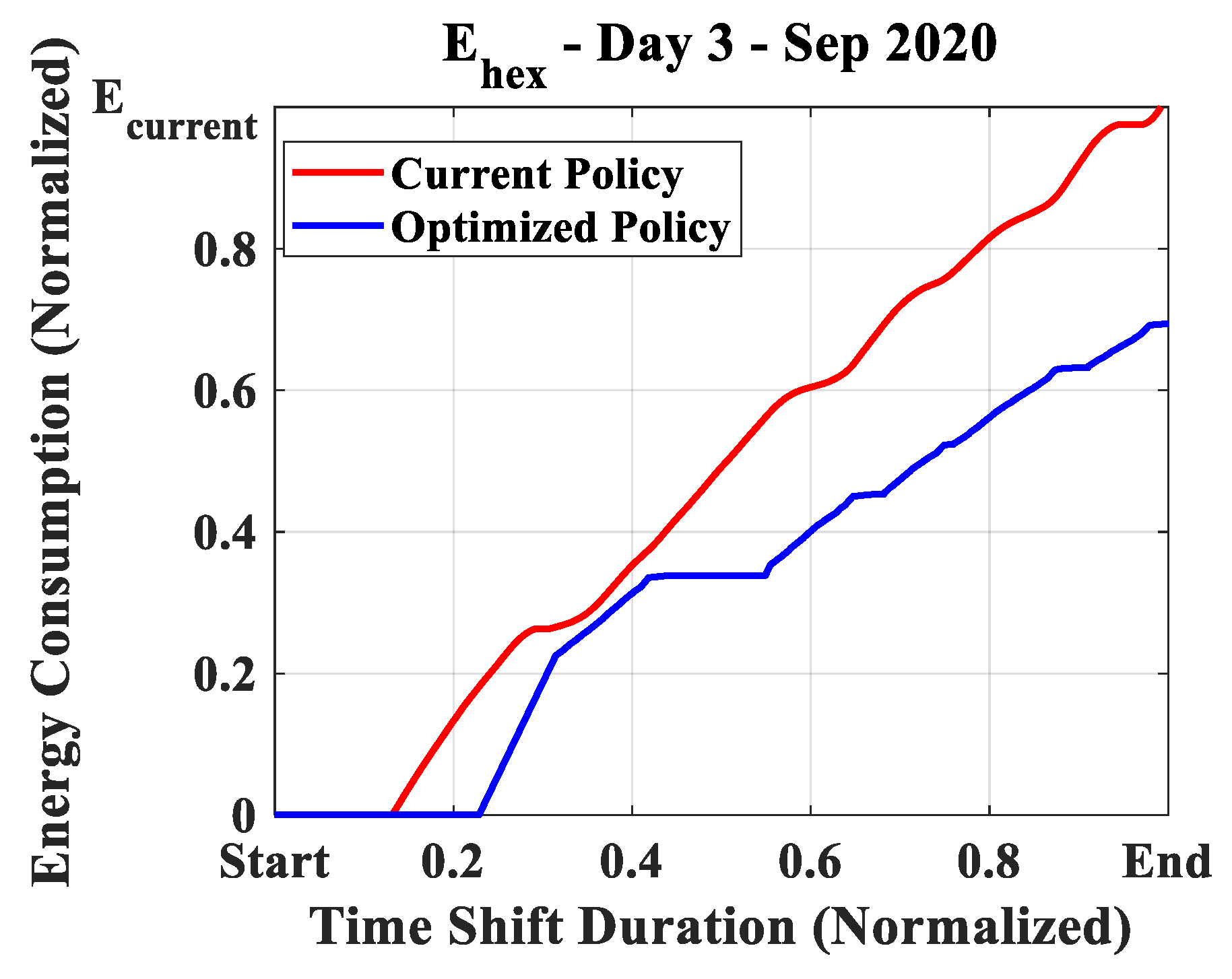
5.2. Optimization with Real Data of the Case Study
5.3. Optimization with New Body Schedule
- (1)
- Each car body must remain in the degreasing tank for a minimum of 3 min, and there is a 1 min waiting time between the entry of two consecutive car bodies in the process.
- (2)
- A setpoint temperature of 50 °C was considered, with an initial temperature of the tank of 30 °C.
- (3)
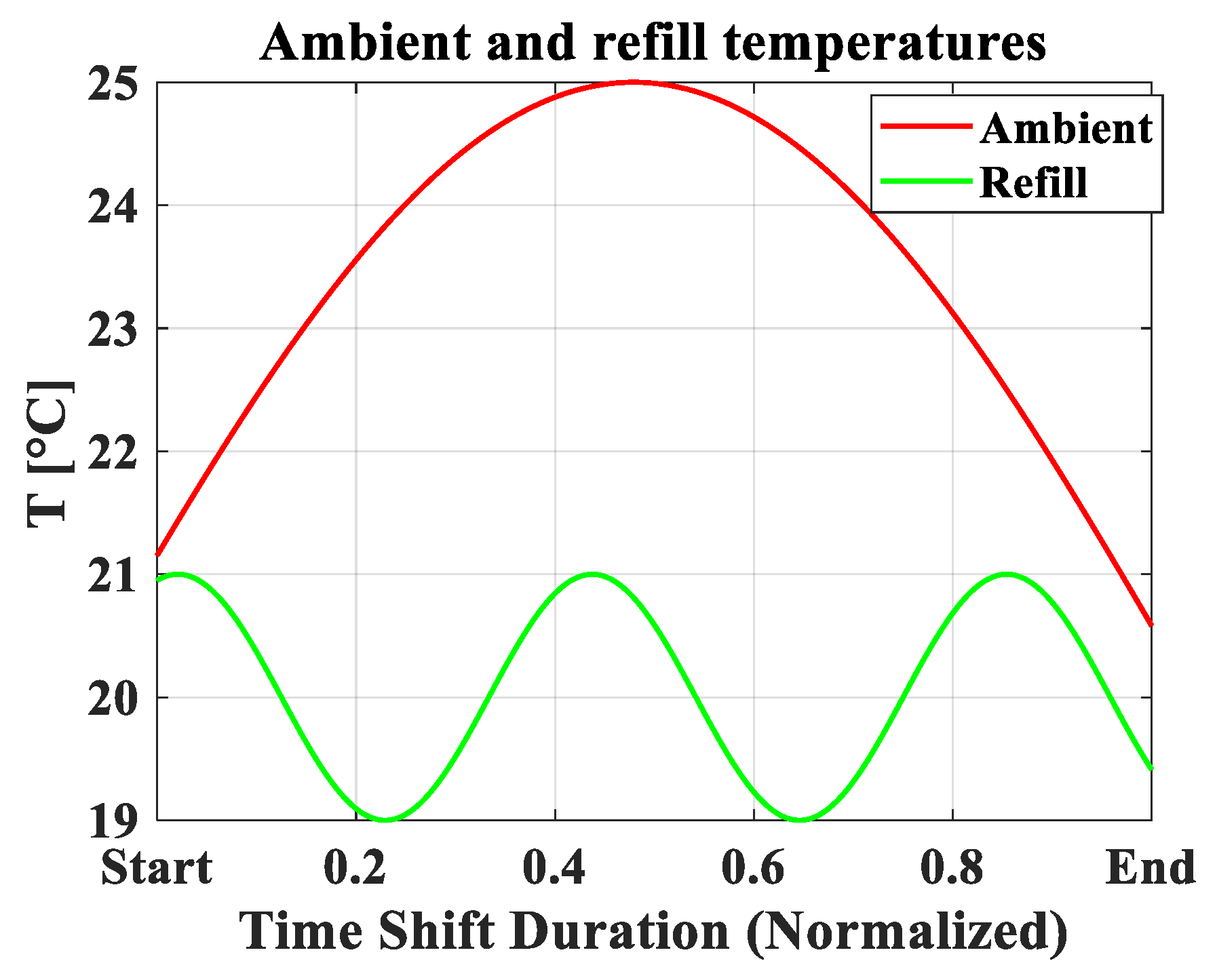
- The ambient and refill temperature trends shown in Figure 11 were determined. It should be clarified that all the input data were chosen solely for the purpose of the results and optimization in this paper, and they do not represent real data on the effective production processes of a company.
6. Conclusions and Future Developments
- Two distinct modeling approaches are presented: a thermodynamic physics-based approach that relies on mass and energy balances of different control volumes of the degreasing tank, and a machine learning approach consisting of three ANNs characterized by different structures, numbers, and typology of inputs and outputs.
- Both modeling approaches were evaluated and compared with the experimental data obtained from a case study of an automotive production facility. For the thermodynamic model, several empirical variables, which cannot be deduced from the case study data, were calibrated using approximately 9000 experimental points. In contrast, the ANNs were calibrated by splitting the whole dataset into subsets for training, validation, and testing purposes.
- The results indicate that, for the analyzed case study, the thermodynamic model exhibited higher prediction accuracy for the tank temperature future trend, achieving an MAE of 1.36 due to all the information from the real data of the company. In contrast, all the ANN approaches exhibited higher MAEs and maximum errors, ranging from 10 to 22 °C, and posing a risk of completely inaccurate predictions.
- The thermodynamic approach was subsequently used to optimize the production process. Based on historical data for a working production day, employing an optimize heat load profile policy recommended by the model could lead to an energy saving of approximately 31% by limiting useless superheating of the water inside the tank and by limiting fluctuations around the desired setpoint value.
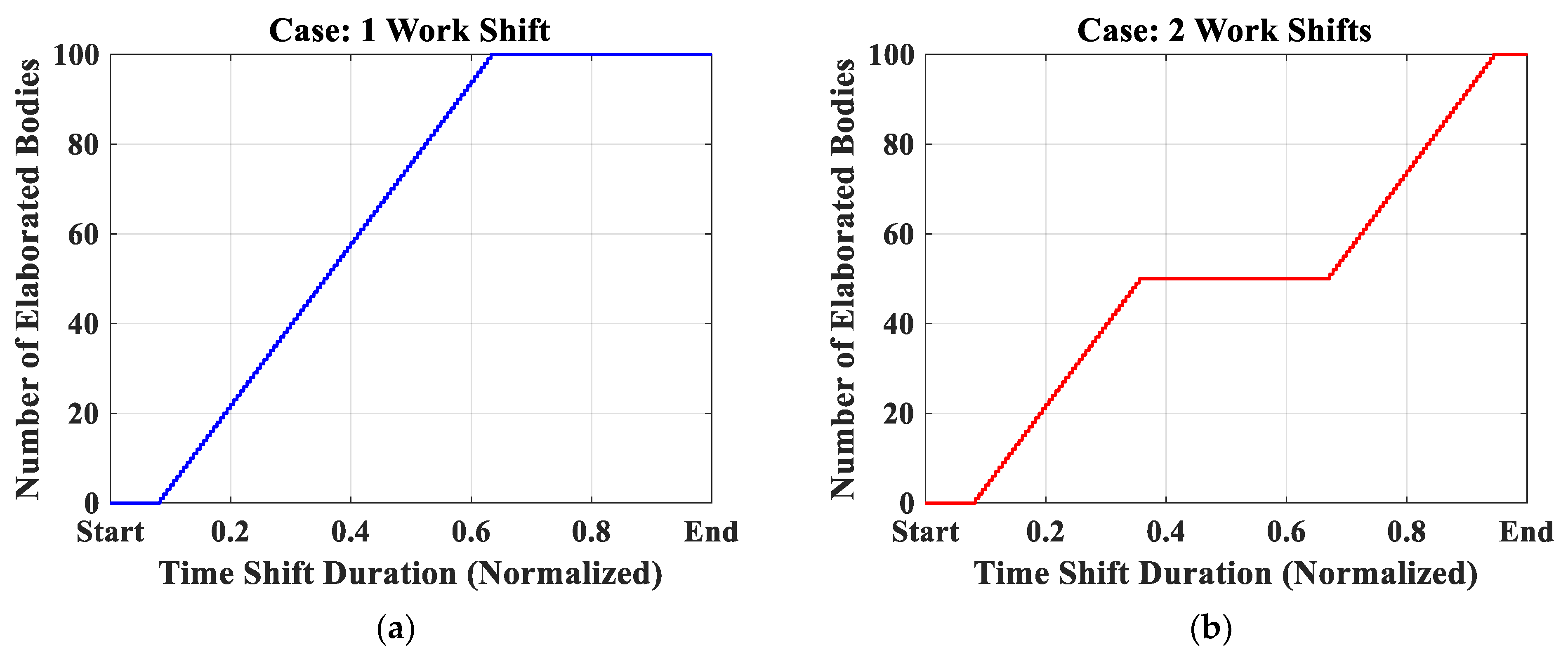
- Considering a supposed production of 100 car bodies, the study explored two hypothetical future production scenarios, the first in which the production is performed in a single work shift, and the second in which the production is divided into two work shifts, potentially due to company constraints or planned maintenance operations. In this case, the model was able to provide an estimation of the extra energy consumption of the second scenario compared to the first, which was approximately 9%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. Industry; IEA: Paris, France, 2022; Available online: https://www.iea.org/reports/industry (accessed on 27 July 2023).
- IEA. Net Zero by 2050, IEA, Paris. 2021. Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 27 July 2023).
- Driving the Motor Industry, 2020 UK Automotive Sustainability Report, 21st ed.; SMMT: London, UK, 2019.
- ANFIA (Associazione Nazionale Filiera Industria Automobilistica). Statistical Data, New Car Registration. Available online: https://www.anfia.it/it/dati-statistici/immatricolazioni-italia (accessed on 15 July 2023).
- Giampieri, A.; Ling-Chin, J.; Ma, Z.; Smallbone, A.; Roskilly, A.P. A review of the current automotive manufacturing practice from an energy perspective. Appl. Energy 2020, 261, 114074. [Google Scholar] [CrossRef]
- Biesinger, F.; Kraß, B.; Weyrich, M. A survey on the necessity for a digital twin of production in the automotive industry. In Proceedings of the 23rd International Conference on Mechatronics Technology (ICMT), Salerno, Italy, 23–26 October 2019; pp. 1–8. [Google Scholar]
- Afram, A.; Janabi-Sharifi, F.; Fung, A.S.; Raahemifar, K. Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: A state of the art review and casestudy of a residential HVAC system. Energy Build. 2017, 141, 96–113. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Review of modeling methods for HVAC systems. Appl. Therm. Eng. 2014, 67, 507–519. [Google Scholar] [CrossRef]
- Forbes, M.G.; Patwardhan, R.S.; Hamadah, H.; Gopaluni, R.B. Model predictive control in industry: Challenges and opportunities. IFAC-PapersOnLine 2015, 48, 531–538. [Google Scholar] [CrossRef]
- Narciso, D.A.; Martins, F.G. Application of machine learning tools for energy efficiency in industry: A review. Energy Rep. 2020, 6, 1181–1199. [Google Scholar] [CrossRef]
- Hu, Y.; Man, Y. Energy consumption and carbon emissions forecasting for industrial processes: Status, challenges and perspectives. Renew. Sustain. Energy Rev. 2023, 182, 113405. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; Iovane, T.; Mauro, G.M.; Napolitano, D.F.; Ruggiano, A.; Viscido, L. A real industrial building: Modeling, calibration and Pareto optimization of energy retrofit. J. Build. Eng. 2020, 29, 101186. [Google Scholar] [CrossRef]
- Kapp, S.; Choi, J.K.; Hong, T. Predicting industrial building energy consumption with statistical and machine-learning models informed by physical system parameters. Renew. Sustain. Energy Rev. 2023, 172, 113045. [Google Scholar] [CrossRef]
- Aruta, G.; Ascione, F.; Bianco, N.; Mauro, G.M.; Vanoli, G.P. Optimizing heating operation via GA-and ANN-based model predictive control: Concept for a real nearly-zero energy building. Energy Build. 2023, 292, 113139. [Google Scholar] [CrossRef]
- Široký, J.; Oldewurtel, F.; Cigler, J.; Prívara, S. Experimental analysis of model predictive control for an energy efficient building heating system. Appl. Energy 2011, 88, 3079–3087. [Google Scholar] [CrossRef]
- Son, Y.H.; Park, K.T.; Lee, D.; Jeon, S.W.; Do Noh, S. Digital twin–based cyber-physical system for automotive body production lines. Int. J. Adv. Manuf. Technol. 2021, 115, 291–310. [Google Scholar] [CrossRef]
- Mendi, A.F. A Digital Twin Case Study on Automotive Production Line. Sensors 2022, 22, 6963. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Zuo, Y.; Tao, F. Equipment energy consumption management in digital twin shop-floor: A framework and potential applications. In Proceedings of the 15th International Conference on Networking, Sensing and Control (ICNSC), Zhuhai, China, 27–29 March 2018; pp. 1–5. [Google Scholar]
- Zhang, H.; Qi, Q.; Tao, F. A multi-scale modeling method for digital twin shop-floor. J. Manuf. Syst. 2022, 62, 417–428. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Q.; Chen, X.; Zhang, D.; Leng, J. A digital twin-based approach for designing and multi-objective optimization of hollow glass production line. IEEE Access 2017, 5, 26901–26911. [Google Scholar] [CrossRef]
- Min, Q.; Lu, Y.; Liu, Z.; Su, C.; Wang, B. Machine learning based digital twin framework for production optimization in petrochemical industry. Int. J. Inf. Manag. 2019, 49, 502–519. [Google Scholar] [CrossRef]
- Karanjkar, N.; Joglekar, A.; Mohanty, S.; Prabhu, V.; Raghunath, D.; Sundaresan, R. Digital twin for energy optimization in an SMT-PCB assembly line. In Proceedings of the IEEE International Conference on Internet of Things and Intelligence System, Bali, Indonesia, 1–3 November 2018; pp. 85–89. [Google Scholar]
- Çamdali, Ü.; Tunc, M. Steady state heat transfer of ladle furnace during steel production process. J. Iron Steel Res. Int. 2006, 13, 18–25. [Google Scholar] [CrossRef]
- Laha, D.; Ren, Y.; Suganthan, P.N. Modeling of steelmaking process with effective machine learning techniques. Expert Syst. Appl. 2015, 42, 4687–4696. [Google Scholar] [CrossRef]
- Paryanto, P.; Brossog, M.; Bornschlegl, M.; Franke, J. Reducing the energy consumption of industrial robots in manufacturing systems. Int. J. Adv. Manuf. Technol. 2015, 78, 1315–1328. [Google Scholar] [CrossRef]
- Atmaca, A.; Kanoglu, M. Reducing energy consumption of a raw mill in cement industry. Energy 2012, 42, 261–269. [Google Scholar] [CrossRef]
- Sanz, E.; Blesa, J.; Puig, V. BiDrac Industry 4.0 framework: Application to an automotive paint shop process. Control Eng. Pract. 2021, 109, 104757. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, L.; Lu, X.; Sen, Y.; Cheng, H. Digital twin for geometric feature online inspection system of car body-in-white. Int. J. Comput. Integr. Manuf. 2021, 34, 752–763. [Google Scholar] [CrossRef]
- Tharma, R.; Winter, R.; Eigner, M. An approach for the implementation of the digital twin in the automotive wiring harness field. In Proceedings of the 15th International Design Conference, Dubrovnik, Croatia, 21–24 May 2018; pp. 3023–3032. [Google Scholar]
- Li, W.; Kara, S. An empirical model for predicting energy consumption of manufacturing processes: A case of turning process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 1636–1646. [Google Scholar] [CrossRef]
- Kara, S.; Li, W. Unit process energy consumption models for material removal processes. CIRP Ann. 2011, 60, 37–40. [Google Scholar] [CrossRef]
- Ma, Z.; Gao, M.; Wang, Q.; Wang, N.; Li, L.; Liu, C.; Liu, Z. Energy consumption distribution and optimization of additive manufacturing. Int. J. Adv. Manuf. Technol. 2021, 116, 3377–3390. [Google Scholar] [CrossRef]
- Corinaldesi, C.; Schwabeneder, D.; Lettner, G.; Auer, H. A rolling horizon approach for real-time trading and portfolio optimization of end-user flexibilities. Sustain. Energy Grids Netw. 2020, 24, 100392. [Google Scholar] [CrossRef]
- Saidu, M.M.; Hall, S.G.; Kolar, P.; Schramm, R.; Davis, T. Efficient Temperature Control in Recirculating Aquaculture Tanks. Appl. Eng. Agric. 2012, 28, 161–167. [Google Scholar] [CrossRef]
- Seung-Hwan, Y.; Jin-Yong, C.; Sang-Hyun, L.; Yun-Gyeong, O.; Koun, Y.D. Climate change impacts on water storage requirements of an agricultural reservoir considering changes in land use and rice growing season in Korea. Agric. Water Manag. 2013, 117, 43–54. [Google Scholar] [CrossRef]
- Zhao, J.; Lyu, L.; Han, X. Operation regulation analysis of solar heating system with seasonal water pool heat storage. Sustain. Cities Soc. 2019, 47, 101455. [Google Scholar] [CrossRef]
- Li, Y.; Ding, Z.; Du, Y. Techno-economic optimization of open-air swimming pool heating system with PCM storage tank for winter applications. Renew. Energy 2020, 150, 878–889. [Google Scholar] [CrossRef]
- EnerMan. ‘EnerMan H2020—Energy Efficient Manufacturing System Management’, EnerMan. 2022. Available online: https://enerman-h2020.eu/ (accessed on 12 July 2022).
- MATLAB Release; The MathWorks, Inc.: Natick, MA, USA, 2023.
- Citarella, B.; Mauro, A.W.; Pelella, F. Use of Artificial Intelligence in the Refrigeration Field. In Proceedings of the 6th IIR TPTPR Conference, Vicenza, Italy, 1–3 September 2021. [Google Scholar] [CrossRef]
- Mohanraj, M.; Jayaraj, S.; Muraleedharan, C. Applications of artificial neural networks for refrigeration, air-conditioning and heat pump systems—A review. Renew. Sustain. Energy Rev. 2012, 16, 1340–1358. [Google Scholar] [CrossRef]
- Minetto, S.; Mauro, A.W.; Martinez, S.; Zhao, Y. Use of Internet of Things and Artificial Intelligence in Refrigeration and Air Conditioning. 55th Informatory Note on Refrigeration Technology; IIF-IIR: Paris, France, 2023. [Google Scholar] [CrossRef]
- Wang, S.C. Chapter 5: Artificial Neural Network. In Interdisciplinary Computing in Java Programming; Springer Science & Business Media: Berlin, Germany, 2003; Volume 743. [Google Scholar]
- Guresen, E.; Kayakutlu, G. Definition of artificial neural networks with comparison to other networks. Procedia Comput. Sci. 2011, 3, 426–433. [Google Scholar] [CrossRef]
- Garud, K.S.; Jayaraj, S.; Lee, M.Y. A review on modeling of solar photovoltaic systems using artificial neural networks, fuzzy logic, genetic algorithm and hybrid models. Int. J. Energy Res. 2021, 45, 6–35. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An algorithm for least-squares estimation of nonlinear parameters. SIAMJ Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]




| Work | Application Sector | Description/Notes |
|---|---|---|
| Ascione et al. [12] | Building | Industrial building, energy, and cost savings of, respectively, 81% and 45% |
| Kapp et al. [13] | Building | Machine learning energy consumption predictor considering 45 manufacturing facilities |
| Aruta et al. [14] | Building | MPC to optimize energy consumption and thermal discomfort in a residential application |
| Siroky et al. [15] | Building | MPC to optimize energy consumption and thermal discomfort in a residential application |
| Son et al. [16] | Industrial production | Occurrence of abnormal scenarios, such as product defects and equipment failures in automotive production lines |
| Mendi et al. [17] | Industrial production | Digital twin to achieve a 6% increase in production and an 88% reduction in downtime in automotive production lines |
| Tao et al. [18,19] | Industrial production | Framework for the implementation of digital twins in shop-floors for smart manufacturing and energy consumption reduction |
| Zhang et al. [20] | Industrial production | Optimization of hollow glass production in terms of load balancing, fast response, high efficiency, low energy consumption, and capacity |
| Min et al. [21] | Industrial production | Production optimization in petrochemical industry |
| Karanjkar et al. [22] | Industrial production | Optimization of an assembly line for surface-mount technology |
| Çamdali and Tunc [23] | Industrial production | Heat transfer model of ladle furnaces in steel production |
| Laha et al. [24] | Industrial production | Machine learning models of steelmaking processes |
| Paryanto et al. [25] | Manufacturing process | Reduction of the energy consumption of industrial robots in manufacturing systems |
| Atmaca and Kanoglu [26] | Manufacturing process | Obtained a 6.7% energy consumption reduction of a grinding process in the cement industry |
| Sanz et al. [27] | Manufacturing process | Framework for the integration of AI tools and IoT for the predictive maintenance of an automotive paint shop process |
| Zheng et al. [28] | Manufacturing process | Anomaly detection of geometric features for car body-in-white |
| Tharma et al. [29] | Manufacturing process | Anomaly detection in the automotive wiring process |
| Li and Kara [30,31] | Manufacturing process | Energy consumption prediction of various material removing processes (e.g., turning etc.) |
| Ma et al. [32] | Manufacturing process | Analytical method for the energy consumption optimization of additive manufacturing equipment |
| Corinaldesi et al. [33] | Different end-user energy-consuming technologies | Definition of the operating strategy for end-users (such as batteries, boilers, heat pumps, electric vehicles, photovoltaic panels) to minimize energy consumptions and costs |
| Saidu et al. [34] | Water tank applications | Efficient temperature control in aquaculture water tanks |
| Hwan et al. [35] | Water tank applications | Estimate the capacity and capability of agricultural water resources |
| Zhao et al. [36] | Water tank applications | Optimize temperature regulation of swimming pools coupled with solar heating |
| Li et al. [37] | Water tank applications | Techno-economic optimization of swimming pool with the employment of PCM |
| Inputs | Output | Hidden Layers | ANN Structure | |
|---|---|---|---|---|
| ANN 1 | 2 | 5-100-100-1 | ||
| ANN 2 | 3 | 5-80-50-20-1 | ||
| ANN 3 | 3 | 5-80-50-20-1 |
| (-) | (-) | (kJ/K) |
|---|---|---|
| 0.893 | 0.947 | 1.664·106 |
| Model | Working Day | MAE (°C) | MRE (°C) | (°C) | (°C) | Std (°C) | |
|---|---|---|---|---|---|---|---|
| Physics- Based | 1 | 1.39 | −0.89 | 2.40 | −2.31 | 68.68 | 1.28 |
| 2 | 1.49 | 1.12 | 4.75 | −1.21 | 72.73 | 1.66 | |
| 3 | 0.84 | 0.58 | 3.84 | −0.81 | 84.86 | 1.07 | |
| 4 | 0.39 | −0.01 | 1.44 | −0.61 | 100.00 | 0.50 | |
| 5 | 1.42 | 1.34 | 3.32 | −0.42 | 63.56 | 1.20 | |
| 6 | 1.78 | 1.77 | 4.31 | −0.10 | 54.78 | 1.57 | |
| ANN 1 | 1 | 2.85 | −2.73 | 1.57 | −9.59 | 36.5 | 2.37 |
| 2 | 9.06 | 9.01 | 19.93 | −0.84 | 40.62 | 7.77 | |
| 3 | 8.45 | 8.28 | 22.01 | −1.34 | 34.74 | 7.81 | |
| 4 | 5.45 | −5.45 | 0.00 | −11.56 | 26.97 | 3.97 | |
| 5 | 0.37 | −0.28 | 0.37 | −0.92 | 100.00 | 0.33 | |
| 6 | 0.25 | 0.25 | 0.76 | −0.04 | 100.00 | 0.17 | |
| ANN 2 | 1 | 0.81 | 0.24 | 4.64 | −3.68 | 88.74 | 1.25 |
| 2 | 1.34 | 0.83 | 6.49 | −1.59 | 80.26 | 2.20 | |
| 3 | 2.87 | 2.63 | 6.37 | −1.78 | 38.50 | 2.28 | |
| 4 | 3.04 | −3.03 | 0.20 | −5.80 | 34.05 | 1.80 | |
| 5 | 0.71 | −0.70 | 0.12 | −1.94 | 100.00 | 0.49 | |
| 6 | 0.26 | −0.03 | 0.49 | −0.84 | 100.00 | 0.32 | |
| ANN 3 | 1 | 5.69 | 5.57 | 11.17 | −0.88 | 19.92 | 3.39 |
| 2 | 1.74 | 1.44 | 4.72 | −1.91 | 63.78 | 1.63 | |
| 3 | 0.93 | −0.56 | 1.99 | −3.15 | 89.67 | 1.07 | |
| 4 | 0.35 | −0.21 | 1.06 | −0.85 | 100.00 | 0.40 | |
| 5 | 1.84 | 1.68 | 3.88 | −0.67 | 50.00 | 1.47 | |
| 6 | 2.09 | 2.00 | 4.47 | −0.47 | 50.09 | 1.70 |
| Model | MAE (°C) | MRE (°C) | (°C) | (°C) | Std (°C) | |
|---|---|---|---|---|---|---|
| Mechanistic physics-based | 1.30 | 0.10 | 7.60 | −3.17 | 72.33 | 1.69 |
| ANN 1 | 3.49 | 1.68 | 22.01 | −11.56 | 62.07 | 6.08 |
| ANN 2 | 1.95 | 1.12 | 10.51 | −5.80 | 66.96 | 2.84 |
| ANN 3 | 1.69 | 1.05 | 11.17 | −3.15 | 69.34 | 2.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pelella, F.; Viscito, L.; Magnea, F.; Zanella, A.; Patalano, S.; Mauro, A.W.; Bianco, N. Comparison between Physics-Based Approaches and Neural Networks for the Energy Consumption Optimization of an Automotive Production Industrial Process. Energies 2023, 16, 6916. https://doi.org/10.3390/en16196916
Pelella F, Viscito L, Magnea F, Zanella A, Patalano S, Mauro AW, Bianco N. Comparison between Physics-Based Approaches and Neural Networks for the Energy Consumption Optimization of an Automotive Production Industrial Process. Energies. 2023; 16(19):6916. https://doi.org/10.3390/en16196916
Chicago/Turabian StylePelella, Francesco, Luca Viscito, Federico Magnea, Alessandro Zanella, Stanislao Patalano, Alfonso William Mauro, and Nicola Bianco. 2023. "Comparison between Physics-Based Approaches and Neural Networks for the Energy Consumption Optimization of an Automotive Production Industrial Process" Energies 16, no. 19: 6916. https://doi.org/10.3390/en16196916
APA StylePelella, F., Viscito, L., Magnea, F., Zanella, A., Patalano, S., Mauro, A. W., & Bianco, N. (2023). Comparison between Physics-Based Approaches and Neural Networks for the Energy Consumption Optimization of an Automotive Production Industrial Process. Energies, 16(19), 6916. https://doi.org/10.3390/en16196916











