Medium Rock-Soil Temperature Distribution Characteristics at Different Time Scales and New Layout Forms in the Application of Medium-Deep Borehole Heat Exchangers
Abstract
:1. Introduction
2. Methodology
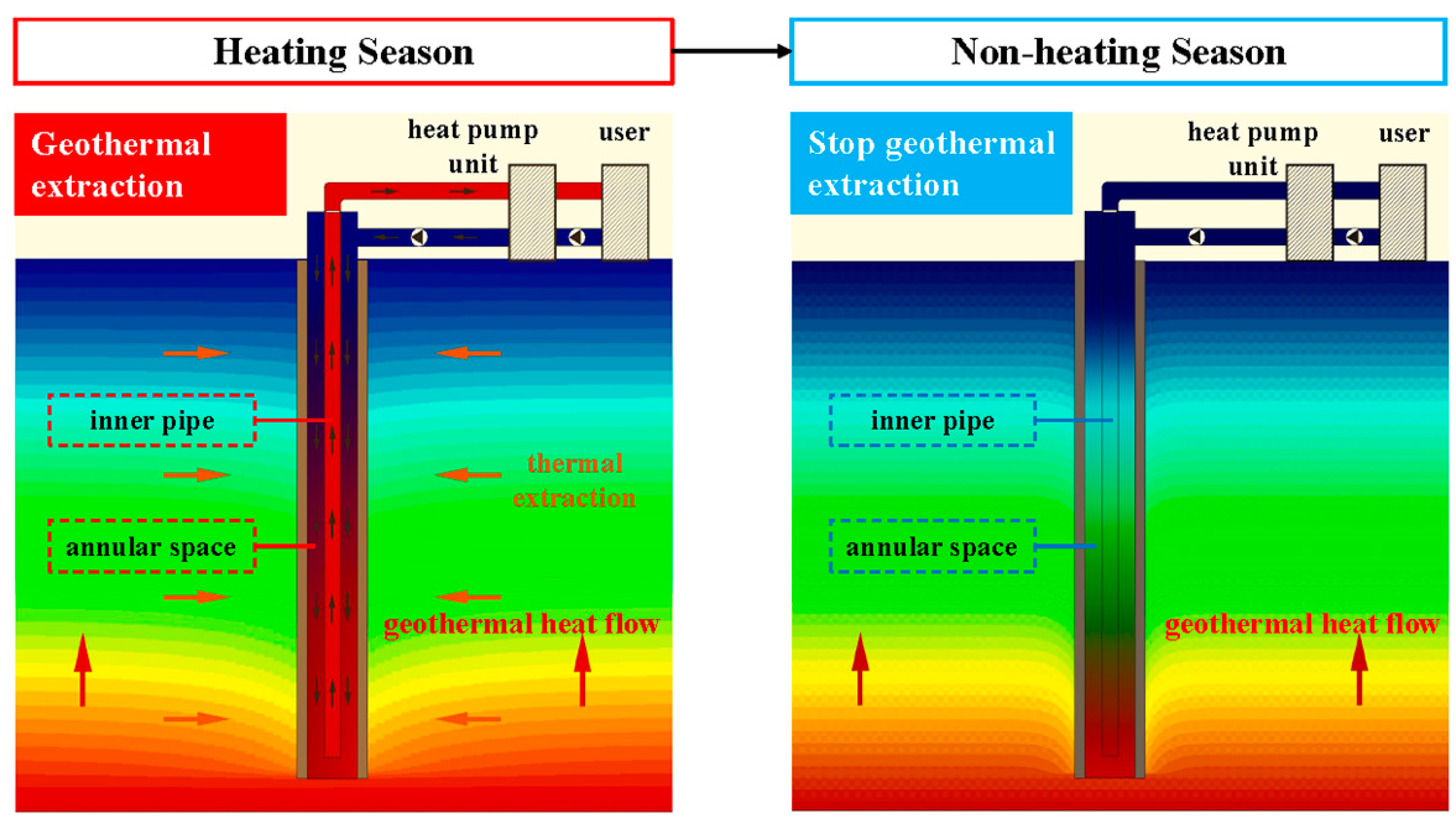
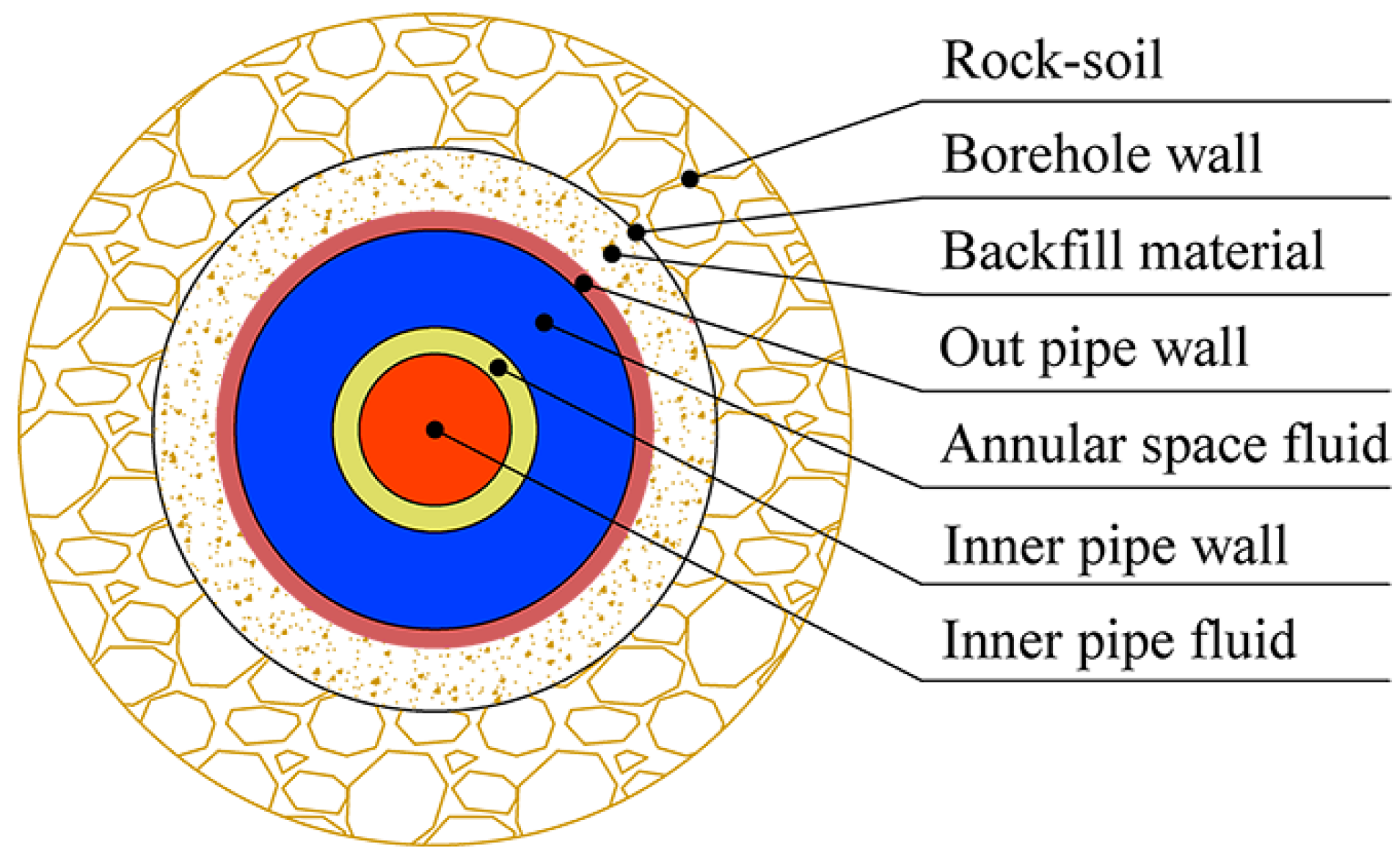
2.1. Heat Transfer between the MBHE and Rock Soil
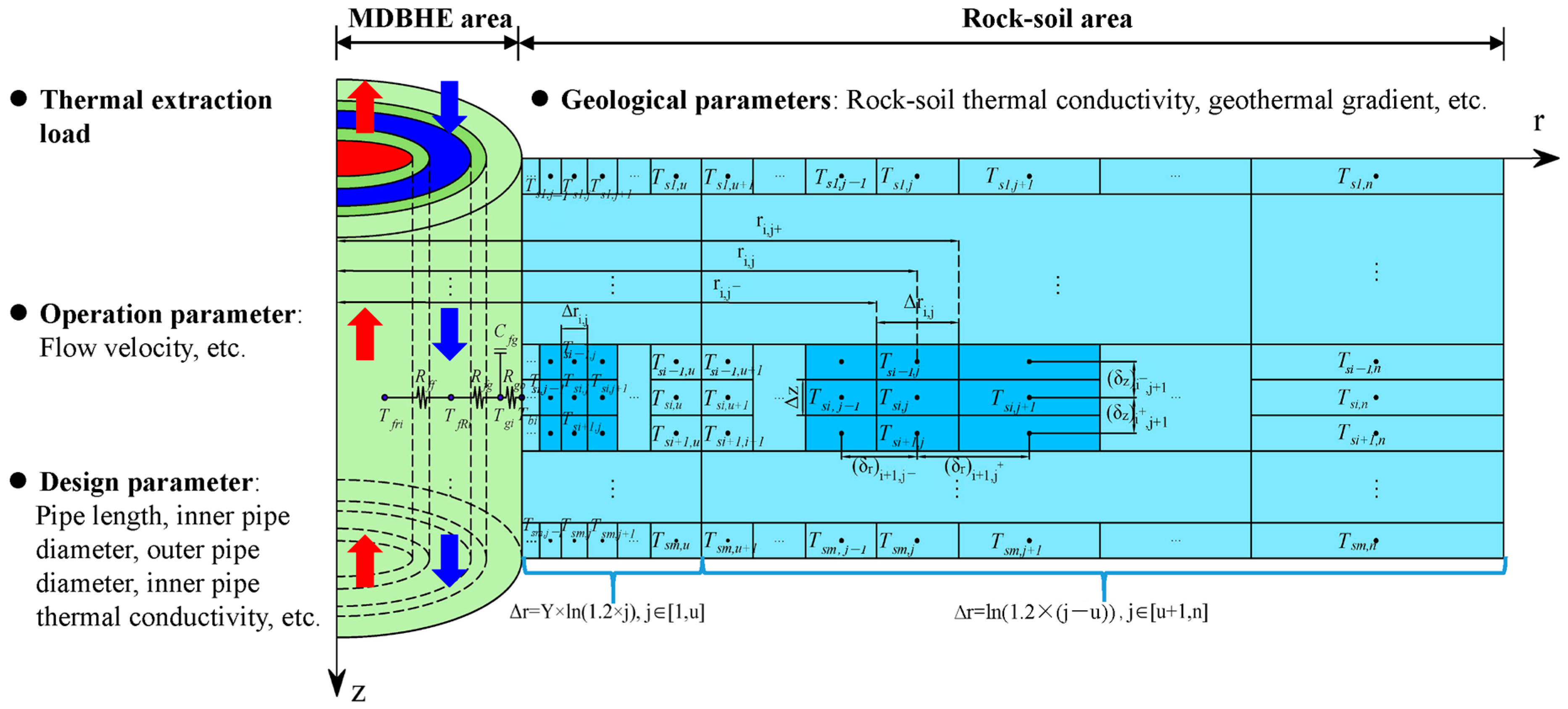
2.2. Numerical Simulation and Analysis Method
2.2.1. Balance Equations in the Numerical Model
2.2.2. Initial and Boundary Conditions
2.2.3. Model Solving and Analysis Method
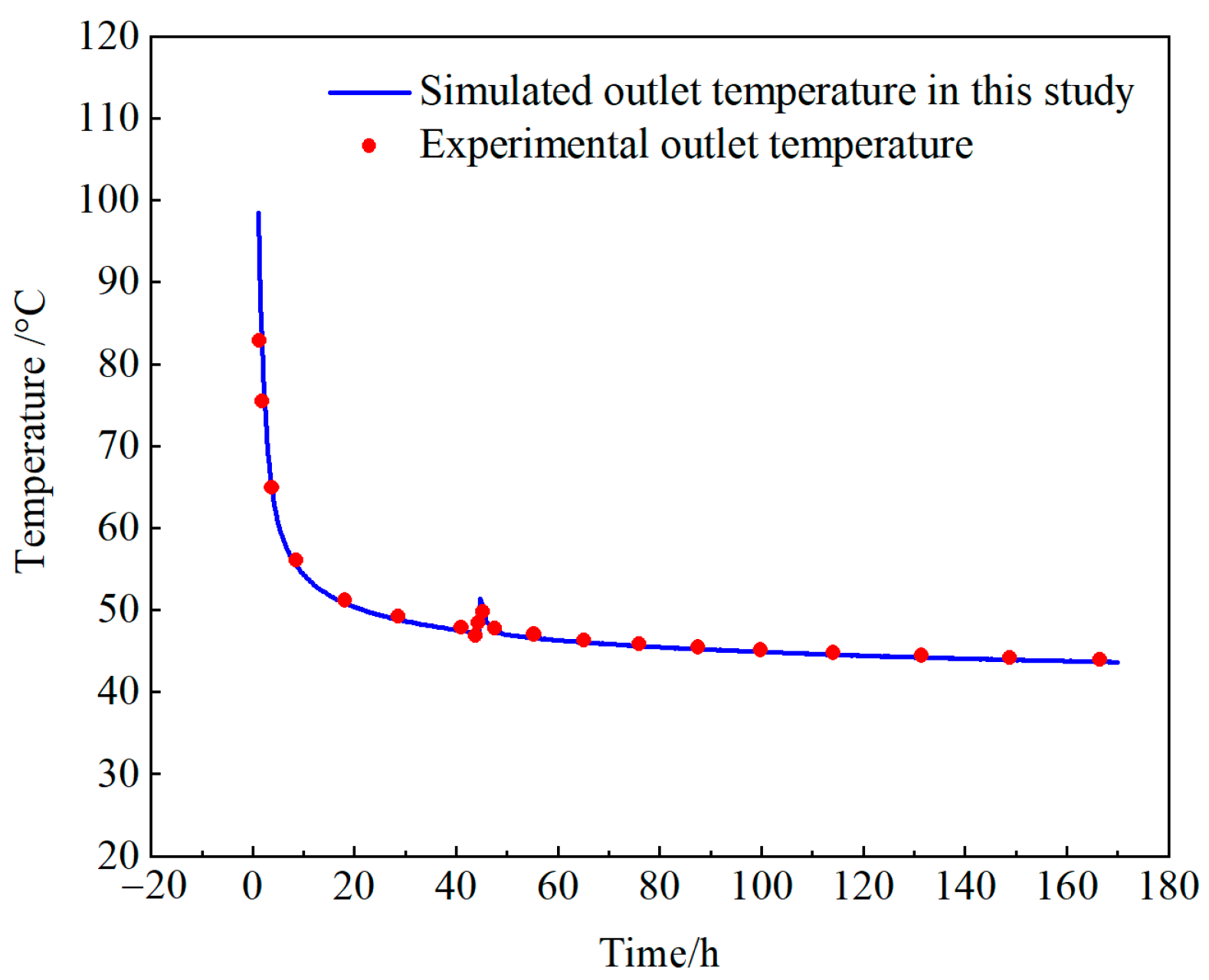
2.2.4. Model Validation
3. Results
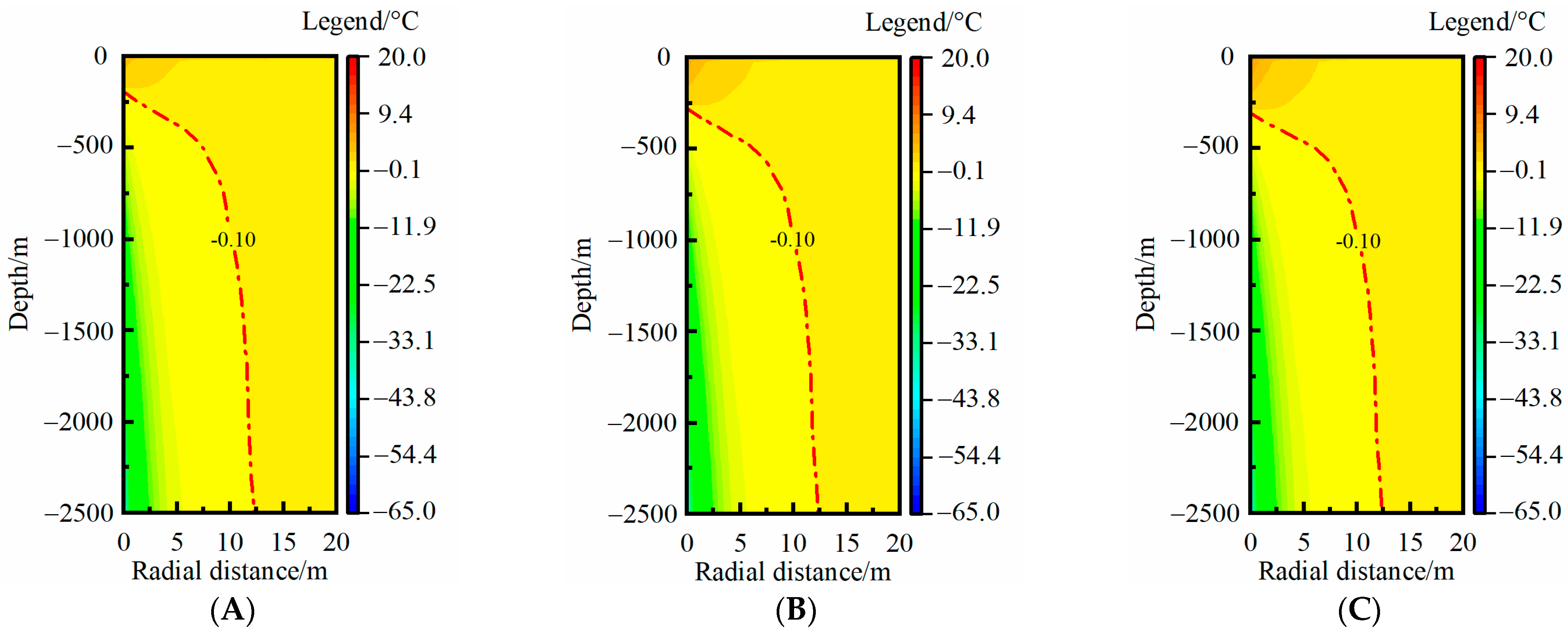
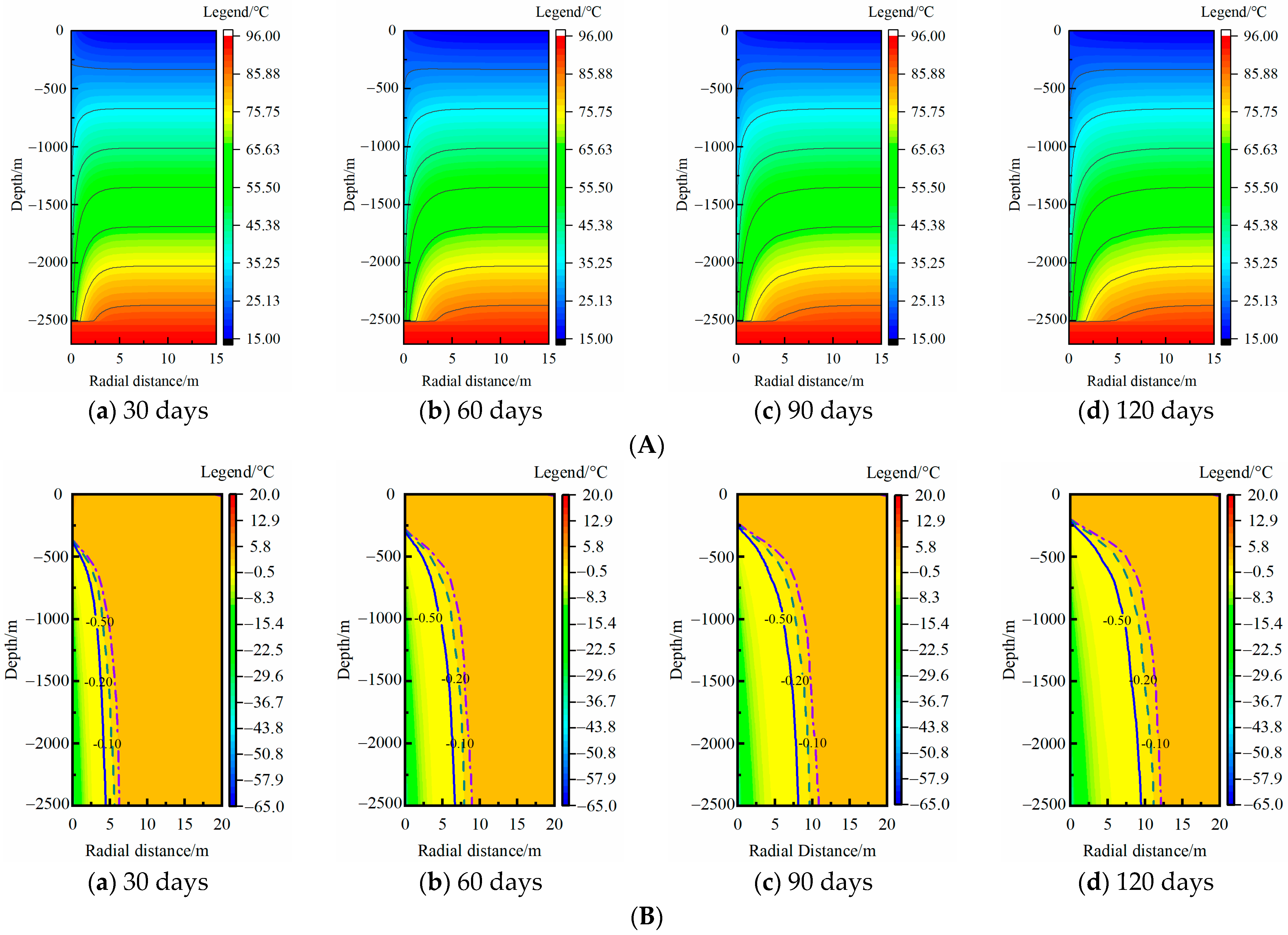
3.1. Rock-Soil Temperature Distribution in One Heating Season
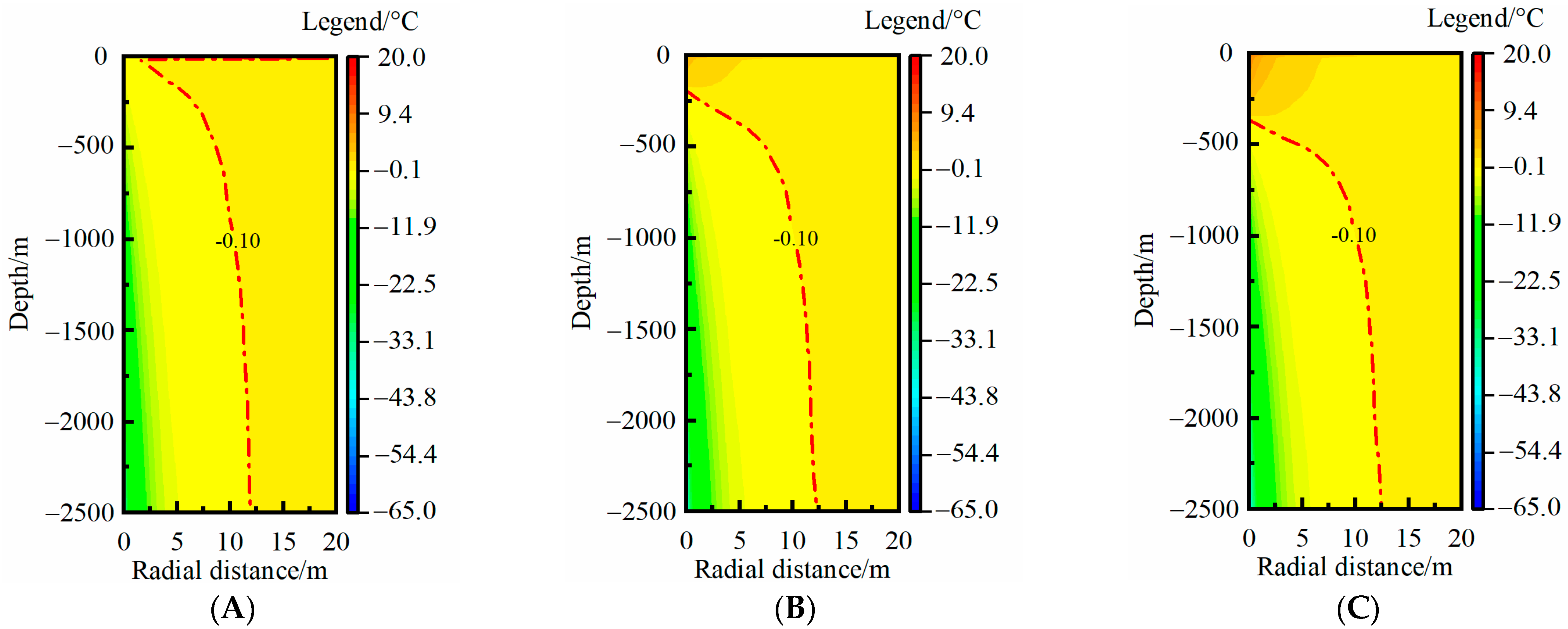
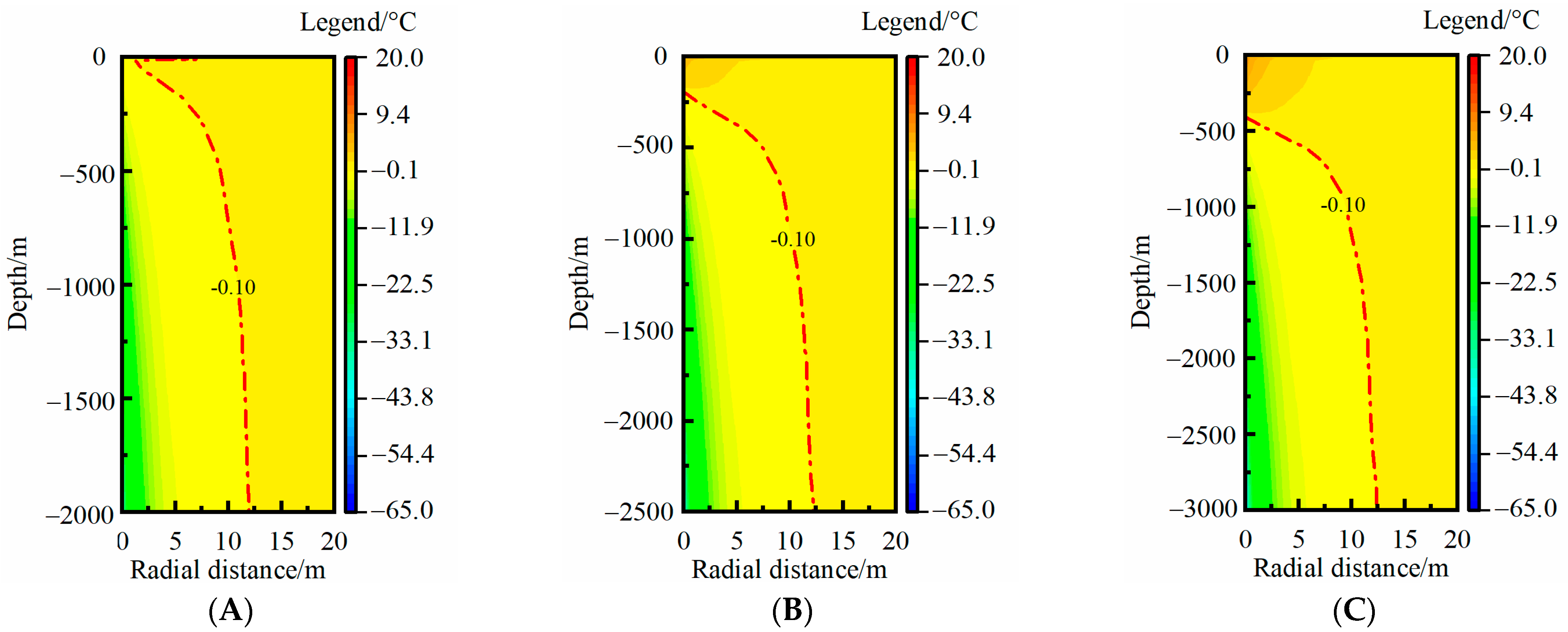
3.2. Effects of Influencing Factors
3.2.1. Thermal Extraction Load
3.2.2. Geological Parameters
3.2.3. Operation Parameters
3.2.4. Design Parameters
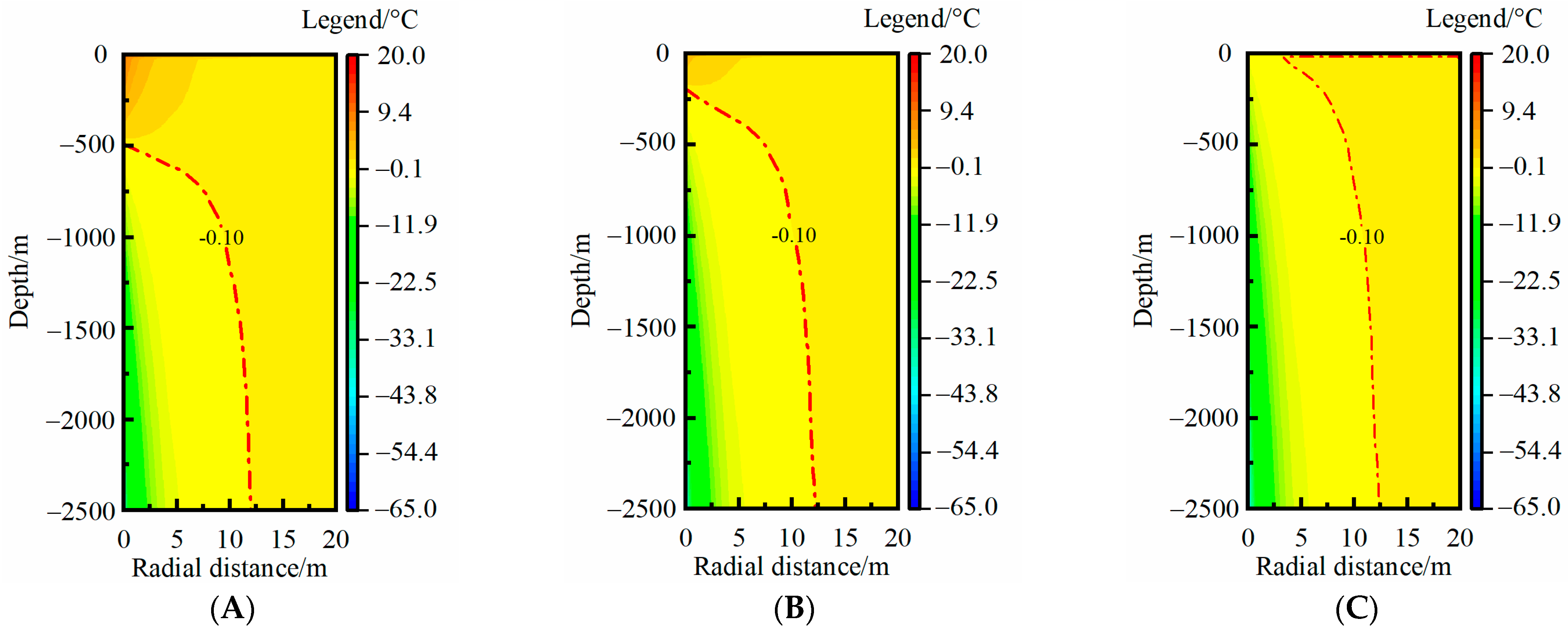
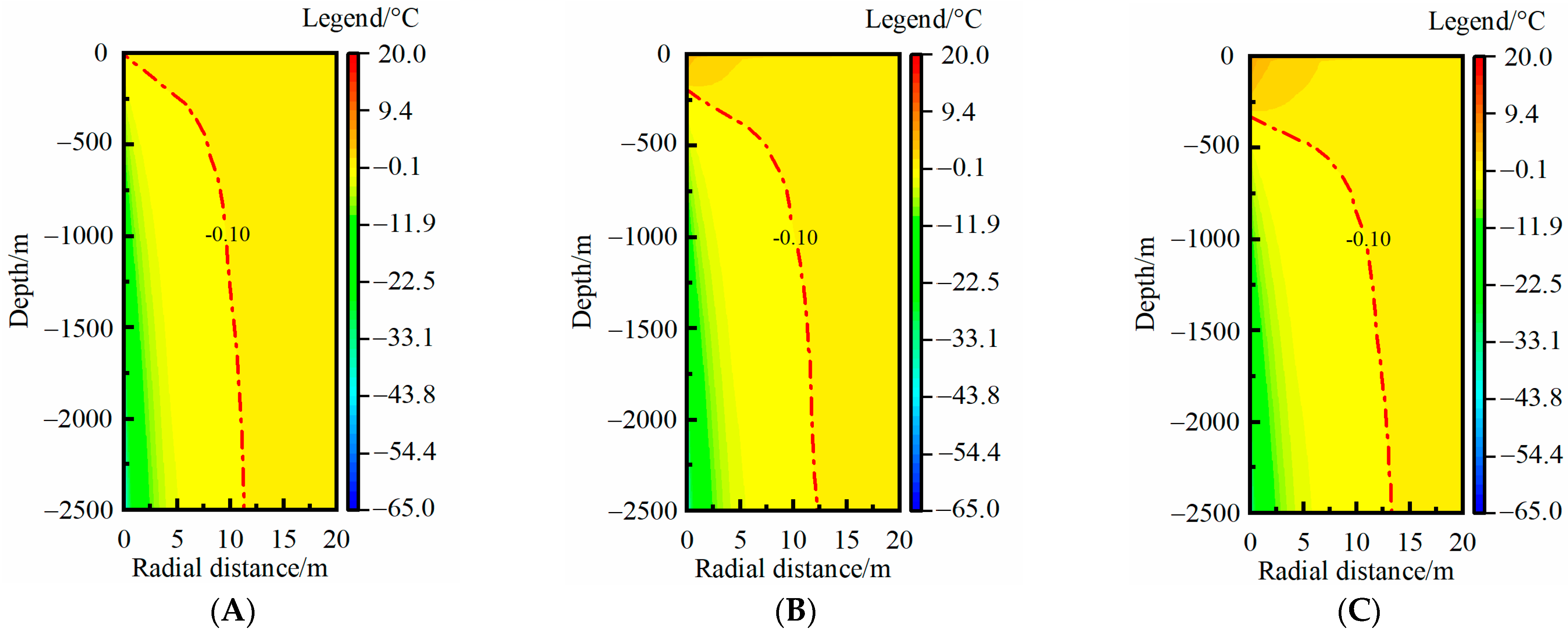
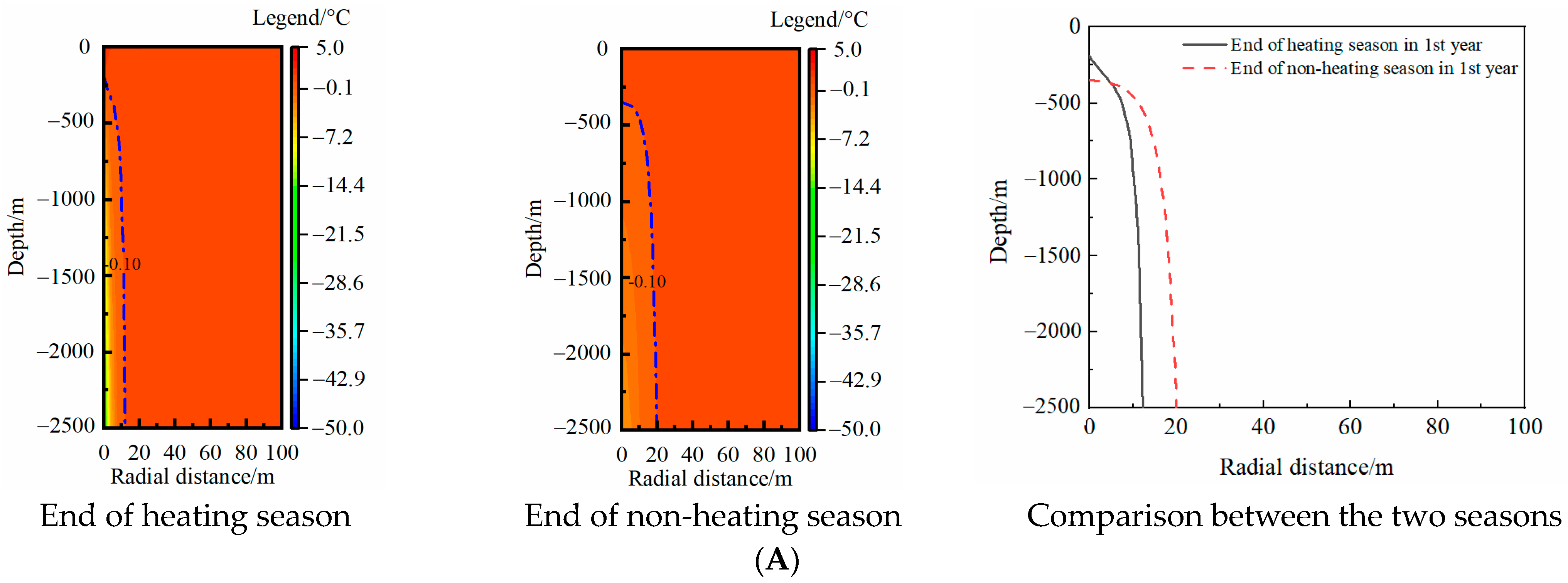
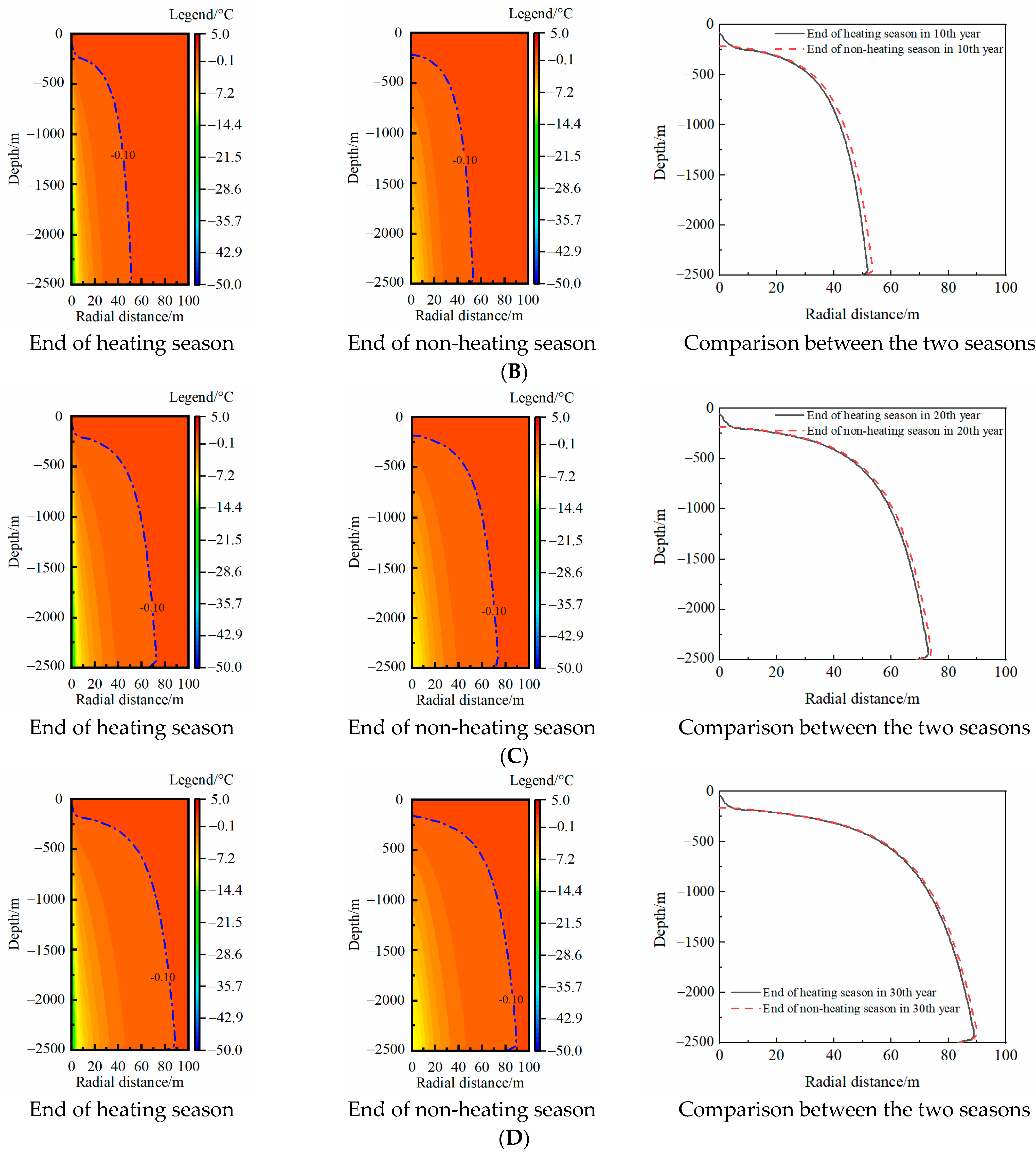
3.3. Rock-Soil Temperature Distribution in the Full Lifecycle
3.3.1. Rock-Soil TAR
3.3.2. Main Influencing Factors Analysis
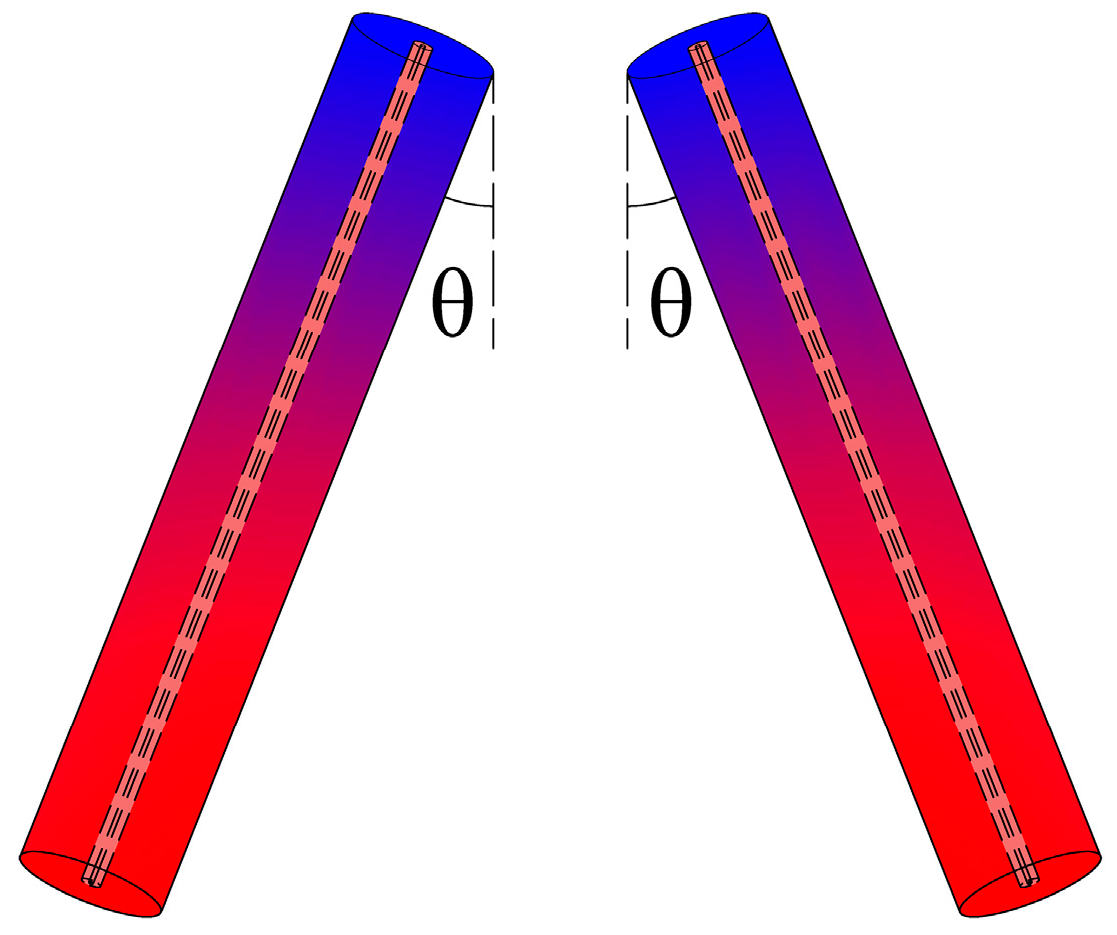
3.4. New Layout Form
3.4.1. Layout Form Proposal
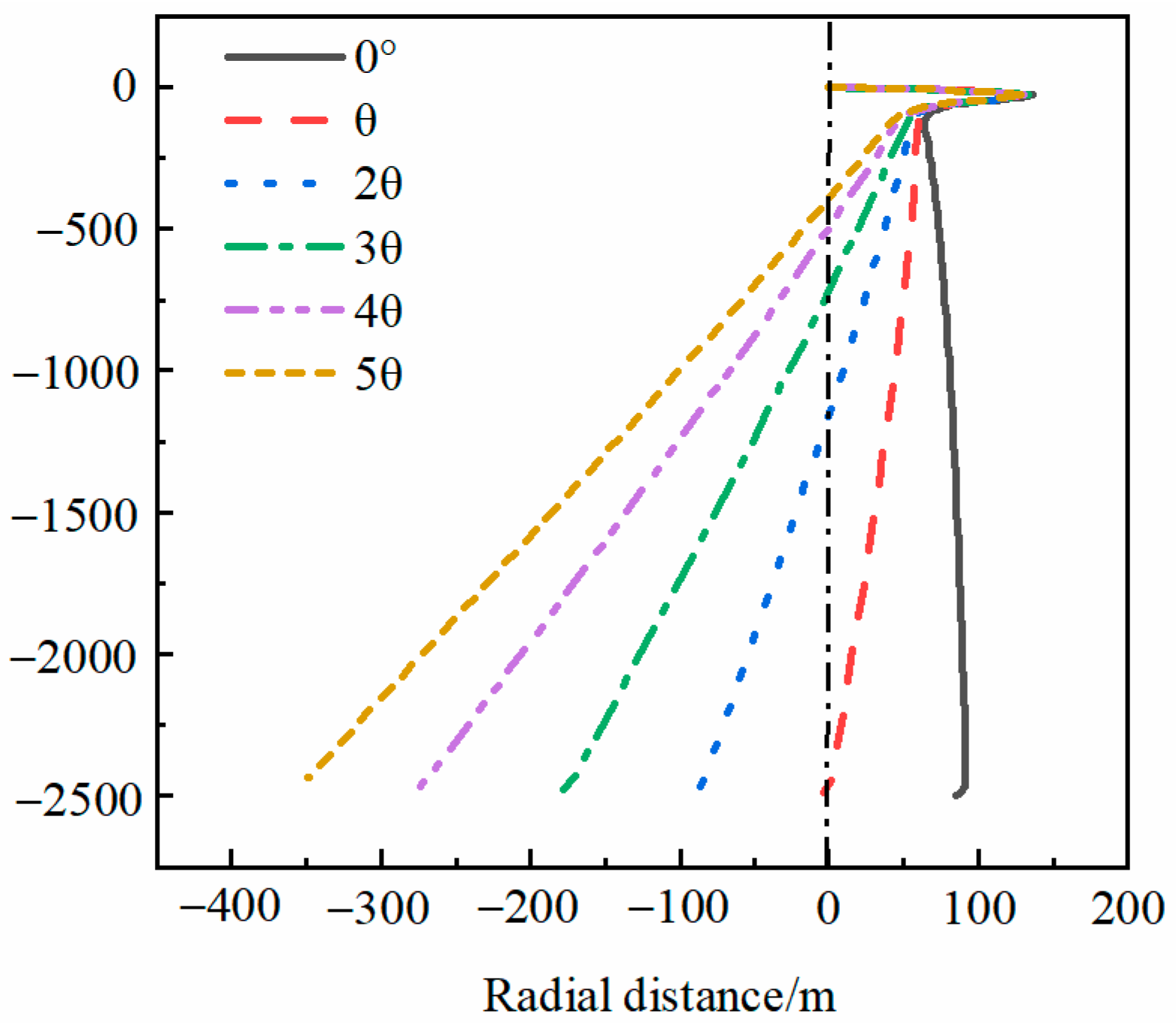
3.4.2. Thermal Affected Area Analysis
4. Discussion
5. Conclusions
- The RTAA continuously expanded in both the radial and vertical directions during a heating season. Among the analyzed influencing factors, only the rock-soil thermal conductivity significantly affected the RTAA in both the radial and vertical directions. The MTAR increased by 17.2% when the thermal conductivity increased from 2.0 to 3.0 W·m−1·K−1, and the increase degree further increased as the thermal conductivity increased. Other factors had impacts on the RTAA only in the vertical direction.
- The temperature recovery mechanism in the non-heating season of medium-deep rock soil varied with the thermal extraction year. In the first year, the temperature difference of the medium-deep rock soil in the radial direction dominated the temperature recovery of the rock soil, whereas the geothermal flow dominated the temperature recovery after 20 years of thermal extraction. In the 30th year, the TAR at the end of the heating season and non-heating season basically coincided.
- The TAR in the 30th year represented the effective MTAR over the full lifecycle. According to the rock-soil temperature distribution characteristics, the main RTAA was focused on the deep part of the rock soil, and the MTAR over the full lifecycle was positioned nearly at the depth of the pipe bottom, so a new layout form with inclining boreholes was proposed. Four times the TAR angle was recommended as optimal incline angle, which could effectively avoid thermal interference between the adjacent MBHEs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Wang, F.; Harindintwali, J.D.; Yuan, Z.Z.; Wang, M.; Wang, F.M.; Li, S.; Yin, Z.G.; Huang, L.; Fu, Y.H.; Li, L.; et al. Technologies and perspectives for achieving carbon neutrality. Innovation 2021, 2, 100180. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wang, F.L.; Wang, Y.L.; Forson, K.; Cao, L.L.; Zhang, C.L.; Zhou, C.; Zhao, B.; Chen, J.S. Experimental investigation on the high-pressure sand suspension and adsorption capacity of guar gum fracturing fluid in low-permeability shale reservoirs: Factor analysis and mechanism disclosure. Environ. Sci. Pollut. Res. 2022, 29, 53050–53062. [Google Scholar] [CrossRef]
- Wang, F.L.; Xiao, Z.X.; Liu, X.; Ren, J.W.; Xing, T.; Li, Z.; Li, X.Y.; Chen, Y.L. Strategic design of cellulose nanofibers@zeolitic imidazolate frameworks derived mesoporous carbon-supported nanoscale CoFe2O4/CoFe hybrid composition as trifunctional electrocatalyst for Zn-air battery and self-powered overall water-splitting. J. Power Sources 2022, 521, 230925. [Google Scholar] [CrossRef]
- Li, Q.C.; Han, Y.; Liu, X.; Ansari, U.; Cheng, Y.F.; Yan, C.L. Hydrate as a by-product in CO2 leakage during the long-term sub-seabed sequestration and its role in preventing further leakage. Environ. Sci. Pollut. Res. 2022, 29, 77737–77754. [Google Scholar] [CrossRef]
- Chahartaghi, M.; Kalami, M.; Ahmadi, M.H.; Kumar, R.; Jilte, R. Energy and exergy analyses and thermo-economic optimization of geothermal heat pump for domestic water heating. Int. J. Low-Carbon Technol. 2019, 14, 108–121. [Google Scholar] [CrossRef]
- Ghazvini, M.; Sadeghzadeh, M.; Ahmadi, M.H.; Moosavi, S.; Pourfayaz, F. Geothermal energy use in hydrogen production: A review. Int. J. Energy Res. 2019, 43, 7823–7851. [Google Scholar] [CrossRef]
- Lund, J.W.; Toth, A.N. Direct utilization of geothermal energy 2020 worldwide review. Geothermics 2020, 90, 101915. [Google Scholar] [CrossRef]
- Tang, F.J.; Nowamooz, H. Long-term performance of a shallow borehole heat exchanger installed in a geothermal field of Alsace region. Renew. Energy 2018, 128, 210–222. [Google Scholar] [CrossRef]
- Zhang, W.K.; Li, W.J.; Sørensen, B.R.; Cui, P.; Man, Y.; Yu, M.Z.; Fang, Z.H. Comparative analysis of heat transfer performance of coaxial pipe and U-type deep borehole heat exchangers. Geothermics 2021, 96, 102220. [Google Scholar] [CrossRef]
- Chen, S.; Cai, W.L.; Witte, F.; Wang, X.R.; Wang, F.H.; Kolditz, O.; Shao, H.B. Long-term thermal imbalance in large borehole heat exchangers array—A numerical study based on the Leicester project. Energy Build. 2021, 231, 110518. [Google Scholar] [CrossRef]
- Kohl, T.; Brenni, R.; Eugster, W. System performance of a deep borehole heat exchanger. Geothermics 2002, 31, 687–708. [Google Scholar] [CrossRef]
- Śliwa, T.; Kotyza, J. Application of existing wells as ground heat source for heat pumps in Poland. Appl. Energy 2003, 74, 3–8. [Google Scholar] [CrossRef]
- Huchtemann, K.; Müller, D. Combined simulation of a deep ground source heat exchanger and an office building. Build. Environ. 2014, 73, 97–105. [Google Scholar] [CrossRef]
- Kelkar, S.; Wolde, G.G.; Rehfeldt, K. Lessons learned from the pioneering hot dry rock project at Fenton Hill, USA. Geothermics 2016, 63, 5–14. [Google Scholar] [CrossRef]
- Ghavidel, A.; Gracie, R.; Dusseault, M.B. Design parameters impacting electricity generation from horizontal multilateral closed-loop geothermal systems in hot dry rock. Geothermics 2022, 105, 102469. [Google Scholar] [CrossRef]
- Liu, D.X.; Zhang, W.; Lu, X.L.; Zhang, J.Q.; Meng, Q.Y.; Hu, M.Q.; Liu, J.L. Research on a novel type of hot dry rock power generation system coupled with Kalina and ORC. Energy Rep. 2022, 8, 65–76. [Google Scholar] [CrossRef]
- Li, J.; Xu, W.; Li, J.F.; Huang, S.; Li, Z.; Qiao, B.; Yang, C.; Sun, D.Y.; Zhang, G.Q. Heat extraction model and characteristics of coaxial deep borehole heat exchanger. Renew. Energy 2021, 169, 738–751. [Google Scholar] [CrossRef]
- Cai, W.L.; Wang, F.H.; Chen, S.; Chen, C.F.; Liu, J.; Deng, J.W.; Kolditz, O.; Shao, H.B. Analysis of heat extraction performance and long-term sustainability for multiple deep borehole heat exchanger array: A project-based study. Appl. Energy 2021, 289, 116590. [Google Scholar] [CrossRef]
- Wang, Z.H.; Wang, F.H.; Liu, J.; Ma, Z.J.; Han, E.S.; Song, M.J. Field test and numerical investigation on the heat transfer characteristics and optimal design of the heat exchangers of a deep borehole ground source heat pump system. Energy Convers. Manag. 2017, 153, 603–615. [Google Scholar] [CrossRef]
- Deng, J.W.; Wei, Q.P.; Liang, M.; He, S.; Zhang, H. Field test on energy performance of medium-depth geothermal heat pump systems (MD-GHPs). Energy Build. 2019, 184, 289–299. [Google Scholar] [CrossRef]
- Deng, J.W.; He, S.; Wei, Q.P.; Li, J.F.; Liu, H.; Zhang, Z.P.; Zhang, H. Field test and optimization of heat pumps and water distribution systems in medium-depth geothermal heat pump systems. Energy Build. 2020, 209, 109724. [Google Scholar] [CrossRef]
- Welsch, B.; Rühaak, W.; Schulte, D.O.; Bär, K.; Sass, I. Characteristics of medium deep borehole thermal energy storage. Int. J. Energy Res. 2016, 40, 1855–1868. [Google Scholar] [CrossRef]
- Hu, X.C.; Banks, J.; Wu, L.P.; Liu, W.V. Numerical modeling of a coaxial borehole heat exchanger to exploit geothermal energy from abandoned petroleum wells in Hinton, Alberta. Renew. Energy 2020, 148, 1110–1123. [Google Scholar] [CrossRef]
- Bu, X.B.; Ma, W.B.; Li, H.S. Geothermal energy production utilizing abandoned oil and gas wells. Renew. Energy 2012, 41, 80–85. [Google Scholar] [CrossRef]
- He, Y.J.; Bu, X.B. A novel enhanced deep borehole heat exchanger for building heating. Appl. Therm. Eng. 2020, 178, 115643. [Google Scholar] [CrossRef]
- Song, X.Z.; Wang, G.S.; Shi, Y.; Li, R.X.; Xu, Z.M.; Zheng, R.; Wang, Y.; Li, J.C. Numerical analysis of heat extraction performance of a deep coaxial borehole heat exchanger geothermal system. Energy 2018, 164, 1298–1310. [Google Scholar] [CrossRef]
- Fang, L.; Diao, N.R.; Shao, Z.K.; Zhu, K.; Fang, Z.K. A computationally efficient numerical model for heat transfer simulation of deep borehole heat exchangers. Energy Build. 2018, 167, 79–88. [Google Scholar] [CrossRef]
- Chen, C.F.; Shao, H.B.; Naumov, D.; Kong, Y.L.; Tu, K.; Kolditz, O. Numerical investigation on the performance, sustainability, and efficiency of the deep borehole heat exchanger System for Building Heating. Geotherm. Energy 2019, 7, 18. [Google Scholar] [CrossRef]
- Le Lous, M.; Larroque, F.; Dupuy, A.; Moignard, A. Thermal performance of a deep borehole heat exchanger: Insights from a synthetic coupled heat and flow model. Geothermics 2015, 57, 157–172. [Google Scholar] [CrossRef]
- Holmberg, H.; Acuna, J.; Næss, E.; Sønju, O. Thermal evaluation of coaxial deep borehole heat exchangers. Renew. Energy 2016, 97, 65–76. [Google Scholar] [CrossRef]
- Liu, J.; Wang, F.H.; Cai, W.L.; Wang, Z.H.; Li, C. Numerical investigation on the effects of geological parameters and layered subsurface on the thermal performance of medium-deep borehole heat exchanger. Renew. Energy 2020, 149, 384–399. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, F.H.; Liu, J.; Li, Y.Z.; Wang, M.; Luo, Y.Q.; Ma, L.X.; Zhu, C.; Cai, W.L. Energy analysis and performance assessment of a hybrid deep borehole heat exchanger heating system with direct heating and coupled heat pump approaches. Energy Convers. Manag. 2023, 276, 116484. [Google Scholar] [CrossRef]
- Liu, J.; Wang, F.H.; Cai, W.L.; Wang, Z.H.; Wei, Q.P.; Deng, J.W. Numerical study on the effects of design parameters on the heat transfer performance of coaxial deep borehole heat exchanger. Int. J. Energy Res. 2019, 43, 6337–6352. [Google Scholar] [CrossRef]
- Huang, Y.B.; Zhang, Y.J.; Xie, Y.Y.; Zhang, Y.; Gao, X.F. Thermal performance analysis on the composition attributes of deep coaxial borehole heat exchanger for building heating. Energy Build. 2020, 221, 110019. [Google Scholar] [CrossRef]
- Cai, W.L.; Wang, F.H.; Chen, C.F.; Chen, S.; Liu, J.; Ren, Z.L.; Shao, H.B. Long-term performance evaluation for deep borehole heat exchanger array under different soil thermal properties and system layouts. Energy 2022, 241, 122937. [Google Scholar] [CrossRef]
- Zhang, F.F.; Fang, L.; Zhu, K.; Yu, M.Z.; Cui, P.; Zhang, W.K.; Zhuang, Z.Y.; Fang, Z.H. Long-term dynamic heat transfer analysis for the borehole spacing planning of multiple deep borehole heat exchanger. Case Stud. Therm. Eng. 2022, 38, 102373. [Google Scholar] [CrossRef]
- Brown, C.S.; Doran, H.; Kolo, I.; Banks, D.; Falcone, G. Investigating the influence of groundwater flow and charge cycle duration on deep borehole heat exchangers for heat extraction and borehole thermal energy storage. Energies 2023, 16, 2677. [Google Scholar] [CrossRef]
- Bidarmaghz, A.; Narsilio, G.A. Is natural convection within an aquifer a critical phenomenon in deep borehole heat exchangers’ efficiency? Appl. Therm. Eng. 2022, 212, 118450. [Google Scholar] [CrossRef]
- Brown, C.S.; Kolo, I.; Falcone, G.; Banks, D. Investigating scalability of deep borehole heat exchangers: Numerical modelling of arrays with varied modes of operation. Renew. Energy 2023, 202, 442–452. [Google Scholar] [CrossRef]
- Liu, J.; Wang, F.H.; Gao, Y.; Zhang, Y.P.; Cai, W.L.; Wang, M.; Wang, Z.H. Influencing factors analysis and operation optimization for the long-term performance of medium-deep borehole heat exchanger coupled ground source heat pump system. Energy Build. 2020, 226, 110385. [Google Scholar] [CrossRef]
- Morita, K.; Bollmeier, W.; Mizogami, H. An experiment to prove the concept of the downhole coaxial heat exchanger (DCHE) in Hawaii. Geotherm. Resour. Counc. Trans. 1992, 16, 9–16. [Google Scholar]



| No | Factor (Unit) | Analyzed Parameters | Benchmark Parameters |
|---|---|---|---|
| (a) | Thermal extraction load (W·m−1) | 75, 100, 125 | 100 |
| (b) | Rock-soil thermal conductivity (W·m−1·K−1) | 2.0, 2.5, 3.0 | 2.5 |
| (c) | Geothermal gradient (°C·km−1) | 25, 30, 35 | 30 |
| (d) | Flow velocity (m·s−1) | 0.5, 0.6, 0.7 | 0.7 |
| (e) | Pipe length (m) | 2000, 2500, 3000 | 2500 |
| (f) | Inner pipe diameter (m) | 0.045, 0.055, 0.0625 | 0.055 |
| (g) | Outer pipe diameter (m) | 0.0889, 0.1096, 0.1223 | 0.0889 |
| (h) | Inner pipe thermal conductivity (W·m−1·K−1) | 0, 0.20, 0.45 | 0.45 |
| No | Factor (Unit) | Benchmark Parameter |
|---|---|---|
| (a) | Heat capacity of rock soil (kJ/(m3·K)) | 2500 |
| (b) | Thermal conductivity of outer pipe (W/(m·K)) | 40 |
| (c) | Heat capacity of inner pipe (kJ/(m3·K)) | 3800 |
| (d) | Heat capacity of outer pipe (kJ/(m3·K)) | 2200 |
| (e) | Thermal conductivity of grout (W/(m·K)) | 1.5 |
| (f) | Heat capacity of grout (kJ/(m3·K)) | 2500 |
| (g) | Ground surface temperature (°C) | 15 |
| Pipe Length/m | TAR Angle/° | Vertical Depth/m | Pipe Length/m | Optimal TAR Angle/° | Vertical Depth/m |
|---|---|---|---|---|---|
| 2000 | 2.1–2.9 | 1997.4–1998.6 | 2000 | 8.4–11.6 | 1958.6–1978.4 |
| 2500 | 1.8–2.4 | 2497.8–2498.8 | 2500 | 7.2–9.6 | 2464.4–2481.2 |
| 3000 | 1.5–2.1 | 2998.0–2999.0 | 3000 | 6.0–8.4 | 2968.6–2983.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhang, Y.; Wang, Z.; Zhou, C.; Liu, B.; Wang, F. Medium Rock-Soil Temperature Distribution Characteristics at Different Time Scales and New Layout Forms in the Application of Medium-Deep Borehole Heat Exchangers. Energies 2023, 16, 6970. https://doi.org/10.3390/en16196970
Liu J, Zhang Y, Wang Z, Zhou C, Liu B, Wang F. Medium Rock-Soil Temperature Distribution Characteristics at Different Time Scales and New Layout Forms in the Application of Medium-Deep Borehole Heat Exchangers. Energies. 2023; 16(19):6970. https://doi.org/10.3390/en16196970
Chicago/Turabian StyleLiu, Jun, Yuping Zhang, Zeyuan Wang, Cong Zhou, Boyang Liu, and Fenghao Wang. 2023. "Medium Rock-Soil Temperature Distribution Characteristics at Different Time Scales and New Layout Forms in the Application of Medium-Deep Borehole Heat Exchangers" Energies 16, no. 19: 6970. https://doi.org/10.3390/en16196970
APA StyleLiu, J., Zhang, Y., Wang, Z., Zhou, C., Liu, B., & Wang, F. (2023). Medium Rock-Soil Temperature Distribution Characteristics at Different Time Scales and New Layout Forms in the Application of Medium-Deep Borehole Heat Exchangers. Energies, 16(19), 6970. https://doi.org/10.3390/en16196970







