A New Method for Determining Interfacial Tension: Verification and Validation

Abstract

Surface tension is a meaningful parameter influencing boiling and condensation in macroscopic scale, in confined spaces, or for nanofluids; it further affects boiling with surfactants. Surface, or interfacial, tension is an important property in the research into increasing heat transfer, enhancing efficiency of photovoltaic systems, improving engine operation, or forming drugs or polymers. It is often determined using axisymmetric drop shape analysis based on the differential equations system formulated by Bashforth and Adams. The closed-form expression of the interface shape states the radii defining the bubbles are the negative numbers, which causes the temperature profile drops along the heat transfer direction, e.g., in the Wiśniewski formulas for the temperature in the vapor bubbles; moreover, the drop, or bubble, possesses only one main radius of curvature, which may reduce the number of the unknowns and equations in the Bashforth and Adams algorithm. An alternative method applying the closed-form expression for the droplet shape is validated for the water (denser) drop flowing down in octane (the lighter liquid); its spare equation is used for verifying the outcomes.

1. Introduction

Heat transfer is the most effective under isothermal processes that take place during phase changes (boiling or condensation); when these processes are evaluated the surface tension forces become an important argument, for other forces are of the same order [1].

Creating and growing the vapor bubbles was thoroughly studied by Wiśniewski [2] under the presumptions that pressure in the bubble is higher than in the surrounding liquid. The bubble expands because heat is transferred from the liquid to the vapor, so the temperature of the boiling liquid (T_s) is higher than the vapor temperature inside the bubble (T_v). Wiśniewski [2] derived four different formulas, under the various assumptions, for determining temperature in the vaporous bubble, as follows:

$$T_v=T_s\left(1+\frac{2\gamma }{R_b}\frac{v_v-v_s}{\Delta H_{vap}}\right)\hspace{1em}\left[K\right]\dots ,$$

(1)

$$T_v=T_{s}exp\left(\frac{2\gamma }{R_b}\frac{v_v-v_s}{\Delta H_{vap}}\right)\hspace{1em}\left[K\right]\dots ,$$

(2)

$$T_v=\frac{T_s}{1-\frac{B_v{T}_s}{\Delta H_{vap}}\ln \left(1+\frac{2\gamma }{R_b{p}_s}\right)}\hspace{1em}\left[K\right]\dots ,$$

(3)

$$T_v=\frac{T_s}{1-\frac{B_v{T}_s}{\Delta H_{vap}}\frac{2\gamma }{R_b{p}_s}}\hspace{1em}\left[K\right]\dots ,$$

(4)

where:

• γ—surface tension [N/m],
• R_b—the radius of the bubble [m],
• v_v—specific volume of the vapor [m³/kg],
• v_s—specific volume of the saturated liquid [m³/kg],
• ΔH_vap—enthalpy of vaporization [J/kg],
• B_v—specific gas constant for vapor [J/(kg·K)],
• p_s—absolute pressure of the saturated liquid [N/m²].

The detailed insight into Equations (1)–(4) leads to the impression that these formulas might be improper, for in every case the temperature in the bubble seems to be higher than in the surrounding liquid. The specific volume of the vapor (v_n) is larger than the specific volume of the liquid (v_s), so the expression in the brackets in Equation (1) is greater than 1, and the exponent in Equation (2) is a positive number, hence T_v > T_s. Since the minuends in the denominators in Equations (3) and (4) are positive fractions, the denominators are less than 1, and T_v > T_s. However, according to the new model, which is presented hereinafter in the subsection, the pressure in the bubble is lower than in the surrounding liquid, and the bubble’s radius is a negative number, so T_v < T_s in Equations (1)–(4); therefore, heat is transferred from the surrounding liquid to the bubble, which is true to form.

Gil et al. [3] report that surface tension makes important impact on the force field that affects the appearance, growth, and detachment of the bubbles during boiling. Greater surface tension markedly shifts the named transition point at the onset of nucleate boiling towards higher values of heat flux; it also increases the forces which are necessary for removing the bubbles from the nucleation surface, which reduces the frequency of bubble removal. These two components may cause a decrease in the boiling heat transfer coefficient.

The major importance of surface tension in analyzing thermal systems operation arises from its influence on surface wettability and bubble growth [4]. For that reason, surface tension, besides the vaporization latent heat and the difference between liquid and vapor phases densities, is the most important parameter in the analyses of boiling and condensation processes. Additionally, for that reason, it is an argument with the most correlations for nucleate pool boiling, especially during critical heat flux conditions.

Estelle et al. (cf. Table 1 in [4]) systematized the heat transfer applications affected by surface tension and emphasized the parameters that correspond to the surface tension. The heat transfer coefficient and Bond number increase in boiling when the surface tension decreases; similarly, the critical heat flux rises under nucleate pool boiling when the surface tension falls. Not at all unlikely is for external conventions boiling, for the Weber number goes up, but the critical heat flux goes down when the surface tension increases. The capillary number and Kandlikar second number increase when the surface tension decreases under flow boiling in microchannels. The Weber number is inversely proportional to the surface tension in the heat pipes. The maximum heat flux decreases and the Kutateladze number increases when the surface tension drops.

Estelle et al. [4] conclude that surface tension and surface wettability are the important properties in formulating a theory for applying nanofluids in heat exchangers or energy systems; these properties have not been studied thoroughly, to date, and dispersion. Surface tension of nanofluids is a function of the nanoparticles’ physical and chemical properties, and their dispersion characteristics. Moreover, variation of the surface tension value may be an indicator of nanoparticle stability and dispersion.

Huang et al. [5] experimentally studied the effect of surface tension and nanoparticle concentration on boiling parameters. Moreover, these authors also did research into the influence of the nanoparticle structure on surface tension and how the boiling process varies when surface tension increases or decreases. They conclude that graphene nanoparticles raise surface tension, which results in a decrease in the heat transfer coefficient and slower bubble separation. Another conclusion relative to surface tension is that added hydrophobic nanoparticles increase surface tension, which causes a reduction in the heat transfer coefficient.

Additionally, nanofluids affect heat transfer in thermosiphons, which achieve a high efficiency of heat transfer because this process is isothermal amid boiling. Kujawska et al. [6] researched changing surface tension and wettability because these properties have an effect on boiling; they employed the pendant drop method for determining surface tension, which was done with a DSA-30 drop shape analyzer. Addition of silica nanofluid at a volume concentration of 2% reduces water surface tension by 4–9% in the range of 15–75 °C; this reduction is sufficient for prohibiting geysering. The graphene oxide nanofluid at a mass concentration of 0.1 g/L has no impact on surface tension because of the low concentration.

Boiling with surfactants is a greatly complicated process, for it is affected by wall heat flux and the physical and chemical properties of the added substances, including the interfacial properties [7]. A surfactant is basically a compound with a low molecular mass; its molecule consists of two parts: one is hydrophilic, but the other is hydrophobic. Even a dilute solution of a surfactant in water has a much lower surface tension than pure water; further addition of the surfactant lowers the surface tension considerably up to the asymptotic limit at the critical micelle concentration. Adding the surfactants increases the boiling heat transfer coefficient; however, some substances possess a local maximum beyond which this coefficient decreases when the concentration rises further.

Although boiling in conventional channels with a diameter larger than 3 mm has been researched exhaustively, the correlations based on these investigations may not be applicable to the narrower channels because the surface tension forces become comparable to those in other channels.

After comprehensive studies of capillary flow and flooding in vertical annular two-phase flows and of heat transfer in limited space, Kew and Cornwell introduced the confinement number [8,9]:

$$Co=\frac{{\left[\frac{\gamma }{\left({\mathsf{\rho }}_l-{\mathsf{\rho }}_v\right)g}\right]}^{1/2}}{d_h}\hspace{1em}\left[-\right]\dots ,$$

(5)

where:

• d_h—hydraulic diameter of a channel [m]
• g—gravitational acceleration [m/s];
• ρ_l—density of a liquid [kg/m³];
• ρ_v—density of a vapor [kg/m³].

If the confinement number for a channel (Co) exceeds 0.5, then surface tension should be included in an analysis and this channel is this channel is named the confined space to be confined space; if Co < 0.5 then the channel is considered to be isolated, and so the effect of surface tension may be ignored.

Mikielewicz [10] derived a correspondence for the heat transfer coefficient in two-phase boiling; this coefficient depends on the pool-boiling heat transfer coefficient, liquid only heat transfer coefficient, and two-phase multiplier, which should be determined using the Lottes and Flinn correlation. However, other correlations for the two-phase multiplier are allowed, e.g., it may be a correlation determined for a particular flow structure. The Mikielewicz correspondence is adapted to the confined channels; this adaptation which was conducted by Mikielewicz et al. [11], consists of applying an empirical correction parameter and modifying the Muller–Steinhagen and Heck correlation for the two-phase multiplier; this modified form of the correlation includes the confinement number that determines the effect of surface tension. Mikielewicz et al. [11] also checked a Chisholm correlation modified by Tran et al.; this modified correlation also included the influence of surface tension expressed by the confinement number; however, this correlation was misadjusted to the reference data.

During boiling, heat transfer rises easily in confined spaces, e.g., in narrow channels; these channels, named surface systems by Pastuszko et al. [12], are used as micro heat exchangers for cooling the processors, or high-power semiconductors in TGV trains. These authors experimentally compared the boiling process in the narrow channels between three working fluids: ethanol, FC-12, and Novec-649. In a channel with a width of 1 mm, height of 5.5 mm, and pitch of 2 mm, the heat flux of the Novec-649 rose by 20% in comparison to that of the FC-72 because of 14% higher surface tension. The higher capillary pressure enhanced the fluid inflow into the mini channel at a depth of 10 mm and at width of 0.6 mm.

One of the methods for increasing the efficiency of photovoltaic systems (PV) is lowering the temperature of the n–p junctions [13]; this temperature is reduced by using a cooling system, for instance a heat pipe that cools using a low-temperature boiling medium [14]. The biggest power gains in the Świnoujście harbor may be obtained on warm days in May at noon [13]; the PV with cooling modules makes power gains of 7–12 kW/m² in the summer, 2.6–25 kW/m² in the spring or autumn, and 0.35–2.9 kW/m² in the winter.

Surface (or interfacial) tension is one of the most important fuel properties to consider when conducting research into improvement of engine operation [15,16]; it is also important in drugs [17,18] and polymer [19] production.

Hossain et al. [20] mention that the excessive emissions of particulate matter are caused by fuels with higher density, viscosity, and surface tension, and lower volatility.

The various methods for determining surface or interface tension employ the Young–Laplace equation depicted by Young [21] and derived by Laplace (after Adamson [22]):

$$\Delta p=\gamma \left(\frac{1}{R_1}+\frac{1}{R_2}\right),$$

(6)

where:

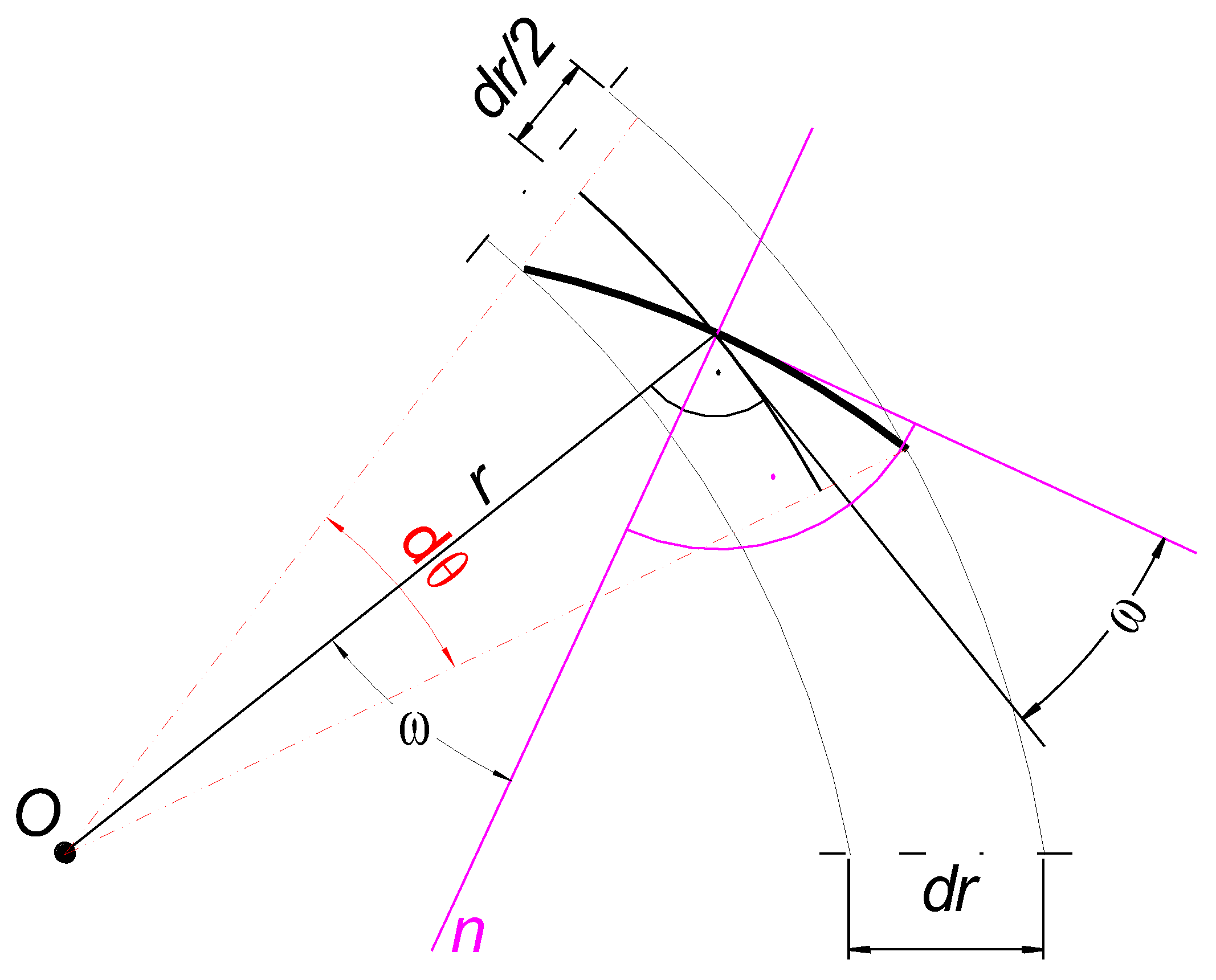
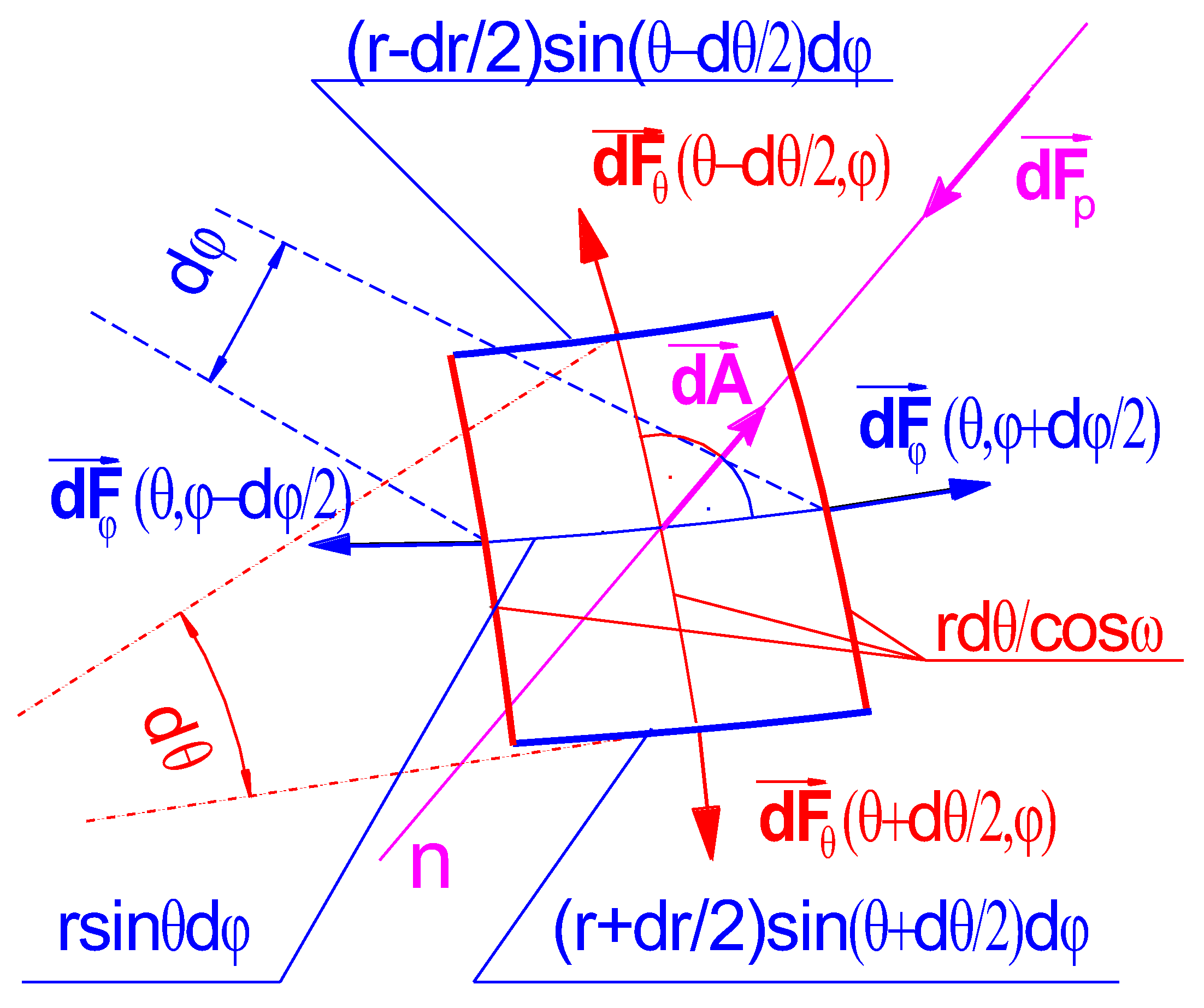
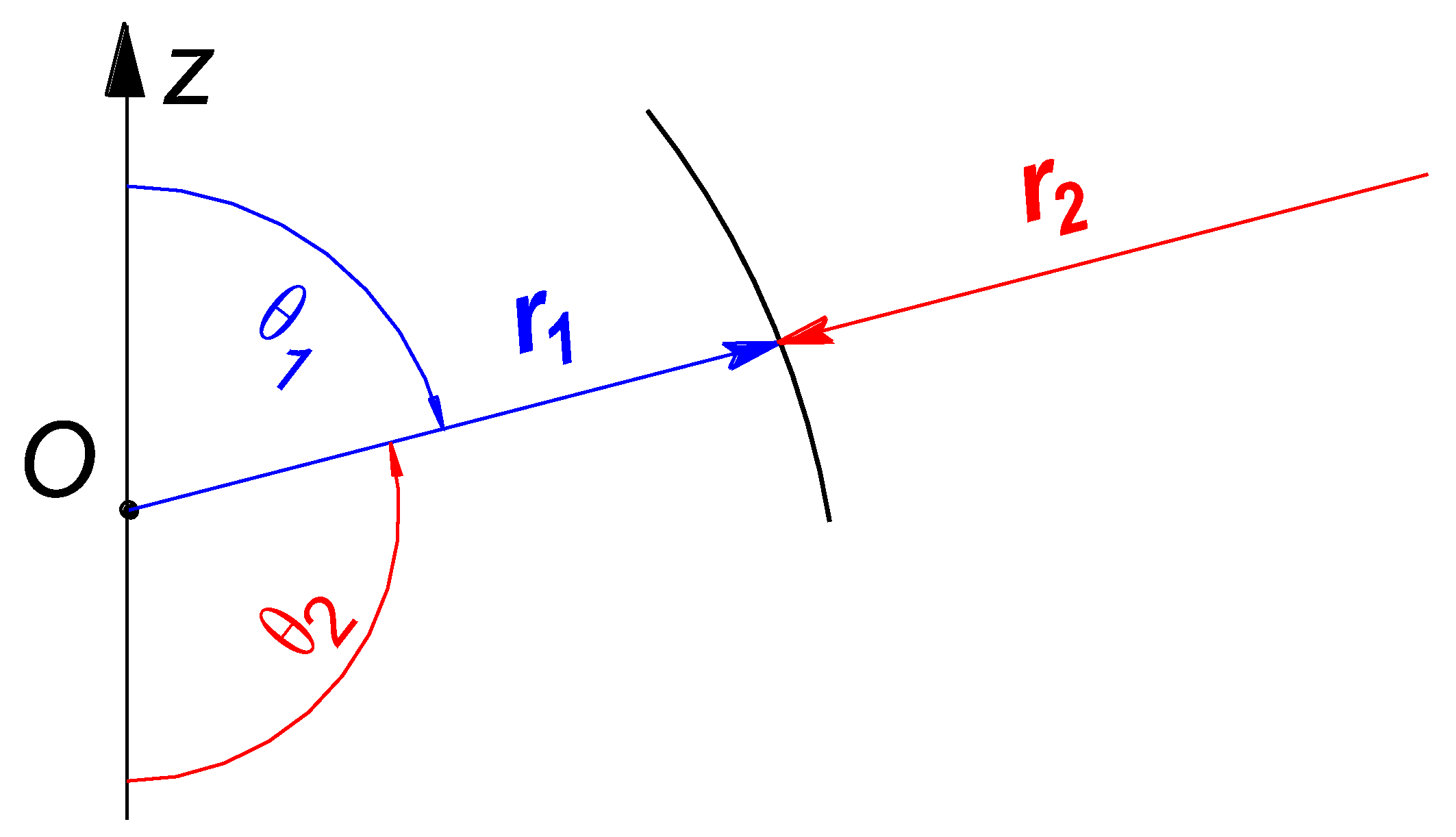
• Δp—pressure difference between two sides of the interface in the bulk phases [Pa];
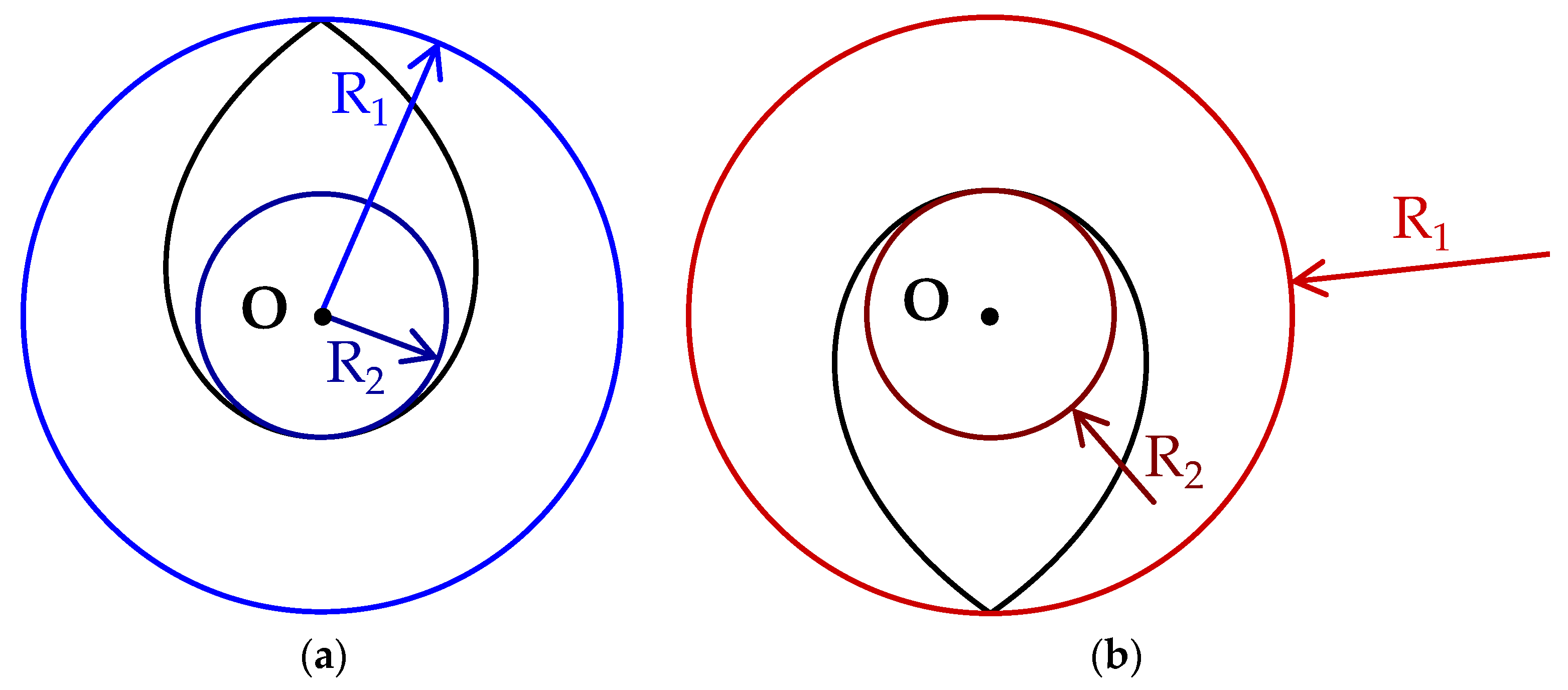
• R₁, R₂—the main radii of curvature [m].

If the interface surface is convex, the gauge pressure is positive; otherwise, if it is concave, the gauge pressure is negative. These conclusions stem from Equation (6). However, these conclusions are invalid when the surface is under hydrostatic pressure, which is proved hereinafter.

Regardless of how the Young-Laplace Equation (6) was derived (cf. Adamson [22] or Gibbs [23]) it is based on the assumptions of the equilibrium thermodynamics, in which all the thermal, mechanical, and material parameters are homogenous. However, it is applied for axisymmetric drop shape analysis, which is a non-equilibrium phenomenon because of the non-homogenous hydrostatic pressure.

Because the interface shape (a contour of a drop or bubble) is not shown explicitly in Equation (6) the surface or interface tension is mostly determined using the Bashforth and Adams [24] algorithm, which is gradually modified [25,26,27,28,29,30,31,32,33,34,35,36,37]. However, the ADSA method possesses some insufficiencies, which are described in [36,38].

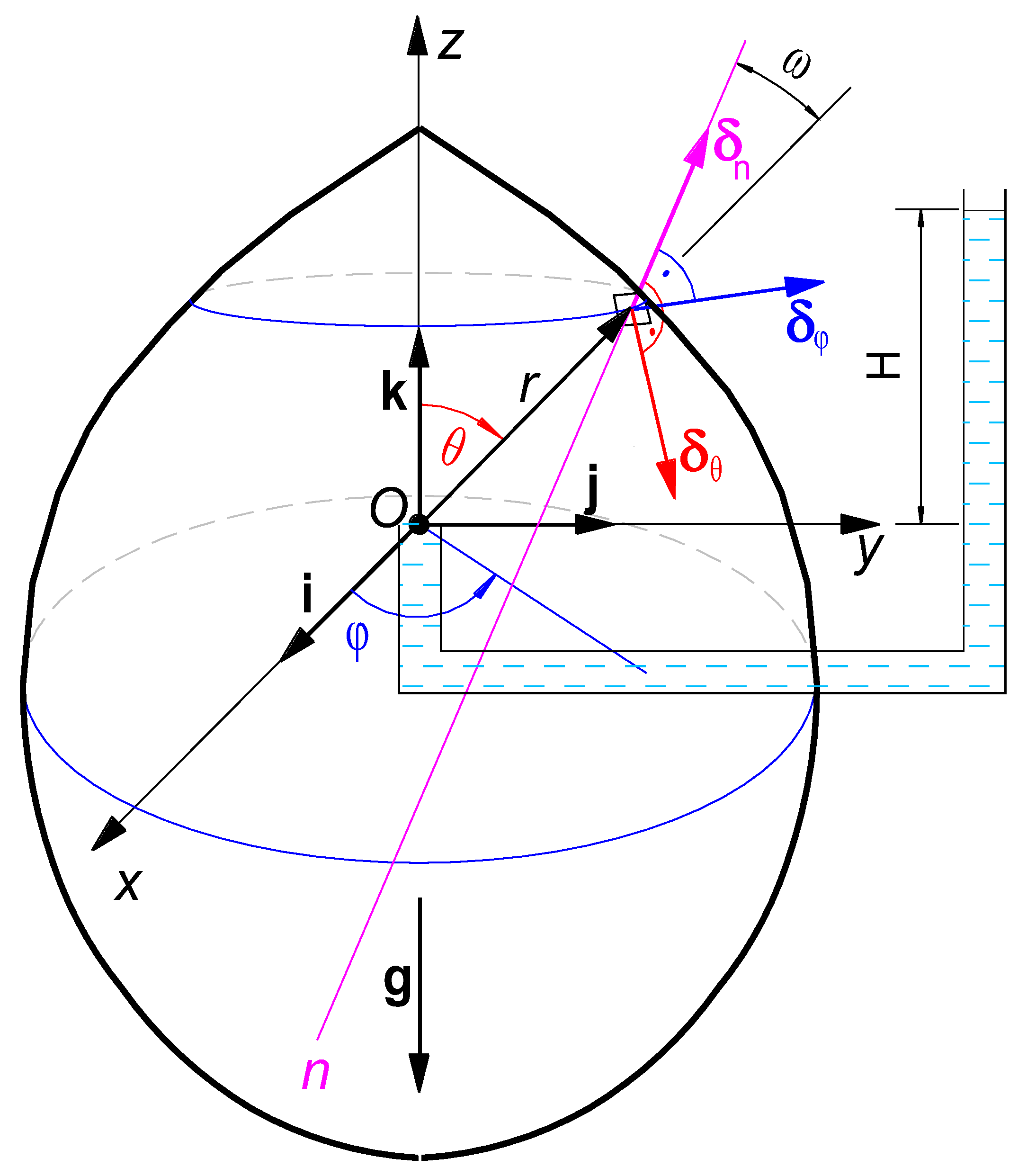
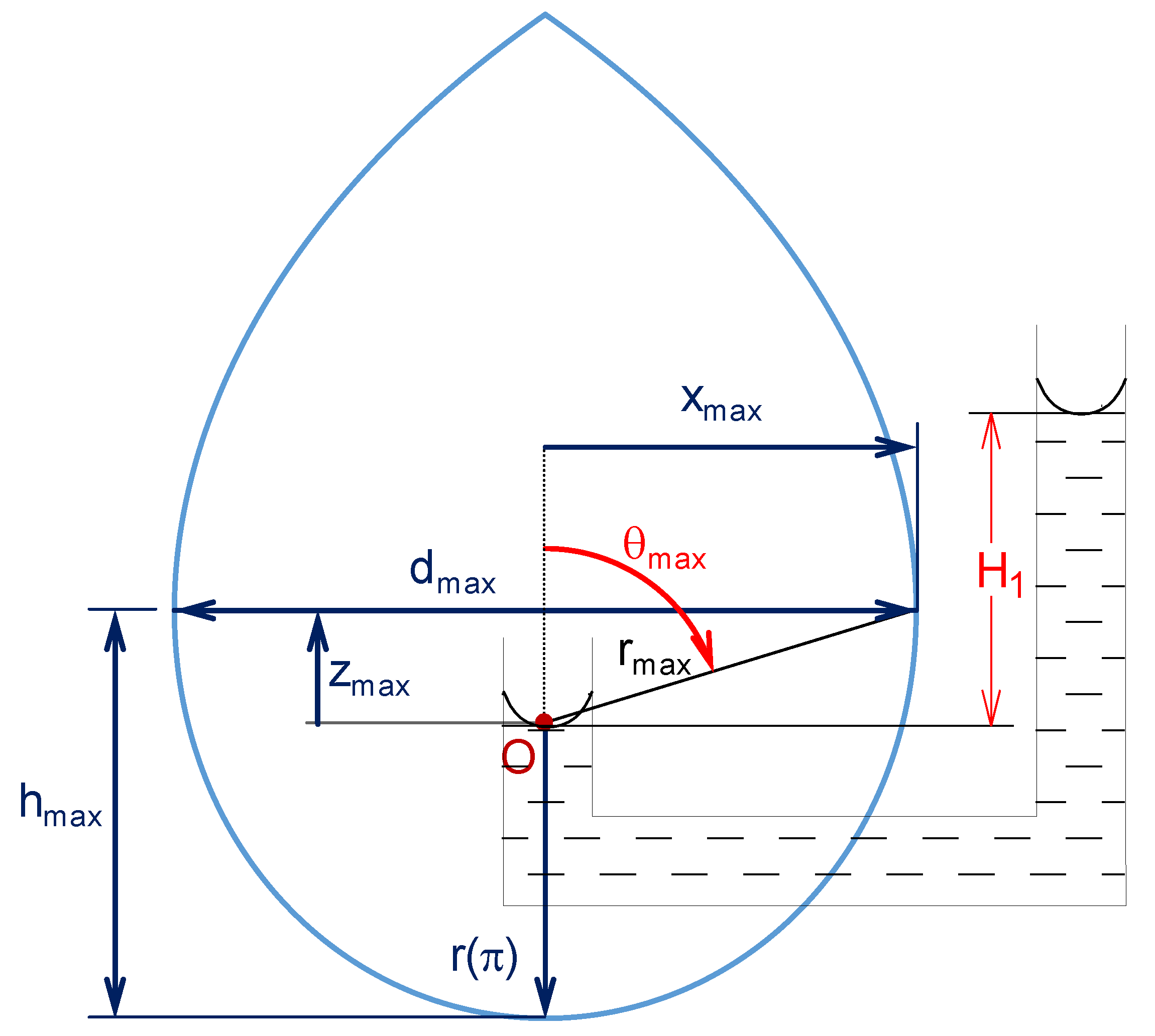
Non-Equilibrium Model for Axisymmetric Drop or Bubble

The limitations of the equilibrium thermodynamics and the Bashforth and Adams method may be overcome by an alternative approach developed by Gajewski (cf. [38,39,40]). For instance, this approach states the drop or bubble has only one main radius of curvature, which might lead to a reduction in the number of unknowns and equations in the Bashforth and Adams method.

This approach is depicted differently than it was done in the works [38,39,40] reviewed hereinafter.

Figure 1 shows both coordinate systems: Cartesian (x, y, z) and surface (θ, φ), created for determining the shape of the interface that is plotted with the thickest line as a drop. This interface encloses a denser liquid and is surrounded by a lighter fluid, which is either a gas (vapor) or a liquid at lower density. The pressure difference between the inner liquid and outer fluid is expressed as hydraulic head (H), which is illustratively shown as a difference in fluid height in a liquid column manometer:

$$H=\frac{p_{dl}-p_{lf}}{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g}=\frac{\Delta p}{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g}\hspace{1em}\left[\mathrm{m}\right],$$

(7)

where

• p_dl—pressure in the interior, which is filled with denser liquid [Pa];
• p_lf—pressure in the exterior, where there is a lighter fluid [Pa],
• Δp—pressure difference between two sides of the interface [Pa],
• ρ_dl—density of a denser liquid [kg/m³];
• ρ_lf—density of a lighter fluid [kg/m³].

Figure 1 also shows the versors i, j, k, and δ_θ, δ_φ in both coordinate systems, respectively. Because the surface is a two-dimensional object embedded in three-dimensional space, a normal vector (δ_n) is also necessary. In general, the radial distance (r) is not the radius of curvature, for it is deviated from the normal to the surface by an angle (ω), shown in Figure 2. In other words, the angle ω is the angle between a sphere at a constant radius (r) and the interface whose radius varies depending on the pressure.

Since hydrostatic pressure depends only on the z coordinate, or polar angle θ in the surface coordinate system, its function in the surface coordinate system is as follows:

$$\Delta p\left(\mathsf{\theta }\right)=\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g\left(H-rcos\mathsf{\theta }\right)\hspace{1em}\left[\mathrm{Pa}\right],$$

(8)

The infinitesimal surface area is the vector product of the meridional arc and the azimuthal one that create this surface. The meridional arc is plotted with the thickest line in Figure 2; if its radius were constant it would be a circle arc that is plotted with a thicker line, and its length (dl_s) would be a projection on a sphere at radius ®

$$d{l}_s=rd\mathsf{\theta }\hspace{1em}\left[\mathrm{m}\right].$$

(9)

Since the infinitesimal surface area is deviated from the sphere by the angle ω, for its radial distance changes along the polar angle, the length of the meridional vector is greater, and given by

$$d{\overrightarrow{l}}_{\mathsf{\theta }}=\frac{rd\mathsf{\theta }}{cos\mathsf{\omega }}{\overrightarrow{\mathsf{\delta }}}_{\mathsf{\theta }}\hspace{1em}\left[\mathrm{m}\right].$$

(10)

The azimuthal vector is equal to

$$d{\overrightarrow{l}}_{\mathsf{\phi }}=rsin\mathsf{\theta }d\mathsf{\phi }{\overrightarrow{\mathsf{\delta }}}_{\mathsf{\phi }}\hspace{1em}\left[\mathrm{m}\right],$$

(11)

for the horizontal cross sections are the circles because of the constant pressure along the azimuthal angle.

Eventually, the vector of the infinitesimal surface area is as follows:

$$d\overrightarrow{A}=\frac{r^{2}sin\mathsf{\theta }d\mathsf{\theta }d\mathsf{\phi }}{cos\mathsf{\omega }}{\overrightarrow{\mathsf{\delta }}}_n\hspace{1em}\left[{\mathrm{m}}^2\right].$$

(12)

Five forces balance on the infinitesimal surface area (dA): the pressure force, which acts on the surface; and four surface tension forces, which act on the four sides of this area (one for each), which is shown in Figure 3. The pressure force $d{\overrightarrow{F}}_p$ is a product of the pressure at the center of the infinitesimal surface area and the vector of this surface area; its sense is opposite to the area vector $d\overrightarrow{A}$, which indicates the minus sign:

$$d{\overrightarrow{F}}_p=-\Delta p\left(\mathsf{\theta }\right)d\overrightarrow{A}\hspace{1em}\left[\mathrm{N}\right].$$

(13)

Eventually, after the substitution of the Formulas (8) and (12) for the pressure and surface area in Equation (13), we have

$$d{\overrightarrow{F}}_p=-\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g\left(H-rcos\mathsf{\theta }\right)\frac{r^{2}sin\mathsf{\theta }d\mathsf{\theta }d\mathsf{\phi }}{cos\mathsf{\omega }}{\overrightarrow{\mathsf{\delta }}}_n\left(\mathsf{\theta },\mathsf{\phi }\right)\hspace{1em}\left[\mathrm{N}\right].$$

(14)

Every surface tension force is the product of the surface tension, the length of the edge arc of the infinitesimal surface area dA, and the unit vector:

$$d{\overrightarrow{F}}_{\mathsf{\theta }}\left(\mathsf{\theta }-\frac{d\mathsf{\theta }}{2},\mathsf{\phi }\right)=-\gamma \left[\left(r-\frac{dr}{2}\right)sin\left(\mathsf{\theta }-\frac{d\mathsf{\theta }}{2}\right)d\mathsf{\phi }\right]{\overrightarrow{\mathsf{\delta }}}_{\mathsf{\theta }}\left(\mathsf{\theta }-\frac{d\mathsf{\theta }}{2},\mathsf{\phi }\right)\hspace{1em}\left[\mathrm{N}\right],$$

(15)

$$d{\overrightarrow{F}}_{\mathsf{\theta }}\left(\mathsf{\theta }+\frac{d\mathsf{\theta }}{2},\mathsf{\phi }\right)=\gamma \left(r+\frac{dr}{2}\right)sin\left(\mathsf{\theta }+\frac{d\mathsf{\theta }}{2}\right)d\mathsf{\phi }{\overrightarrow{\mathsf{\delta }}}_{\mathsf{\theta }}\left(\mathsf{\theta }+\frac{d\mathsf{\theta }}{2},\mathsf{\phi }\right)\hspace{1em}\left[\mathrm{N}\right],$$

(16)

$$d{\overrightarrow{F}}_{\mathsf{\phi }}\left(\mathsf{\theta },\mathsf{\phi }-\frac{d\mathsf{\phi }}{2}\right)=-\gamma \frac{rd\mathsf{\theta }}{cos\mathsf{\omega }}{\overrightarrow{\mathsf{\delta }}}_{\mathsf{\phi }}\left(\mathsf{\phi }-\frac{d\mathsf{\phi }}{2}\right)\hspace{1em}\left[\mathrm{N}\right],$$

(17)

$$d{\overrightarrow{F}}_{\mathsf{\phi }}\left(\mathsf{\theta },\mathsf{\phi }+\frac{d\mathsf{\phi }}{2}\right)=\gamma \frac{rd\mathsf{\theta }}{cos\mathsf{\omega }}{\overrightarrow{\mathsf{\delta }}}_{\mathsf{\phi }}\left(\mathsf{\phi }+\frac{d\mathsf{\phi }}{2}\right)\hspace{1em}\left[\mathrm{N}\right].$$

(18)

Figure 2 indicates a geometrical correspondence

$$tan\mathsf{\omega }=\frac{\frac{dr}{2}}{r\frac{d\mathsf{\theta }}{2}}\hspace{1em}\left[-\right]$$

(19)

which converts the system of the differential equations into the system of the trigonometrical equations, which greatly facilitates the solution. After a certain number of mathematical transformations, we obtain the force balance in the tangential (meridional in the surface coordinate system) direction in a simplified form:

$$1+tan\mathsf{\omega }tan\mathsf{\theta }-{\left(1+{tan}^2\mathsf{\omega }\right)}^{1/2}=0\hspace{1em}\left[-\right],$$

(20)

whereas the simplificative force balance in the normal direction is as follows:

$$tan\mathsf{\omega }-{\left\{\frac{1}{{\left[\frac{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)gr\left(H-rcos\mathsf{\theta }\right)}{\gamma }-1\right]}^2}-1\right\}}^{1/2}=0.$$

(21)

Equation (20) has two roots:

$$tan\mathsf{\omega }=0\hspace{1em}\left[-\right],$$

(22)

and

$$tan\mathsf{\omega }=tan2\mathsf{\theta }\hspace{1em}\left[-\right].$$

(23)

Equation (21) has four roots for each root of Equation (20). The second four roots, which satisfy Equations (23) and (21), have not been connected to any researched object.

Equation (22) leads to the conclusion that the radial distance (r) is simultaneously the main radius of curvature, and this radius is the only one. Equation (21), after substituting Equation (22), is decomposed into three equations:

$$\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g\left(H-rcos\mathsf{\theta }\right)=\frac{2\gamma }{r},$$

(24)

$$\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g\left(H-rcos\mathsf{\theta }\right)=0, \mathrm{and}$$

(25)

$$r=0.$$

(26)

Equation (25) is the horizontal plane, while Equation (26) explicitly states the lack of the surface.

The quadratic Equation (24) draws the shapes of either a drop or bubble. Its first root describes the drop of a denser liquid surrounded by a lighter fluid, and ω equals 0:

$$r_1\left(\mathsf{\theta }\right)=\frac{H_1-{\left[H_1^2-8\frac{\gamma }{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g}cos{\mathsf{\theta }}_1\right]}^{1/2}}{2cos{\mathsf{\theta }}_1}.$$

(27)

Its second root is in the shape of either a drop of lighter liquid or a gaseous bubble placed in a denser liquid, in which case, ω is equal to π:

$$r_2\left(\mathsf{\theta }\right)=\frac{H_2+{\left[H_2^2-8\frac{\gamma }{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g}cos{\mathsf{\theta }}_2\right]}^{1/2}}{2cos{\mathsf{\theta }}_2}.$$

(28)

It should be emphasized that the variables with the subscript 1 in Equation (27) are the positive numbers, whilst the subfix 2 in Equation (28) denotes a negative value. The negative hydraulic head (H₂) means the pressure in the drop or bubble is lower than in the surrounding denser liquid. The negative radius (r₂) is measured from the exterior to the outside part of the surface; the negative polar angle θ₂ is measured counterclockwise; see Figure 4.

Since the numerical values at θ = π/2 in Equations (27) and (28) approach infinity, the following limits are determined:

$$\underset{x\to \frac{\pi }{2}}{lim}{r}_1=\frac{2\gamma }{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g{H}_1},$$

(29)

$$\underset{x\to \frac{\pi }{2}}{lim}{r}_2=\frac{2\gamma }{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g{H}_2},$$

(30)

where the first limit is a positive number, whilst the second limit is less than zero; each limit gives a spare equation which is used for the verification of the results.

The radius (r₁) or (r₂) will be a real number if the radicand in Equations (27) or (28) is not negative; hence, there is a boundary value of hydrostatic pressure that is required for creating a drop or bubble; if at any polar angle the radicand is negative then a closed interface will not come into being, and a pendant drop is observed, for instance. The minimal hydraulic head for a drop creation equals

$$H_{1\hspace{0.33em}min}=\sqrt{8\gamma /\left[\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g\right]}\hspace{1em}\left[\mathrm{m}\right].$$

(31)

While a fully developed bubble occurs when the hydraulic head falls to

$$H_{2\hspace{0.33em}max}=-\sqrt{8\gamma /\left[\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g\right]}\hspace{1em}\left[\mathrm{m}\right]$$

(32)

or a lower value.

The tips that are the pointed ends shown in Figure 5 will occur only when the hydraulic head is equal to one of these boundary values. A tip rounds off at the hydraulic head, either above H_{1 min} or below H_{2 max}; if the hydraulic head is lower than H_{1 min}, then a pendant drop occurs; when the hydraulic head is higher than H_{2 max}, a sessile bubble appears.

Although the separate solutions for the drop and bubble seem to be an advantage of this model, the negative quantities of the hydraulic head, radius of curvature, and polar angle may sound odd. To prove this, Young–Laplace equation for a surface under uniform pressure is applied; this surface possesses only one main radius of curvature (R), for a force acting on an isotropic body creates the same deformation independently of the direction:

$$\Delta p=\frac{2\gamma }{R}.$$

(33)

Equation (33) states that a surface under uniform pressure difference (Δp) and surface tension (γ) is a sphere at radius (R); the longer radius R is, the lower the pressure gauge is inside the sphere.

Figure 5a shows a water drop at a density (ρdl) of 998 kg/m³ surrounded by air (ρ_lf = 1.2 kg/m³); the surface tension γ is 0.0727 N/m and gravitational acceleration g = 9.81 m/s². At the highest point of the drop, where θ = 0, the radius of curvature R₁(0) = 3.86 mm, while at the lowest point, where θ = π, R₂(π) = 1.60 mm. If the pressure inside the drop were homogenous and outside pressure were uniform, the sphere at radius R₁ would enclose water at a gauge pressure Δp₁ = 37.71 Pa (calculated from Equation (8) for H_{1 min} = 3.86 mm) and inside the sphere at radius R₂, Δp₂ would be 91.03 Pa (also calculated in the same way).

For an analysis of Figure 5b with an air bubble in water and the hydraulic head at the origin being H_{2 min}, the material properties and constants are as above. At the highest point θ = −π and R₂(−π) = −1.60 mm, which corresponds to gauge pressure Δp₂ = −91.03 Pa (obtained from Equation (8) for H_{2 max} = −3.86 mm). At the lowest point, the radius of curvature R₁(0) = −3.86 mm and corresponding gauge pressure Δp₁ = −37.71 Pa. Consequently, the pressure at the apex is lower than at the tip. The same values of gauge pressure are obtained from Equation (33).

Figure 6 shows that an interface under hydrostatic pressure may possess an inflection point, for instance, a convex pendant drop dents at the upper part and becomes concave; this shape change occurs without changing the sign of the gauge pressure. This outcome has not been achieved from the models based on the Young–Laplace equation.

The new method for determining the surface or interface tension is based on Equations (27) and (28), which are solved at the widest diameter of the drop or bubble. When the diameter (d_max) lies in the horizontal plane, it is given by

$$d_{max}=2x_{max}=2r_{max}sin{\mathsf{\theta }}_{max}\hspace{1em}\left[m\right],$$

(34)

while the vertical distance between this diameter and the drop bottom or bubble top is obtained as follows:

$$h_{max}=z_{max}+r\left(\pi \right)=r_{max}cos{\mathsf{\theta }}_{max}+r\left(\pi \right)\hspace{1em}\left[m\right],$$

(35)

where the all the variables in Equations (34) and (35) are defined in Figure 7. After substituting the correspondence (27) we have:

$$d_{max}=\left\{H_1-{\left[H_1^2-8\frac{\gamma }{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g}cos{\mathsf{\theta }}_{max}\right]}^{1/2}\right\}\frac{{\left(1-{cos}^2{\mathsf{\theta }}_{max}\right)}^{1/2}}{cos{\mathsf{\theta }}_{max}}\hspace{1em}\left[m\right],$$

(36)

and

$$h_{max}=\frac{1}{2}\left\{-{\left[H_1^2-8\frac{\gamma }{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g}cos{\mathsf{\theta }}_{max}\right]}^{1/2}+{\left[H_1^2+8\frac{\gamma }{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g}\right]}^{1/2}\right\}\hspace{1em}\left[m\right],$$

(37)

where there are three unknowns γ, H₁, and θ_max; the last two are marked in red in Figure 7, while the origin “O”, whose location has also been the unknown before the solution, is marked in dark red. The dimensions d_max and h_max have been measured, while the densities ρ_dl and ρ_lf have been determined in other experiments. Hence, Equations (36) and (37) create an underdetermined system. The third equation which is needed is a necessary condition for extremum diameter:

$$\frac{\partial d}{\partial \mathsf{\theta }}=\frac{\partial 2x}{\partial \mathsf{\theta }}=\frac{2\partial rsin\mathsf{\theta }}{\partial \mathsf{\theta }}=0\hspace{1em}\left[m\right].$$

(38)

This necessary condition is given by

$$0=H_1^2-H_1{\left[H_1^2-8\frac{\gamma }{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g}cos{\mathsf{\theta }}_{max}\right]}^{1/2}-4\frac{\gamma }{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g}cos{\mathsf{\theta }}_{max}\left(1+{cos}^2{\mathsf{\theta }}_{max}\right)\hspace{1em}\left[m^2\right].$$

(39)

The finite equations set (36), (37), and (39) is solved; the solution is given by:

$$cos{\mathsf{\theta }}_{max}=-1-\frac{h_{max}}{2a^2}\left[h_{max}-{\left(H_1^2+8a^2\right)}^{\frac{1}{2}}\right],$$

(40)

$$H_1=d_{max}\frac{cos{\mathsf{\theta }}_{max}}{{\left(1-{cos}^2{\mathsf{\theta }}_{max}\right)}^{\frac{1}{2}}}+\frac{4a^2}{d_{max}}{\left(1-{cos}^2{\mathsf{\theta }}_{max}\right)}^{\frac{3}{2}}\hspace{1em}\left[\mathrm{m}\right],$$

(41)

$$a^2=\frac{d_{max}}{8\left(1-{cos}^2{\mathsf{\theta }}_{max}\right)}\left[2H_1{\left(1-{cos}^2{\mathsf{\theta }}_{max}\right)}^{\frac{1}{2}}-d_{max}cos{\mathsf{\theta }}_{max}\right]\hspace{1em}\left[{\mathrm{m}}^2\right],$$

(42)

where a is the capillary constant:

$$a={\left[\frac{\gamma }{\left({\mathsf{\rho }}_{dl}-{\mathsf{\rho }}_{lf}\right)g}\right]}^{1/2}\hspace{1em}\left[\mathrm{m}\right].$$

(43)

The set (40)–(42) is numerically solved quite easily. Afterwards the surface tension is determined from Equation (43).

The aim of the present investigation is a validation of the solution for the first root, and the accentuation of the spare equation in the verification of the outcomes.

2. Materials and Methods

Mezger [41] derived a surface tension function of temperature for the surface tension between the liquid and vapor phases of a substance:

$$\gamma ={\Delta }_{l-s}{U}_0{N}_A^{2/3}\left[1-{\left(\frac{t}{t_c}\right)}^2\right]\left[\frac{1}{{\left({\mathsf{\nu }}_l^{1/3}-l\right)}^2}-\frac{1}{{\left({\mathsf{\nu }}_v^{1/3}-l\right)}^2}\right]\hspace{1em}\left[J/m^2\right],$$

(44)

where:

• Δ_l-sU₀—internal energy change from the liquid phase to the surface at the reference temperature [J];
• N_A—Avogadro number [-];
• T—temperature [°C];
• t_c—critical temperature [°C];
• ν_l—molar volume of liquid phase [m³];
• ν_v—molar volume of vapor phase [m³];
• l—a correction factor [m].

There are two unknowns, except for the surface tension, in Equation (44): Δ_l-sU₀ and l, which are determined experimentally; these experiments should be conducted at two different temperatures.

The Mezger formula (44) was derived for one substance in two phases; whilst the area of the present research is the interface between two substances in the liquid phase, so the Mezger formula (44) may be transformed to

$$\gamma =b\left[1-{\left(\frac{t}{t_c}\right)}^2\right]\hspace{1em}\left[N/m\right],$$

(45)

and eventually is expressed as follows:

$${\gamma }_{reg}=b-a{t}^2\hspace{1em}\left[\mathrm{N}/\mathrm{m}\right].$$

(46)

After the substitution,

$$x=-t^2$$

(47)

Equation (46) converts to a linear function

$${\gamma }_{reg}=ax+b\hspace{1em}\left[\mathrm{N}/\mathrm{m}\right],$$

(48)

in which the constants (a) and (b) may be determined using a linear regression.

The previous validation [42] was done for the air bubbles flowing up in denser water, so the present experiments are performed for the denser water flowing down in the lighter n-octane. Two variables, d_max and h_max, are measured in the digital photographs and substituted into the equation system (40)–(42), which contains three unknowns, hydraulic head at the origin (H₁), square capillary constant (a²), and the cosine of the polar angle for the longest diameter (cosθ_max). When the capillary constant (a) and the densities (ρ_dl) and (ρ_lf) are determined, Equation (43) yields the interface tension (γ).

Inasmuch as the method described in [38] possesses a spare equation

$$\frac{r\left(\pi \right)}{r\left(\pi /2\right)}+\frac{H_1\left[H_1-{\left(H_1^2+8a^2\right)}^{\frac{1}{2}}\right]}{4a^2}=0$$

(49)

the interface tension determination may be verified quite easily; the radii r(π) and r(π/2) are measured in the stills, while H₁ and a² are the solutions of the equation system (40)–(42). When Equation (49) is satisfied, the interface tension is determined correctly. Otherwise, the measurements of d_max and h_max as well as the computations must be repeated.

Figure 8 shows the system of apparatus applied for determining water–octane (n-octane) interfacial tension. Since a water drop flowing out of the needle (1) and a benchmark of a linear dimension (2) are placed very close in the tank (5) filled with octane, they are captured by the CCD camera (8) and the pictures are displayed on the monitor (9). A temperature equalizer (3) enables equalization of the temperatures of octane and water, which are measured by the thermocouple K (4) connected with the gauge Testo-435-4, not seen in the photograph. The desired temperature is controlled by the heat exchanger (6) connecting to the circulating bath (7). A photographic lamp (10) lights the drops through the dispersion filter (11). The Testo 435-4 gauge with the thermocouple K (4) shows the temperature in the range of −200 to +1370 °C; its confirmed accuracy in the range −60.0 ± 60.0 °C is ±0.3 °C and resolution is 0.1 °C.

3. Results and Discussion

Figure 9 shows the lack of significant discrepancies between the results of Harkins and Brown [43], Zepperi et al. [44], Goebel (after Knovel [45]), and the current experiment, especially at the temperature of ca. 20 °C. The outcomes of Zepperi et al. [44] at a range from 10 °C to 60 °C, arrange linearly; the presented experimental results are not as orderly, but they might be approximated by a linear function up to 90.6 °C. Nevertheless, the numerical approximation of the experimental results

$${\gamma }_{num}=\frac{1}{18.8+0.0325t+1.9\cdot {10}^{-42}{e}^t}\hspace{1em}\left[\mathrm{N}/\mathrm{m}\right]$$

(50)

with Pearson coefficient R² = 0.982, corresponds with the outcomes of Zepperi et al. [44]. At temperatures above 90 °C, the water–octane interface tension sharply decreases.

Equation (46), after determining the coefficients a and b, is as follows:

$${\gamma }_{reg}=0.0528276-1.52819\cdot {10}^{-6}{t}^2\hspace{1em}\left[\mathrm{N}/\mathrm{m}\right].$$

(51)

However, the value of the Pearson coefficient R² = 0.721645 is too low. This regression line gives slightly higher values in the range from 10 °C to 42 °C. In contrast, the values between 58 °C and 96 °C are too low. Eventually, the interface tension drops faster than γ_reg in Equation (51) when the temperature approaches the water boiling point, which is shown in Figure 9.

Table 1. The results of the spare equation (49) for the determined interface tensions.

Lp.	T	g	Equation (49)
-	[°C]	[N/m]	-
1	2.2	0.053198	−0.000049
2	2.7	0.05281	−0.000072
3	4.9	0.052871	0.008169
4	9.8	0.052291	0.000670
5	20	0.051852	0.000246
6	20.5	0.050945	−0.000763
7	20.8	0.051838	0.000149
8	24.9	0.050735	0.000231
9	25	0.050212	0.001298
10	29.7	0.050015	0.000003
11	30.5	0.051458	0.000178
12	40.3	0.049252	0.000088
13	40.9	0.04944	0.000119
14	50	0.048893	0.000040
15	51.4	0.049131	0.000045
16	60	0.049071	0.000015
17	60.4	0.049268	0.000058
18	70.9	0.047458	−0.000134
19	72	0.047163	0.000391
20	80.7	0.047217	0.000053
21	90.6	0.046874	−0.001967
22	96.4	0.042011	−0.000003
23	97.8	0.033906	0.000068
24	98.9	0.027326	0.000383

shows the results of Equation (49) in the last column. This equation is applied for verifying the measured values, d_max and h_max, which were the input data in the equation sets (40)–(42). The greatest discrepancy is at the 3rd row of 0.008169, which seems to be a relatively small quantity.