Computational Fluid Dynamic Simulation of Leakage Acoustic Waves Propagation Model for Gas Pipelines
Abstract
:1. Introduction
2. Theoretical Analysis
2.1. CFD Method in Time-Domain
2.2. The Calculation Method of Propagation Loss
2.3. Establishment of Three-Dimensional (3-D) Time-Domain Pulse Method
3. Simulation Analysis
3.1. Establishment of Simulation Model
3.2. Flow Field Analysis Obtained by CFD Simulation
3.2.1. Acoustic Waves Propagate Downstream
3.2.2. Acoustic Waves Propagate Upstream
3.3. Validation of the Simulation Results with the Experimental Data
3.3.1. Establishing the Experimental Facility
3.3.2. Analyzing of Experimental Data
- (1)
- When acoustic waves propagate downstream, compared with ACs obtained by experiments, the errors of the ones obtained by simulation are smaller than 10%. Additionally, the ACs obtained by experiments are larger than the ones obtained by simulation.
- (2)
- When acoustic waves propagate upstream, compared with ACs obtained by experiments, the errors of the ones obtained by simulation are smaller than 10%. In addition, the ACs obtained by experiments are larger than the ones obtained by simulation.
- (1)
- For amplitude ACs, compared with the non-viscosity and static flow model, the ones of the viscosity and static flow model become larger due to viscosity, while the ones of non-viscosity and flow models become smaller due to gas flow, which shows that the influence of viscosity is much larger than the one of gas flow. Compared with the viscosity and static flow model, the ones of the viscosity and flow models become larger due to gas flow. The former two comparative analyses show that the existence of viscosity makes the opposite influences of gas flow, and the ones obtained when downstream are smaller than the ones obtained when upstream.
- (2)
- For TCs and their factors, with the increase of distance, TCs of the non-viscosity and static flow model become larger of which the law obeys exponential function. The viscosity makes the TCs factor much larger. When gas flow was introduced without viscosity, downstream helped to keep the waveform, while upstream aggravates the waveform change, and the influence of downstream is larger than the one of upstream. Then, viscosity is taken into consideration. It can be found that when downstream, viscosity help to keep the waveform, while when upstream viscosity aggravates the waveform change. In a word, compared with the results of the non-viscosity and static flow model, viscosity makes the smoothing speed of the rising section become larger; gas flow has different changing speeds of the rising section according to different directions. Generally, the rising section becomes smooth though downstream reduces the smoothing trend, while upstream enhances the trend. The Reynolds number can combine the influences of viscosity and gas flow.
3.4. Simulation Analysis under Variable Conditions
3.4.1. Simulation under Different Reynolds Numbers
3.4.2. Simulation under Different Diameters
4. Application of Propagation Model
5. Conclusions
- (1)
- Three-dimensional (3-D) time-domain pulse method is established in this paper through which the propagation characteristics, including flow field and acoustic field, are obtained. The propagation model, including amplitude attenuation coefficients and time coefficients of acoustic waves propagating downstream and upstream, can be obtained by simulation.
- (2)
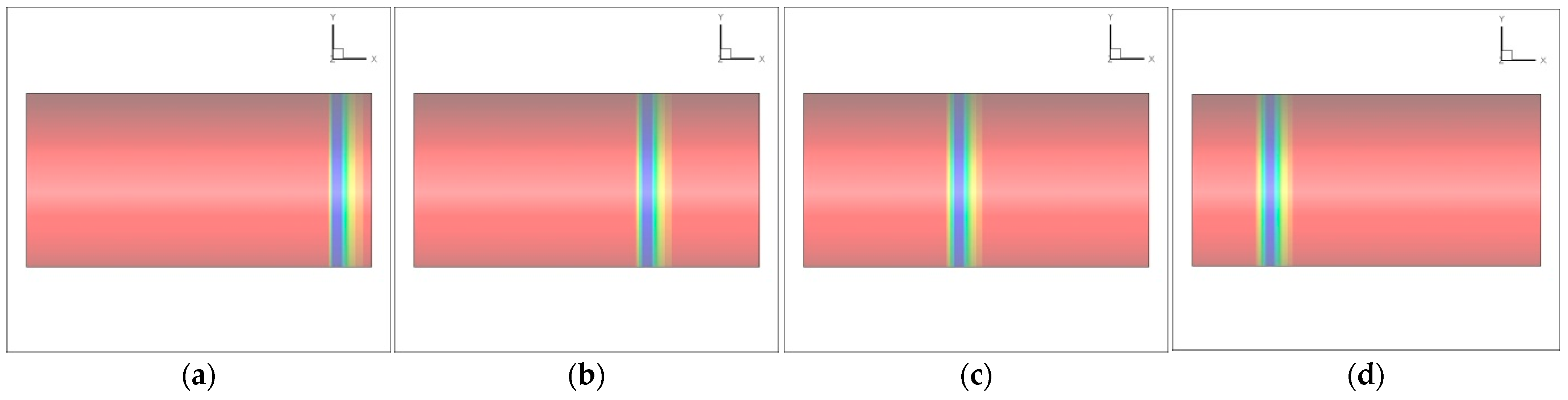
- By simulation, there is a negative pressure zone in the pipe with the input of pressure pulse. The negative pressure zone shows regular pressure layers between which the interfaces are plane. In the propagation process, the negative pressure zone becomes wider, especially the front of the zone.
- (3)
- By simulation, the amplitude attenuation process along the pipeline follows exponential law of which attenuation coefficients can be calculated. The time coefficient changing process with the increase of propagation distance follows exponential law of which the factors can be calculated.
- (4)
- The ACs obtained by simulation are verified by the ones obtained by experiments under five pressure levels, which shows the accuracy of the simulation. Compared with ACs obtained by experiments, the errors of the ones obtained by simulation are smaller than 10%. The ACs obtained by experiments are larger than the ones obtained by simulation.
- (5)
- Propagation characteristics including AC and TC factors of different simulation models can be obtained, which shows the influences of gas viscosity and gas flowing. The propagation characteristics under different Reynolds numbers and diameters are simulated.
- (6)
- The propagation model is applied for leak location by which the method based on amplitude attenuation model is proposed. For leak location, the errors calculated by the simulation ACs are located at 1%, even 0.1% of which the largest one is 8.427%, while the ones calculated by the experimental ACs are located at 1%, even 0.1% of which the largest one is 2.423%. Though there are errors of the method based on the amplitude propagation model, the new method can be effective and promising in the future.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Murvay, P.S.; Silea, I. A survey on gas leak detection and localization techniques. J. Loss Prev. Process Ind. 2012, 25, 966–973. [Google Scholar] [CrossRef]
- Hunaidi, O.; Chu, W.T. Acoustical characteristics of leak signals in plastic water distribution pipes. Appl. Acoust. 1999, 58, 235–254. [Google Scholar] [CrossRef] [Green Version]
- Muggleton, J.M.; Brennan, M.J.; Pinnington, R.J. Wavenumber prediction of waves in buried pipes for water leak detection. J. Sound Vib. 2002, 249, 939–954. [Google Scholar] [CrossRef]
- Prek, M. Analysis of wave propagation in fluid-filled viscoelastic pipes. Mech. Syst. Signal Proc. 2007, 21, 1907–1916. [Google Scholar] [CrossRef]
- Mostafapour, A.; Davoudi, S. Analysis of leakage in high pressure pipe using acoustic emission method. Appl. Acoust. 2013, 74, 335–342. [Google Scholar] [CrossRef]
- Mostafapour, A.; Davoudi, S. A theoretical and experimental study on acoustic signals caused by leakage in buried gas-filled pipe. Appl. Acoust. 2015, 87, 1–8. [Google Scholar] [CrossRef]
- Liu, C.W.; Li, Y.X.; Fu, J.T.; Liu, G.X. Experimental study on acoustic propagation-characteristics-based leak location method for natural gas pipelines. Process Saf. Environ. Prot. 2015, 96, 43–60. [Google Scholar]
- Almeida, F.C.L.; Brennan, M.J.; Joseph, P.F.; Dray, S.; Whitfield, S.; Paschoalini, A.T. Towards an in-situ measurement of wave velocity in buried plastic water distribution pipes for the purposes of leak location. J. Sound Vib. 2015, 359, 40–55. [Google Scholar] [CrossRef]
- Brennan, M.J.; Lima, F.K.; Almeida, F.C.L.; Joseph, P.F.; Paschoalini, A.T. A virtual pipe rig for testing acoustic leak detection correlators: Proof of concept. Appl. Acoust. 2016, 102, 137–145. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Li, S.Z. Acoustic emission (AE) based small leak detection of galvanized steel pipe due to loosening of screw thread connection. Appl. Acoust. 2017, 120, 85–89. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, Y.; Muggleton, J.M. Axisymmetric fluid-dominated wave in fluid-filled plastic pipes: Loading effects of surrounding elastic medium. Appl. Acoust. 2017, 116, 43–49. [Google Scholar] [CrossRef]
- Butterfield, J.D.; Krynkin, A.; Collins, R.P.; Beck, S.B.M. Experimental investigation into vibro-acoustic emission signal processing techniques to quantify leak flow rate in plastic water distribution pipes. Appl. Acoust. 2017, 119, 146–155. [Google Scholar] [CrossRef]
- Gao, Y.; Brennan, M.J.; Liu, Y.; Almeida, F.C.L.; Joseph, P.F. Improving the shape of the cross-correlation function for leak detection in a plastic water distribution pipe using acoustic signals. Appl. Acoust. 2017, 127, 24–33. [Google Scholar] [CrossRef] [Green Version]
- Brennan, M.J.; Karimi, M.; Muggleton, J.M.; Almeida, F.C.L.; Lima, F.K.; Ayala, P.C.; Obata, D.; Paschoalini, A.T.; Kessissoglou, N. On the effects of soil properties on leak noise propagation in plastic water distribution pipes. J. Sound Vib. 2018, 427, 120–133. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.W.; Li, Y.X.; Meng, L.Y.; Wang, W.C.; Zhao, F.S.; Fu, J.T. Computational fluid dynamic simulation of pressure perturbations generation for gas pipelines leakage. Comput. Fluids 2015, 119, 213–223. [Google Scholar] [CrossRef]
- Liu, E.; Li, D.; Zhao, W.; Peng, S.; Chen, Q. Correlation analysis of pipeline corrosion and liquid accumulation in gas gathering station based on computational fluid dynamics. J. Nat. Gas Sci. Eng. 2022, 102, 104564. [Google Scholar] [CrossRef]








| Pressure /kPa | Leakage Orifice/mm | Fitted Signals | Simulated Values | ||||
|---|---|---|---|---|---|---|---|
| Acoustic Amplitude/Pa | Leakage Time/s | TCs/10−4 s | Acoustic Amplitude/Pa | Leakage Time/s | TCs/s | ||
| 1150 | 0.6 | −13,089.05 | 16.767 | 3.871 | −2,042,173.8 | 0.01 | −500 |
| 0.7 | −15,306.29 | 11.402 | 3.649 | −2,388,074.2 | 0.01 | −500 | |
| 0.8 | −14,094.59 | 15.105 | 4.090 | −2,199,132.6 | 0.01 | −500 | |
| Simulation Model | Steady State Calculation Model | Transient State Calculation Model | Inlet Pressure/Pa | Outlet Pressure/Pa |
|---|---|---|---|---|
| Non-viscosity and static flow | No | Inviscid | Equation (5) | 1,150,000 |
| Viscosity and static flow | No | Laminar flow | Equation (5) | 1,150,000 |
| Non-viscosity and flow | Yes | Inviscid | Equation (5) | 1,149,800 |
| Viscosity and flow | Yes | Realizable | Equation (5) | 1,149,800 |
| Propagation Distance/m | Drop Points | Amplitude /Pa | Amplitude Corresponding Point | Difference Value | 1/TC /(1/s) | TC/s | Coefficient of Curve Fitting |
|---|---|---|---|---|---|---|---|
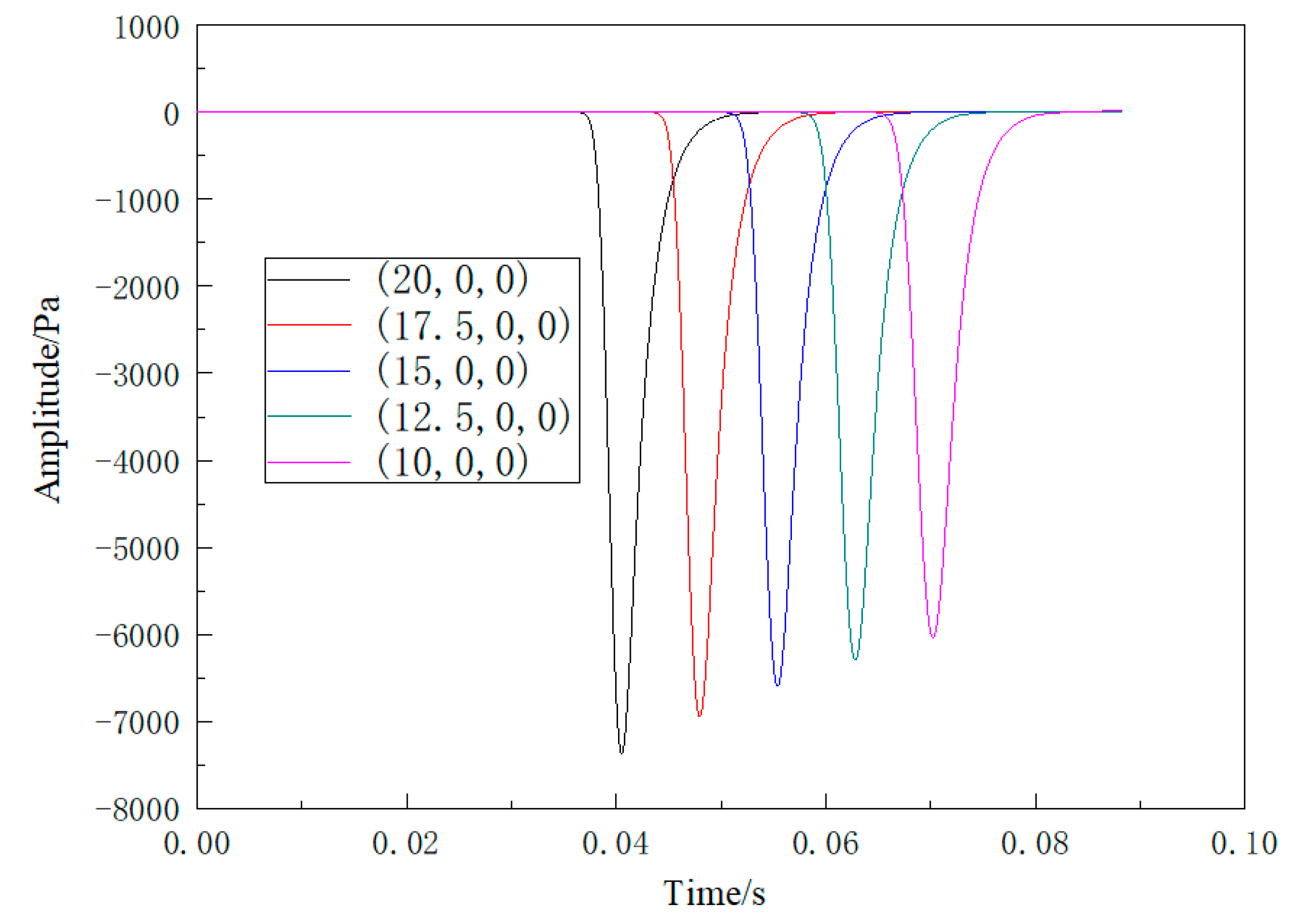
| 10 | 1450 | −7414.63 | 1618 | 168 | 497.82 | 0.002009 | 0.9994 |
| 12.5 | 1732 | −6998.25 | 1915 | 183 | 497.57 | 0.002010 | 0.9991 |
| 15 | 2011 | −6653.75 | 2211 | 200 | 497.20 | 0.002011 | 0.9987 |
| 17.5 | 2299 | −6360.50 | 2507 | 208 | 496.51 | 0.002014 | 0.9983 |
| 20 | 2583 | −6106.13 | 2803 | 220 | 494.05 | 0.002024 | 0.9979 |
| Propagation Distance/m | Drop Points | Amplitude/Pa | Amplitude Corresponding Point | Difference Value | 1/TC/(1/s) | TC/s | Coefficient of Curve Fitting |
|---|---|---|---|---|---|---|---|
| 10 | 1454 | −7369.38 | 1621 | 167 | 517.51 | 0.001932 | 0.9987 |
| 12.5 | 1733 | −6945.38 | 1918 | 185 | 517.71 | 0.001932 | 0.9981 |
| 15 | 2018 | −6594.88 | 2215 | 197 | 518.50 | 0.001929 | 0.9974 |
| 17.5 | 2298 | −6294.50 | 2512 | 214 | 520.12 | 0.001923 | 0.9965 |
| 20 | 2585 | −6031.88 | 2809 | 224 | 522.86 | 0.001913 | 0.9954 |
| Pressure/MPa | Leakage Orifice/mm | Distance/m | Amplitude/kPa | ACs | Average |
|---|---|---|---|---|---|
| 1 | 0.1 | 0.1 | −12.48503 | 0.020119 | 0.020861 |
| 48.3 | −4.63913 | ||||
| 109.1 | −1.54617 | ||||
| 160.49 | −0.47318 | ||||
| 0.45 | 0.1 | −14.27095 | 0.020796 | ||
| 48.3 | −5.35099 | ||||
| 109.1 | −1.77649 | ||||
| 160.49 | −0.47906 | ||||
| 0.9 | 0.1 | −22.47467 | 0.021669 | ||
| 48.3 | −8.76786 | ||||
| 109.1 | −2.89263 | ||||
| 160.49 | −0.64574 |
| Pressure/MPa | Leakage Orifice/mm | Distance/m | Amplitude/kPa | ACs | Average |
|---|---|---|---|---|---|
| 1 | 0.1 | −0.1 | −21.63334 | 0.023398 | 0.023027 |
| 60.7 | −4.25644 | ||||
| 108.9 | −1.53141 | ||||
| 151.11 | −0.61887 | ||||
| 0.45 | −0.1 | −17.74594 | 0.022693 | ||
| 60.7 | −3.72122 | ||||
| 108.9 | −1.54179 | ||||
| 151.11 | −0.53928 | ||||
| 0.9 | −0.1 | −19.03354 | 0.022990 | ||
| 60.7 | −3.87986 | ||||
| 108.9 | −1.54738 | ||||
| 151.11 | −0.55907 |
| Pressure/ kPa | Downstream | Upstream | ||||||
|---|---|---|---|---|---|---|---|---|
| Gas Velocity /m/s | ACs by Simulation | ACs by Experiment | Errors/% | Gas Velocity/m/s | ACs by Simulation | ACs by Experiment | Errors/% | |
| 1150 | 5.465 | 0.019355 | 0.020861 | −7.22 | 5.448 | 0.021958 | 0.023027 | −4.64 |
| 2050 | 3.386 | 0.013107 | 0.014479 | −9.48 | 3.315 | 0.015702 | 0.016260 | −3.43 |
| 3170 | 2.291 | 0.009680 | 0.009791 | −1.13 | 2.238 | 0.011478 | 0.012376 | −7.26 |
| 4060 | 1.295 | 0.006680 | 0.007016 | −4.79 | 1.274 | 0.008656 | 0.009122 | −5.11 |
| 5060 | 1.488 | 0.006532 | 0.006963 | −6.19 | 1.423 | 0.008586 | 0.009500 | −9.62 |
| Simulation Model | Direction | Distance/m | ACs | TCs/s | TCs Factors |
|---|---|---|---|---|---|
| Non-viscosity and static flow | -- | 0 | 0.017872 | 0.002000 | 0.00089 |
| 10 | 0.002012 | ||||
| 12.5 | 0.002018 | ||||
| 15 | 0.002024 | ||||
| 17.5 | 0.002032 | ||||
| 20 | 0.002043 | ||||
| Viscosity and static flow | -- | 0 | 0.019015 | 0.002000 | 0.00222 |
| 10 | 0.002059 | ||||
| 12.5 | 0.002065 | ||||
| 15 | 0.002070 | ||||
| 17.5 | 0.002075 | ||||
| 20 | 0.002081 | ||||
| Non-viscosity and flow | Downstream | 0 | 0.017518 | 0.002000 | 0.00060 |
| 10 | 0.002004 | ||||
| 12.5 | 0.002011 | ||||
| 15 | 0.002017 | ||||
| 17.5 | 0.002022 | ||||
| 20 | 0.002030 | ||||
| Upstream | 0 | 0.017647 | 0.002000 | 0.00097 | |
| 10 | 0.002013 | ||||
| 12.5 | 0.002021 | ||||
| 15 | 0.002028 | ||||
| 17.5 | 0.002035 | ||||
| 20 | 0.002045 | ||||
| Viscosity and flow | Downstream | 0 | 0.019355 | 0.002000 | 0.00046 |
| 10 | 0.002009 | ||||
| 12.5 | 0.002010 | ||||
| 15 | 0.002011 | ||||
| 17.5 | 0.002014 | ||||
| 20 | 0.002024 | ||||
| Upstream | 0 | 0.019958 | 0.002000 | −0.00245 | |
| 10 | 0.001932 | ||||
| 12.5 | 0.001932 | ||||
| 15 | 0.001929 | ||||
| 17.5 | 0.001923 | ||||
| 20 | 0.001913 |
| Gas | Kinematics Viscosity under Normal Condition/10−5 | Velocity/(m/s) | Reynolds Numbers |
|---|---|---|---|
| Air | 1.711 | 5.362 | 3024.224 |
| Nitrogen | 1.663 | 5.452 | 3161.373 |
| Methane | 1.027 | 7.207 | 6738.122 |
| Reynolds Numbers | Direction | AC | TCs Factors |
|---|---|---|---|
| 3024 | Downstream | 0.019355 | 0.00046 |
| Upstream | 0.019958 | −0.00245 | |
| 3161 | Downstream | 0.019204 | 0.00110 |
| Upstream | 0.019871 | −0.00233 | |
| 6738 | Downstream | 0.018082 | 0.00242 |
| Upstream | 0.018984 | −0.00194 |
| Diameter/mm | Direction | ACs |
|---|---|---|
| 20 | Downstream | 0.014787 |
| Upstream | 0.014971 | |
| 10 | Downstream | 0.015905 |
| Upstream | 0.016532 | |
| 8 | Downstream | 0.017072 |
| Upstream | 0.017898 |
| Pressure/ kPa | Leakage Orifice/mm | Number of Sensors | Distance between the Sensor and Sensor 1/m | Sampling Point | Amplitude /kPa | Location by ACs by Simulation | Location by ACs by Experiments | Location by Traditional Method | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Location Point | Location Error | Location Point | Location Error | Location Point | Location Error | ||||||
| 11,765 | −5.341 | ||||||||||
| 3 | 48.20 | 11,621 | −15.771 | 48.790 | 1.639 | 47.582 | −0.867 | 47.998 | −0.005 | ||
| 4 | 109.00 | 11,797 | −4.959 | 49.270 | 1.165 | 50.120 | 1.945 | 47.646 | −0.325 | ||
| 5 | 160.39 | 11,948 | −1.571 | 45.522 | −1.545 | 48.359 | 0.224 | 47.452 | −0.342 | ||
| 0.45 | 2 | 9755 | −5.137 | ||||||||
| 3 | 48.20 | 9615 | −15.098 | 48.677 | 1.405 | 47.474 | −1.091 | 47.827 | −0.360 | ||
| 4 | 109.00 | 9789 | −4.648 | 48.645 | 0.592 | 49.529 | 1.403 | 47.988 | −0.011 | ||
| 5 | 160.39 | 9938 | −1.592 | 46.786 | −0.757 | 49.549 | 0.966 | 47.452 | −0.342 | ||
| 0.9 | 2 | 14,438 | −5.342 | ||||||||
| 3 | 48.20 | 14,297 | −15.494 | 48.357 | 0.740 | 47.173 | −1.716 | 47.998 | −0.005 | ||
| 4 | 109.00 | 14,470 | −4.864 | 48.797 | 0.731 | 49.676 | 1.538 | 47.475 | −0.482 | ||
| 5 | 160.39 | 14,621 | −1.554 | 45.254 | −1.712 | 48.096 | 0.060 | 10.516 | −23.371 | ||
| 2 | 0.1 | 2 | 16,813 | −11.038 | |||||||
| 3 | 48.20 | 16,674 | −23.248 | 47.785 | −0.446 | 46.936 | −2.207 | 47.909 | −0.189 | ||
| 4 | 109.00 | 16,848 | −10.570 | 48.087 | 0.080 | 49.933 | 1.773 | 47.957 | −0.039 | ||
| 5 | 160.39 | 16,999 | −4.309 | 40.321 | −4.788 | 44.946 | −1.904 | 47.297 | −0.438 | ||
| 0.45 | 2 | 16,035 | −13.396 | ||||||||
| 3 | 48.20 | 15,896 | −29.846 | 49.736 | 3.602 | 48.763 | 1.584 | 47.909 | −0.189 | ||
| 4 | 109.00 | 16,070 | −12.106 | 46.076 | −1.765 | 48.048 | 0.044 | 48.129 | 0.119 | ||
| 5 | 160.39 | 16,220 | −5.203 | 40.144 | −4.898 | 44.779 | −2.009 | 47.469 | −0.331 | ||
| 0.9 | 2 | 11,896 | −12.217 | ||||||||
| 3 | 48.20 | 11,754 | −25.864 | 47.964 | −0.076 | 47.104 | −1.859 | 47.909 | −0.189 | ||
| 4 | 109.00 | 11,930 | −11.456 | 47.358 | −0.589 | 49.251 | 1.148 | 47.957 | −0.039 | ||
| 5 | 160.39 | 12,082 | −5.130 | 42.852 | −3.210 | 47.320 | −0.424 | 47.125 | −0.545 | ||
| 3 | 0.1 | 2 | 19,936 | −19.240 | |||||||
| 3 | 48.20 | 19,514 | −33.939 | 48.877 | 1.820 | 46.893 | −2.297 | 47.995 | −0.011 | ||
| 4 | 109.00 | 20,043 | −19.826 | 51.287 | 3.015 | 49.497 | 1.374 | 48.080 | 0.074 | ||
| 5 | 160.39 | 20,503 | −10.925 | 46.632 | −0.853 | 45.311 | −1.677 | 47.058 | −0.587 | ||
| 0.45 | 2 | 29,253 | −16.538 | ||||||||
| 3 | 48.20 | 28,824 | −29.461 | 49.342 | 2.785 | 47.336 | −1.377 | 47.995 | −0.011 | ||
| 4 | 109.00 | 29,357 | −17.093 | 51.429 | 3.146 | 49.632 | 1.497 | 48.080 | 0.074 | ||
| 5 | 160.39 | 29,815 | −9.493 | 47.144 | −0.534 | 45.799 | −1.372 | 47.058 | −0.587 | ||
| 0.9 | 2 | 32,133 | −20.412 | ||||||||
| 3 | 48.20 | 31,704 | −36.424 | 49.422 | 2.951 | 47.415 | −1.214 | 47.995 | −0.011 | ||
| 4 | 109.00 | 32,238 | −20.773 | 50.697 | 2.474 | 48.936 | 0.859 | 48.080 | 0.074 | ||
| 5 | 160.39 | 32,700 | −12.544 | 50.368 | 1.477 | 48.878 | 0.547 | 47.058 | −0.587 | ||
| 4 | 0.1 | 2 | 19,794 | −24.860 | |||||||
| 3 | 48.20 | 19,367 | −38.113 | 48.857 | 1.778 | 47.431 | −1.180 | 47.894 | −0.221 | ||
| 4 | 109.00 | 19,901 | −26.201 | 50.904 | 2.664 | 50.642 | 2.423 | 48.039 | 0.036 | ||
| 5 | 160.39 | 20,362 | −17.439 | 46.743 | −0.784 | 47.759 | −0.150 | 46.682 | −0.821 | ||
| 0.45 | 2 | 22,981 | −26.656 | ||||||||
| 3 | 48.20 | 22,558 | −41.014 | 49.092 | 2.266 | 47.657 | −0.712 | 47.837 | −0.339 | ||
| 4 | 109.00 | 23,088 | −27.444 | 49.377 | 1.264 | 49.195 | 1.096 | 48.039 | 0.036 | ||
| 5 | 160.39 | 23,547 | −17.803 | 43.542 | −2.780 | 44.718 | −2.046 | 46.910 | −0.680 | ||
| 0.9 | 2 | 20,156 | −33.459 | ||||||||
| 3 | 48.20 | 19,736 | −52.363 | 50.199 | 4.563 | 48.708 | 1.469 | 47.951 | −0.103 | ||
| 4 | 109.00 | 20,268 | −34.852 | 50.138 | 1.961 | 49.915 | 1.757 | 48.039 | 0.036 | ||
| 5 | 160.39 | 20,738 | −24.174 | 48.667 | 0.416 | 49.589 | 0.991 | 46.682 | −0.821 | ||
| 5 | 0.1 | 2 | 22,215 | −32.929 | |||||||
| 3 | 48.20 | 21,800 | −51.707 | 50.673 | 5.547 | 47.796 | −0.423 | 47.834 | −0.345 | ||
| 4 | 109.00 | 22,324 | −35.120 | 51.356 | 3.079 | 50.015 | 1.848 | 48.095 | 0.088 | ||
| 5 | 160.39 | 22,780 | −22.986 | 45.522 | −1.545 | 46.003 | −1.245 | 47.102 | −0.560 | ||
| 0.45 | 2 | 20,584 | −36.974 | ||||||||
| 3 | 48.20 | 20,166 | −59.290 | 52.062 | 8.427 | 49.070 | 2.220 | 47.834 | −0.345 | ||
| 4 | 109.00 | 20,693 | −38.394 | 49.588 | 1.457 | 48.390 | 0.358 | 48.095 | 0.088 | ||
| 5 | 160.39 | 21,146 | −25.768 | 45.415 | −1.612 | 45.904 | −1.307 | 47.159 | −0.525 | ||
| 0.9 | 2 | 24,299 | −41.189 | ||||||||
| 3 | 48.20 | 23,883 | −65.228 | 51.234 | 6.710 | 48.310 | 0.643 | 47.891 | −0.226 | ||
| 4 | 109.00 | 24,409 | −43.798 | 51.158 | 2.897 | 49.832 | 1.680 | 48.095 | 0.088 | ||
| 5 | 160.39 | 24,865 | −30.586 | 49.612 | 1.005 | 49.758 | 1.096 | 47.159 | −0.525 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Xue, Y.; Li, Y.; Feng, Q. Computational Fluid Dynamic Simulation of Leakage Acoustic Waves Propagation Model for Gas Pipelines. Energies 2023, 16, 615. https://doi.org/10.3390/en16020615
Li X, Xue Y, Li Y, Feng Q. Computational Fluid Dynamic Simulation of Leakage Acoustic Waves Propagation Model for Gas Pipelines. Energies. 2023; 16(2):615. https://doi.org/10.3390/en16020615
Chicago/Turabian StyleLi, Xuejie, Yuan Xue, Yuxing Li, and Qingshan Feng. 2023. "Computational Fluid Dynamic Simulation of Leakage Acoustic Waves Propagation Model for Gas Pipelines" Energies 16, no. 2: 615. https://doi.org/10.3390/en16020615





