Adaptive Mixed-Integer Linear Programming-Based Energy Management System of Fast Charging Station with Nuclear–Renewable Hybrid Energy System
Abstract
:1. Introduction
2. System Modelling
2.1. Micro Modular Reactor (MMR)
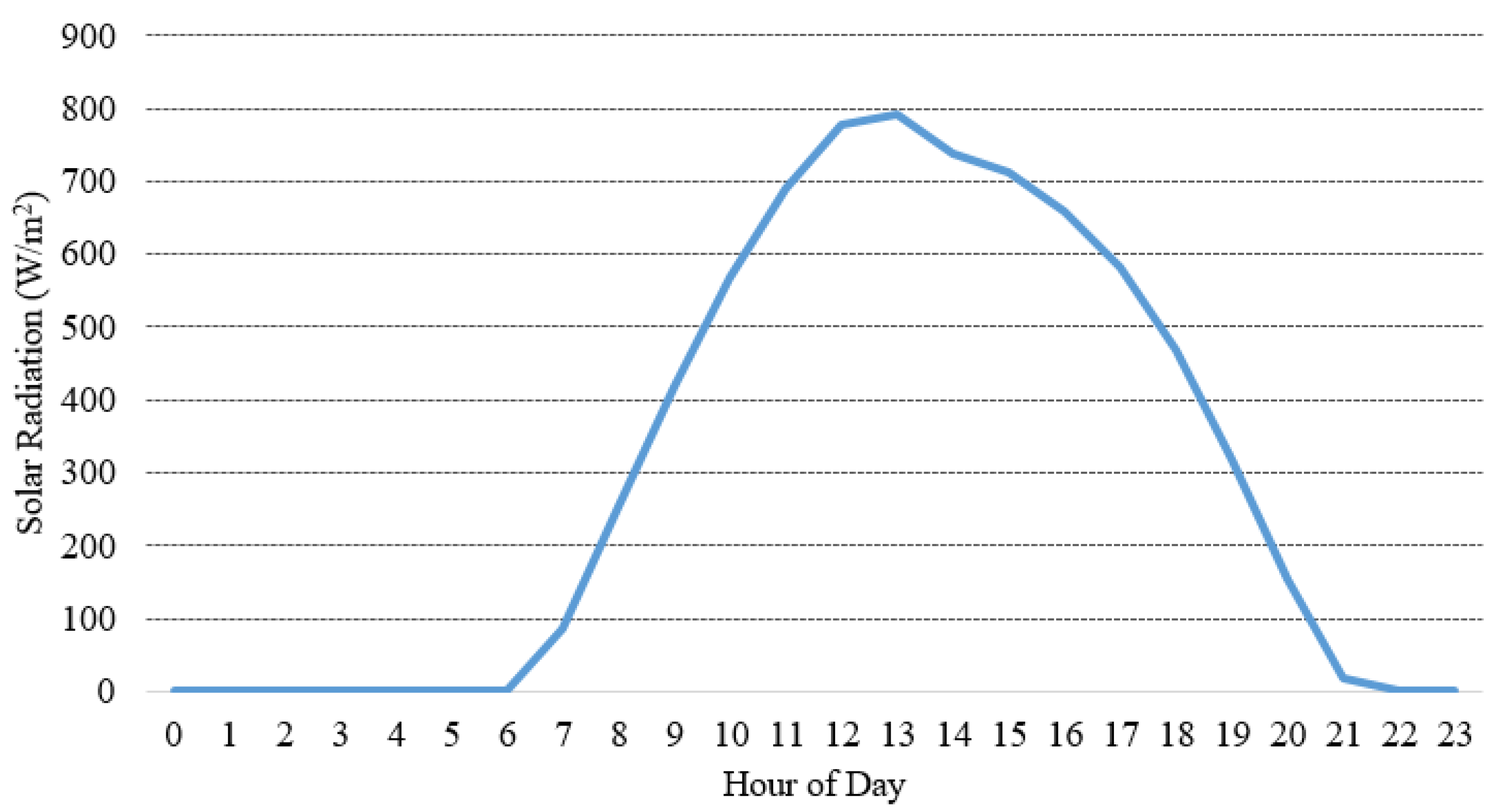
2.2. Solar Energy
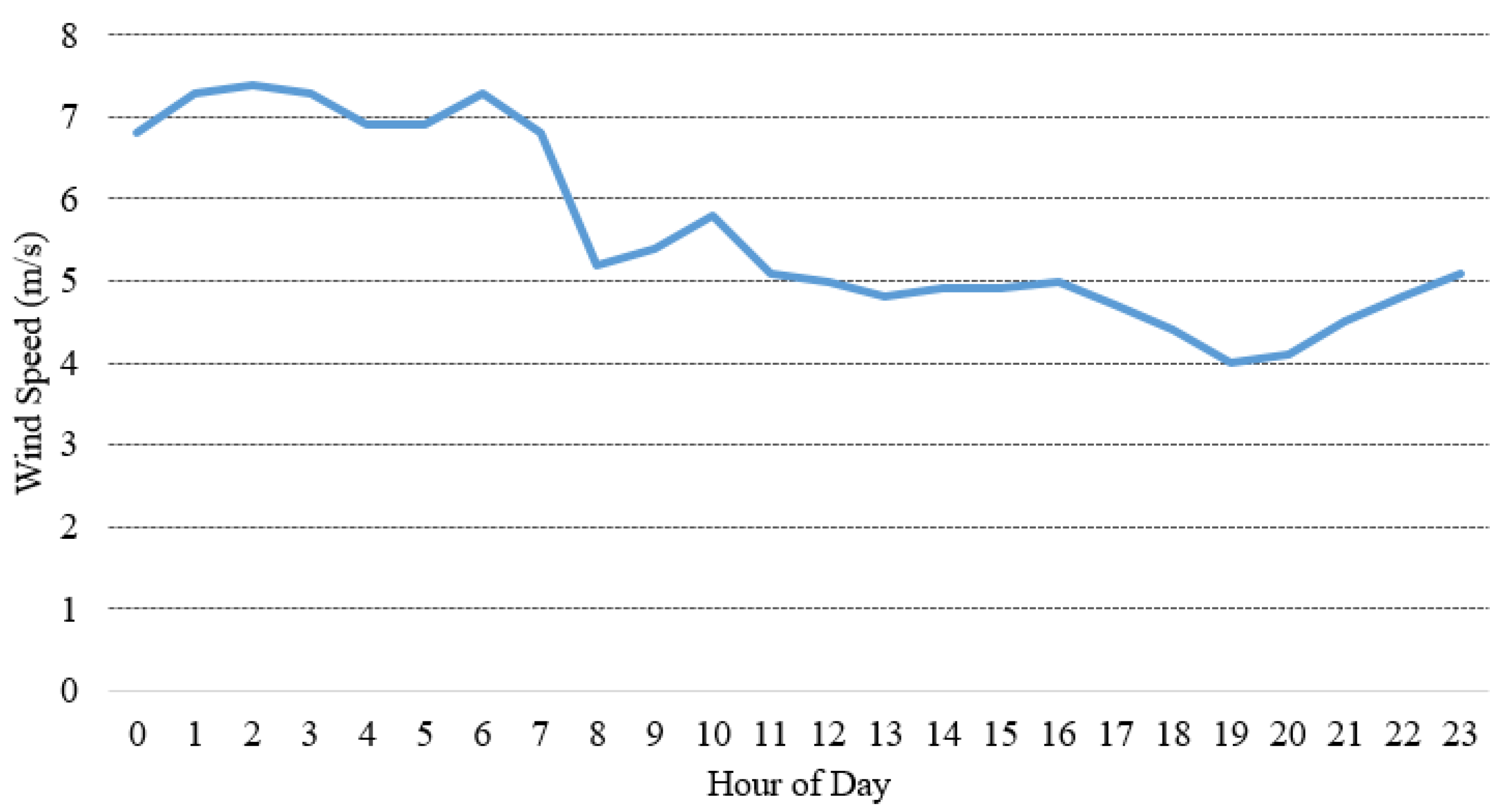
2.3. Wind Energy
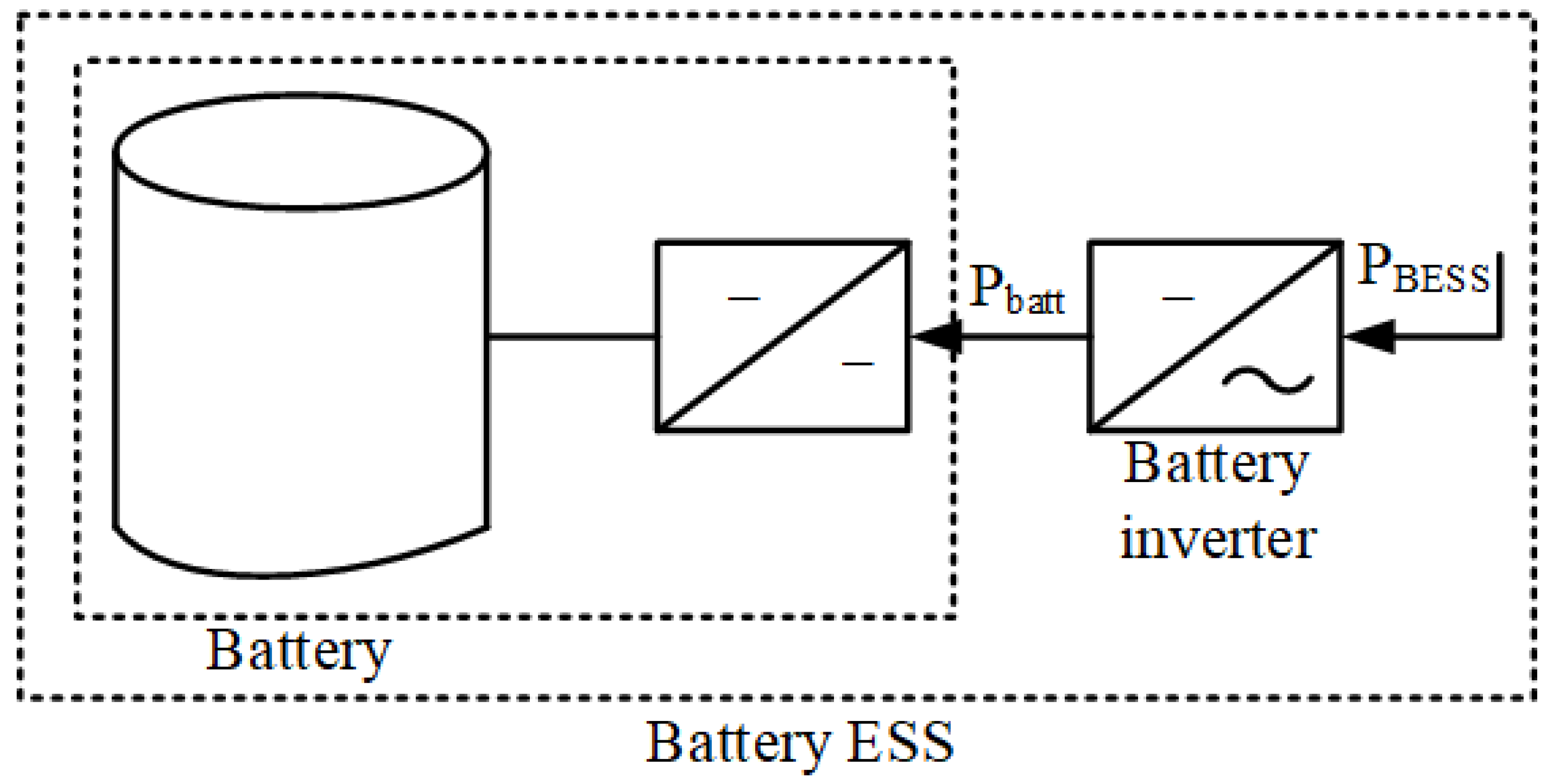
2.4. Battery Storage System
2.5. Fast Charging Station
3. Design of Energy Management System
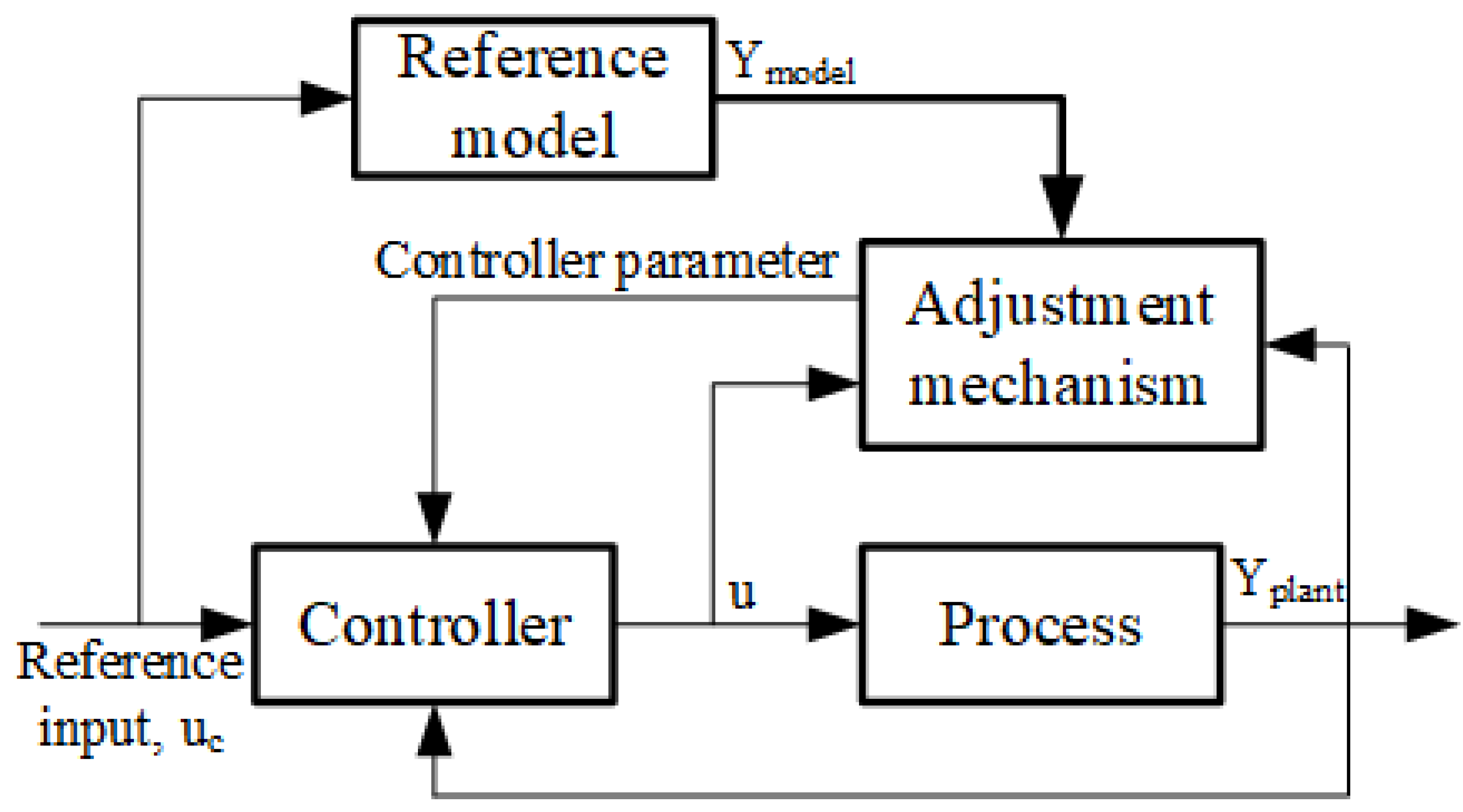
3.1. Control System Design
3.2. Objective Function
3.3. Constraints
3.4. Mrac with Mixed-Integer Linear Programming
3.4.1. Optimization Problem Formulation
- the vector is used to collect the decision variables for ;
- the integer constraints are represented as a vector called , and the integer-valued components of decision vector u are indicated by the values;
- a vector form with linear coefficients is used to define the objective function R (18);
- and denote the lower limit and upper limit of the decision variable (28);
- Matrix , vector , and decision vector u are used to define the inequality constraint (29);
- Matrix , vector , and decision vector u are used to represent the equality constraint (34).
3.4.2. Optimization Problem Solution
3.4.3. Control Set-Points Execution
3.4.4. Shift the Prediction Horizon
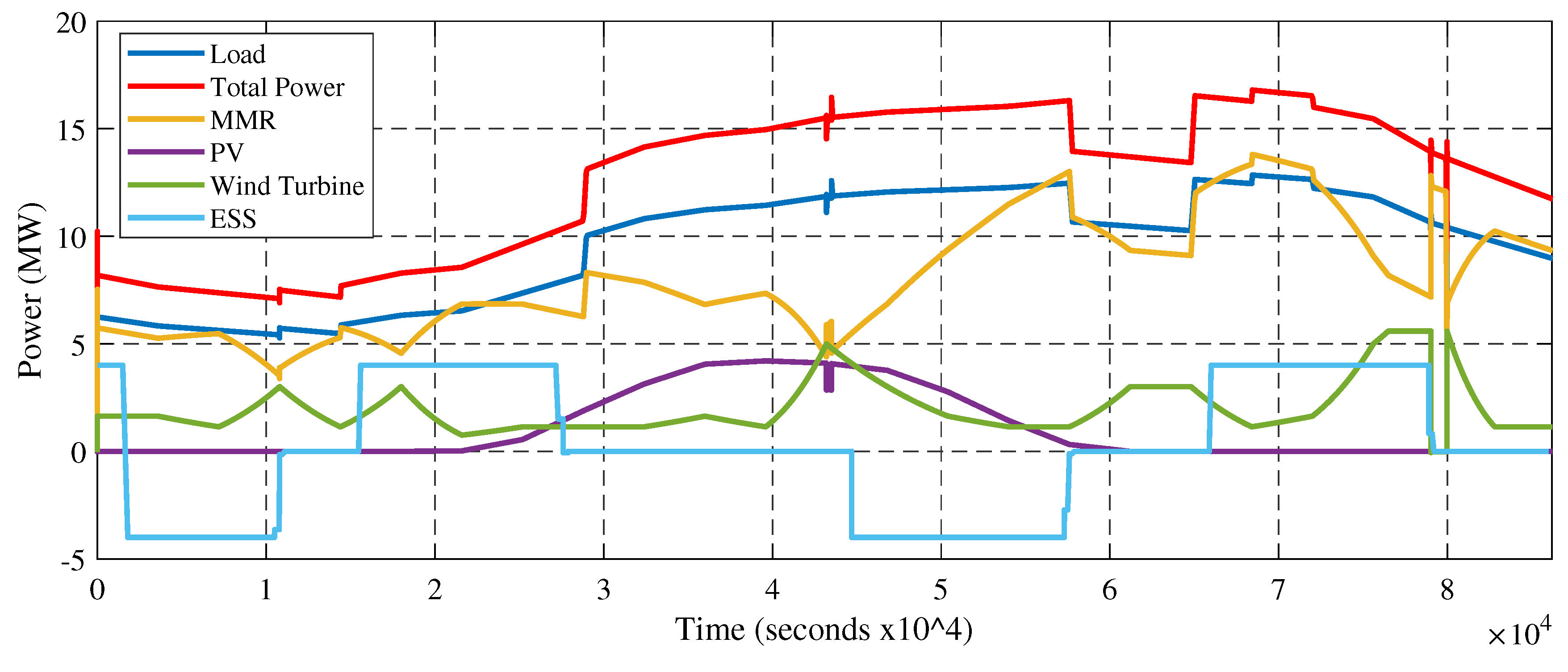
4. Performance Evaluation
- SoC values estimated from the energy storage block;
- The step horizon of forecasting;
- MILP’s sampling rate, or the number of times it calls itself in Simulink;
- Predicted statistics on the cost of electricity produced by a forecasting function for PV, WT, and MMR generation and the demand for electricity;
- the nominal storage capacity;
- efficiency of the power electronics which is updated at each time step.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barone, G.; Buonomano, A.; Calise, F.; Forzano, C.; Palombo, A. Building to vehicle to building concept toward a novel zero energy paradigm: Modelling and case studies. Renew. Sustain. Energy Rev. 2019, 101, 625–648. [Google Scholar] [CrossRef]
- Sujitha, N.; Krithiga, S. RES based EV battery charging system: A review. Renew. Sustain. Energy Rev. 2017, 75, 978–988. [Google Scholar] [CrossRef]
- Hansen, K.; Mathiesen, B.V.; Skov, I.R. Full energy system transition towards 100% renewable energy in Germany in 2050. Renew. Sustain. Energy Rev. 2019, 102, 1–13. [Google Scholar] [CrossRef]
- Rhys-Tyler, G.; Legassick, W.; Bell, M. The significance of vehicle emissions standards for levels of exhaust pollution from light vehicles in an urban area. Atmos. Environ. 2011, 45, 3286–3293. [Google Scholar] [CrossRef]
- Medora, N.K. Electric and Plug-in Hybrid Electric Vehicles and Smart Grids. In The Power Grid; Elsevier: Amsterdam, The Netherlands, 2017; pp. 197–231. [Google Scholar]
- Tan, Z.; Tan, Q.; Rong, M. Analysis on the financing status of PV industry in China and the ways of improvement. Renew. Sustain. Energy Rev. 2018, 93, 409–420. [Google Scholar] [CrossRef]
- Chen, W.; Hong, J.; Yuan, X.; Liu, J. Environmental impact assessment of monocrystalline silicon solar photovoltaic cell production: A case study in China. J. Clean. Prod. 2016, 112, 1025–1032. [Google Scholar] [CrossRef]
- Lee, H.; Lovellette, G. Will Electric Cars Transform the US Vehicle Market. An Analysis of the Key Determinants; Belfer Center for Science and International Affairs: Cambridge, MA, USA, 2011. [Google Scholar]
- Xu, Z.; Hu, Z.; Song, Y.; Luo, Z.; Zhan, K.; Wu, J. Coordinated charging strategy for PEVs charging stations. In Proceedings of the 2012 IEEE Power and eNergy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Cao, Y.; Tang, S.; Li, C.; Zhang, P.; Tan, Y.; Zhang, Z.; Li, J. An optimized EV charging model considering TOU price and SOC curve. IEEE Trans. Smart Grid 2011, 3, 388–393. [Google Scholar] [CrossRef]
- Fazelpour, F.; Vafaeipour, M.; Rahbari, O.; Rosen, M.A. Intelligent optimization to integrate a plug-in hybrid electric vehicle smart parking lot with renewable energy resources and enhance grid characteristics. Energy Convers. Manag. 2014, 77, 250–261. [Google Scholar] [CrossRef]
- Vermaak, H.J.; Kusakana, K. Design of a photovoltaic–wind charging station for small electric Tuk–tuk in DR Congo. Renew. Energy 2014, 67, 40–45. [Google Scholar] [CrossRef]
- Hafez, O.; Bhattacharya, K. Optimal design of electric vehicle charging stations considering various energy resources. Renew. Energy 2017, 107, 576–589. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel wind powered electric vehicle charging station with vehicle-to-grid (V2G) connection capability. Energy Convers. Manag. 2017, 136, 229–239. [Google Scholar] [CrossRef]
- Tushar, M.H.K.; Assi, C.; Maier, M.; Uddin, M.F. Smart microgrids: Optimal joint scheduling for electric vehicles and home appliances. IEEE Trans. Smart Grid 2014, 5, 239–250. [Google Scholar] [CrossRef]
- Hutson, C.; Venayagamoorthy, G.K.; Corzine, K.A. Intelligent scheduling of hybrid and electric vehicle storage capacity in a parking lot for profit maximization in grid power transactions. In Proceedings of the 2008 IEEE Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008; pp. 1–8. [Google Scholar]
- Acha, S.; Green, T.C.; Shah, N. Effects of optimised plug-in hybrid vehicle charging strategies on electric distribution network losses. In Proceedings of the IEEE PES T&D 2010, New Orleans, LA, USA, 19–22 April 2010; pp. 1–6. [Google Scholar]
- Vaya, M.G.; Andersson, G. Centralized and decentralized approaches to smart charging of plug-in vehicles. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Torreglosa, J.P.; García-Trivi no, P.; Fernández-Ramirez, L.M.; Jurado, F. Decentralized energy management strategy based on predictive controllers for a medium voltage direct current photovoltaic electric vehicle charging station. Energy Convers. Manag. 2016, 108, 1–13. [Google Scholar] [CrossRef]
- García-Trivi no, P.; Torreglosa, J.P.; Fernández-Ramírez, L.M.; Jurado, F. Control and operation of power sources in a medium-voltage direct-current microgrid for an electric vehicle fast charging station with a photovoltaic and a battery energy storage system. Energy 2016, 115, 38–48. [Google Scholar] [CrossRef]
- González-Rivera, E.; Sarrias-Mena, R.; García-Trivi no, P.; Fernández-Ramírez, L.M. Predictive energy management for a wind turbine with hybrid energy storage system. Int. J. Energy Res. 2020, 44, 2316–2331. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Y.; Hill, D.J. Optimal scheduling for EV charging stations in distribution networks: A convexified model. IEEE Trans. Power Syst. 2016, 32, 1574–1575. [Google Scholar] [CrossRef]
- Zheng, H.; Wu, J.; Wu, W.; Wang, Y. Integrated motion and powertrain predictive control of intelligent fuel cell/battery hybrid vehicles. IEEE Trans. Ind. Informatics 2019, 16, 3397–3406. [Google Scholar] [CrossRef]
- Hu, J.; Shan, Y.; Guerrero, J.M.; Ioinovici, A.; Chan, K.W.; Rodriguez, J. Model predictive control of microgrids–An overview. Renew. Sustain. Energy Rev. 2021, 136, 110422. [Google Scholar] [CrossRef]
- Rodriguez, J.; Heydari, R.; Rafiee, Z.; Young, H.A.; Flores-Bahamonde, F.; Shahparasti, M. Model-free predictive current control of a voltage source inverter. IEEE Access 2020, 8, 211104–211114. [Google Scholar] [CrossRef]
- Chen, T.; Abdel-Rahim, O.; Peng, F.; Wang, H. An Improved Finite Control Set-MPC-Based Power Sharing Control Strategy for Islanded AC Microgrids. IEEE Access 2020, 8, 52676–52686. [Google Scholar] [CrossRef]
- Jayachandran, M.; Ravi, G. Predictive power management strategy for PV/battery hybrid unit based islanded AC microgrid. Int. J. Electr. Power Energy Syst. 2019, 110, 487–496. [Google Scholar] [CrossRef]
- Abdeltawab, H.H.; Mohamed, Y.A.R.I. Market-oriented energy management of a hybrid wind-battery energy storage system via model predictive control with constraint optimizer. IEEE Trans. Ind. Electron. 2015, 62, 6658–6670. [Google Scholar] [CrossRef]
- e Silva, D.P.; Salles, J.L.F.; Fardin, J.F.; Pereira, M.M.R. Management of an island and grid-connected microgrid using hybrid economic model predictive control with weather data. Appl. Energy 2020, 278, 115581. [Google Scholar] [CrossRef]
- Nair, U.R.; Costa-Castelló, R. A model predictive control-based energy management scheme for hybrid storage system in islanded microgrids. IEEE Access 2020, 8, 97809–97822. [Google Scholar] [CrossRef]
- Žilinskas, A. Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms; INFORMS: Houston, TX, USA, 2006. [Google Scholar]
- Zhao, Y.; Lu, Y.; Yan, C.; Wang, S. MPC-based optimal scheduling of grid-connected low energy buildings with thermal energy storages. Energy Build. 2015, 86, 415–426. [Google Scholar] [CrossRef]
- Parisio, A.; Rikos, E.; Glielmo, L. A model predictive control approach to microgrid operation optimization. IEEE Trans. Control. Syst. Technol. 2014, 22, 1813–1827. [Google Scholar] [CrossRef]
- Jiang, Q.; Xue, M.; Geng, G. Energy management of microgrid in grid-connected and stand-alone modes. IEEE Trans. Power Syst. 2013, 28, 3380–3389. [Google Scholar] [CrossRef]
- De Angelis, F.; Boaro, M.; Fuselli, D.; Squartini, S.; Piazza, F.; Wei, Q. Optimal home energy management under dynamic electrical and thermal constraints. IEEE Trans. Ind. Informatics 2012, 9, 1518–1527. [Google Scholar] [CrossRef]
- Bordons, C.; Garcia-Torres, F.; Ridao, M.A. Model Predictive Control of Microgrids; Springer: Berlin/Heidelberg, Germany, 2020; Volume 358. [Google Scholar]
- Oettingen, M. Modelling of the reactor cycle cost for thorium-fuelled PWR and environmental aspects of a nuclear fuel cycle. Geol. Geophys. Environ. 2019, 45, 207. [Google Scholar] [CrossRef]
- Ruth, M.F.; Zinaman, O.R.; Antkowiak, M.; Boardman, R.D.; Cherry, R.S.; Bazilian, M.D. Nuclear–renewable hybrid energy systems: Opportunities, interconnections, and needs. Energy Convers. Manag. 2014, 78, 684–694. [Google Scholar] [CrossRef]
- Bragg-Sitton, S.M.; Boardman, R.; Rabiti, C.; Suk Kim, J.; McKellar, M.; Sabharwall, P.; Chen, J.; Cetiner, M.S.; Harrison, T.J.; Qualls, A.L. Nuclear–Renewable Hybrid Energy Systems: 2016 Technology Development Program Plan; Technical report; Idaho National Lab.(INL): Idaho Falls, ID, USA, 2016. [Google Scholar]
- Ruth, M.; Cutler, D.; Flores-Espino, F.; Stark, G. The Economic Potential of Nuclear–Renewable Hybrid Energy Systems Producing Hydrogen; Technical report; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2017. [Google Scholar]
- Ruth, M.; Cutler, D.; Flores-Espino, F.; Stark, G.; Jenkin, T.; Simpkins, T.; Macknick, J. The Economic Potential of Two Nuclear–Renewable Hybrid Energy Systems; Technical report; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2016. [Google Scholar]
- Subki, H. Advances in Small Modular Reactor Technology Developments; International Atomic Energy Agency (IAEA): Vienna, Austria, 2020. [Google Scholar]
- USNC. Available online: https://usnc.com/ (accessed on 9 March 2022).
- Small Nuclear Power Reactors—World Nuclear Association. Available online: https://www.world-nuclear.org/information-library/nuclear-fuel-cycle/nuclear-power-reactors/small-nuclear-power-reactors.aspx (accessed on 9 March 2022).
- Kaur, D.; Cheema, P. Software tools for analyzing the hybrid renewable energy sources: A review. In Proceedings of the 2017 International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 19–20 January 2017; pp. 1–4. [Google Scholar]
- Edson, N.; Willson, P.; Rakshi, B.; Kekwick, I. Market and technical assessment of micro nuclear reactors. Nuvia Ltd. 2016. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/787411/Market_and_Technical_Assessment_of_Micro_Nuclear_Reactors.pdf (accessed on 29 December 2022).
- Nichol, M.; Desai, H. Cost Competitiveness of Micro-Reactors for Remote Markets; Nuclear Energy Institute (NEI): Washington, DC, USA, 2019. [Google Scholar]
- Solar Panel Size Guide: How Big is a Solar Panel. Available online: https://unboundsolar.com/blog/solar-panel-size-guide (accessed on 28 April 2022).
- Meteoblue: Weather Oshawa Airport. Available online: https://www.meteoblue.com/en/weather/week/oshawa-airport_canada_7668135 (accessed on 2 May 2022).
- Lu, L.; Yang, H.; Burnett, J. Investigation on wind power potential on Hong Kong islands—an analysis of wind power and wind turbine characteristics. Renew. Energy 2002, 27, 1–12. [Google Scholar] [CrossRef]
- Toliyat, H.A.; Lipo, T.A. Transient analysis of cage induction machines under stator, rotor bar and end ring faults. IEEE Trans. Energy Convers. 1995, 10, 241–247. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Lu, L.; Zhou, W. A novel optimization sizing model for hybrid solar-wind power generation system. Sol. Energy 2007, 81, 76–84. [Google Scholar] [CrossRef]
- Yang, H.; Lu, L.; Burnett, J. Weather data and probability analysis of hybrid photovoltaic–wind power generation systems in Hong Kong. Renew. Energy 2003, 28, 1813–1824. [Google Scholar] [CrossRef]
- Mulder, G.; Six, D.; Claessens, B.; Broes, T.; Omar, N.; Van Mierlo, J. The dimensioning of PV-battery systems depending on the incentive and selling price conditions. Appl. Energy 2013, 111, 1126–1135. [Google Scholar] [CrossRef]
- Alternative Fuels Data Center (AFDC). Available online: https://afdc.energy.gov/evi-pro-lite/load-profile (accessed on 21 March 2022).
- Azuatalam, D.; Paridari, K.; Ma, Y.; Förstl, M.; Chapman, A.C.; Verbič, G. Energy management of small-scale PV-battery systems: A systematic review considering practical implementation, computational requirements, quality of input data and battery degradation. Renew. Sustain. Energy Rev. 2019, 112, 555–570. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| Capacity (kW) | 1000 |
| Initial cost (USD) | 11,250,000 |
| Replacement cost (USD) | 2,300,000 |
| O&M cost (USD/lifetime) | 1,510,000 |
| Fuel type | Uranium |
| Fuel price (USD/Kg) | 1390 |
| Efficiency (%) | 40 |
| Lifetime (years) | 60 |
| Heat recovery ration (%) | 40 |
| Parameter | Value |
|---|---|
| Area occupied by unit PV panel () | 5 |
| Capacity (kW) | 1 |
| Initial cost (USD) | 640 |
| Replacement cost (USD) | 640 |
| O&M cost (USD/year) | 0 |
| Lifetime (years) | 30 |
| Efficiency of the MPPT unit (%) | 95 |
| Nominal operating cell temperature () | 40 |
| PV panel reference temperature () | 25 |
| Parameter | Value |
|---|---|
| Capacity (kW) | 10 |
| Initial cost (USD) | 13,000 |
| Replacement cost (USD) | 13,000 |
| O&M cost (USD/year) | 400 |
| Lifetime (years) | 20 |
| Hub Height (m) | 55 |
| Rotor size (m) | 33 |
| Minimum wind speed (m/s) | 4 |
| Rated wind speed (m/s) | 8 |
| Maximum wind speed (m/s) | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddique, A.B.; Gabbar, H.A. Adaptive Mixed-Integer Linear Programming-Based Energy Management System of Fast Charging Station with Nuclear–Renewable Hybrid Energy System. Energies 2023, 16, 685. https://doi.org/10.3390/en16020685
Siddique AB, Gabbar HA. Adaptive Mixed-Integer Linear Programming-Based Energy Management System of Fast Charging Station with Nuclear–Renewable Hybrid Energy System. Energies. 2023; 16(2):685. https://doi.org/10.3390/en16020685
Chicago/Turabian StyleSiddique, Abu Bakar, and Hossam A. Gabbar. 2023. "Adaptive Mixed-Integer Linear Programming-Based Energy Management System of Fast Charging Station with Nuclear–Renewable Hybrid Energy System" Energies 16, no. 2: 685. https://doi.org/10.3390/en16020685
APA StyleSiddique, A. B., & Gabbar, H. A. (2023). Adaptive Mixed-Integer Linear Programming-Based Energy Management System of Fast Charging Station with Nuclear–Renewable Hybrid Energy System. Energies, 16(2), 685. https://doi.org/10.3390/en16020685







