Next Article in Journal
How Does the Digital Economy Affect Carbon Emission Efficiency? Evidence from Energy Consumption and Industrial Value Chain
Previous Article in Journal
A New Method of Fault Localization for 500 kV Transmission Lines Based on FRFT-SVD and Curve Fitting
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 16
Issue 2
10.3390/en16020760
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Implementation of Artificial Intelligence in Modeling and Control of Heat Pipes: A Review

by
Abdul Ghani Olabi
1,2,*,
Salah Haridy
1,3,
Enas Taha Sayed
4,
Muaz Al Radi
5,
Abdul Hai Alami
1,
Firas Zwayyed
1,
Tareq Salameh
1 and
Mohammad Ali Abdelkareem
1,4,*
1
Sustainable Energy & Power Systems Research Centre, RISE, University of Sharjah, Sharjah P.O. Box 27272, United Arab Emirates
2
Mechanical Engineering and Design, School of Engineering and Applied Science, Aston University, Aston Triangle, Birmingham B4 7ET, UK
3
Benha Faculty of Engineering, Benha University, Benha 13511, Egypt
4
Chemical Engineering Department, Faculty of Engineering, Minia University, Minya 61519, Egypt
5
Department of Electrical Engineering and Computer Science, Khalifa University, Abu Dhabi P.O. Box 127788, United Arab Emirates
*
Authors to whom correspondence should be addressed.
Energies 2023, 16(2), 760; https://doi.org/10.3390/en16020760
Submission received: 25 November 2022 / Revised: 31 December 2022 / Accepted: 3 January 2023 / Published: 9 January 2023
Browse Figures
Versions Notes

Abstract

:
Heat pipe systems have attracted increasing attention recently for application in various heat transfer-involving systems and processes. One of the obstacles in implementing heat pipes in many applications is their difficult-to-model operation due to the many parameters that affect their performance. A promising alternative to classical modeling that emerges to perform accurate modeling of heat pipe systems is artificial intelligence (AI)-based modeling. This research reviews the applications of AI techniques for the modeling and control of heat pipe systems. This work discusses the AI-based modeling of heat pipes focusing on the influence of chosen input parameters and the utilized prediction models in heat pipe applications. The article also highlights various important aspects related to the application of AI models for modeling heat pipe systems, such as the optimal AI model structure, the models overfitting under small datasets conditions, and the use of dimensionless numbers as inputs to the AI models. Also, the application of hybrid AI algorithms (such as metaheuristic optimization algorithms with artificial neural networks) was reviewed and discussed. Next, intelligent control methods for heat pipe systems are investigated and discussed. Finally, future research directions are included for further improving this technology. It was concluded that AI algorithms and models could predict the performance of heat pipe systems accurately and improve their performance substantially.

1. Introduction

Heat pipes are among the most efficient passive heat transfer technologies capable of transporting large quantities of heat over long distances by latent heat (phase-change process) [1,2]. Figure 1 shows a schematic diagram of a conventional heat pipe. A heat pipe consists of a sealed container/evacuated tube and a wick structure. It is partially filled with working fluid at liquid/vapor equilibrium and does not incorporate moving parts [3]. The heat pipe is basically divided into three sections: (1) an evaporator section where the heat is absorbed from the source, and the working fluid evaporates; (2) a condenser section where the heat is dissipated into the surrounding environment (sink) and the working fluid returns to its liquid state; and (3) an adiabatic section [4].
The advantages of heat pipes include lightweight, minimal maintenance requirements, high reliability, extensive working life, low cost, and high performance [5,6]. Heat pipes come in various shapes and sizes, each with different properties. Thus, they can be implemented in a wide range of applications [7,8,9,10,11,12]. For example, Ando et al. developed a flat-plate heat pipe with good heat transfer performance for spacecraft applications [13]. Krishna et al. explored the application of heat pipes with nano-enhanced phase change material (PCM) for electronic cooling [14]. Putra et al. [15] investigated developing a passive battery cooling system for electric vehicles using heat pipes. Additionally, Zhang et al. designed a heat pipe radiator for nuclear application [16]. Different types of heat pipes are loop heat pipe (LHP) [17], pulsating/oscillating heat pipe (PHP/OHP) [18], variable conductance heat pipe (VCHP) [19], thermosyphon [20], sorption heat pipe (SHP) [21], annular heat pipe [22], and rotating heat pipe (RHP) [23].
Predicting the thermal performance of a heat pipe is difficult, as it is influenced by several parameters, which can be classified into three categories: (1) operational parameters such as heat input and filling ratio; (2) property parameters such as surface tension and thermal conductivity; (3) geometrical parameters such as lengths of evaporator and condenser sections, and shape of cross-section [24]. As several parameters affect the operation and performance of heat pipe systems and their effects overlap, the modeling of heat pipes is of very high complexity. A promising alternative to classical modeling that can overcome these issues is artificial intelligence (AI)-based modeling. The development of artificial intelligence (AI) technologies has been of great benefit to scientific research [25,26,27]. AI algorithms mainly point to an artificial neural network (ANN), fuzzy logic (FL), genetic algorithm (GA), particle swarm optimization (PSO), etc. Such algorithms have been widely used to develop reliable and accurate prediction models for different systems in different fields [28,29,30,31]. AI models can be used to model various operational aspects of heat pipe systems while implicitly taking the internal complexities of the model into consideration.
Recently, Ahmadi et al. summarized the applications of machine learning methods in modeling various types of heat pipes [32]. However, at the time of publication of that work, the progress on utilizing machine learning models for modeling of heat pipe systems was significantly limited compared to the current progress, as several works on this topic have been published in the last years [33,34,35,36,37,38,39,40], and thus a recent review that covers the current state-of-the-art is required. Furthermore, the previous work by Ahmadi et al. [32] did not discuss various aspects of the implementation of AI models for modeling of heat pipe systems, including the optimal AI model structure, the models overfitting under small datasets conditions, the use of dimensionless numbers as inputs to the AI models, and the AI-based control of heat pipe systems. This work covers this research gap by providing a recent review of the current progress while discussing several important aspects related to the successful implementation of AI models in heat pipe systems to provide a practical guideline for future research on this topic. Moreover, this work provides critical future research directions for improving the current technologies. This work reviews AI methods in modeling and controlling systems in heat pipe applications. Section 2 provides an overview of different fundamental AI methods. Next, Section 3 investigates and discusses the use of AI technology in predicting and controlling heat pipe systems. Finally, the conclusions and future research directions are introduced in Section 4.

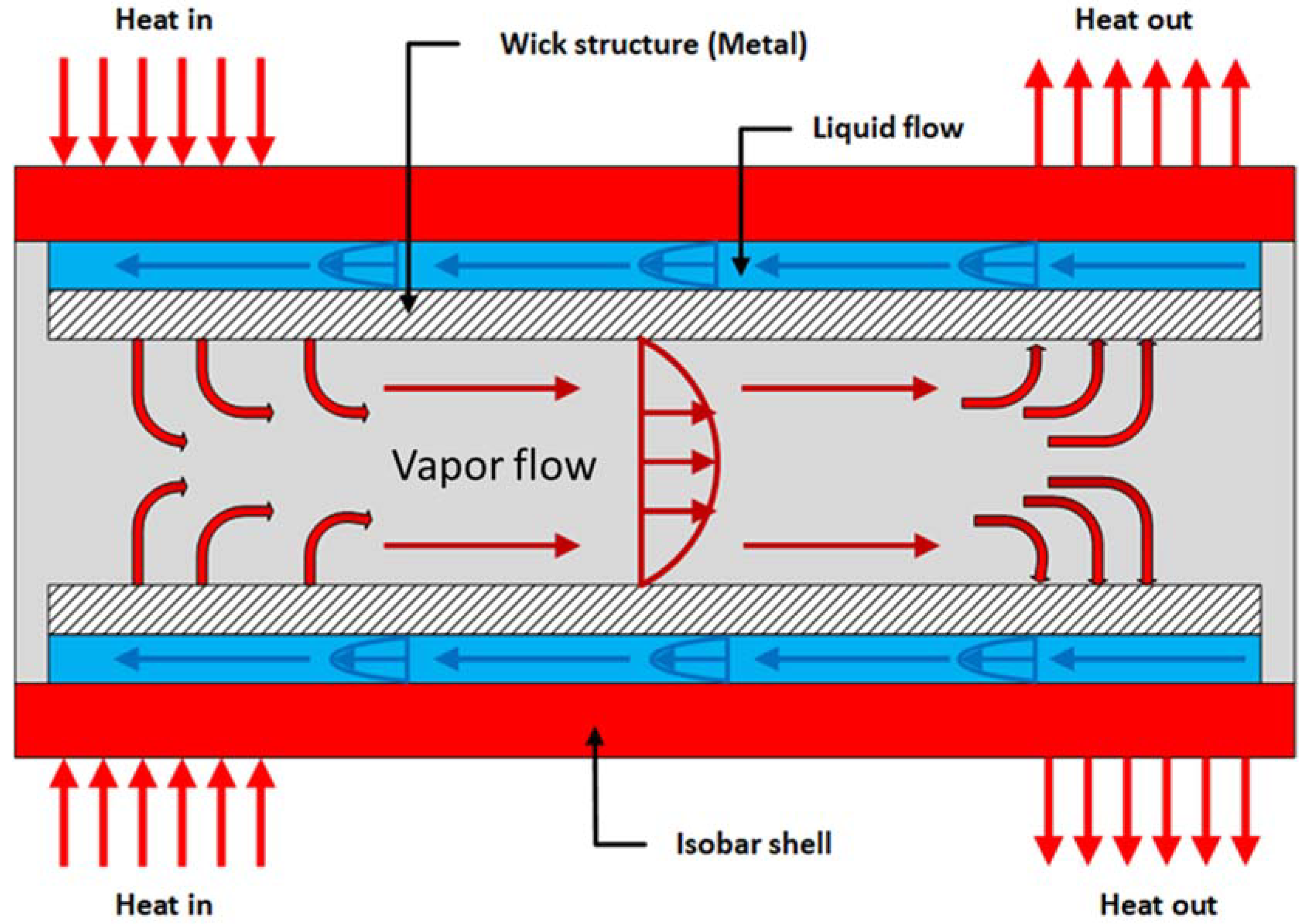
2. Background

Several AI techniques have previously been applied in the literature for the modeling and optimization of heat pipe systems. These techniques include artificial neural networks, fuzzy logic, adaptive neuro-fuzzy inference system (ANFIS), and metaheuristic optimization algorithms. In this section, a brief background on the applied AI techniques is included. Artificial neural networks (ANN) were the first AI algorithms used for modeling heat pipe systems. An ANN is a computational model capable of simulating the brain’s behavior and performing various computational tasks by predicting a number of outputs using a number of inputs [41]. There are various types of neural networks based on different training algorithms, such as the multilayer perceptron neural network (MLPNN), radial basis function (RBF) neural network, convolutional neural network (CNN), etc. ANNs are employed in forecasting, control, modeling, and pattern classification applications [42].
Another type of AI algorithm that was applied in the modeling of heat pipe systems is fuzzy logic, which uses fuzzy if–then statements to perform the model prediction and decision-making. Fuzzy logic can be applied in different applications such as temperature control, aircraft control, robotics, and many other control applications [43]. A hybrid AI model that combines the principles of ANNs and fuzzy logic and was applied for modeling of heat pipe systems is the adaptive neuro-fuzzy inference system (ANFIS). ANFIS can model a large class of complex nonlinear systems to an anticipated grade of precision. ANFIS has previously been applied in the literature for forecasting, modeling, and control tasks [44]. Finally, metaheuristic optimization algorithms have been used in the literature to model heat pipe systems, mostly via hybridization with other types of AI models. Such algorithms include genetic algorithms (GA) [36], particle swarm optimization (PSO) [45], and the grey wolf optimizer (GWO) [46]. In summary, Table 1 compares the AI algorithms applied to model heat pipe systems.

3. Current Progress and Discussion

Several works in the literature have discussed the application of various AI techniques for the modeling and optimization of heat pipe systems. AI techniques have been used to predict heat pipe systems’ performance and operational parameters and optimize the design and operational variables for maximizing the system’s performance and response. In this section, the current progress on the application of AI techniques in heat pipe systems is reviewed and discussed.

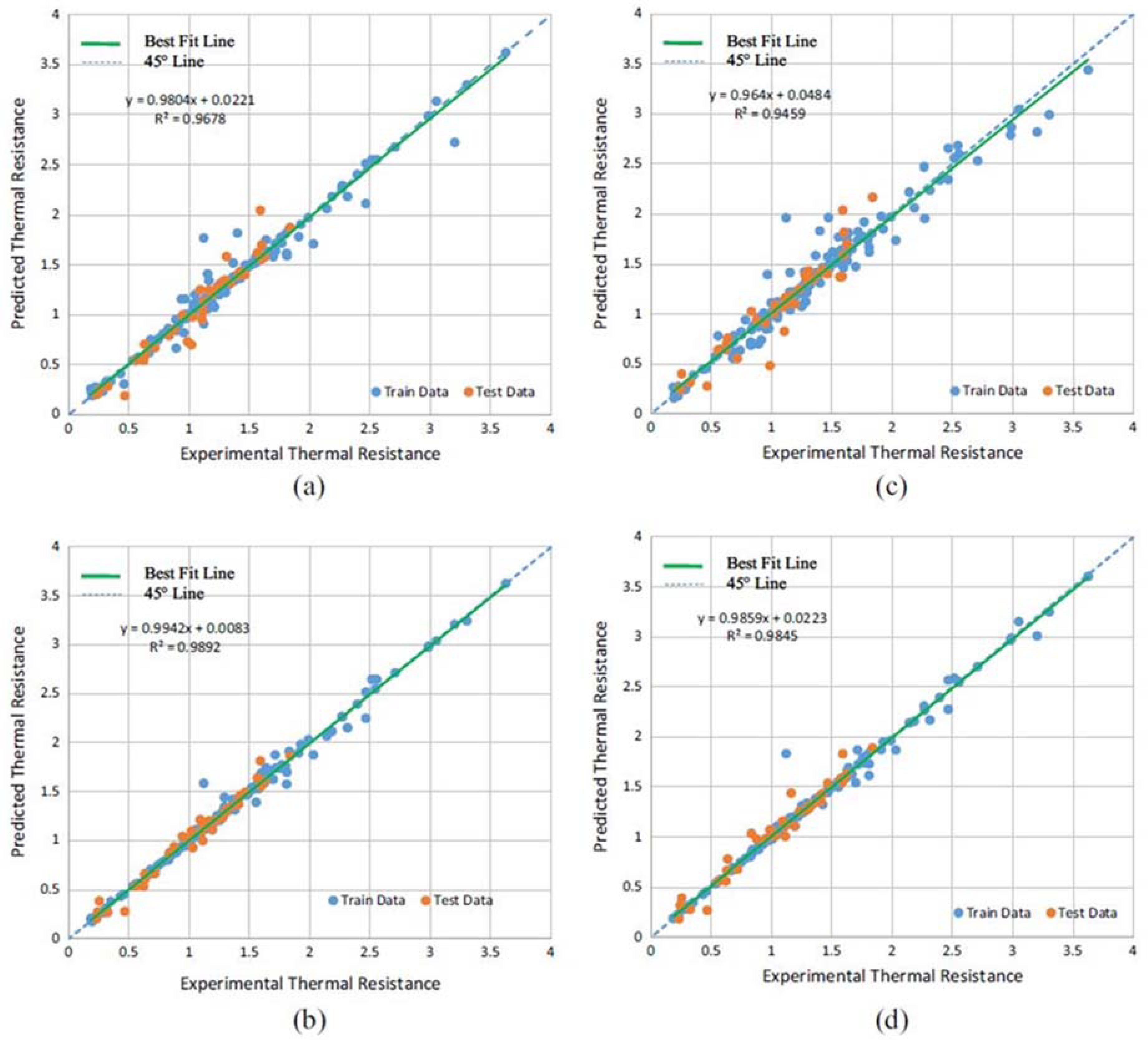
3.1. Optimal ANN Structure for Heat Pipe Modeling

The performance and accuracy of an artificial neural network are influenced by its structure (number of hidden layers and neurons) and training algorithm. Artificial neural network (ANN) modeling was conducted by Patel and Mehta [52] to predict the thermal performance of a closed loop pulsating heat pipe (CLPHP). Eighteen different ANN models (radial basis, generalized regression, linear layer, cascade forward back propagation, feed-forward backpropagation; feed-forward distributed time delay, layer recurrent and Elman backpropagation) involving different activation functions (linear (PURELIN), logistic sigmoid (LOGSIG), tangent sigmoid (TANSIG), and radial basis Gaussian function) were tested. It was found that a generalized regression neural network with radial basis Gaussian function had the lowest mean absolute relative deviation among all ANN models and predicted the thermal performance of CLPHP in the error range of ±1.81% compared to the experimental data. Furthermore, thermal performance prediction models for a pulsating heat pipe (PHP) using an artificial neural network (ANN) were discussed by Patel and Mehta [53]. A feed-forward backpropagation neural network was adopted. Eleven ANN models with different numbers of neurons were constructed based on 1652 experimentally obtained data. The most accurate model was that with 14 neurons (R = 0.9447).
Another study by Salehi et al. [54] designed an optimized neural network using a genetic algorithm to predict the heat transfer characteristics of a silver/water nanofluid two-phase closed thermosyphon that is thermally enhanced by a magnetic field. The genetic algorithm was applied to optimize the number of neurons in the hidden layer, the coefficient of the learning rate, and momentum. The optimal model was achieved with two hidden layers with nine and six neurons structure. The results showed excellent accuracy compared to the experimental results. A 96-neuron artificial neural network (ANN) model was constructed by Chavda [39] to investigate the thermal performance of a two-layer screen mesh-type cylindrical heat pipe using silver nanofluid. The built ANN models were divided into three categories in which the heat pipe’s performance was predicted based on: (1) one output parameter (thermal resistance); (2) two output parameters (thermal resistance and thermal conductivity); and (3) three output parameters (thermal resistance, thermal conductivity, and overall heat transfer coefficient). A single-layer feed-forward backpropagation network with six hidden layer neurons predicted the values with the lowest prediction error for one output parameter (normalized mean square error NMSE = 0.000041). For two output parameters, a cascade feed-forward backpropagation network with 11 hidden layer neurons predicted the thermal performance of the heat pipe with minimum errors (NMSE = 0.00000019), and a forward backpropagation network with 12 hidden layer neurons predicted the values with least error of prediction for three outputs (NMSE = 0.000001). Lee and Chang [55] presented the application of a nonlinear autoregressive algorithm with an exogenous (NARX) neural network to study the thermal dynamics of a pulsating heat pipe in both time and frequency domains. There was good agreement between the predicted and experimentally measured results, which demonstrates the effectiveness of the model/method in analyzing PHP dynamics.
In summary, optimizing the structure of the used AI model is highly important, as it directly affects the model’s prediction accuracy and processing time. The current works mainly relied on trial-and-error for finding the optimal structure of the AI model with best prediction capability.

3.2. Overfitting of Trained Prediction Models without Validation Sets

Some heat pipe modeling studies have constructed successful prediction models without including a dataset for validation (only training and testing), and few studies have excluded the testing dataset (only training and validation), meaning there are no specific criteria for establishing accurate prediction models. Implementing an AI-based heat pipe model that was only evaluated on specific scenarios without validating its generalizability for other scenarios could be of highly negative effect as the model could perform very poorly and thus worsen the system’s performance. For example, Kahani and Vatankhah [37] investigated the effect of Al2O3 as a working fluid on the thermal performance of wickless heat pipe (WHP) by developing an optimized artificial neural network (multilayer perceptron MLP) using 52 experimentally obtained datasets (75% for training and 25% for testing). The effect of different parameters on heat pipe solar collector (HPSC) was analyzed by Sivaraman and Mohan [56] using an artificial neural network (ANN). The study implemented a multilayer feed-forward ANN architecture consisting of two layers with six inputs and one output. A 168 data were used for training the network, and 66 data for testing without validation. The simulated and experimental results were found to be very close, with a mean square error of 0.9234. However, such small dataset with no validation set could result in an overfitted model, in which the model only memorizes the received data and does not generalize well for general cases.
Meanwhile, Khandekar et al. [57] adopted a fully connected feed-forward multilayer ANN configuration using a backpropagation momentum learning algorithm to model pulsating heat pipe thermal performance. Two models were analyzed, the first model was trained with 52 datasets (out of 72 datasets) within the typical operation range, i.e., data of fill ratios between 20–85%. The second model was trained with the whole dataset (72 sets). Both models showed satisfying results, but the model trained with the typical PHP operation range dataset provided better results than the model trained with the whole dataset. This demonstrates that the output of an ANN model might get negatively affected by those training datasets which represent different phenomenological regimes of the system, as the ANN model is a typical black box, unaware of the physical phenomena guiding the system dynamics.
In summary, training AI models with a small dataset results in the model only performing well on the training set and achieving lower performance on the testing set. Moreover, using a validation set helps in verifying the robustness and accuracy of the models in cases different from the training case.

3.3. Prediction Models’ Input and Output Parameters

Artificial intelligence technologies (mostly artificial neural networks) have proven reliable and efficient for predicting the thermal performance of different heat pipes. The input parameters of artificial neural networks are mainly the parameters that have a significant influence on the heat pipe operation, such as heat flux/input, filling ratio, number of turns and lengths of evaporator and condenser; while the thermal resistance is considered as one of the most common output parameters of the network usually used to measure the performance and efficiency of the heat pipe system.
Jia-qiang et al. [58] used a function chain neural network to predict the heat transfer performance of a looped copper–water oscillating heat pipe based on grey relational analysis (GRA). GRA was used to determine the main influencing factors based on experimentally obtained data. It was found that the charging ratio, inclination angle, and heat input are the main influencing factors (relational grade more than 0.5). Thus, two function chain neural networks with three inputs (charging ratio, inclination angle, and heat input) and four inputs (charging ratio, inclination angle, heat input, and number of turns) were built. The relative error and fitting degree of both neural networks were almost the same (4% error for the three-input model and 5% error for four-input model) when tested several times in different conditions. Still, the four-input neural network was more complicated than the three-input neural network. Thus, the results suggest that only input variables of a relational grade of more than 0.5 should be considered when constructing a function chain neural network to save computing time and guarantee an acceptable fitting precision.
To predict the thermal resistance of pulsating heat pipes filled with ethanol, Ahmadi et al. [59] proposed four models, including multilayer perceptron (MLP), radial bias function combined with genetic algorithm (GA-RBF), least square support vector machine (LSSVM), and a conjugated hybrid of particle swarm optimization and adaptive neuro-fuzzy inference system (CHPSO ANFIS). The filling ratio, the thermal conductivity of the tube, inclination angle, lengths of adiabatic, condenser and evaporator sections, heat input, and inner and outer diameters were used as input parameters. A genetic algorithm (GA) was applied to the RBF model to obtain the optimum number of parameters. PSO was applied to the ANFIS model to train the FIS and optimize the tuning process. The results showed that the GA-RBF model was the most accurate in predicting the PHP’s thermal resistance with a determination coefficient (R2) of 0.9892, as shown in Figure 2. The same input parameters were used by Ahmadi et al. [35] to estimate the thermal resistance and thermal conductivity of pulsating heat pipe (PHP) with water as a working fluid using the group method of data handling (GMDH) neural network. The maximum relative error was approximately 35.8%, reaching less than 5% for a thermal resistance higher than 10 K/W. In addition, it was notable that the average relative deviation decreases and reaches zero for effective thermal conductivity higher than 10,000 W/K.m. The results demonstrated that the GMDH method is an effective tool for predicting the thermal performance/heat transfer characteristics of PHPs and can be applied to PHPs filled with various operating fluids such as ethanol, acetone, etc.
In a study conducted by Wen [40], two types of artificial neural networks, multilayer perceptron (MLP) and group method of data handling (GMDH), were employed to model the thermal resistance of vertical-oriented oscillating heat pipes filled with acetone. Heat load, filling ratio, lengths of different sections of the heat pipe, inner and outer diameters, and several turns were the models’ inputs. The results demonstrated that both models accurately predict the OHPs thermal performance. However, the complex architecture of the MLP model (MSE = 0.0045, R2 = 0.9893) and its ability to employ functions with higher ability in training the network are the reasons behind its higher accuracy than the GMDH model (MSE = 0.0144, R2 = 0.9651). Similarly, Wang et al. [60] presented a fully connected feed-forward neural network model to predict the thermal resistance of closed vertical meandering pulsating heat pipe (PHP) with water as a working fluid. The input parameters were the same as those of Wen [40] except for the outer diameter. The model results indicated a satisfactory prediction of the PHP thermal performance (MSE = 0.0025, correlation coefficient R = 0.9962).
Nanofluids are being used in heat transfer applications due to their high thermal transfer properties and high thermal conductivity compared to base fluids. Nanofluid concentration and thermal conductivity are essential parameters that should be considered when analyzing nanofluid-filled heat pipe systems.
Shanbedi et al. [61] designed an MLPNN model to predict the temperature performance of a two-phase closed thermosyphon using two synthesized nanofluids, including carbon nanotube (CNT)/water and CNT-Ag/water. According to the experimental results, the appropriate range of weight fraction to obtain a suitable (ΔT) was 0.91–1.1% wt, 0.2–0.3% wt, and 0.95–1% wt for CNT/water and CNT-Ag/water, respectively. These results indicate that the weight fraction of nanoparticles is a crucial parameter for predicting the thermal efficiency of a two-phase closed-loop thermosyphon. The MLPNN model attained a correlation coefficient (R) above 0.99 and a small RMSE value of 0.3338 with only minor prediction errors reported. Three artificial intelligent approaches: multilayer feed-forward neural network (MLFFNN), adaptive neuro-fuzzy inference system (ANFIS), and group method of data handling (GMDH) type neural network was employed by Malekan et al. [38] to investigate the thermal resistance of a closed loop oscillating heat pipe (OHP) filled with γFe2O3/water and Fe3O4/water nanofluids. The input parameters were heat input, the thermal conductivity of working fluids, and the ratio of inner diameter to the length of OHP. Several MLFFNN, ANFIS, and GMDH models were built and tested. The MLFFNN model with one hidden layer with five neurons and the Levenberg–Marquardt training algorithm was the most accurate with an RMSE value of 0.0508, while the GMDH models showed the highest error value of 0.0569. Moreover, the prediction of thermal performance (thermal resistance) of a two-phase closed thermosyphon was conducted by Shanbedi et al. [62] using an adaptive neuro-fuzzy inference system (ANFIS). Two water-based nanofluids were used: pristine carbon nanotube (CNT) and CNT with ethylenediamine (CNT–EDA). The considered input parameters were nanofluid type, nanofluid concentration, input power, length, and temperature difference. The R2 of the model was equal to 0.9999, indicating a very high accuracy and reliability.
Maddah et al. [63] predicted the efficiency of Cu/O water nanofluid in a heat pipe exchanger using a three-layered forward neural network and the Levenberg–Marquardt training algorithm. Filling ratio, nanofluid concentration, and input power were selected as the input parameters, and the output parameter was the heat exchanger efficiency. The predicted results matched the experimental results with a high accuracy indicated by a testing the R-value of 0.9978.
In summary, various input and output parameters have been used in the literature for the modeling of heat pipe systems. Some parameters were general and applied in modeling all types of heat pipes, while other parameters were related to specific types of heat pipes. Thus, carefully choosing the input and output parameters is crucial for achieving excellent overall modeling.

3.4. Dimensionless Numbers as Input Parameters

The prediction of the thermal performance (thermal resistance) of some types of heat pipes (PHP, for example) are sometimes tricky, as many parameters affect the operation (performance), such as heat input, inner diameter, filling ratio, etc. Therefore, heat transfer correlations (dimensionless numbers) have been used to develop reliable heat transfer prediction methods.
A novel method for predicting the thermal performance of a closed pulsating heat pipe with different working fluids and a variety of operational conditions usng a fully connected feed-forward neural network was proposed by Wang et al. [24]. The input parameters were the Kutateladze number (Ku), Bond number (Bo), Morton number (Mo), Prandtl number (Pr), Jacob number (Ja), number of turns (N), and the ratio of the evaporation section length to the diameter (Le/d), while the output parameter of the ANN model was the thermal resistance. The system’s property parameters were evaluated at the coolant temperature as it was known in the initial stages. A backpropagation learning algorithm was used in building the ANN due to its adaptability. The results indicated that the developed model is reliable and can predict thermal performance accurately (MSE = 0.0138, R = 0.9824). The working fluid highly influenced the variation of the predicted values. In a similar approach, Liang et al. [64] conducted a thermal performance investigation of miniature revolving heat pipes (MRVHPs) using a backpropagation neural network and genetic algorithm (GA-BPNN). However, Bo, Ja, Pr, Fr, and filling ratio were the considered input parameters, and Ku was the output parameter. It was concluded that the maximum error for estimating the best filling ratio under several operational conditions is 11.4% for a heating load of 200 W and rotation speed of 500 rpm, while others were within the 10% range. The trained model achieved a high R value of 0.9260 indicating the model’s accuracy in modeling the heat pipe system.
Qian et al. [65] proposed a novel heat transfer prediction model for oscillating heat pipes based on an extreme gradient boosting algorithm (XGBoost), which requires a smaller dataset for prediction compared to ANNs and can evaluate the contribution of each parameter in influencing the output and final decision. The ratio of inner diameter to evaporator section length (Di/Le), Ku, and Ja were the most important parameters influencing the output.
In summary, the use of dimensionless numbers as inputs and outputs of AI models is a very promising method for modeling the highly complex behavior of heat pipe systems as they combine several parameters of the heat pipe system at once.

3.5. AI-Based Prediction Models for Heat Pipe Applications

AI technologies are not limited to only simulating the performance of individual heat pipe systems but have also been implemented to model heat pipe applications such as solar energy (e.g., solar collectors) and electronic cooling applications. By implementing AI models, the difficulty of the modeling process becomes significantly lower compared to other classical and computational methods, such as computational fluid dynamics (CFD), as AI methods could directly model the entire system with all its internal processes directly from the collected experimental data. This data-driven approach could be faster and computationally less expensive than full models of the developed systems.
For instance, the precision of various data-based and energy balance-based methods for modeling the performance of heat pipe solar collectors (HPSC) for a whole year under the climatic conditions of Western Australia was investigated and compared by Shafieian et al. [34]. The models included an artificial neural network (multilayer perceptron—MLP), thermal resistance network (TRN), artificial neuro-fuzzy inference system (ANFIS), and fuzzy methods. The input parameters were inlet temperature of HPSC, ambient temperature, and solar radiation, whereas outlet temperature (the main contributing parameter in the thermal efficiency of solar collectors) was the output parameter. Regarding R2, the best prediction method for the HPSC’s performance was the ANN (R2 = 0.98079, 0.98974, 0.98903, 0.99209 for spring, summer, autumn, and winter, respectively) followed by ANFIS and TRN. Due to large errors, the fuzzy method was not recommended for modeling HPSCs. Sivaraman and Mohan [56] studied the effects of different parameters on heat pipe solar collectors (HPSCs) using multilayer feed-forward ANN. It was found that a decrease in the total length/inner diameter of the heat pipe (L/di) ratio results in an improvement in HPSC performance. This is justifiable since the transport capability of heat pipe increases with increasing the internal diameter, which mainly determines heat transport. The ANN analysis of HPSC showed that the collector (L/di ratio = 52.63, Lc/Le = ratio 0.3333, water inlet temperature = 34 °C) is better than other cases for water flow rate of 0.0033 kg/s. The results demonstrated that the proposed model can successfully predict the effects of different parameters on the HPSC performance, as indicated by a high R2 value of 0.9234. Two different types ANN for predicting the thermal performance of hybrid solar collectors (heated gas + solar radiation as heat sources) were compared by Facão et al. [66]. Different configurations of multiple layer perceptron (MLP) and radial basis functions (RBF) were considered. MLP, despite being simpler, showed slightly better performance than that of the RBF. Tolon et al. [67] evaluated thermodynamic analysis of evacuated tube heat pipe (ETHP) solar energy systems integrated into sustainable buildings with an artificial neural network (ANN). The ANN was applied to analyze the effects of radiation (I), mass (m), and ambient temperature (Tair) (input parameters) on the exergy of the system. A backpropagation neural network (BPNN) with hidden layer (two hidden layers) feedback was the chosen form of ANN. The results indicated that the effect of mass on the exergy was approximately double that of mass and radiation and the trained model achieved excellent prediction capability indicated by a small average error value of 0.0006 at the end of the training process.
Furthermore, Taheri et al. [33] presented a new design of a liquid-cooled heat sink for the thermal management of the printed circuit board (PCB), as an electronic device, by altering the heat sink heat pipe application. Two methods of ANN (radial basis function (RBF) and multilayer perceptron (MLP)) were used to predict PCB steady-state temperature (based on the experimentally obtained results) under different operating conditions that are not studied in the experiments. The results indicated both ANN methods demonstrate practically accurate estimates of the heatsink module, but RBFANN has more precise prediction results (R2 = 0.7223 for MLPNN and R2 = 0.9966 for RBFNN).
In summary, various AI models were used for the modeling of heat pipe systems employed in various applications. AI models can model the heat pipe systems separately or modeling the entire system incorporating heat pipes. Modeling the operation of the entire system could be of benefit in cases where the internal interactions and processes in the system are very complex and is better to incorporate them implicitly in the AI model.

3.6. Hybrid AI Methods for Working Condition Optimization

Optimization algorithms can be implemented into a heat pipe’s performance prediction models to optimize the operating conditions to achieve the optimal working rate (highest efficiency). Optimization of finned heat pipe operation conditions/parameters was conducted by Naresh [36] using a combined artificial neural network (ANN) and genetic algorithm (GA). The objective of the optimization was to obtain the optimum conditions of a number of fins and fill ratio for a given heat input at which the minimum thermal resistance can be achieved. The network was trained using the Levenberg–Marquardt algorithm. The optimum average fill ratio and the number of fins were found to be 52% and seven, respectively. Jalilian et al. [68] investigated the behavior of a pulsating heat pipe flat-plate solar collector (PHPFPSC) using the artificial neural network method and optimized the solar collector’s parameters using a genetic algorithm. Multilayer perceptron (MLP), specifically, two-layer perceptron (with one hidden layer) and three-layer perceptron (with two hidden layers) neural networks, were used to investigate the system because of the nonlinearity of PHPs and solar collectors. The results demonstrated that the evaporator length, inclination angle, and filling ratio were the most influencing factors on the system’s efficiency. The optimal values of the parameters were an evaporator length of 108.3 cm, a filling ratio of 56.9%, and an inclination angle of 25.01°, and the optimal thermal efficiency, based on the optimal parameters, was 61.4%, which was 4.0% higher than that in the nonoptimal case. Moreover, the results indicated that a decrease in the temperature of the input water of the water tank leads to an increase in the system’s thermal efficiency (efficiency increases by about 1% for a decrease of 1 °C). The average error was less than 7.5%, which indicates that neural networks are capable of predicting the performance of PHPFPSC systems with high accuracy. Using a similar approach, the simulation and optimization of a pulsating heat pipe (PHP) was conducted by Jokar et al. [69] using a novel approach that consists of an artificial multilayer perceptron (MLP) neural network and genetic algorithm (GA). The optimum operation point obtained by the GA was heat flux (q”) = 39.93 W, filling ratio (FR) = 38.25%, inclination angle (IA) = 55.6°, and the obtained results by the GA were validated by comparison to experimental results.
In summary, hybrid models combining optimization algorithms with AI-based models have shown excellent performance in modeling and optimizing various types of heat pipe systems. The incorporation of optimization algorithms in the modeling process helps in improving the overall model’s accuracy and can be employed for optimizing the operational parameters of the heat pipe system.

3.7. Intelligent Control Methods for Heat Pipes

Control algorithms are usually applied to AI models/systems to establish intelligent control systems for heat pipe systems. As shown in Table 2, all of the intelligent control systems that were applied in the literature are based on fuzzy logic models.
Dong et al. [71] proposed a fuzzy incremental control algorithm for controlling loop heat pipe space cooling system (LHP-SCS) consisting of an LHP with ammonia as working fluid and a variable emittance radiator with MEMS louver. This intelligent control technique takes advantage of minor overshoots, no steady error, and strong operating properties. The proposed FIC strategy was compared with the traditional PID approach. The former demonstrated an improvement in the heat flux tracking effect and temperature control than the latter, as indicated with lower overshoot values by more than 15% for considered control parameters combined with shorter settling times by more than 30%. Furthermore, it showed potential for more stable thermal and hydraulic conditions for safe operation of the LHP structures and working fluid. Dual-driven intelligent combination control (TQ-ICC) of a heat pipe space cooling system (HP-SCS) was developed by Yunze at al. [72] to improve the temperature control and heat flux tracking effects. The combination control strategy improves the final control action by employing temperature regulation and heat flux tracking errors to the proposed dual-driven system and adaptively adjusting their contributions using a fuzzy fusing rule. The results suggested that the proposed model can considerably enhance the thermal control effects and promote safe operation of heat pipe space cooling system as well, which was indicated by a more than 75% smaller settling time and more than 89% smaller overshoot compared to a base PID controller. Zhang et al. [70] designed and simulated a nonlinear adaptive fuzzy controller to control the heat pipe radiator with a new-type function of contraction–expansion factor. The controller was designed to resolve the energy (heat) wastage in the heat pipe radiator due to its complex nonlinear nature. The model was found to be feasible and adaptive.
A particle swarm optimization (PSO) algorithm was also used by Xi et al. [45] to tune the proportional–integral–derivative (PID) control parameters to optimize the parameters of heat pipe temperature control during a vacuum thermal test. The temperature control model was constructed based on the heat response data of the heat pipe. The time integral of the absolute value of the control error was used as the objective function. Compared to the attenuation curve method, the PSO method achieved better results in reducing overshoot by more than 63%, shortening the time to reach steady-state, and improving performance by reducing the maximum overshoot by more than 15%.
In summary, the control of heat pipe systems using AI algorithms was discussed previously in the literature for controlling various parameters such as temperature and heat release. However, ANN has not previously been used for the intelligent control of heat pipe systems. Thus, the implementation of ANN in this task is limited, and future research on this gap is highly recommended.

3.8. Summary

Several studies in the literature have discussed the application of various AI techniques for the modeling and optimization of heat pipe systems. Table 3 summarizes the progress made on modeling heat pipes’ performance using AI techniques. It can be observed from the table that several AI techniques, including MLPNN, GMDH, and ANFIS, were used for modeling different parameters of heat pipe systems, including the thermal resistance, the water outlet temperature, the heat transfer rate, and the thermal efficiency. It is observable from the table that the AI model that was used the most is the MLPNN due to its ease of application and excellent ability to model highly nonlinear relationships between the parameters. Several types of heat pipe systems were discussed for optimization using AI in the literature, including PHP, OHP, thermosyphons, and heat pipe heat exchangers.

4. Conclusions and Future Research Directions

This work reviewed and discussed the recent developments of AI technologies in heat pipe applications. Most of the studies reviewed in this work primarily focus on predicting the thermal performance of heat pipe systems. Hybrid AI algorithms and intelligent control systems for heat pipes were also covered. The following highlights can be concluded from this review:
  • Most of the work on AI in heat pipes involves pulsating/oscillating heat pipes. This is mainly due to the difficulty of experimentally analyzing the effects of different parameters on the performance of a heat pipe, since its performance depends on several parameters. Furthermore, the numerical modeling of PHPs using computational fluid dynamics (CFD) is relatively complex due to the chaotic nature of PHPs, which shows the potential of AI-based modeling methods.
  • ANN is the most widely used AI technology in predicting the performance of heat pipes and has proven its ability to be one of the most effective techniques for predicting performance accurately. As a result, it can be used for the efficient design of heat pipes.
  • Multilayer perceptron neural networks (MLPNNs) achieved the highest accuracy in predicting the performance of heat pipe systems compared to other similar models.
  • The AI model structure (number of hidden layers and neurons) is an important factor that influences the model’s prediction accuracy.
  • The most common influencing input parameters are heat flux, filling ratio, and length of each heat pipe section (evaporator and condenser sections). In the case of nanofluid-filled heat pipes, nanofluid properties (such as concentration and thermal conductivity of nanofluid) are the most common input parameters that should be considered, as they most significantly influence the operation.
  • Optimization algorithms and a combination of optimization algorithms and AI models can identify the optimum operating conditions of heat pipe systems.
  • Fuzzy (and hybrid fuzzy) controllers are the most widely used controllers for heat pipes and heat pipe systems.
Despite the wide application of AI models for modeling various heat pipe systems, some important research gaps still need to be addressed to improve this technology and move it closer to practical application. These research gaps include:
  • Hybrid models combining metaheuristic optimization algorithms with AI-based models have shown excellent performance in modeling heat pipe systems. However, the current progress on hybridizing AI models with optimization algorithms is very limited, and further research on this topic is highly recommended. Optimization algorithms that were not hybridized previously with AI models for heat pipe modeling include grey wolf optimizer [74], ant colony optimization (ACO) [75], and the whale optimization algorithm (WOA) [76].
  • Several recent AI models have performed superior tasks that were not previously applied for modeling heat pipe systems. These models include the recurrent neural networks (RNN) [77,78] and transformer networks [79,80] that showed excellent performance in sequential data prediction and modeling tasks, as well as generative adversarial networks (GAN) [81,82] that showed excellent performance in various AI tasks in general and modeling tasks in specific. Further works discussing the applications of these state-of-the-art models for modeling various aspects of heat pipe systems are highly recommended and are expected to improve the currently achieved limits of the AI-based modeling of heat pipes.
  • The progress made on the AI-based control of heat pipe systems is very limited, and various types of intelligent control algorithms and target parameters have not previously been discussed in the literature. Most importantly, ANN showed excellent performance in different system control tasks and has not previously been used to control heat pipe systems’ operation. Thus, developing ANN-based methods for the operational control of heat pipe systems is highly recommended and expected to achieve higher performance compared to the currently applied techniques.

Author Contributions

Conceptualization, A.G.O., M.A.R. and A.H.A.; methodology, S.H., E.T.S., F.Z., T.S. and M.A.A.; formal analysis, A.G.O., S.H., E.T.S., M.A.R., A.H.A., F.Z., T.S. and M.A.A.; investigation, A.G.O., A.H.A. and M.A.A.; data curation, S.H., E.T.S., M.A.R., F.Z. and T.S.; writing—original draft, A.G.O., S.H., E.T.S., M.A.R., A.H.A., F.Z., T.S. and M.A.A.; draft preparation, A.G.O., S.H., E.T.S., M.A.R., A.H.A., F.Z., T.S. and M.A.A. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the University of Sharjah, Project No. 19020406129.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Jouhara, H.; Chauhan, A.; Nannou, T.; Almahmoud, S.; Delpech, B.; Wrobel, L. Heat pipe based systems-Advances and applications. Energy 2017, 128, 729–754. [Google Scholar] [CrossRef]
  2. Sintered Wicks. Available online: https://www.1-act.com/resources/heat-pipe-resources/heat-pipe-wicks/sintered-wicks/ (accessed on 1 August 2020).
  3. Blet, N.; Lips, S.; Sartre, V. Heats pipes for temperature homogenization: A literature review. Appl. Therm. Eng. 2017, 118, 490–509. [Google Scholar] [CrossRef] [Green Version]
  4. Abdelkareem, M.A.; Maghrabie, H.M.; Abo-Khalil, A.G.; Adhari, O.H.K.; Sayed, E.T.; Radwan, A.; Rezk, H.; Jouhara, H.; Olabi, A.G. Thermal management systems based on heat pipes for batteries in EVs/HEVs. Journal of Energy Storage 2022, 51, 104384. [Google Scholar] [CrossRef]
  5. Behi, H.; Ghanbarpour, M.; Behi, M. Investigation of PCM-assisted heat pipe for electronic cooling. Appl. Therm. Eng. 2017, 127, 1132–1142. [Google Scholar] [CrossRef]
  6. Werner, T.C.; Yan, Y.; Mullen, D.; Halimic, E. Experimental analysis of a high temperature water heat pipe for thermal storage applications. Therm. Sci. Eng. Prog. 2020, 19, 100564. [Google Scholar] [CrossRef]
  7. Singh, R.; Mochizuki, M.; Nguyen, T.; Akbarzadeh, A. Applications of heat pipes in energy conservation and renewable energy based systems. Front. Heat Pipes (FHP) 2011, 2, 033003. [Google Scholar]
  8. Abdelkareem, M.A.; Maghrabie, H.M.; Sayed, E.T.; Kais, E.-C.A.; Abo-Khalil, A.G.; Al Radi, M.; Baroutaji, A.; Olabi, A. Heat pipe-based waste heat recovery systems: Background and applications. Therm. Sci. Eng. Prog. 2022, 29, 101221. [Google Scholar] [CrossRef]
  9. Maghrabie, H.M.; Olabi, A.; Alami, A.H.; Al Radi, M.; Zwayyed, F.; Salamah, T.; Wilberforce, T.; Abdelkareem, M.A. Numerical simulation of heat pipes in different applications. Int. J. Thermofluids 2022, 16, 100199. [Google Scholar] [CrossRef]
  10. Reay, D.A. Thermal energy storage: The role of the heat pipe in performance enhancement. Int. J. Low-Carbon Technol. 2015, 10, 99–109. [Google Scholar] [CrossRef] [Green Version]
  11. Lips, S.; Sartre, V.; Lefevre, F.; Khandekar, S.; Bonjour, J. Overview of Heat Pipe Studies during The Period 2010–2015. Interfacial Phenom. Heat Transf. 2016, 4, 33–53. [Google Scholar] [CrossRef] [Green Version]
  12. Behi, H.; Behi, M.; Karimi, D.; Jaguemont, J.; Ghanbarpour, M.; Behnia, M.; Berecibar, M.; Van Mierlo, J. Heat pipe air-cooled thermal management system for lithium-ion batteries: High power applications. Appl. Therm. Eng. 2020, 183, 116240. [Google Scholar] [CrossRef]
  13. Ando, M.; Okamoto, A.; Tanaka, K.; Maeda, M.; Sugita, H.; Daimaru, T.; Nagai, H. On-orbit demonstration of oscillating heat pipe with check valves for space application. Appl. Therm. Eng. 2018, 130, 552–560. [Google Scholar] [CrossRef]
  14. Krishna, J.; Kishore, P.; Solomon, A. Heat pipe with nano enhanced-PCM for electronic cooling application. Exp. Therm. Fluid Sci. 2017, 81, 84–92. [Google Scholar] [CrossRef] [Green Version]
  15. Putra, N.; Anggoro, T.; Winarta, A. Experimental study of heat pipe heat exchanger in hospital HVAC system for energy conservation. Int. J. Adv. Sci. Eng. Inf. Technol. 2017, 7, 871–877. [Google Scholar] [CrossRef]
  16. Zhang, W.; Wang, C.; Chen, R.; Tian, W.; Qiu, S.; Su, G. Preliminary design and thermal analysis of a liquid metal heat pipe radiator for TOPAZ-II power system. Ann. Nucl. Energy 2016, 97, 208–220. [Google Scholar] [CrossRef]
  17. Maydanik, Y.; Vershinin, S.; Chernysheva, M. Investigation of thermal characteristics of a loop heat pipe in a wide range of external conditions. Int. J. Heat Mass Transf. 2020, 147, 118967. [Google Scholar] [CrossRef]
  18. Babu, E.; Reddappa, H.; Reddy, G. Effect of filling ratio on thermal performance of closed loop pulsating heat pipe. Mater. Today Proc. 2018, 5, 22229–22236. [Google Scholar] [CrossRef]
  19. Law, R.; Reay, D.; Mustaffar, A.; McGlen, R.; Underwood, C.; Ng, B. Experimental investigation into the feasibility of using a variable conductance heat pipe for controlled heat release from a phase-change material thermal store. Therm. Sci. Eng. Prog. 2018, 7, 125–130. [Google Scholar] [CrossRef] [Green Version]
  20. Huminic, G.; Huminic, A.; Morjan, I.; Dumitrache, F. Experimental study of the thermal performance of thermosyphon heat pipe using iron oxide nanoparticles. Int. J. Heat Mass Transf. 2011, 54, 656–661. [Google Scholar] [CrossRef]
  21. Yu, Y.; Wang, L. Solid sorption heat pipe coupled with direct air cooling technology for thermal control of rack level in internet data centers: Design and numerical simulation. Int. J. Heat Mass Transf. 2019, 145, 118714. [Google Scholar] [CrossRef]
  22. Cao, Y.; Gao, X.; Li, R. A liquid plug moving in an annular pipe–Heat transfer analysis. Int. J. Heat Mass Transf. 2019, 139, 1065–1076. [Google Scholar] [CrossRef]
  23. Yau, Y.H.; Foo, Y. Comparative study on evaporator heat transfer characteristics of revolving heat pipes filled with R134a, R22 and R410A. Int. Commun. Heat Mass Transf. 2011, 38, 202–211. [Google Scholar] [CrossRef]
  24. Wang, X.; Yan, Y.; Meng, X.; Chen, G. A general method to predict the performance of closed pulsating heat pipe by artificial neural network. Appl. Therm. Eng. 2019, 157, 113761. [Google Scholar] [CrossRef]
  25. Abdelkareem, M.A.; Soudan, B.; Mahmoud, M.S.; Sayed, E.T.; AlMallahi, M.N.; Inayat, A.; Al Radi, M.; Olabi, A.G. Progress of artificial neural networks applications in hydrogen production. Chem. Eng. Res. Des. 2022, 182, 66–86. [Google Scholar] [CrossRef]
  26. Olabi, A.; Abdelkareem, M.A.; Semeraro, C.; Al Radi, M.; Rezk, H.; Muhaisen, O.; Al-Isawi, O.A.; Sayed, E.T. Artificial Neural Networks Applications in Partially Shaded PV Systems. Therm. Sci. Eng. Prog. 2022, 37, 101612. [Google Scholar] [CrossRef]
  27. Moayedi, H.; Mosavi, A. An innovative metaheuristic strategy for solar energy management through a neural networks framework. Energies 2021, 14, 1196. [Google Scholar] [CrossRef]
  28. Khajeh, M.G.; Maleki, A.; Rosen, M.A.; Ahmadi, M.H. Electricity price forecasting using neural networks with an improved iterative training algorithm. Int. J. Ambient Energy 2018, 39, 147–158. [Google Scholar] [CrossRef]
  29. Yuan, H.; Dai, H.; Wu, W.; Xie, J.; Shen, J.; Wei, X. A fuzzy logic PI control with feed-forward compensation for hydrogen pressure in vehicular fuel cell system. Int. J. Hydrog. Energy 2021, 46, 5714–5728. [Google Scholar] [CrossRef]
  30. Bahiraei, M.; Nazari, S.; Safarzadeh, H. Modeling of energy efficiency for a solar still fitted with thermoelectric modules by ANFIS and PSO-enhanced neural network: A nanofluid application. Powder Technol. 2021, 385, 185–198. [Google Scholar] [CrossRef]
  31. Wang, Y.; Wei, C. Design optimization of office building envelope based on quantum genetic algorithm for energy conservation. J. Build. Eng. 2021, 35, 102048. [Google Scholar] [CrossRef]
  32. Ahmadi, M.H.; Kumar, R.; Assad, M.E.H.; Ngo, P.T.T. Applications of machine learning methods in modeling various types of heat pipes: A review. J. Therm. Anal. Calorim. 2021, 146, 2333–2341. [Google Scholar] [CrossRef]
  33. Taheri, A.; Moghadam, M.G.; Mohammadi, M.; Passandideh-Fard, M.; Sardarabadi, M. A new design of liquid-cooled heat sink by altering the heat sink heat pipe application: Experimental approach and prediction via artificial neural network. Energy Convers. Manag. 2020, 206, 112485. [Google Scholar] [CrossRef]
  34. Shafieian, A.; Parastvand, H.; Khiadani, M. Comparative and performative investigation of various data-based and conventional theoretical methods for modelling heat pipe solar collectors. Sol. Energy 2020, 198, 212–223. [Google Scholar] [CrossRef]
  35. Ahmadi, M.H.; Sadeghzadeh, M.; Raffiee, A.H.; Chau, K.-W. Applying GMDH neural network to estimate the thermal resistance and thermal conductivity of pulsating heat pipes. Eng. Appl. Comput. Fluid Mech. 2019, 13, 327–336. [Google Scholar] [CrossRef] [Green Version]
  36. Naresh, Y. Numerical investigation on the heat transfer performance and optimisation of a finned heat pipe using artificial neural networks and genetic algorithm. Int. J. Ambient. Energy 2020, 43, 2231–2238. [Google Scholar] [CrossRef]
  37. Kahani, M.; Vatankhah, G. Thermal performance prediction of wickless heat pipe with Al2O3/water nanofluid using artificial neural network. Chem. Eng. Commun. 2019, 206, 509–523. [Google Scholar] [CrossRef]
  38. Malekan, M.; Khosravi, A.; Goshayeshi, H.R.; Assad, M.E.H.; Pabon, J.J.G. Thermal resistance modeling of oscillating heat pipes for nanofluids by artificial intelligence approach. J. Heat Transf. 2019, 141, 072402. [Google Scholar] [CrossRef]
  39. Chavda, N. Investigation of Thermal Performance of Cylindrical Heat Pipe Using Silver Nanofluid: Part-II: Prediction Using Artificial Neural Network. J. Inst. Eng. (India) Ser. C 2020, 101, 115–124. [Google Scholar] [CrossRef]
  40. Wen, J. Thermal resistance modeling of oscillating heat pipes filled with acetone by using artificial neural network. J. Therm. Anal. Calorim. 2021, 144, 1873–1881. [Google Scholar] [CrossRef]
  41. Bre, F.; Gimenez, J.; Fachinotti, V. Prediction of wind pressure coefficients on building surfaces using Artificial Neural Networks. Energy Build. 2017, 158, 1429–1441. [Google Scholar] [CrossRef]
  42. Suman, S. Artificial intelligence in nuclear industry: Chimera or solution? J. Clean. Prod. 2020, 278, 124022. [Google Scholar] [CrossRef]
  43. Youssef, A.; El-Telbany, M.; Zekry, A. The role of artificial intelligence in photo-voltaic systems design and control: A review. Renew. Sustain. Energy Rev. 2017, 78, 72–79. [Google Scholar] [CrossRef]
  44. Ghenai, C.; Al-Mufti, O.A.A.; Al-Isawi, O.A.M.; Amirah, L.H.L.; Merabet, A. Short-term building electrical load forecasting using adaptive neuro-fuzzy inference system (ANFIS). J. Build. Eng. 2022, 52, 104323. [Google Scholar] [CrossRef]
  45. Xi, Z.; Chunlin, D.; Yao, F.; Jing, W.; Lin, Z. Temperature Control Optimization for Heat Pipe Based on Particle Swarm Optimization. In Proceedings of the 2018 Eighth International Conference on Instrumentation & Measurement, Computer, Communication and Control (IMCCC), Harbin, China, 19–21 July 2018. [Google Scholar]
  46. Dehghani, M.; Riahi-Madvar, H.; Hooshyaripor, F.; Mosavi, A.; Shamshirband, S.; Zavadskas, E.K.; Chau, K.-W. Prediction of hydropower generation using grey wolf optimization adaptive neuro-fuzzy inference system. Energies 2019, 12, 289. [Google Scholar] [CrossRef] [Green Version]
  47. Said, S.Z.; Thiaw, L.; Wabuge, C. Maximum Power Point Tracking of Photovoltaic Generators Partially Shaded Using an Hybrid Artificial Neural Network and Particle Swarm Optimization Algorithm. Int. J. Energy Power Eng. 2017, 6, 91–99. [Google Scholar] [CrossRef]
  48. Kambalimath, S.; Deka, P. A basic review of fuzzy logic applications in hydrology and water resources. Appl. Water Sci. 2020, 10, 1–14. [Google Scholar] [CrossRef]
  49. Shariati, M.; Mafipour, M.S.; Haido, J.H.; Yousif, S.T.; Toghroli, A.; Trung, N.T.; Shariati, A. Identification of the most influencing parameters on the properties of corroded concrete beams using an Adaptive Neuro-Fuzzy Inference System (ANFIS). Steel Compos. Struct. 2020, 34, 155. [Google Scholar]
  50. Imran, M.; Alsuhaibani, S. Chapter 7—A Neuro-Fuzzy Inference Model for Diabetic Retinopathy Classification. In Intelligent Data Analysis for Biomedical Applications; Academic Press: Cambridge, MA, USA, 2019; pp. 147–172. [Google Scholar]
  51. Song, B.; Wang, Z.; Zou, L. On Global Smooth Path Planning for Mobile Robots using a Novel Multimodal Delayed PSO Algorithm. Cogn. Comput. 2017, 9, 5–17. [Google Scholar] [CrossRef]
  52. Patel, V.M.; Mehta, H. Artificial neural network modeling of a closed loop pulsating heat pipe. World Acad. Sci. Eng. Technol.-Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2016, 10, 1754–1757. [Google Scholar]
  53. Patel, V.M.; Mehta, H. Thermal performance prediction models for a pulsating heat pipe using Artificial Neural Network (ANN) and Regression/Correlation Analysis (RCA). Sādhanā 2018, 43, 1–16. [Google Scholar] [CrossRef] [Green Version]
  54. Salehi, H.; Heris, S.Z.; Salooki, M.K.; Noei, S.H. Designing a neural network for closed thermosyphon with nanofluid using a genetic algorithm. Braz. J. Chem. Eng. 2011, 28, 157–168. [Google Scholar] [CrossRef] [Green Version]
  55. Lee, Y.-W.; Chang, T.-L. Application of NARX neural networks in thermal dynamics identification of a pulsating heat pipe. Energy Convers. Manag. 2009, 50, 1069–1078. [Google Scholar] [CrossRef]
  56. Sivaraman, B.; Mohan, N. Analysis of heat pipe solar collector using artificial neural network. J. Sci. Ind. Res. 2007, 66, 995–1001. [Google Scholar]
  57. Khandekar, S.; Cui, X.; Groll, M. Thermal performance modeling of pulsating heat pipes by artificial neural network. In Proceedings of the 12th International Heat Pipe Conference, Moscow, Russia, 19–24 May 2002; pp. 215–219. [Google Scholar]
  58. E, J.; Li, Y.; Gong, J. Function chain neural network prediction on heat transfer performance of oscillating heat pipe based on grey relational analysis. J. Cent. South Univ. Technol. 2011, 18, 1733. [Google Scholar] [CrossRef]
  59. Ahmadi, M.H.; Tatar, A.; Nazari, M.A.; Ghasempour, R.; Chamkha, A.J.; Yan, W.-M. Applicability of connectionist methods to predict thermal resistance of pulsating heat pipes with ethanol by using neural networks. Int. J. Heat Mass Transf. 2018, 126, 1079–1086. [Google Scholar] [CrossRef]
  60. Wang, X.; Li, B.; Yan, Y.; Gao, N.; Chen, G. Predicting of thermal resistances of closed vertical meandering pulsating heat pipe using artificial neural network model. Appl. Therm. Eng. 2019, 149, 1134–1141. [Google Scholar] [CrossRef]
  61. Shanbedi, M.; Jafari, D.; Amiri, A.; Heris, S.Z.; Baniadam, M. Prediction of temperature performance of a two-phase closed thermosyphon using artificial neural network. Heat Mass Transf. 2013, 49, 65–73. [Google Scholar] [CrossRef]
  62. Shanbedi, M.; Amiri, A.; Rashidi, S.; Heris, S.Z.; Baniadam, M. Thermal performance prediction of two-phase closed thermosyphon using adaptive neuro-fuzzy inference system. Heat Transf. Eng. 2015, 36, 315–324. [Google Scholar] [CrossRef]
  63. Maddah, H.; Ghazvini, M.; Ahmadi, M. Predicting the efficiency of CuO/water nanofluid in heat pipe heat exchanger using neural network. Int. Commun. Heat Mass Transf. 2019, 104, 33–40. [Google Scholar] [CrossRef]
  64. Liang, F.; Gao, J.; Xu, L. Thermal performance investigation of the miniature revolving heat pipes using artificial neural networks and genetic algorithms. Int. J. Heat Mass Transf. 2020, 151, 119394. [Google Scholar] [CrossRef]
  65. Qian, N.; Wang, X.; Fu, Y.; Zhao, Z.; Xu, J.; Chen, J. Predicting heat transfer of oscillating heat pipes for machining processes based on extreme gradient boosting algorithm. Appl. Therm. Eng. 2020, 164, 114521. [Google Scholar] [CrossRef]
  66. Facão, J.; Varga, S.; Oliveira, A. Evaluation of the use of artificial neural networks for the simulation of hybrid solar collectors. Int. J. Green Energy 2004, 1, 337–352. [Google Scholar] [CrossRef]
  67. Tolon, F.E.; Karabuga, A.; Tolon, M.; Utlu, Z. Evaluation of thermodynamic analysis of solar energy systems integrated into sustainable buildings with artificial neural network: A case study. Procedia Comput. Sci. 2019, 158, 91–98. [Google Scholar] [CrossRef]
  68. Jalilian, M.; Kargarsharifabad, H.; Godarzi, A.A.; Ghofrani, A.; Shafii, M.B. Simulation and optimization of pulsating heat pipe flat-plate solar collectors using neural networks and genetic algorithm: A semi-experimental investigation. Clean Technol. Environ. Policy 2016, 18, 2251–2264. [Google Scholar] [CrossRef]
  69. Jokar, A.; Godarzi, A.A.; Saber, M.; Shafii, M.B. Simulation and optimization of a pulsating heat pipe using artificial neural network and genetic algorithm. Heat Mass Transf. 2016, 52, 2437–2445. [Google Scholar] [CrossRef]
  70. Zhang, P.; Hao, X.-H.; Xu, W.-T. Design and simulation of a nonlinear adaptive fuzzy controller for the heat pipe-radiator. In Proceedings of the 2007 International Conference on Wavelet Analysis and Pattern Recognition, Beijing, China, 2–4 November 2007. [Google Scholar]
  71. Dong, S.-J.; Li, Y.-Z.; Wang, J.; Wang, J. Fuzzy incremental control algorithm of loop heat pipe cooling system for spacecraft applications. Comput. Math. Appl. 2012, 64, 877–886. [Google Scholar] [CrossRef] [Green Version]
  72. Yunze, L.; Mingmin, L.; Lee, K. A dual-driven intelligent combination control of heat pipe space cooling system. Chin. J. Aeronaut. 2012, 25, 566–574. [Google Scholar]
  73. Lei, L. Testing algorithm for heat transfer performance of nanofluid-filled heat pipe based on neural network. Open Phys. 2020, 18, 751–760. [Google Scholar] [CrossRef]
  74. Mirjalili, S.; Mirjalili, S.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
  75. Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
  76. Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
  77. Jung, Y.; Jung, J.; Kim, B.; Han, S. Long short-term memory recurrent neural network for modeling temporal patterns in long-term power forecasting for solar PV facilities: Case study of South Korea. J. Clean. Prod. 2020, 250, 119476. [Google Scholar] [CrossRef]
  78. Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
  79. Liu, D.; Wang, Y.; Liu, C.; Yuan, X.; Yang, C.; Gui, W. Data Mode Related Interpretable Transformer Network for Predictive Modeling and Key Sample Analysis in Industrial Processes. IEEE Trans. Ind. Inform. 2022. [Google Scholar] [CrossRef]
  80. Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021. [Google Scholar]
  81. Cheng, M.; Fang, F.; Pain, C.; Navon, I. Data-driven modelling of nonlinear spatio-temporal fluid flows using a deep convolutional generative adversarial network. Comput. Methods Appl. Mech. Eng. 2020, 365, 113000. [Google Scholar] [CrossRef]
  82. Zotov, E.; Tiwari, A.; Kadirkamanathan, V. Towards a digital twin with generative adversarial network modelling of machining vibration. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Halkidiki, Greece, 5–7 June 2020; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
Energies 16 00760 g001 550
Figure 1. Schematic diagram of heat pipe structure and operation.
Figure 1. Schematic diagram of heat pipe structure and operation.
Energies 16 00760 g001
Energies 16 00760 g002 550
Figure 2. Predicted thermal resistance values by (a) MLP, (b) RBF, (c) ANFIS, and (d) LSSVM models compared to experimental data [59], with permission No. 5435490825671.
Figure 2. Predicted thermal resistance values by (a) MLP, (b) RBF, (c) ANFIS, and (d) LSSVM models compared to experimental data [59], with permission No. 5435490825671.
Energies 16 00760 g002
Table
Table 1. Summary and comparison between various AI algorithms.
Table 1. Summary and comparison between various AI algorithms.
AI AlgorithmAdvantagesDrawbacksSample Applications
Artificial Neural Network (ANN)Easy to implement. Excellent capacity to predict several parameters together. It can be used to predict complex systems.Training of the network is required. Larger network sizes require more data and longer training and processing time. Optimizing photovoltaic systems [47], and modeling hydrogen production [25].
Fuzzy LogicFlexible and allows modifications. Output decisions can be interpreted easily. Can handle multiple different inputs at the same time.Mainly dependent on the expertise of the designer. Inaccurate designs result in wrong outputs. Requires extensive testing with equipment.Water resource prediction [48], control of fuel cell vehicles [29].
Adaptive Neuro-Fuzzy Inference System (ANFIS)Capable of modeling highly nonlinear processes. Achieves superior performance on tasks with a small number of inputs.High computational cost. The trade-off between output accuracy and interpretability. Generated intermediate representations could be hard to interpret.Analysis of concrete structures [49], medical imaging analysis [50].
Metaheuristic OptimizationFaster convergence speed compared to the classical optimization algorithm. Lower computational cost. Broad applicability. Easy to hybridize with other algorithms.Not guaranteed to perform effectively on all tasks. Some problems could result in significantly longer processing times. It could be trapped in a local maxima. Requires careful parameter tuning. Robot path planning [51], temperature control [45].
Table
Table 2. Intelligent control methods for heat pipes.
Table 2. Intelligent control methods for heat pipes.
Control MethodTarget ParameterRef.
PIDTemperature[45]
Nonlinear adaptive fuzzy controllerEnergy (heat) wastage in the heat pipe radiator[70]
Fuzzy incremental controlLHP temperatures, condensing pressure, and mass flow rate[71]
Dual intelligent model (fuzzy fusing rules)Temperature control and heat flux tracking effects[72]
Table
Table 3. Different AI models for predicting heat pipe thermal performance (*: MSE value, **: RMSE value, x: Accuracy measure not available).
Table 3. Different AI models for predicting heat pipe thermal performance (*: MSE value, **: RMSE value, x: Accuracy measure not available).
AI MethodType of Heat PipeInput ParametersOutput ParametersDataset SplitAccuracyRef.
Training/Testing/ValidationMSE (*)
RMSE (**)		R
MLPNNTube heat pipe and flat heat pipe solar collectorsSolar radiation, ambient temperature, inlet gas temperature, inlet water temperature, evaporator length, condenser length, gas mass flow rate, and water mass flow rate.Collector efficiency and heat output70%/15%/15%0.0050 *0.9460[66]
MLPNN0.0002 *0.9995
GA-MLPNNPHPFilling ratio, inclined angle, and input heat flux to the evaporatorThermal resistance70%/30%/xxx[69]
MLPNNPHPHeat flux, number of turns, filling ratio, length ratio of evaporation section, and inner diameterThermal resistance70%/15%/15%0.0025 *0.9962[60]
MLPNNPHPHeat input and fill ratioOverall thermal resistance64%/18%/18%xx[57]
MLPNNHeat pipe solar collectorTotal length/ inner diameter of heat pipe (L/di), condenser length/evaporator length (Lc/Le), water inlet temperature, collector tilt angle, and solar intensityWater outlet temperature72%/28%/x0.9234 *x[56]
MLPNNCLPHPHeat input and filling ratioThermal resistance70%/15%/15% [52]
MLPNNPHPFilling ratio, thermal conductivity of tube, inclination angle, lengths of adiabatic, condenser and evaporator sections, heat input, and inner and outer diametersThermal resistance80%/20%/x0.1121 **0.9838[59]
GA-RBFNN0.065 **0.9946
CHPSO ANFIS0.1455 **0.9726
MLPNNHeat pipe heat exchangerFilling ratio, nanofluid concentration, and input powerHeat exchanger efficiencyx/x/xx0.99388[63]
MLPNNPHPKutateladze number (Ku), Bond number (Bo), Morton number (Mo), Prandtl number (Pr), Jacob number (Ja), number of turns (N), and the ratio of the evaporation section length to the diameter (Le/d)Thermal resistance70%/15%/15%0.0138 *0.9824[24]
MLPNNEvacuated tube heat pipeThe radiation (I), mass (m), and ambient temperature (Tair)Exergy55%/30%/15%xx[67]
RBFNNHeat sink heat pipeNanofluid mass fraction, the coolant flow rate, and the heat flux of the PCBPCB steady-state temperature80%/20%/x0.6357 **0.9983[33]
MLPNN70%/15%/15%0.7223 **0.9978
MLPNNPHPInner diameter (Di), outer diameter (Do), evaporator length (Le), condenser length (Lc), number of turns (N), working fluids (WFs), orientation (θ), filling ratio (FR), and heat input (Q)Thermal resistance70%/15%/15%x0.9434[53]
NARX neural networkPHPWall temperature measured by thermocouple T7 at evaporatorTemperature T1 at condenserx/x/x [55]
MLPNNHeat pipe solar collectorsInlet temperature of the HPSC, ambient temperature, and solar radiationOutlet temperature80%/x/20%0.00525 **0.9960[34]
ANFISx/x/x0.00461 **0.9706
fuzzy methodx/x/xxx
GMDHPHPInner and outer diameters, tube thermal conductivity, turns, length of each section, heat input, filling ratio, and (sine of) inclination angleThermal resistancex/x/x 0.9779[35]
Thermal conductivity 0.9906
Function chain NN (3 inputs)OHPCharging ratio, inclination angle, and heat inputHeat transfer ratex/x/xxx[58]
Function chain NN (4 inputs)Charging ratio, inclination angle, heat input, and number of turnsHeat transfer ratex/x/xxx
GA-ANNTwo-phase closed thermosyphonHeat input, number of fins, and filling ratioThermal resistance80%/x/20%x0.9950[36]
MLPNNWickless heat pipe (WHP)Input power, volume concentration of nanofluid, filling ratio and mass rate in condenser sectionThermal efficiency75%/25%/x0.00994 * (for testing dataset)0.9911[37]
MLPNNOHPHeat input, thermal conductivity of working fluids, and ratio of inner diameter to the length of OHPThermal resistance70%/30%/x0.0025 *0.9966[38]
ANFIS0.0031 *0.9953
GMDH0.0032 *0.9862
GA-MLPNN (2-layer)PHPSolar radiation, inlet temperature of the water tank, the evaporator length, filling ratio, and inclination angleGained heat70%/30%/xxx[68]
GA-MLPNN (3-layer)xx
MLPNNTwo-layer screen mesh-type cylindrical heat pipeHeat load, size of silver nanoparticles, concentration of silver nanoparticles in water, inclination angle, average evaporator temperature, and average condenser temperatureThermal resistance, thermal conductivity, and overall heat transfer coefficient70%/15%/15% x[39]
Cascade MLPNN x
RBFNN x
Generalized regression x
GA-MLPNNMiniature revolving heat pipe (MRVHP)Bo, Ja, Pr, Fr, and filling ratioKu (Kutateladze number)70%/30%/xx0.9623[64]
XGBoostOHPKu (Kutateladze number), Ja (Jacob number), Prliq (Prandtl number), Mo (Morton number), heat flux, target evaporator temperature, and geometric parameters (Di/Le and Do/Di)Effective heat transfer coefficient93%/7%/xxx[65]
MLPNNNanofluid-filled heat pipeHeating power and nanofluid concentrationThermal resistancex/x/xxx[73]
MLPNNOHPHeat load, filling ratio, lengths of different sections, inner and outer diameters, and number of turnsThermal resistance70%/15%/15%0.0045 *0.9946[40]
GMDH70%/30%/x0.0144 *0.9824
GA-MLPNNTwo-phase closed thermosyphonMagnetic field strength, volume fraction of nanofluid in water, and inlet powerThermal efficiency80%/20%/x0.0000315 *0.9800[54]
Thermal resistance0.001 *0.999
MLPNNTwo-phase closed thermosyphonHeat input, concentration of nanofluid, and type of nanofluidTemperature difference between evaporator and condenser75%/25%/x0.333757843 **0.9999[61]
Temperature difference between the input and the output
water streams of condenser section (ΔT)		0.001891019 **0.9997
ANFISTwo-phase closed thermosyphonType of nanofluid, concentration of nanofluid,
input power, length, and temperature difference		Thermal resistance70%/15%/15%4.175 × 10−12 *0.9999[62]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Olabi, A.G.; Haridy, S.; Sayed, E.T.; Radi, M.A.; Alami, A.H.; Zwayyed, F.; Salameh, T.; Abdelkareem, M.A. Implementation of Artificial Intelligence in Modeling and Control of Heat Pipes: A Review. Energies 2023, 16, 760. https://doi.org/10.3390/en16020760

AMA Style

Olabi AG, Haridy S, Sayed ET, Radi MA, Alami AH, Zwayyed F, Salameh T, Abdelkareem MA. Implementation of Artificial Intelligence in Modeling and Control of Heat Pipes: A Review. Energies. 2023; 16(2):760. https://doi.org/10.3390/en16020760

Chicago/Turabian Style

Olabi, Abdul Ghani, Salah Haridy, Enas Taha Sayed, Muaz Al Radi, Abdul Hai Alami, Firas Zwayyed, Tareq Salameh, and Mohammad Ali Abdelkareem. 2023. "Implementation of Artificial Intelligence in Modeling and Control of Heat Pipes: A Review" Energies 16, no. 2: 760. https://doi.org/10.3390/en16020760

APA Style

Olabi, A. G., Haridy, S., Sayed, E. T., Radi, M. A., Alami, A. H., Zwayyed, F., Salameh, T., & Abdelkareem, M. A. (2023). Implementation of Artificial Intelligence in Modeling and Control of Heat Pipes: A Review. Energies, 16(2), 760. https://doi.org/10.3390/en16020760

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop