Abstract
As the important technology of renewable energy systems, power electronics technology is directly bound up with the prospect and development of renewable energy technology. As the output end of renewable energy systems, a single-phase H-bridge converter needs to stabilize the output current. When predictive current control (PCC) tracks the reference current, the dynamic response is the fastest, but the control delay and the changes in model parameters will cause the output current steady-state error. The sliding mode predictive current control (SMPCC) algorithm is proposed to control the output current better. The proposed SMPCC scheme uses the combination of traditional PCC and variable structure scheme, and it establishes the mathematical model according to the state equation of the converter. Taking the exponential reaching law as control law, the expression of the variable structure controller is obtained. The MATLAB experimental and simulation results show that SMPCC can not only improve its robustness to the parameter changes but also obtain better steady-state performance while enhancing the rapidity of the current changes. In conclusion, SMPCC has a better control effect in the converter.
1. Introduction
The integration of large-scale renewable energy sources is essential in the efforts towards reaching carbon neutrality, and it will fundamentally reshape modern power systems. Power electronics technologies have seen significant advancements in recent years, and now they have an important role in the development of renewable energy systems. This has contributed to advances in materials, design, modeling, controls, manufacturing, and applications of new power electronics technologies that provide high performance, low cost, and high reliability for converters and renewable energy systems. As the important technology of renewable energy systems, power electronics technology is directly bound up with the prospect and development of renewable energy technology, and it is closely linked to social demand and progress. Renewable energy systems have been widely used with the consecutive development of power electronics technology, and there are applications such as solar photovoltaic systems [,,], wind generation systems [,], and hybrid energy systems [,]. In the paper, a renewable energy system is used in high-power occasions, so the output current can achieve 3000 A. As an important part of renewable energy systems, the research on DC/DC converter is mainly divided into two directions: one is to develop a novel topology to improve the conversion efficiency of the converter; the other is to propose new control methods and optimization algorithms to improve the converter performance. The switch voltage stress of a single-phase H-bridge converter is lower, and fewer components are important to improve the power density. Furthermore, the polarity of the output voltage can be changed.
DC/DC converters are strongly nonlinear, so the common algorithm cannot obtain a better effect. The simplest algorithm is proportional-integral (PI) control; many algorithms appeared later, such as bilinear theory [], sliding mode control [], adaptive control [], and other algorithms. Sliding mode variable structure control is embodied as discontinuous, and it has the characteristics of changing like a switch with the change of time. This is consistent with the DC/DC converter’s characteristic of realizing electric energy conversion by controlling the switches, so there are many applications of variable structure control in the research of many DC/DC converters. Through the established predictive model, the future state variable is predicted by using predictive control. In order to output the control variable, the error between the predicted value and the given value is used []. Comparing with using the error between the given value and the measured value, the method is better.
Predictive current control (PCC) has a better prospect with the consecutive development of digital signal processors []. As a model-based technology, PCC has many advantages, such as fast dynamic response, high current tracking accuracy, and fixed switching frequency [,,,]. In practical applications, renewable energy systems are time-varying control systems. However, PCC performance is decided by the model accuracy, and the inductor parameter cannot be accurately acquired []. The parameter perturbation leads to the mismatch of model parameters, which leads to an unsatisfactory system response and further deteriorates the control performance of the system. Reference [] improves its sensitivity to the change of inductance parameter by the online look-up table method, but its accuracy is not high. Reference [] proposed a variable-step adaptive filtering algorithm to achieve predictive control, but its steady-state error is relatively large. Reference [] improved the current equation to eliminate control delay influence, but its steady-state error still exists.
The sliding-mode algorithms have been applied to the high-performance control of power converters and motor drives for a long time []. For example, the first-order sliding-mode controller [] and the high-order sliding-mode controller []. Reference [] proposes a discrete control algorithm to suppress the influence of various disturbances on the low-speed gimbal servo system, and the constraint between controller parameters and sampling time is established to ensure the stability of the system. Reference [] demonstrates the robust performance and robust stability of the system with respect to the filter parameters uncertainties, grid impedance, grid frequency, and grid voltage, as well as the unknown load dynamics that include unbalanced loads and nonlinear loads with harmonic currents.
In order to improve the robustness, stability, and dynamic performance, this paper applies sliding mode predictive current control (SMPCC) to renewable energy systems, and it uses carrier-based pulse width modulation (PWM) control to obtain a fixed switching frequency. Compared with traditional PCC, SMPCC is less sensitive to changes in the system parameters. Firstly, the converter’s discrete model is obtained by using the mathematical model. By minimizing the error between the reference current and the predicted current, a reasonable sliding mode variable structure controller is designed. The sensitivity of the controller to the inductance parameter is reduced, and it eliminates the steady-state error in traditional PCC. In order to improve the estimation accuracy of output current, A state observer is constructed in the delay compensation. The controller is simulated and experimented with to verify the controller design rationality. Finally, simulation and experiments show that SMPCC can ensure the current dynamic response and it reduces the current steady-state error. This SMPCC reduces the sensitivity to the inductance parameter, and it achieves the expected effect in the control of renewable energy systems. The correctness and validity of SMPCC are proved.
2. Sliding Mode Predictive Current Control
2.1. Establishment of System Model
Figure 1 shows the topology, which is made up of a load , a capacitor , a parasitic resistance , an inductor , four switches, and an input voltage source . PWM1, with a control period of and a duty cycle of , is used to control M1 and M4, while PWM2, which is complementary to PWM1, controls M2 and M3. In the power-on process, the inductance and parasitic resistance will change with the magnitude of the current and the power-on time. Let the inductance value offset be .
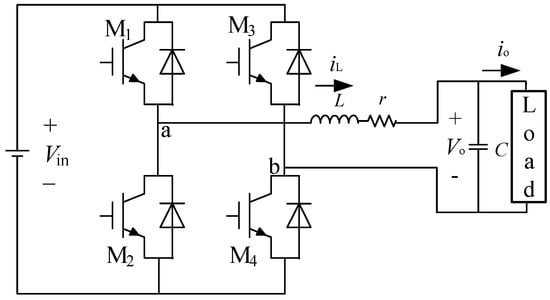
Figure 1.
The topology of single-phase H-bridge converter.
It is supposed that the converter works in continuous current mode, so the inductor current is always not equal to zero, the parasitic resistance current . is the output current, .
The system state expression can be obtained by circuit analysis as
The matrix equation is expressed as
is the switch function:
2.2. Design of Sliding Mode Controller
In order to control and at the same time, The sliding mode controller is designed according to the system state equation, and the sliding surface is designed according to the PI control idea, so the system errors are defined as follows:
in the formula, is the output reference current.
Then integrate to attain :
Then differentiate , and respectively and sort them out to attain:
Taking , and as state variables, (8)–(10) are written in the form of state equation:
where , , , can be written
The sliding mode variable of the sliding mode controller is defined as
where , , and , and are positive or negative constants at the same time.
Taking the sliding mode variable derivative and the first derivative of can be obtained.
The controller robustness and stability can be improved by selecting an appropriate reaching law for the sliding mode controller. This design adopts the exponential reaching law as a control law, which has the characteristics of fast response and small chattering []. The exponential approach law can be written:
where is the sign function.
The sign function in (15) is:
According to (14) and (15), the expression can be obtained:
Arranging (17) and replacing the switching function with , the expression can be obtained:
Chattering may occur in the process of input control, so is replaced by the saturation function , which can effectively reduce chattering so that the final expression of the controller is obtained as
where the expression of is
In the formula, , is the upper limit of the boundary layer of the switching surface, and the saturation function is used to switch the moving points outside the boundary layer while the moving points inside the boundary layer change linearly. By choosing an appropriate value, the error can converge to zero, thereby reducing chattering.
Because MATLAB deals with discrete data, the system needs to be discretized first, and
Therefore, (11) can be changed to discrete form as
In the formula, , is the third-order unit matrix and is the sampling period.
In the same way, the discrete exponential reaching law can be obtained (the sign function has been replaced by the saturation function):
From (22) and (23), the discrete sliding mode controller is obtained as
where of is substituted by the predicted value, and the discrete sliding mode predictive controller is obtained by (24).
2.3. System Stability Analysis
The Lyapunov function is used to verify the stability of the system:
is derivative to attain:
The equal sign holds if and only if .
Equation (26) shows that the sliding mode variable is asymptotically stable, and it satisfies the Lyapunov stability condition, which verifies that the system is stable.
2.4. Traditional PCC and Control Delay Compensation
The mathematical model is also
where is the voltage between point a and point b.
A cost function is used in traditional PCC. The function which defines the error of the inductor current can be written:
Equation (28) is the Euclidean distance between the estimated current and the reference current.
From (27), the inductor current predicted value which is at the time
The inductor voltage in the next moment can be obtained.
can be expressed to
The average value of in one control cycle is
The above equation is solved to attain
In order to eliminate a one-step delay of digital execution, is used in (29) instead of .
It is difficult to acquire the actual value of in the system, so the control effect is affected. The specific form of the state observer of the error is:
In the equation, is the estimated value of which is at the time, and is the gain of the state observer. In (34), the observer of consists of Equation (29) and a correction part, which is based on the error between and .
Define the state error , (34) is subtracted from (29) to obtain the dynamics error.
And we will know
where is the initial error.
By adjusting , the predicted current can gradually approach the actual current.
The inductor current ripple varies with the inductor value. The inductor current ripple equation is shown below.
where is volt seconds, and is the voltage when the inductor is conducting forward.
When the inductance parameter is inaccurate, the inductance parameter is , and the inductance current ripple can be obtained
Therefore, the difference between the inductance current ripple when the inductance parameter is inaccurate and the ideal inductance current ripple
3. Results
3.1. Simulation
In order to verify the effectiveness of SMPCC, a model is built for simulation. The control diagram is shown in Figure 2. is the carrier signal of M1 and M4, is modulated signal of M1 and M4, is the time when M4 is turned on in a control cycle, is the time when M4 is turned off in a control cycle.
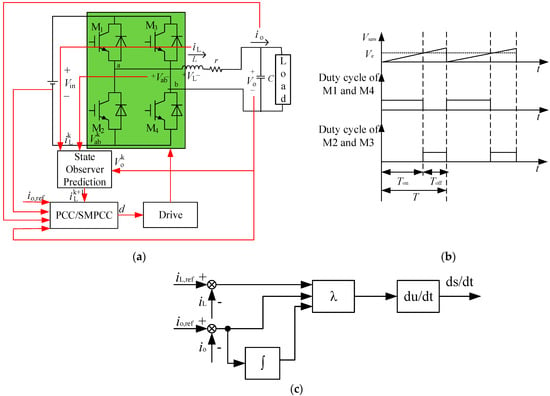
Figure 2.
The converter control algorithm. (a) The converter control diagram; (b) Pulse width modulation (PWM) algorithm; (c) The detailed block diagram of the proposed sliding mode predictive current control (SMPCC).
The parameters are: the capacitor , the switching frequency , the load resistance and parasitic resistance , the inductor , the input voltage . Take , , , , and the sampling period is 100 μs. Traditional PCC and SMPCC are simulated.
The gain of the state observer in the simulation. In Figure 3, the steady-state current analysis shows the output reference current and output control current of traditional PCC and SMPCC. The average output control current of traditional PCC is 2290 A, while that of SMPCC is 2299 A. The output control current of traditional PCC has a certain tracking error, while SMPCC can eliminate the steady-state error well, and it can accurately track the reference current. Through the comparative analysis of the simulation results, under ideal conditions, it can be found that after using SMPCC, the output control current steady-state error is reduced, so the steady-state performance is improved.
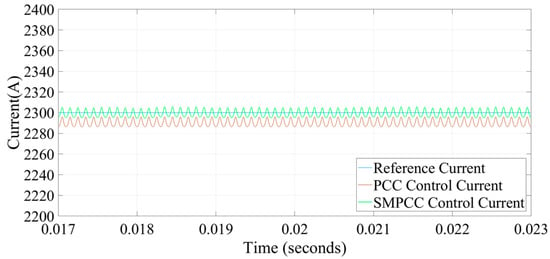
Figure 3.
The simulation analysis of steady-state current.
The output reference current increases at 0.02 s from 2300 A to 3000 A when the input voltage is unchanged; Figure 4 shows the simulation. From Figure 4a, it can be found that when the output reference current increases suddenly, the system response will lag by one cycle, which is the inherent control delay. The output control current is quickly adjusted to 3000 A and into a steady state. The total adjustment time (rise time plus adjustment time) of SMPCC is shorter than that of traditional PCC, indicating that the controller of SMPCC has a faster response speed. From Figure 4b, it can be found that the output voltage of traditional PCC is adjusted quickly to 409 V, while the output voltage of SMPCC can be adjusted faster to the theoretical value, which is 411 V. The duty cycle change diagram of M1 and M4 in SMPCC is shown in Figure 4c. In order to keep the output of the controller stable, it can be found that a larger duty cycle is given at 0.02 s. The duty cycle will not change significantly after the output is stable, and with the system fluctuation, it will change in real time. The theoretical value of the duty cycle is smaller than the actual value because there is a certain voltage at the parasitic resistance. The difference between the output voltage obtained from the actual value of the duty cycle minus the voltage at the parasitic resistance is basically consistent with the actual output voltage.
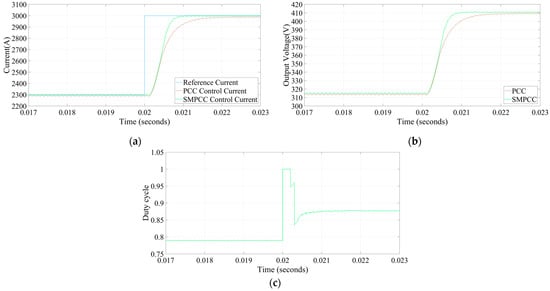
Figure 4.
The simulation when output reference current abruptly increases. (a) The output current changes; (b) The output voltage changes; (c) The duty cycle changes of M1 and M4 in SMPCC.
When the input voltage is unchanged, Figure 5 shows the simulation waveform by tracking sinusoidal current as an example. It can be found from Figure 5 that the output control current smoothly reverses. The output reference current is sinusoidal when the input voltage is unchanged; Figure 5 shows the simulation. It can be found from Figure 5a that when the output reference current is sinusoidal, the response of the system will lag by one cycle, which is the inherent control delay. Soon, the output control current can change sinusoidally when the output reference current changes, while the controller of SMPCC has a faster response speed. From Figure 5b, it can be found that the output voltage of traditional PCC can also change sinusoidally soon when the output reference current changes, while the controller of SMPCC has a faster response speed as well. Figure 5c shows the duty cycle change diagram of M1 and M4 in SMPCC. It can be found from Figure 5c that when the output reference current is sinusoidal, the controller will give the duty cycle of sinusoidal change at this time due to the sinusoidal change of output voltage, and with the system fluctuation, the duty cycle will change in real time.
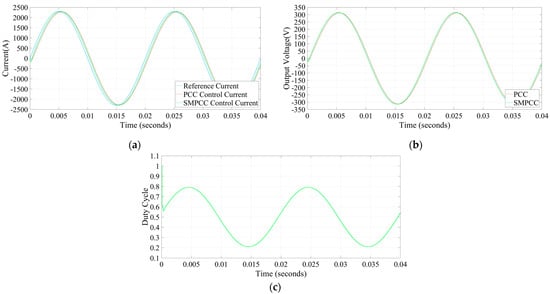
Figure 5.
The simulation when the output reference current is sinusoidal. (a) The output current changes; (b) The output voltage changes; (c) The duty cycle changes of M1 and M4 in SMPCC.
Fast Fourier transform (FFT) analysis is conducted for the output current of the two methods. Figure 6a and Figure 6b show total harmonic distortion (THD) analysis of the output current waveform under traditional PCC and SMPCC, respectively. The fundamental wave content of the output current in Figure 6a is 2280 A, and the THD of the output current is 0.27%, while that in Figure 6b is 2294 A, and the THD of the output current is 0.27% as well. Comparing Figure 6a and Figure 6b, it can be found that the output current fundamental wave content of SMPCC is closer to the output reference current value than that of traditional PCC, and the THD of SMPCC is the same as that of traditional PCC. Through the comparative analysis of the results, it can be found that under ideal conditions, the output current steady-state error is reduced, and the system’s steady-state performance is improved after using SMPCC.
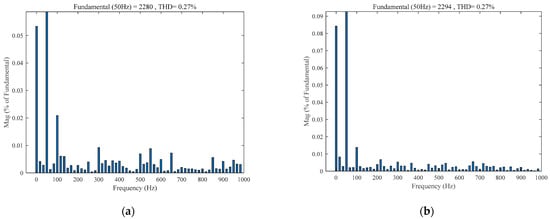
Figure 6.
Output current fast Fourier transform (FFT) analysis. (a) Traditional predictive current control (PCC); (b) Improved SMPCC.
Figure 7 shows the amplitude response waveforms of the two control methods, and the output reference currents of both methods are suddenly applied from to when . Comparing traditional PCC and SMPCC, it can be found that after the sudden change of output reference current, the system response will lag by one cycle, which is the inherent control delay. It can be found that the output control current tracking time of traditional PCC is longer than that of SMPCC after the inherent switching cycle delay of the system. In conclusion, the current response of SMPCC is faster than that of traditional PCC, which is consistent with the dynamic performance analysis.
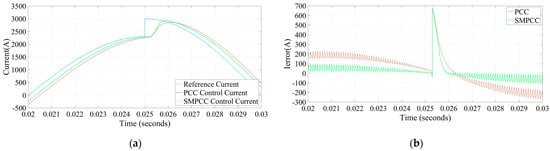
Figure 7.
Simulation of a sudden increase in the output reference current amplitude. (a) Control current; (b) Current error.
The frequency response waveforms of the two control methods are shown in Figure 8, and the output reference currents of both methods are suddenly applied from to when . Comparing traditional PCC and SMPCC, it can be found that after the sudden change of output reference current, the system response will lag by one cycle, which is the inherent control delay. It can be found that the output control current tracking time of traditional PCC is longer than that of SMPCC after the inherent switching cycle delay of the system. In conclusion, the current response of SMPCC is faster than that of traditional PCC, which is consistent with the dynamic performance analysis.
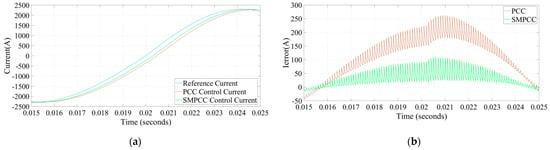
Figure 8.
Simulation of a sudden increase in the output reference current frequency. (a) Control current; (b) Current error.
To check the robustness of traditional PCC, Figure 9 shows the case where its true inductance value is different from the control value (0.1 mH). Compared with the performance under ideal conditions, it can be observed from Figure 9a that the ripple of the inductor current becomes larger in the steady state when ; in Figure 9b, the ripple of the inductor current becomes smaller when the inductor current is steady when . The simulation results are consistent with the theoretical analysis.
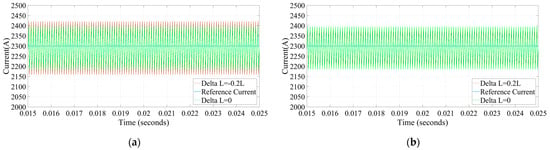
Figure 9.
When the real inductance value is different from the control value. (a) Comparison of and ; (b) Comparison of and .
To check the robustness of SMPCC, Figure 10 shows the case where its real inductance value is different from the control value (0.1 mH). It can be seen that when , the inductor current ripple value of traditional PCC is 262 A, and the current ripple error becomes 53 A. Comparing the performance under ideal conditions, it can be found that the inductor current ripple value becomes larger when , and the change is obvious. Similarly, when , the inductor current ripple value of SMPCC is 213 A, and the current ripple error becomes 2 A. It is also larger than the inductor current ripple value in the case of , but the change is smaller. Similarly, when , it can be found that the current ripple error of traditional PCC and SMPCC and the inductor current ripple value are larger than the ideal performance, but the impact on SMPCC is smaller. This shows that the inaccuracy of the inductor parameter has an impact on the steady-state performance of traditional PCC and SMPCC, but its impact on SMPCC is much smaller than that of traditional PCC. When the inductor parameter is at −20% to 20% deviation, the steady-state performance of SMPCC can still achieve satisfactory results. This is because traditional PCC only relies on the system model of the converter, and it has a greater dependence on the inductance in the control delay compensation and current prediction, while in the control delay compensation, SMPCC adds a state observer to correct its prediction of the state at the time, and it uses the combination of predictive control and variable structure scheme to greatly improve the accuracy of its model prediction. So far, the results show that in the same simulation environment, SMPCC performance is greater than that of traditional PCC.
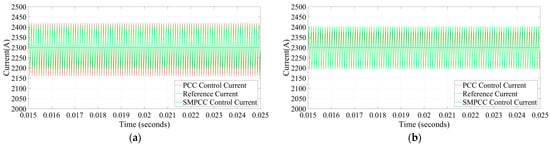
Figure 10.
When the real parasitic resistance value is different from the control value. (a) Comparison of and ; (b) Comparison of and .
3.2. Experimental
To further verify the effectiveness of SMPCC, many experiments are carried out in the prototype, which is shown in Figure 11. The main control CPU is TMS320F28335 from TI. During the experiments, the sampling frequency is 10 kHz. The experimental parameters are: the capacitance , the load resistance , the parasitic resistance , the inductance , the input voltage , other control parameters are the same as that in the simulation.

Figure 11.
The single-phase H-bridge experimental prototype.
The results under traditional PCC are presented here for comparison. The steady-state waveforms under these two methods are shown in Figure 12, and the output reference current is . Figure 12a,b are the output currents of traditional PCC and SMPCC, respectively. The average output current of traditional PCC is 2.28 A, and the average output current of SMPCC is 2.30 A, which is equal to the output reference current. The results show that both traditional PCC and SMPCC can track the output reference current well. SMPCC can greatly reduce the steady-state current error because SMPCC has many advantages, such as anti-interference and insensitivity to parameter changes. Simulation results and experimental tests show that the output current amplitude of proposed SMPCC is very close to the expected control value, and the performance is satisfactory.
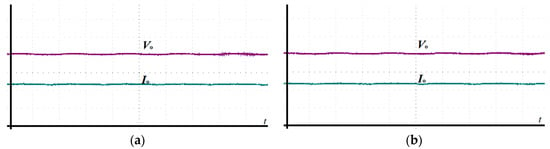
Figure 12.
Steady-state response of single-phase H-bridge converter, (10 V/div), (1 A/div). (a) traditional PCC; (b) SMPCC.
In addition to the steady-state performance comparison, Figure 13 presents the dynamic response of traditional PCC and SMPCC to sudden changes in the output reference current. In Figure 13, the output reference current is suddenly added from to , Figure 13a is the output reference current response waveform under traditional PCC, and Figure 13b is the output reference current response waveform under SMPCC. Comparing the output current responses of the two control methods, it can be found that after the output reference current changes abruptly, the steady-state error of SMPCC is smaller than that of traditional PCC, and the corresponding speed is faster, which is consistent with the situation in the simulation.
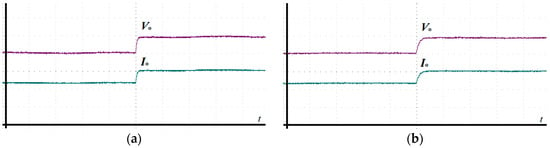
Figure 13.
Dynamic response when the output reference current changes suddenly, (10 V/div), (1 A/div). (a) traditional PCC; (b) SMPCC.
Figure 14 shows the dynamic response of traditional PCC and SMPCC when the output reference current is sinusoidal and the output reference current is . Figure 14a shows the output voltage and output control current response waveform under traditional PCC, and Figure 14b shows the output voltage and output control current response waveform under SMPCC. According to the output current response of the two control methods, the output control current of traditional PCC and SMPCC smoothly reverses when the output reference current is sinusoidal, which is consistent with the situation in the simulation.
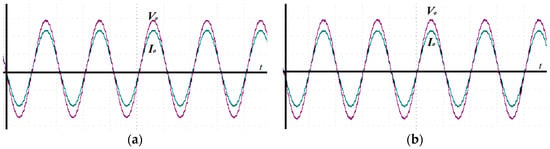
Figure 14.
Dynamic response when the output reference current is sinusoidal, (10 V/div), (1 A/div). (a) traditional PCC; (b) SMPCC.
Figure 15 shows the dynamic response of SMPCC when the amplitude of output reference current changes suddenly. After the amplitude of output reference current is suddenly added from to , SMPCC can quickly track the change of output reference current, which is consistent with the situation in the simulation.
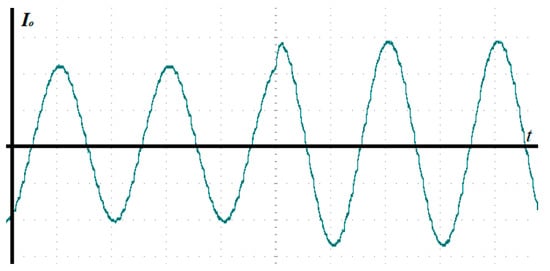
Figure 15.
Dynamic response when the amplitude of output reference current changes suddenly, (1 A/div).
Figure 16 shows the dynamic response of SMPCC when the frequency of output reference current changes suddenly. After the frequency of output reference current is suddenly added from to , SMPCC can quickly track the change of output reference current, which is consistent with the situation in the simulation.
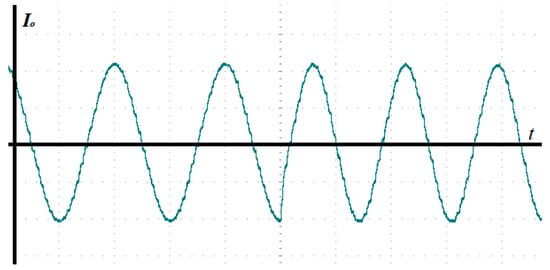
Figure 16.
Dynamic response when the frequency of output reference current changes suddenly, (1 A/div).
Through experimental and simulation analysis, the effectiveness of traditional PCC and proposed SMPCC is demonstrated. The proposed SMPCC dynamic performance is greater than that of traditional PCC. SMPCC also eliminates the steady-state error, and it is insensitive to system parameter changes. SMPCC has superior performance in practical applications.
4. Conclusions
This paper uses SMPCC to stabilize the output current quickly to the output reference current without an overshoot.
In order to reduce the control delay influence, a state observer is proposed in this paper. In view of the problem of steady-state error, a mathematical model is obtained for a renewable energy system, and the combination of traditional PCC and variable structure scheme eliminates the steady-state error in traditional PCC, and it reduces its sensitivity to inductance parameters.
Finally, the experimental and simulation results show that SMPCC has a good effect on renewable energy systems. The theoretical analysis in this paper is consistent with the experimental conclusions, which proves the effectiveness of SMPCC.
Author Contributions
Conceptualization, methodology, validation, formal analysis, investigation, data curation, writing—original draft preparation, writing—review and editing, visualization, W.Z.; resources, project administration, funding acquisition, Z.S.; software, supervision, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pandit, D.; Nguyen, N.; Elsaiah, S.; Mitra, J. Reliability evaluation of solar PV system incorporating insolation-dependent failure rates. In Proceedings of the International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021. [Google Scholar]
- Zhao, Y.; Gong, S.; Zhang, C.; Ge, M.; Xie, L. Performance analysis of a solar photovoltaic power generation system with spray cooling. Case Stud. Therm. Eng. 2022, 29, 1–12. [Google Scholar] [CrossRef]
- Vo, T.T.E.; Ko, H.; Huh, J.; Park, N. Overview of possibilities of solar floating photovoltaic systems in the offshore industry. Energies 2021, 14, 6988. [Google Scholar] [CrossRef]
- Jassim, A.K.; Ateeq, A.A. Wind energy applied as a sustainable technology to produce electrical energy in Basra. In Proceedings of the 5th International Scientific Conference on Advanced Engineering Technologies (ISC-AET) 2020 (Virtual Conference), Basra, Iraq, 18–19 August 2020. [Google Scholar]
- Tong, Y.; Fan, W.; Liu, Z. Influence of wind power generation system accessing to traction power supply system on power quality. In Proceedings of the 5th International Conference on Electrical Engineering and Information Technologies for Rail Transportation (EITRT) 2021, Qingdao, China, 21–23 October 2021. [Google Scholar]
- Saadaoui, F.; Youcef, M.; Mammar, K. Energy management of a hybrid energy system (PV/PEMFC and lithium battery) using macroscopic energy representation. In Proceedings of the Artificial Intelligence and Heuristics for Smart Energy Efficiency in Smart Cities, Tipasa, Algeria, 24–26 November 2021. [Google Scholar]
- Kumar, A.; Mishra, V.M.; Ranjan, R. A survey on hybrid renewable energy system for standalone and grid connected applications: Types, storage options, trends for research and control strategies. WSEAS Trans. Electron. 2020, 11, 80–85. [Google Scholar] [CrossRef]
- Chen, F.; Cai, X.S. Design of feedback control laws for switching regulators based on the bilinear large signal model. IEEE Trans. Power Electron. 1990, 5, 236–240. [Google Scholar] [CrossRef]
- Malesani, L.; Spiazzi, R.G.; Tenti, P. Performance optimization of Cuk converters by sliding-mode control. IEEE Trans. Power Electron. 1995, 10, 302–309. [Google Scholar] [CrossRef]
- Ramirez, H.S.; Esteban, M.G.; Zinober, A.S.I. Dynamical adaptive pulse-width-modulation control of DC-to-DC power converters: A backstepping approach. Int. J. Control 1996, 65, 205–222. [Google Scholar] [CrossRef]
- Xi, Y.; Li, D.W.; Lin, S. Model predictive control—Status and challenge. Acta Autom. Sin. 2013, 39, 222–236. [Google Scholar] [CrossRef]
- Ma, J.; Song, W.; Wang, S.; Feng, X. Deadbeat predictive direct power control of single-phase three-level pulse rectifiers. Proc. Chin. Soc. Electr. Eng. 2015, 35, 935–943. [Google Scholar] [CrossRef]
- Yu, B.; Chang, L. Improved predictive current controlled PWM for single-phase grid-connected voltage source inverters. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005. [Google Scholar]
- Zhang, X.; Hou, B.; Mei, Y. Deadbeat predictive current control of permanent-magnet synchronous motors with stator current and disturbance observer. IEEE Trans. Power Electron. 2016, 32, 3818–3834. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, G.; Rong, F.; Feng, J.; Jia, L.; He, J.; Huang, S. Robust fault-tolerant predictive current control for permanent magnet synchronous motors considering demagnetization fault. IEEE Trans. Ind. Electron. 2018, 65, 5324–5334. [Google Scholar] [CrossRef]
- Mohamed, Y.A.I.; El-Saadany, E.F. Robust high bandwidth discrete-time predictive current control with predictive internal model—A unified approach for voltage-source PWM converters. IEEE Trans. Power Electron. 2008, 23, 126–136. [Google Scholar] [CrossRef]
- Nishida, Y.; Miyashita, O.; Haneyoshi, T.; Tomita, H.; Maeda, A. A predictive instantaneous-current PWM controlled rectifier with AC-side harmonic current reduction. IEEE Trans. Ind. Electron. 1997, 44, 337–343. [Google Scholar] [CrossRef]
- Wu, T.F.; Sun, K.H.; Kuo, C.L.; Chang, C.H. Predictive current controlled 5-kW single-phase bidirectional inverter with wide inductance variation for DC-microgrid applications. IEEE Trans. Power Electron. 2010, 25, 3076–3084. [Google Scholar] [CrossRef]
- Wu, Z.; Zou, Y.; Zhang, Z.; Zhang, Y. Adaptive predictive controller of supply current applied in single-phase PWM rectifier. Trans. China Electrotech. Soc. 2010, 25, 73–79. [Google Scholar]
- Yang, L.; Yang, S.; Zhang, W.; Chen, Z.; Xu, L. The improved deadbeat predictive current control method for single-phase PWM rectifiers. Proc. Chin. Soc. Electr. Eng. 2015, 35, 5842–5850. [Google Scholar] [CrossRef]
- Cavallo, A.; Canciello, G.; Russo, A. Supervised energy management in advanced aircraft applications. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018; pp. 2769–2774. [Google Scholar] [CrossRef]
- Li, H.; Chen, X.; Zhang, H.; Cui, X. High-precision speed control for low-speed gimbal systems using discrete sliding mode observer and controller. IEEE J. Em. Sel. Top. P. 2022, 10, 2871–2880. [Google Scholar] [CrossRef]
- Dehkordi, N.M.; Sadati, N.; Hamzeh, M. A robust backstepping high-order sliding mode control strategy for grid-connected DG units with harmonic/interharmonic current compensation capability. IEEE Trans. Sustain. Energ. 2017, 8, 561–572. [Google Scholar] [CrossRef]
- Le, J.Y.; Xie, Y.X.; Ji, Y.P.; Zhang, Z. Sliding-mode variable-structure control of CCM buck converter based on exact feedback linearization. J. South China Univ. Technol. 2012, 40, 130–135+160. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).