Contagion Spillover from Bitcoin to Carbon Futures Pricing: Perspective from Investor Attention
Abstract
:1. Introduction
2. Related Literature
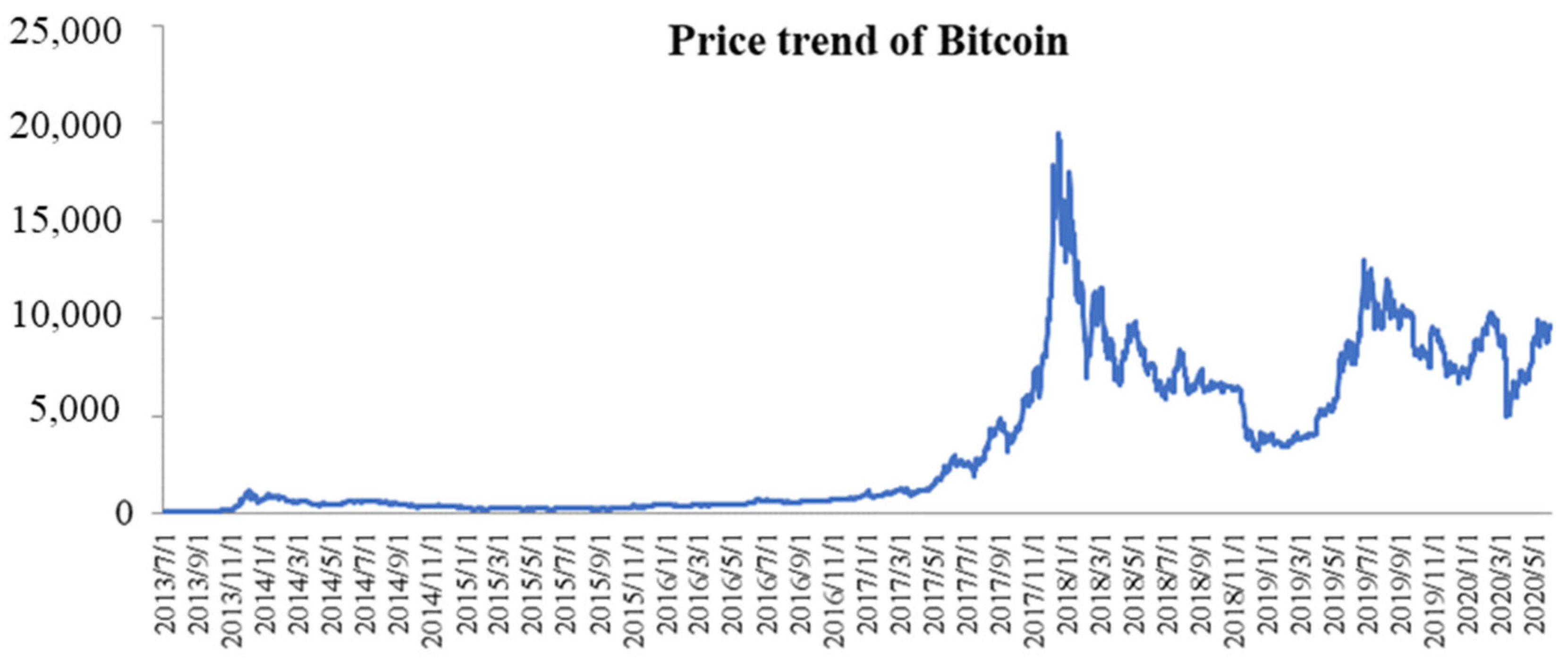
3. Data
4. Methods
4.1. VAR and Granger Causality
4.2. Squared Bitcoin Attention
4.3. Interactive Terms
4.4. Controlling Other Variables
4.5. Models and Indicators for Out-of-Sample Forecasting
5. Results for In-Sample and Out-of-Sample
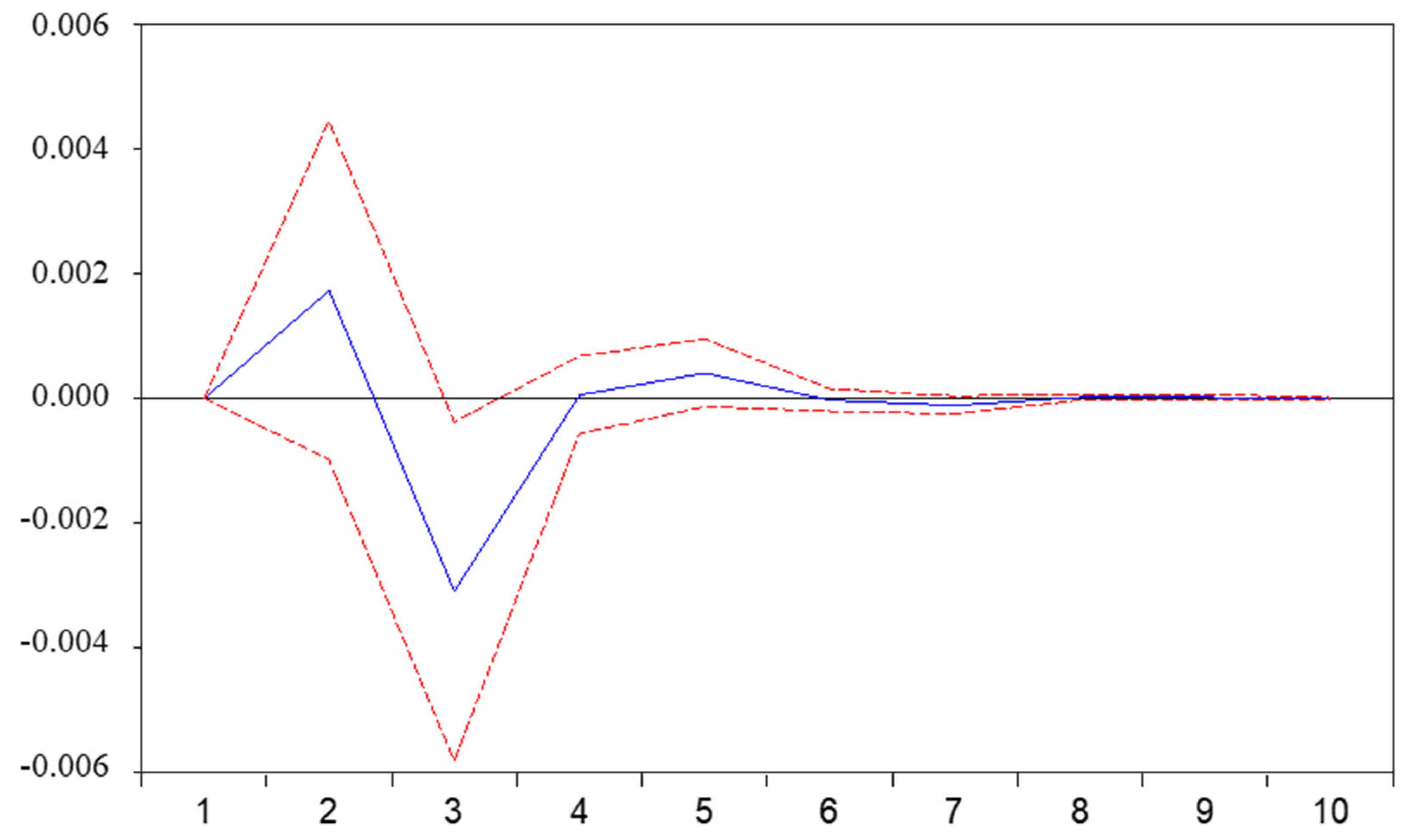
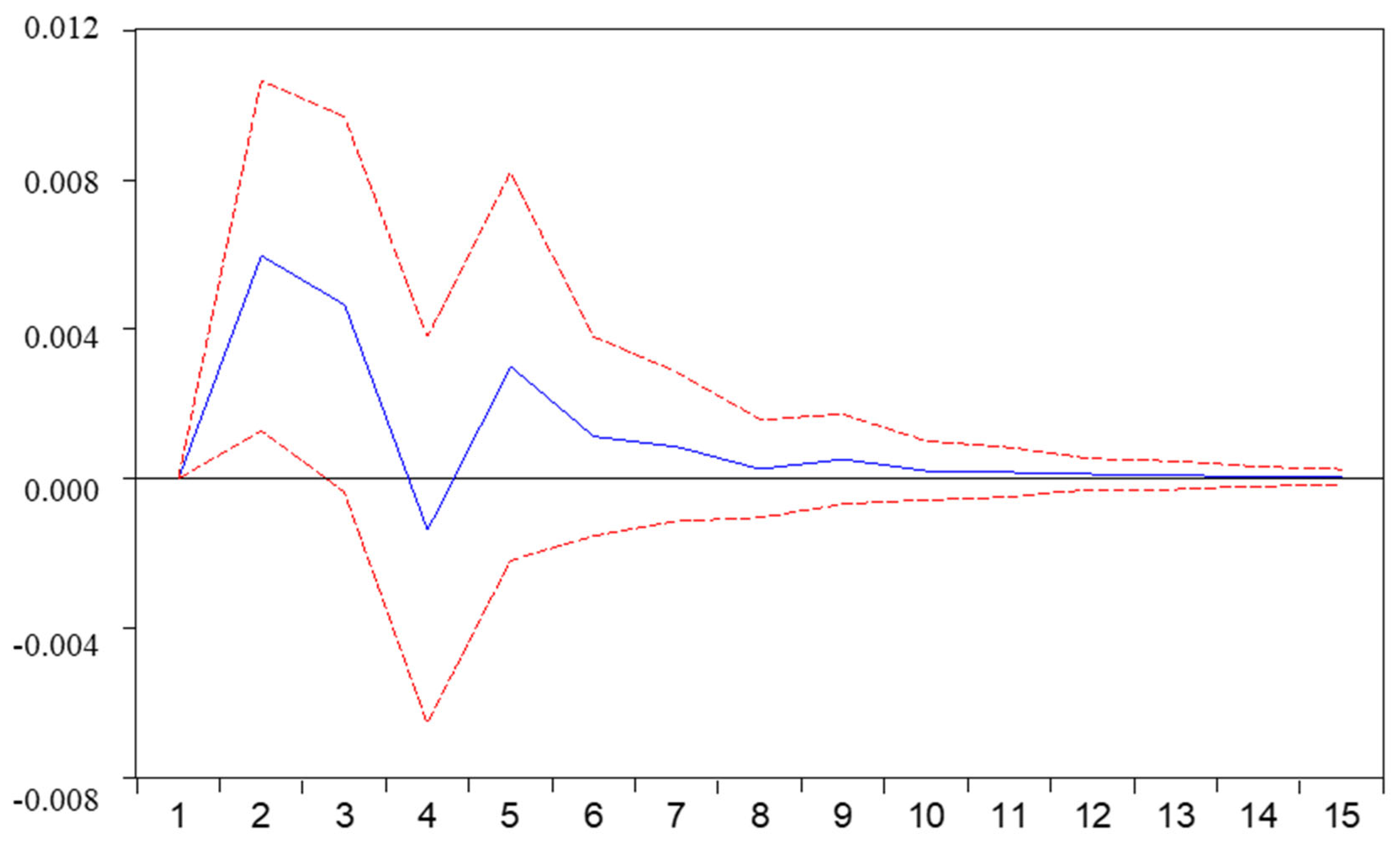
5.1. VAR and Granger Causality
5.2. Nonlinear Impact of Bitcion Attention
5.3. Interactive Terms
5.4. Controlling Other Variables
5.5. Out-of-Sample Forecasts
6. Economic Values
7. Robustness Checks
7.1. Update Sample Frequency
7.2. Twitter Based Investor Attention
7.3. Twitter Based Uncertainty
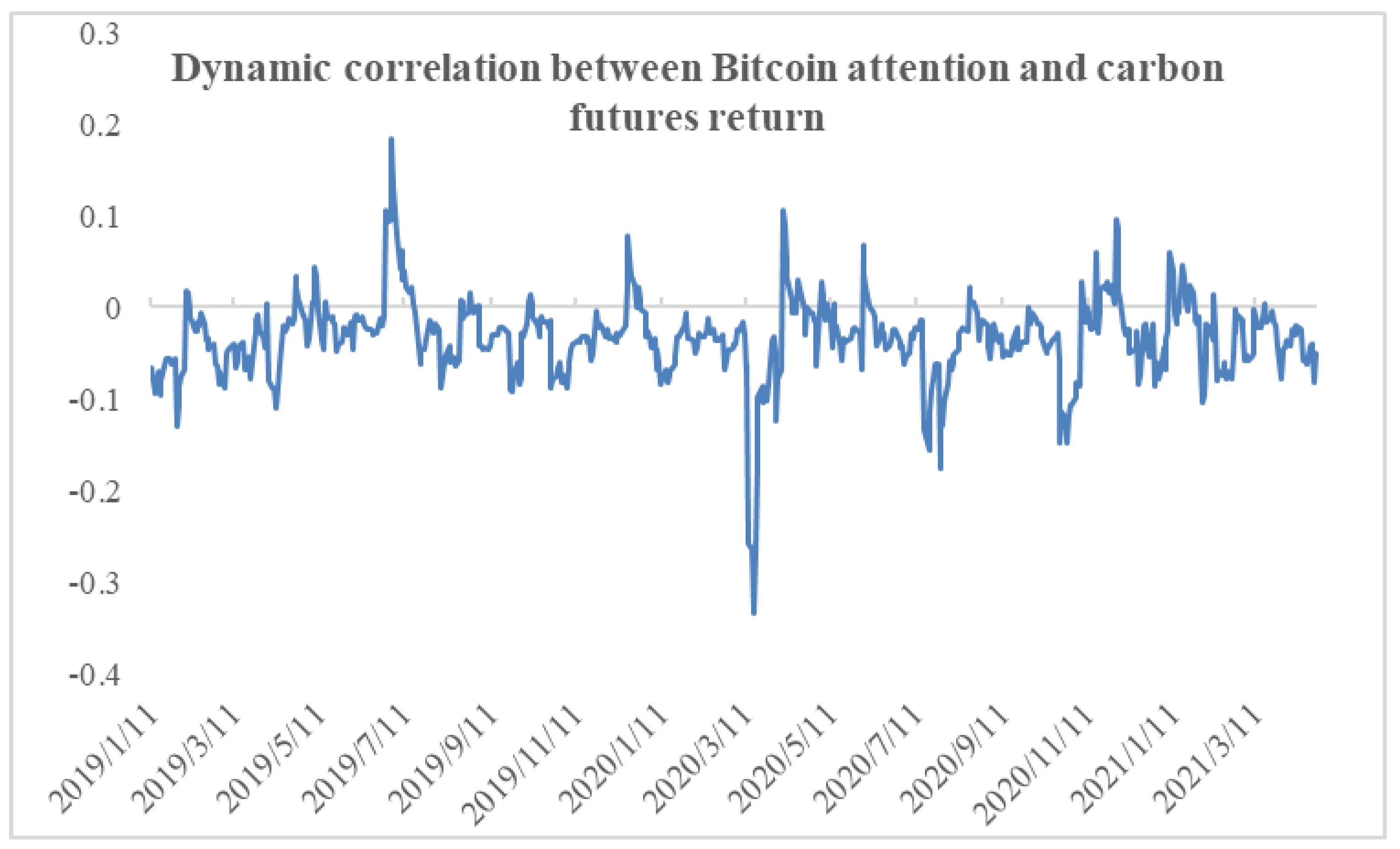
7.4. VAR-DCC-GARCH Based Dynamic Correlation
8. Further Discussions
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teixidó, J.; Verde, S.F.; Nicolli, F. The impact of the EU emissions trading system on low-carbon technological change: The empirical evidence. Ecol. Econ. 2019, 164, 106347. [Google Scholar] [CrossRef]
- Zhao, X.; Han, M.; Ding, L.; Kang, W. Usefulness of economic and energy data at different frequencies for carbon price forecasting in the EU ETS. Appl. Energy 2018, 216, 132–141. [Google Scholar] [CrossRef]
- Aatola, P.; Ollikainen, M.; Toppinen, A. Price determination in the EU ETS market: Theory and econometric analysis with market fundamentals. Energy Econ. 2013, 36, 380–395. [Google Scholar] [CrossRef]
- Zhu, P.; Zhang, X.; Wu, Y.; Zheng, H.; Zhang, Y. Investor attention and cryptocurrency: Evidence from the Bitcoin market. PLoS ONE 2021, 16, e0246331. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Duan, K.; Urquhart, A. Time-varying dependence between Bitcoin and green financial assets: A comparison between pre-and post-COVID-19 periods. J. Int. Financ. Mark. Inst. Money 2023, 82, 101687. [Google Scholar] [CrossRef]
- Jiang, S.; Li, Y.; Lu, Q.; Hong, Y.; Guan, D.; Xiong, Y.; Wang, S. Policy assessments for the carbon emission flows and sustainability of Bitcoin blockchain operation in China. Nat. Commun. 2021, 12, 1938. [Google Scholar] [CrossRef] [PubMed]
- Paolella, M.S.; Taschini, L. An econometric analysis of emission allowance prices. J. Bank Financ. 2008, 32, 2022–2032. [Google Scholar] [CrossRef] [Green Version]
- Benz, E.; Trück, S. Modeling the price dynamics of CO2 emission allowances. Energy Econ. 2009, 31, 4–15. [Google Scholar] [CrossRef]
- Feng, Z.H.; Zou, L.L.; Wei, Y.M. Carbon price volatility: Evidence from EU ETS. Appl. Energy 2011, 88, 590–598. [Google Scholar] [CrossRef]
- Dutta, A. Modeling and forecasting the volatility of carbon emission market: The role of outliers, time-varying jumps and oil price risk. J. Clean. Prod. 2018, 172, 2773–2781. [Google Scholar] [CrossRef]
- Milunovich, G.; Joyeux, R. Pricing efficiency and arbitrage in the EU ETS carbon futures market. J. Invest. Strategy 2007, 2, 23–26. [Google Scholar]
- Kanen, J.L.M. Carbon Trading and Pricing; Environmental Finance Publications: London, UK, 2006. [Google Scholar]
- Arouri, M.E.H.; Nguyen, D.K. Oil prices, stock markets and portfolio investment: Evidence from sector analysis in Europe over the last decade. Energy Policy 2010, 38, 4528–4539. [Google Scholar] [CrossRef] [Green Version]
- Ciner, C. Energy shocks and financial markets: Nonlinear linkages. Stud. Nonlinear Dyn. Econom. 2001, 5, 203–212. [Google Scholar] [CrossRef]
- Ren, X.; Dou, Y.; Dong, K.; Yan, C. Spillover effects among crude oil, carbon, and stock markets: Evidence from nonparametric causality-in-quantiles tests. Appl. Econ. 2022, 1–24. [Google Scholar] [CrossRef]
- Chevallier, J.; Sévi, B. On the realized volatility of the ECX CO2 emissions 2008 futures contract: Distribution, dynamics and forecasting. Ann. Financ. 2011, 7, 1–29. [Google Scholar] [CrossRef]
- Zhu, B.; Wei, Y. Carbon price forecasting with a novel hybrid ARIMA and least squares support vector machines methodology. Omega-Int. J. Manag. Sci. 2013, 41, 517–524. [Google Scholar] [CrossRef]
- Zhu, B.; Han, D.; Wang, P.; Wu, Z.; Zhang, T.; Wei, Y.M. Forecasting carbon price using empirical mode decomposition and evolutionary least squares support vector regression. Appl. Energy 2017, 191, 521–530. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Li, D.; Hao, Y.; Tan, Z. A hybrid model using signal processing technology, econometric models and neural network for carbon spot price forecasting. J. Clean. Prod. 2018, 204, 958–964. [Google Scholar] [CrossRef]
- Hao, Y.; Tian, C.; Wu, C. Modelling of carbon price in two real carbon trading markets. J. Clean. Prod. 2020, 244, 118556. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, B. Forecasting Regional Carbon Prices in China Based on Secondary Decomposition and a Hybrid Kernel-Based Extreme Learning Machine. Energies 2022, 15, 3562. [Google Scholar] [CrossRef]
- Adra, S.; Barbopoulos, L.G. The valuation effects of investor attention in stock-financed acquisitions. J. Empir. Financ. 2018, 45, 108–125. [Google Scholar] [CrossRef]
- Audrino, F.; Sigrist, F.; Ballinari, D. The impact of sentiment and attention measures on stock market volatility. Int. J. Forecast. 2020, 36, 334–357. [Google Scholar] [CrossRef]
- Pham, L.; Huynh, T.L.D. How does investor attention influence the green bond market? Financ. Res. Lett. 2020, 35, 101533. [Google Scholar] [CrossRef]
- Wang, Y. Volatility spillovers across NFTs news attention and financial markets. Int. Rev. Financ. Anal. 2022, 83, 102313. [Google Scholar] [CrossRef]
- Vozlyublennaia, N. Investor attention, index performance, and return predictability. J. Bank Financ. 2014, 41, 17–35. [Google Scholar] [CrossRef]
- Da, Z.; Engelberg, J.; Gao, P. In search of attention. J. Financ. 2011, 66, 1461–1499. [Google Scholar] [CrossRef]
- Han, L.; Lv, Q.; Yin, L. Can investor attention predict oil prices? Energy Econ. 2017, 66, 547–558. [Google Scholar] [CrossRef]
- Yao, T.; Zhang, Y.J.; Ma, C.Q. How does investor attention affect international crude oil prices? Appl. Energy 2017, 205, 336–344. [Google Scholar] [CrossRef]
- Han, L.; Xu, Y.; Yin, L. Does investor attention matter? The attention-return relationships in FX markets. Econ. Model. 2018, 68, 644–660. [Google Scholar] [CrossRef]
- Kou, Y.; Ye, Q.; Zhao, F.; Wang, X. Effects of investor attention on commodity futures markets. Financ. Res. Lett. 2018, 25, 190–195. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhu, P.; Wu, Y.; Zhang, Y. Research on the Volatility of the Cotton Market under Different Term Structures: Perspective from Investor Attention. Sustainability 2022, 14, 14389. [Google Scholar] [CrossRef]
- Chen, R.; Qian, Q.; Jin, C.; Xu, M.; Song, Q. Investor attention on internet financial markets. Financ. Res. Lett. 2020, 36, 101421. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, Y. Coronation Day of Financial Market, Investor Attention, and Stock Return: A Perspective of Local and Global Media. Emerg. Mark. Financ. Trade 2021, 58, 1–14. [Google Scholar] [CrossRef]
- Ibikunle, G.; McGroarty, F.; Rzayev, K. More heat than light: Investor attention and bitcoin price discovery. Int. Rev. Financ. Anal. 2020, 69, 101459. [Google Scholar] [CrossRef]
- Su, X.; Zhan, W.; Li, Y. Quantile dependence between investor attention and cryptocurrency returns: Evidence from time and frequency domain analyses. Appl. Econ. 2021, 53, 6439–6471. [Google Scholar] [CrossRef]
- Wang, C.; Shen, D.; Li, Y. Aggregate investor attention and Bitcoin return: The long short-term memory networks perspective. Financ. Res. Lett. 2022, 49, 103143. [Google Scholar] [CrossRef]
- Neto, D. Examining interconnectedness between media attention and cryptocurrency markets: A transfer entropy story. Econ. Lett. 2022, 214, 110460. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Wu, Y.; Zhu, P. Investor attention and carbon return: Evidence from the EU-ETS. Ekon. Istraz. 2021, 35, 709–727. [Google Scholar] [CrossRef]
- Pan, D.; Zhang, C.; Zhu, D.; Hu, S. Carbon price forecasting based on news text mining considering investor attention. Environ. Sci. Pollut. Res. 2022, 1–14. [Google Scholar] [CrossRef]
- Wu, Y.; Han, L.; Yin, L. Our currency, your attention: Contagion spillovers of investor attention on currency returns. Econ. Model. 2019, 80, 49–61. [Google Scholar] [CrossRef]
- Yin, L.; Feng, J. Can investors attention on oil markets predict stock returns? N. Am. Econ. Financ. 2019, 48, 786–800. [Google Scholar] [CrossRef]
- Ding, Q.; Huang, J.; Zhang, H. Time-frequency spillovers among carbon, fossil energy and clean energy markets: The effects of attention to climate change. Int. Rev. Financ. Anal. 2022, 83, 102222. [Google Scholar] [CrossRef]
- Ali, F.; Bouri, E.; Naifar, N.; Shahzad, S.J.H.; AlAhmad, M. An examination of whether gold-backed Islamic cryptocurrencies are safe havens for international Islamic equity markets. Res. Int. Bus. Financ. 2022, 63, 101768. [Google Scholar] [CrossRef]
- Han, L.; Wu, Y.; Yin, L. Investor attention and currency performance: International evidence. Appl. Econ. 2018, 50, 2525–2551. [Google Scholar] [CrossRef]
- Guidolin, M.; Hyde, S. Can VAR models capture regime shifts in asset returns? A long-horizon strategic asset allocation perspective. J. Bank Financ. 2012, 36, 695–716. [Google Scholar] [CrossRef] [Green Version]
- Anggraeni, W.; Andri, K.B.; Mahananto, F. The performance of ARIMAX model and Vector Autoregressive (VAR) model in forecasting strategic commodity price in Indonesia. Procedia Comput. Sci. 2017, 124, 189–196. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Lin, J.J. Can the VAR model outperform MRS model for asset allocation in commodity market under different risk preferences of investors? Int. Rev. Financ. Anal. 2019, 66, 101395. [Google Scholar] [CrossRef]
- Ren, X.; Dou, Y.; Dong, K.; Li, Y. Information spillover and market connectedness: Multi-scale quantile-on-quantile analysis of the crude oil and carbon markets. Appl. Econ. 2022, 54, 4465–4485. [Google Scholar] [CrossRef]
- Yin, L.; Feng, J.; Liu, L.; Wang, Y. It’s not that important: The negligible effect of oil market uncertainty. Int. Rev. Econ. Financ. 2019, 60, 62–84. [Google Scholar] [CrossRef]
- Welch, I.; Goyal, A. A comprehensive look at the empirical performance of equity premium prediction. Rev. Financ. Stud. 2008, 21, 1455–1508. [Google Scholar] [CrossRef]
- Clark, T.E.; West, K.D. Approximately normal tests for equal predictive accuracy in nested models. J. Econom. 2007, 138, 291–311. [Google Scholar] [CrossRef]
- Neely, C.J.; Rapach, D.E.; Tu, J.; Zhou, G. Forecasting the equity risk premium: The role of technical indicators. Manag. Sci. 2014, 60, 1772–1791. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wei, Y.; Wu, C.; Yin, L. Oil and the short-term predictability of stock return volatility. J. Empir. Financ. 2018, 47, 90–104. [Google Scholar] [CrossRef]
- Ferreira, M.A.; Santa-Clara, P. Forecasting stock market returns: The sum of the parts is more than the whole. J. Financ. Econ. 2011, 100, 514–537. [Google Scholar] [CrossRef] [Green Version]
- Shen, D.; Urquhart, A.; Wang, P. Does twitter predict bitcoin? Econ. Lett. 2019, 174, 118–122. [Google Scholar] [CrossRef]
- Ustaoğlu, E. Return and Volatility Spillover between Cryptocurrency and Stock Markets: Evidence from Turkey. J. Account. Financ. 2022, 93, 117–126. [Google Scholar] [CrossRef]
- Ren, X.; Li, J.; He, F.; Lucey, B. Impact of climate policy uncertainty on traditional energy and green markets: Evidence from time-varying granger tests. Renew. Sust. Energy Rev. 2023, 173, 113058. [Google Scholar] [CrossRef]


| Panel A: Descriptive Statistics | ||||||
| Mean | std. dev | min | max | Skewness | Kurtosis | |
| Carbon futures return | 0.0014 | 0.0281 | −0.1594 | 0.1331 | −0.0973 | 2.776 |
| Bitcoin attention | 0.0218 | 0.1457 | −0.4260 | 0.7985 | 1.2130 | 4.6775 |
| Bitcoin return | 0.0039 | 0.0388 | −0.3918 | 0.1941 | −0.7493 | 15.0439 |
| Panel B: ADF Stationary Test | ||||||
| Type | T-Statistics | |||||
| Carbon Futures Return | Bitcoin Attention | Bitcoin Return | ||||
| Intercept | −21.4022 *** | −18.6729 *** | −31.8958 *** | |||
| Trend and intercept | −21.3944 *** | −18.6801 *** | −31.9082 *** | |||
| None | −21.4216 *** | −17.8842 *** | −31.5704 *** | |||
| Lag | LR | FPE | AIC | SC | HQ |
|---|---|---|---|---|---|
| 1 | 5.9447 | 1.53 × 10−5 | −5.4130 | −5.3564 | −5.3906 |
| 2 | 27.2447 | 1.46 × 10−5 | −5.4584 | −5.3640 * | −5.4211 * |
| 3 | 7.7233 | 1.46 × 10−5 | −5.4580 | −5.3260 | −5.4059 |
| 4 | 12.4481 * | 1.45 × 10−5 * | −5.4690 * | −5.2992 | −5.4019 |
| −0.0354 (0.0478) | −0.4005 * (0.2218) | |
| 0.0682 (0.0474) | −0.0967 (0.2203) | |
| −0.0106 (0.0471) | 0.0935 (0.2186) | |
| 0.0401 (0.0470) | −0.1360 (0.2183) | |
| 0.0065 (0.0104) | −0.0956 ** (0.0481) | |
| −0.0292 *** (0.0103) | −0.2265 *** (0.0481) | |
| −0.0201 ** (0.0104) | −0.1040 ** (0.0484) | |
| −0.0312 *** (0.0104) | −0.0708 (0.0485) | |
| Constant | 0.0021 (0.0014) | 0.0320 *** (0.0067) |
| 0.0517 | 0.0663 | |
| 23.5008 *** | 30.6262 *** | |
| Granger Causality test | F-statistics | |
| Carbon return does not Granger cause Bitcoin attention | 0.9521 | |
| Bitcoin attention does not Granger cause carbon return | 4.5617 *** | |
| Coefficient | Standard Error | |
|---|---|---|
| −0.0351 | 0.0482 | |
| 0.0669 | 0.0479 | |
| −0.0113 | 0.0476 | |
| 0.0354 | 0.0475 | |
| −0.0005 | 0.0131 | |
| −0.0344 *** | 0.0129 | |
| −0.0221 * | 0.0126 | |
| −0.0197 | 0.0127 | |
| 0.0315 | 0.0329 | |
| 0.0177 | 0.0321 | |
| 0.0047 | 0.0318 | |
| −0.0655 ** | 0.0321 | |
| Constant | 0.0024 | 0.0016 |
| 0.0623 | ||
| F-statistic | 2.32 *** | |
| Coefficient | Standard Error | |
|---|---|---|
| −0.0545 | 0.0496 | |
| 0.0210 | 0.0493 | |
| 0.0019 | 0.0487 | |
| 0.0444 | 0.0486 | |
| 0.0081 | 0.0104 | |
| −0.0244 ** | 0.0104 | |
| −0.0180 * | 0.0104 | |
| −0.0296 *** | 0.0105 | |
| 0.2976 | 0.3398 | |
| 1.1354 *** | 0.3382 | |
| 0.0140 | 0.3419 | |
| 0.4089 | 0.3409 | |
| Constant | 0.0021 | 0.0014 |
| 0.0856 | ||
| F-statistic | 3.26 *** | |
| Equation (5) | Equation (6) | |
|---|---|---|
| −0.0623 (0.0506) | −0.0896 * (0.0504) | |
| 0.0503 (0.0500) | 0.0550 (0.0494) | |
| −0.0490 (0.0498) | −0.0258 (0.0490) | |
| 0.0224 (0.0500) | 0.0299 (0.0493) | |
| 0.0085 (0.0105) | 0.0119 (0.0105) | |
| −0.0299 *** (0.0104) | −0.0242 ** (0.0103) | |
| −0.0205 * (0.0105) | −0.0189 * (0.0104) | |
| −0.0318 *** (0.0105) | −0.0283 *** (0.0104) | |
| 0.0280 (0.0414) | 0.0543 (0.0460) | |
| 0.0254 (0.0416) | −0.0362 (0.0461) | |
| 0.1031 ** (0.0415) | 0.0461 (0.0461) | |
| 0.0599 (0.0414) | 0.0134 (0.0458) | |
| −0.3756 * (0.2152) | ||
| 0.5439 ** (0.2103) | ||
| 0.4136 * (0.2121) | ||
| 0.6790 *** (0.2189) | ||
| Constant | 0.0021 (0.0015) | 0.0021 (0.0014) |
| 0.0756 | 0.1216 | |
| F-statistic | 2.85 *** | 3.58 *** |
| Equation (7) | Equation (8) | Equation (9) | Equation (10) | Equation (11) | |
|---|---|---|---|---|---|
| −0.0201 | −0.0713 | −0.0615 | −0.0293 | 0.0262 | |
| 1.0050 | 0.4195 | 0.4665 | 0.9442 | 1.8268 ** |
| Equation (7) | Equation (8) | Equation (9) | Equation (10) | Equation (11) | |
|---|---|---|---|---|---|
| Panel A: forecast horizon is 2 | |||||
| −0.0180 | −0.0712 | −0.0615 | −0.0286 | 0.0282 | |
| 1.0609 | 0.4702 | 0.4825 | 0.9735 | 1.8489 ** | |
| Panel B: forecast horizon is 3 | |||||
| −0.0209 | −0.0766 | −0.0650 | −0.0317 | 0.0248 | |
| 0.9968 | 0.3634 | 0.4178 | 0.9189 | 1.7941 ** | |
| Panel C: forecast horizon is 4 | |||||
| −0.0186 | −0.0732 | −0.0635 | −0.0290 | 0.0279 | |
| 1.0521 | 0.4558 | 0.4709 | 0.9728 | 1.8454 ** | |
| Panel D: forecast horizon is 5 | |||||
| −0.0240 | −0.0806 | −0.0691 | −0.0329 | 0.0246 | |
| 0.9285 | 0.3307 | 0.3723 | 0.8890 | 1.7554 ** | |
| Forecast Horizon = 1 | Forecast Horizon = 2 | Forecast Horizon = 3 | Forecast Horizon = 4 | Forecast Horizon = 5 | |
|---|---|---|---|---|---|
| : Equation (11) | 0.0262 | 0.0282 | 0.0248 | 0.0279 | 0.0246 |
| : Equation (14) | 0.0156 | 0.0172 | 0.0163 | 0.0169 | 0.0172 |
| Indicator | Benchmark | Equation (7) | Equation (8) | Equation (9) | Equation (10) | Equation (11) | ||
|---|---|---|---|---|---|---|---|---|
| b_cp = 0 | 3 | Utility | 0.0010 | 0.0039 | 0.0038 | 0.0033 | 0.0031 | 0.0048 |
| SR | 0.1251 | 0.1696 | 0.1718 | 0.1430 | 0.1284 | 0.2114 | ||
| 6 | Utility | 0.0009 | 0.0030 | 0.0025 | 0.0023 | 0.0023 | 0.0036 | |
| SR | 0.1251 | 0.1749 | 0.1475 | 0.1363 | 0.1361 | 0.2067 | ||
| 9 | Utility | 0.0009 | 0.0022 | 0.0019 | 0.0019 | 0.0018 | 0.0028 | |
| SR | 0.1251 | 0.1651 | 0.1463 | 0.1440 | 0.1348 | 0.1976 | ||
| b_cp = 10 | 3 | Utility | 0.0010 | 0.0032 | 0.0031 | 0.0026 | 0.0024 | 0.0040 |
| SR | 0.1227 | 0.1393 | 0.1379 | 0.1157 | 0.1011 | 0.1773 | ||
| 6 | Utility | 0.0009 | 0.0024 | 0.0019 | 0.0018 | 0.0017 | 0.0030 | |
| SR | 0.1227 | 0.1433 | 0.1124 | 0.1085 | 0.1048 | 0.1733 | ||
| 9 | Utility | 0.0009 | 0.0018 | 0.0015 | 0.0016 | 0.0013 | 0.0023 | |
| SR | 0.1227 | 0.1326 | 0.1114 | 0.1167 | 0.1031 | 0.1670 | ||
| b_cp= 20 | 3 | Utility | 0.0010 | 0.0025 | 0.0024 | 0.0020 | 0.0017 | 0.0032 |
| SR | 0.1202 | 0.1087 | 0.1037 | 0.0880 | 0.0735 | 0.1426 | ||
| 6 | Utility | 0.0009 | 0.0018 | 0.0012 | 0.0013 | 0.0011 | 0.0024 | |
| SR | 0.1203 | 0.1114 | 0.0769 | 0.0803 | 0.0730 | 0.1392 | ||
| 9 | Utility | 0.0009 | 0.0013 | 0.0011 | 0.0012 | 0.0008 | 0.0018 | |
| SR | 0.1203 | 0.0998 | 0.0762 | 0.0889 | 0.0709 | 0.1357 |
| Panel A: Lag Length Equals to 1 | ||
| VAR estimation | ||
| −0.0178 (0.0906) | 0.0908 (0.3230) | |
| −0.0531 ** (0.0257) | −0.0830 (0.0918) | |
| Constant | 0.0027 ** (0.0013) | 0.0233 *** (0.0046) |
| 0.0345 | 0.0080 | |
| Granger Causality test | -statistics | |
| Carbon return does not Granger cause Bitcoin attention | 0.079 | |
| Bitcoin attention does not Granger cause carbon return | 4.255 ** | |
| Panel B: lag length equals to 2 | ||
| VAR estimation | ||
| 0.0093 | 0.0466 | |
| (0.0916) | (0.3312) | |
| −0.0971 | −0.0205 | |
| (0.0895) | (0.3237) | |
| −0.0492 * | −0.0873 | |
| (0.0256) | (0.0925) | |
| 0.0257 | −0.0391 | |
| (0.0262) | (0.0947) | |
| Constant | 0.0020 | 0.0246 *** |
| (0.0014) | (0.0052) | |
| 0.0541 | 0.0092 | |
| Granger Causality test | -statistics | |
| Carbon return does not Granger cause Bitcoin attention | 0.0242 | |
| Bitcoin attention does not Granger cause carbon return | 5.1272 * | |
| Panel C: lag length equals to 4 | ||
| VAR estimation | ||
| 0.0029 | 0.1254 | |
| (0.0922) | (0.3432) | |
| −0.1173 | 0.0147 | |
| (0.0908) | (0.3379) | |
| −0.1250 | 0.1799 | |
| (0.0900) | (0.3350) | |
| −0.0105 | 0.3604 | |
| (0.0890) | (0.3311) | |
| −0.0511 ** | −0.0896 | |
| (0.0250) | (0.0929) | |
| 0.0233 | −0.0337 | |
| (0.0257) | (0.0955) | |
| −0.0152 | −0.0054 | |
| (0.0257) | (0.0958) | |
| 0.0395 | −0.0074 | |
| (0.0257) | (0.0958) | |
| Constant | 0.0020 | 0.0239 *** |
| (0.0017) | (0.0063) | |
| 0.0980 | ||
| Granger Causality test | -statistics | |
| Carbon return does not Granger cause Bitcoin attention | 1.4584 | |
| Bitcoin attention does not Granger cause carbon return | 8.3173 * | |
| −0.0632 (0.0774) | −0.2957 (0.3662) | |
| 0.0806 (0.0772) | 0.1051 (0.3649) | |
| −0.0440 (0.0765) | 0.1405 (0.3616) | |
| 0.0839 (0.0765) | −0.2934 (0.3618) | |
| −0.0087 (0.0164) | −0.2418 (0.0776) | |
| −0.0361 ** (0.0168) | −0.2388 (0.0792) | |
| −0.0298 * (0.0168) | −0.1177 (0.0796) | |
| −0.0403 ** (0.0165) | −0.1809 (0.0780) | |
| Constant | 0.0045 (0.0031) | 0.0609 (0.0147) |
| 0.0823 | 0.1078 | |
| 14.43241 * | 19.45013 ** | |
| Granger Causality test | F-statistics | |
| Carbon return does not Granger cause Twitter-based Bitcoin attention | 0.3372 | |
| Twitter-based Bitcoin attention does not Granger cause carbon return | 2.5307 ** | |
| Equation (15) | Equation (16) | Equation (17) | Equation (18) | |
|---|---|---|---|---|
| −0.0546 (0.0411) | −0.0574 (0.0411) | −0.0565 (0.0412) | −0.0744 * (0.0410) | |
| 0.0755 * (0.0406) | 0.0775 * (0.0408) | 0.0751 * (0.0407) | 0.0642 (0.0405) | |
| −0.0282 (0.0405) | −0.0245 (0.0406) | −0.0275 (0.0406) | −0.0307 (0.0402) | |
| 0.0590 (0.0404) | 0.0601 (0.0406) | 0.0599 (0.0404) | 0.0579 (0.0404) | |
| 0.0024 (0.0080) | 0.0039 (0.0080) | 0.0022 (0.0081) | 0.0056 (0.0080) | |
| −0.0163 ** (0.0080) | −0.0162 ** (0.0080) | −0.0153 * (0.0081) | −0.0191 ** (0.0080) | |
| −0.0146 * (0.0080) | −0.0163 ** (0.0080) | −0.0147 * (0.0081) | −0.0196 ** (0.0080) | |
| −0.0174 ** (0.0080) | −0.0178 ** (0.0081) | −0.0173 * (0.0081) | −0.0220 *** (0.0081) | |
| −0.0053 (0.0052) | −0.0054 (0.0053) | |||
| 0.0022 (0.0054) | 0.0035 (0.0055) | |||
| −0.0132 ** (0.0054) | −0.0127 ** (0.0055) | |||
| −0.0034 (0.0052) | −0.0031 (0.0053) | |||
| 0.0002 (0.0044) | −0.0012 (0.0045) | |||
| −0.0053 (0.0045) | −0.0033 (0.0046) | |||
| −0.0012 (0.0045) | 0.0013 (0.0046) | |||
| −0.0040 (0.0044) | −0.0010 (0.0045) | |||
| −0.0002 (0.0335) | ||||
| −0.0443 (0.0335) | ||||
| −0.0178 (0.0336) | ||||
| −0.0078 (0.0337) | ||||
| 0.0160 (0.0240) | ||||
| −0.0593 ** (0.0239) | ||||
| −0.0621 ** (0.0240) | ||||
| −0.0533 ** (0.0242) | ||||
| Constant | 0.0023 * (0.0012) | 0.0023 * (0.0012) | 0.0025 ** (0.0012) | 0.0025 * (0.0012) |
| 0.0522 | 0.0420 | 0.0558 | 0.0702 | |
| F-statistic | 2.70 *** | 2.14 ** | 2.15 *** | 2.75 *** |
| Mean | Min | Max | |
|---|---|---|---|
| Value | −0.0330 | −0.3343 | 0.1834 |
| 0.3195 *** (0.0919) | −0.1049 (0.1770) | |
| 0.1197 (0.0952) | 0.0933 (0.1833) | |
| 0.0086 (0.0948) | −0.0807 (0.1826) | |
| 0.1053 (0.0900) | −0.1294 (0.1734) | |
| 0.1294 *** (0.0481) | −0.0916 (0.0927) | |
| 0.0714 (0.0498) | −0.0318 (0.0959) | |
| −0.0662 (0.0503) | −0.0140 (0.0968) | |
| 0.0588 (0.0503) | −0.0345 (0.0969) | |
| Constant | 0.0208 *** (0.0074) | 0.0382 *** (0.0142) |
| 0.2477 | 0.0236 | |
| 38.1981 *** | 2.8044 | |
| Granger Causality test | F-statistics | |
| Realized volatility does not Granger cause Bitcoin attention | 0.3826 | |
| Bitcoin attention does not Granger cause realized volatility | 2.9860 ** | |
| Coefficient | Standard Error | |
|---|---|---|
| 0.3403 *** | 0.0926 | |
| 0.1410 | 0.0960 | |
| −0.1556 | 0.0957 | |
| 0.1887 ** | 0.0812 | |
| −0.1335 ** | 0.0604 | |
| 0.1175 * | 0.0617 | |
| −0.1100 * | 0.0609 | |
| −0.0282 | 0.0617 | |
| 2.9213 *** | 0.4679 | |
| −0.5571 | 0.5333 | |
| 0.3980 | 0.5329 | |
| 1.4290 *** | 0.5265 | |
| Constant | 0.0202 *** | 0.0066 |
| 0.4885 | ||
| F-statistic | 8.20 *** | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Zhu, P.; Zhang, Y. Contagion Spillover from Bitcoin to Carbon Futures Pricing: Perspective from Investor Attention. Energies 2023, 16, 929. https://doi.org/10.3390/en16020929
Zhou Q, Zhu P, Zhang Y. Contagion Spillover from Bitcoin to Carbon Futures Pricing: Perspective from Investor Attention. Energies. 2023; 16(2):929. https://doi.org/10.3390/en16020929
Chicago/Turabian StyleZhou, Qingjie, Panpan Zhu, and Yinpeng Zhang. 2023. "Contagion Spillover from Bitcoin to Carbon Futures Pricing: Perspective from Investor Attention" Energies 16, no. 2: 929. https://doi.org/10.3390/en16020929
APA StyleZhou, Q., Zhu, P., & Zhang, Y. (2023). Contagion Spillover from Bitcoin to Carbon Futures Pricing: Perspective from Investor Attention. Energies, 16(2), 929. https://doi.org/10.3390/en16020929





