A Hybrid Master–Slave Control Strategy for Multiple Distributed Generators in Microgrid
Abstract
:1. Introduction
- (1)
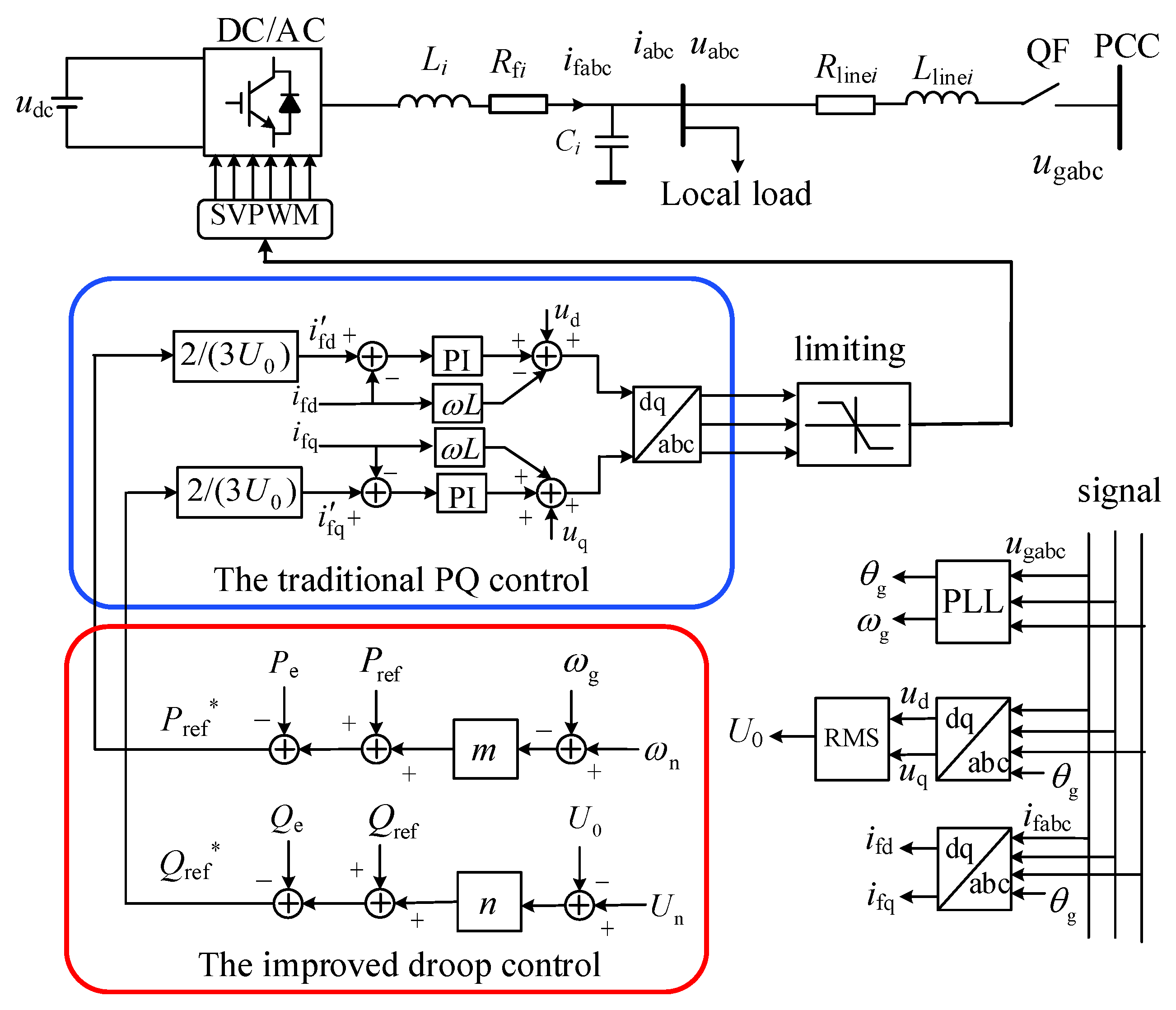
- For the slave DG using traditional PQ control, an improved droop control strategy is introduced to ensure that the slave DG has a droop output characteristic and can respond to load disturbances with the master DG. The master DG is controlled by a virtual synchronous generator (VSG) to provide voltage and frequency support for the power system.
- (2)
- Virtual coordinate transformation and virtual impedance control are introduced to realize decoupling and accurate distribution of output power of multiple DGs in a low-voltage microgrid.
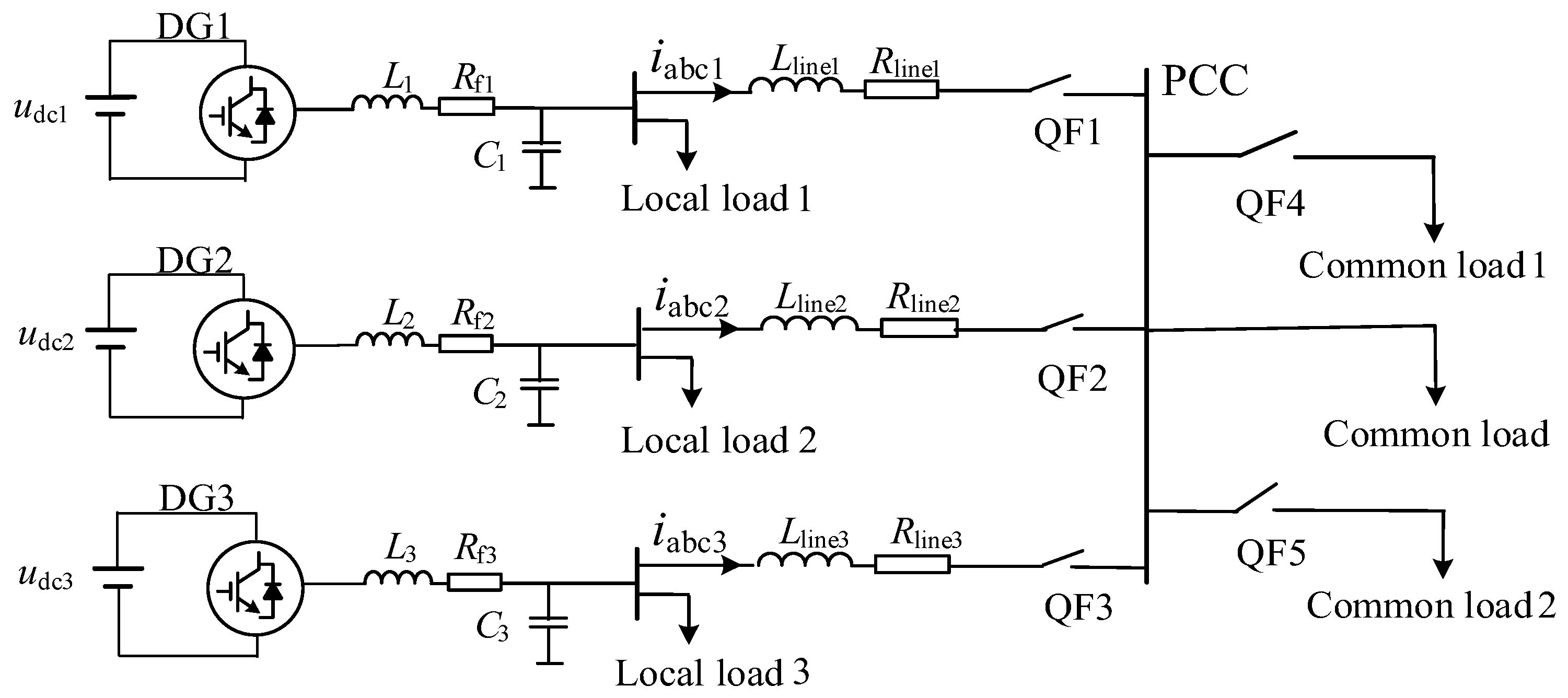
2. Topological Structure and Control Principle of Multi- DGs Hybrid Master–Slave Control
2.1. The Topology of the Multi-DGs Hybrid Master–Slave Control
2.2. Virtual Synchronous Generator Control
2.3. Improved Droop Control
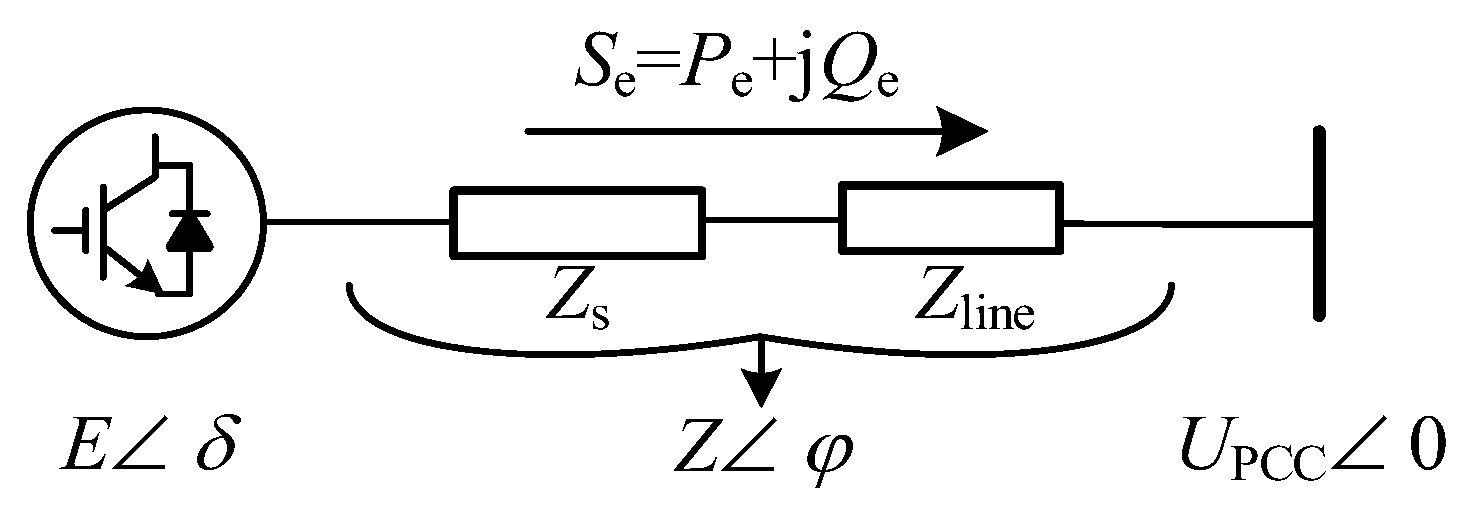
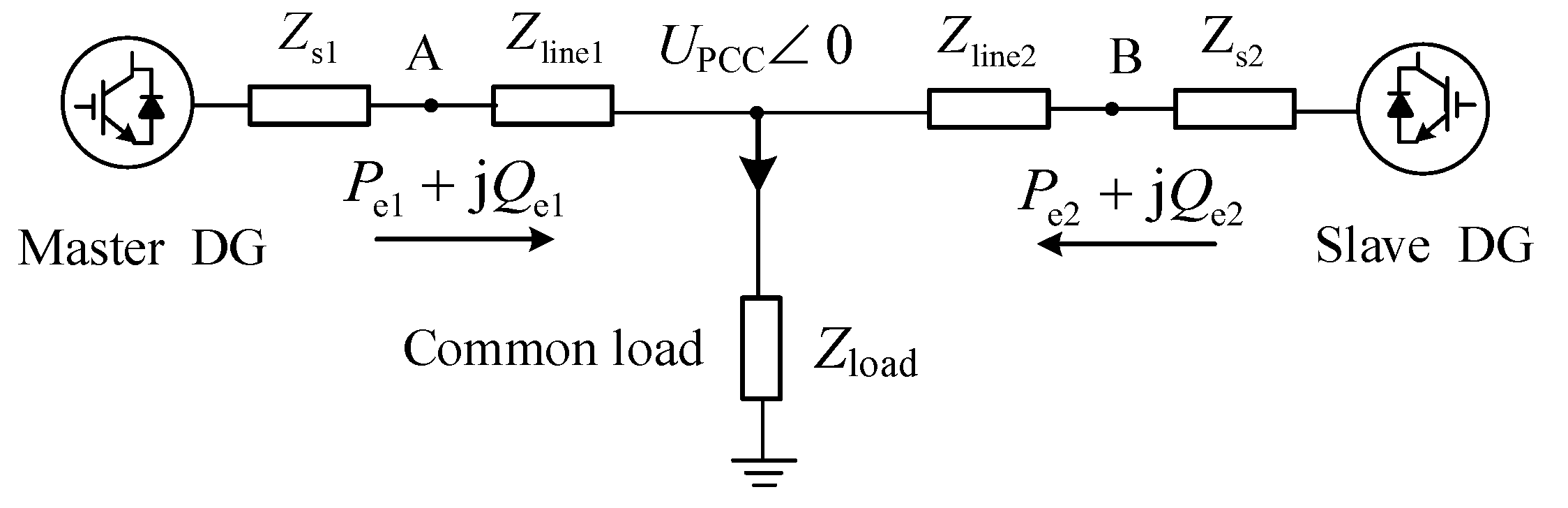
3. Precise Power Distribution for Multi-DGs Hybrid Master–Slave Control
3.1. Virtual Coordinate Transformation
3.2. Virtual Impedance Control
4. Simulation Results
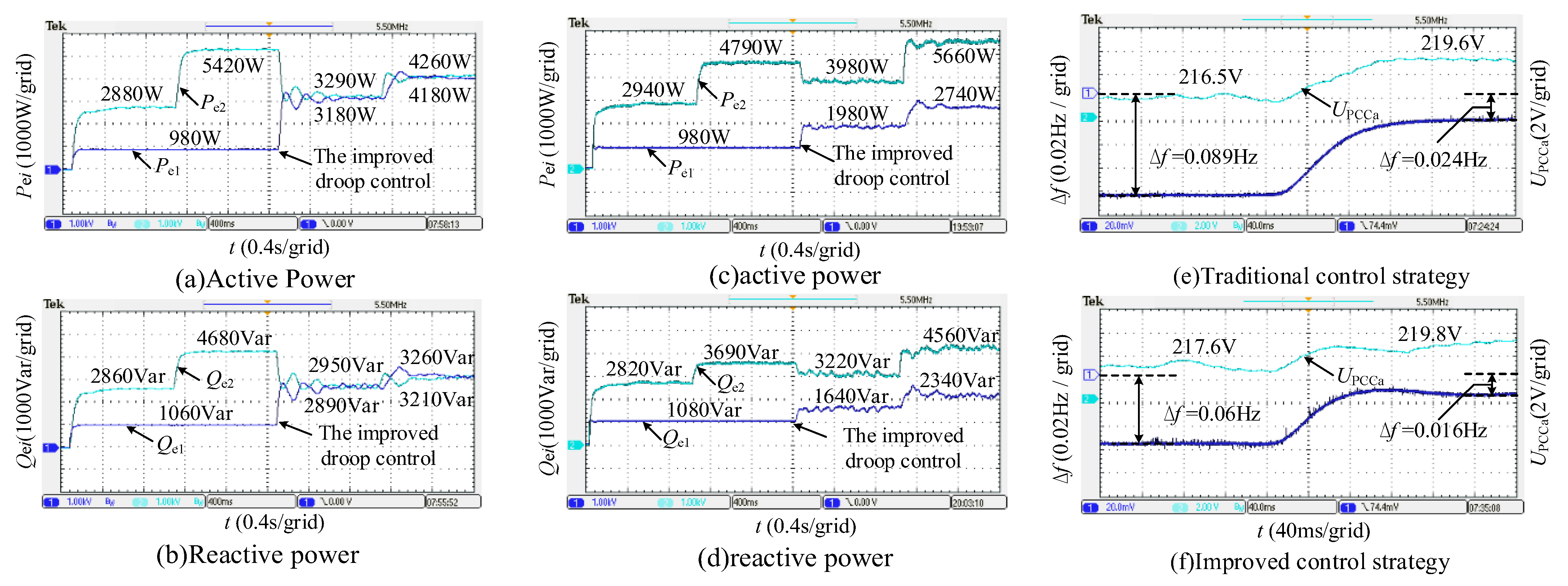
5. Experimental Results
5.1. Two DG Capacity According to 1:1 Configuration
5.2. Two DG Capacity According to 2:1 Configuration
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, G.D.; Wang, Z.Y.; Iu, H.C.; Chen, S.Z.; Ye, Y.M.; Zhang, B.; Zhang, Y. Unique modular structure of multi-cell high-boost converters with reduced component currents. IEEE Trans. Power Electron. 2017, 33, 7795–7804. [Google Scholar] [CrossRef]
- Elsaraf, H.; Jamil, M.; Pandey, B. Techno-economic design of a combined heat and power microgrid for a remote community in newfoundland Canada. IEEE Access. 2021, 9, 91548–91563. [Google Scholar] [CrossRef]
- Zhong, Q.C. Power-electronics-enabled autonomous power systems: Architecture and technical routes. IEEE Trans. Ind. Electron. 2017, 64, 5907–5918. [Google Scholar] [CrossRef]
- Yang, L.; Cao, T.; Cai, Z.; Xia, X.; Jia, C.; Dong, X.; Zhang, S. Stability analysis and robust control method for LCL-type three-phase four-wire split capacitor inverter considering zero-sequence loop. Electronics 2022, 11, 3286. [Google Scholar] [CrossRef]
- Chen, J.; Yue, D.; Dou, C.; Chen, L.; Weng, S.; Li, Y. A virtual complex impedance based P-V droop method for parallel-connected inverters in low-voltage AC Microgrids. IEEE Trans. Ind. Informat. 2021, 17, 1763–1773. [Google Scholar] [CrossRef]
- Yan, X.; Ma, H.; Jia, J.; Aslam, W.; Wang, C.; Zhang, S.; Liang, B. Precise reactive power-voltage droop control of parallel virtual synchronous generators that considers line impedance. Electronics 2021, 10, 1344. [Google Scholar] [CrossRef]
- Gupta, Y.; Chatterjee, K.; Doolla, S. A simple control scheme for improving reactive power sharing in islanded microgrid. IEEE Trans. Power Syst. 2020, 35, 3158–3169. [Google Scholar] [CrossRef]
- Li, T.; Wen, B.; Wang, H. A self-adaptive damping control strategy of virtual synchronous generator to improve frequency stability. Processes 2020, 8, 291. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Wang, C.; Wang, Z.; Ma, H.; Liang, B.; Wei, X. A united control strategy of photovoltaic-battery energy storage system based on voltage-frequency controlled VSG. Electronics 2021, 10, 2047. [Google Scholar] [CrossRef]
- Qin, B.; Xu, Y.; Yuan, C.; Jia, J. A unified method of frequency oscillation characteristic analysis for multi-vsg grid-connected system. IEEE Trans. Power Deliv. 2021, 99, 279–289. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed power system virtual inertia implemented by grid-connected power converters. IEEE Trans. Power Electron. 2017, 33, 8488–8499. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.Q.; Qiu, D.Y.; Zhang, B.; Zhang, G.D. High-performance quasi-z-source inverter with low capacitor voltage stress and small inductance. IET Power Electron. 2015, 8, 2331–2337. [Google Scholar] [CrossRef]
- Fang, J.; Li, X.; Li, H.; Tang, Y. Stability improvement for three-phase grid-connected converters through impedance reshaping in quadrature-axis. IEEE Trans. Power Electron. 2018, 33, 8365–8375. [Google Scholar] [CrossRef]
- Wu, H.; Ruan, X.; Yang, D.; Chen, X.; Zhao, W.; Lv, Z.; Zhong, Q.C. Small-signal modeling and parameters design for virtual synchronous generators. IEEE Trans. Ind. Electron. 2016, 63, 4292–4303. [Google Scholar] [CrossRef]
- Fang, J.; Zhang, R.; Li, H. Frequency derivative- based inertia enhancement by grid-connected power converters with a frequency-locked-loop. IEEE Trans. Smart Grid. 2019, 10, 4918–4927. [Google Scholar] [CrossRef]
- Dashtdar, M.; Nazir, M.S.; Bajaj, M.; Srikanth, G.B.; Hosseinimoghadam, S.M.S. Improving the sharing of active and reactive power of the islanded microgrid based on load voltage control. Smart Sci. 2022, 10, 142–157. [Google Scholar] [CrossRef]
- Zhou, X.; Tang, F.; Loh, P.C.; Jin, X.; Cao, W. Four-leg converters with improved common current sharing and selective voltage- quality enhancement for islanded microgrids. IEEE Trans. Power Deliv. 2016, 31, 522–531. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| udc1, udc2, udc3/(V) | 400 | Un/(V) | 220 |
| L1, L2, L3/(mH) | 4 | ωn/(rad/s) | 314.16 |
| J/(kg·m2) Rf1, Rf2, Rf3/(Ω) | 0.15 0.02 | K/(Var/V) C1, C2, C3/(uF) | 0.1 10 |
| m1, m2/(kW/Hz) n1, n2/(kVar/V) | 1.38 0.4 | Dp/(W/Hz) Dq/(kVar/V) | 8.8 0.8 |
| Rline1 + Xline1/(Ω) | 0.35 + j0.20 | Rv1 + Xv1/(Ω) | 0.35 + j0.3 |
| Rline2 + Xline2/(Ω) | 0.6 + j0.15 | Rv2 + Xv2/(Ω) | 0.1 + j0.35 |
| Rline3 + Xline3/(Ω) | 0.5 + j0.40 | Rv3 + Xv3/(Ω) | 0.2 + j0.1 |
| Time | UPCC/V | f/Hz | ∆UPCC/V | ∆f/Hz |
|---|---|---|---|---|
| 0 ≤ t < 0.5 | 219.96 | 49.99 | 0.04 | -0.01 |
| 0.5 ≤ t < 1 | 217.82 | 49.92 | −2.14 | −0.07 |
| 1 ≤ t < 1.5 | 215.62 | 49.85 | −2.20 | −0.07 |
| 1.5 ≤ t < 2 | 217.73 | 49.94 | 2.11 | 0.09 |
| 2 ≤ t < 3 | 216.85 | 49.89 | −0.08 | −0.05 |
| 3 ≤ t < 4 | 214.6 | 49.84 | −2.25 | −0.05 |
| Capacity Settings | Time | Pei/(∑Pei)/% | Qei/(∑Qei)/% | Does It Meet the Settings | ||
|---|---|---|---|---|---|---|
| DG1 | DG2 | DG1 | DG2 | |||
| 1:1 | 0 ≤ t < 1 | 25.4 | 74.6 | 27.0 | 73.0 | No |
| 1 ≤ t < 2 | 15.3 | 84.7 | 18.5 | 81.5 | No | |
| 2 ≤ t < 3 | 49.1 | 50.9 | 49.5 | 50.5 | Yes | |
| 3 ≤ t < 4 | 49.5 | 50.5 | 49.6 | 50.4 | Yes | |
| 2:1 | 0 ≤ t < 1 | 25.0 | 75.0 | 27.7 | 72.3 | No |
| 1 ≤ t < 2 | 17.0 | 83.0 | 22.7 | 77.3 | No | |
| 2 ≤ t < 3 | 33.2 | 66.8 | 33.7 | 66.3 | Yes | |
| 3 ≤ t < 4 | 32.6 | 67.4 | 33.9 | 66.1 | Yes | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Li, J.; Wen, Y.; Sehnan, M.; Xu, W. A Hybrid Master–Slave Control Strategy for Multiple Distributed Generators in Microgrid. Energies 2023, 16, 968. https://doi.org/10.3390/en16020968
Chen Y, Li J, Wen Y, Sehnan M, Xu W. A Hybrid Master–Slave Control Strategy for Multiple Distributed Generators in Microgrid. Energies. 2023; 16(2):968. https://doi.org/10.3390/en16020968
Chicago/Turabian StyleChen, Yanxia, Jing Li, Yu Wen, Moeed Sehnan, and Wanyu Xu. 2023. "A Hybrid Master–Slave Control Strategy for Multiple Distributed Generators in Microgrid" Energies 16, no. 2: 968. https://doi.org/10.3390/en16020968
APA StyleChen, Y., Li, J., Wen, Y., Sehnan, M., & Xu, W. (2023). A Hybrid Master–Slave Control Strategy for Multiple Distributed Generators in Microgrid. Energies, 16(2), 968. https://doi.org/10.3390/en16020968







