Intelligent Control Schemes for Maximum Power Extraction from Photovoltaic Arrays under Faults
Abstract
1. Introduction
- Maximization of a PV power system is achieved by developing FLC and PSO schemes in numerous fault scenarios. A comparison of PSO and FL schemes with the P&O scheme is performed on both a thin film and a crystalline PV array under a variety of faulty conditions, which is not reported in the literature [13,14,15]. Comparative analysis of a conventional control scheme with the FLC strategy on changing irradiance conditions is performed in the referenced works [16,17] without consideration of different PV arrays like CIGS thin film and crystalline PV arrays.
- Performance of the presented FLC scheme is also analyzed under a special case of multiple faults known as a day-to-night transition fault, in which the combined effect of the faults is examined. This special fault is also analyzed as a combined fault in this research study. Various authors [18,19,20,21,22,23,24] have designed control schemes for tracking global power peaks under shading conditions, but the introduction of multiple faults under shading makes the tracking more difficult and challenging. For the proposed study, the fuzzy logic-based MPPT and PSO schemes are designed for the analysis of multiple faults under shading conditions, which is an addition to the new aspect of the presented research work.
- Importantly, the influence of all the considered faults on current (I) and power (P) with consideration of TF and crystalline PV technology is finely inspected in this study, which is not explained comprehensively in previous work [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. The proposed FLC scheme is suitable for handling imprecise data and control of non-linear systems under fault occurrences. The occurrence of multiple faults under shading can severely impact the performance of the conventional controllers, but FLC can extract maximum power under severe multiple fault conditions, which is also performed as a significant part of the contributions of this paper.
- In this study, the challenging task of defining 49 fuzzy rules for IMFs and OMFs is performed for designing the FLC scheme to accurately track global peak power under various fault scenarios for thin film and crystalline PV arrays, which is an addition to the contributions of this paper. The proposed FLC scheme offers an optimized performance of the PV system in terms of accuracy.
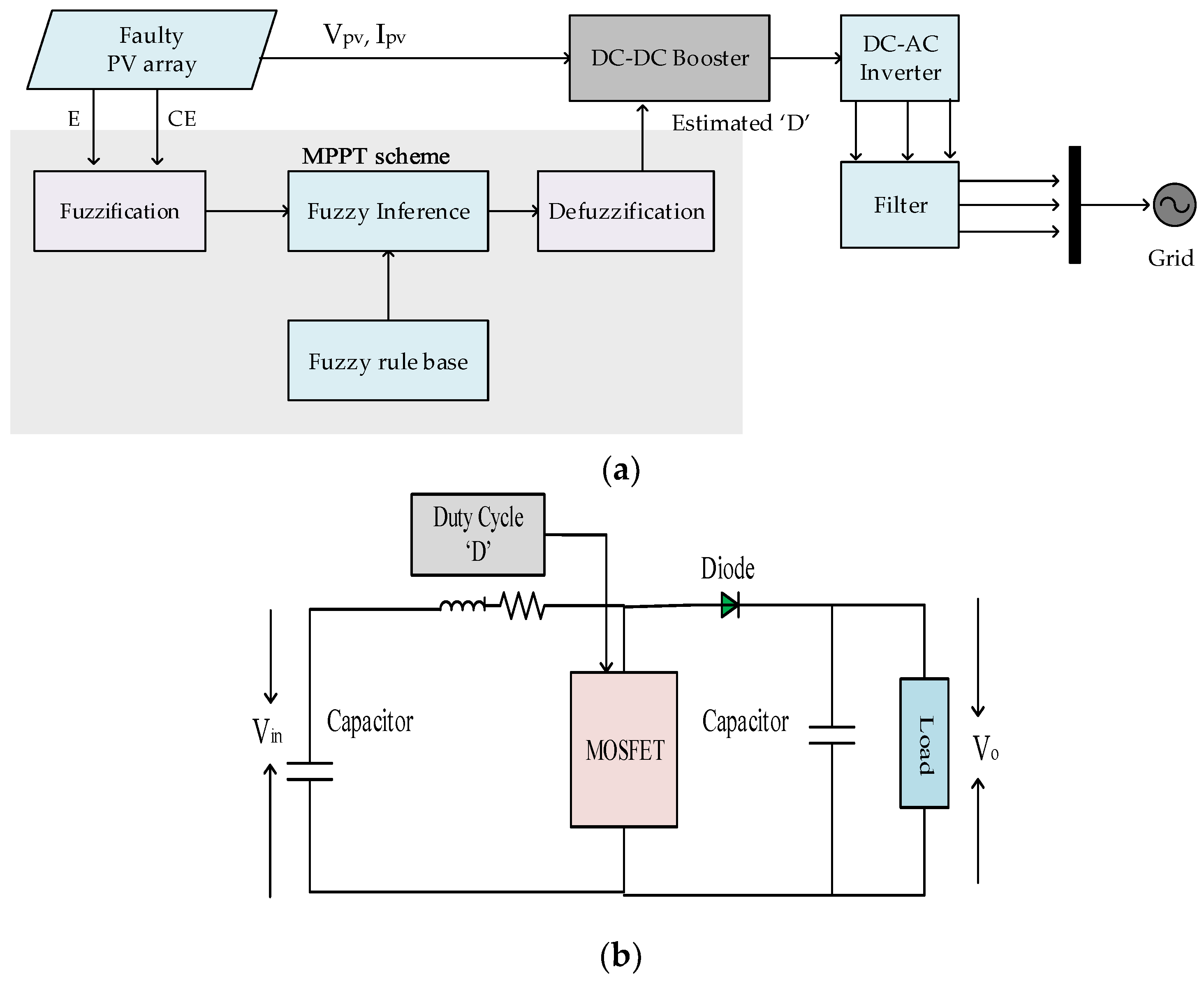
2. Proposed System Model
2.1. Operation of Boost Converter
2.2. PV Array
3. Studied Faults
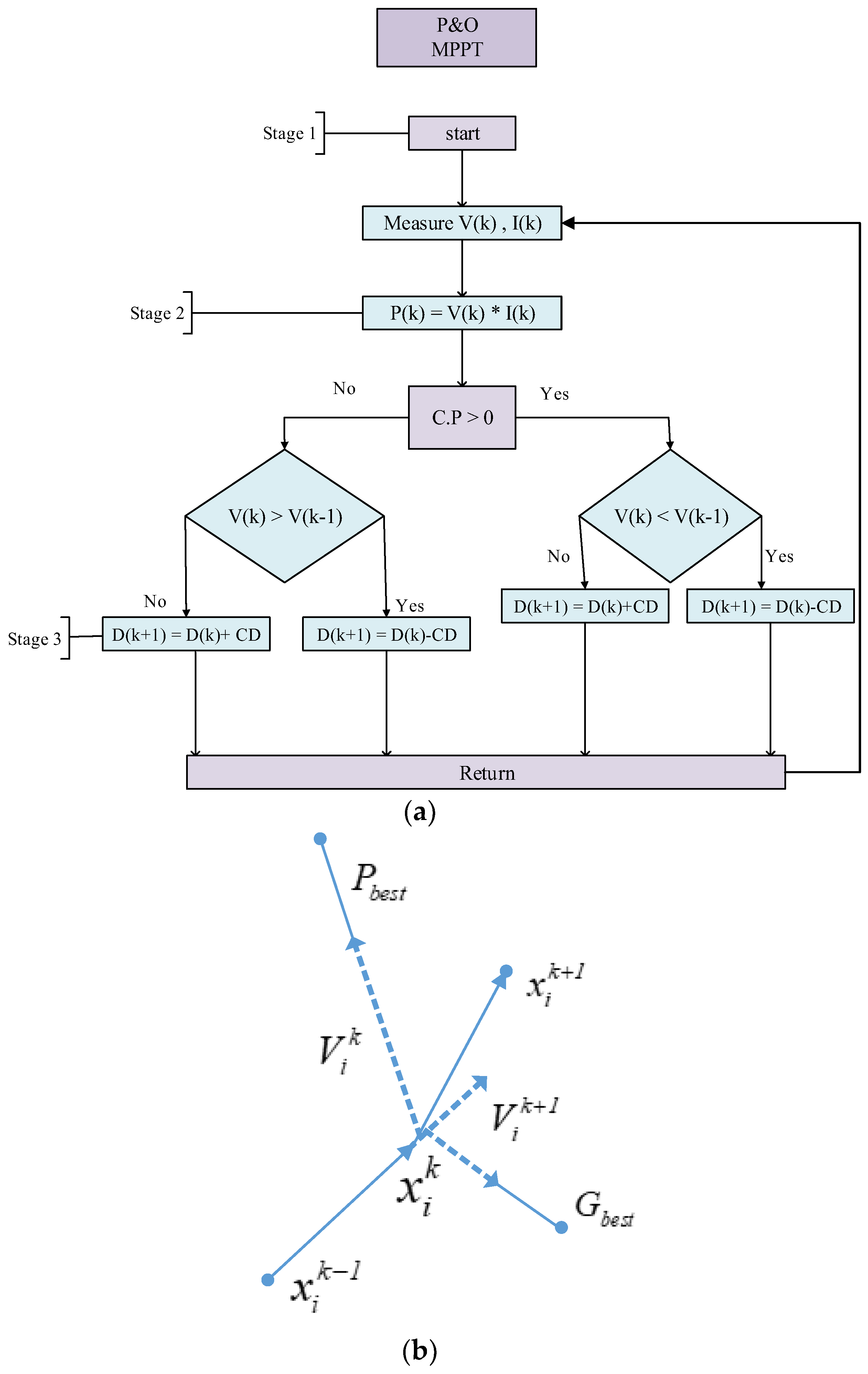
4. Adopted Strategies for Maximum Power Extraction
4.1. P&O MPPT
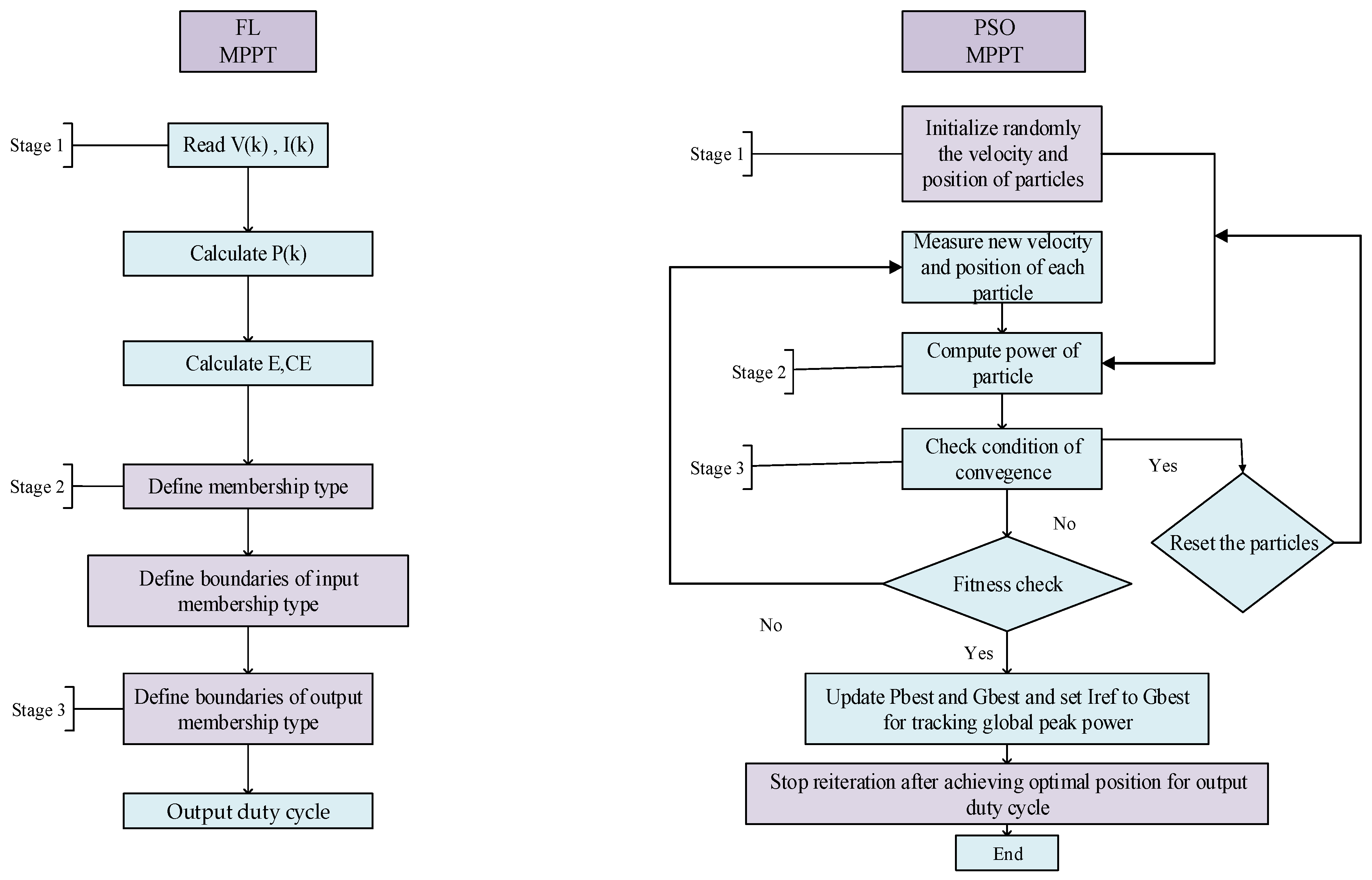
4.2. PSO-Based MPPT Scheme
4.3. FL-Based Control Scheme
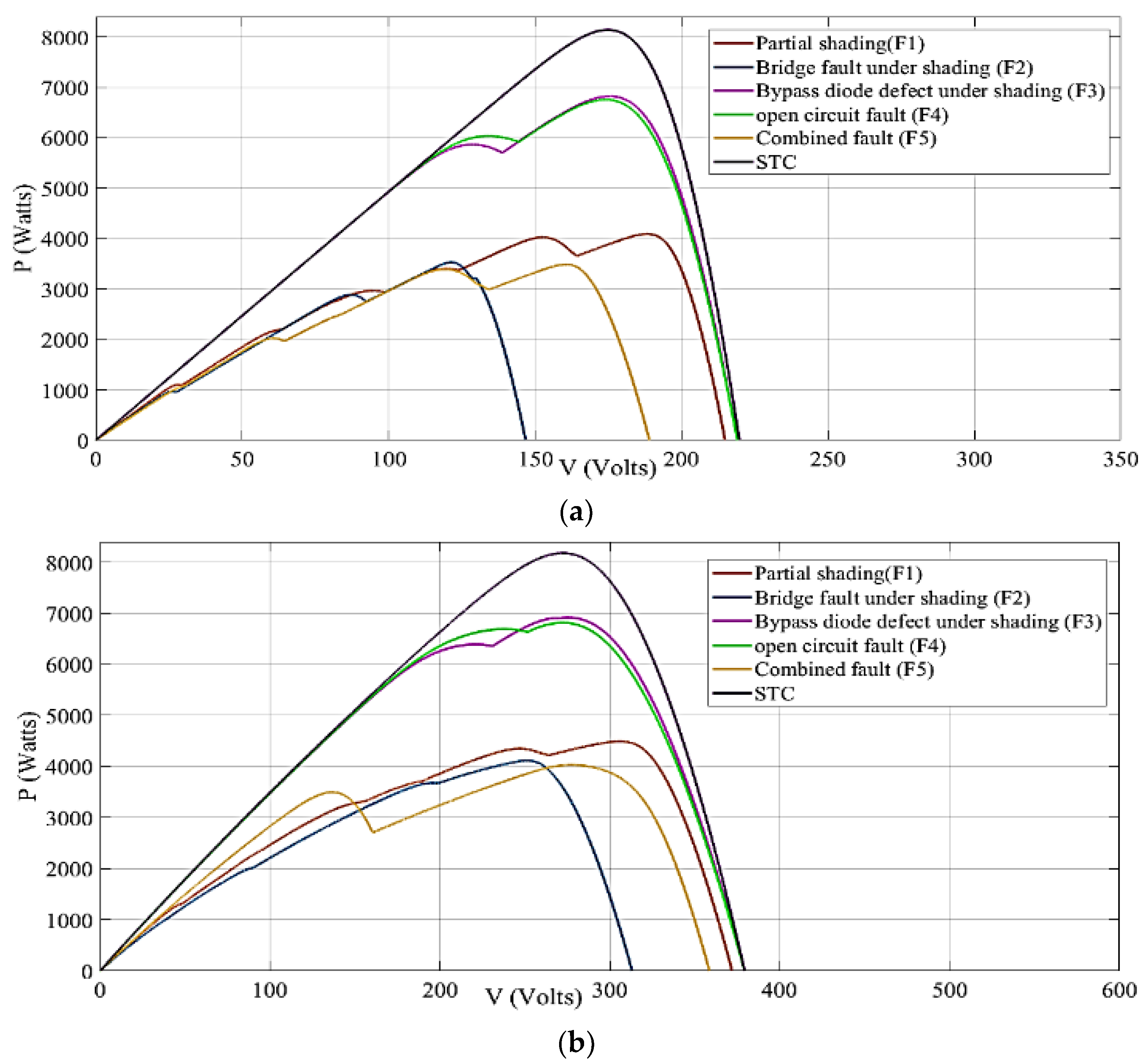
5. Numerical Analysis
Results of Faulty PV Arrays with Enabled MPPT Strategies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kivimäki, S.J. Revisited perturbation frequency design guideline for direct fixed-step maximum power point tracking algo-rithms. IEEE Trans. Ind. Elec. 2017, 64, 4601–4609. [Google Scholar] [CrossRef]
- Meral, M.; Çelík, D. A comprehensive survey on control strategies of distributed generation power systems under normal and abnormal conditions. Annu. Rev. Control 2019, 47, 112–132. [Google Scholar] [CrossRef]
- Meral, M.; Çelík, D. Comparison of SRF/PI- and STRF/PR-based power controllers for grid-tied distributed generation systems. Electr. Eng. 2018, 100, 633–643. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Shoyama, M. Scaling Factor Design Based Variable Step Size Incremental Resistance Maximum Power Point Tracking for PV Systems. J. Power Electron. 2012, 12, 164–171. [Google Scholar] [CrossRef]
- Hu, K.; Cao, S.; Li, W.; Zhu, F. An Improved Particle Swarm Optimization Algorithm Suitable for Photovoltaic Power Tracking Under Partial Shading Conditions. IEEE Access 2019, 7, 143217–143232. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- Kaced, K.; Larbes, C.; Ramzan, N.; Bounabi, M.; Dahmane, Z.E. Bat algorithm based maximum power point tracking for photovoltaic system under partial shading conditions. Sol. Energy 2017, 158, 490–503. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Al-Saud, M.S.; Abokhalil, A.G. A Novel Bat Algorithm Strategy for Maximum Power Point Tracker of Photovoltaic Energy Systems Under Dynamic Partial Shading. IEEE Access 2020, 8, 10048–10060. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. An enhanced adaptive P&O MPPT for fast and efficient tracking under varying environmental conditions. IEEE Trans. Sust. Energy 2018, 9, 1487–1496. [Google Scholar]
- Elobaid, L.M.; Abdelsalam, A.K.; Zakzouk, E.E. Artificial neural network-based photovoltaic maximum power point tracking techniques: A survey. IET Renew. Power Gen. 2015, 9, 1043–1063. [Google Scholar] [CrossRef]
- Seyedmahmoudian, B.M. State of the art artificial intelligence-based MPPT techniques for mitigating partial shading effects on PV systems–A review. Renew. Sust. Energy Rev. 2016, 64, 435–455. [Google Scholar] [CrossRef]
- Yi, Z.; Etemadi, A.H. Fault Detection for Photovoltaic Systems Based on Multi-Resolution Signal Decomposition and Fuzzy Inference Systems. IEEE Trans. Smart Grid 2016, 8, 1274–1283. [Google Scholar] [CrossRef]
- Bounechba, H.; Bouzid, A.; Nabti, K.; Benalla, H. Comparison of Perturb & Observe and Fuzzy Logic in Maximum Power Point Tracker for PV Systems. Energy Procedia 2014, 50, 677–684. [Google Scholar] [CrossRef]
- Dorji, S.; Wangchuk, D.; Choden, T.; Tshewang, T. Maximum Power Point Tracking of solar pho-tovoltaic cell using Perturb & Observe and fuzzy logic controller algorithm for boost converter and quadratic boost converter. Mater. Today Proc. 2020, 27, 1224–1229. [Google Scholar]
- Al-Majidi, S.D.; Abbod, M.F.; Al-Raweshidy, H.S. A novel maximum power point tracking technique based on fuzzy logic for photovoltaic systems. Int. J. Hydrogen Energy 2018, 43, 14158–14171. [Google Scholar] [CrossRef]
- Algarín, C.R.; Giraldo, J.T.; Alvarez, O.R. Fuzzy Logic Based MPPT Controller for a PV System. Energies 2017, 10, 2036. [Google Scholar] [CrossRef]
- Hong, Y.-Y.; Buay, P.P.M. Robust design of type-2 fuzzy logic-based maximum power point tracking for photovol-taics. Sustain. Energy Technol. Assess. 2020, 38, 100669. [Google Scholar]
- Saidi, A.; Benachaiba, C. Comparison of IC and P&O algorithms in MPPT for grid connected PV module. In Proceedings of the 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016; pp. 213–218. [Google Scholar] [CrossRef]
- Elkhateb, A.; Rahim, N.A.; Selvaraj, J.; Uddin, M.N. Fuzzy-logiccontroller-based SEPIC converter for maximum power point tracking. IEEE Trans. Ind. Appl. 2014, 50, 2349–2358. [Google Scholar] [CrossRef]
- Karmouni, H.; Chouiekh, M.; Motahhir, S.; Qjidaa, H.; Jamil, M.; Sayyouri, M. A novel modified sine-cosine optimized MPPT algorithm for grid integrated PV system under real operating conditions. IEEE Access 2019, 7, 10467–10477. [Google Scholar]
- Hamouda, N.; Babes, B.; Boutaghane, A.; Kahla, S.; Talbi, B. An enhanced MPPT method combining fractional-order and fuzzy logic control. IEEE J. Photovolt. 2017, 7, 640–650. [Google Scholar]
- Al Nabulsi, A.; Dhaouadi, R. Efficiency optimization of a DSP-based standalone PV system using fuzzy logic and dual-MPPT control. IEEE Trans. Ind. Inf. 2012, 8, 573–584. [Google Scholar] [CrossRef]
- Han, G.; Zhang, S.; Boix, P.; Wong, L.; Sun, L.; Lien, S.-Y. Towards high efficiency thin film solar cells. Prog. Mater. Sci. J. 2017, 87, 246–291. [Google Scholar] [CrossRef]
- Quansah, D.A.; Adaramola, M.S. Comparative study of performance degradation in poly- and mono-crystalline-Si solar PV modules deployed in different applications. Int. J. Hydrogen Energy 2018, 43, 3092–3109. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Sanjeevikumar, P.; Ranjana, M.S.B.; Blaabjerg, F.; Sharma, A. Fuzzy SVPWM-based inverter control realization of grid integrated photovoltaic-wind system with fuzzy particle swarm optimisation maximum power point tracking algorithm for a grid-connected PV/wind power generation system: Hardware implementation. IET Electr. Power Appl. 2018, 12, 962–971. [Google Scholar] [CrossRef]
- Firth, S.; Lomas, K.; Rees, S. A simple model of PV system performance and its use in fault detection. Sol. Energy 2010, 84, 624–635. [Google Scholar] [CrossRef]
- Bostan, V.; Toma, A.R.; Tudorache, T.; Paţurcă, S.V.; Dumitrescu, A.-M.; Bostan, I. Performance analysis of polycrystalline and CIS thin-film PV panels in real operation conditions. In Proceedings of the 2017 5th International Symposium on Electrical and Electronics Engineering (ISEEE), Galati, Romania, 20–22 October 2017; pp. 1–4. [Google Scholar]
- Ozden, T.; Akinoglu, B.G.; Kurtz, S. Performance and Degradation Analyses of two Different PV Modules in Central Anatolia. In Proceedings of the 2018 International Conference on Photovoltaic Science and Technologies (PVCon), Ankara, Turkey, 4–6 July 2018; pp. 1–4. [Google Scholar]
- Pachauri, R.K.; Chauhan, Y.K. Hybrid PV/FC Stand Alone Green Power Generation: A Perspective for Indian Rural Telecommunication Systems. In Proceedings of the 2014 International Conference on Issues and Challenges in Intelligent Computing Techniques (ICICT), Ghaziabad, India, 7–8 February 2017; pp. 807–815. [Google Scholar]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive approach to modeling and sim-ulation of photovoltaic arrays. IEEE Trans. Power Elect. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A critical evaluation on maximum power point tracking methods for partial shading in PV systems. Renew. Sustain. Energy Rev. 2015, 47, 933–953. [Google Scholar] [CrossRef]
- Sun, X.; Silverman, T.; Garris, R.; Deline, C.; Alam, M.A. An Illumination- and Temperature-Dependent Analytical Model for Copper Indium Gallium Diselenide (CIGS) Solar Cells. IEEE J. Photovolt. 2016, 6, 1298–1307. [Google Scholar] [CrossRef]
- Silverman, T.J.; Deceglie, M.G.; Sun, X.; Garris, R.L.; Alam, M.A.; Deline, C.; Kurtz, S. Thermal and electrical effects of partial shade in monolithic thin-film photovoltaic modules. IEEE J. Photovolt. 2015, 5, 1742–1747. [Google Scholar] [CrossRef]
- Ul-Haq, A.; Alammari, R.; Iqbal, A.; Jalal, M.; Gul, S. Computation of Power Extraction from Photo-voltaic Arrays under Various Fault Conditions. IEEE Access 2020, 8, 47619–47639. [Google Scholar] [CrossRef]
- Blaifi, S.-A.; Moulahoum, S.; Benkercha, R.; Taghezouit, B.; Saim, A. M5P model tree based fast fuzzy maximum power point tracker. Sol. Energy 2018, 163, 405–424. [Google Scholar] [CrossRef]
- Zaki, S.A.; Zhu, H.; Yao, J. Fault detection and diagnosis of photovoltaic system using fuzzy logic control. E3S Web Conf. 2019, 107, 02001. [Google Scholar] [CrossRef]
- Kandemir, E.; Cetin, N.S.; Borekci, S. A Comparison of Perturb & Observe and Fuzzy-Logic Based MPPT Methods for Uniform Environment Conditions. Period. Eng. Nat. Sci. (PEN) 2017, 5, 16–23. [Google Scholar] [CrossRef]
- Bendib, B.; Krim, F.; Belmili, H.; Almi, M.; Boulouma, S. Advanced Fuzzy MPPT Controller for a Stand-alone PV System. Energy Procedia 2014, 50, 383–392. [Google Scholar] [CrossRef]
- Ilyas, A.; Ayyub, M.; Khan, M.R.; Jain, A.; Husain, M.A. Realisation of incremental conductance the MPPT algorithm for a solar photovoltaic system. Int. J. Amb. Energy 2018, 39, 873–884. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Padmanaban, S.; Maroti, P.K.; Sharma, A. An extensive practical investigation of FPSO-based MPPT for grid integrated PV system under variable operating conditions with anti-islanding protection. IEEE Syst. J. 2019, 13, 1861–1871. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Padmanaban, S.; Holm-Nielsen, J.B.; Blaabjerg, F.; Bhaskar, M.S. An Experimental Estimation of Hybrid ANFIS–PSO-Based MPPT for PV Grid Integration Under Fluctuating Sun Irradiance. IEEE Syst. J. 2020, 14, 1218–1229. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Bhaskar, M.S.; Padmanaban, S.; Blaabjerg, F.; Azam, F. New CUK–SEPIC converter based photovoltaic power system with hybrid GSA–PSO algorithm employing MPPT for water pumping applications. IET Power Electron. 2020, 13, 2824–2830. [Google Scholar] [CrossRef]
- Fahad, S.; Mahdi, A.J.; Tang, W.H.; Huang, K.; Liu, Y. Particle Swarm Optimization Based DC-Link Voltage Control for Two Stage Grid Connected PV Inverter. In Proceedings of the 2018 International Conference on Power System Technology POWERCON, Guangzhou, China, 6–9 November 2018; pp. 2233–2241. [Google Scholar]
- Natarajan, K.; Bala, P.K.; Sampath, V. Fault Detection of Solar PV System Using SVM and Thermal Image Processing. IJRER 2020, 10, 967–977. [Google Scholar]
- Alwar, S.; Samithas, D.; Boominathan, M.S.; Balachandran, P.K.; Mihet-Popa, L. Performance Analysis of Thermal Image Processing-Based Photovoltaic Fault Detection and PV Array Reconfiguration—A Detailed Experimentation. Energies 2022, 15, 8450. [Google Scholar] [CrossRef]
- Devarakonda, A.K.; Karuppiah, N.; Selvaraj, T.; Balachandran, P.K.; Shanmugasundaram, R.; Senjyu, T. A Comparative Analysis of Maximum Power Point Techniques for Solar Photovoltaic Systems. Energies 2022, 15, 8776. [Google Scholar] [CrossRef]
- Selvaraj, T.; Rengaraj, R.; Venkatakrishnan, G.; Soundararajan, S.; Natarajan, K.; Balachandran, P.; David, P.; Selvarajan, S. Environmental Fault Diagnosis of Solar Panels Using Solar Thermal Images in Multiple Convolutional Neural Networks. Int. Trans. Electr. Energy Syst. 2022, 2022, 2872925. [Google Scholar] [CrossRef]
- Fahad, S.; Goudarzi, A.; Li, Y.; Xiang, J. A coordination control strategy for power quality enhancement of an active distribution network. Energy Rep. 2022, 8, 5455–5471. [Google Scholar] [CrossRef]
- Shang, Y. Resilient Multiscale Coordination Control against Adversarial Nodes. Energies 2018, 11, 1844. [Google Scholar] [CrossRef]
- Fahad, S.; Goudarzi, A.; Xiang, J. From Grid Feeding to Grid Supporting Converters: A Constant Power Active Distribution Network Perspective. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 862–867. [Google Scholar] [CrossRef]




| Ref. | Techniques of MPPT Used in the Literature | Research Gaps |
|---|---|---|
| [10] | Neural network for MPPT | No need for accurate panel data but needs large input data set for training of algorithm |
| [11] | Genetic algorithm | No need for accurate panel data but needs large input data set for training of algorithm |
| [18] | Modified fuzzy logic MPPT for more accuracy | Uses convergent distribution type MFs instead of symmetrical MFs with lack of adaptivity for various operating points |
| [21] | Dual MPPT using FL and P&O | Slower performance and complex design |
| [25] | Particle swarm optimization (PSO) with FL-based MPPT | Lack of dynamic adjustment of MF boundaries and types |
| [19] | Modified sine–cosine method with FL and sliding mode control | Lack of dynamic adjustment of MF boundaries and types |
| [20] | Fractional order combined with fuzzy logic | Enhanced tracking efficiency, but high complexity in design of the controller and computation of alpha factor limits the controller |
| [13] | Comparative analysis of different control schemes (P&O and FLC) |
|
| [14] | Evaluation of P&O and FLC schemes for single PV module | Carried out for boost converter and quadratic boost converter |
| [15] | Novel MPPT based on both P&O and fuzzy | Only rapidly changing weather conditions are considered in this study |
| [16] | Implementation of fuzzy controller | Changing insulation conditions are considered in this study |
| [17] | Novel MPPT scheme for type-2 FLC system |
|
| [7,8] | BAT algorithm for MPPT scheme | Tested only for shading patterns |
| [5] | PSO for MPPT scheme | Tested only for shading fault |
| [6] | Cuckoo search algorithm for tracking peak power | Used only for shading condition |
| [35] | Fast fuzzy MPPT scheme |
|
| [31] | Fuzzy logic | No need for large data set and highly compatible with nonlinear systems, but needs to define membership functions (MFs) |
| [38] | Novel MPPT scheme with fast mutable duty cycle | Fast tracking and high efficiency, but limited range of tracking and only for specified panel temperature and irradiance |
| [39] | PV system with GSA and PSO-based MPPT for water pumping application | New hybrid MPPT used for water pumping application |
| IMFs | (CE) | ||||||
|---|---|---|---|---|---|---|---|
| NBS | NMS | NSS | ZES | PSS | PMS | PBS | |
| E | |||||||
| NBS | NBS | NBS | NBS | NBS | NMS | NSS | ZES |
| NMS | NBS | NBS | NBS | NMS | NSS | ZES | PSS |
| NSS | NBS | NBS | NMS | NSS | ZES | PSS | PMS |
| ZES | NBS | NMS | NSS | ZES | PSS | PMS | PBS |
| PSS | NMS | NSS | ZES | PSS | PMS | PBS | PBS |
| PMS | NSS | ZES | PSS | PMS | PBS | PBS | PBS |
| PBS | ZES | PSS | PMS | PBS | PBS | PBS | PBS |
| Sr. No. | Parameter | Monocrystalline Module | CIGS Module |
|---|---|---|---|
| 1 | Open-circuit voltage (V) | 36.5 | 63.2 |
| 2 | Short-circuit current (A) | 8.26 | 6.1 |
| 3 | Max. peak power (W) | 230 | 230 |
| 4 | Max. peak voltage (V) | 29.5 | 46 |
| 5 | Max. peak current (A) | 7.8 | 5 |
| 6 | Photocurrent (A) | 8.26 | 6.33 |
| 7 | Diode saturation current (A) | ||
| 8 | Diode ideality factor | 0.95 | 0.95 |
| 9 | Shunt resistance | 476.1 | 56.1 |
| 10 | Series Resistance | 0.41 | 2.1 |
| Faults | Peak Power (kW) | Peak Voltage (V) | Peak Current (A) |
|---|---|---|---|
| Monocrystalline PV | |||
| F1 | 4.01 | 188 | 21.3 |
| F2 | 3.45 | 135 | 25.5 |
| F3 | 6.75 | 172 | 39.2 |
| F4 | 6.7 | 172 | 38.9 |
| F5 | 3.3 | 158 | 20.8 |
| Thin Film PV | |||
| F1 | 4.3 | 302 | 14.2 |
| F2 | 4.01 | 255 | 15.7 |
| F3 | 6.81 | 260 | 26.1 |
| F4 | 6.78 | 258 | 26.2 |
| F5 | 4.05 | 290 | 13.9 |
| Fault Case | Monocrystalline (MC) | Thin Film (TF) | ||
|---|---|---|---|---|
| Peak Power with PSO Strategy (Watt) | Peak Power with Fuzzy Logic Scheme (Watt) | Peak Power with PSO Strategy (Watt) | Peak Power with Fuzzy Logic Scheme (Watt) | |
| F1 | 4010 | 4010 | 4300 | 4300 |
| F2 | 3450 | 3440 | 4010 | 4010 |
| F3 | 6750 | 6750 | 6805 | 6800 |
| F4 | 6700 | 6700 | 6780 | 6780 |
| F5 | 3300 | 3300 | 4005 | 4005 |
| Fault Case | Monocrystalline (MC) | Thin Film (TF) | ||
|---|---|---|---|---|
| Peak Power by FL Scheme | Peak Power by PSO Scheme | Peak Power by FL Scheme | Peak Power by PSO Scheme | |
| F1 | 14.5% | 14.5% | 7.2% | 7.2% |
| F2 | 10.9% | 11.2% | 11.3% | 11.3% |
| F3 | 10.6% | 10.6% | 9.6% | 9.7% |
| F4 | 11.5% | 11.5% | 11.1% | 11.1% |
| F5 | 13.7% | 13.7% | 26% | 26% |
| Faults | PV Material | Impact on Current | Impact on Power Grid |
|---|---|---|---|
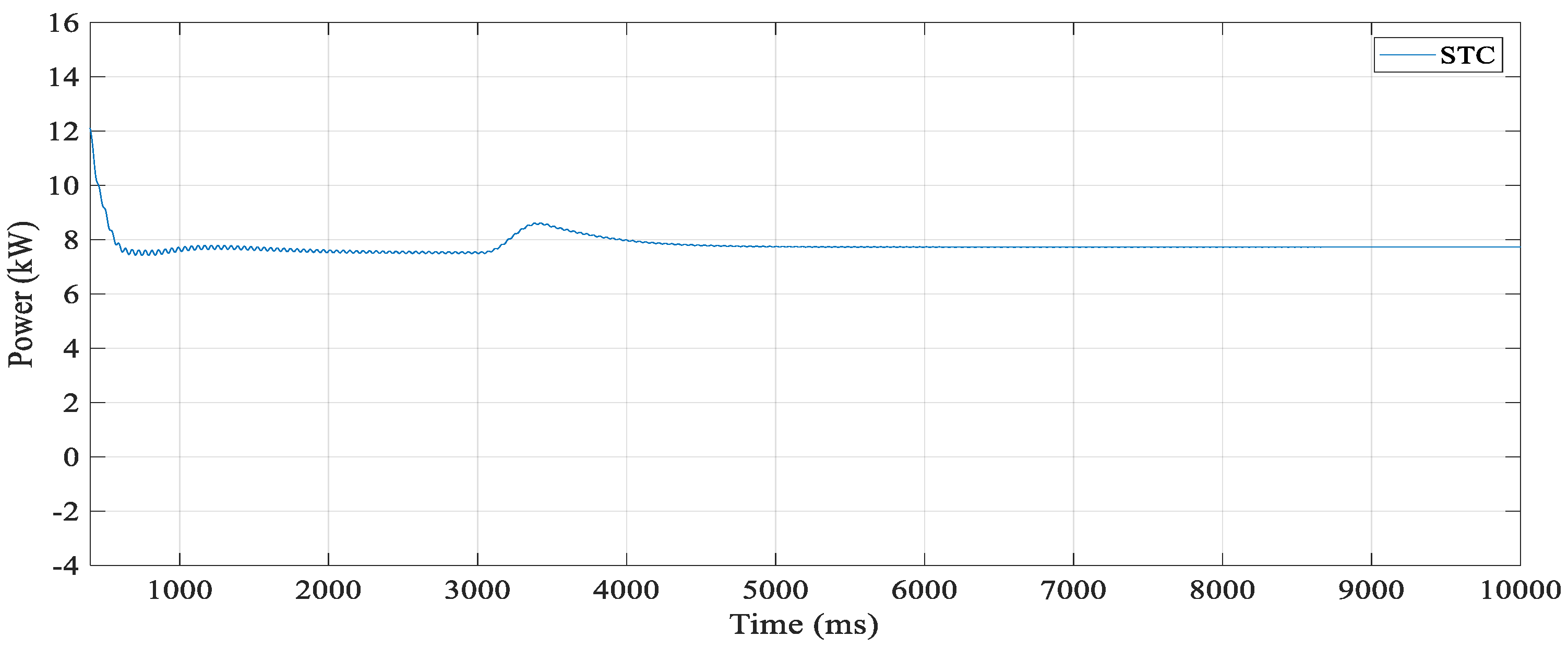
| F1 | CIGS |  | 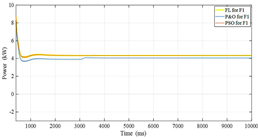 |
| Monocrystalline | 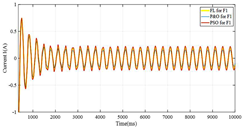 | 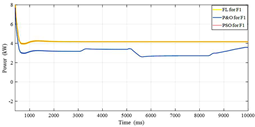 | |
| F2 | CIGS | 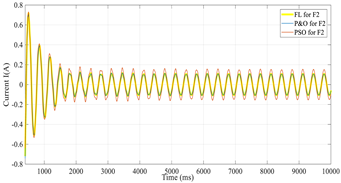 | 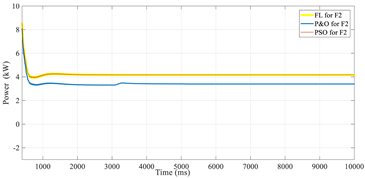 |
| Monocrystalline | 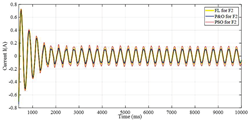 |  | |
| F3 | CIGS | 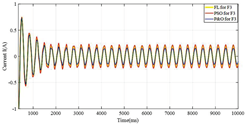 | 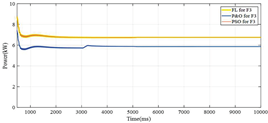 |
| Monocrystalline |  | 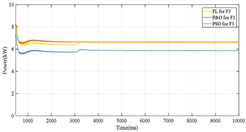 | |
| F4 | CIGS |  | 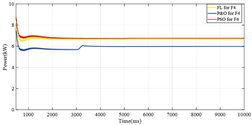 |
| Monocrystalline | 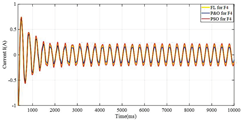 | 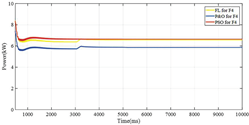 | |
| F5 | CIGS | 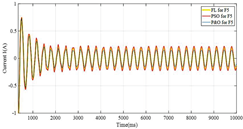 | 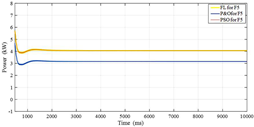 |
| Monocrystalline |  | 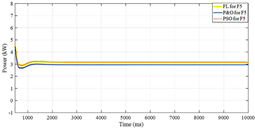 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ul-Haq, A.; Fahad, S.; Gul, S.; Bo, R. Intelligent Control Schemes for Maximum Power Extraction from Photovoltaic Arrays under Faults. Energies 2023, 16, 974. https://doi.org/10.3390/en16020974
Ul-Haq A, Fahad S, Gul S, Bo R. Intelligent Control Schemes for Maximum Power Extraction from Photovoltaic Arrays under Faults. Energies. 2023; 16(2):974. https://doi.org/10.3390/en16020974
Chicago/Turabian StyleUl-Haq, Azhar, Shah Fahad, Saba Gul, and Rui Bo. 2023. "Intelligent Control Schemes for Maximum Power Extraction from Photovoltaic Arrays under Faults" Energies 16, no. 2: 974. https://doi.org/10.3390/en16020974
APA StyleUl-Haq, A., Fahad, S., Gul, S., & Bo, R. (2023). Intelligent Control Schemes for Maximum Power Extraction from Photovoltaic Arrays under Faults. Energies, 16(2), 974. https://doi.org/10.3390/en16020974







