Computational Study of Deflagration-to-Detonation Transition in a Semi-Confined Slit Combustor
Abstract
:1. Introduction
2. Materials and Methods
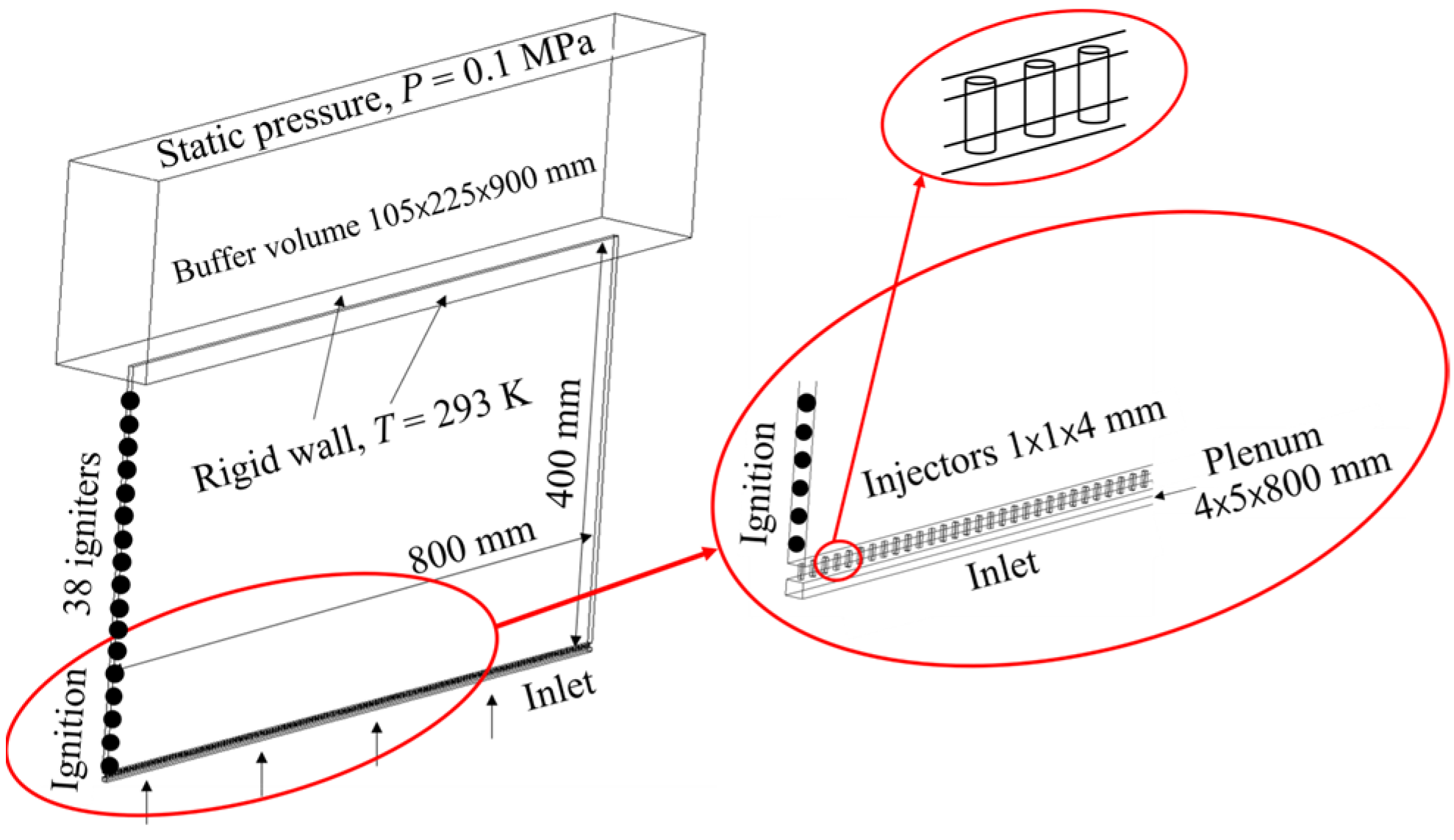
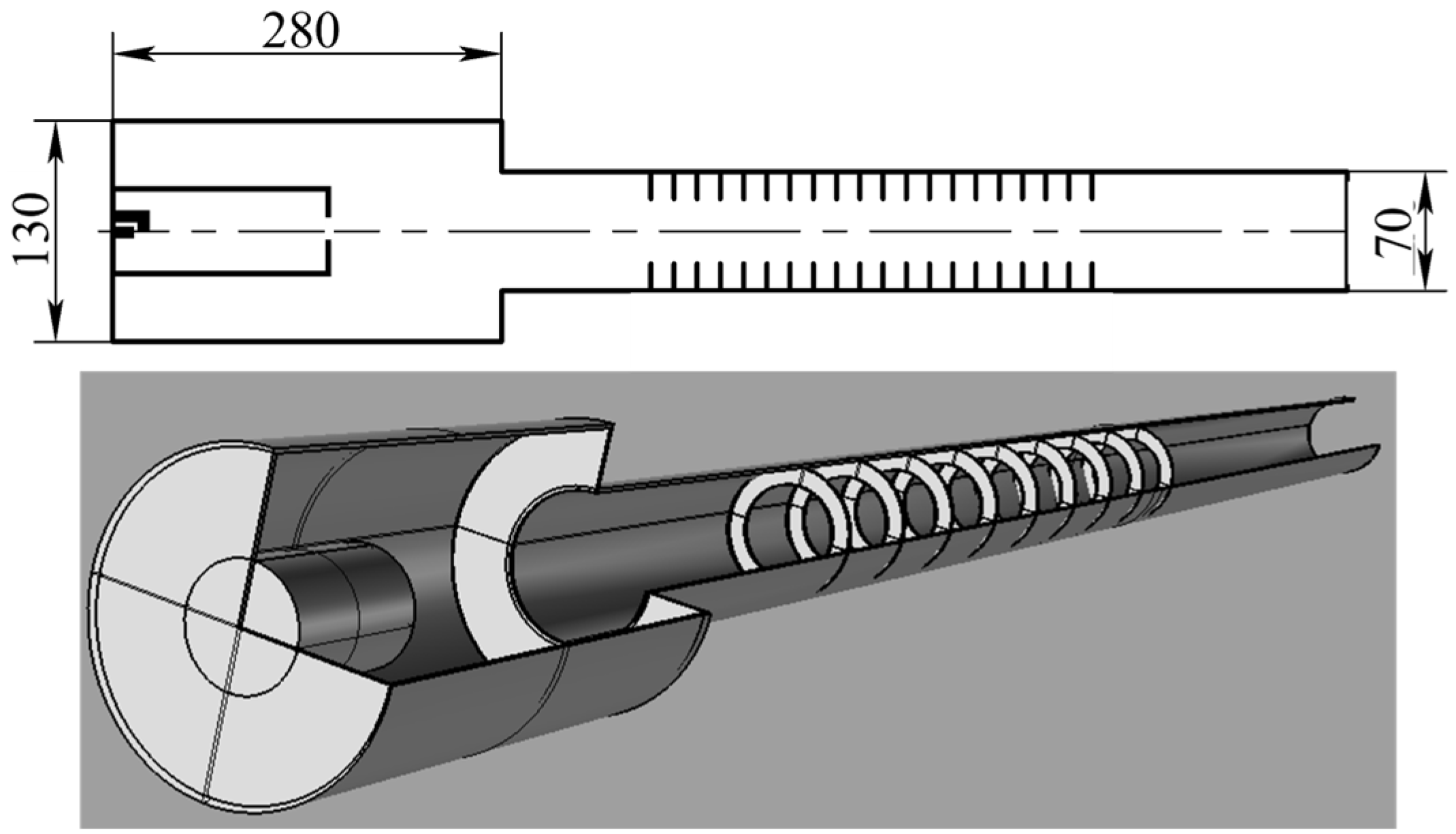
2.1. Slit Combustor
2.2. Mathematical Statement of the Problem
2.2.1. Mean Flow Equations
2.2.2. Combustion Model
Flame Tracking Method
Particle Method
2.2.3. Boundary Conditions
2.3. Numerical Procedure
3. Results
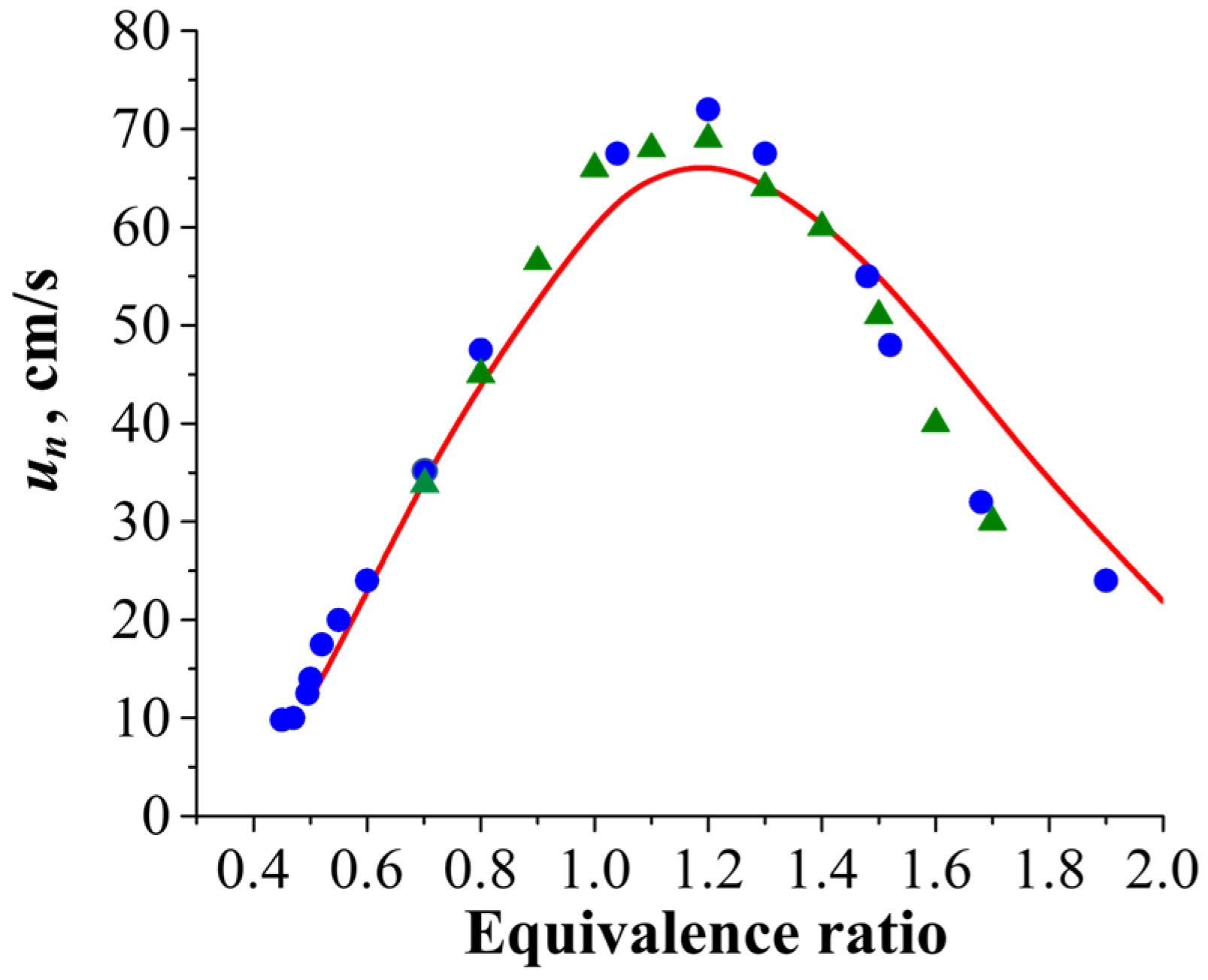
3.1. Model Validation
3.1.1. Validation Test I
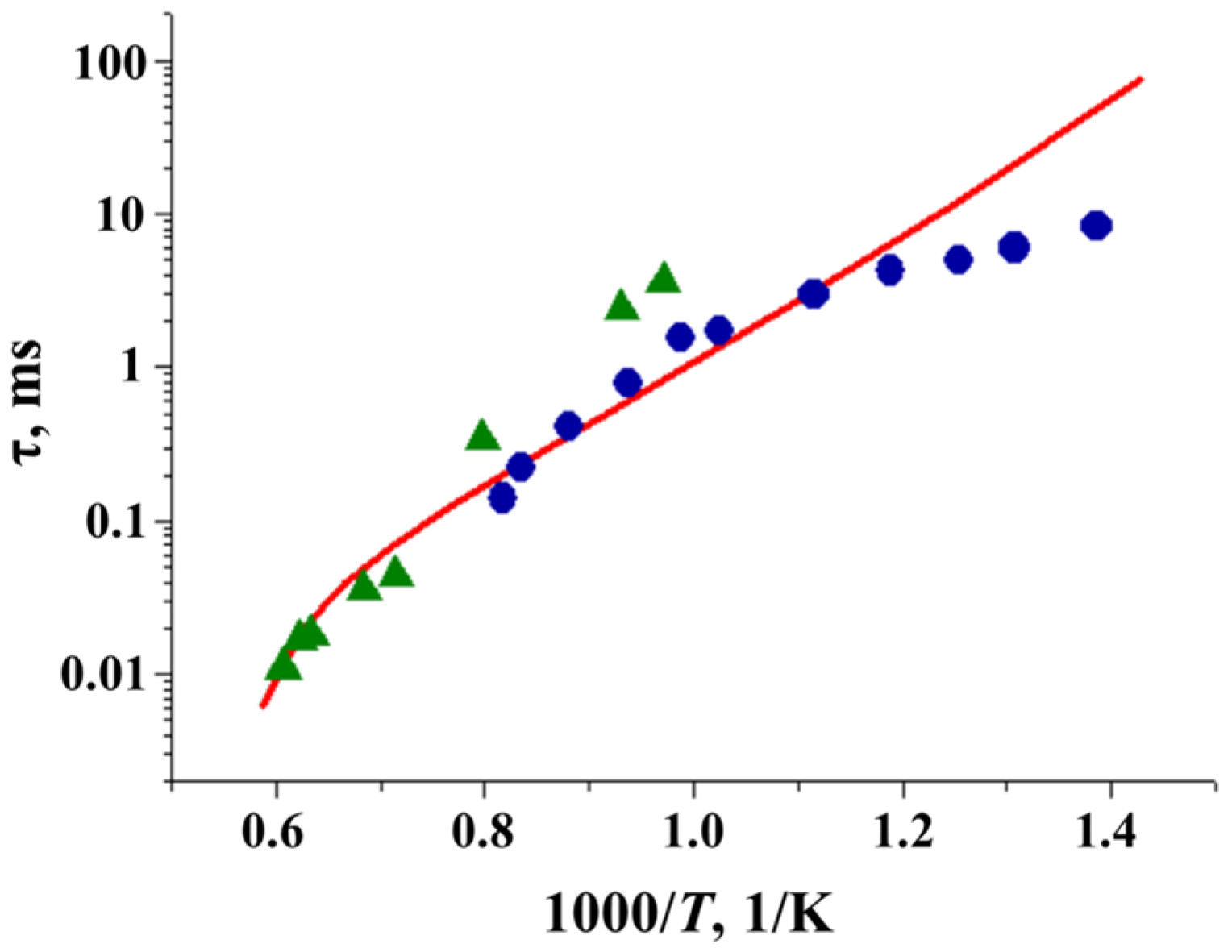
3.1.2. Validation Test II
3.1.3. Validation Test III
3.2. Results of Calculations
3.2.1. Mesh Sensitivity
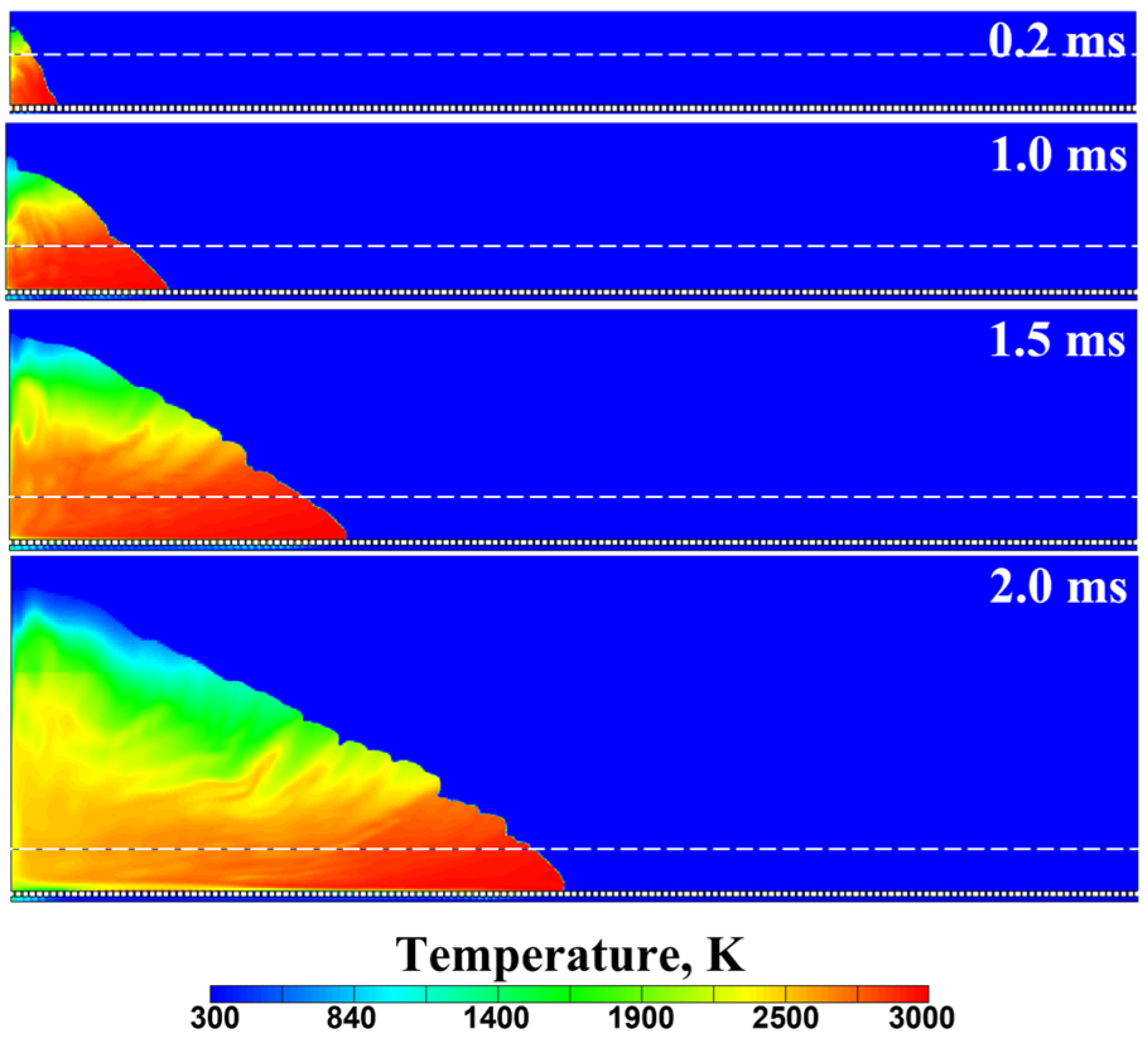
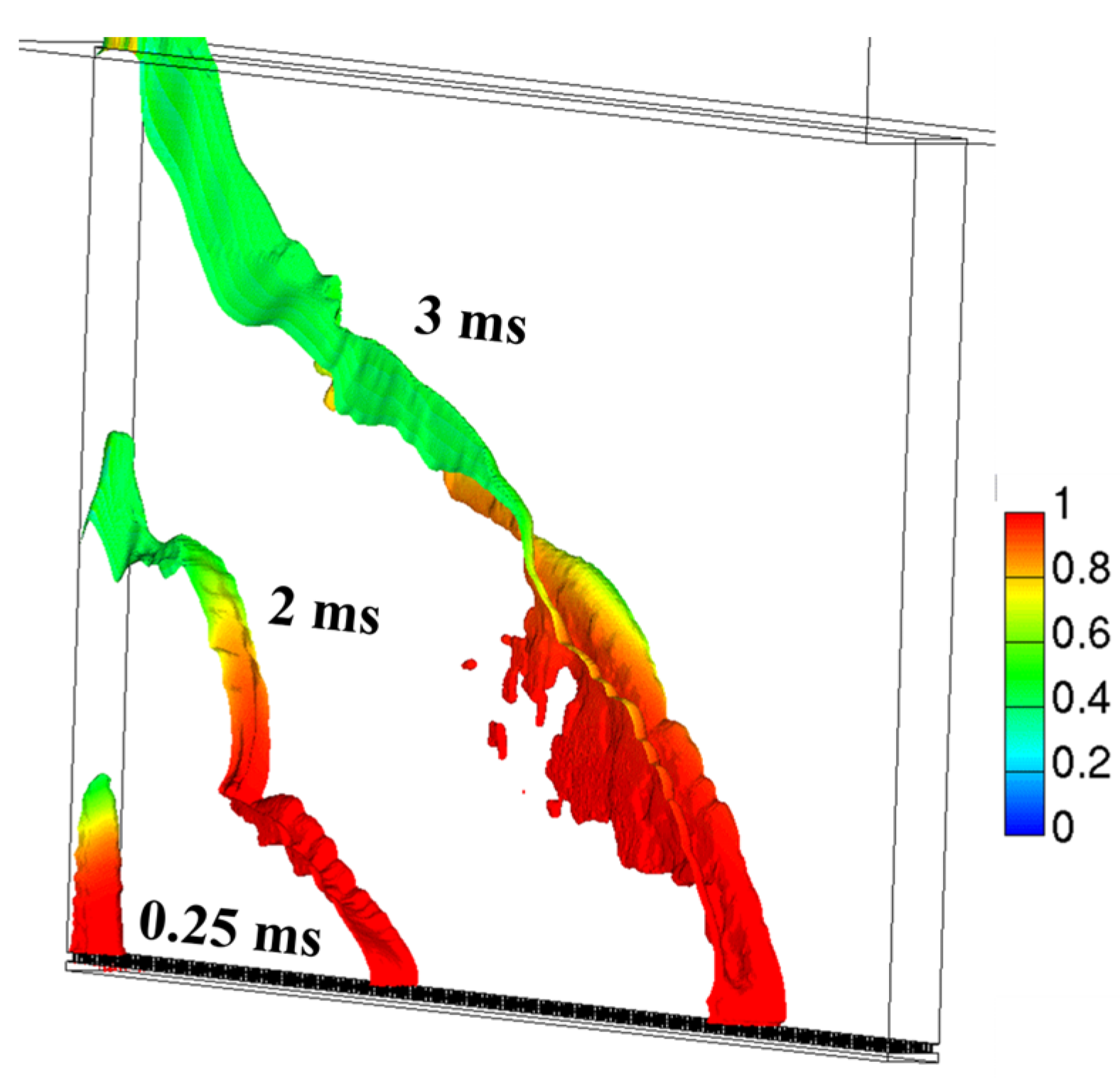
3.2.2. Slit Filling
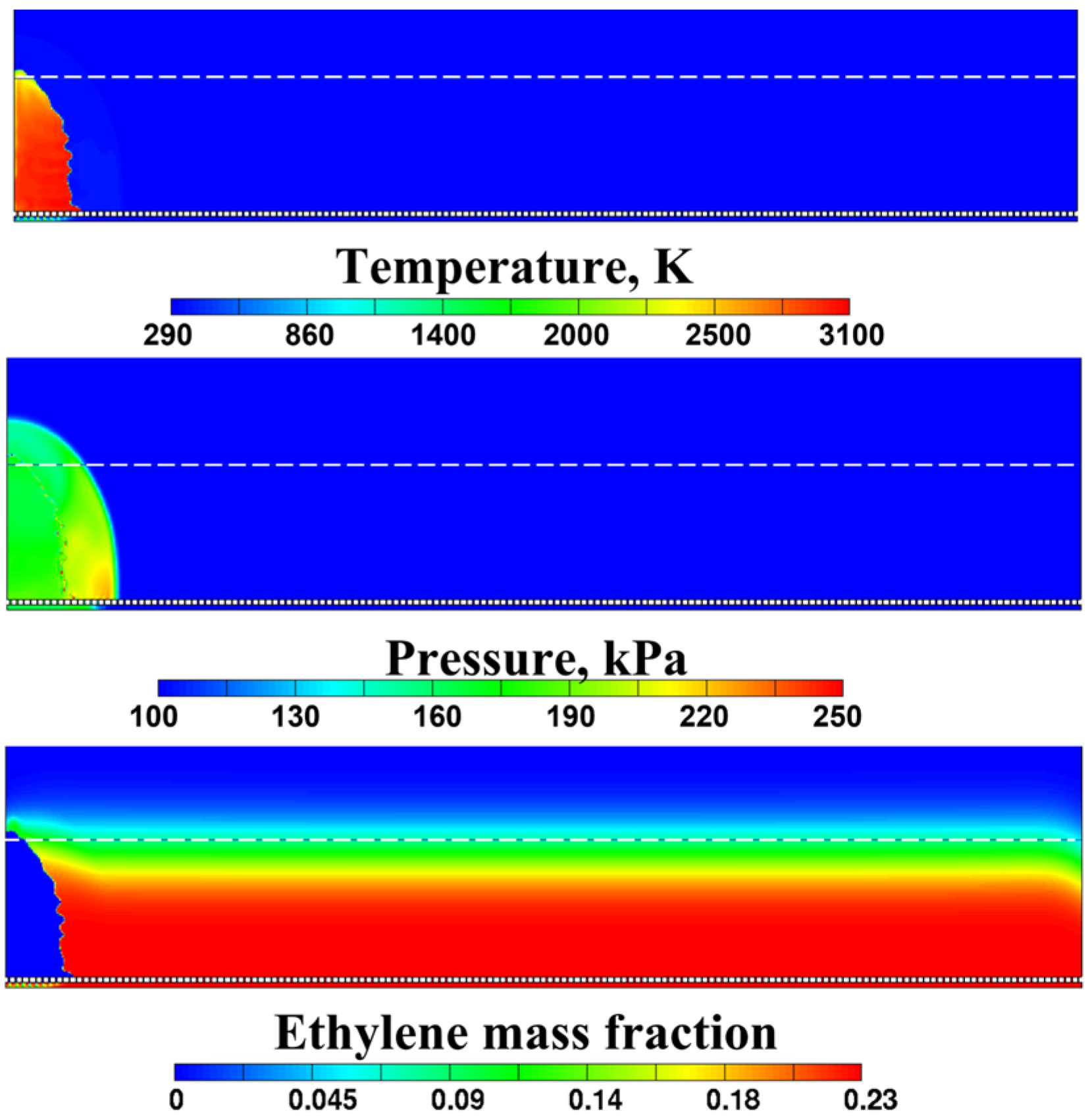
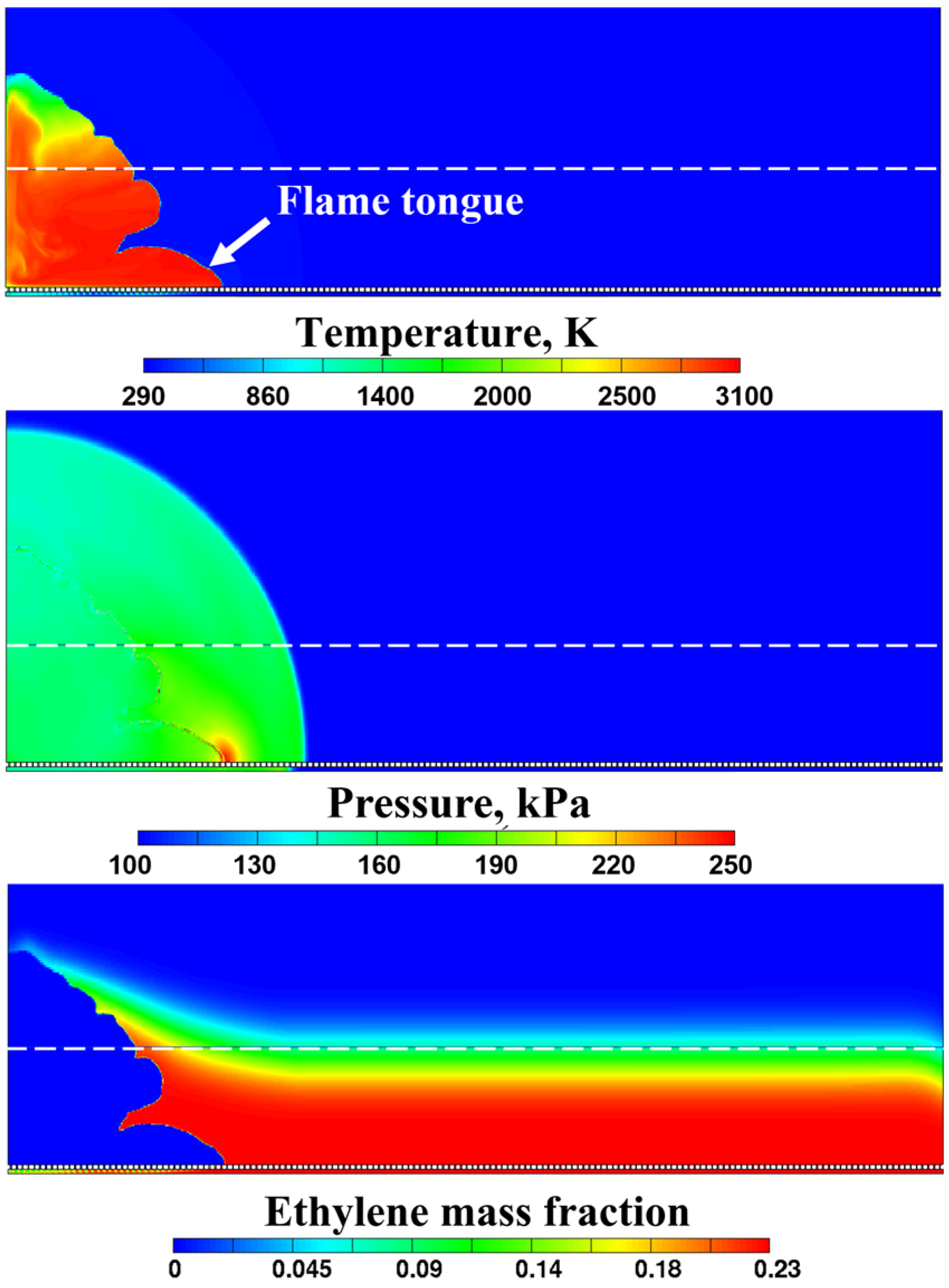
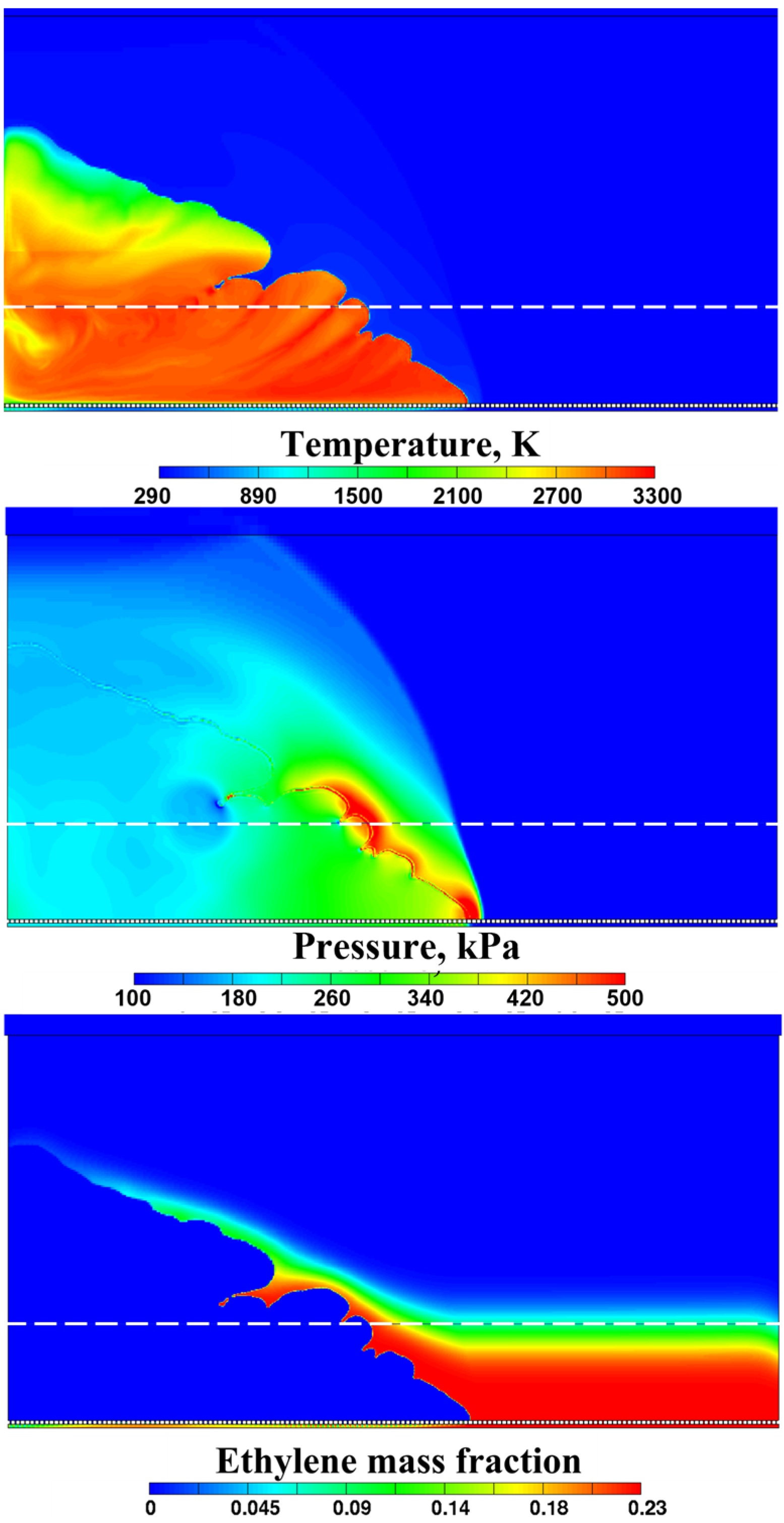
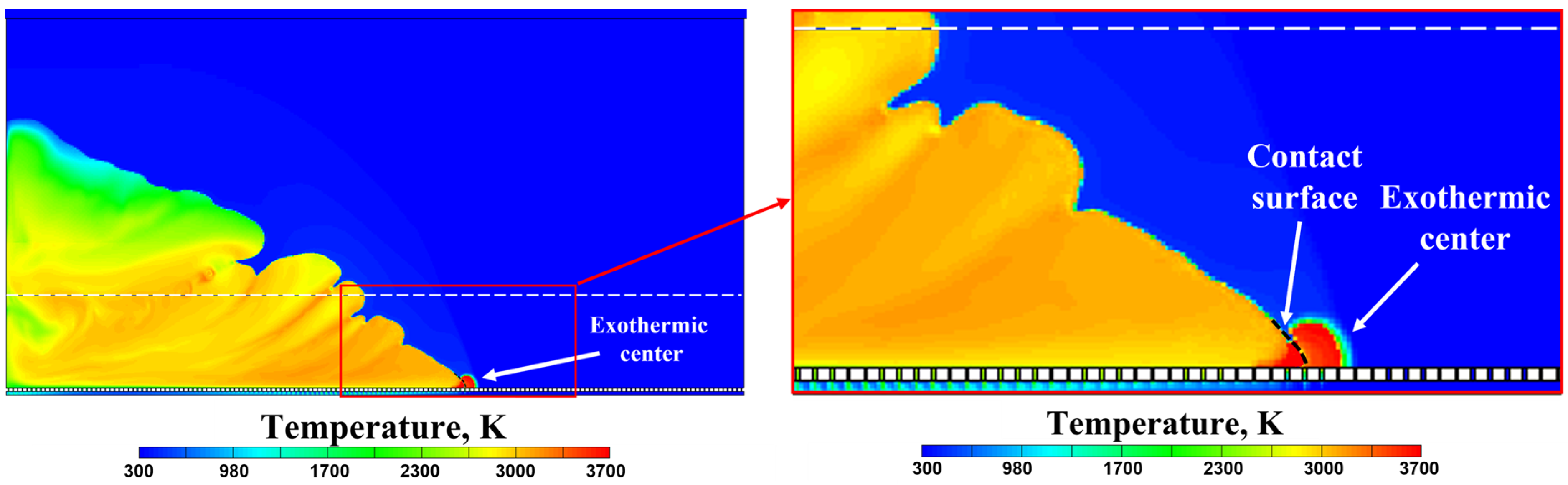
3.2.3. Deflagration-to-Detonation Transition
3.2.4. Effect of Layer Height on DDT
3.2.5. Effect of Nitrogen Dilution on DDT
3.2.6. Effect of Slit Width on DDT
4. Discussion
5. Conclusions
- (1)
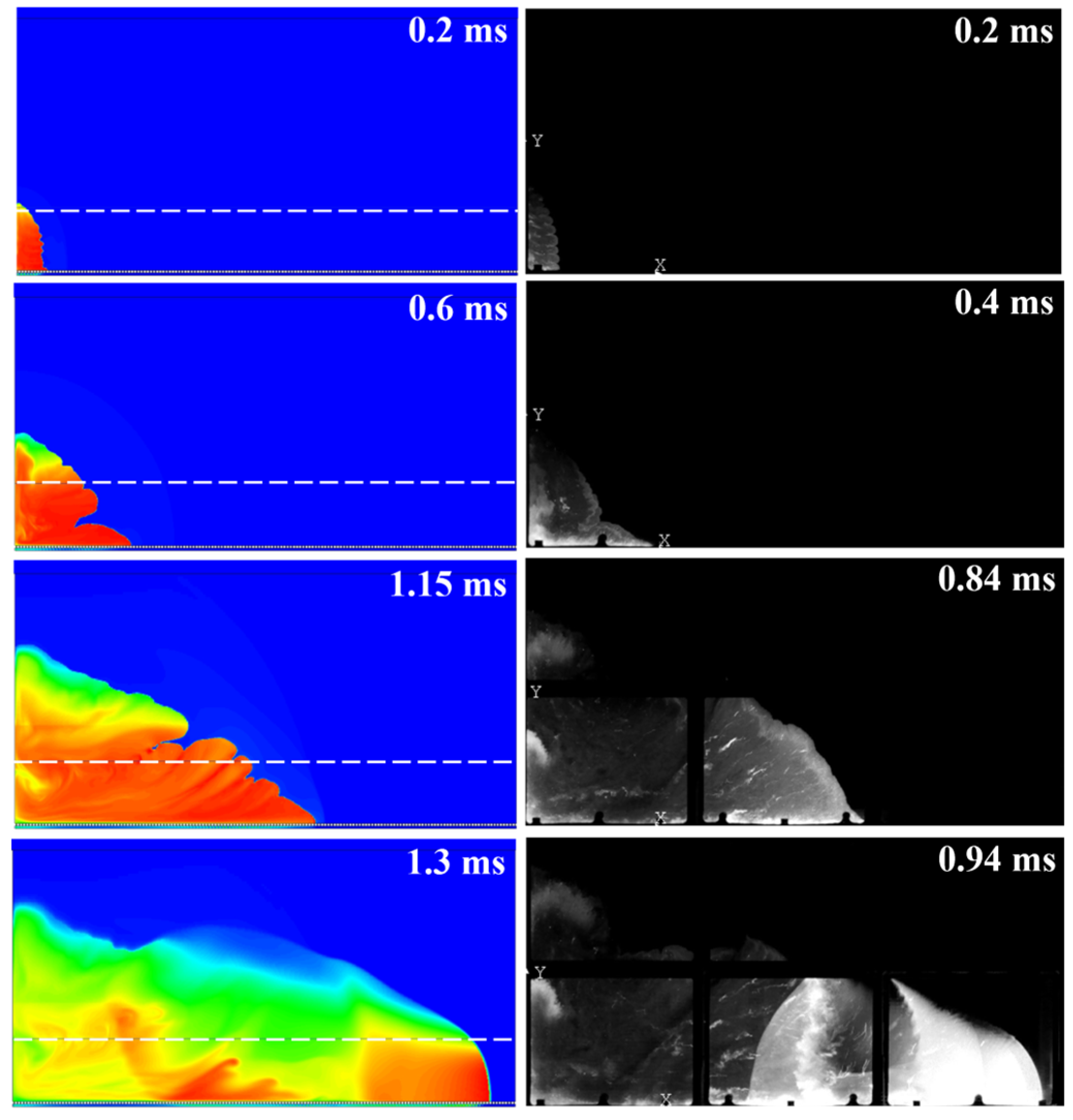
- The calculation results agree satisfactorily with the experimental data [31] on the slit-filling dynamics, flame structure, the occurrence of preflame self-ignition centers, and DDT.
- (2)
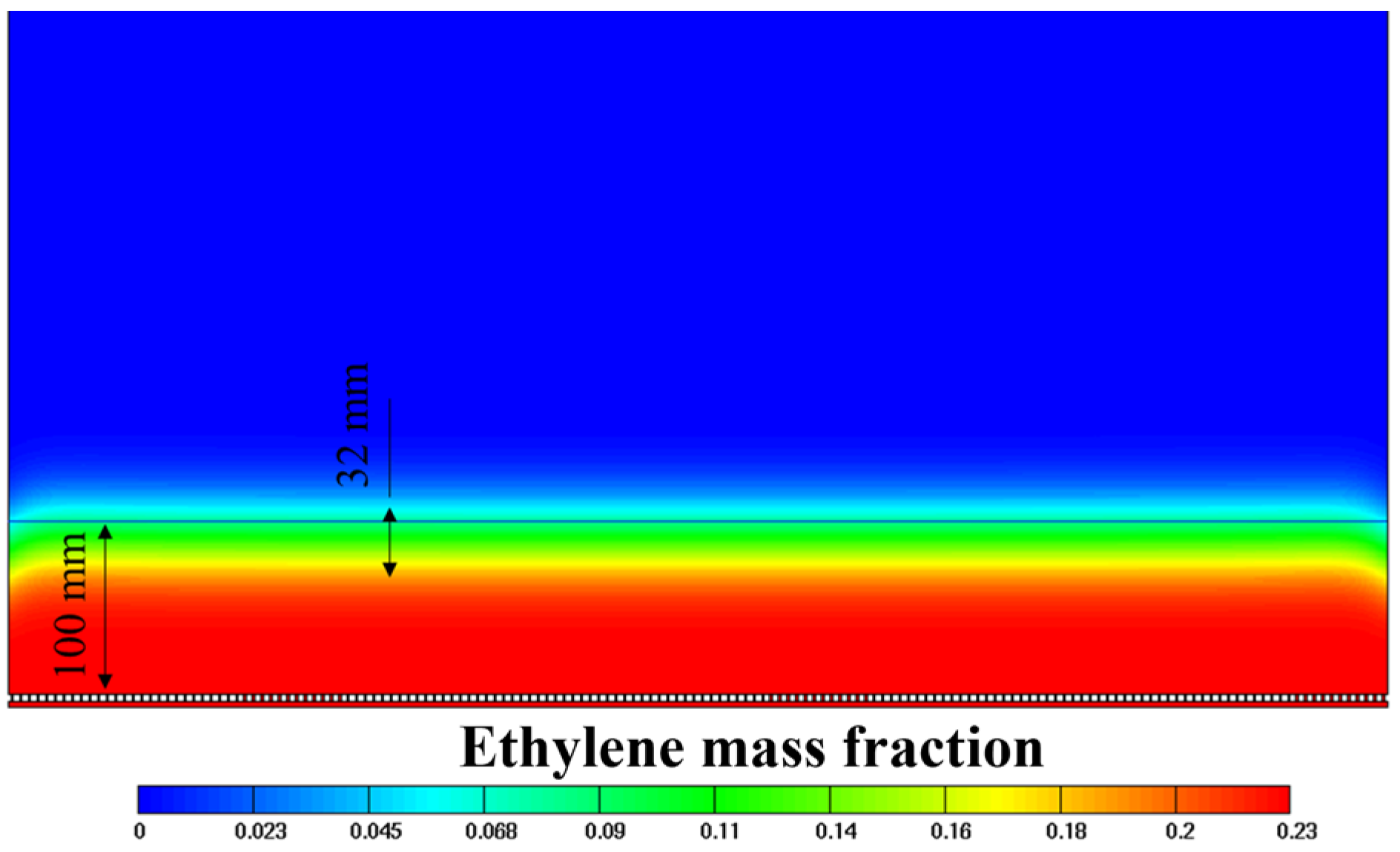
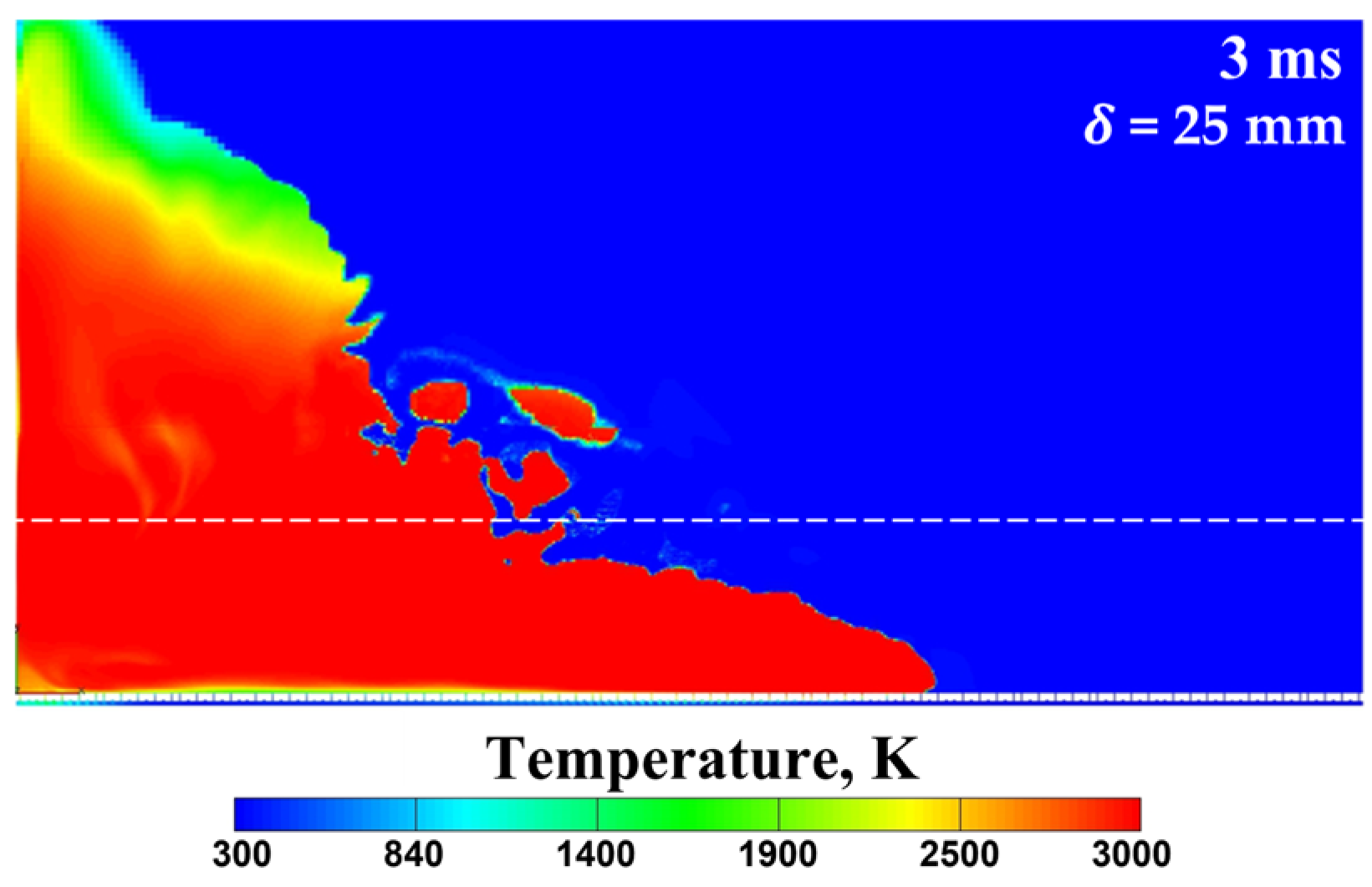
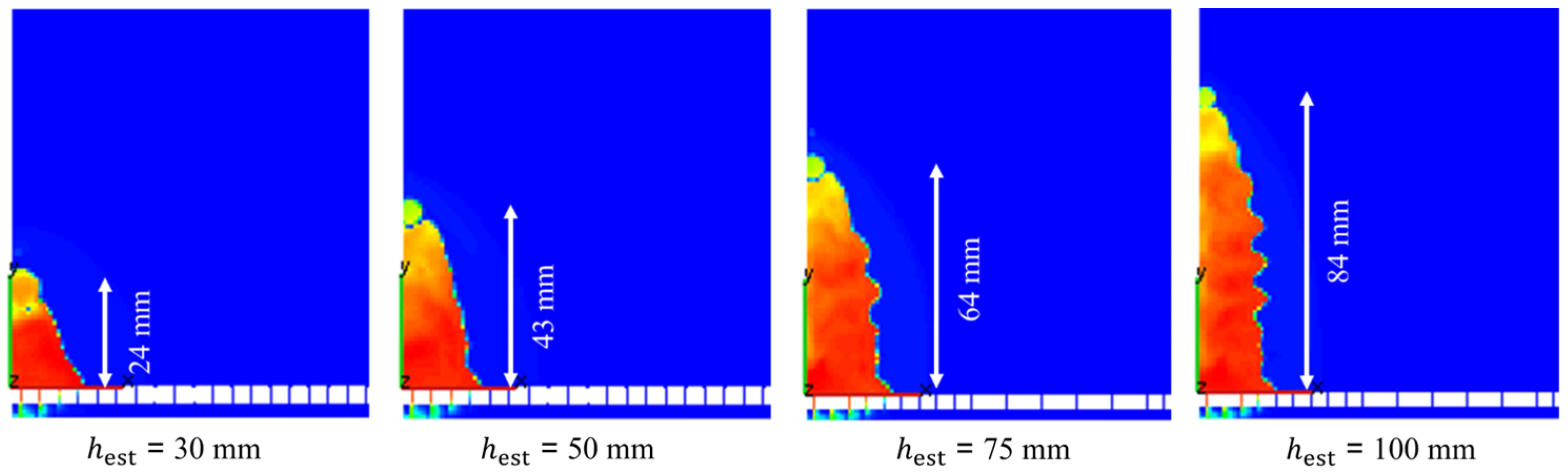
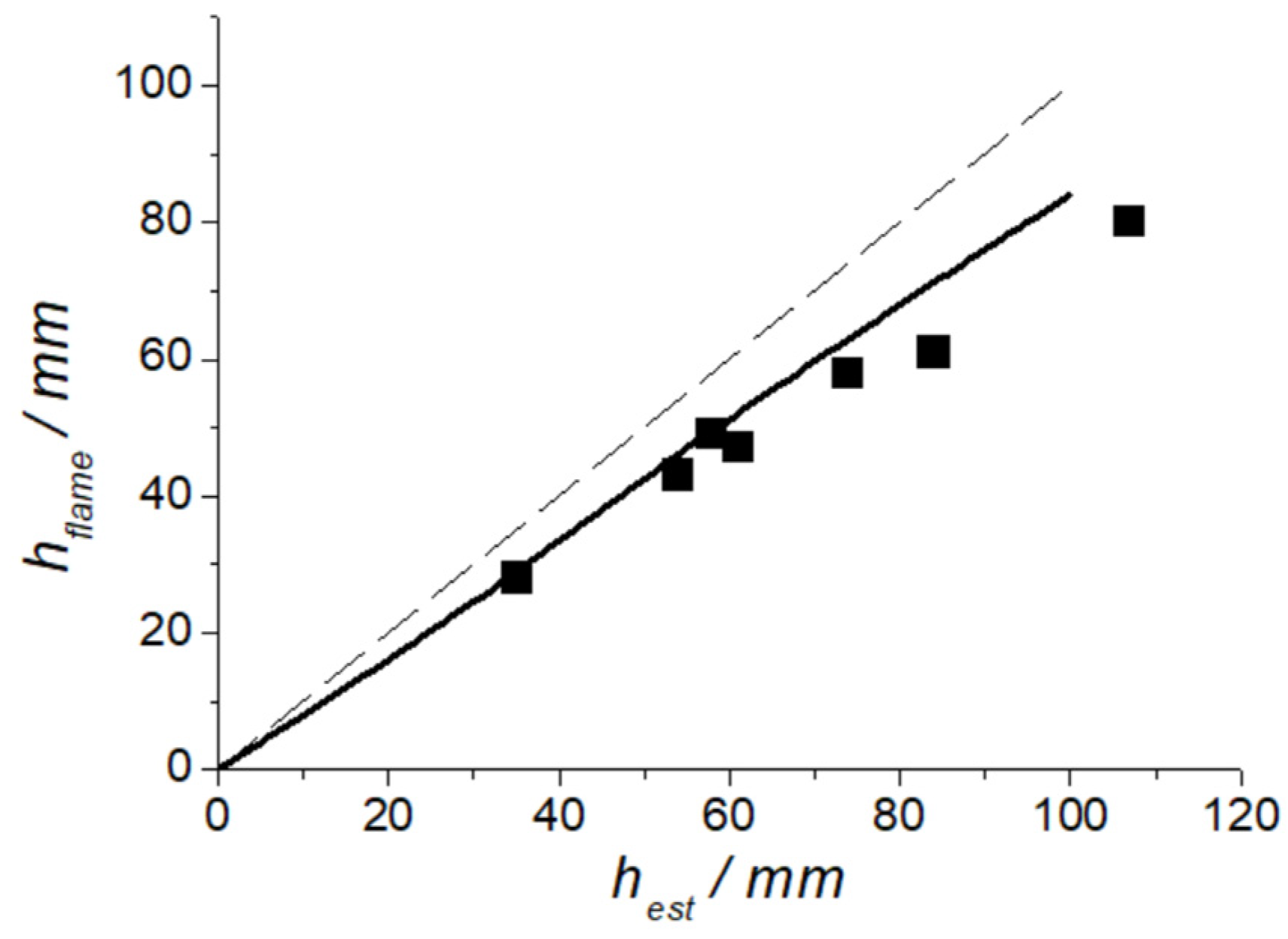
- Slit filling with the combustible mixture is accompanied by blurring the contact surface between the mixture and the ambient air, causing the mixture to dilute with air. As a result, the true height of the layer, which is still possible to ignite, is smaller than the estimated height of the layer by up to 16%.
- (3)
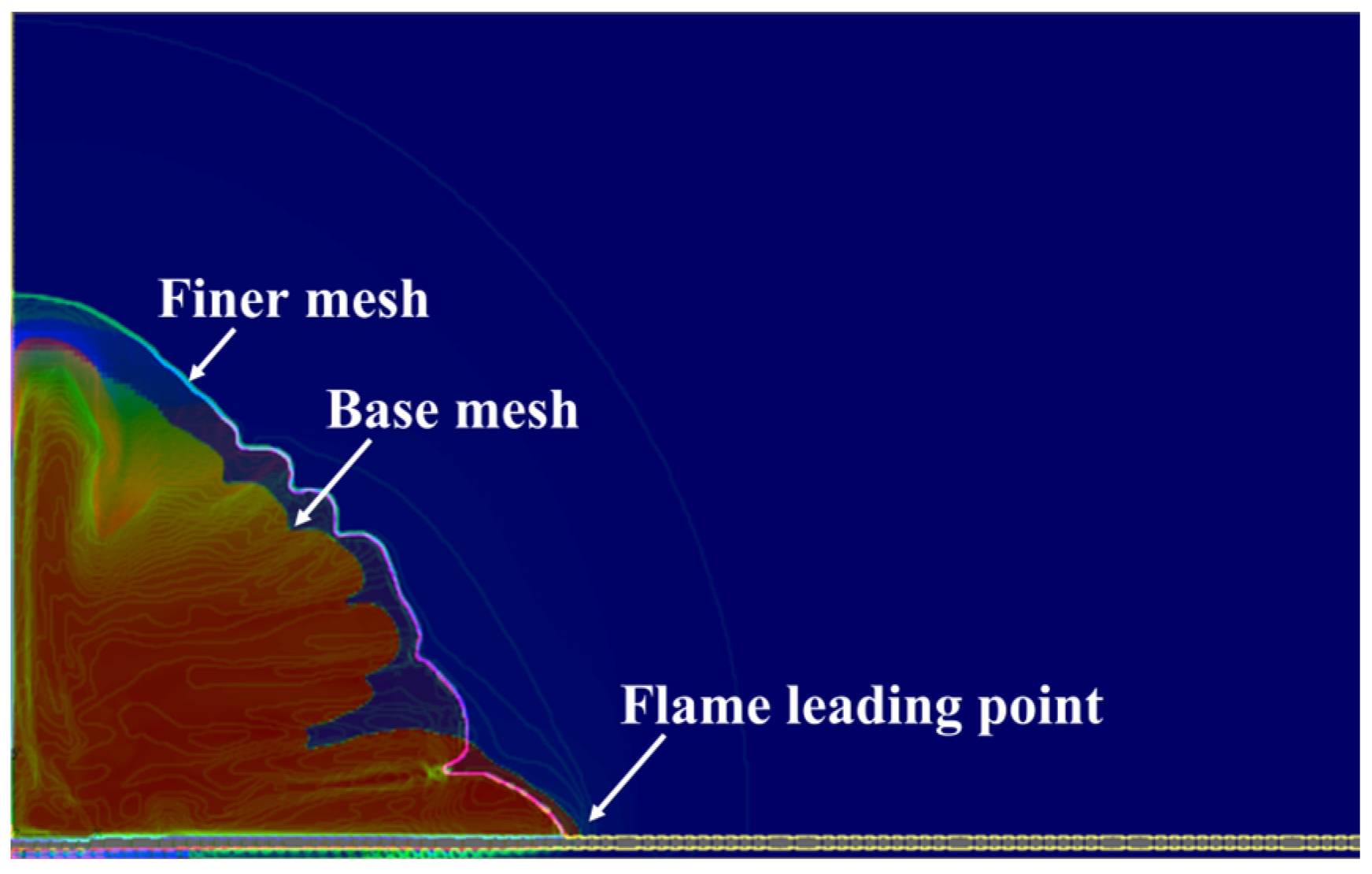
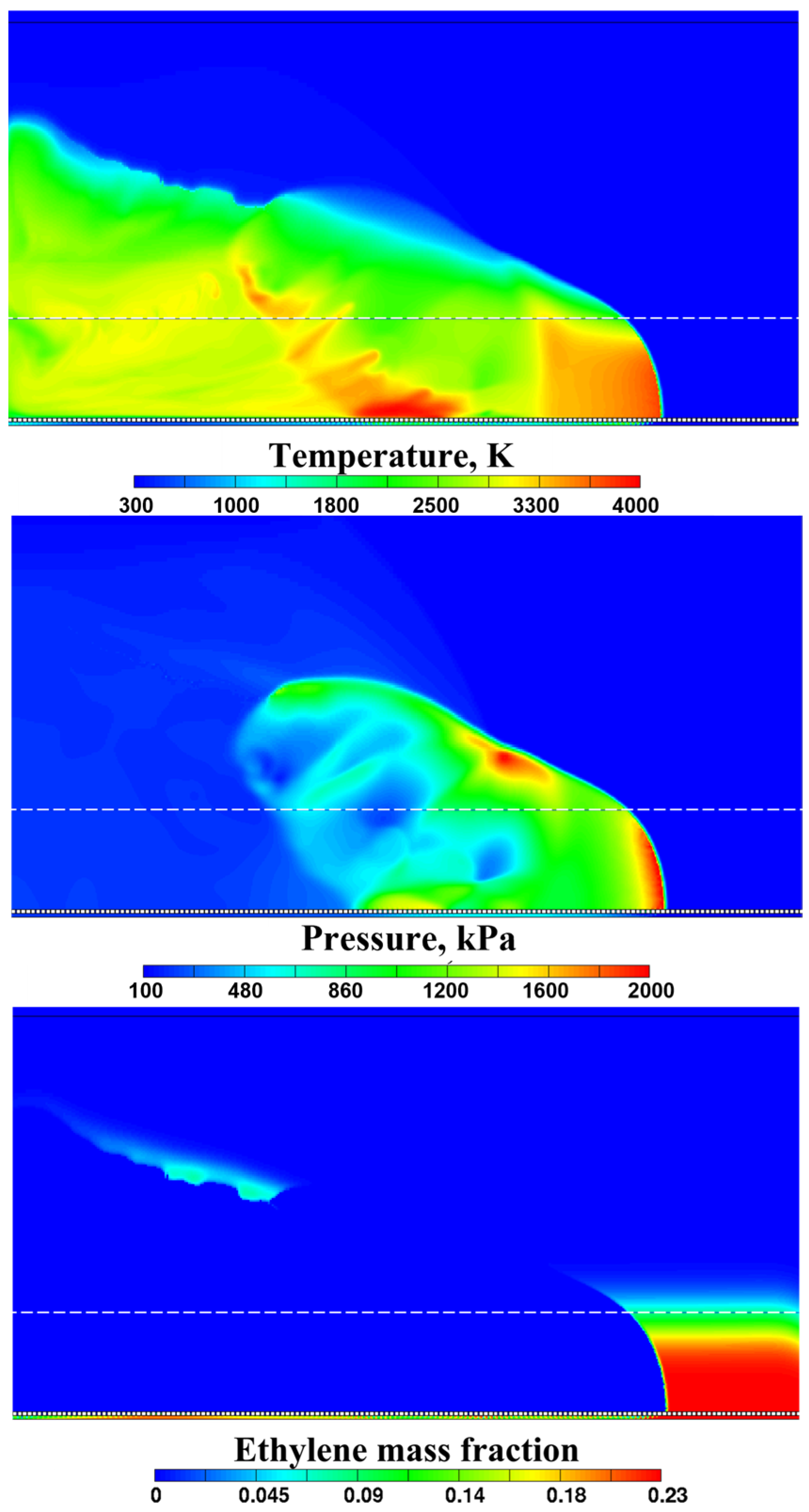
- DDT can occur in the layer at a time instant very close to the instant when the flame-born shock wave overtakes the precursor shock wave caused by flame ignition. DDT most probably occurs near the slit bottom due to the formation of the exothermic self-ignition center ahead of the leading edge of the flame as a result of shock wave reflections from the walls of injector holes at the slit bottom and from the corners of conjugation of the slit bottom and side walls.
- (4)
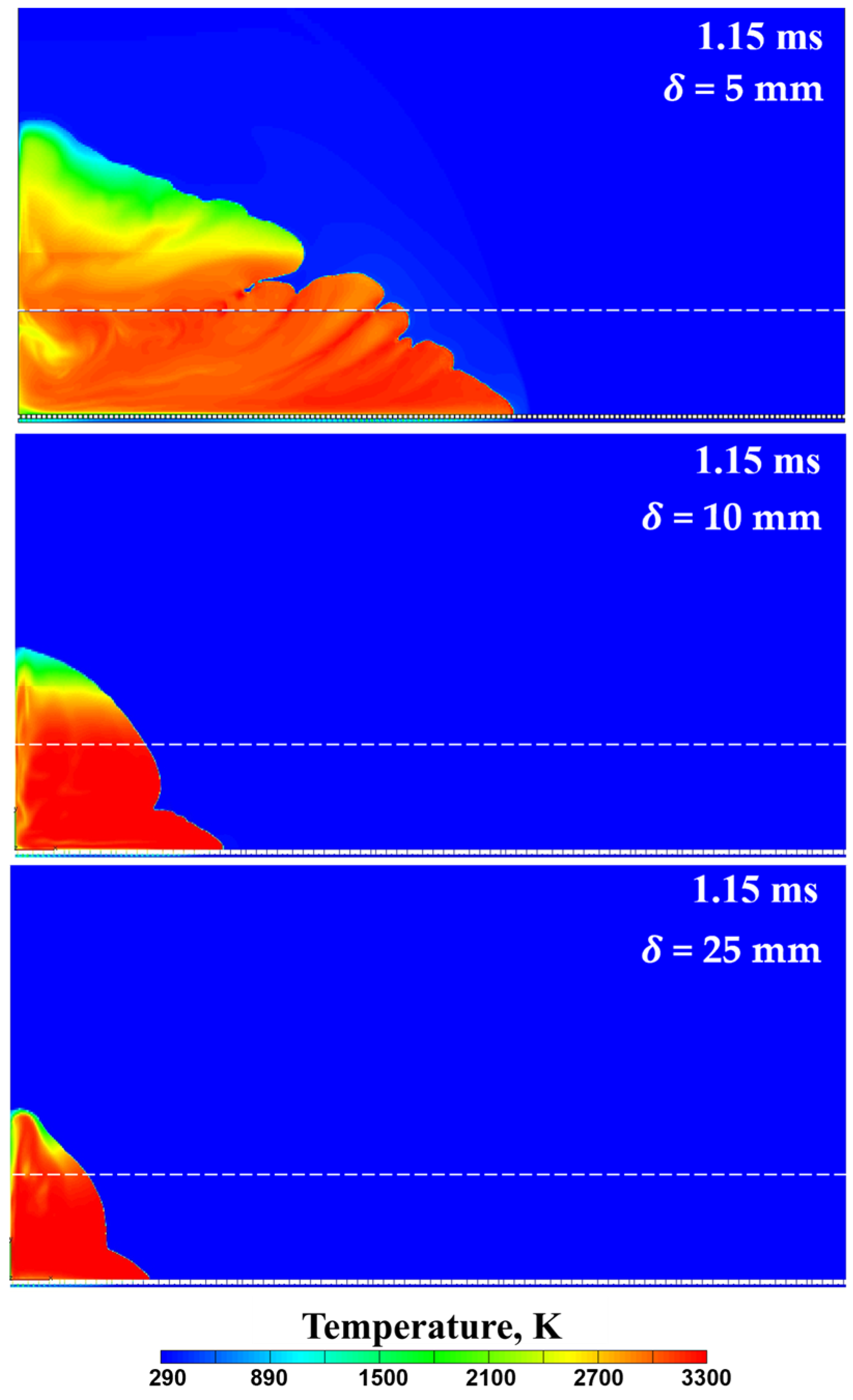
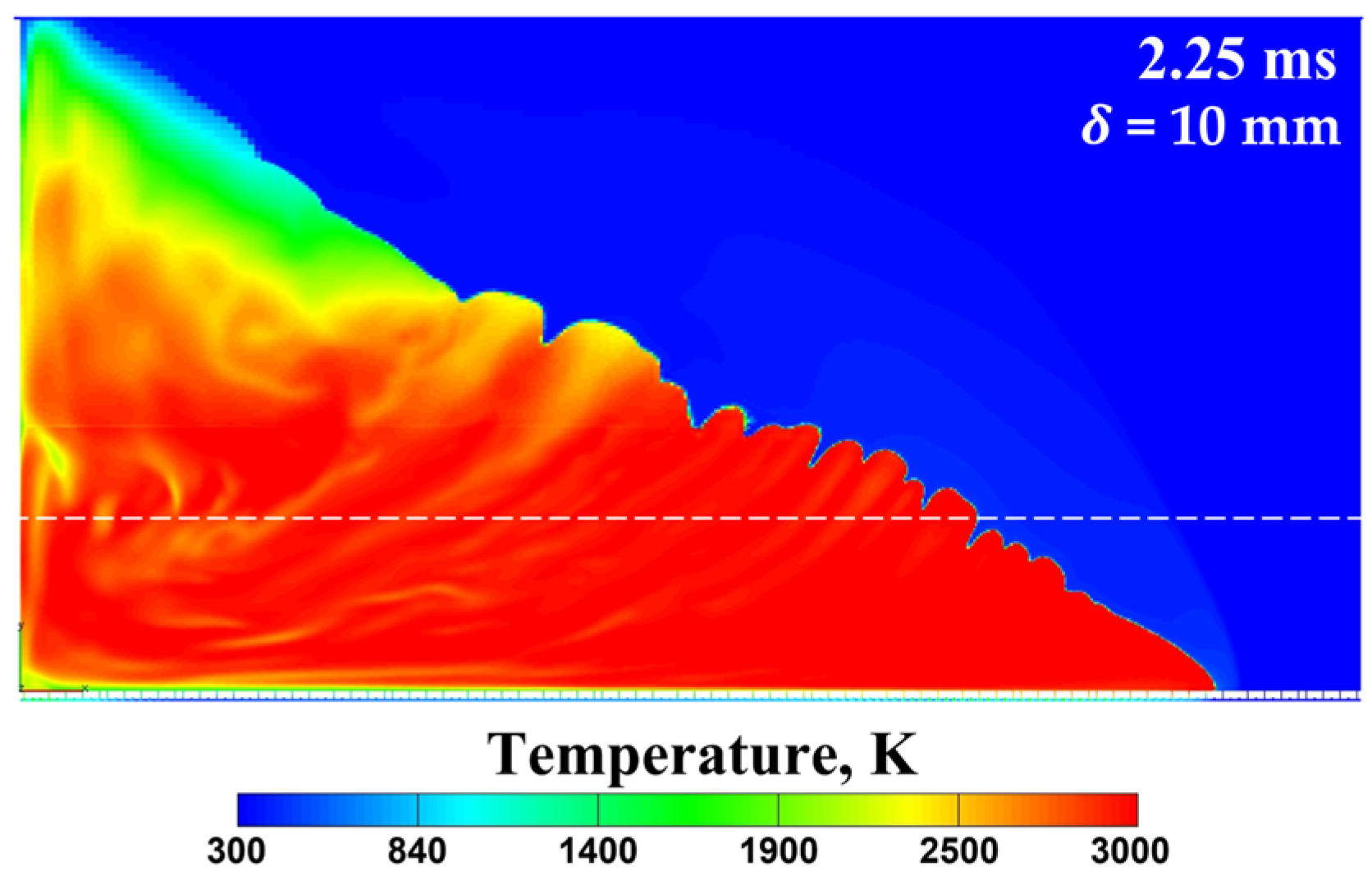
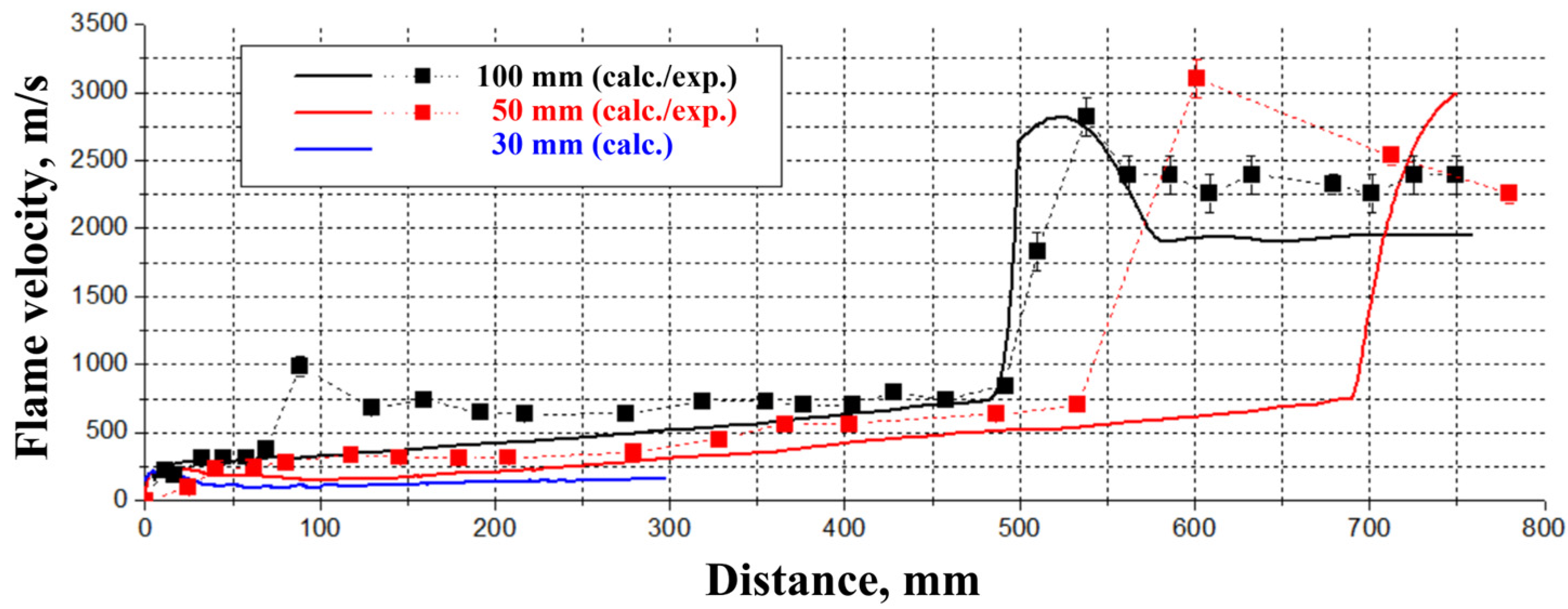
- A decrease in the height of the layer of the combustible mixture leads to a decrease in the intensity of the precursor shock wave and the flame-born shock wave, and therefore, to a decrease in the level of turbulence and the flame propagation velocity in the vicinity of the slit bottom, thus increasing the DDT run-up distance and time up to the critical value when DDT fails.
- (5)
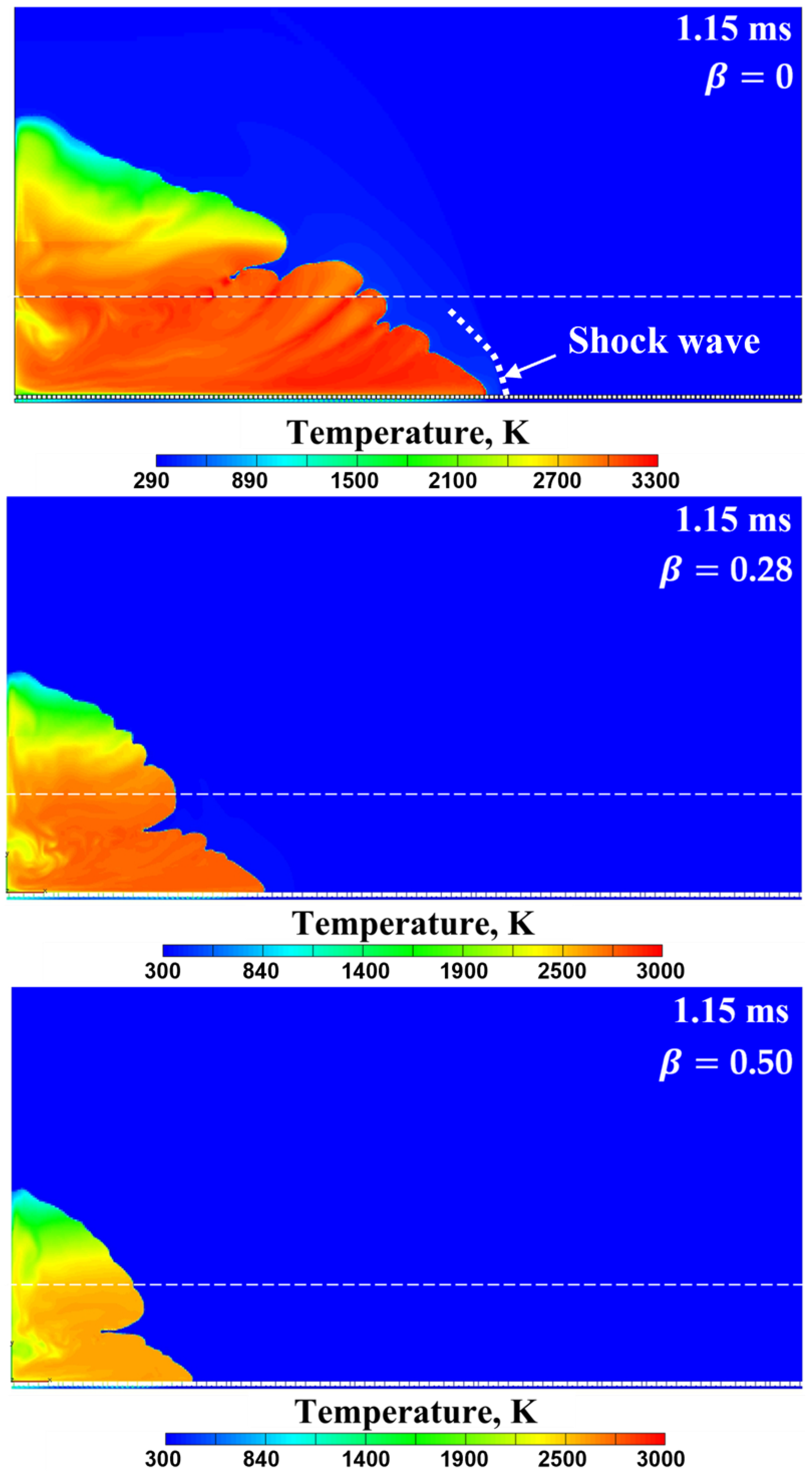
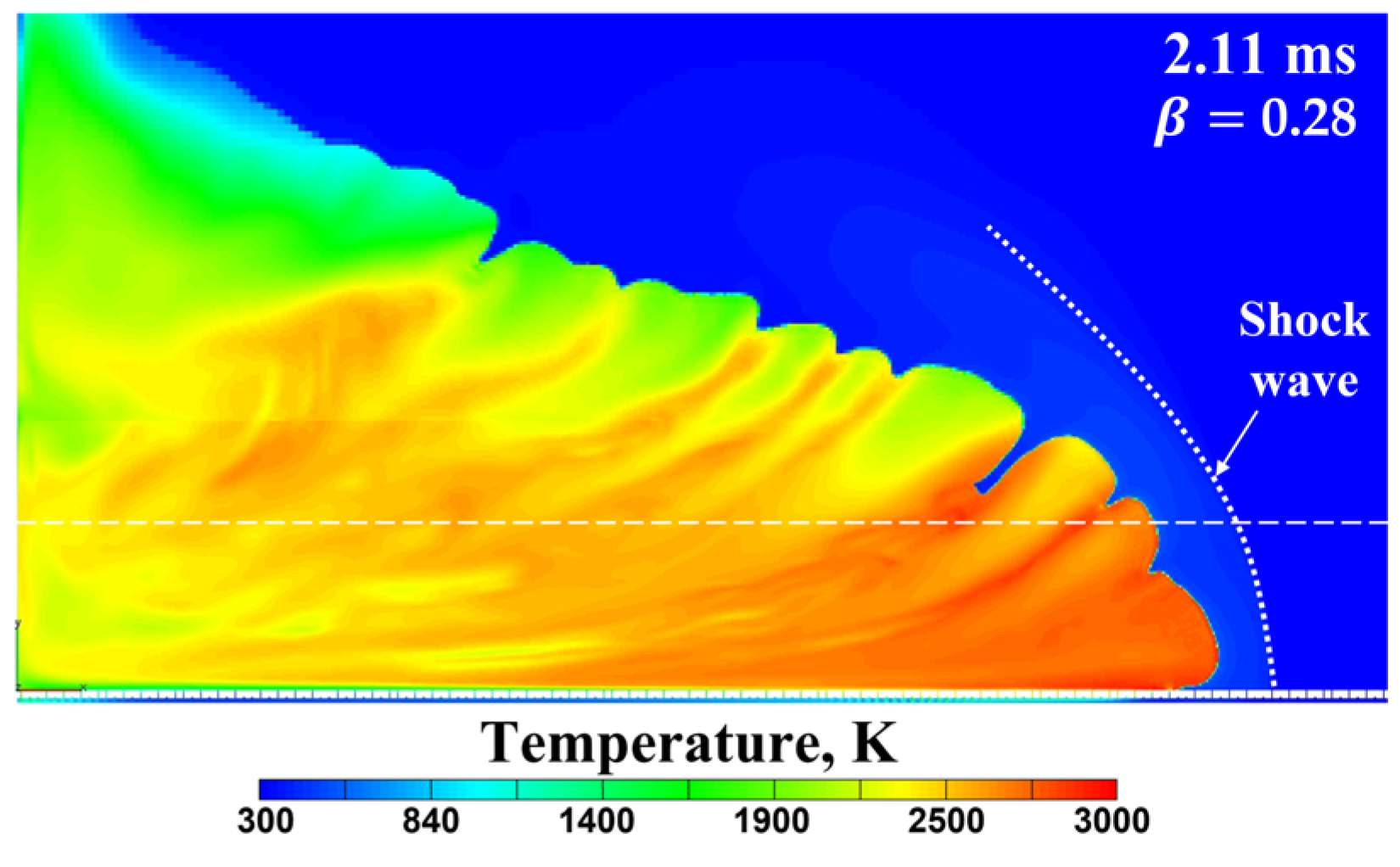
- The dilution of the combustible mixture with nitrogen leads to the same effect as the decrease in the height of the layer of the combustible mixture, as it leads to a decrease in the rate of energy release and a corresponding weakening of the precursor and the flame-born shock waves, thus increasing the DDT run-up distance and time up to the critical value when DDT fails.
- (6)
- The increase in the slit width at a fixed ignition energy leads to the same effects as the decrease in the height of the layer of the combustible mixture and the dilution of the combustible mixture with nitrogen. The deterioration of the conditions for DDT in a wider slit is mainly associated with a longer delay of flame arrival to the side walls of the slit causing slower flame propagation and acceleration.
- (7)
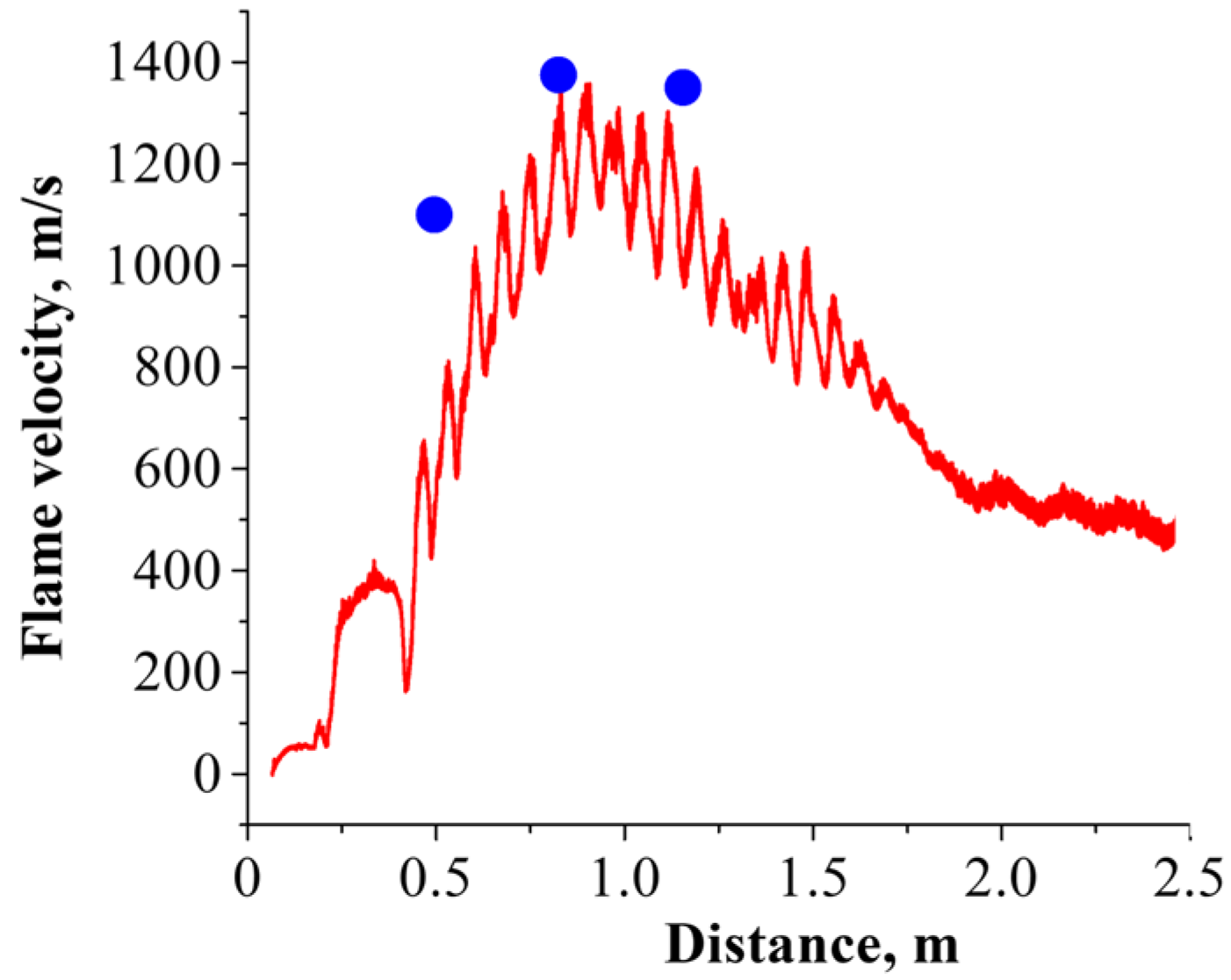
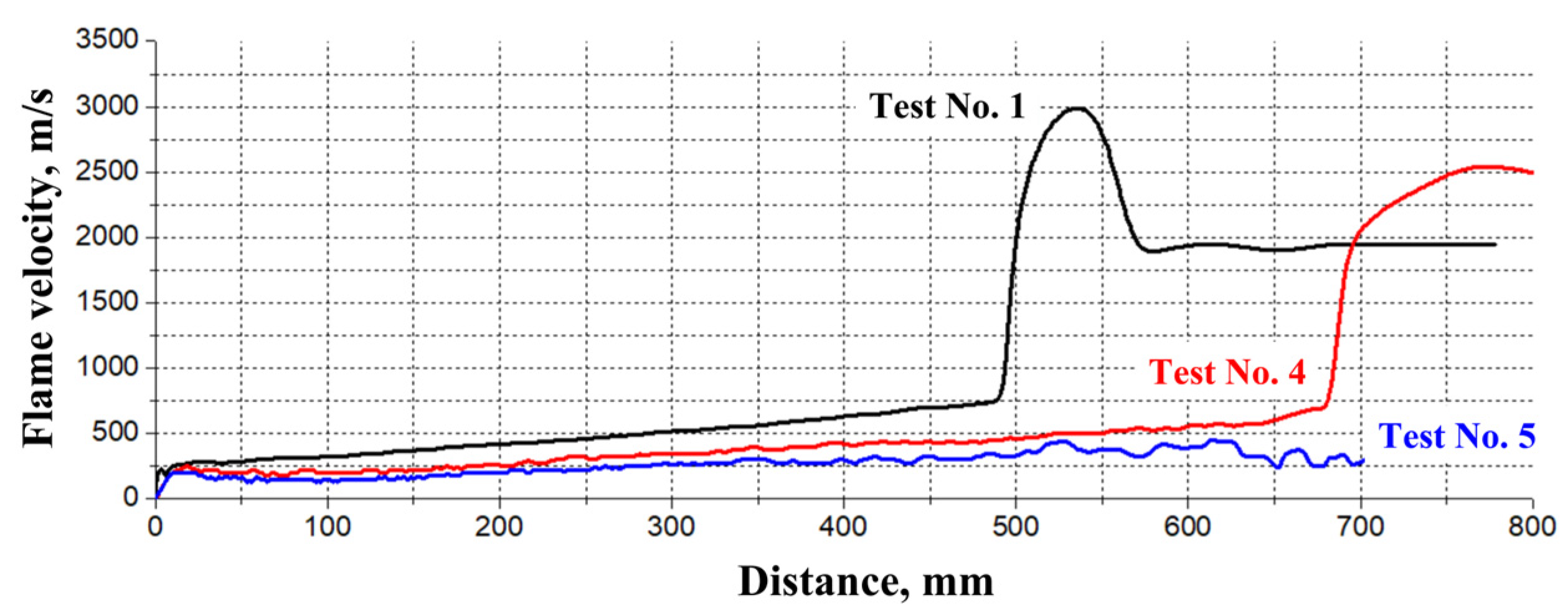
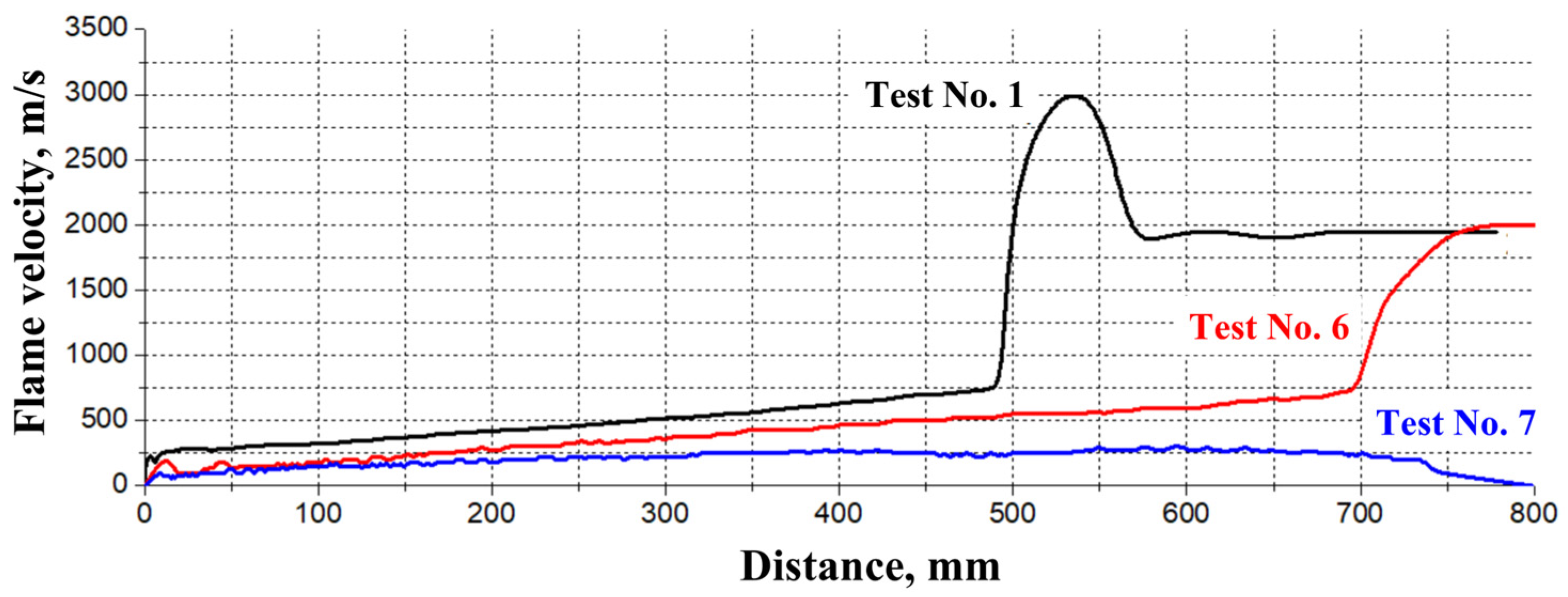
- A comparison of the calculation results and experimental data on the flame propagation velocity shows that the calculation satisfactorily describes the flame acceleration stage, as well as the apparent flame velocity at which DDT occurs (about 750 m/s for a stoichiometric ethylene–oxygen mixture). In addition, the calculation correctly predicts the minimum height of the combustible mixture layer required for DDT.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bykovskii, F.A.; Zhdan, S.A.; Vedernikov, E.F. Continuous spin detonations. J. Propul. Power 2006, 22, 1204–1216. [Google Scholar] [CrossRef]
- Dubrovskii, A.V.; Ivanov, V.S.; Frolov, S.M. Three-dimensional numerical simulation of the operation process in a continuous detonation combustor with separate feeding of hydrogen and air. Russ. J. Phys. Chem. B 2015, 9, 104–119. [Google Scholar] [CrossRef]
- Zhou, R.; Wu, D.; Wang, J.-P. Progress of continuously rotating detonation engines. Chin. J. Aeron. 2016, 29, 15–29. [Google Scholar] [CrossRef]
- Voitsekhovskii, B.V. Stationary detonation. Dokl. Akad. Nauk. SSSR 1959, 129, 1254–1256. [Google Scholar]
- Sommers, W.P.; Morrison, R.B. Simulation of condensed-explosive detonation phenomena with gases. Phys. Fluids 1962, 5, 241–248. [Google Scholar] [CrossRef]
- Dabora, E.K.; Nicholls, J.A.; Morrison, R.B. The influence of a compressible boundary on the propagation of gaseous detonations. Proc. Symp. Combust. 1965, 10, 817–830. [Google Scholar] [CrossRef]
- Adams, T.G. Do weak detonation waves exist? AIAA J. 1978, 16, 1035–1040. [Google Scholar] [CrossRef]
- Ivanov, M.F.; Fortov, V.E.; Borisov, A.A. Numerical simulation of the development of a detonation in gas volumes of finite thickness. Combust. Explos. Shock Waves 1981, 17, 332–338. [Google Scholar] [CrossRef]
- Bone, W.A.; Fraser, R.P.; Wheeler, W.H. A photographic investigation of flame movements in gaseous explosions. Part VII: The phenomenon of spin in detonation. Phil. Trans. A 1935, 235, 29–68. [Google Scholar]
- Strehlow, R.A.; Adamczyk, A.A.; Stiles, R.J. Transient studies of detonation waves. Astron. Acta 1972, 17, 509–527. [Google Scholar]
- Gavrilenko, T.P.; Krasnov, A.N.; Nikolaev, Y.A. Transfer of a gas detonation through an inert gas plug. Combust. Explos. Shock. Waves 1982, 18, 240–244. [Google Scholar] [CrossRef]
- Bjerketvedt, D.; Sonju, O.K.; Moen, I.O. The influence of experimental condition on the reinitiatirm of detonation across an inert region. Progr. Astron. Aeron. 1986, 106, 109–113. [Google Scholar]
- Thomas, G.O.; Sutton, P.; Edwards, D.H. The behavior of detonation waves at concentration gradients. Combust. Flame 1991, 84, 312–322. [Google Scholar] [CrossRef]
- Teodorczyk, A.; Benoan, F. Interaction of detonation with inert gas zone. Shock Waves 1996, 6, 211–223. [Google Scholar] [CrossRef]
- Teodorczyk, A.; Thomas, G.O.; Ward, S.M. Transmission of a detonation across an air gap. In Proceedings of the 20th International Symposium Shock Waves, Pasadena, CA, USA, 31 May 1996; pp. 1095–1100. [Google Scholar]
- Kuznetsov, M.S.; Alekseev, V.I.; Dorofeev, S.B.; Matsukov, I.D.; Boccio, J.L. Detonation propagation, decay, and reinitiation in nonuniform gaseous mixtures. Proc. Combust. Inst. 1998, 27, 2241–2247. [Google Scholar] [CrossRef]
- Liu, J.C.; Liou, J.J.; Sichel, M.; Kauffman, C.W.; Nicholls, J.A. Diffraction and transmission of a detonation into a bounding explosive layer. Proc. Combust. Inst. 1988, 21, 1639–1647. [Google Scholar] [CrossRef]
- Tonello, N.A.; Sichel, M.; Kauffman, C.W. Mechanisms of detonation transmission in layered H2-O2 mixtures. Shock Waves 1995, 5, 225–238. [Google Scholar] [CrossRef]
- Oran, E.S.; Jones, D.A.; Sichel, M. Numerical simulation of detonation transmission. Proc. R. Soc. Lond. A 1992, 436, 267–297. [Google Scholar] [CrossRef]
- Ishii, K.; Kojima, M. Propagation of detonation in mixtures with concentration gradients. In Application of Detonation to Propulsion; Roy, G., Frolov, S., Shepherd, J., Eds.; TORUS Press: Moscow, Russia, 2004; pp. 32–37. [Google Scholar]
- Calhoon, W.; Sinha, N. Detonation wave propagation in concentration gradients. AIAA Paper 2005-1167. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar] [CrossRef]
- Ishii, K.; Kojima, M. Behavior of detonation propagation in mixtures with concentration gradients. Shock Waves 2007, 17, 95–102. [Google Scholar] [CrossRef]
- Kessler, D.A.; Gamezo, V.N.; Oran, E.S. Gas-phase detonation propagation in mixture composition gradients. Phil. Trans. R. Soc. A 2012, 370, 567–596. [Google Scholar] [CrossRef]
- Houim, R.W.; Fievisohn, R.T. The influence of acoustic impedance on gaseous layered detonations bounded by an inert gas. Combust. Flame 2017, 179, 185–198. [Google Scholar] [CrossRef]
- Rudy, W.; Kuznetsov, M.; Porowski, R.; Teodorczyk, A.; Grune, J.; Sempert, K. Critical conditions of hydrogen–air detonation in partially confined geometry. Proc. Combust. Inst. 2013, 34, 1965–1972. [Google Scholar] [CrossRef]
- Kuznetsov, M.; Yanez, J.; Grune, J.; Friedrich, A.; Jordan, T. Hydrogen combustion in a flat semiconfined layer with respect to the Fukushima Daiichi accident. Nucl. Eng. Des. 2015, 286, 36–48. [Google Scholar] [CrossRef]
- Li, J.; Mi, X.; Higgins, A.J. Geometric scaling for a detonation wave governed by a pressure-dependent reaction rate and yielding confinement. Phys. Fluids 2015, 27, 027102. [Google Scholar] [CrossRef]
- Reynaud, M.; Virot, F.; Chinnayya, A. A computational study of the interaction of gaseous detonations with a compressible layer. Phys. Fluids 2017, 29, 056101. [Google Scholar] [CrossRef]
- Grune, J.; Sempert, K.; Haberstroh, H.; Kuznetsov, M.; Jordan, T. Experimental investigation of hydrogen–air deflagrations and detonations in semiconfined flat layers. J. Loss Prevent. Proc. Ind. 2013, 26, 317–323. [Google Scholar] [CrossRef]
- Shamshin, I.O.; Ivanov, V.S.; Aksenov, V.S.; Gusev, P.A.; Frolov, S.M. Experimental study of the initial stage of the operation process in detonation rocket and air-breathing engines. In Advances in Detonation Research; Frolov, S.M., Ed.; TORUS Press: Moscow, Russia, 2022; pp. 17–20. [Google Scholar] [CrossRef]
- Shamshin, I.O.; Ivanov, V.S.; Aksenov, V.S.; Gusev, P.A.; Frolov, S.M. Deflagration-to-detonation transition in a semi-confined slit combustor filled with nitrogen diluted ethylene-oxygen mixture. Energies 2023, 16, 1098. [Google Scholar] [CrossRef]
- Nettleton, M.A. Gaseous Detonations; Chapman and Hall: London, UK, 1987. [Google Scholar]
- Frolov, S.M.; Ivanov, V.S.; Basara, B.; Suffa, M. Numerical simulation of flame propagation and localized preflame autoignition in enclosures. J. Loss Prev. Process Industr. 2013, 26, 302–309. [Google Scholar] [CrossRef]
- Shchelkin, K.I. Fast Combustion and Spin Detonation of Gases; Voenizdat Publishing: Moscow, Russia, 1949. [Google Scholar]
- Frolov, S.M. Acceleration of the deflagration-to-detonation transition in gases: From Shchelkin to our days. Combust. Explos. Shock Waves 2012, 48, 258–268. [Google Scholar] [CrossRef]
- Belyaev, A.A.; Basevich, V.Y.; Frolov, S.M. Database for calculating laminar and turbulent combustion of aviation kerosene—Air mixtures. Combust. Explos. 2015, 8, 29–36. [Google Scholar]
- Basevich, V.Y.; Belyaev, A.A.; Posvyanskii, V.S.; Frolov, S.M. Mechanisms of the oxidation and combustion of normal paraffin hydrocarbons: Transition from C1–C10 to C11–C16. Russ. J. Phys. Chem. B 2013, 7, 161–169. [Google Scholar] [CrossRef]
- Egolfopoulos, F.N.; Zhu, D.L.; Law, C.K. Experimental and numerical determination of laminar flame speeds: Mixtures of C2-hydrocarbons with oxygen and nitrogen. Proc. Combust. Inst. 1991, 23, 471–478. [Google Scholar] [CrossRef]
- Hirasawa, T.; Sung, C.J.; Joshi, A.; Yang, Z.; Wang, H.; Law, C.K. Determination of laminar flame speeds using digital particle image velocimetry: Binary fuel blends of ethylene, n-butane, and toluene. Proc. Combust. Inst. 2002, 29, 1427–1434. [Google Scholar] [CrossRef]
- Pope, S.B. PDF methods for turbulent reactive flows. Progr. Energy Combust. Sci. 1985, 11, 119–192. [Google Scholar] [CrossRef]
- Frolov, S.M.; Basevich, V.Y.; Neuhaus, M.G.; Tatshl, R. A joint velocity–scalar PDF method for modeling premixed and nonpremixed combustion. In Advanced Computation and Analysis of Combustion; Roy, G.D., Frolov, S.M., Givi, P., Eds.; ENAS Publishing House: Moscow, Russia, 1997; pp. 537–562. [Google Scholar]
- Saxena, S.; Kahandawala, M.S.P.; Sidhu, S.S. A shock tube study of ignition delay in the combustion of ethylene. Combust. Flame 2011, 158, 1019–1031. [Google Scholar] [CrossRef]
- Wan, Z.; Zheng, Z.; Wang, Y.; Zhang, D.; Li, P.; Zhang, C. A shock tube study of ethylene/air ignition characteristics over a wide temperature range. Combust. Sci. Technol. 2019, 192, 2297–2305. [Google Scholar] [CrossRef]
- Marthur, S.R.; Murthy, J.Y. A pressure–based method for unstructured meshes. Numer. Heat Transf. B 1997, 31, 195–215. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1510–1520. [Google Scholar] [CrossRef]
- Kawasaki, A.; Kasahara, J. A novel characteristic length of detonation relevant to supercritical diffraction. Shock Waves 2020, 30, 1–12. [Google Scholar] [CrossRef]
- Kerampran, S.; Desbordes, D.; Veyssiere, B. Influence of the pressure waves generated at the initial stage of flame propagation on the DDT process in smooth tubes. In Confined Detonations and Pulse Detonation Engines; Roy, G., Frolov, S., Santoro, W., Tsyganov, S., Eds.; TORUS Press: Moscow, Russia, 2003; pp. 3–16. [Google Scholar]
- Borisov, A.A.; Koval, A.S.; Mailkov, A.E.; Smetanyuk, V.A.; Frolov, S.M. Transient modes of propagation of the shock wave–reaction zone complex in methane–air mixtures. Russ. J. Phys. Chem. B 2014, 8, 158–164. [Google Scholar] [CrossRef]
- Gelfand, B.E.; Frolov, S.M.; Nettleton, M.A. Gaseous detonations-a selective review. Prog. Energy Combust. Sci. 1991, 17, 327–371. [Google Scholar] [CrossRef]
- Frolov, S.M.; Aksenov, V.S.; Ivanov, V.S.; Medvedev, S.N.; Shamshin, I.O. Flow structure in rotating detonation engine with separate supply of fuel and oxidizer: Experiment and CFD. In Detonation Control for Propulsion: Pulse Detonation and Rotating Detonation Engines; Li, J.-M., Teo Boo, C.J., Khoo, C., Wang, J.-P., Wang, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 39–59. [Google Scholar] [CrossRef]


| No. | Reaction | , (L, mol, s) | , kcal/mol |
|---|---|---|---|
| 1 | C2H4 + 2O2 → 2CO + 2H2O | 2∙108 | 25 |
| 2 | CO + H2O → CO2 + H2 | 1∙1012/ | 42 |
| 3 | CO2 + H2 → CO + H2O | 3.1∙1013/ | 50 |
| 4 | H2 + H2 + O2 → H2O + H2O | 7.0∙1013/ | 21 |
| 5 | CO + CO + O2 → CO2 + CO2 | 8.5∙1012/ | 21 |
| Test No. | mm | vol.% | , L/min | , s | , mm | |
|---|---|---|---|---|---|---|
| 1 | 5 | 0 | 0 | 2.36 | 10 | 100 |
| 2 | 5 | 0 | 0 | 2.36 | 5 | 50 |
| 3 | 5 | 0 | 0 | 2.36 | 3 | 30 |
| 4 | 5 | 0.28 | 22 | 2.36 | 10 | 100 |
| 5 | 5 | 0.50 | 33 | 2.36 | 10 | 100 |
| 6 | 10 | 0 | 0 | 5.72 | 10 | 100 |
| 7 | 25 | 0 | 0 | 11.80 | 10 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanov, V.S.; Shamshin, I.O.; Frolov, S.M. Computational Study of Deflagration-to-Detonation Transition in a Semi-Confined Slit Combustor. Energies 2023, 16, 7028. https://doi.org/10.3390/en16207028
Ivanov VS, Shamshin IO, Frolov SM. Computational Study of Deflagration-to-Detonation Transition in a Semi-Confined Slit Combustor. Energies. 2023; 16(20):7028. https://doi.org/10.3390/en16207028
Chicago/Turabian StyleIvanov, Vladislav S., Igor O. Shamshin, and Sergey M. Frolov. 2023. "Computational Study of Deflagration-to-Detonation Transition in a Semi-Confined Slit Combustor" Energies 16, no. 20: 7028. https://doi.org/10.3390/en16207028
APA StyleIvanov, V. S., Shamshin, I. O., & Frolov, S. M. (2023). Computational Study of Deflagration-to-Detonation Transition in a Semi-Confined Slit Combustor. Energies, 16(20), 7028. https://doi.org/10.3390/en16207028








