Real-Time Implementation of Sensorless DTC-SVM Applied to 4WDEV Using the MRAS Estimator
Abstract
:1. Introduction
- Low robustness to variations in rotor parameters;
- Presence of coordinate transformations that depend on an estimated angle;
- Use of a mechanical sensor (fragile and costly). When not using this sensor (Sensorless drive), the machine’s performance is degraded.
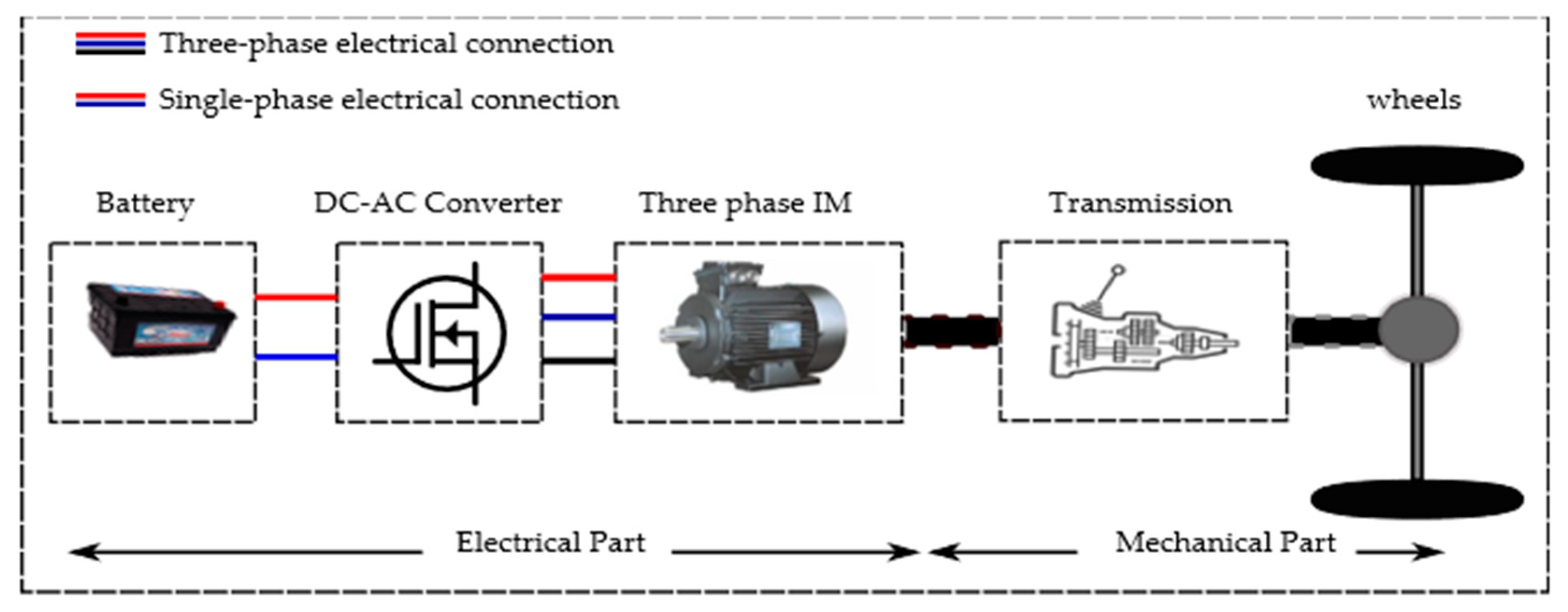
2. Electric Vehicle Powertrain
2.1. Electric Vehicle Diagram
2.1.1. Principle
2.1.2. The Battery
- -
- High specific power to ensure good vehicle acceleration;
- -
- A large number of charge/discharge cycles without significant performance degradation;
- -
- Reduced production cost;
- -
- Application safety;
- -
- Fast recharging;
2.1.3. The DC-AC Converter
2.1.4. The Induction Motor
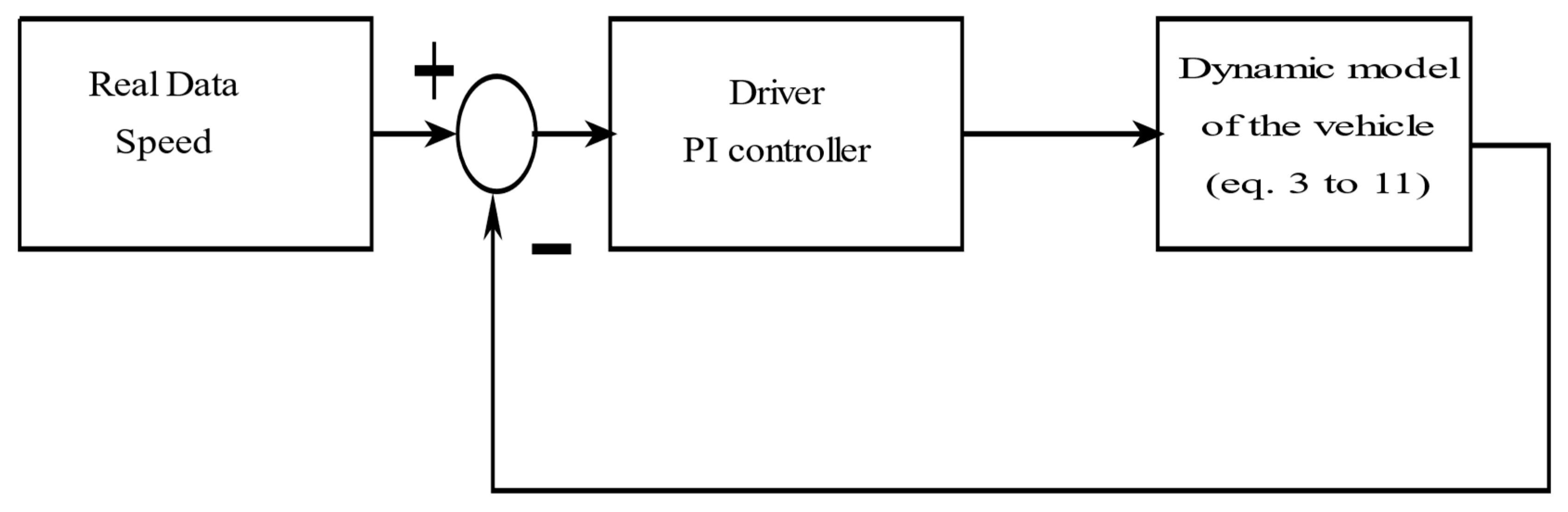
2.2. Dynamic Modelling of the Vehicle
- the force generated by the powertrain;
- The aerodynamic friction force;
- : The force of wheel friction;
- : The force of gravity when driving on non-horizontal roads.
2.3. Experimental Test
| Latitude | Longitude | Altitude (m) | Speed (Km/h) | Time/Date |
|---|---|---|---|---|
| 32.35699 | −9.274521 | 113.9 | 0 | 15:20:53/13 May 2022 |
| 32.36787 | −9.273886 | 113.9 | 28.5 | 15:21:08/13 May 2022 |
| 32.3784 | −9.273513 | 113.7 | 28.5 | 15:21:24/13 May 2022 |
| ………. | ………. | ………. | ………. | ………. |
| ………. | ………. | ………. | ………. | ………. |
| ………. | ………. | ………. | ………. | ………. |
| 33.98274 | −6.944687 | 70.8 | 95.4 | 19:25:30/13 May 2022 |
| 33.9849 | −6.944562 | 72.5 | 70.8 | 19:25:48/13 May 2022 |
| 33.98707 | −6.940218 | 73.6 | 91.3 | 19:27:05/13 May 2022 |

2.4. Simulation Results and Discussion
- Scenario 1: SR Route (Safi–Rabat).
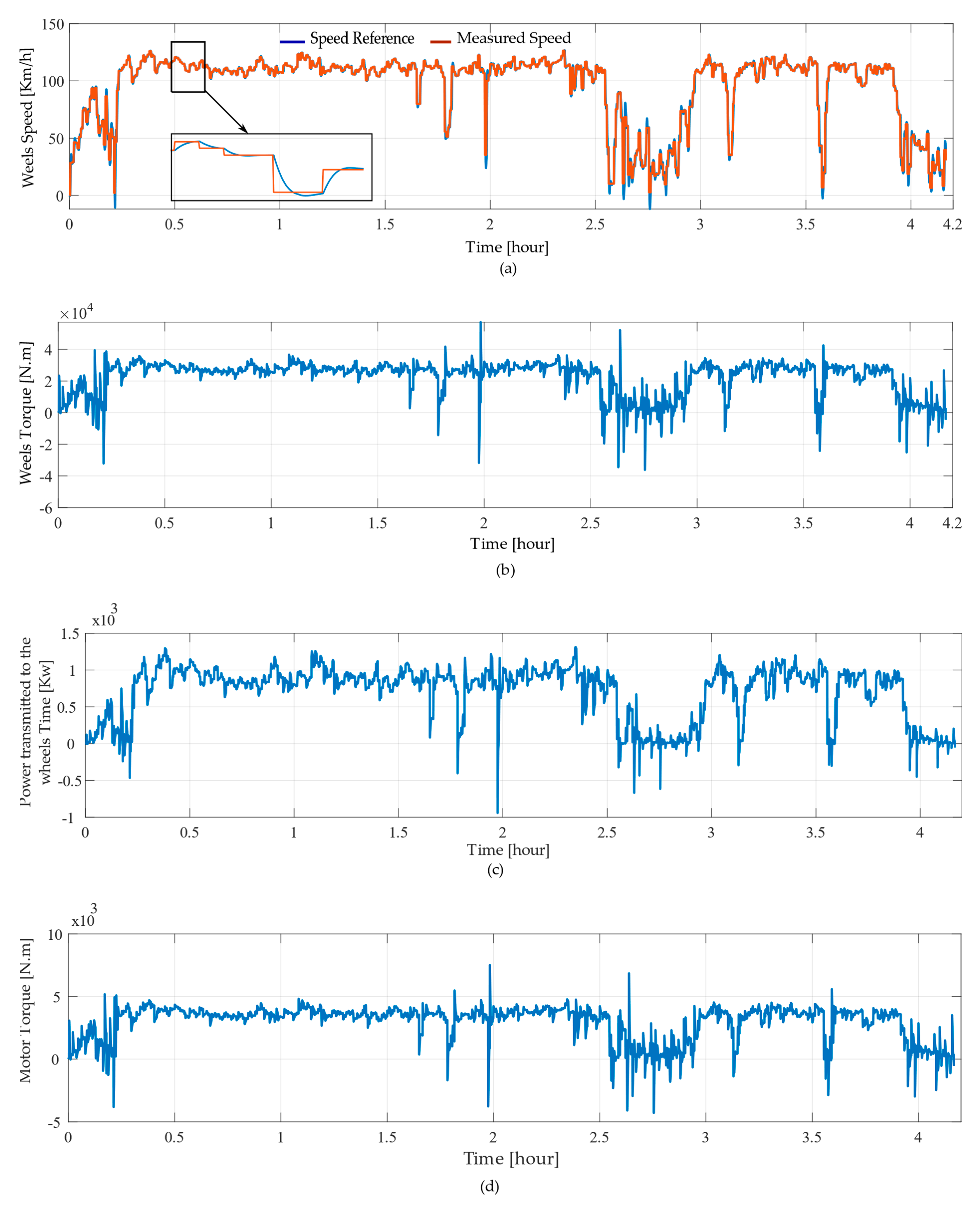
- Scenario 2: Driving cycle FTP75.

3. Direct Torque Control Modeling
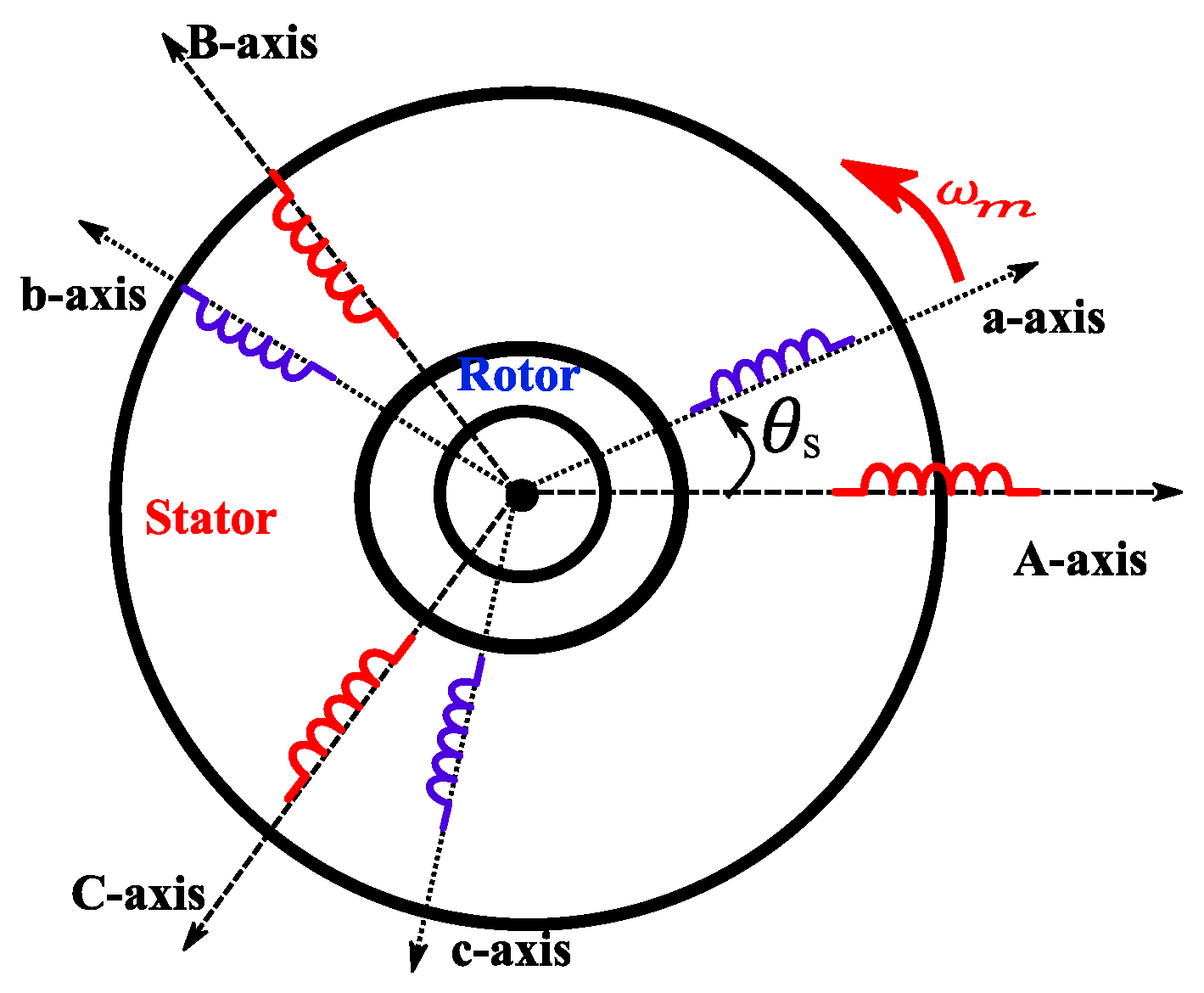
3.1. Induction Motor Modeling
- Electrical equations:
- Magnetic equations:
- Mechanical equations:
3.2. Two-Level Voltage Source Inverter Modeling
- Si = 1 if is closed and is opened.
- Si = 0 if is opened and is closed.
3.3. The DTC-SVM Strategy
3.4. Elaboration of the Switching Table
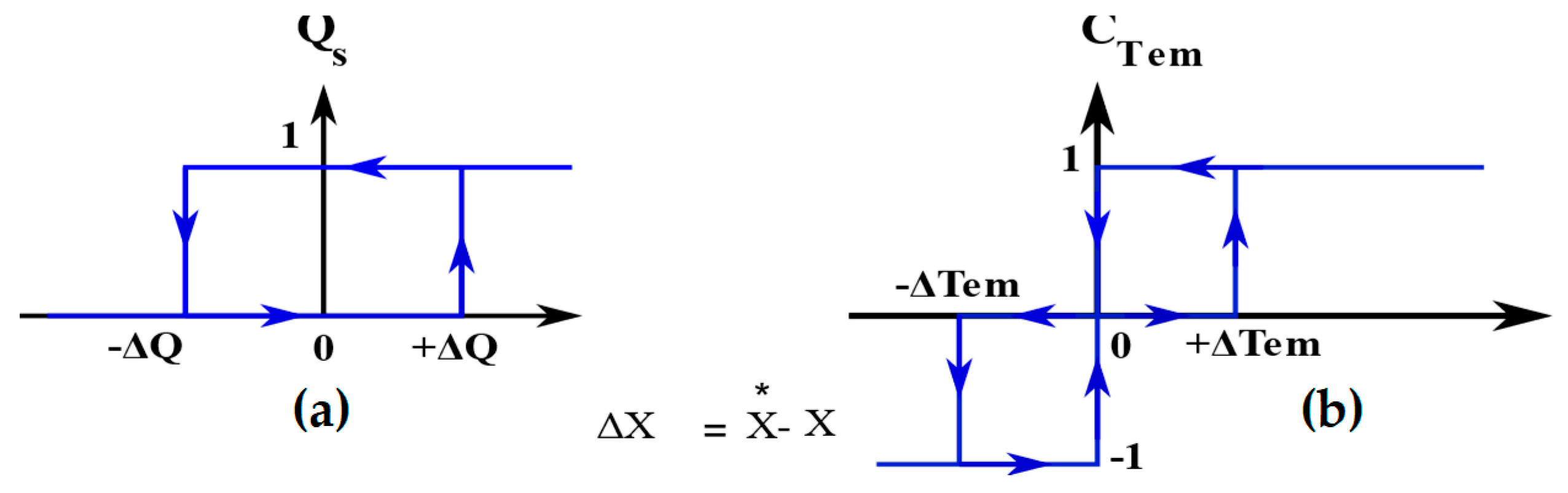
| Sector | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
↑ | ↑ | ||||||
| ↓ | |||||||
↓ | ↑ | ||||||
| ↓ | |||||||
3.5. Design of a Rotor Flux Model Reference Adaptive System Observer
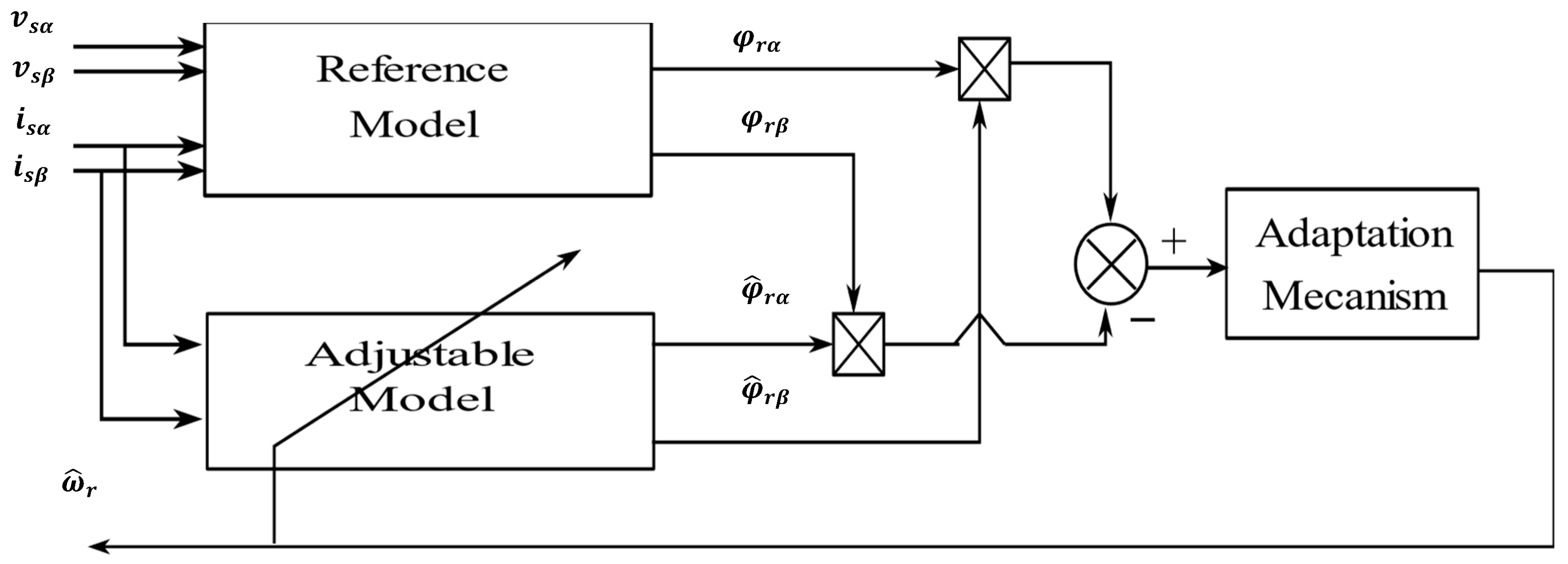
3.6. Simulation Results
3.6.1. Speed Step Response
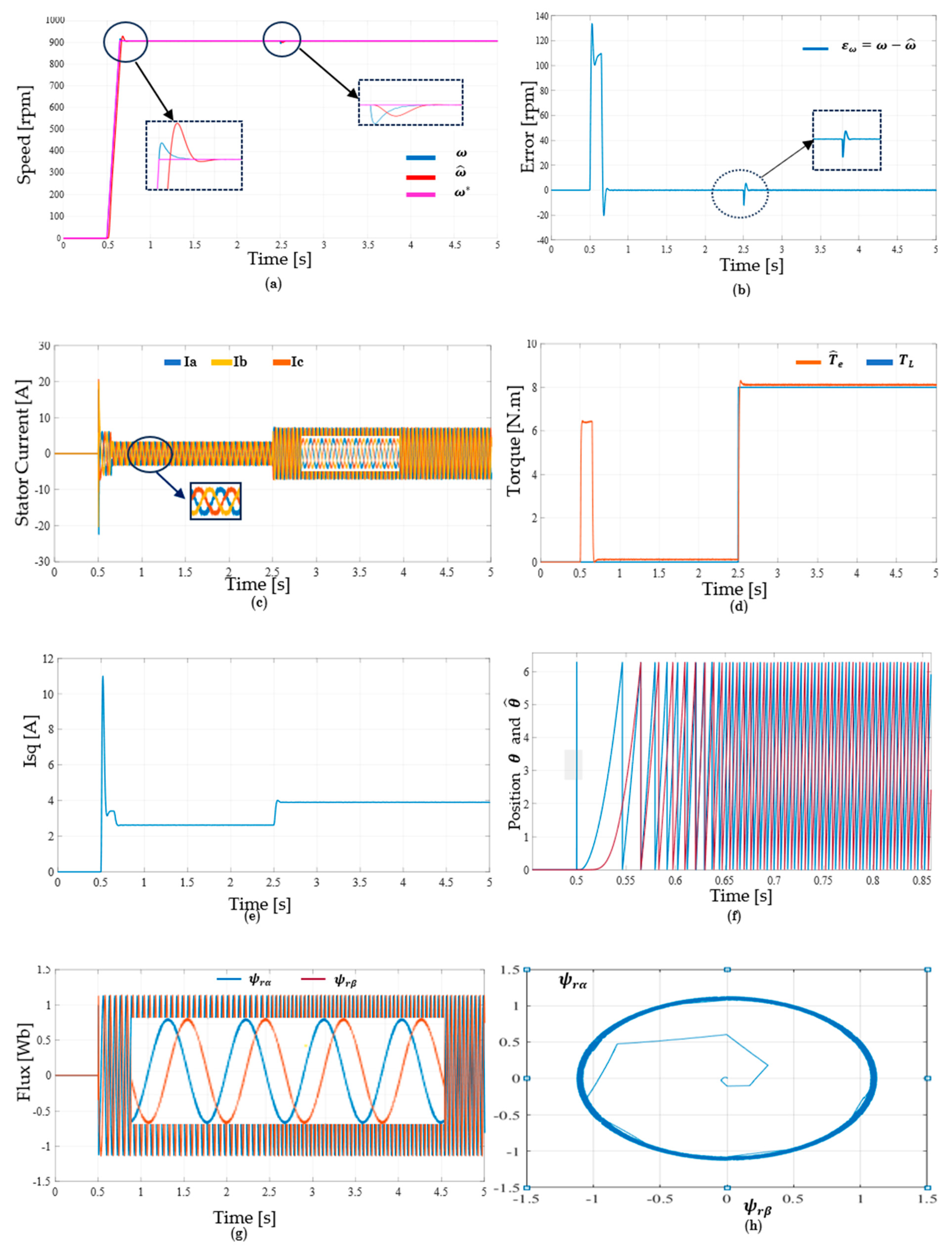
3.6.2. Variable Speed Response
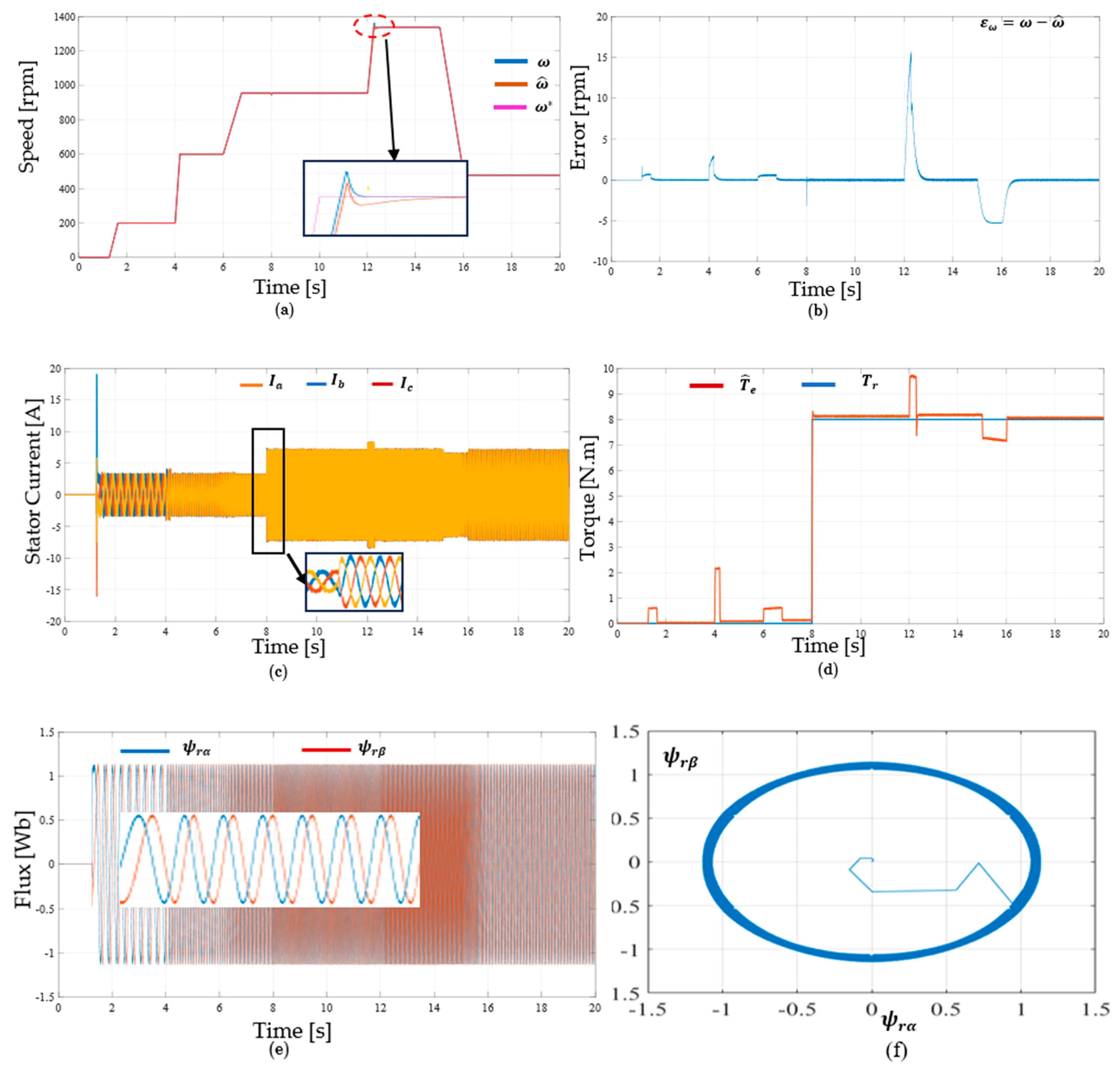
3.7. DTC-SVM Control Implementation
3.7.1. Experimental Test Bench
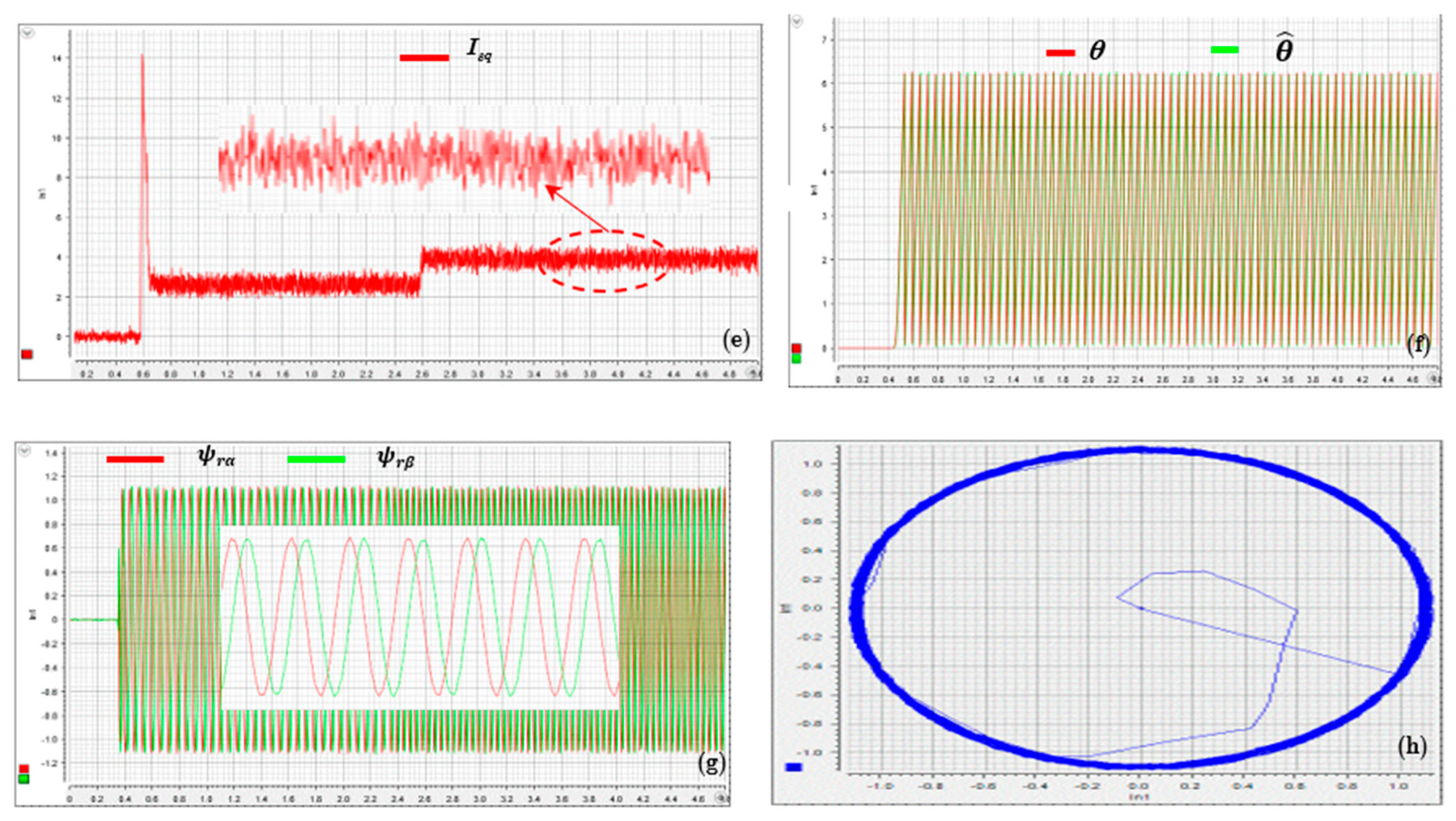
3.7.2. Experimental Results
4. Electronic Differential System
4.1. The Electronic Differential System


| Vehicle reference speed | |
| Steering angle (°) | |
| Turning angle of left front wheel (°) | |
| Turning angle of right front wheel (°) | |
| Length of vehicle (m) | |
| Width of vehicle (m) | |
| Steering radius of center of rear axle | |
| Steering radius of inside rear wheel | |
| Steering radius of outside rear wheel | |
| Steering radius of center of front axle | |
| Steering radius of inside front wheel | |
| Steering radius of outside front wheel | |
| Linear speed of left front in wheel and right front in wheel | |
| Linear speed of left rear in wheel and right rear in wheel |
4.2. Speed Controller Design of IM Drive
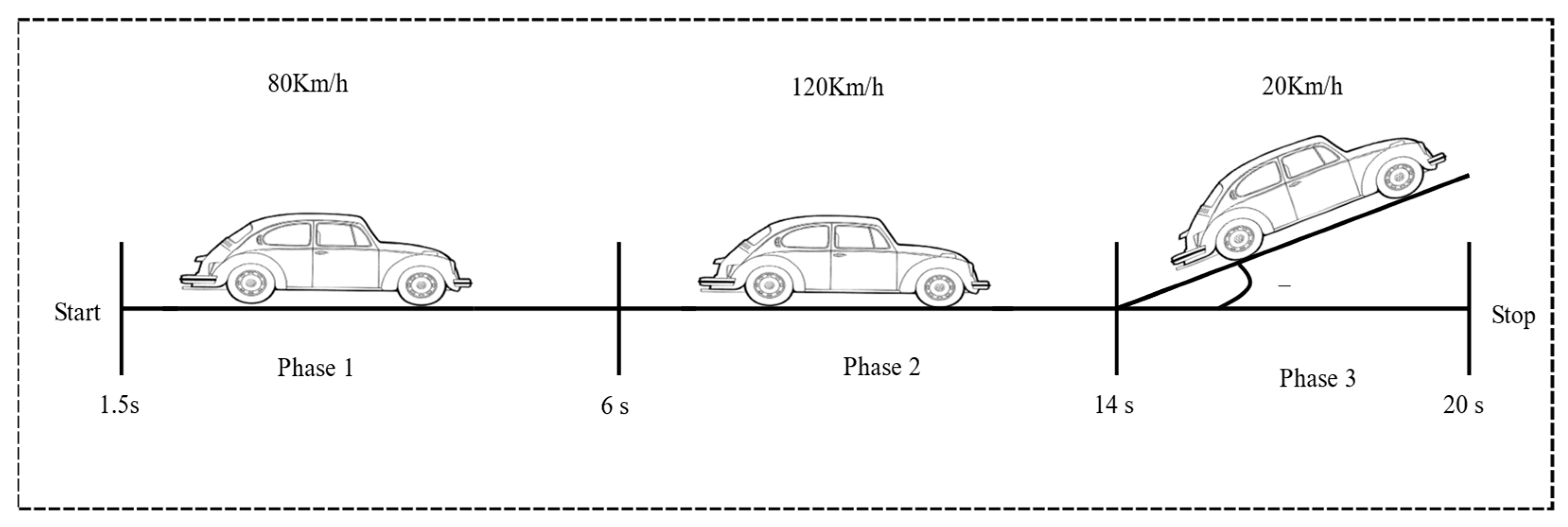
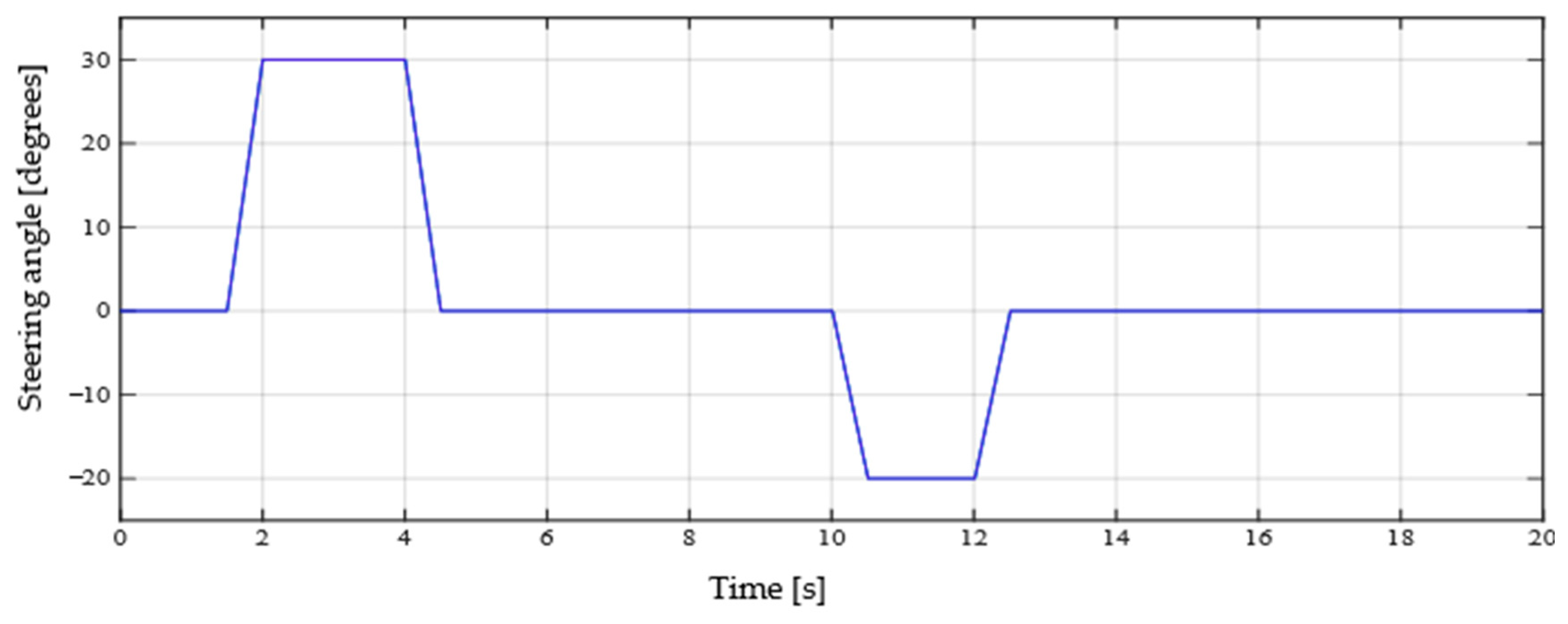
4.3. Vehicle Speed Profile
4.4. Simulation Results
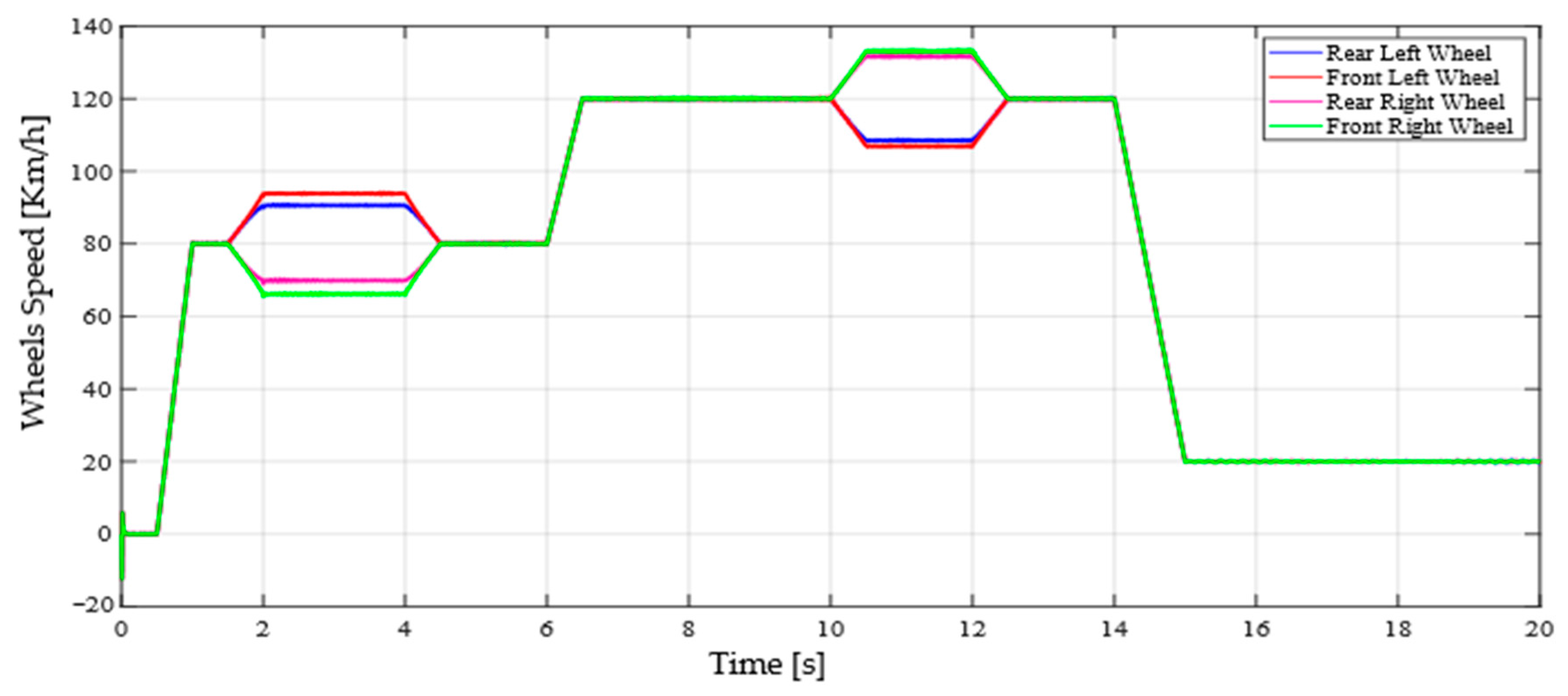
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boulmane, A.; Zidani, Y.; Belkhayat, D. Comparative study of direct and indirect field oriented control. In Proceedings of the 2017 International Renewable and Sustainable Energy Conference (IRSEC), Tangier, Morocco, 4–7 December 2017; pp. 1–6. [Google Scholar]
- Esparza Sola, T.; Chiu, H.-J.; Liu, Y.-C.; Rahman, A.N. Extending DC bus utilization for induction motors with stator flux oriented direct torque control. Energies 2022, 15, 374. [Google Scholar] [CrossRef]
- Soon, T.C.; Ping, H.W.; Rahim, N.A. SVM Direct Torque Control of an induction machine. In Proceedings of the 2012 IEEE Conference on Sustainable Utilization and Development in Engineering and Technology (STUDENT), Kuala Lumpur, Malaysia, 6–9 October 2012; pp. 123–128. [Google Scholar]
- Sengamalai, U.; Thamizh Thentral, T.; Ramasamy, P.; Bajaj, M.; Hussain Bukhari, S.S.; Elattar, E.E.; Althobaiti, A.; Kamel, S. Mitigation of circulating bearing current in induction motor drive using modified ANN based MRAS for Traction Application. Mathematics 2022, 10, 1220. [Google Scholar] [CrossRef]
- Benlaloui, I.; Drid, S.; Chrifi-Alaoui, L.; Ouriagli, M. Implementation of a new MRAS speed sensorless vector control of induction machine. IEEE Trans. Energy Convers. 2014, 30, 588–595. [Google Scholar] [CrossRef]
- Zbede, Y.B.; Gadoue, S.M.; Atkinson, D.J. Model predictive MRAS estimator for sensorless induction motor drives. IEEE Trans. Ind. Electron. 2016, 63, 3511–3521. [Google Scholar] [CrossRef]
- Lokriti, A.; Salhi, I.; Doubabi, S. PI-flou avec une seule entrée pour la commande sans capteur mécanique du MAS exceptée de la rotation directe de Park. In Actes des 22èmes Rencontres Francophones sur la Logique Floue et ses Applications, 10–11 Octobre 2013, Reims, France; Université de Reims Champagne-Ardenne: Reims, France, 2013; p. 179. [Google Scholar]
- Comanescu, M.; Xu, L. Sliding-mode MRAS speed estimators for sensorless vector control of induction machine. IEEE Trans. Ind. Electron. 2006, 53, 146–153. [Google Scholar] [CrossRef]
- Loron, L.; Laliberte, G. Application of the extended Kalman filter to parameters estimation of induction motors. In Proceedings of the 1993 Fifth European Conference on Power Electronics and Applications, Brighton, UK, 13–16 September 1993; pp. 85–90. [Google Scholar]
- Salvatore, L.; Stasi, S.; Cupertino, F. Improved rotor speed estimation using two Kalman filter-based algorithms. In Proceedings of the Conference Record of the 2001 IEEE Industry Applications Conference. 36th IAS Annual Meeting (Cat. No. 01CH37248), Chicago, IL, USA, 30 September–4 October 2001; pp. 125–132. [Google Scholar]
- El Ouanjli, N.; Motahhir, S.; Derouich, A.; El Ghzizal, A.; Chebabhi, A.; Taoussi, M. Improved DTC strategy of doubly fed induction motor using fuzzy logic controller. Energy Rep. 2019, 5, 271–279. [Google Scholar] [CrossRef]
- Rashag, H.F.; Koh, S.; Abdalla, A.N.; Tan, N.M.; Chong, K. Modified direct torque control using algorithm control of stator flux estimation and space vector modulation based on fuzzy logic control for achieving high performance from induction motors. J. Power Electron. 2013, 13, 369–380. [Google Scholar] [CrossRef]
- Nanda, G.; Kar, N.C. A survey and comparison of characteristics of motor drives used in electric vehicles. In Proceedings of the 2006 Canadian Conference on Electrical and Computer Engineering, Ottawa, ON, Canada, 7–10 May 2006; pp. 811–814. [Google Scholar]
- Wu, X.; Freese, D.; Cabrera, A.; Kitch, W.A. Electric vehicles’ energy consumption measurement and estimation. Transp. Res. Part D Transp. Environ. 2015, 34, 52–67. [Google Scholar] [CrossRef]
- Yu, Z.; Huai, R.; Xiao, L. State-of-charge estimation for lithium-ion batteries using a kalman filter based on local linearization. Energies 2015, 8, 7854–7873. [Google Scholar] [CrossRef]
- Fiori, C.; Ahn, K.; Rakha, H.A. Power-based electric vehicle energy consumption model: Model development and validation. Appl. Energy 2016, 168, 257–268. [Google Scholar] [CrossRef]
- Grunditz, E.A.; Thiringer, T. Performance analysis of current BEVs based on a comprehensive review of specifications. IEEE Trans. Transp. Electrif. 2016, 2, 270–289. [Google Scholar] [CrossRef]
- Wong, J.Y. Theory of Ground Vehicles; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Boudallaa, A.; Chennani, M.; Belkhayat, D.; Rhofir, K. Vector Control of Asynchronous Motor of Drive Train Using Speed Controller H∞. Emerg. Sci. J. 2022, 6, 834–850. [Google Scholar] [CrossRef]
- Gdaim, S.; Mtibaa, A.; Mimouni, M.F. Design and experimental implementation of DTC of an induction machine based on fuzzy logic control on FPGA. IEEE Trans. Fuzzy Syst. 2014, 23, 644–655. [Google Scholar] [CrossRef]
- Wahab, H.A.; Sanusi, H. Simulink model of direct torque control of induction machine. Am. J. Appl. Sci. 2008, 5, 1083–1090. [Google Scholar]
- Shi, L.; Jin, S. Direct torque control and space vector modulation-based direct torque control of brushless doubly-fed reluctance machines. IET Electr. Power Appl. 2023, 17, 1069–1080. [Google Scholar] [CrossRef]
- Ghezouani, A. Commande Directe du Couple par Modes Glissants (DTC-SMC) d’un Véhicule Électrique à Quatre Roues Motrices (EV4WD); Université de Béchar-Mohamed Tahri: Béchar, Algeria, 2019. [Google Scholar]
- Farajpour, Y.; Alzayed, M.; Chaoui, H.; Kelouwani, S. A novel switching table for a modified three-level inverter-fed DTC drive with torque and flux ripple minimization. Energies 2020, 13, 4646. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Idris, N.R.N.; Lee, K.-B. Dynamic hysteresis torque band for improving the performance of lookup-table-based DTC of induction machines. IEEE Trans. Power Electron. 2017, 33, 7959–7970. [Google Scholar] [CrossRef]
- Mossa, M.A.; Echeikh, H.; Diab, A.A.Z.; Haes Alhelou, H.; Siano, P. Comparative study of hysteresis controller, resonant controller and direct torque control of five-phase IM under open-phase fault operation. Energies 2021, 14, 1317. [Google Scholar] [CrossRef]
- Bacha, S.; Saadi, R.; Ayad, M.Y.; Sahraoui, M.; Laadjal, K.; Cardoso, A.J.M. Autonomous Electric-Vehicle Control Using Speed Planning Algorithm and Back-Stepping Approach. Energies 2023, 16, 2459. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Akl, M.M.; M Rashad, E.E. A comparative dynamic analysis between model predictive torque control and field-oriented torque control of IM drives for electric vehicles. Int. Trans. Electr. Energy Syst. 2021, 31, e13089. [Google Scholar] [CrossRef]
- Bose, B.K. Modern Power Electronics and AC Drives; Prentice Hall Upper Saddle River: Upper Saddle River, NJ, USA, 2002; Volume 123. [Google Scholar]
- Vas, P. Sensorless Vector and Direct Torque Control; Oxford University Press: Oxford, UK, 1998; Volume 42. [Google Scholar]
- Rind, S.J.; Ren, Y.; Shi, K.; Jiang, L.; Tufail, M. Rotor flux-MRAS based speed sensorless non-linear adaptive control of induction motor drive for electric vehicles. In Proceedings of the 2015 50th International Universities Power Engineering Conference (UPEC), Stoke-on-Trent, UK, 1–4 September 2015; pp. 1–6. [Google Scholar]
- Yıldırım, M.; Öksüztepe, E.; Tanyeri, B.; Kürüm, H. Electronic differential system for an electric vehicle with in-wheel motor. In Proceedings of the 2015 9th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 26–28 November 2015; pp. 1048–1052. [Google Scholar]






| Vehicle Parameters | |
|---|---|
| Vehicle mass | Mveh = 1400 Kg; |
| Wheel radius | Rwheel = 0.29 m; |
| Frontal surface area | S = 2.59 m2; |
| Inertia of the wheels | Jwheel = 0.65 Kg.m2; |
| Aerodynamic drag coefficient | Cx = 0.37; |
| Engine power | Pmot = 75 Kw; |
| Engine shaft inertia | Jmot = 0.103 Kg.m2; |
| Gear ratio | rred = 8; |
| Reducer efficiency Rolling resistance coefficients | ηred = 0.95; ; |
| Motor Specifications | Motor Parameters |
|---|---|
| Rated power: 1.5 kW | Ls = 0.42 H; |
| Rated current: 2.65 A | Lr = 0.072 H; |
| Rated frequency: 50 Hz | M = 0.1636 H; |
| Rated speed: 1425 rpm | Rs = 4.75 Ω; |
| Rated voltage: 400 V | Rr = 1.2 Ω; |
| Number of pole pairs: p = 2 | fr = 0.0025 Nm.s.rad−1; |
| J = 0.02 kg.m2; |
| Phase | Time (s) | Information | Vehicle Speed |
|---|---|---|---|
| Phase 01 | 1.5–6 s | Curved road at right side | 80 Km/h |
| Phase 02 | 6–14 s | Acceleration and curved road | 120 Km/h |
| Phase 04 | 14–20 s | Climbing a slope | 20 Km/h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boudallaa, A.; Belkhadir, A.; Chennani, M.; Belkhayat, D.; Zidani, Y.; Rhofir, K. Real-Time Implementation of Sensorless DTC-SVM Applied to 4WDEV Using the MRAS Estimator. Energies 2023, 16, 7090. https://doi.org/10.3390/en16207090
Boudallaa A, Belkhadir A, Chennani M, Belkhayat D, Zidani Y, Rhofir K. Real-Time Implementation of Sensorless DTC-SVM Applied to 4WDEV Using the MRAS Estimator. Energies. 2023; 16(20):7090. https://doi.org/10.3390/en16207090
Chicago/Turabian StyleBoudallaa, Abdelhak, Ahmed Belkhadir, Mohammed Chennani, Driss Belkhayat, Youssef Zidani, and Karim Rhofir. 2023. "Real-Time Implementation of Sensorless DTC-SVM Applied to 4WDEV Using the MRAS Estimator" Energies 16, no. 20: 7090. https://doi.org/10.3390/en16207090
APA StyleBoudallaa, A., Belkhadir, A., Chennani, M., Belkhayat, D., Zidani, Y., & Rhofir, K. (2023). Real-Time Implementation of Sensorless DTC-SVM Applied to 4WDEV Using the MRAS Estimator. Energies, 16(20), 7090. https://doi.org/10.3390/en16207090






