LLC Resonant Converters as Isolated Power Factor Corrector Pre-Regulators—Analysis and Performance Evaluation

Abstract

The power supply of many applications running off the power line is made up of an isolated dc-dc converter powered by a front-end power factor corrector (PFC) stage. The PFC stage ensures compliance with the electromagnetic compatibility regulations but does not usually provide safety isolation since it is typically implemented with a boost converter. Lately, the increase in multi-output power supplies, especially in lighting and USB Power Delivery applications, has raised the need for an isolated PFC at power levels where currently there is not an industry standard solution. This isolated PFC is intended to power one or more non-isolated post-regulators to enable a substantial simplification of the overall architecture and a cost reduction. The usage of an LLC resonant converter as an isolated PFC has been considered and demonstrated only quite recently, raising the industry’s attention due to the favorable converter’s characteristics that have led to its success as a dc-dc converter. This paper provides two significant contributions. Firstly, it provides a quantitative assessment of the difference in the results obtained by designing an LLC-based PFC converter based on the first harmonic approximation analysis or the time-domain analysis by applying them to the design of the same converter. Secondly, it demonstrates that designing an LLC-based PFC converter to work also in the above-resonance region optimizes its performance by reducing the (magnetizing) reactive current in the resonant tank and, therefore, the rms currents on both the input and the output side and the related power loss.

1. Introduction

The industry standard solution to address the compliance of mains-operated power supplies with the IEC 61000-3-2 regulation [1], which sets limits to the harmonic content of their input current, is the addition of an electronic front-end circuit, the so-called power factor corrector (PFC). It is a switch-mode converter directly supplied by the rectified mains and controlled to draw a sinusoidal current in phase with the voltage. This results in a low total harmonic distortion (THD) and near-unity power factor (PF = 1), hence the name PFC, as if the electronic equipment was a resistive load.

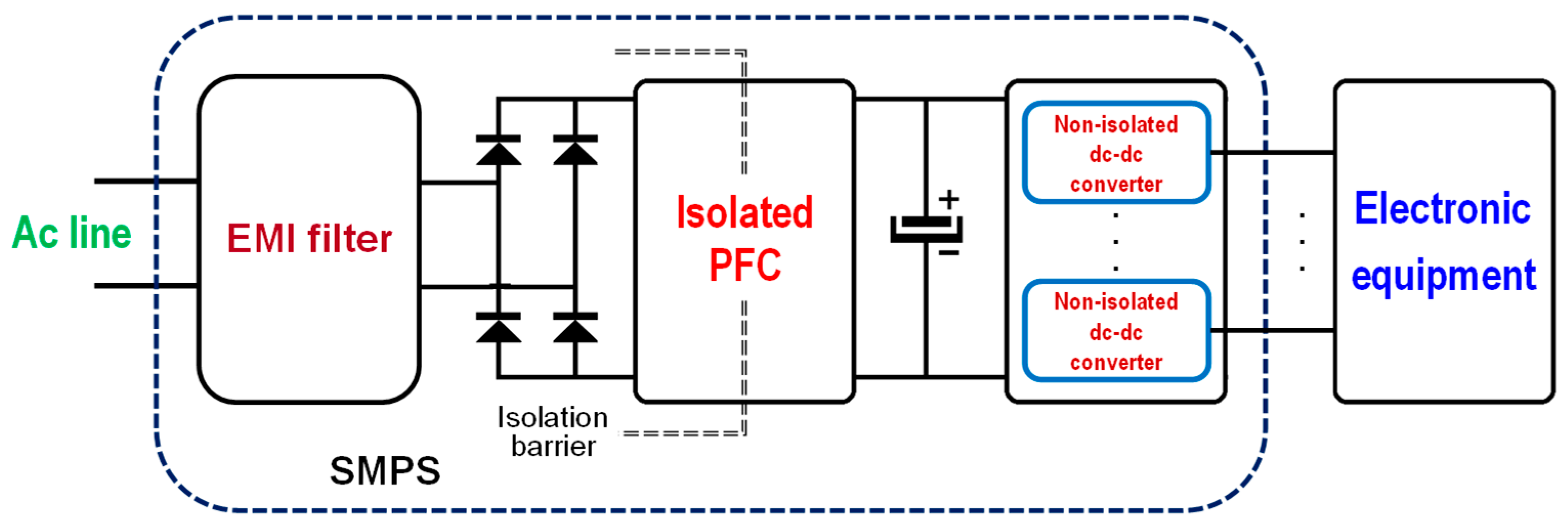
Figure 1 shows the most common architecture of a power-factor-corrected switch-mode power supply (SMPS): a PFC pre-regulator front end providing a regulated output voltage and powering a cascaded dc-dc converter.

In most applications, the PFC pre-regulator is realized using a boost converter, a non-isolated topology. The cascaded dc-dc converter is therefore responsible for providing the isolation required in most power supplies operated from the mains to meet safety requirements and regulations.

The boost converter can cover a broad power range, whereas the cascaded dc-dc converter uses different topologies depending on the power level. Flyback converters are commonly used in the lower power range. LLC resonant converters [2] have become very popular at higher power levels because of their nice properties conferred by soft-switching operation (low power loss, high efficiency, high operating frequency, low electromagnetic emissions, high power density) without significant drawbacks.

There are applications, however, where an isolated PFC cascaded by one or more non-isolated converters might be a better option: multi-output isolated converters involve a more complicated design and are more difficult to fine-tune, while non-isolated dc-dc converters are quite standard building blocks, can be very efficient and compact and eliminate cross-regulation issues among the various outputs. This is the case, for example, of multi-output SMPS or LED drivers, or chargers for mobile equipment, single and multiport [3], required to comply with the USB Power Delivery (USB-PD) protocol.

Figure 2 shows this type of architecture.

Additionally, there are other SMPS applications (e.g., battery chargers) where the load is tolerant to the low-frequency ripple of a PFC output. In this case, an isolated PFC might enable a single-stage architecture (see Figure 3) with a substantial cost saving.

Flyback-based isolated PFCs are a good choice up to 50–60 W: they are often used in lighting equipment [4,5,6,7]. For higher power levels, though the literature presents plenty of different solutions [8], none have become an industry standard like the flyback PFC.

Isolated boost converters [9] are not easy to handle, and the provisions needed to make them operate properly make them less cost-effective; other topologies, such as SEPIC [10], Ćuk [11] and Zeta [12] converters, can effectively work as an isolated PFC, but they are seldom used.

Likewise, a lot of new topologies combining a boost-type front end with an isolated converter that share the same control have been proposed over the years [13,14,15,16,17,18,19,20] but did not find broad industrial usage, with very few exceptions [20]. Many of them [15,16,17,18,19] considered the LLC converter to be the isolated converter.

Only recently, research has concentrated on the standalone LLC converter used as a PFC stage (an LLC-PFC in short), therefore supplied by a rectified sinusoidal voltage and not by a dc voltage like in two-stage SMPS architectures.

Ref. [21] uses the first harmonic approximation (FHA) analysis to demonstrate LLC’s ability to work as a PFC stage, keeping its previously mentioned benign properties. It sets up a design procedure that is used in [22] to prove the feasibility of an LLC-PFC at the kW level and in [23] for the design of a modular PFC stage operated from the three-phase line. In these papers, it is assumed that the converter always works in the so-called “below-resonance” operating region, and the design constraints required to ensure soft switching in this region are not addressed.

As for the control of the output voltage/current of an LLC-PFC, the previously mentioned works consider average current mode control (ACMC), like in boost PFC operated in Continuous Conduction Mode [24], to achieve extremely low distortion of the input current. The implementation is microcontroller-based.

Other authors [25,26] consider modulating the switching frequency directly (they call it voltage-mode control) to simplify the control system at the price of a significantly higher THD of the input current, though still sufficient to comply with the IEC 61000-3-2 regulation.

In [25,27], the accuracy limits of the FHA approach are highlighted, and the time-domain (TD) analysis is proposed to overcome these limitations. Ref. [27] shows that the FHA approach results in a too-conservative design that does not fully utilize the operating region of the converter, whereas by using the TD approach, the operating region of the converter can be fully utilized. However, the degree of conservativeness of the FHA approach is shown only qualitatively, the TD-based design procedure is just sketched, and the details on how the design is carried out are few.

Based on these premises, the first objective of the present work is to assess how the usage of the TD approach can improve an FHA-based design. This goal is achieved by addressing the design of a specified converter with the two approaches and comparing the results. A more detailed TD-based design procedure is provided in this paper.

A second objective is to demonstrate that designing the LLC-PFC converter to work also in the above-resonance region optimizes its performance by reducing the reactive current in the resonant tank, which in turn reduces the rms currents on both the input and the output sides.

Thirdly, to assess the feasibility of implementing ACMC using low-cost analog components, this control is considered and verified by simulations and bench experiments.

Ultimately, the goal of the present work is to demonstrate that an LLC-PFC can be an attractive solution in many use cases, with all the credentials to become an industry standard for an isolated PFC at the power levels that a flyback PFC cannot support.

Therefore, the paper is organized as follows.

In Section 2, the FHA analysis is reviewed; compared to previously published procedures, here, operation above the upper resonance frequency is accounted for. The resulting step-by-step design procedure is given in Appendix A.

In Section 3, the TD analysis is reviewed. Due to its mathematical complexity, only the basic definitions and the results are provided in this section, the details of the analysis are given in Appendix B.

Section 4 provides the electrical specification of an LLC-PFC intended for a high-power LED lamp driver and uses two different design strategies with the FHA approach: the first one assumes that the converter operates at the upper resonance frequency on the peak of the maximum ac input voltage, whereas the second one assumes that the converter operates at the upper resonance frequency on the peak of the nominal ac input voltage, thus utilizing the above-resonance region to handle ac input voltages higher than the nominal one. The same is done with the TD approach.

Section 5 shows a prototype constructed so that the two designs based on the TD approach can be implemented in a single board and provides the results of their bench evaluation. The results are commented on to provide the basis for the conclusions drawn in Section 6.

2. First Harmonic Approximation (FHA) Analysis of the LLC-PFC

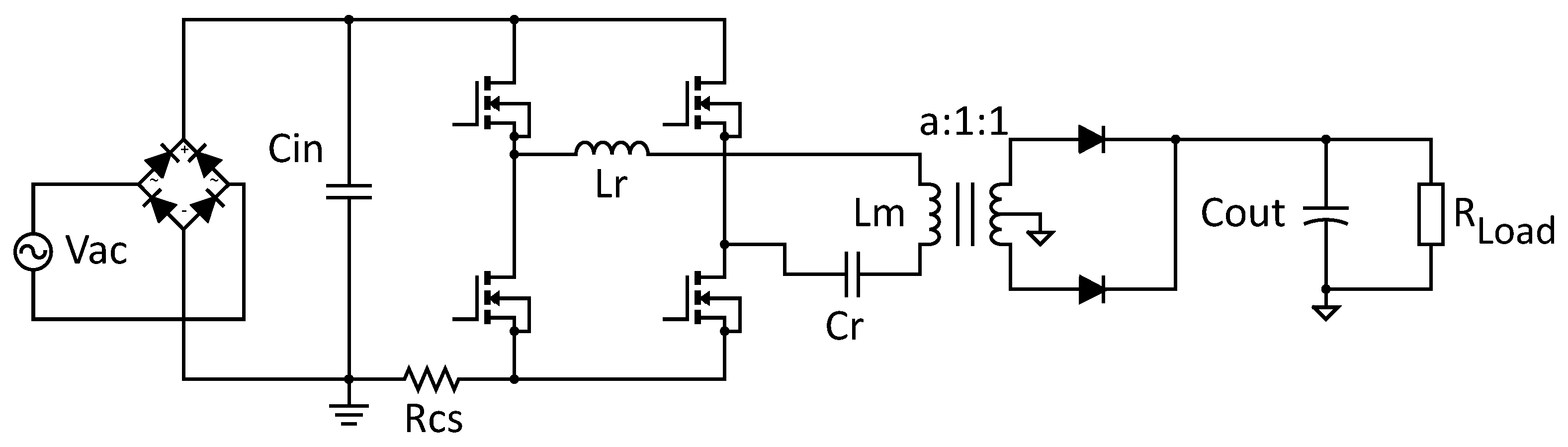
The simplified circuit diagram of the LLC-PFC converter is shown in Figure 4. The input capacitor $Cin$ is not a bulk capacitor as it is usually placed after the input bridge in a non-power-factor-corrected converter; it is only a filter for the high-frequency switching noise, like a standard boost PFC.

The FHA analysis, whose foundations were laid in a paper published in 1988 [28], is now widely used when designing an LLC resonant converter, especially because a handy design procedure can be found that starts from the electrical specification and leads to the definition of the resonant tank’s parameter ($a$, $Lr$, $Lm$, $Cr$), e.g., like the 10-step procedure in [29].

Before extending this procedure to the design of an LLC-PFC, it is convenient to remember some basic definitions used in the FHA analysis:

Primary-to-secondary turn ratio	$a=\frac{Np}{Ns}$
Topology factor	$\alpha =\left\{\begin{array}{c}2a \mathrm{half} \mathrm{bridge}\\ a \mathrm{full} \mathrm{bridge}\end{array}\right.$
Normalized voltage conversion ratio (voltage gain)	$\left|M\left(f_n,\lambda ,Q\right)\right|=\alpha \frac{Vout}{Vin}=\frac{1}{\sqrt{{\left[1+\lambda \left(1-\frac{1}{f_n^2}\right)\right]}^2+Q^2{\left(f_n-\frac{1}{f_n}\right)}^2}}$	(1)
Resonance frequencies	$f_{R1}=\frac{1}{2\pi \sqrt{Lr Cr}}; f_{R2}=\frac{1}{2\pi \sqrt{(Lr+Lm)Cr}}$
Characteristic impedance	$Z_{R1}=\sqrt{\frac{Lr}{Cr}}=2\pi f_{R1} Lr=\frac{1}{2\pi f_{R1} Cr}$
Series-to-magnetizing inductance ratio	$\lambda =\frac{Lr}{Lm}=\frac{f_{R2}^2}{f_{R1}^2-f_{R2}^2}$
Normalized switching frequency	$f_n=\frac{f_{sw}}{f_{R1}}$
Output ac resistance	${Rout}_{ac}=\frac{8}{{\pi }^2}\frac{{Vout}^2}{Pout}=\frac{8}{{\pi }^2}{R}_{Load}$
Quality factor	$Q=\frac{Z_{R1}}{R_{ac}}=\frac{Z_{R1}}{a^2{Rout}_{ac}}=\frac{{\pi }^2}{8}\frac{Z_{R1} Pout}{ a^2 Vou{t}^2}$

The FHA analysis developed for LLC converters supplied by a substantial dc input voltage can be extended to the PFC case, based on a quasi-static approximation. In fact, although the input voltage is a rectified sinusoid that goes all the way from zero to the peak, the line frequency $f_{line}$ is such that the variations are much slower than the converter dynamics, making it possible to consider the system operating in steady-state conditions for all the instantaneous phase angles $\theta$ of the rectified sinusoid.

In order to act as a PFC stage and achieve a unity PF, the instantaneous input power along a line half cycle, $Pi\left(\theta \right)$, swings from zero at the zero crossing of the input voltage and current to twice the average power $Pin$ (equal to the output power $Pout$ divided by the efficiency $\eta$) at the peak of the input voltage, as plotted in Figure 5:

$$Pi\left(\theta \right)=\left(Vi{n}_{pk}\mathit{sin}\theta \right) \left(Ii{n}_{pk}\mathit{sin}\theta \right)=2Vin Iin {\sin }^2\theta =2Pin {\sin }^2\theta =2\frac{Pout}{\eta }{\sin }^2\theta .$$

(2)

where $Vin$ and $Iin$ are the rms values, and $Vi{n}_{pk}$ and $Ii{n}_{pk}$ are the peak values of the input voltage and current, respectively.

Evaluating (2) at $\theta =\pi /2$, we obtain

$$Pi\left(\pi /2\right)=2 Vin Iin=2 Pin=Vi{n}_{pk}Ii{n}_{pk}.$$

(3)

This means that at the peak of the sinusoidal line voltage, the converter is powered with an equivalent dc line voltage $Vi{n}_{pk}$ and absorbs an equivalent dc current equal to $Ii{n}_{pk}$, resulting in the input power being twice the average value. Based on the concept of quasi-static approximation, the design based on the FHA approach can be carried out treating the peak values of the line voltage and current as if they were dc values.

To ensure proper operation as a PFC-LLC, some additional analysis is needed. To this purpose, it is fundamental to consider that not only the instantaneous input power but also the instantaneous output power varies along $\theta$ too:

$$Po\left(\theta \right)=\eta Pi\left(\theta \right)=2 \eta Pin {\sin }^2\theta =2 Pout {\sin }^2\theta ,$$

(4)

and so do the ac resistance and the quality factor. Substituting (4) in (1), we get

$$\begin{gathered} {Rout}_{ac}\left(\theta \right)=\frac{4}{{\pi }^2}\frac{{Vout}^2}{Pout {\sin }^2\theta } \\ Q\left(\theta \right)=\frac{{\pi }^2}{4}\frac{Z_{R1}}{a^2}\frac{Pout}{{Vout}^2}{\sin }^2\theta =Q_0 {\sin }^2\theta . \end{gathered}$$

(5)

Finally, also the voltage gain $\left|M\right|$ becomes a function of $\theta$:

$$\left|M\left(f_n,\lambda ,Q_0,\theta \right)\right|=\frac{1}{\sqrt{{\left[1+\lambda \left(1-\frac{1}{f_n^2}\right)\right]}^2+Q_0^2{\sin }^4\theta {\left(f_n-\frac{1}{f_n}\right)}^2}}.$$

(6)

This voltage gain needs to be compared to the voltage gain of an LLC converter supplied by a rectified sinusoid $Vi{n}_{pk}\sin \theta =\sqrt{2} Vin\sin \theta$ required to provide a regulated output voltage $Vout$:

$$M_{req}\left(Vin,\theta \right)=\alpha \frac{Vout}{\sqrt{2} Vin\sin \theta }=\alpha \frac{Vout}{Vi{n}_{pk}\sin \theta }.$$

(7)

The plot of (7) vs. $\theta$ is shown in Figure 6: $M_{req}$ is minimum on the peak of the sinusoid ($\theta =\pi /2$) and tends to infinity approaching the zero crossings.

To ensure that the converter can regulate the output voltage, with fixed $Q_0$ and $\lambda$, it must be $\left|M\right|>M_{req}$ at some frequency for all $\theta$ values. Also, the operating points must be in the inductive region, where the converter works with zero-voltage switching (ZVS).

We can visualize this constraint considering a hypothetical LLC converter and plotting its voltage gain $\left|M\right|$ vs. the normalized frequency $f_n$ at a fixed power level (i.e., at a fixed $Q_0$) with the phase angle $\theta$ as a parameter, as shown in Figure 7. In particular, the plot is drawn with $\theta$ equal to $\mathsf{\pi }/2$, $\mathsf{\pi }/3$ and $\mathsf{\pi }/4$ (due to the symmetry of the sin function, these plots represent the supplementary angles too). The highest required gain $M_{req}$ (calculated at the minimum input voltage $Vi{n}_{{pk}_{min}}$ and, in case of variable output voltage, at $Vout={Vout}_{max}$) for the same phase angles is plotted in dashed lines.

For all of these three phase angles of the input voltage, there is an intersection between the required gain and the LLC voltage gain: these are the operating points for those phase angles. This means that the condition $\left|M\right|>M_{req}$ is met at some frequency. These points are in the inductive region, so the converter works with ZVS as required.

However, we need to ensure that this condition is verified for any phase angle $\theta$ included in $[0,\mathsf{\pi }/2]$ (if it is so, for symmetry, it will be also in $[\mathsf{\pi }/2,\mathsf{\pi }]$).

The $\left|M\right|$ curves also show that the gain has a peak $M_{pk}$ in the capacitive region and the maximum useful value $M_{MAX}$ at the boundary between the capacitive and the inductive region. Notice that the difference between $M_{MAX}$ and $M_{req}$ gets smaller as $\theta$ tends to $\mathsf{\pi }/2$ or, equivalently, when $Q_0$ increases. Also notice that $M_{MAX}$ is larger than the gain at $f_{sw}=f_{R2}$ (or, equivalently, at $f_n=f_{R2}/f_{R1}$). The latter gain can be easily calculated by inserting $f_n=f_{R2}/f_{R1}$ in (6) and considering the definitions in (1):

$$\left|M\left(f_{R2}/f_{R1},\lambda ,Q_0,\theta \right)\right|=\frac{\sqrt{\lambda \left(1+\lambda \right)}}{Q_0{\sin }^2\theta }.$$

(8)

Imposing that (8) be greater than (or at least equal to) the required voltage gain (7) evaluated at the minimum input voltage and maximum output voltage, where the needed gain is at a maximum, we will make sure that the gain will be always sufficient to achieve output voltage regulation:

$$M_{MAX}\left(\lambda ,Q_0,\theta \right)\ge \frac{\sqrt{\lambda \left(1+\lambda \right)}}{Q_0{\sin }^2\theta }\ge \alpha \frac{Vou{t}_{max}}{\sqrt{2} Vi{n}_{min}\sin \theta }.$$

(9)

Since the inequality ${1/\sin }^2\theta \ge 1/\sin \theta$ is always true for any phase angle between zero and $\pi$, the condition that must be fulfilled to ensure output voltage regulation is:

$$\frac{\sqrt{\lambda \left(1+\lambda \right)}}{Q_0}\ge \alpha \frac{Vou{t}_{max}}{\sqrt{2} Vi{n}_{min}}.$$

(10)

Likewise, the maximum value of the minimum voltage gain occurs when $f_{sw}>f_{R1}$ and $Q_0=0$ (i.e., the output load is zero):

$$\left|M\left(f_n,\lambda ,0,\theta \right)\right|=\frac{1}{1+\lambda \left(1-\frac{1}{f_n^2}\right)}=\left|M_{OL}\left(f_n,\lambda \right)\right|.$$

(11)

Its minimum value is called $M_{\infty }$ and occurs when $f_{sw}\gg f_{R1}$, as shown in Figure 8.

Indeed, if the maximum switching frequency is fixed at $f_{max}>f_{R1}$, the maximum value of the minimum voltage gain can be evaluated:

$$\left|M_{OL}\left(f_{max}/f_{R1},\lambda \right)\right|=\frac{1}{1+\lambda \left[1-{\left(\frac{f_{R1}}{f_{max}}\right)}^2\right]}.$$

(12)

Imposing that (12) be lower than the required voltage gain (7) evaluated at the peak of the maximum input voltage and the minimum output voltage, where the required gain is at a minimum, it is possible to find the minimum inductance ratio $\lambda$ that fulfills the minimum gain requirement:

$$\frac{1}{1+\lambda \left[1-{\left(\frac{f_{R1}}{f_{max}}\right)}^2\right]}\le \alpha \frac{V{out}_{min} }{\sqrt{2} {Vin}_{max}}=M_{re{q}_{min}}\to \lambda \ge \frac{\frac{1}{M_{re{q}_{min}}}-1}{1-{\left(\frac{f_{R1}}{f_{max}}\right)}^2}.$$

(13)

The FHA-based design procedure used in [21,22,23] and described step-by-step in [30] sets the maximum operating frequency at the upper resonance frequency $f_{R1}$(or equivalently $f_n=1$) where the gain is unity and independent of the load. Since this gain must be lower than or equal to the minimum required voltage gain $M_{re{q}_{min}}$, it is possible to derive the following constraint on $\alpha$:

$$1\le \alpha \frac{Vou{t}_{min}}{\sqrt{2} Vi{n}_{max}}\to \alpha \ge \frac{\sqrt{2} Vi{n}_{max}}{Vou{t}_{min}}.$$

(14)

If we extend the operating region at frequencies higher than $f_{R1}$(i.e., $f_n>1$), the constraint on $\alpha$ can be derived from (13):

$$\alpha \ge \frac{\sqrt{2} Vi{n}_{max}}{Vou{t}_{min}}\left\{1+\lambda \left[1-{\left(\frac{f_{R1}}{f_{max}}\right)}^2\right]\right\}.$$

(15)

From (14) or (15), along with (1), it is possible to derive the required turn ratio $a$.

Condition (10), along with (14) (or (15), depending on the design), is a fundamental design constraint because it determines the maximum and minimum gain of the LLC converter to fulfill the necessary gain to perform as a PFC.

By equating the required gain (7) to the voltage gain (6), it is possible to find how the normalized switching frequency varies along the phase angle $\theta$ of a line half cycle, as illustrated in the plot of Figure 9.

The switching frequency peaks at $\theta =\pi /2$ and decreases as the instantaneous line voltage moves toward the zero crossing, where it reaches the lower resonance frequency $f_{R2}$ (the only possible equilibrium point when $Vin\left(\theta \right) \mathrm{and} Iin\left(\theta \right)$ are both zero). The relationship is strongly nonlinear and dependent on the rms input voltage, difficult to synthesize in an analog circuit or in a look-up table. This explains why controlling the switching frequency directly like in [25,26] results in a high THD of the input current.

Unfortunately, as already said, the accuracy of the FHA analysis is quite good when the system is working near the upper resonance frequency $f_{R1}$ but is worse if we move away from this point. Since the LLC converter is designed to work in the entire range between the lower and the upper resonance frequencies and above when working as a PFC, a time-domain analysis is necessary to assess how the approximations inherent in the FHA analysis affect the results.

3. Time Domain (TD) Analysis of the LLC-PFC

The study of the differential equations of the current and voltages of the resonant tank allows us to better understand the behavior below the upper resonance frequency without the approximations inherent in the FHA approach.

As with the FHA, the quasi-static approximation allows us to solve the system of differential equations considering the input voltage fixed.

There are some takeaways from the FHA theory that can be used also in the TD analysis. One is the fact that the most stringent condition for the gain is at the peak of the minimum input voltage, where the difference between the available gain and the required gain is minimized, as shown in Figure 7. Also, the transformer turn ratio $a$ can be derived considering (14) or (15), depending on whether the maximum switching frequency $f_{max}$ is set at $f_{R1}$ or above $f_{R1}$.

It is convenient to start the TD analysis by inspecting the key waveforms of voltage and current in the resonant tank. We will assume that at the peak of $Vi{n}_{min}$ (i.e., $Vi{n}_{{min}_{pk}}$) and full output load, the resonant tank operating mode is DCMB2 as defined in [2] and characterized by two distinct time intervals in each switching half cycle.

Figure 10 shows the typical resonant tank currents and resonant capacitor voltage during the below resonance operation, in the first half switching cycle in DCMB2 mode. The waveforms in the second half switching cycle are mirror symmetric with respect to the horizontal axis (the initial conditions and the evolution in time are just opposite).

The plots of the currents in Figure 10 show the following:

• The red portion is the resonant current $i_{RT}$ during the time interval $(0-Tm)$ during which current flows on the secondary side as well.
• The blue portion is the magnetizing current $i_M$ flowing into $Lm$ during the time interval $(0-Tm)$; this current is subtracted from $i_{RT}$ and does not contribute to the secondary current to form the output dc current.
• The black portion is the tank circuit current $i_{mag}$ in the time interval $(Tm-Tsw/2)$; this is a magnetizing current too, flowing in both $Lr$ and $Lm$; in this interval, the secondary current is zero.

The following analysis is performed supposing that the primary switch configuration is a half bridge (then, $\alpha =2a$).

The circuit is described by two sets of differential equations in the two-time intervals $(0-Tm)$ and $(Tm-Tsw/2)$. Referring to Figure 10 for the symbolism, in the time interval $\left(0-Tm\right)$, it is possible to write:

$$\left\{\begin{array}{c}{Vin}_{pk}=Lr\frac{d}{dt}{i}_{RT}\left(t\right)+v_{Cr}\left(t\right)+a Vout\\ i_{RT}\left(t\right)=Cr\frac{d}{dt}{v}_{Cr}\left(t\right)\\ a Vout=Lm\frac{d}{dt}{i}_M\left(t\right)\end{array}\right.$$

(16)

with initial conditions:

$$\left\{\begin{array}{c}{i}_{RT}\left(0\right)=i_M\left(0\right)=-I_o\\ v_{Cr}\left(0\right)=V_{{Cr}_0}\end{array}\right..$$

(17)

The solution of the system (16) is:

$$\left\{\begin{array}{c}{v}_{Cr}\left(t\right)=-Z_{R1} I_o\sin \left(2\pi f_{R1}t\right)-\left(Vi{n}_{pk}-aVout-V_{{Cr}_0}\right)\cos \left(2\pi f_{R1}t\right)+\left(Vi{n}_{pk}-aVout\right)\\ i_{RT}\left(t\right)=-I_o\cos \left(2\pi f_{R1}t\right)+\frac{1}{Z_{R1}}\left(Vi{n}_{pk}-aVout-V_{{Cr}_0}\right)\sin \left(2\pi f_{R1}t\right)\\ i_M\left(t\right)=a\frac{Vout}{Lm}t-I_o\end{array}\right.,$$

(18)

where $f_{R1}$ and $Z_{R1}$ are those defined by (1).

During the same time interval, there is a current flowing on the secondary side of the converter:

$$i_{sec}\left(t\right)=a\left[i_{RT}\left(t\right)-i_M\left(t\right)\right].$$

(19)

During the second time interval $(Tm-Tsw/2)$, there is no current flowing on the secondary side, and the inductances $Lr$ and $Lm$ are effectively in series. The second set of differential equations is:

$$\left\{\begin{array}{c}{Vin}_{pk}=\left(Lr+Lm\right)\frac{d}{dt}{i}_{RT}\left(t\right)+v_{Cr}\left(t\right)\\ i_{mag}\left(t\right)=Cr\frac{d}{dt}{v}_{Cr}\left(t\right)\end{array}\right.$$

(20)

with initial conditions:

$$\left\{\begin{array}{c}{i}_{mag}\left(Tm\right)=I_m\\ v_{Cr}\left(Tm\right)=V_{{Cr}_{Tm}}\end{array}\right..$$

(21)

The solution of the system (20) is:

$$\left\{\begin{array}{c}{v}_{Cr}\left(t\right)=Z_{R2}·I_m\sin \left[2\pi f_{R2}\left(t-Tm\right)\right]-\left(Vi{n}_{pk}-V_{{Cr}_{Tm}}\right)\cos \left[2\pi f_{R2}\left(t-Tm\right)\right]+Vi{n}_{pk}\\ i_{mag}\left(t\right)=I_m\cos \left[2\pi f_{R2}\left(t-Tm\right)\right]+\frac{1}{Z_{R2}}\left(Vi{n}_{pk}-V_{{Cr}_{Tm}}\right)\sin \left[2\pi f_{R2}\left(t-Tm\right)\right]\end{array},\right.$$

(22)

where $f_{R2}$ has been already defined in (1), while it is:

$$Z_{R2}=\sqrt{\frac{Lr+Lm}{Cr}}=2\pi f_{R2}\left(Lr+Lm\right)=\frac{1}{2\pi f_{R2}Cr}.$$

(23)

The complete TD analysis is detailed in Appendix B. Here, we show only the results, in particular, the following system of four nonlinear equations in the four unknowns $I_o$, $I_m$, $Tm$ and $Tsw$ that are highlighted in Figure 10:

$$\left\{\begin{array}{c}{Iout}_{pk}=a\frac{I_m-I_o}{Tsw}\left[\frac{\tan \left(\pi f_{R1}Tm\right)}{\pi f_{R1}}-Tm\right]\\ {Iin}_{pk}-\frac{{Iout}_{pk}}{2a}=\frac{1}{2Tsw}\left[Tm\left(I_m-I_o\right)+\left(I_m+I_o\right)\frac{\tan \left(\pi f_{R2}\left(\frac{Tsw}{2}-Tm\right)\right)}{\pi f_{R2}}\right]\\ {\left[\frac{I_m+I_o}{2\pi f_{R1}Tm}\frac{K_V-1}{\lambda }+\pi f_{R1}TswIi{n}_{pk}\right]}^2={\left[\frac{I_m+I_o\cos \left(2\pi f_{R1}Tm\right)}{\sin \left(2\pi f_{R1}Tm\right)}\right]}^2\\ \tan \left({\phi }_{min}\right)=\frac{I_o\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi f_{R1}Tm\right)}{I_m+I_o\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi f_{R1}Tm\right)}\end{array}\right..$$

(24)

All the other parameters are known quantities:

• $Ii{n}_{pk}$ is the peak input current (averaged on a complete switching cycle) evaluated at the peak of the minimum input voltage (i.e., with phase angle $\mathsf{\theta }=\mathsf{\pi }/2$):

  $$Ii{n}_{pk}=2\frac{Pin}{Vi{n}_{pk}}\approx 2\frac{Pout}{\eta Vi{n}_{pk}}.$$
• $Iou{t}_{pk}$ is the peak output current (averaged on a complete switching cycle) evaluated at the peak of the minimum input voltage that is equal to twice the rated output current for a PFC circuit:

  $$Iou{t}_{pk}=2\frac{Pout}{Vout}.$$
• $K_V$ is the inverse of the voltage gain required of the converter that is the ratio between the minimum input voltage and the nominal input voltage at resonance:

  $$K_V\frac{{Vin}_{min}}{Vi{n}_{res}}=\frac{\sqrt{2}Vi{n}_{min}}{\alpha Vout}.$$
• ${\phi }_{min}$ is the minimum phase angle between the resonant current and the half-bridge voltage, to ensure ZVS operation, strictly correlated to the dead time $T_{\mathrm{D}}$ that is purposely inserted between the turn-off of one switch of the half-bridge leg and the turn-on of the other one to allow ZVS and the turn-off delay $T_{off}$ of the power switch:

  $${\phi }_{min}=2\pi f_{R1}\left(T_{\mathrm{D}}-T_{off}\right).$$

The system (24) needs to be solved with a numerical method using a calculation tool. Once solutions ($I_o$, $I_m$, $Tm$ and $Tsw$) are found, the parameters of the resonant tank circuit and the operating frequency can be calculated:

$$Lm=aVout\frac{Tm}{I_m+I_o};Lr=\lambda Lm;Cr=\frac{1}{{\left(2\pi f_{R1}\right)}^{2}Lr};fsw=\frac{1}{Tsw}.$$

4. Design of an LLC-PFC with Both FHA and TD Analysis

Table 1. Electrical specification of the reference LLC-PFC for a high-power LED lamp driver.

Symbol	Name	Value	Unit
$Vi{n}_{min}-Vi{n}_{max}$	Input voltage range (rms)	176–305	$\mathrm{V}\mathrm{a}\mathrm{c}$
$Vi{n}_{nom}$	Nominal input voltage (rms)	$230$	$\mathrm{V}\mathrm{a}\mathrm{c}$
$Vout$	Regulated output voltage (dc)	$60\pm 5\%$	$\mathrm{V}\mathrm{d}\mathrm{c}$
$V_{Rect}$	Secondary rectifier voltage drop (dc)	$0.1$	$\mathrm{V}\mathrm{d}\mathrm{c}$
$Pou{t}_{max}$	Maximum output power	$240$	$\mathrm{W}$
$\eta$	Estimated efficiency @ $Pou{t}_{max},Vi{n}_{min}$	$94$	$\%$
$f_{R1}$	Upper resonance frequency	$150$	$\mathrm{k}\mathrm{H}\mathrm{z}$
$f_{R2}$	Lower resonance frequency (*)	$60$	$\mathrm{k}\mathrm{H}\mathrm{z}$
$f_{max}$	Maximum switching frequency (*)	$300$	$\mathrm{k}\mathrm{H}\mathrm{z}$
$C_{HB}$	Half-bridge midpoint estimated capacitance	$660$	$\mathrm{p}\mathrm{F}$
$T_D$	Dead time	$270$	$\mathrm{n}\mathrm{s}$

⁽*⁾ these two specifications are mutually exclusive: $f_{R2}$ is specified if the design is to be carried out with $f_{max}=f_{R1}$; $f_{max}$ is specified if the design is to be carried out with $f_{max}>f_{R1}$ ($f_{R2}$ will be the result of computation).

shows the electrical specification of an LLC-PFC for a high-power LED lamp driver supplied by the European mains.

Based on this specification, two different design strategies are used.

The first one is such that the converter works at the upper resonance frequency $f_{R1}$ at the peak of the maximum input voltage $Vi{n}_{max}$. This automatically sets $f_{max}=f_{R1}$.

The second one is designed to work at the upper resonance frequency $f_{R1}$ at the peak of the nominal input voltage $Vi{n}_{nom}$, which is lower than $Vi{n}_{max}$. As a result, the switching frequency will exceed $f_{R1}$ in the voltage range included between $Vi{n}_{nom}$ and $Vi{n}_{max}$. The maximum switching frequency $f_{max}$ is specified, and the lower resonance frequency $f_{R2 }$ is determined by $f_{max}$.

The two design strategies are carried out using the FHA and the TD approach, for a total of four designs, which are labeled and summarized in

Table 2. Summary of the four designs and their label.

Name	Description	Frequency Range
FHA1	$\mathrm{Design} \mathrm{with} \mathrm{FHA}—f_{R1}$$\mathrm{at} Vi{n}_{{max}_{pk}}$	$f_{R2}\le f_{sw}\le f_{R1}$
FHA2	$\mathrm{Design} \mathrm{with} \mathrm{FHA}—f_{R1}$$\mathrm{at} Vi{n}_{{nom}_{pk}}$	$f_{R2}\le f_{sw}\le f_{max}$
TD1	$\mathrm{Design} \mathrm{with} \mathrm{TD}—f_{R1}$$\mathrm{at} Vi{n}_{{max}_{pk}}$	$f_{R2}\le f_{sw}\le f_{R1}$
TD2	$\mathrm{Design} \mathrm{with} \mathrm{TD}—f_{R1}$$\mathrm{at} Vi{n}_{{nom}_{pk}}$	$f_{R2}\le f_{sw}\le f_{max}$

. These design labels are used hereafter in this document.

The resulting LLC resonant tanks are given in

Table 3. Calculation results for the four designs listed in Table 2.

Symbol	Name	FHA1	TD1	FHA2	TD2	Unit
$a$	Primary-to-secondary turn ratio	$3.8$	$3.8$	$2.8$	$2.8$	---
$Vi{n}_{res}$	Input voltage at the resonance (rms)	$323$	$323$	$238$	$238$	$\mathrm{V}\mathrm{a}\mathrm{c}$
$Cr$	Resonant capacitor	$54$	$44$	$44$	$22$	$\mathrm{n}\mathrm{F}$
$Lr$	Series resonant inductance	$20.8$	$25.5$	$25.6$	$51$	$\mathsf{\mu }\mathrm{H}$
$Lm$	Parallel resonant inductance	$109.2$	$134$	$68.2$	$101$	$\mathsf{\mu }\mathrm{H}$
$f_{R1}$	Upper resonance frequency	$150.2$	$150.2$	$150$	$150.2$	$\mathrm{k}\mathrm{H}\mathrm{z}$
$f_{R2}$	Lower resonance frequency	$60.1$	$60.1$	$78.3$	$87$	$\mathrm{k}\mathrm{H}\mathrm{z}$
$I_o$	Initial resonant current for ZVS	$3.2$	$2.09$	$3.93$	$2.02$	$\mathrm{A}$

. Figure 11 shows the corresponding currents in the resonant tank circuit and the secondary side. The pictures with the same physical quantity have identical time bases and magnitudes, to easily compare the waveforms.

Table 4. Calculated rms currents for the four designs listed in Table 2. Rows #1–5: values averaged over a switching cycle at $Vi{n}_{{min}_{pk}}.$ Rows #6–7: values averaged over a line cycle at $Vi{n}_{min}$.

#	Parameter	FHA1	TD1	FHA2	TD2	Unit
1	Resonant tank current	4.563	4.535	4.962	4.622	A
2	Magnetizing current	2.927	2.482	2.869	1.919	A
3	Initial current (instantaneous value)	3.203	2.096	3.929	2.022	A
4	Secondary current (x diode)	8.851	9.075	7.380	7.302	A
5	Secondary current (total)	12.517	12.834	10.437	10.327	A
6	Resonant tank current (over a line cycle)	3.843	3.524	4.026	3.318	A
7	Secondary current (total, over a line cycle)	7.37	7.615	6.343	6.293	A

shows the corresponding calculated current stress.

With reference to Table 3, comparing the FHA designs with the TD designs (FHA1 vs. TD1, FHA2 vs. TD2), the FHA designs have a larger resonant capacitor $Cr$ with both design strategies. Consequently, the resonant inductances obtained from the FHA designs are lower, and this leads to some key facts:

• The lower $Lm$ increases its peak-to-peak current (magnetizing current) when the output current is flowing because the voltage across it is fixed and proportional to the output voltage times the transformer turn ratio, which is the same in both cases. This also increases the rms current and, therefore, the power dissipation. Analytical calculations (please refer to Table 4) show an increment of the rms value by more than 15% in the FHA1 vs. TD1 comparison and by more than 33% in the FHA2 vs. TD2 comparison. Of course, this positively affects the total rms current as well.
• The higher resonant capacitor $Cr$ reduces the impedance of the resonant tank and, therefore, the quality factory $Q_0$. According to the FHA theory, the lower the quality factor, the higher the maximum gain that the converter can achieve, hence moving the converter’s operation away from the capacitive region. This is confirmed by the initial resonant tank current $I_o$ at the peak of the minimum input voltage, which is more than 34% greater in the FHA1 design with respect to the TD1 design, while it is over 48% larger in the FHA2 design compared to the TD2 design.

Comparing the two analytical results of the FHA analysis (FHA1 vs. FHA2) FHA2 has an initial current over 22% greater than FHA1, but there is a reduction in the rms secondary current by more than 16%. Vice versa, comparing the two results of the TD analysis (TD1 vs. TD2), the initial current is essentially the same since it mostly depends on the capacitance of the half-bridge node, while the rms currents in $Lm$ and the output diodes are reduced by more than 22% and 19%, respectively, in the TD2 design compared to TD1. Table 4 summarizes all these results.

The same remarks can be made by observing the waveforms of Figure 11. Comparing FHA1 with TD1, we notice that the initial current $I_o$ is lower in TD1, which means that the converter operates closer to the inductive-capacitive boundary and utilizes a larger portion of the available operating region. Also, it is confirmed that the peak-to-peak (and, consequently, the rms) magnetizing current, which is purely reactive, is smaller in TD1.

The advantage of designing with $f_{max}>f_{R1}$ is even more conspicuous. Comparing FHA1 with FHA2, the $(Tm-Tsw/2)$ interval is much shorter in FHA2, and, consequently, the conduction angle of the secondary current is larger, which significantly reduces their peak and rms value. Comparing FHA2 with TD2, we observe a reduction in the initial current $I_o$ in TD2, with the same consequences.

It is interesting to visualize the difference between the results of the FHA approach with those of the TD approach shown in Table 3, using the key tool of the FHA approach.

The plots of the voltage gain evaluated with the FHA analysis at the peak of the input voltage for FHA1 and TD1 designs are shown in Figure 12.

The TD1 design (blue line) seems not to be working: the peak voltage gain gets very close to but does not reach the required gain, and this happens in the capacitive region. The conclusion would be that the converter cannot regulate the output voltage and works in capacitive mode, then without ZVS. In contrast, there is enough gain margin with the FHA design (red line). However, the time-domain analysis shows that the TD1 design works, and with ZVS. This depends, as already said, on the approximation of the FHA analysis that is less accurate when moving away from the upper resonance frequency $f_{R1}$.

Regarding the FHA2 and TD2 designs, they cannot be compared in the same plot because the lower resonance frequencies are quite different, and so they are the curves of the gain, but the same remarks apply if we look at their plots separately in Figure 13 and Figure 14.

The conclusion is that the FHA designs are more conservative with respect to the TD designs and, consequently, more lossy, and less efficient. Therefore, the FHA approach is useful for carrying out a preliminary design or a design where efficiency and power density are not the primary concerns. In fact, the real advantage of the FHA is the possibility to make a design easily and quickly without sophisticated calculation tools. For an optimized design, the TD analysis must be used, which allows for a reduction in the rms magnetizing current while still ensuring the ZVS of the primary switches.

The other key point worth highlighting is that designing the converter to work also in the above resonance region improves the shape of the magnetizing and secondary currents, thus reducing their peak and rms values. As a result, power dissipation is reduced too, and efficiency is increased. However, if the design is based on the FHA approach, this efficiency gain could be completely offset by the higher losses in the resonant tank, due to the excess of magnetizing current.

Before building the prototype, a series of simulations were run to check the paper designs and, if needed, refine them. The results, not shown here, do not differ significantly from those calculated and listed in Table 4. Also, the waveforms were very similar to those shown in Figure 11.

5. Prototype and Performance

A prototype was built able to accommodate both TD designs. Its picture, with the key components highlighted, is shown in Figure 15.

Table 5. Electrical characteristics of the realized resonant tanks.

Symbol	Name	TD1	TD2	Unit
$a$	Primary-to-secondary turn ratio	$4$	$2.8$	---
$Cr$	Resonant capacitor	$2\times 22$	$22$	$\mathrm{n}\mathrm{F}$
$Lr$	Series resonant inductance	$23.7$	$50$	$\mathsf{\mu }\mathrm{H}$
$Lm$	Parallel resonant inductance	$138$	$101$	$\mathsf{\mu }\mathrm{H}$
$f_{R1}$	Upper resonance frequency	$155.9$	$151.7$	$\mathrm{k}\mathrm{H}\mathrm{z}$
$f_{R2}$	Lower resonance frequency	$59.7$	$87.3$	$\mathrm{k}\mathrm{H}\mathrm{z}$

shows the electric characteristics of the resonant tank of both prototypes.

Table 6. Measured current stress (rms values) over a line cycle at the minimum input voltage for the two TD designs listed in Table 5.

Parameter	TD1	TD2	Unit
Resonant tank current	3.79	3.53	A
Secondary current (total)	8.01	6.54	$\mathrm{A}$

shows the measured current stress at the line frequency time scale. The values are slightly larger than those predicted by the calculations (shown in Table 4, lines #6–7) which took power loss sources into account quite roughly.

Figure 16 and Figure 17 show the most important waveform of both TD designs over one line cycle at the minimum mains voltage. In particular, the half-bridge voltage (CH1, gold color) follows the ac input voltage (CH5, gray color), and the resonant current (CH4, green color) is modulated over the line cycle. Also, the output voltage (CH3, blue color) has a low-frequency ripple (twice the line frequency), typical of an active PFC circuit.

At the peak of the minimum input voltage and maximum load, the HB node swings inside the dead time, and both switches operate with ZVS, as shown in Figure 18 and Figure 19 for the TD1 and TD2 designs, respectively.

As predicted by both the FHA and the TD analysis, when the instantaneous input voltage is below the peak, there is more margin for ZVS. Figure 20 and Figure 21 show the resonant tank current and the HB voltage for the TD1 and TD2 designs, respectively, at a phase of the minimum input voltage $\theta =\pi /4$, while Figure 22 and Figure 23 show the same waveforms at the valley of the minimum input voltage. Notice that the reactive (magnetizing) current is in quadrature with the applied voltage (inferable from the gate-drive signal), consistent with the instantaneous input power being zero at the zero crossing of the line voltage.

Finally, the input current and voltage at the minimum and nominal input voltage are shown in Figure 24: the shape of the current tracks the shape of the input voltage very closely and with very low phase shift, consistently with the low THD and high PF measured values, thus confirming the effectiveness of the topology.

The efficiency comparison between the TD designs is shown in Figure 25. The peak efficiency is 96% for both of them at 100% load, but the TD2 design outperforms the TD1 design at lower loads, where the dissipation due to the greater reactive current of the TD1 design is more impacting. At 10% load, TD2 is about 4% more efficient. The four-point average efficiency (mean value of the efficiency at 100%, 75%, 50% and 25% load) of TD2 is notably higher as well.

The total power loss at 100% load is about 10W and seems to be distributed quite evenly among the various parts that handle power (EMI filter, input bridge, primary MOSFETs, synchronous rectifier MOSFETs, resonant transformer). The transformer is the hottest spot, which suggests that its construction needs to be considered carefully.

Figure 26 shows the THD and the PF of the TD2 design. The THD is below 10% down to 60W (25% of output load), while the PF peaks at 0.997 at full load and stays above 0.9 down to 25% load. These figures are comparable to those of boost PFC converters of similar power [31].

6. Conclusions

In this paper, the usage and the design of an LLC resonant converter as a power factor corrector, the LLC-PFC, were discussed. An LLC-PFC has many interesting features: safety isolation between the mains and the user, the ability to address any output voltage by adjusting the turn ratio of the transformer and soft-switching operation with high efficiency and low EMI emissions. From the system perspective, the usage of an isolated PFC enables the use of non-isolated downstream dc-dc converters (e.g., buck converters) to generate the final voltage for the equipment, which is particularly advantageous in multiple output systems.

The first harmonic approximation (FHA) analysis can prove that the LLC converter can perform as a PFC, but its accuracy as a design tool was questioned because of the approximations inherent in it. For this reason, a time domain (TD) analysis was performed, showing that the FHA analysis leads to a more conservative design of the resonant tank. If efficiency is a primary design target, a design based on the TD analysis is preferable despite its higher complexity because it results in a lower reactive current in the resonant tank, especially when the converter is designed to work partly above the upper resonance frequency.

Finally, two different designs (one working always below the upper resonance frequency, the other working also above this frequency) based on the TD analysis were carried out, and a prototype was realized, to compare and validate the results found. The experiments showed a significant reduction in the reactive current in the transformer and a higher efficiency, especially at low loads, when the converter is designed to work at the upper resonance frequency with the nominal input voltage.

Based on these results, the next steps will be the preparation of properly engineered hardware to evaluate the level of power density achievable with this converter. Another target of future work is the development of a PFC-LLC able to work with a wide range of mains, from 90 to 305 Vac. In both cases, the biggest expected challenge is in the transformer.