A Low Common-Mode SVPWM for Two-Level Three-Phase Voltage Source Inverters
Abstract
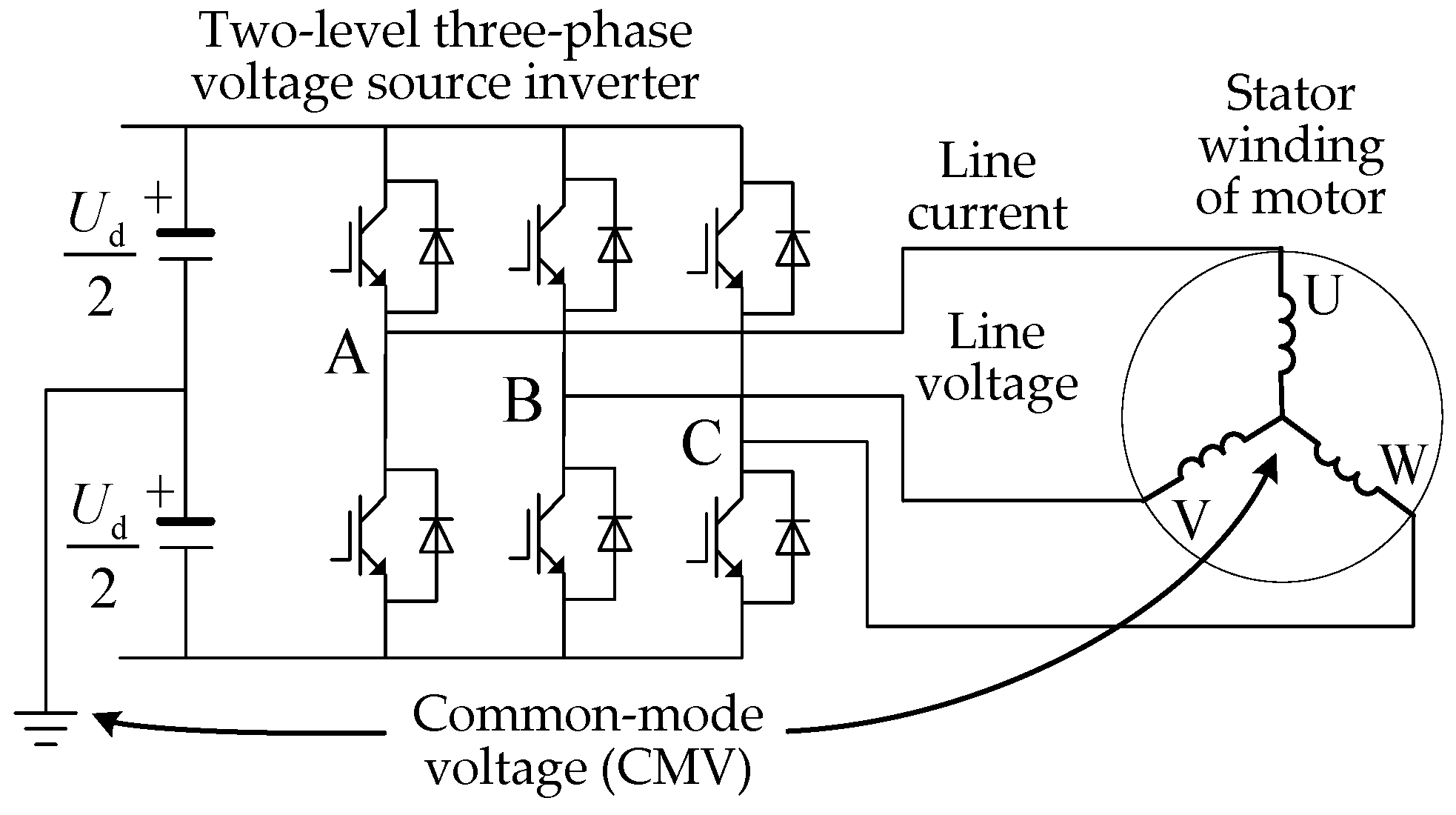
:1. Introduction
2. Low Common-Mode SVPWM Method
2.1. Classification of Basic Vectors
2.2. Synthesis of Expected Vectors
2.3. Sequences of Basic Vectors
2.4. Waveform of Common-Mode Voltages
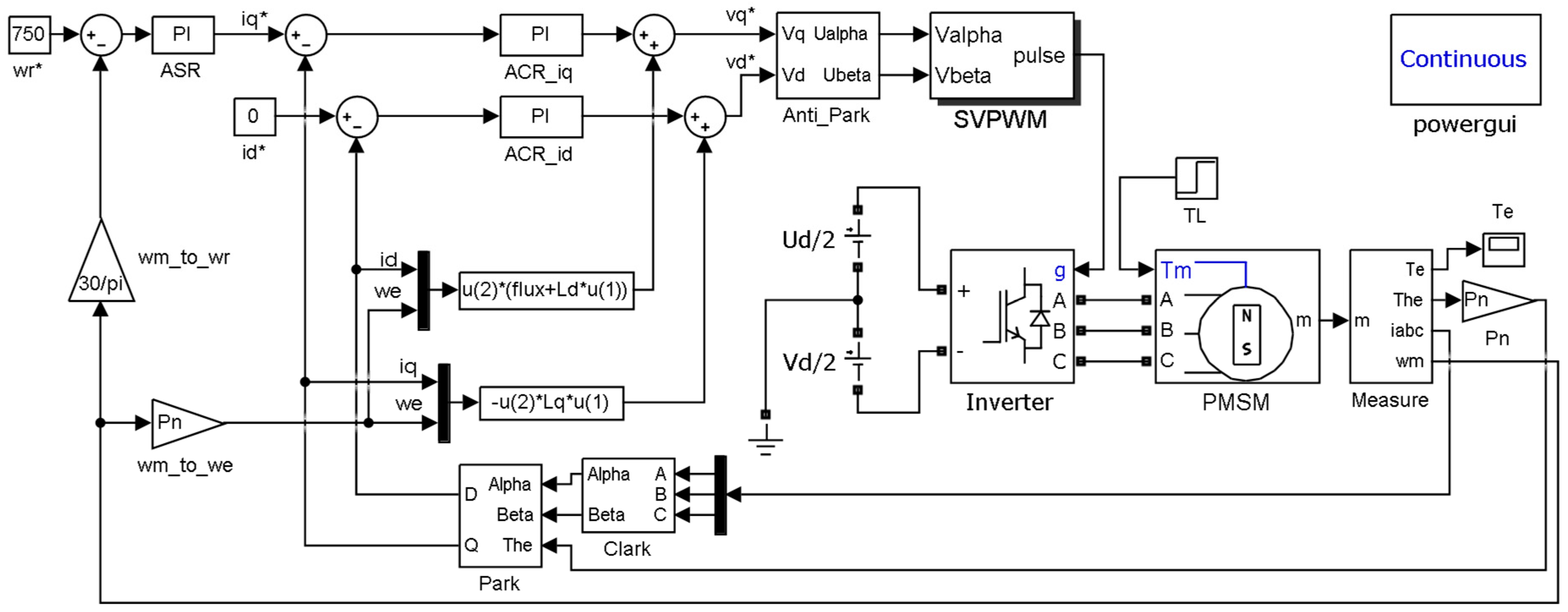
3. Simulation and Experimental Results
3.1. Simulation Results
3.2. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mirafzal, B. Power Electronics in Energy Conversion Systems; McGraw-Hill Education: New York, NY, USA, 2022; pp. 206–210. ISBN 978-1-260-46380-4. [Google Scholar]
- Suntio, T.; Messo, T. Power Electronics in Renewable Energy Systems; MDPI: Basel, Switzerland, 2019; pp. 1–8. ISBN 978-3-03921-045-9. [Google Scholar]
- Geyer, T. Model Predictive Control of High Power Converters and Industrial Drives; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 77–84. ISBN 978-1-119-01090-6. [Google Scholar]
- Fan, L.; Liu, Z.; Liang, Y.; Li, H.; Rao, B.; Yin, S.; Jiang, D. Analysis and utilization of common-mode voltage in inverters for power supply. IEEE Trans. Power Electron. 2023, 7, 8811–8824. [Google Scholar] [CrossRef]
- Luo, Q.; Zheng, J.; Sun, Y.; Yang, L. Optimal modeled six-phase space vector pulse width modulation method for stator voltage harmonic suppression. Energies 2018, 18, 2598. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Malinowski, M.; Al-Haddad, K. Power Electronics for Renewable Energy Systems, Transportation and Industrial Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014; pp. 664–671. ISBN 978-1-118-63403-5. [Google Scholar]
- Zheng, J.; Rong, F.; Li, P.; Huan, S.; He, Y. Six-phase SVPWM with common-mode voltage suppression. IET Power Electron. 2018, 15, 2461–2469. [Google Scholar] [CrossRef]
- Sudhoff, S.D. Power Magnetic Devices: A Multi-Objective Design Approaches, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 543–572. ISBN 978-1-119-67465-8. [Google Scholar]
- Wu, B.; Narimni, M. High-Power Converters and AC Drives, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 101–109. ISBN 978-1-119-15603-1. [Google Scholar]
- Tan, B.; Gu, Z.; Shen, K.; Ding, X. Third harmonic injection SPWM method based on alternating carrier polarity to suppress the common mode voltage. IEEE Access 2019, 7, 9805–9816. [Google Scholar] [CrossRef]
- Dai, J.; Li, G.; Hu, C. Study on a new method to eliminate the common-mode voltage based on improved SHEPWM. IEEE Conf. Ind. Electron. Appl. 2015, 1633–1636. [Google Scholar]
- Guo, L.; Jin, N.; Gan, C.; Luo, K. Hybrid voltage vector preselection-based model predictive control for two-level voltage source inverters to reduce the common-mode voltage. IEEE Trans. Ind. Electron. 2020, 6, 4680–4691. [Google Scholar] [CrossRef]
- Cetin, N.O.; Hava, A.M. Interaction between the filter and PWM units in the sine filter configuration utilizing three-phase AC motor drives employing PWM inverters. In Proceedings of the IEEE Energy Conversion Congress & Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 2592–2599. [Google Scholar]
- Ün, E.; Hava, A.M. A near-state PWM method with reduced switching losses and reduced common-mode voltage for three-phase voltage source inverters. IEEE Trans. Ind. Appl. 2009, 2, 782–793. [Google Scholar] [CrossRef]
- Tian, K.; Wang, J.; Wu, B.; Xu, D.; Cheng, Z.; Zargari, N.R. A virtual space vector modulation technique for the reduction of common-mode voltages in both magnitude and third-order component. IEEE Trans. Power Electron. 2016, 1, 839–848. [Google Scholar] [CrossRef]
- Zheng, J.; Lyu, M.; Li, S.; Luo, Q.; Huang, K. Common-mode reduction SVPWM for three-phase motor fed by two-level voltage source inverter. Energies. 2020, 12, 3884. [Google Scholar] [CrossRef]
- Lee, J.; Park, J. Selection of PWM methods for common-mode voltage and DC-link capacitor current reduction of three-phase VSI. IEEE Trans. Ind. Appl. 2023, 1, 1064–1076. [Google Scholar] [CrossRef]
- Singh, H.; Sudhoff, S.D. A common-mode shorting network to reduce common-mode excitation of three-phase two-level electric drives. IEEE Open Access J. Power Energy 2023, 10, 14–24. [Google Scholar] [CrossRef]
- Jiang, D.; Shen, Z.; Liu, Z.; Hun, X.; Wang, Q.; He, Z. Progress in active mitigation technologies of power electronics noise for electrical propulsion system. Proc. CSEE 2020, 16, 5291–5301. [Google Scholar]
- Zhao, R.; Jiang, X.; Wang, C.; Wang, Y.; Xu, H.; Yan, Q. A novel zero-sequence-voltage-balanced SVPWM with the analyses of common-mode voltage and differential-mode current. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2483–2496. [Google Scholar] [CrossRef]
- Xu, X.; Wu, M.; Wang, K.; Zhang, M.; Li, H.; Li, Y.W.; Li, Y. Common-mode voltage reduction for back-to-back two-level converters based on zero-sequence voltage injection. IEEE Trans. Ind. Electron. 2023, 12, 11971–11982. [Google Scholar] [CrossRef]
- Li, X.; Xie, M.; Ji, M.; Yang, J.; Wu, X.; Shen, G. Restraint of common-mode voltage for PMSM-inverter systems with current ripple constraint based on voltage-vector MPC. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 2, 688–697. [Google Scholar] [CrossRef]
- Wu, X.; Tan, G.; Ye, Z.; Liu, Y.; Xu, S. Optimized common-mode voltage reduction PWM for three-phase voltage-source inverters. IEEE Trans. Power Electron. 2016, 4, 2959–2969. [Google Scholar] [CrossRef]













| Classes | Basic Vectors | SA | SB | SC | CMV Values |
|---|---|---|---|---|---|
| Class (i) | V0 | 0 | 0 | 0 | −Ud/2 |
| V1 | 1 | 0 | 0 | ||
| Class (ii) | V3 | 0 | 1 | 0 | −Ud/6 |
| V5 | 0 | 0 | 1 | ||
| V2 | 1 | 1 | 0 | ||
| Class (iii) | V4 | 0 | 1 | 1 | Ud/6 |
| V6 | 1 | 0 | 1 | ||
| Class (iv) | V7 | 1 | 1 | 1 | Ud/2 |
| Sectors | Basic Vectors | Action Time | Sectors | Basic Vectors | Action Time |
|---|---|---|---|---|---|
| S1′ | V0 V1 V3 | Equation (2) | S7′ | V0 V4 V6 | Similar to (2) |
| S2′ | V0 V2 V6 | Equation (4) | S8′ | V0 V3 V5 | Similar to (4) |
| S3′ | V0 V2 V4 | Similar to (2) | S9′ | V0 V1 V5 | Similar to (2) |
| S4′ | V0 V1 V3 | Similar to (4) | S10′ | V0 V4 V6 | Similar to (4) |
| S5′ | V0 V3 V5 | Similar to (2) | S11′ | V0 V2 V6 | Similar to (2) |
| S6′ | V0 V2 V4 | Similar to (4) | S12′ | V0 V1 V5 | Similar to (4) |
| Sequence Number | Sequences of Basic Vectors within One Switching Cycle | Number of Switches | Current Sampling Synchronized with Zero Vector |
|---|---|---|---|
| sequence 1 | V0V6V2V2V6V0 | 8 | convenient |
| sequence 2 | V0V2V6V6V2V0 | 8 | convenient |
| sequence 3 | V6V2V0V0V2V6 | 8 | convenient |
| sequence 4 | V2V6V0V0V6V2 | 8 | convenient |
| sequence 5 | V6V0V2V2V0V6 | 8 | inconvenient |
| sequence 6 | V2V0V6V6V0V2 | 8 | inconvenient |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Inverter DC link voltage | 311 V | Motor stator resistance | 0.958 Ω |
| Inverter switching frequency | 5 kHz | Motor stator d-axis inductance | 0.00525 H |
| Line current sampling frequency | 5 kHz | Motor stator q-axis inductance | 0.012 H |
| Speed command value | 750 r/min | Motor rotor flux linkage | 0.1827 W |
| Motor-rated voltage | 130 V/50 Hz | Motor damping coefficient | 0.008 N·m·s |
| Motor moment of inertia | 0.003 kg·m2 | Motor number of pole pairs | 4 |
| Method Number | SVPWM Method | CMV Peak Value | CMV Valley Value | Number of CMV Jumps in a Period | Number of Switches in a Period | Whether to Use Zero Vector | Line Voltage Quality | Current Sampling Quality |
|---|---|---|---|---|---|---|---|---|
| 1 | Conventional SVPWM | Ud/2 | −Ud/2 | 6 | 6 | Yes | Excellent | Excellent |
| 2 | DPWMmax | Ud/2 | −Ud/6 | 4 | 4 | Yes | Good | Good |
| 3 | DPWMmin | Ud/6 | −Ud/2 | 4 | 4 | Yes | Good | Good |
| 4 | Active zero-state PWM | Ud/6 | −Ud/6 | 6 | 6 | No | Medium | Medium |
| 5 | Near-state PWM | Ud/6 | −Ud/6 | 4 | 4 | No | Medium | Medium |
| 6 | Virtual vector PWM | Ud/6 | −Ud/6 | 6 | 6 | No | Medium | Medium |
| 7 | Odd–even alternating PWM | −Ud/6 | −Ud/6 | 0 | 8 | No | Medium | Medium |
| 8 | Low common-mode SVPWM | Ud/6 | −Ud/2 | 2 | 6 or 8 | Yes | Good | Good |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Peng, C.; Zhao, K.; Lyu, M. A Low Common-Mode SVPWM for Two-Level Three-Phase Voltage Source Inverters. Energies 2023, 16, 7294. https://doi.org/10.3390/en16217294
Zheng J, Peng C, Zhao K, Lyu M. A Low Common-Mode SVPWM for Two-Level Three-Phase Voltage Source Inverters. Energies. 2023; 16(21):7294. https://doi.org/10.3390/en16217294
Chicago/Turabian StyleZheng, Jian, Cunxing Peng, Kaihui Zhao, and Mingcheng Lyu. 2023. "A Low Common-Mode SVPWM for Two-Level Three-Phase Voltage Source Inverters" Energies 16, no. 21: 7294. https://doi.org/10.3390/en16217294






