Power Density Increase in Permanent-Magnet Synchronous Machines Considering Active Thermal Control

Abstract

The power density of electric machines for future battery electric vehicles must be further increased to improve customer benefits. To this end, this paper compares two state-of-the art electrical traction machines and evaluates the potential for increasing the power density using a third, novel high-speed machine design. The analysis is performed using an electromagnetic finite element analysis, a thermal network with lumped parameters, and a coupled electromagnetic–thermal simulation. The simulations of the three machines evaluate the potential for increasing the power density and overload margins, as well as reducing material consumption. With regard to the active thermal control, the new design aims for reduced thermal capacities and increased loss density to optimize the thermal controllablity and overall performance. The thermal active control is analyzed in thermal transient simulations and electromagnetic simulations with different magnet temperatures. The results show that higher magnet temperatures benefit efficiency and reduce losses for low torque at high speeds. However, a colder magnet is needed for maximum torque at base speed. A maximum loss reduction of 24% is achieved with a 100 °C magnet-temperature difference at maximum speed and low torque.

1. Introduction

The need to reduce emissions has made the requirements for electrical machines even more demanding, with the cost and availability of materials being critical factors in the development of electric drive units, as well as improving their efficiency and range. Increasing the power density of electrical machines is a promising approach to meet these requirements, as presented by various methods highlighted in this paper. This not only helps in meeting the demands, but also leads to more sustainable electrical machine designs.

In recent years, development trends show an increased component power in the electric drive train, and also in electrical traction machines, as depicted in Figure 1 [1]. Increasing the maximum machine speed is the second distinctive trend which can be observed. Advantages in power density and efficiency have led to the predominant use of interior permanent magnet synchronous machine (IPMSM)s in electrical traction applications [2]. It is well known that active thermal control of electrical machines can be used to minimize losses. In this work, we combine this degree of freedom with common measures to increase the power density and investigate the synergies.

Although not the topic of this work, it is worth mentioning that lightweight construction approaches, such as the use of carbon-reinforced fiber material or topology and shape optimization in several components can also result in higher power density [3,4].

This work is structured as follows: First, an overview of existing traction machines in production vehicles is given. Then, the basic specifications of the three simulated machines are given. Next, fundamentals of the definition of power density are recapitulated and the simulation setups are described. Two representative passenger vehicle traction machines are analyzed with regards to their power density and power loss density in electromagnetic–thermal simulations. These two state-of-the-art machines are compared to the third new developed high-speed, i.e., 25,000 rpm maximum speed, machine. This machine is especially designed for active thermal control operation, which has further potential for obtaining a higher power density.

In this work, different measures for power density improvement are presented and discussed. Afterwards, four common approaches to increase the power density are examined:

• An electromagnetic design approach aimed at increased speed and reduced torque, which leads to smaller machines at the same mechanical power.
• An improved thermal layout, resulting in higher power limits and more efficient operation in certain ranges, at the same machine size.
• Thermal active-component-wise control that reduces losses in large operation areas.
• A reduction in loss with the same thermal layout, allowing operation at increased mechanical power, at the same machine size.

Figure 1. Overview of performance of traction drives [5,6,7,8,9,10,11].

Figure 1. Overview of performance of traction drives [5,6,7,8,9,10,11].

Overview of Current Electric Vehicle Traction Machines

There is a general trend to increase the speed, as can be seen in Figure 1: starting from 6000 rpm between the years 1997 and 2002, to 12,000 rpm and 13,000 rpm around 2012, and finally reaching around 17,000 rpm in the most recent electrical vehicles (EVs), from 2016.

Considering the Prius as a representative hybrid electrical vehicle (HEV), from generation 2 to generation 3, a $1.5$ kW/kg (45%) increase was realized. The Prius generation 4 has an additional increase of $0.9$ kW/kg ($18.7$%) compared to generation 3 [5,6,7]. This could be achieved by an optimization in the electromagnetic design. The obvious measures are:

• Increasing the speed. Assuming a similar corner speed to the maximal speed ratio, the maximal speed can be used as an indicator for increased speed at peak power. Early designs have a maximum speed of 6000 rpm, which is successively increased to 17,000 rpm by 2017, depicted in Figure 1.
• Reduction in the amount of electrical steel used in the rotor, as discussed in [1,5,6], which results in an overall lower weight at the same power, thus increasing the power density.
• The rotor pole geometry is altered significantly throughout the generations, which probably improved the electromagnetic characteristics.

Although it cannot directly be concluded from the specifications presented in Figure 1, it can be stated that more sophisticated cooling systems are utilized for improved performance (regarding efficiency, power density, and maximal power) [12]; cf. Section 3.3.

2. Investigated Electrical Machines

The investigated electrical machines are three IPMSMs. Two machines are very similar to existing series electric vehicles’ traction drives. These machines (electrical machine model 1 (M1) and electrical machine model 2 (M2)) represent the state of the art considering their motor topology, power class, and cooling systems. Electrical machine model 3 (M3) is a development which tries to capture trends beyond the state of the art, regarding operating speed, power density, and thermal design.

An overview of the machines’ specifications is given in

Table 1. Specifications of investigated machines.

	M1	M2	M3
Motor Type	IPMSM	IPMSM	IPMSM
Rotor Poles	8	8	6
Slot Number	48	48	54
Winding Type	Distributed	Distributed	Distributed
Active Length (mm)	230	175	73.5
Stator Outer Diameter (mm)	220	190	175
Magnet Weight Share (%)	4.52	4.06	4.3
DC-link Voltage (V)	355	350	400
Max. Speed (rpm)	16,000	14,500	25,000
Max. Torque ($\mathrm{N}$$\mathrm{m}$)	284	171	129
Max. Power (kW)	158	109	86
Max. Power per Weight ($\frac{\mathrm{kW}}{\mathrm{k}\mathrm{g}}$)	2.09	2.51	4.68

. The performance data are determined at winding temperature (${\vartheta }_{\mathrm{winding}}$) = 160 ${}^{°}$C and magnet temperature (${\vartheta }_{\mathrm{magnet}}$) = 160 ${}^{°}$C from the electromagnetic simulation. The DC link voltages are all in the similar range of a 400 $\mathrm{V}$ system, and the winding type is hairpin-distributed winding for all three machines. M1 and M2 both have a 48 slot, 8 pole configuration, whereas M3 has a 54 slot, 6 pole configuration due to its higher operating speed. Machines M1 and M2 are, in general, bigger and heavier than M3. Machine M1 weighs $75.68$ $\mathrm{k}\mathrm{g}$ and M2 $43.44$ $\mathrm{k}\mathrm{g}$ (about 310%, and 136% heavier than M3). For the weight distributions, see

Table 2. Weights of investigated machines.

	Component	Material	Volume (l)	Weight (kg)	Share (%)
M1	Winding	Copper	0.8	7.39	9.8
	Stator	N27	2.9	22.37	29.6
	Rotor	N27	2.8	21.58	28.5
	Magnet	N42UH	0.5	3.42	4.5
	Shaft	Structural Steel	0.8	6.25	8.3
	Housing	Aluminum	5	13.98	18.5
	Total	-	-	75.68	-
M2	Winding	Copper	0.6	5.33	12.3
	Rotor	N20	1.7	13.05	30.0
	Magnet	N30UH	0.2	1.76	4.1
	Shaft	Structural Steel	0.3	2.71	6.2
	Housing	Aluminum	2.2	6.09	14.0
	Total	-	-	43.44	-
M3	Winding	Copper	0.4	4	21.8
	Stator	N20	0.7	5.34	29.1
	Rotor	N20	0.5	3.55	19.3
	Magnet	N30UH	0.1	0.79	4.3
	Shaft	Structural Steel	0.1	0.94	5.1
	Housing	Aluminum	1.2	3.42	18.6
	Total	-	-	18.37	-

.

The cross-sections of the machines’ rotors and stators are given in Figure 2. Electrical machine M1 has a delta-shaped pole and measures 220 mm active axial length and 190 mm stator outer diameter. It has a maximum speed of 16,000 rpm and a maximum torque of 284 $\mathrm{N}$$\mathrm{m}$, which is higher than the torque of the compared machines. Machine M1 has a peak power of 150 kW.

The second electrical machine, M2, has a V-shaped pole, an active length of 175 mm, and a stator outer diameter of 190 mm, and reaches 14,500 rpm and a maximum torque of 190 $\mathrm{N}$$\mathrm{m}$ at a maximum power of 109 kW.

With the double V-shaped pole and the smallest overall volume ($73.5$ mm active axial length and 175 mm stator outer diameter) and weight ($18.37$ $\mathrm{k}\mathrm{g}$) of M3, the machine still reaches 80 kW, with a maximum speed of 25,000 rpm.

Both reference machines, i.e., M1 and M2, exhibit similar specific power per weight (${\rho }_{\mathrm{grav}}$) of $2.09$ $\frac{\mathrm{kW}}{\mathrm{k}\mathrm{g}}$ and $2.51$ $\frac{\mathrm{kW}}{\mathrm{k}\mathrm{g}}$. M3 has a significantly higher specific power per weight of $4.68$ $\frac{\mathrm{kW}}{\mathrm{k}\mathrm{g}}$.

In Table 2, the weight shares of the machines are shown. The magnet weight share is around 4% for all machines. Also, the stator makes up around 30% for all machines. M3 shows a higher share for the winding ($21.8$%), and reduced rotor share of $19.3$%, whereas the compared machines show around 30% for the rotor and $9.8$% (M1) and $12.3$% (M2) for the winding.

Although machine M3 has a significantly lower maximum power than machines M1 and M2, the amount of converted energy in machine M3 is the same in the assumed drive cycles. The occurring losses in machine M3 can be assumed to be very similar, since the efficiency is also similar. Considering the smaller volume and mass of machine M3, the loss density is in general higher in M3. In particular, this will be quantified in Section 5.1 for all three machines. This higher specific loss per volume also allows the active conditioning of each machine component, as explained in Section 6.

All the machines use housing water jacket cooling. Although machine M3 can optionally be used with additional sophisticated component-specific cooling concepts (direct stator and rotor magnet cooling cf. [13]), these are not considered in the following. Instead, further investigations are planned to show the specific thermal conditioning possibilities. These machines are selected for comparison because they represent a typical range of machines for passenger vehicles with similar system specifications and the same topology and basic design concepts.

3. Methods and Fundamentals

The mechanical power at the shaft, mechanical power ($P_{\mathrm{mech}}$), is defined by the torque (T) and speed (n):

$$P_{\mathrm{mech}}=2\pi ·T·n.$$

(1)

To ensure proper comparability, the electric machine is used with a generic housing, and the performances are derived from simulations, with the simulation setups and boundary conditions being identical.

The overall mass of the electrical machine is defined by:

$$\begin{array}{c}\hfill m_{\mathrm{EM},\mathrm{total}}=m_{\mathrm{winding}}+m_{\mathrm{stator}}+m_{\mathrm{rotor}}+\\ \hfill m_{\mathrm{magnet}}+m_{\mathrm{shaft}}+m_{\mathrm{housing}},\end{array}$$

(2)

where $m_{\mathrm{winding}}$ is the mass of the copper of the winding, $m_{\mathrm{stator}}$ is the mass of the stator lamination sheets, $m_{\mathrm{rotor}}$ is the mass of the rotor lamination sheets, $m_{\mathrm{shaft}}$ is the mass of the shaft, and $m_{\mathrm{housing}}$ is the mass of the generic housing. Each of the investigated machines is separated into these component weights in Table 2. A straightforward way to roughly estimate the machine’s overall electromagnetic active volume,

$$V_{\mathrm{EM},\mathrm{total}}=l·\frac{D_{\mathrm{S},\mathrm{OD}}^2}{4},$$

(3)

is to consider the active length of an electrical machine (l) and the stator outer diameter ($D_{\mathrm{S},\mathrm{OD}}$). The actual volumes and masses of each component are used for the power loss density.

The power density (gravimetric) is defined as power per weight:

$${\rho }_{\mathrm{grav}}=\frac{P_{\max }}{m_{\mathrm{EM},\mathrm{total}}}$$

(4)

or volumetric; power per volume:

$${\rho }_{\mathrm{vol}}=\frac{P_{\max }}{V_{\mathrm{EM},\mathrm{total}}},$$

(5)

with maximal mechanical output power ($P_{\max }$) and total mass of the electrical machine ($m_{\mathrm{total}}$), or the simplified machine volume ($V_{\mathrm{EM},\mathrm{total}}$), defined in (2), (3), respectively. However, the initial quantities are often not properly defined, especially in specifications for commercial use. In fact, there is no clear definition of power and weight, but a variety of possible interpretations are used. It is a significant difference whether comparing the weight for the complete electric drive unit (EDU), the electrical machine including power electronics, or only the electrical machine. Another example is the choice of the specified maximum power. Both continuous power and peak power are used, where 10 or 30 s are specified for the latter. The same definition can be used to give a specific loss per volume (specific loss per volume (${\rho }_{\mathrm{L},\mathrm{vol}}$)) for each component i

$${\rho }_{\mathrm{L},\mathrm{vol}}=\frac{P_{\mathrm{L},\mathrm{i}}}{V_{\mathrm{EM},\mathrm{i}}},$$

(6)

as given in (6), where $P_{\mathrm{L},\mathrm{i}}$ are the losses in one component, i, and $V_{\mathrm{EM},\mathrm{i}}$ is the corresponding volume of component i.

The power for continuous operation is defined by the same maximal operating temperatures (i.e., 160 °C for winding and magnets) coming from the electromagnetic–thermal simulation. The overload power is set as the maximum power before significant saturation effects are noticeable, considering the electromagnetic simulation results only. The detailed investigated electrical machines are modeled in ANSYS MotorCAD for the electromagnetic investigations in 2D finite element analysis (FEA), and for the thermal investigations in a lumped parameter thermal network (LPTN).

3.1. Losses Analysis

Total losses, as shown in (7), can be separated into copper losses ($P_{\mathrm{L},\mathrm{Cu}}$) in the windings, iron losses ($P_{\mathrm{L},\mathrm{iron}}$) in the laminations of the stator and rotor, magnet losses ($P_{\mathrm{L},\mathrm{magnet}}$) in the magnets, and mechanical loss ($P_{\mathrm{L},\mathrm{mech}}$) such as windage losses and bearing friction losses.

$$P_{\mathrm{L},\mathrm{tot}}=P_{\mathrm{L},\mathrm{Cu}}+P_{\mathrm{L},\mathrm{iron}}+P_{\mathrm{L},\mathrm{magnet}}+P_{\mathrm{L},\mathrm{mech}},$$

(7)

For the investigated IPMSM designs, iron losses and copper losses show the highest share in the average load range. Considering the speed ranges of the other machines in the benchmark in Figure 1, $P_{\mathrm{L},\mathrm{iron}}$ may be the major loss and its reduction could be a promising approach for increasing the power density. Although magnet losses have only a small share in the total losses, a reduction in $P_{\mathrm{L},\mathrm{magnet}}$ could be advantageous for operation in high-speed ranges, since often the loss density in the rotor is one limiting factor in this range. In the base speed range, $P_{\mathrm{L},\mathrm{Cu}}$ is usually the dominant loss type.

For machine M3, the loss separation is shown for the complete operating range in Figure 3. The main loss is $P_{\mathrm{L},\mathrm{Cu}}$, with up to 90% in the base speed range and up to 70% in the field-weakening range. In the lower-torque range, meaning up to 25 $\mathrm{N}$$\mathrm{m}$, $P_{\mathrm{L},\mathrm{iron}}$ has a share of around 70%, and in field weakening, also in the high-torque range, still a share of 20% to 30%. $P_{\mathrm{L},\mathrm{magnet}}$ generally has its maximum of around 2.5% in the field-weakening range.

3.1.1. Copper Losses

The copper losses can be separated into DC (copper losses DC part ($P_{\mathrm{L},\mathrm{Cu},\mathrm{DC}}$)) and AC (copper losses AC part ($P_{\mathrm{L},\mathrm{Cu},\mathrm{AC}}$)) parts, and considering a linearized temperature dependence represented as (8), where $R_{\mathrm{DC}}$ is the DC-equivalent resistance and $R_{\mathrm{ac}}$ the equivalent AC resistance, and I is the current, as described in (8), where ${\alpha }_{\mathsf{\theta }}$ is the temperature coefficient of copper and $\Delta \theta$ the temperature change with respect to the reference temperature ${\theta }_{\mathrm{ref}}$.

$$\begin{array}{c}\hfill P_{\mathrm{L},\mathrm{Cu}}\left(\vartheta \right)=P_{\mathrm{L},\mathrm{Cu},\mathrm{DC}}\left(\vartheta \right)+P_{\mathrm{L},\mathrm{Cu},\mathrm{AC}}\left(\vartheta \right)\\ \hfill =\left(R_{\mathrm{DC}}\left({\vartheta }_{\mathrm{ref}}\right)·[1+{\alpha }_{DC,\vartheta }·\Delta \vartheta ]\right)·I^2\\ \hfill +\left(R_{\mathrm{ac}}\left({\vartheta }_{\mathrm{ref}}\right)·[1+{\alpha }_{AC,\vartheta }·\Delta \vartheta ]\right)·I^2\end{array}$$

(8)

3.1.2. Iron Losses

The nature of the iron losses has been investigated and discussed in depth: [14,15]. With respect to the loss distribution over the operating range, as shown in Figure 3, iron losses account for up to 90% and over wide ranges up to 25% of the total losses. Considering the loss shift due to higher speeds mentioned in Section 3.4, reducing iron losses is one important task in future designs. In general, iron losses can be most effectively reduced by the choice of low-loss materials, which are determined either by the material composition or by the lamination sheet thickness; however, in this study, the new designed machine M3 already uses low-loss core materials and, therefore, the potential is limited here.

3.1.3. Magnet Losses

The main origin of magnet losses are eddy currents; hysteresis losses can be neglected [16,17]. Since eddy current losses are proportional to the square of frequency [18], magnet losses have to be considered, especially in high-speed operation, as can be seen in Figure 3. Also, eddy current losses are temperature-dependent, and are lower at increased temperatures [17].

Although magnet losses make up only a small part of the total losses in common radial flux machines with distributed windings (in the case of machine M3 maximal 2.5%), it can be useful to reduce $P_{\mathrm{L},\mathrm{magnet}}$. Magnet losses can be significantly reduced by axial and or tangential magnet segmentation [19,20]. In general, the improvement should hold against overall machine loss, specific operating limits (e.g., magnet operating temperatures), and the higher manufacturing costs. An example of a real-world traction drive which uses magnet segmentation is Tesla’s Model 3 [1].

3.2. Reduction of Losses

A favorable way to increase the power density is by reducing the total losses in the electrical machine. On the one hand, the reduced losses will increase the reachable $P_{\mathrm{mech}}$ at the same input power. On the other hand, reduced losses will result in a lower thermal loading, resulting in the same temperature at a higher power. Therefore, a loss reduction will have a double beneficial effect on the power density increase.

In the electromagnetic design process, the most relevant operating range for efficiency has to be defined prior to choosing the measures for loss reduction. As briefly described in Section 3.4, the different types of losses can be shifted for different electromagnetic design concepts.

Since copper losses make up a large share of the total losses, it makes sense to focus on a decrease in the current I or on reducing the phase resistance [21]. The assumption of a reduced current I can be implemented both by the concept of active thermal-field weakening (cf. Section 6) and by the choice of the electromagnetic design (cf. Section 3.4).

Since the phase resistance, in the case of copper, is temperature-dependent, cooler windings will result in a significant reduction in the DC part of copper losses. However, the AC part of copper losses has an anti-proportional behavior since eddy currents will be higher for an increased conductivity in the material. In the end, it has to be estimated which loss share is more predominant and which target temperature should be selected for minimum losses. Reducing copper losses and having the same cooling boundaries generally results in cooler windings.

It is obvious that improved cooling of the stator windings leads to a higher power density. Sophisticated cooling systems can be specifically used to dynamically and precisely control the winding temperature to the optimal target temperature. In the end, the maximal heat dissipation is limited and further power density increases have to be investigated considering the tradeoffs for each individual design.

3.3. Improved Loss Dissipation

The maximum operating temperature of an electrical machine is defined by the material limits of the components (e.g., housing, bearings, shaft, lamination sheets, windings, insulation, permanent magnets). Usually, the components which are closest to their temperature limits are the windings (insulation) [22] and magnets [23]. However, the magnet limit is harder to specify, since it is also dependent on the operating point of the magnet; an example calculation can be found in [24].

Improved cooling concepts can ensure the temperature limits in the machine’s hot spots, at an increased mechanical power, and total losses, respectively. A thorough review is given in [12]. In general, methods are categorized by the location of cooling, i.e., direct contact with the cooled components (spray cooling, flushing, channels in active components), and indirect (cooling jackets, housing fins, and shaft cooling). The second distinctive characteristic is the choice of cooling medium. Commonly, gas or liquid (water-based or oil-based) coolants are used. Cooling of electrical machines was always a topic of interest, as can be seen by early patents, e.g., [25]. Nowadays, especially in mobile applications, increases in power density are becoming more relevant. Recent developments include direct-end winding cooling concepts [26], direct winding cooling [27], as well as improved housing jacket cooling [28]. All these approaches mainly target the winding temperature. Realizations of rotor cooling, to dissipate loss from the rotor to extend the operating range and increase efficiency, which reduce losses and increase the driving range, are becoming more important [24].

Rotor-cooling concepts can be categorized, as in [12], into rotor shaft cooling, direct liquid-cooled rotor, rotor spray cooling, and combinations of those concepts. Furthermore, air-cooled rotor and rotor jet impingement cooling have to be named. In the following, the focus is on direct liquid-cooled rotor concepts, since these probably offer the highest potential regarding magnet conditioning.

The first patent dealing with dedicated rotor cooling was filed in 1990 and patented in 1993 [29]. It consists of a hollow shaft and multiple cooling channels in the rotor. Subsequent patents were disclosed in 2009 [30], also a liquid hollow shaft with coaxial design, and 2013 [31], a hollow shaft with air cooling. In 2014, in [32], a closed hollow shaft solution with heat exchanger and phase-change approach was published. In 2017, a patent considering a hollow shaft was disclosed [33]. Following that, commercial approaches were realized by Equipmake [34] and Audi [8]. It is obvious that dedicated conditioning of separate machine components is an upcoming technology trend, which enables higher power density, higher efficiency, in particular in certain operating ranges (cf. Section 6), and finally, enables smaller-sized machines. These smaller machines, i.e., machines with higher power density, with dedicated conditioning, are the key to the effective dynamic active-thermal-control strategy for further performance optimization.

3.4. Electromagnetic High-Speed Design

The mechanical power can be defined in analytical sizing [35] by

$$P_{\mathrm{mech}}=C·D_{\mathrm{S},\mathrm{ID}}^2·l·n,$$

(9)

where the defined quantities are the stator inner diameter ($D_{\mathrm{S},\mathrm{ID}}$), the utilization factor (C), the active length of an electrical machine (l), and the speed. The mechanical power is proportional to the torque and to the speed, and the torque is proportional to the square of the stator inner diameter $D_{\mathrm{S},\mathrm{ID}}$. Consequentially, the same mechanical power can be realized by reduced torque and increased speed. This results in a shift from copper losses to increased iron losses, magnet losses, and mechanical loss, which must be taken into account in the design phase.

The maximum torque–speed characteristic of the high-speed machine M3 can provide the same power at higher speeds and significantly lower torque. Thus, the overall volume and weight of an electrical machine can be reduced, c.f. Section 5.1. As shown in Table 1, high-speed machine M3 has a 123% higher gravimetric power density compared to the state-of-the-art machine M1. Additionally, the component weights, and along with this the thermal capacities, will be decreased, leading to a more dynamic thermal behavior.

Nevertheless, in the end, the electromagnetic benefits of high-speed machine designs needs to be weighted, on a system level, against a higher gear ratio in transmission, special bearings, and material choices, which is not part of this study.

3.5. Active Thermal Control

As mentioned in Section 3.3, the majority of (rotor) conditioning concepts aim at either an extended operating range or performance improvement by ensuring that magnet temperature stays below the defined limit.

For the winding, a faster controlled and limited heat-up can be beneficial for the reduction in the AC part of the copper losses.

An intentionally hot-conditioned magnet has a significant potential to reduce losses, as described in this work by the electromagnetic investigations.

IPMSMs cannot modify the rotor flux, which is chosen to reach maximum torque. For field weakening, this flux then needs to be compensated for by direct axis current ($I_{\mathrm{d}}$). This results in increased loss, and further, increased cost, requiring either higher-energy magnets or more magnetic material, which additionally reduces the power density. The only possible way to change the magnetic flux, excluding $I_{\mathrm{d}}$, is increasing the magnet’s temperature [36]. The commonly used Neodymium Iron Boron (NdFeB) magnets show a temperature-dependent remanence flux density. The used magnet material in the investigated machine M3 is given in [37], and exhibits an averaged linear reversible temperature coefficient of $-0.1125$ $\frac{\%}{°\mathrm{C}}$.

With an appropriate conditioning system, dedicated to controlling magnet temperature, scenarios with hot as well as cold magnets and additionally transient changes in magnet temperature can be achieved. Especially for the operating range at lower torques, where a hot magnet is beneficial; c.f. Section 7. Given a machine with such a conditioning system, the loss can be minimized in all operating regions, increasing the effective power density and driving range. For identification of the loss reduction potential, electromagnetic simulations for the IPMSMs are performed, which are described in Section 4.

Current EVs have unnecessarily high power reserves in the base speed and field-weakening range. This over-performance is usually achieved by higher torques, e.g., machine M1 has 200 $\mathrm{N}$$\mathrm{m}$ to 350 $\mathrm{N}$$\mathrm{m}$ [1]. In simplified terms, torque is proportional to the size of the machine. Large machines have higher thermal capacities and a slower thermal response. On the one hand, this allows for longer or higher overload operation with a standard housing water jacket, but on the other hand, it limits the power density and makes active-component conditioning more difficult.

For identification of the loss reduction potential by active thermal-field weakening, electromagnetic simulations for the IPMSMs are performed.

4. Simulation Setup

For a holistic comparison, every physical domain that affects the performance of the machines needs to be simulated. The investigation is split into a stand-alone 2D electromagnetic FEA simulation, a thermal LPTN stand-alone simulation, and a coupled electromagnetic–thermal simulation. The electromagnetic simulation is used to identify the maximum torque–speed performance as well as providing an estimation of the efficiency. Furthermore, the resulting losses are used as input for the thermal simulations. The stand-alone thermal simulation is used to compare the temperature development in high-speed- and high-torque-case operating points. The coupled electromagnetic–thermal simulation evaluates the machines’ behavior in common drive cycles such as WLTC or Artemis motorway 150 (Artemis motorway 150), considering the efficiency, temperature development, and main ranges of energy conversion. In the following, the simulation approaches are briefly described.

4.1. Electromagnetic Model

The electromagnetic model represents the rotational symmetric part of the machine as a two-dimensional stationary electromagnetic FEA. The outlines for the simulation model are taken from Figure 2. The materials are characterized on the basis of [38,39] for the electrical steel and on the basis of [37,40] for the magnets. The material data for copper is taken from the MotorCAD database; it has a defined electrical resistivity of $17.24$ $\mathsf{\mu }$$\mathsf{\Omega }$$\mathrm{m}$. The simulations are current-fed with sinusoidal current wave forms, i.e., they are fundamental wave models, which means that no harmonic effects from, e.g., inverter-based current wave forms, are accounted for. The conductors are represented by homogeneous areas of constant current density. The temperature effects are defined by material characterization in pre-processing only, i.e., the resistance of the winding and remanence of the permanent magnet. The temperature is assumed to be constant in each electromagnetic simulation step. The control strategies maximum torque per ampere (MTPA) and maximum torque per flux (MTPF) are adjusted for each magnet temperature to achieve minimal losses, with an assumed 5% voltage reserve [41]. The control parameters, i.e., $I_{\mathrm{d}}$ and quadrature axis current ($I_{\mathrm{q}}$) are identified a priori using ANSYS MotorCAD Lab.

The operating maps, with temperature-optimized control parameters. are simulated by steady-state simulations for defined torque and speed set points using ANSYS MotorCAD. The resulting loss data are interpolated in post-processing. The rotational speed, amplitude, and phase of the current is defined for each simulation point. The iron losses and magnet losses are calculated in the FEA, while the copper losses are only represented as in (8). The winding temperature is assumed to be 160 $°$C as a possible worst case for copper losses and the temperature limit of insulation class H (180 $°$C according to [22]), with a feasible margin.

To perform an in-depth analysis of power and loss densities, the different machines are compared at specific operating points.

4.2. Thermal Lumped Parameter Model

The thermal transient simulations of the electrical machines are performed using lumped parameter thermal network (LPTN) models. The thermal networks depict the radial cross-section of the motor. For each motor, one pole is modeled and thermal resistances and capacities are scaled to values for the whole machine. In addition, the axial heat flow is modeled with a front and rear section, so that the networks depict the machines in three axial layers (front, rear, and the main section in between). For reference, the resulting thermal network is depicted in Appendix A. Cooling is modeled assuming fixed temperatures at the cooling inlet and thermal resistances from the inlet to the cooled machine components. Depending on the individual geometry, each LPTN network consists of around 70 nodes. The recommended values, given for the materials in

Table 3. Material specifications in thermal model.

Material	Thermal Conductivity ($\frac{\mathbf{W}\mathbf{K}}{\mathbf{m}}$)	Specific Heat ($\frac{\mathbf{J}\mathbf{K}}{\mathbf{kg}}$)	Density ($\frac{\mathbf{kg}}{{\mathbf{m}}^3}$)
Electrical steel	27	460	7650
Aluminum	168	833	2790
Copper	401	385	8933
Structural Steel	52	460	7800
Magnet	7.6	460	7500
Insulation	0.2	1000	1400
Slot Liner	0.21	1000	700

, from the ANSYS MotorCAD database were used for each machine; no parameter identification of the heat transfer coefficients (HTCs) was performed. The thermal conductance of the stator-to-housing is set to 1057 $\frac{\mathrm{W}\mathrm{K}}{{\mathrm{m}}^2}$, and of housing-to-bearing shields, rotor lamination-to-shaft and magnets-to-lamination are set to 6341 $\frac{\mathrm{W}\mathrm{K}}{{\mathrm{m}}^2}$. The effective bearing conductance is speed independent and set to $75.8$ $\frac{\mathrm{W}\mathrm{K}}{{\mathrm{m}}^2}$. The effective air-gap resistance is speed-dependent and given in Figure 4. The identification of the critical heat transfer coefficient (HTC)s from the winding to the stator and convective heat transfer from the rotor to the stator and winding would result in more realistic values for the temperatures. For reasons of comparability, and since no particular features are implemented in the investigated machines, the used values are considered to be accurate enough. The coolant boundaries are constant and set to be same for each machine at a volume flow of 6 $\frac{\mathrm{l}}{\min }$ and 60 °C inlet temperature. The ambient temperature is set at 24 °C, and only natural convection is assumed at the machine’s outer surface. The simulation step time is 1 $\mathrm{s}$.

4.3. Transient Electromagnetic–Thermal Model

Since drive-cycle simulations have a quite extensive time frame, the coupled simulation model is simplified. Therefore, the electromagnetic behavior is represented by a map-based model, where flux linkages and inductances are $I_{\mathrm{d}}$- and $I_{\mathrm{q}}$-dependent and losses are speed- and torque-dependent. In each time step, the requested torque and speed is input to this model (as well as the temperatures of the magnets and windings resulting from the LPTN model). The corresponding machine behavior is fed back and the losses in particular are fed into the LPTN model.

Housing cooling with a flow rate of 6 $\frac{\mathrm{l}}{\min }$ and a coolant temperature of 60 $°\mathrm{C}$ is used. The coolant is an ethylene glycol–water mixture in the proportions of 50% for water and ethylene glycol. The start temperature for the drive-cycle simulations of the complete machines is the ambient temperature of 24 °C. The temperatures used for steady-state simulations are the resulting temperatures after five drive cycles using the Artemis motorway 150. For all simulations, the same 1800 $\mathrm{k}\mathrm{g}$ vehicle model is used. The gear ratio is adapted for each machine to match the maximum motor speed to a vehicle speed of 180 $\frac{\mathrm{km}}{\mathrm{h}}$. For each machine, the drive cycle is simulated five times in a row.

5. Simulation Results

For a holistic evaluation, the machines are compared in driving cycles and explicit stationary operating points, as well as stationary points over the entire operating range. The focus is first placed separately on the electromagnetic and thermal behavior. Subsequently, a dedicated thermal–electromagnetic coupled investigation is considered.

5.1. Stationary Electromagnetic Performance Analysis

Efficiency maps, including maximum and continuous torque as well as markers of the operating points of the considered machines, are given in Figure 5. Continuous torque curves are shown in dashed lines for a resulting maximal winding and magnet temperature of 160 $°\mathrm{C}$.

Four operating points are defined for specific power requirements. The resulting loss densities are calculated using (6).

• The OPHT is a high-torque, low-speed operating point at 35 $\mathrm{k}$$\mathrm{W}$, the loss density is shown in Figure 6a.
• The OPHS is a high-speed, low-torque operating point at 40 $\mathrm{k}$$\mathrm{W}$, the loss density is shown in Figure 6b.
• The OPMS is an operating point defined for the maximum speed and a power of 30 $\mathrm{k}$$\mathrm{W}$, the loss density is depicted in Figure 6c.
• The OPA150 is an operating point which is derived from the average torque and speed of the considered machines in the Artemis motorway 150 cycle. The loss density of operating point averaged from Artemis 150 cycle (OPA150) is shown in Figure 6d.

Due to the different operating ranges, these operating points are differently placed within the operating range of each machine, the torque–speed positions are shown in Figure 5. The operating point high torque (OPHT), operating point high speed (OPHS), and operating point maximum speed (OPMS) conditions represent the limits of the operating ranges and can be used to consider special use cases such as rotor heat-up on a long high-speed trip (OPMS and OPHS), or stator heat-up during extreme acceleration or hill climbing (OPHT).

5.1.1. High-Torque Operating Point

In operating point high torque (OPHT), a typical behavior for high-torque, low-speed operation can be observed. The highest loss density occurs in the windings for all machines. Loss density in the windings is especially high for OPHT due to high currents for the high torque demand. Machine M3 shows the highest loss density, of around 12,000 $\frac{\mathrm{W}}{\mathrm{l}}$, compared to 3800 $\frac{\mathrm{W}}{\mathrm{l}}$ (M2) and 2400 $\frac{\mathrm{W}}{\mathrm{l}}$ (M1). This results also in a rather fast temperature rise of the complete machine. The frequency-dependent losses, i.e., $P_{\mathrm{L},\mathrm{iron}}$ and $P_{\mathrm{L},\mathrm{magnet}}$ are comparable for all machines and significantly below all other analyzed operating points.

5.1.2. High-Speed Operating Points

For high-speed, low-torque operating points OPHS and OPMS, the loss density in the windings is roughly halved but still high. It is notable that M1 shows an increase of around 142% in the winding loss density from OPHS to OPMS, compared to M2 of only 69% and M3, which shows a reduction of 7%. This indicates that the magnets of M1 are clearly oversized, which results in a substantial field-weakening current being needed and leads also to a lower efficiency in this operating region, as can also be seen in Figure 5, where M1 shows a wider range with low efficiency at very low torques compared to M2 and M3. The loss density in the stator is increased significantly, by around 300%, for all machines, due to the increased frequency in the excitation current and the resulting stator rotational field. Higher harmonics in the rotor flux density lead also to increased loss density in the rotor, which is visible in the roughly five-times-higher rotor loss density and ten-times-higher magnet loss density, similar for all machines. The magnet loss density does not show a general trend from OPHS to OPMS: M1 shows the commonly expected increase, but M2 only marginally increases and M3 shows a reduced magnet loss density, by around 44%.

5.1.3. Artemis Motorway 150 Operating Point

The operating point OPA150 is derived from the Artemis motorway 150, i.e., average speed and torque of the cycle. OPA150 represents a more realistic long-term operating point in the high-speed region compared to OPHS and OPMS. For M2 and M3, OPA150 is located in the maximum-efficiency region, but for M1 it is torque-wise well below the maximum-efficiency region. The winding shows the lowest loss density of all the depicted operating points, but the ratios between the three machines are similar, as for the other operating points. The stator loss density is in a range between 450 $\frac{\mathrm{W}}{\mathrm{L}}$ (M2) and 497 $\frac{\mathrm{W}}{\mathrm{L}}$.

The common observation from all of the investigated operating points is that machine M3 has higher loss densities for all components, the only exceptions are the loss densities of the magnet and rotor for OPMS, where M1 has a similar rotor loss density and 85% higher magnet loss density. While a similar distribution can be observed for the stator loss density for all machines (cf. Figure 6c,d), machine M3 shows a significantly higher winding loss share of 51%.

5.2. Electromagnetic Transient Drive-Cycle Analysis

For further comparison of the investigated machines, transient drive-cycle simulations are performed in Artemis motorway 150 to compare the machines in a highway operation. The magnet and winding temperatures are set to 160 $°\mathrm{C}$ as a worst-case estimate.

Figure 7, Figure 8 and Figure 9 show the operating point distribution, i.e., the energy conversion share, of the drive cycle for each machine plotted onto the corresponding efficiency map. The color scheme allows for the differentiation of the energy conversion at the different operating points. Furthermore, the operating range of highest efficiency, i.e., always higher than 96%, is marked by a blue outline. The total electromagnetic losses are shown as contour levels and are marked with labels.

The drive-cycle analysis for M1 shows that the main energy conversion is below 100 $\mathrm{N}$$\mathrm{m}$ and between 8000 rpm and 13,000 rpm. As can be seen in Figure 7, even for highway situations, M1 operates only in a limited region of the map and outside of the maximum efficiency region, for which a higher torque would be needed. For the case of the Artemis motorway 150, this machine can clearly be considered oversized. As can be seen in Figure 8, M2 only partly has energy conversion outside of the most efficient region, because partly the torque range in the drive cycle is lower than the highest-efficiency region. Already, the smaller M2 shows a better matching of the maximal efficiency area and the area of most converted energy in the Artemis motorway 150 cycle.

As is depicted in Figure 9, M3 mainly operates in a range below 50 $\mathrm{N}$$\mathrm{m}$ and between 12,000 rpm and 20,000 rpm. The torque reaches the maximum torque for speeds higher than 15,000 rpm. Therefore, compared to the other machines, the operating points are more distributed over the possible torque range in this machine’s operating range. M3 generally operates at a lower torque but higher speed than machines M1 and M2. The energy conversion is observable mainly in the high-efficiency region of the operating range.

It can be concluded from the results shown in Figure 7, Figure 8 and Figure 9 that M3, as the smallest machine, best matches this representative cycle’s requirements. Machines M1 and M2 could be downsized to a lower target maximum torque without having an effect on the driving scenario and are, therefore, considered to be oversized. A small, high-speed machine, such as M3, is more suitable in this highway drive cycle.

5.3. Thermal Transient Analysis

For further analysis, the drive cycles WLTC class 3 and Artemis motorway 150, and two extreme operating point heat-ups (OPHT and OPHS) are simulated. The temperature development in the drive cycles is used for benchmarking the novel, small high-speed machine M3 against M1 and M2. The single-operating-point heat-ups are used to evaluate the temperature rise rates and, therefore, the overload and thermal-field-weakening potentials.

5.3.1. Drive-Cycle Thermal Transients

Over the course of five drive-cycle simulations, a convergence to a quasi-stationary temperature range can be observed. The temperature results of WLTC are depicted in Figure 10. The different magnet temperatures and the different thermal dynamics between M1 and M2 compared to M3 are particularly significant in the first cycle, where the machines heat up. As the WLTC is a rather low-performance drive cycle, a similar temperature for the magnets and windings is achieved, around 80 $°\mathrm{C}$ in quasi-steady state. The magnet temperatures vary by around 5 $°\mathrm{C}$ and, thus, show lower dynamics than the windings, which fluctuate in the range of 20 $°\mathrm{C}$. In Figure 11, the temperature profiles for the maximum temperature of the magnets and windings are depicted for the Artemis motorway 150 drive-cycle simulation.

In general, the temperature of the windings remains higher than the magnet temperatures. The lowest magnet temperature is reached with machine M1. This machine also has the slowest change in temperature, especially in the first drive cycle up to 1200 $\mathrm{s}$, where the initial temperature is low and, therefore, heat up is fast compared to the following cycles. A steady-state temperature level is established for all machines after around three cycles. M1 shows the lowest temperatures, for the winding of 100 $°\mathrm{C}$ to 117 $°\mathrm{C}$ and for the magnet around 100 $°\mathrm{C}$. The temperatures of M2 and M3 are very close, with the magnets (117 $°\mathrm{C}$) and windings at (117 $°\mathrm{C}$ to 130 $°\mathrm{C}$). However, machine M3 has a more dynamic magnet temperature during the cycle and fluctuates by around 5 $°\mathrm{C}$. This can be explained by the higher loss density in the rotor and magnets, as can be seen from Figure 6d. The higher temperature level can be explained by a higher loss density for M3 and the lower operating speed of M2, which results in a higher thermal resistance from rotor to coolant.

In comparison, M3, whose performance map matches the operating requirements for Artemis motorway 150 well (see Figure 9), shows a lower thermal inertia, which means a faster heat-up or cool-down. Both investigated drive cycles can be easily performed with a large temperature margin (max. temperature assumed 160 $°\mathrm{C}$) by M3. Also, without any special considered cooling concepts (only waterjacket cooling is used for all three machines), the resulting temperatures of all the machines are in a very similar range.

5.3.2. Single-Operating-Point Thermal Transients

To evaluate the heat-up at more extreme operating points, the cases of OPHT and OPHS are simulated with the LPTN model. The thermal dynamics of the windings and magnet define, on the one hand, the overload capability, and on the other hand, the potential for the faster achievement of the desired component temperature.

The starting temperatures are derived from the steady-state temperatures at the end of the Artemis motorway 150. As can be seen in Figure 12, M1 and M2 clearly show a similar rise in the winding temperature of $0.398$ $\frac{°\mathrm{C}}{\mathrm{s}}$ and $0.312$ $\frac{°\mathrm{C}}{\mathrm{s}}$, respectively. Motor M3 shows a significantly increased rise rate of $2.38$ $\frac{°\mathrm{C}}{\mathrm{s}}$. Despite this high rate, M3 reaches 160 $°\mathrm{C}$ after 21 $\mathrm{s}$ and 180 $°\mathrm{C}$ after 33 $\mathrm{s}$, which is still a feasible overload time. Furthermore, M1 is designed to be operated with dedicated cooling systems for a higher heat dissipation, including in the windings, which would result in a slower temperature rise, if needed. The temperature rise in the magnet in OPHT is insignificant for M1 and M2, and despite that, M3 rises 4.25 times faster than M2, which is still very low at $0.02$ $\frac{°\mathrm{C}}{\mathrm{s}}$ and would not limit the overload time at OPHT operation.

It is a clear finding that temperature changes in specific motor components, especially those such as magnets, are faster in machines which are the right size for the planned application. Oversizing and the resulting use of too much material, in contrast, leads to a slower thermal behavior. In Figure 13, for an operating point (OPHS) which has significantly higher loss density in the rotor components, it can be observed that the small high-speed machine (M3) shows the highest temperature rise rate for the magnet, of about $0.1$ $\frac{°\mathrm{C}}{\mathrm{s}}$, compared to M1 of about $0.04$ $\frac{°\mathrm{C}}{\mathrm{s}}$ and $0.05$ $\frac{°\mathrm{C}}{\mathrm{s}}$ for (M2). The reason is the increased power and loss density. However, the rise rate is still rather slow and considering the targeted temperature rise rates needed for an active dynamic thermal control of the machine, a sophisticated cooling concept is essential; the component temperatures could then be dynamically controlled, enabling a better overall performance of the machine. This shows the best opportunities for M3 in the method described in Section 6. Looking at the temperature rise rates for the windings hot-spot in the operating point OPHS, machines M2 and M3 show almost the same behavior, with rise rates of $0.35$ $\frac{°\mathrm{C}}{\mathrm{s}}$, compared to a slightly lower rise rate for M1 of about $0.25$ $\frac{°\mathrm{C}}{\mathrm{s}}$.

A downside of a small and thermally highly dynamic machine can be the overall high temperatures in specific machine components. The high temperature of the windings of M3 result from the high winding loss density, which is depicted in Figure 6a–d. However, it can be concluded that M3 indeed can be used for the investigated applications, the same as M1 and M2, since M3 is in a feasible temperature range for typical drive-cycle cases. Given that, it can be stated that, due to its design, machine M3 realizes a 76% reduction in magnet material and a $75.7$% total weight reduction (M3 vs. M1); and a $49.3$% reduction in magnet material and a $57.7$% total weight reduction (M3 vs. M2).

6. Active Thermal Control for Electromagnetic Performance Improvement

At the moment, a particular conditioning design is under development, the layout of which has a direct link to the magnets, granting precise and dynamic temperature control. Given this background, the following electromagnetic simulation cases are considered.

For the magnet temperature ${\vartheta }_{\mathrm{magnet}}$, a range between 60 ${}^{°}$C and 160 ${}^{°}$C is assumed. The resulting remanence used in the simulations is calculated in pre-processing according to the linear reversible temperature coefficient stated in the data sheet [37]; cf. [2]. Demagnetization for increased temperature operation is considered; no demagnetization took place. For this investigation, the worst case is the operation with hot magnets (i.e., here, the defined maximum magnet temperature of 160 $°\mathrm{C}$), and maximum field-weakening current. This operating point is identified and simulated in FEA for each investigated machine at the maximum speed and highest torque for each machine. The knee point of the magnets is the flux density below which irreversible damage to the magnets takes place. The knee point is identified as $0.31$ $\mathrm{T}$ for machine M1, $0.14$ $\mathrm{T}$ for machine M2, and $0.31$ $\mathrm{T}$ for machine M3. The results of the FEA simulation for checking whether demagnetization occurs is shown in Figure 14. It can be seen that the flux density stays above the critical knee point for all machines. Therefore, the feasibility of this operating range has been checked.

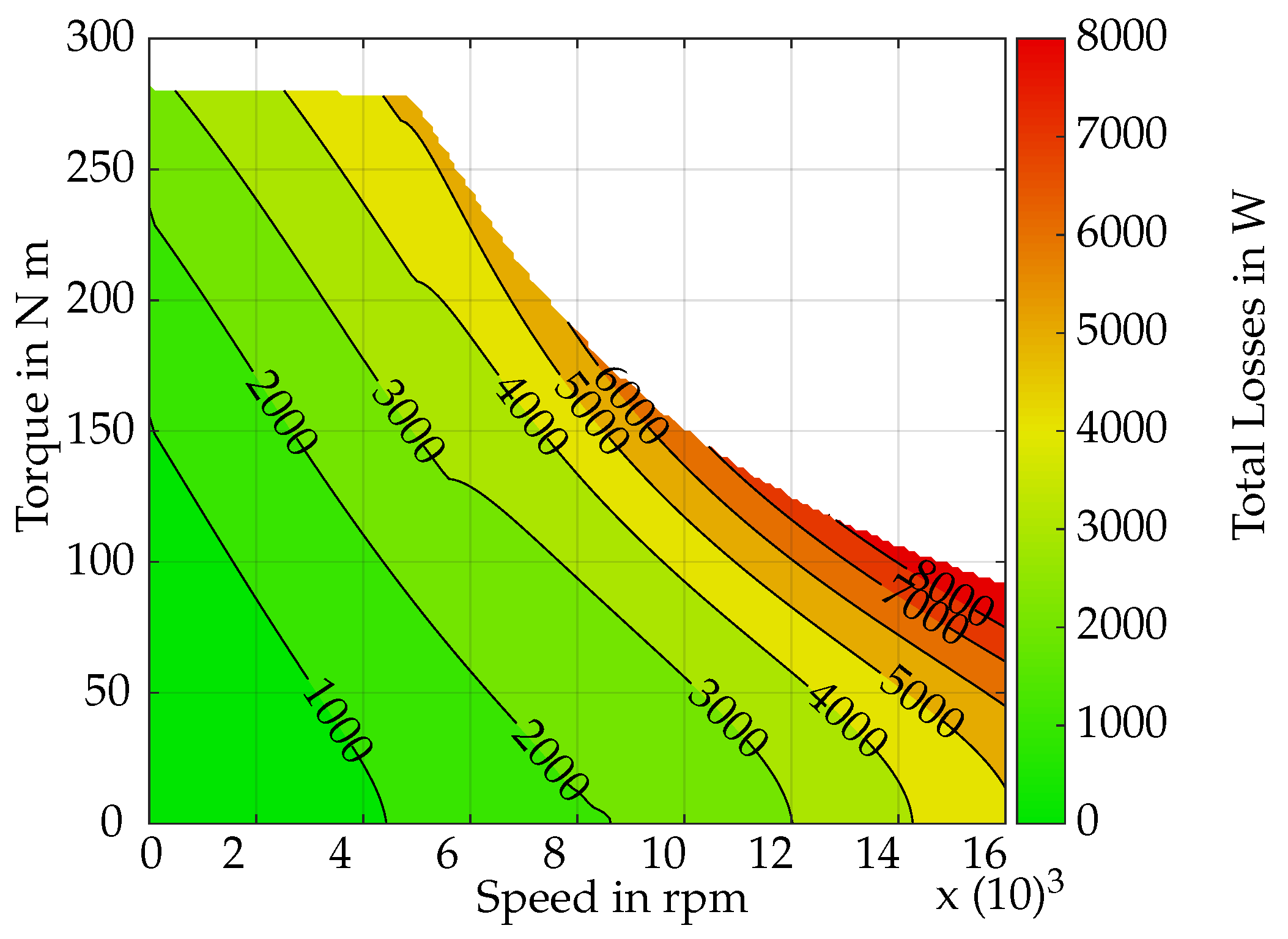
Since the loss reduction is more relevant in this investigation, the operating maps are represented as loss maps rather than efficiency maps, the losses type maps are given in Figure 15a,b. For a temperature distribution of ${\vartheta }_{\mathrm{winding}}$ = 160 ${}^{°}$C and ${\vartheta }_{\mathrm{magnet}}$ = 60 ${}^{°}$C, the loss map is given for machine M1 in Figure 16. The ranges of maximal loss, around 5 kW to 8 kW, are predictable in the high-torque regions in base speed as well as in field weakening. But also in low load at high speed, higher losses are observed, i.e., around 4 kW at 15,000 rpm.

For comparison, the loss maps are shown for the assumed highest difference in ${\vartheta }_{\mathrm{magnet}}$ of 100 $°\mathrm{C}$, from the operation of 160 ${}^{°}$C subtracted from 60 ${}^{°}$C. In Figure 17a,b, the total loss difference in the operation of the hot magnet (160 $°\mathrm{C}$) minus operation of the cold magnet (60 $°\mathrm{C}$) is shown.

In general, regions with a loss difference $\Delta$$P_{\mathrm{L},\mathrm{tot}}$ < 0 W (marked as orange to green) represent a range where a higher magnet temperature is beneficial. For all cases, ranges which exhibit lower losses for hot magnets are identified in the field-weakening range at low torques. Ranges that show a significant performance deterioration are for high torque, especially in the base speed range. It can be observed for M1 that the region with the highest energy conversion for Artemis motorway 150 and the region for optimal operation with a hot magnet match.

In the investigated cases, the highest difference in losses is observed also for the highest temperature difference ($\Delta$ ${\vartheta }_{\mathrm{magnet}}$ = 100 ${}^{°}$C), depicted in Figure 17a. The maximal loss reduction for a hot magnet of around 1600 W is achieved in the field-weakening range at 16,000 rpm. For cases with lower $\Delta$${\vartheta }_{\mathrm{magnet}}$, the loss savings are also smaller, but the ranges where hot or cold magnets are beneficial stay nearly the same compared to the maximal $\Delta$${\vartheta }_{\mathrm{magnet}}$.

Further, the loss distribution is examined in Figure 15a for machine M1, and for machine M3 in Figure 15b. Here, only the major loss shares, i.e., copper losses and iron losses, are shown, because magnet losses are contributing less than 2% to the total losses and even less to the loss differences. It is clearly observable that the main loss difference results from lower copper losses in the field-weakening area and higher copper losses in the high-torque area. The iron losses only contribute a small amount to the total loss difference and show for both machines the highest increase in the beginning of the field-weakening area, and a reduction in the high-speed field-weakening area. In the base speed range, there is only a marginal change in the iron losses. The difference in the field-weakening area can be explained by a different operating condition with different control parameters, i.e., in particular, the different field-weakening current.

When comparing the potential loss reduction in machine M1 and machine M3, it shows that M3, i.e., the smaller, right-sized machine, has a lower loss reduction potential in the field-weakening region, of only 400 W, whereas machine M1 shows a higher reduction, of around 1600 W. The consequent trend is also seen in the overload-torque region in the base speed range, where the oversized machine M1 only has a reduction potential for a cold magnet of around 400 W and machine M3 of 1000 W. This shows just the regions for which the machines are designed, and for which the amplitude of the rotor flux is chosen. For machine M1, this is for reaching high torques, and it exhibits its best efficiency in the mid-speed and high-torque ranges; c.f. Figure 7. For machine M3, this is for lower loads and mid- to higher-speed ranges and the mid-torque range; c.f. Figure 8.

7. Conclusions of Simulation Results

The three machines, M1, M2, and M3, are compared at steady operating points; in general, this shows that all the machines offer similar efficiencies, in the range of the highest efficiency, all machines reach above 96%, though machine M2 has the highest efficiency, of over 97%. Machine M3 shows higher efficiency over a wider speed range and up to deep field weakening, but has a significantly lower efficiency in the high-torque overload case at around corner speed compared to the other machines, due to a lower permanent magnet flux. The comparison of the ranges of the highest energy conversion of Artemis motorway 150 and the ranges of the highest efficiency are most overlaid for machine M3, which results in the lowest cumulative loss.

In the drive-cycle simulation machine, M3 shows the best overlay in the range of highest efficiency and the range of highest energy conversion. The thermal drive-cycle simulations reveal that for typical drive cycles the crucial magnet and winding temperatures of all three machines, although M3 is designed for a significantly lower maximum power, are at similar temperature ranges, which are far from the common temperature limits. In conclusion, a general loss reduction for hot magnets in field-weakening operation of IPMSM is proven. Also, it is shown that in most cases in the base speed range, a cold magnet is beneficial for loss reduction. Machine M1 shows a higher potential for loss reduction in the field-weakening range, and shows a lower impact of hot magnets in the high-torque base speed range. But M1 cannot change internal temperatures as fast as M3 (c.f. Figure 12 and Figure 13), which then leads to higher losses in normal operation, especially in the field-weakening range.

8. Summary and Outlook

A detailed overview of three current state-of-the-art electrical machines is given. It is concluded that currently one major design goal is increasing the power density. Approaches to reaching this goal are discussed regarding their further potential. The component-wise power density loss for the complete operating range is analyzed using example operating points for the investigated machines. The thermal behavior of the three machines is discussed for the Artemis motorway 150 and WLTC drive cycles. The idea of altering the remanence of the permanent magnet by changing its temperature is presented. With electromagnetic simulations, the potential to operate more efficiently with active thermal-field weakening over the operating range is identified for the investigated IPMSM. The highest potential to reduce losses at high magnet temperatures is in the field-weakening and low-torque regions, for a selected difference in magnet temperature of 100 ${}^{°}$C (60 ${}^{°}$C to 160 ${}^{°}$C); the maximum loss reduction of 1750 W (70% decrease) is achieved for machine M1 at around its maximum speed, 16,000 rpm. The improvement for an intentionally cold magnet at maximum torque in the base speed range is around 400 W.

The relatively large machine M1 shows a higher loss reduction in this operating range compared to machine M3, which also shows reduced losses with hot magnets in the field-weakening range, but only has a maximum loss reduction of around 600 W at its maximum speed of 25,000 rpm and around 1000 W at maximum torque in the base speed range with cold magnets. But the comparable small machine, M3, shows the fastest thermal heat-up in the simulated drive cycles WLTC and Artemis motorway 150, even without any special cooling concept. This fast thermal behavior is beneficial for the dedicated thermal control to achieve the target magnet temperature in an acceptable time. By means of a newly developed conditioning concept, designed for dedicated magnet-temperature control, an adapted model is going to be built. For a holistic assessment, a coupled simulation (thermal and electromagnetic) representing the new concept will be carried out for transient, especially drive-cycle, investigations, with a focus on energy savings and overload capability. Furthermore, the models of the machines are going to be validated on the test bench. Fast changes in magnet temperatures can probably be achieved, and an optimal efficiency and power density over the complete operating range is going to be realized by a proper control strategy. For real-world applications, online magnet-temperature knowledge is needed, and the demagnetization risk always has to be considered. Additionally, the aging of magnets due to the often fast thermal cycles of magnets will be considered.