An Analysis of Mechanical and Thermal Stresses, Temperature and Displacement within the Transparent Cylinder and Piston Top of a Small Direct-Injection Spark-Ignition Optical Engine
Abstract
:1. Introduction
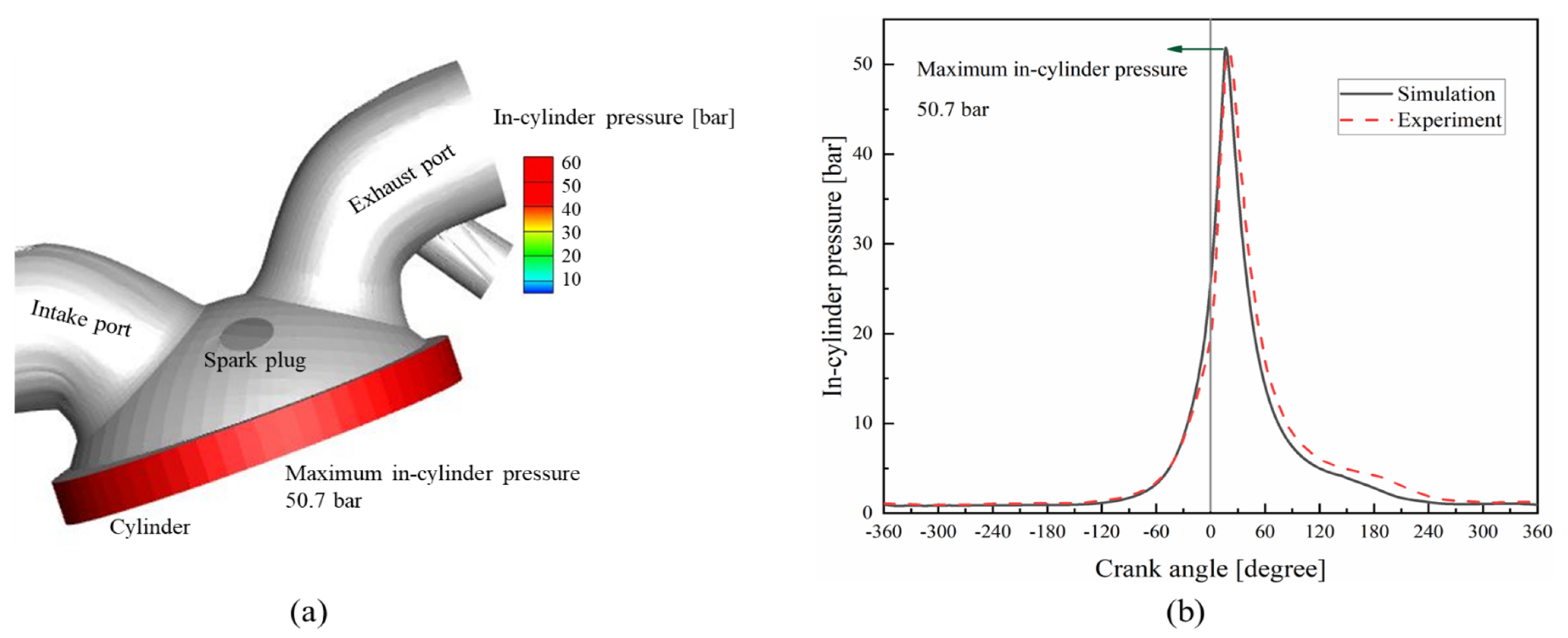
- A small DISI optical engine is designed while maintaining the bore and stroke dimensions of its conventional metal counterpart from which (and its validated CFD model) loads and measured boundary conditions are derived. This design’s geometric specifics serve as the initial dimensions for the transparent cylinder and piston top when initiating the coupled finite element analysis for thickness optimization.
- A coupled finite element analysis methodology is developed to analyze the combined stresses, temperatures and displacements. This methodology is then applied to the transparent components of the small DISI optical engine.
- The optimum thicknesses of both the transparent cylinder and piston top are determined to ensure their resilience against complex loads and boundary conditions, thereby ensuring an enhanced factor of safety.
- The research methodology outlined in this study can be applied to the advancement of optical engines, including technologies such as PFI, DISI and CI, irrespective of the fuel type. This is achievable by utilizing thermal and mechanical load data obtainable from experimental data (along with validated CFD models) of their corresponding metal counterparts.
2. Methodology of Coupled Finite Element Analysis in ABAQUS/CAE
3. Application of the Coupled Finite Element Analysis for the Quartz Cylinder
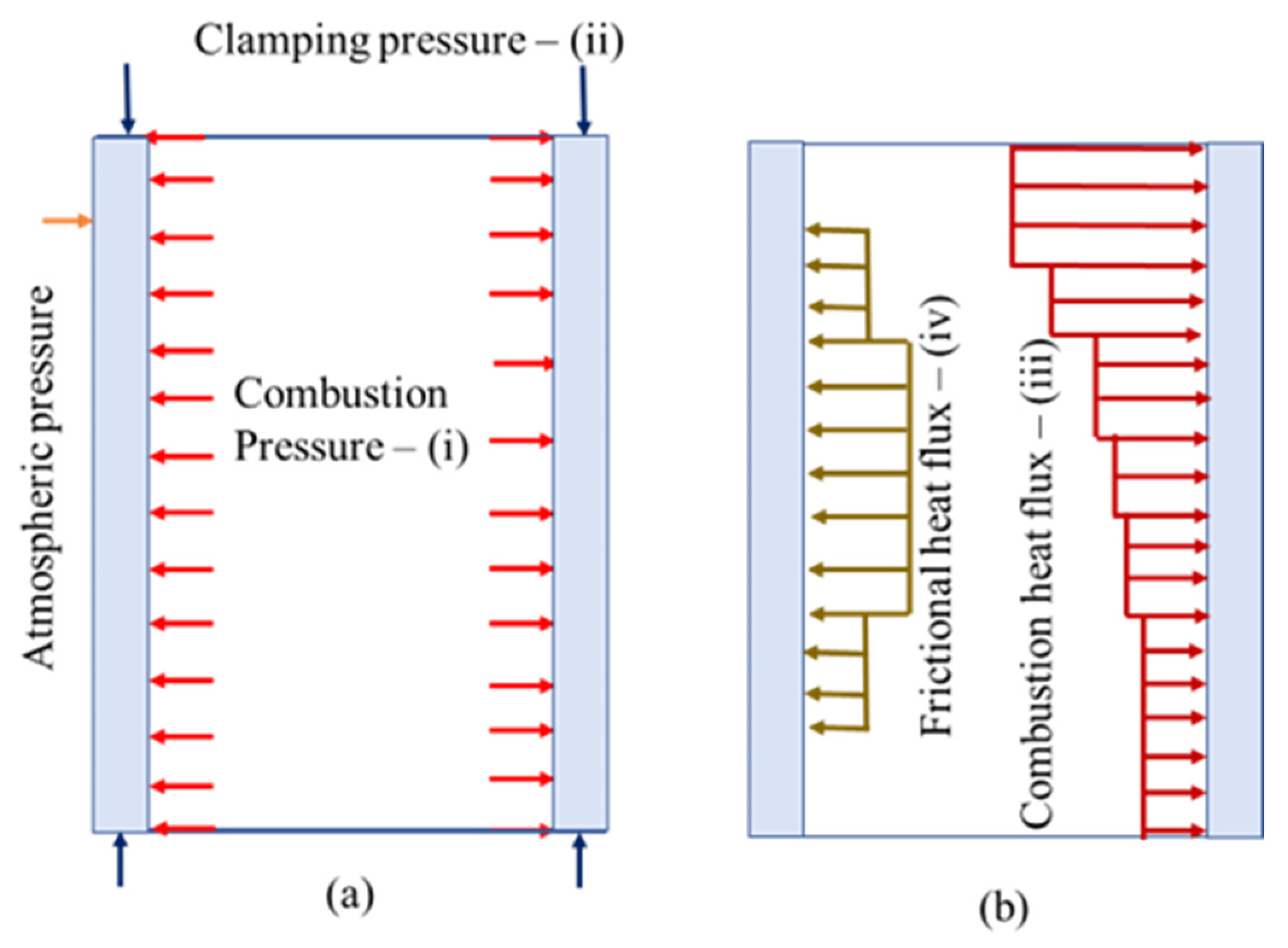
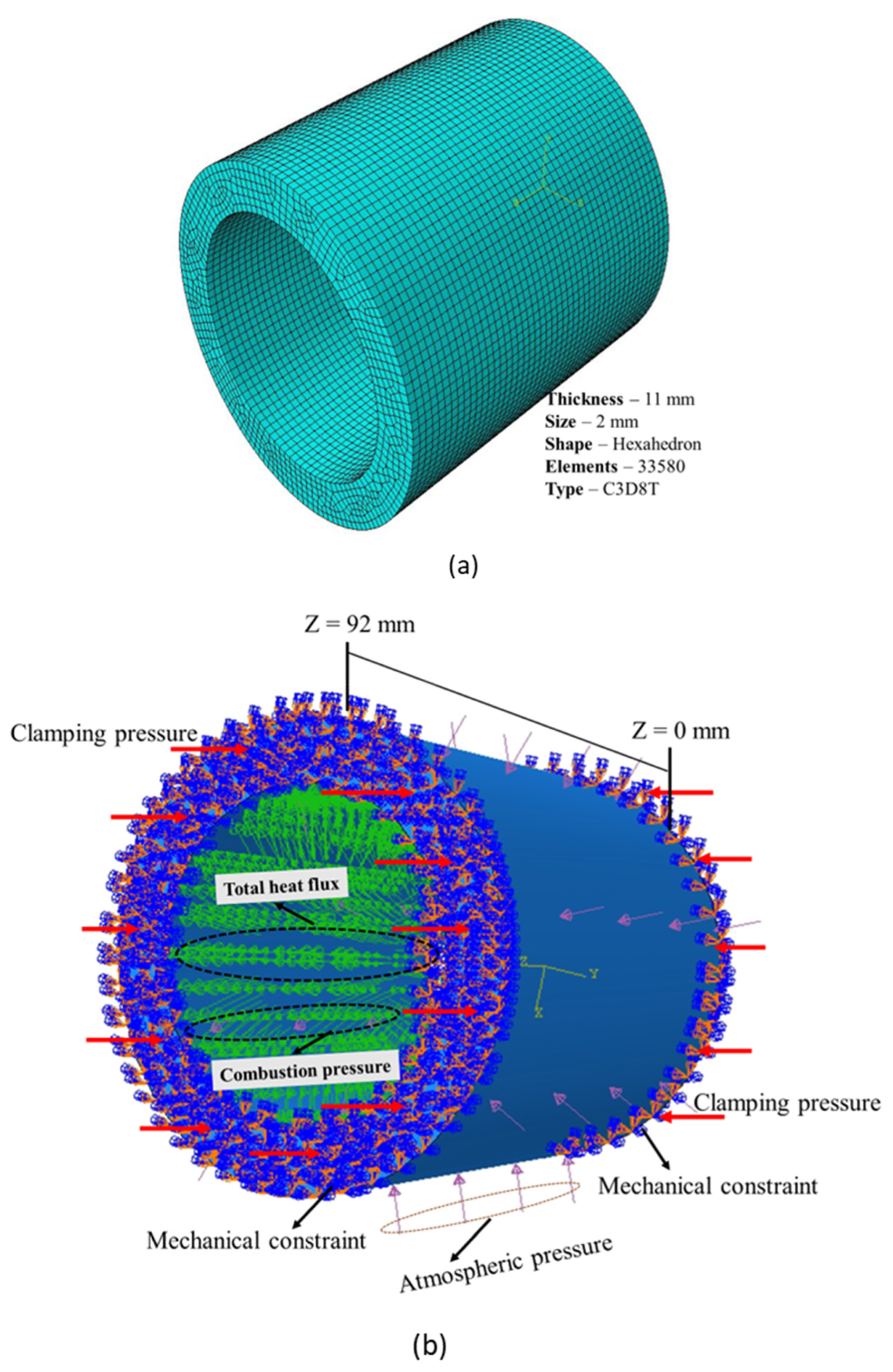
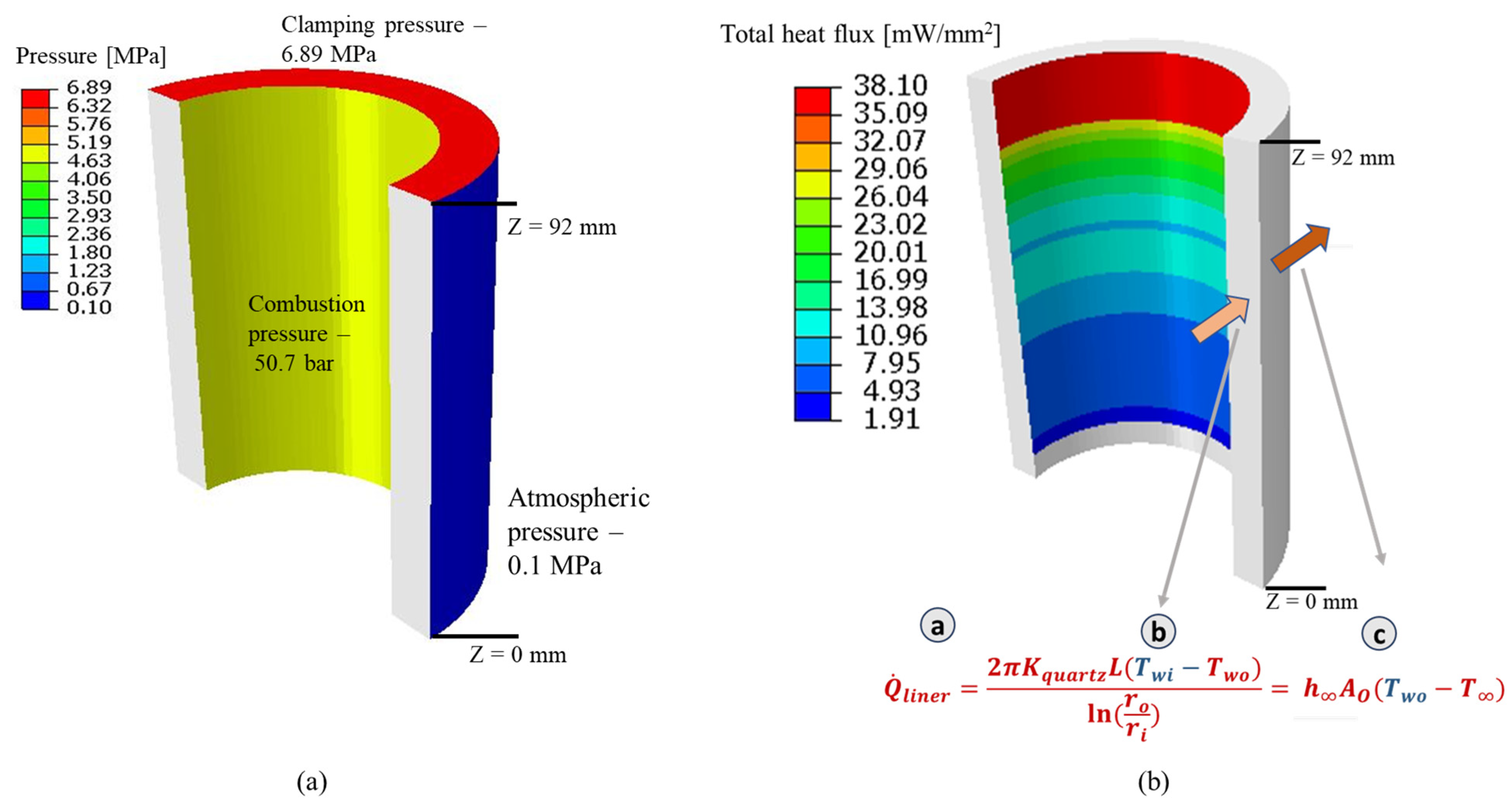
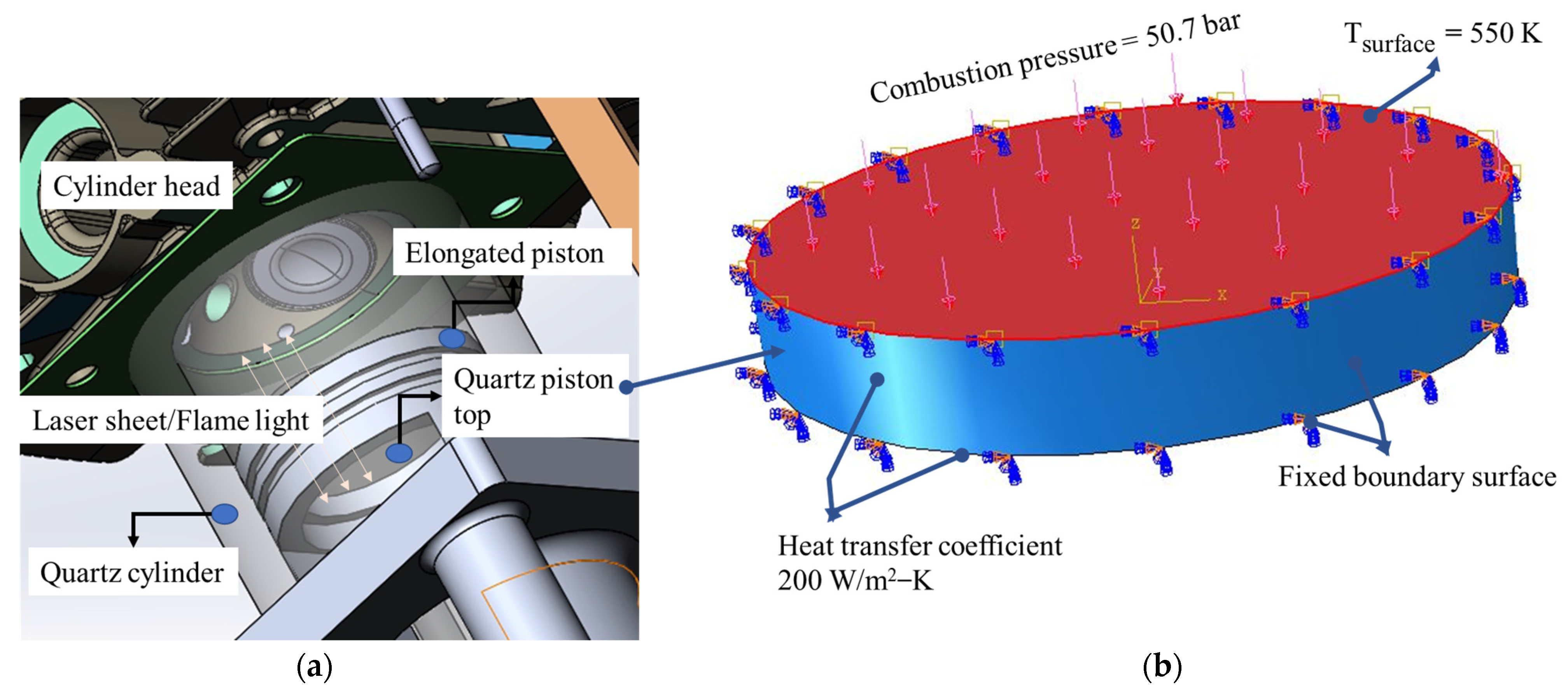
3.1. Basic Assumptions and Boundary Conditions
- Combustion pressure, applied to the inside surface of the cylinder, was assumed to be constant with respect to time and uniform over the axial length.
- Clamping force was converted to pressure and was assumed to be applied uniformly at the top and bottom surfaces of the cylinder [17].
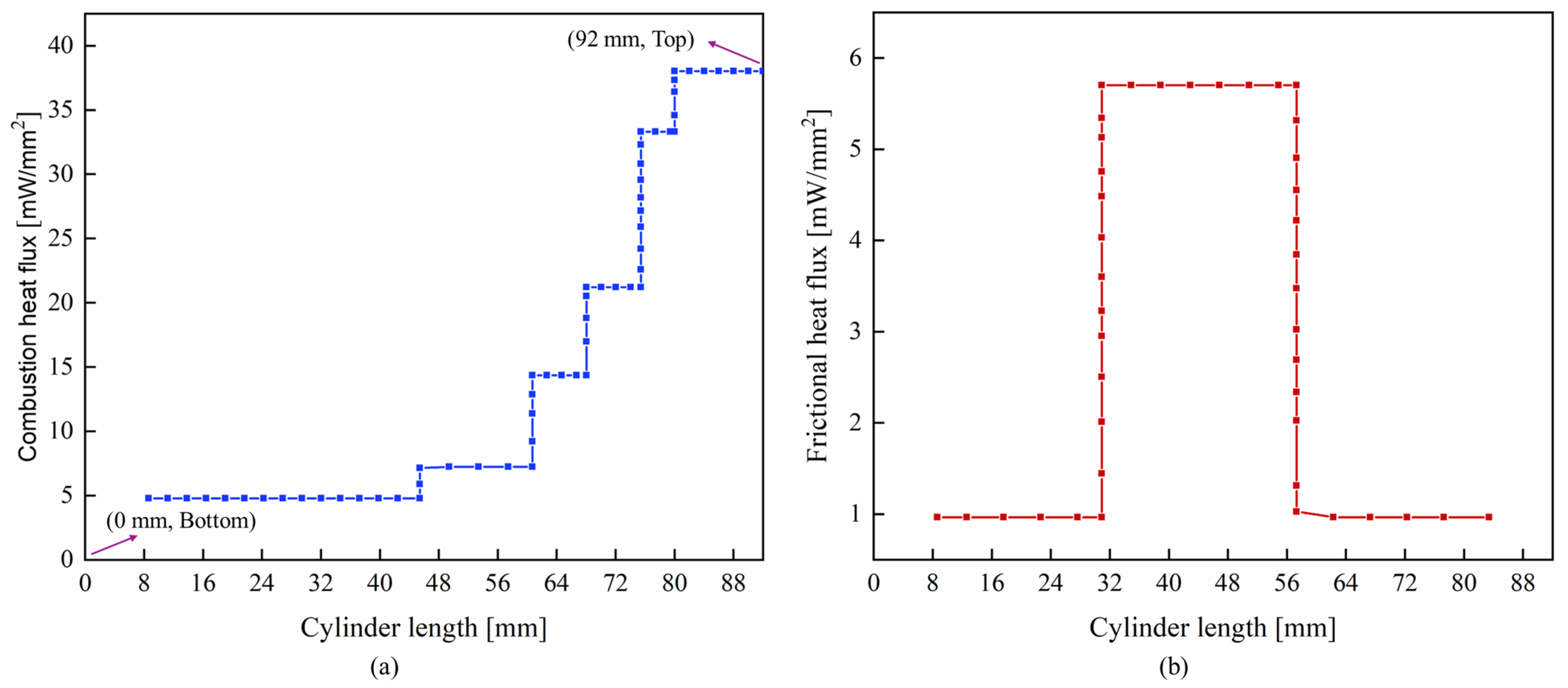
- Combustion heat flux, applied to the inside surface of the cylinder, was assumed to be constant with respect to time but reduced from top to bottom along its longitudinal axis [17].
- Frictional heat flux was assumed to be constant with respect to time and had a stepwise profile with maximum magnitude at the middle of the cylinder [17]. This is due to the greater lateral force present near the middle of the stroke, thus producing more frictional heat.
3.2. Thermal and Mechanical Load Profiles
3.3. Finite Element Model of the Quartz Cylinder
4. Application of the Coupled Finite Element Analysis Methodology for the Quartz Piston Top
5. Results and Discussion
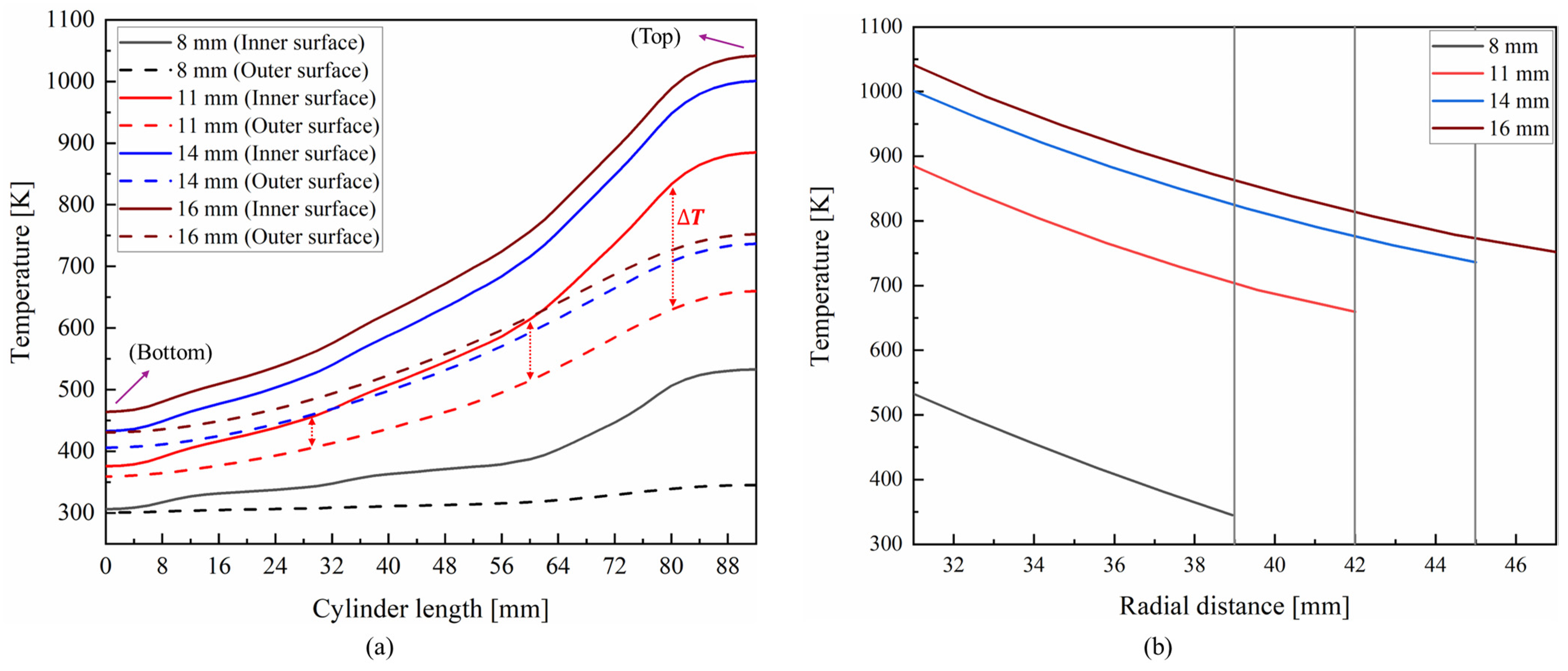
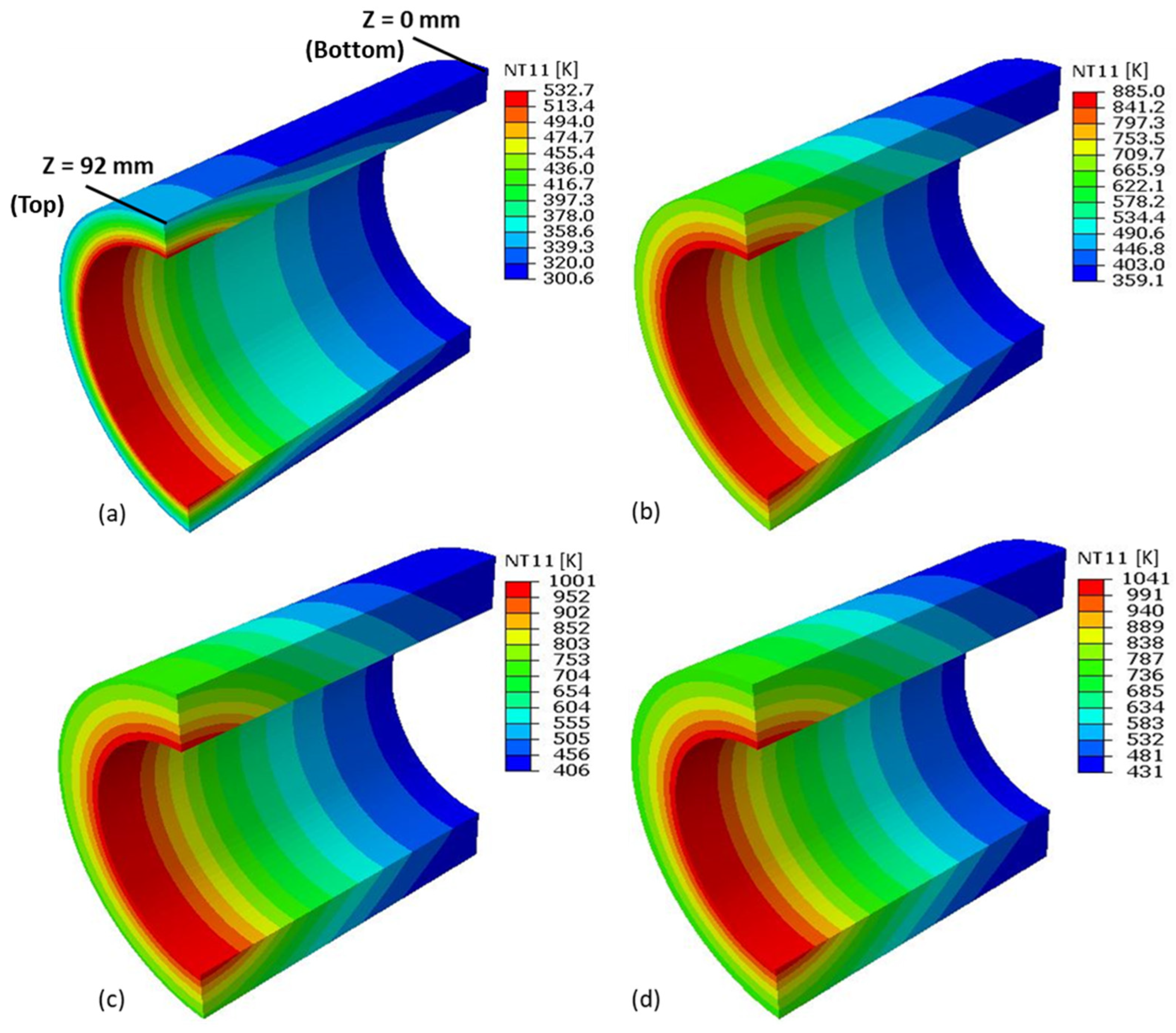
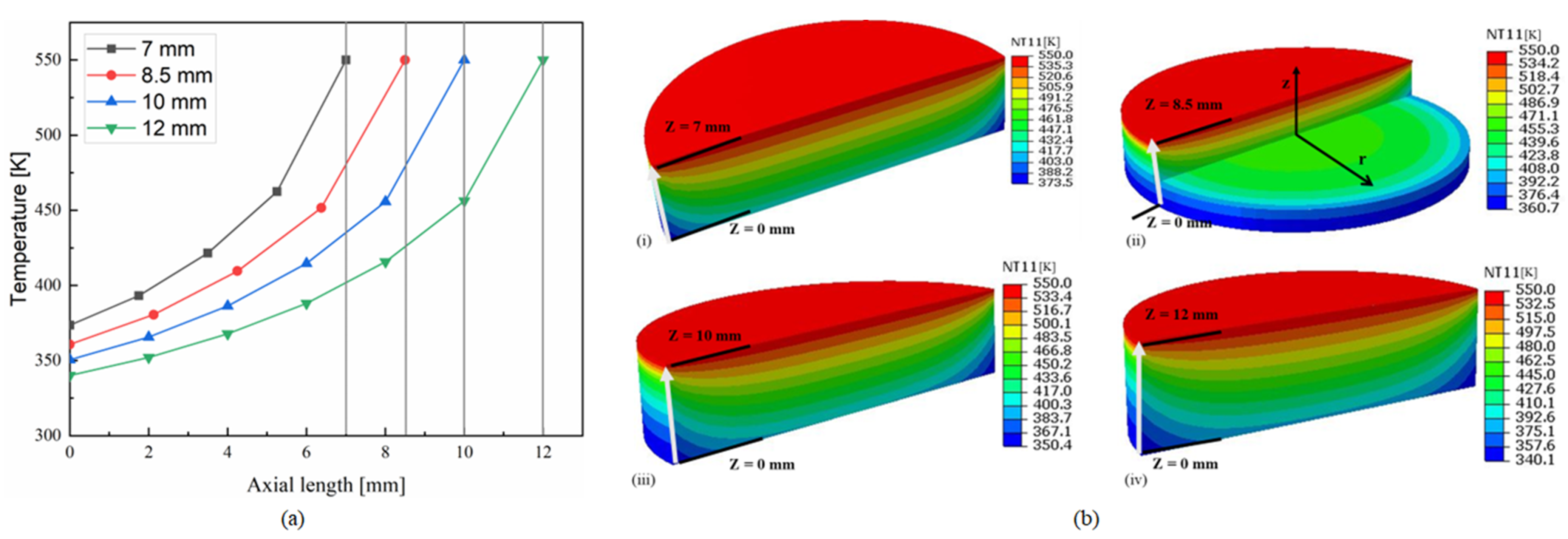
5.1. Temperature Distributions in the Quartz Cylinder and Piston Top under Combined Loading Conditions
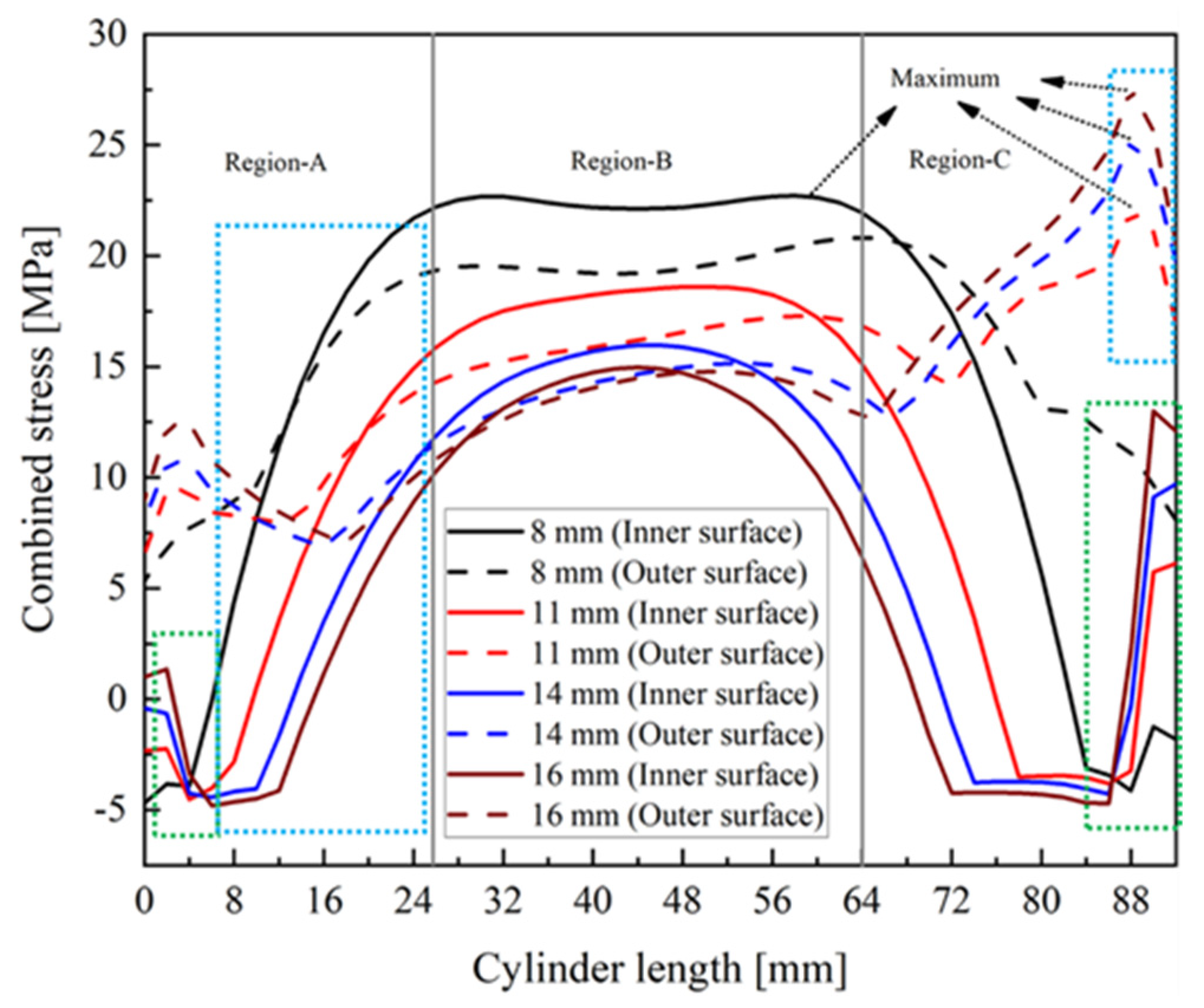
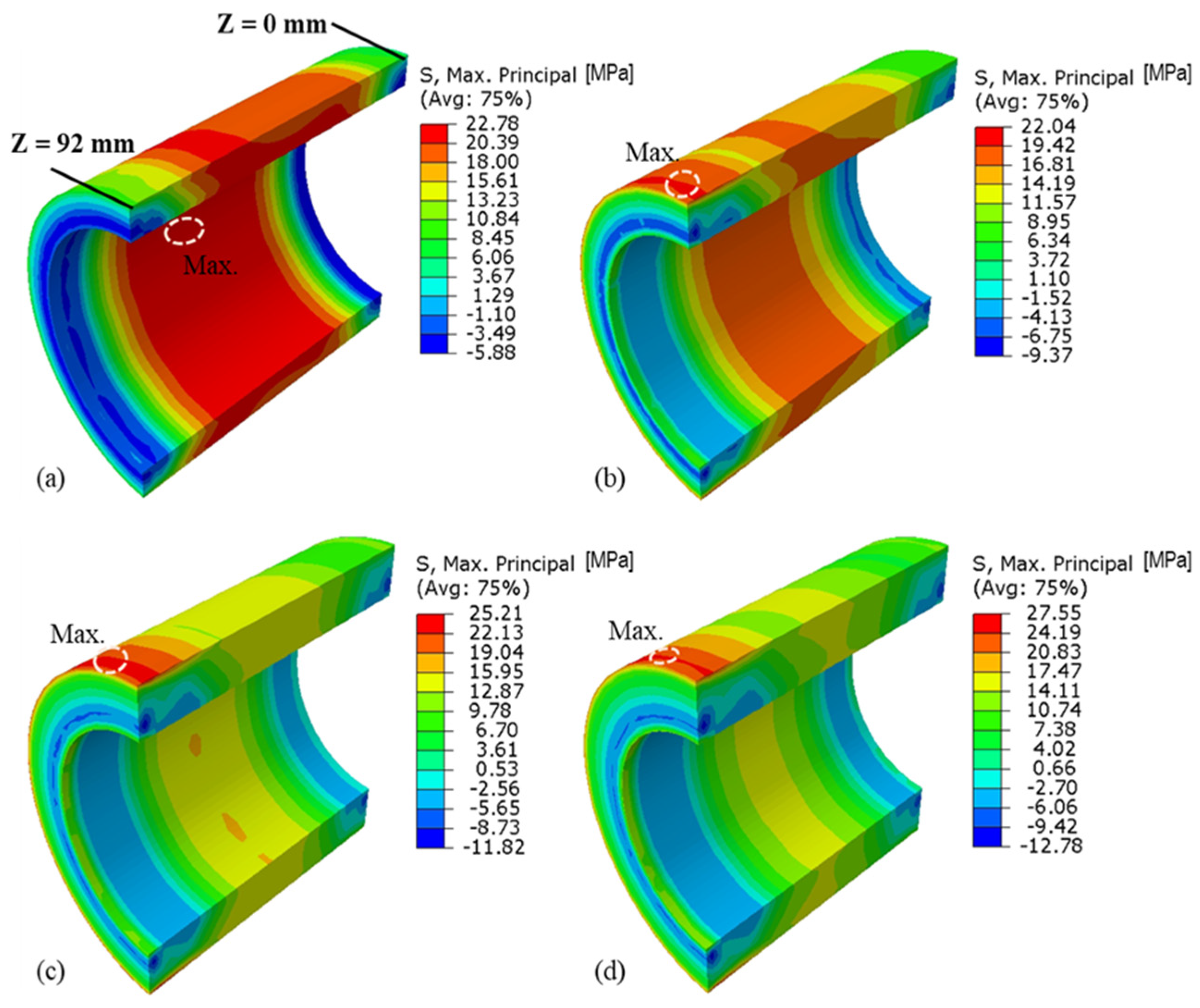
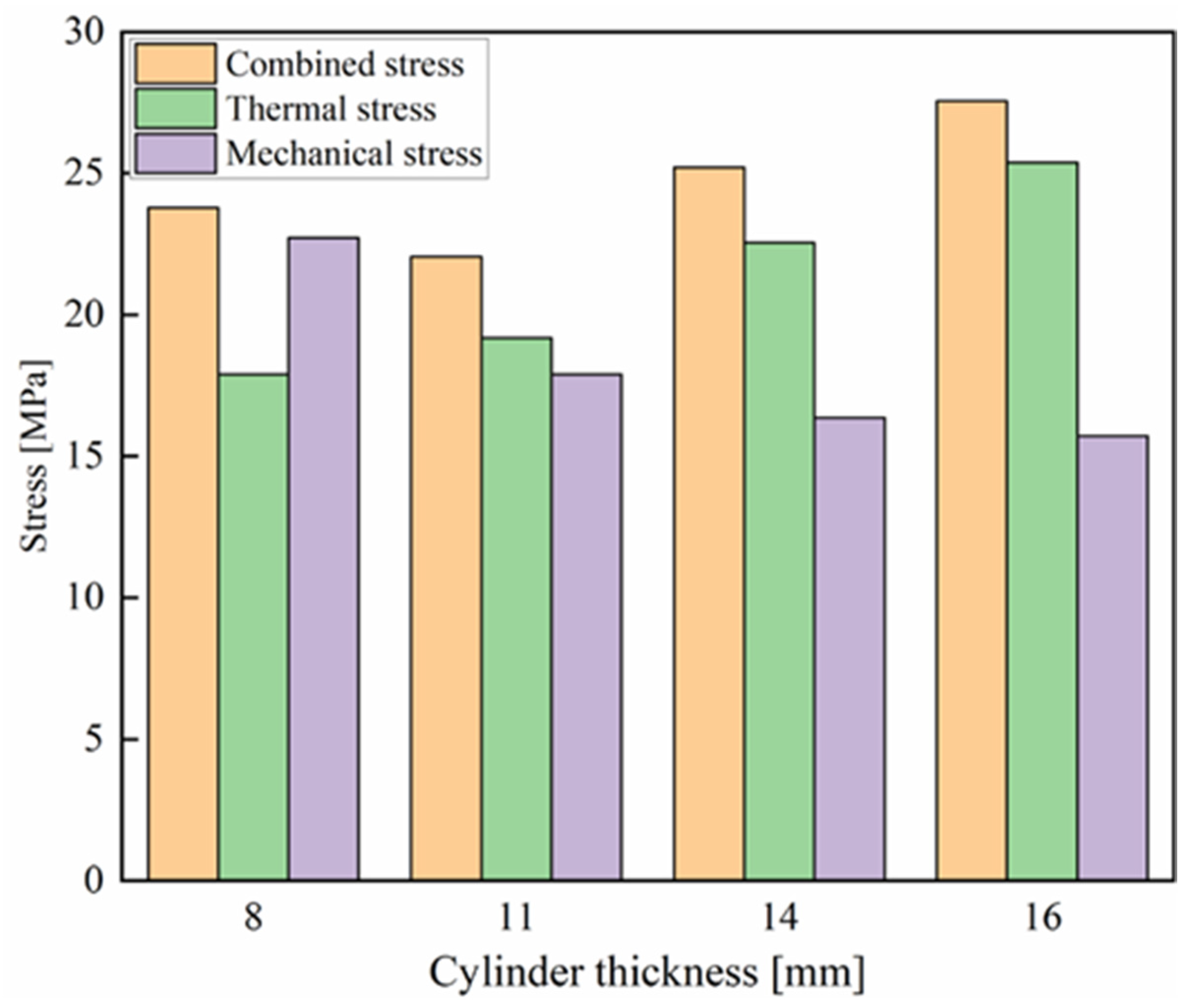
5.2. Combined Stress Distributions in the Quartz Cylinder and Piston Top under Combined Loading Conditions
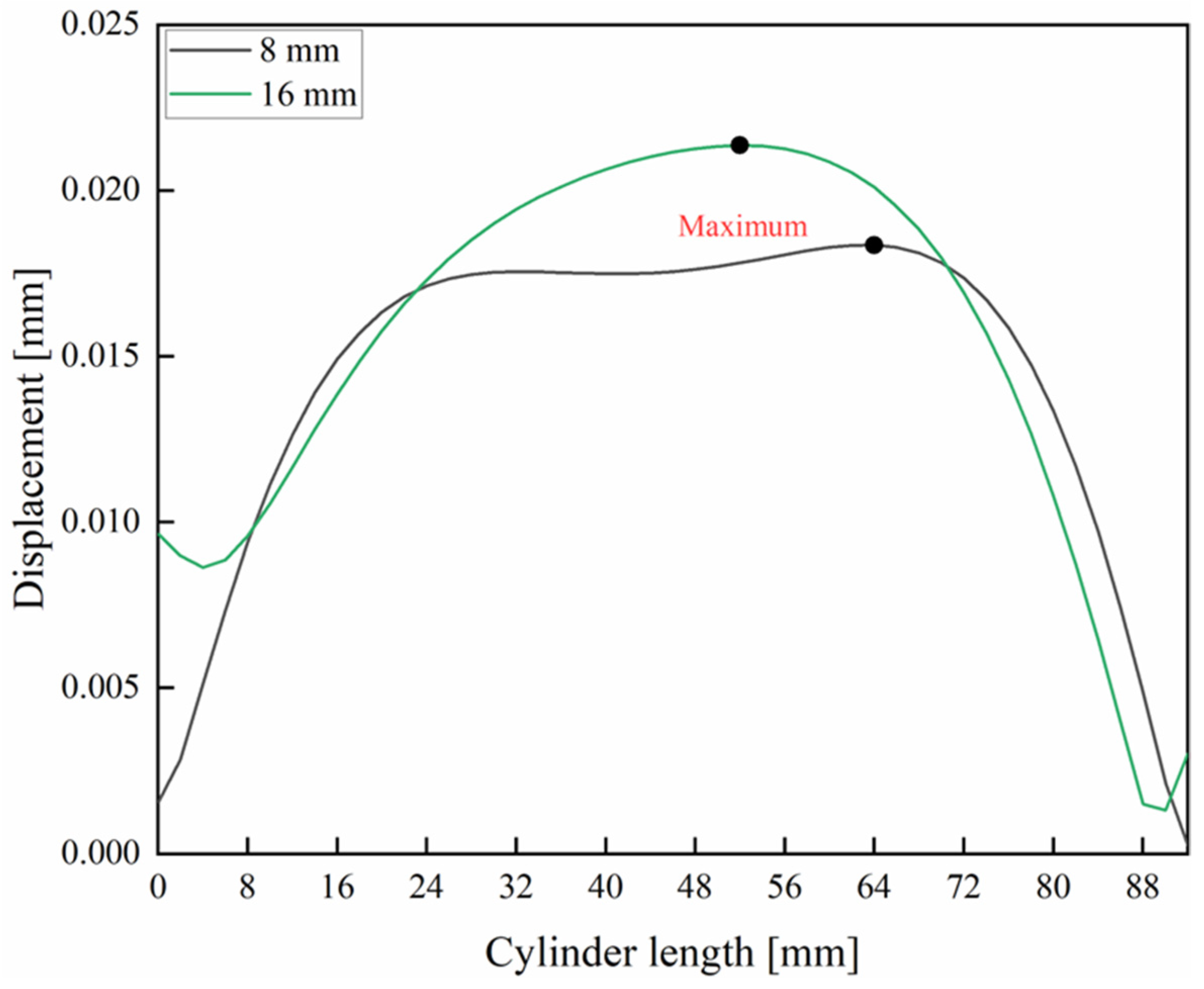
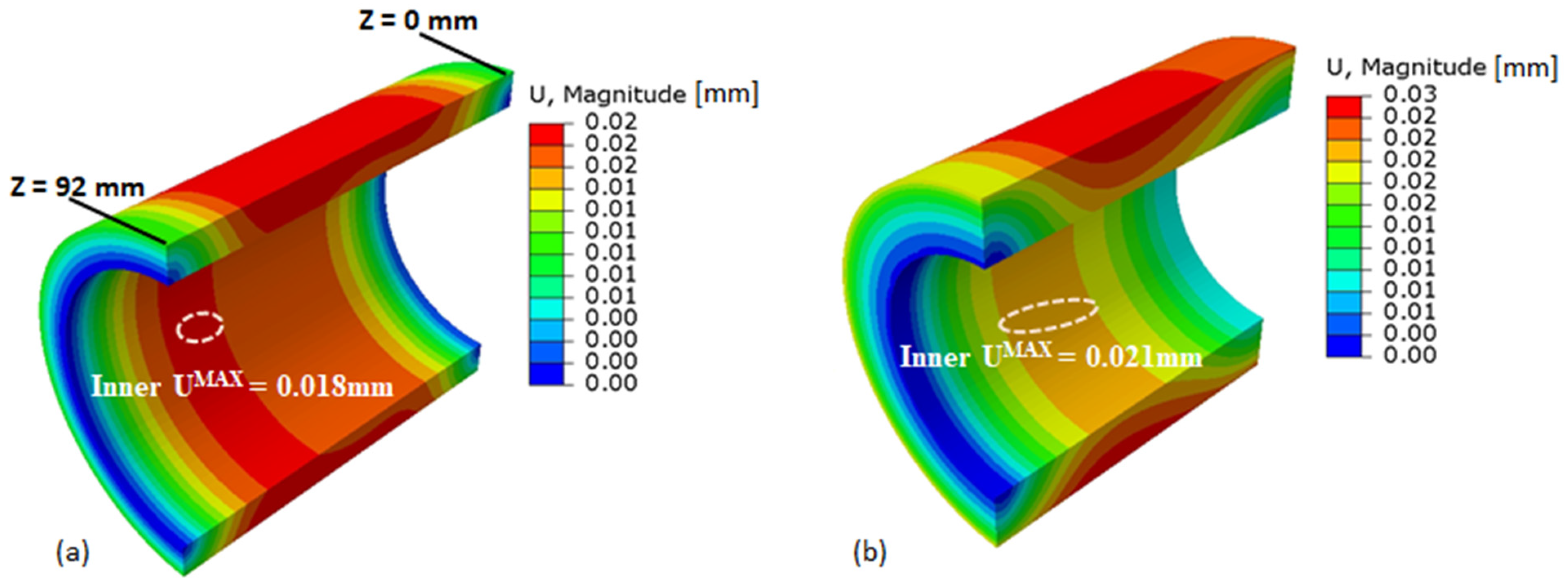
5.3. Displacement Distributions in the Quartz Cylinder and Piston Top under Combined Loading Conditions
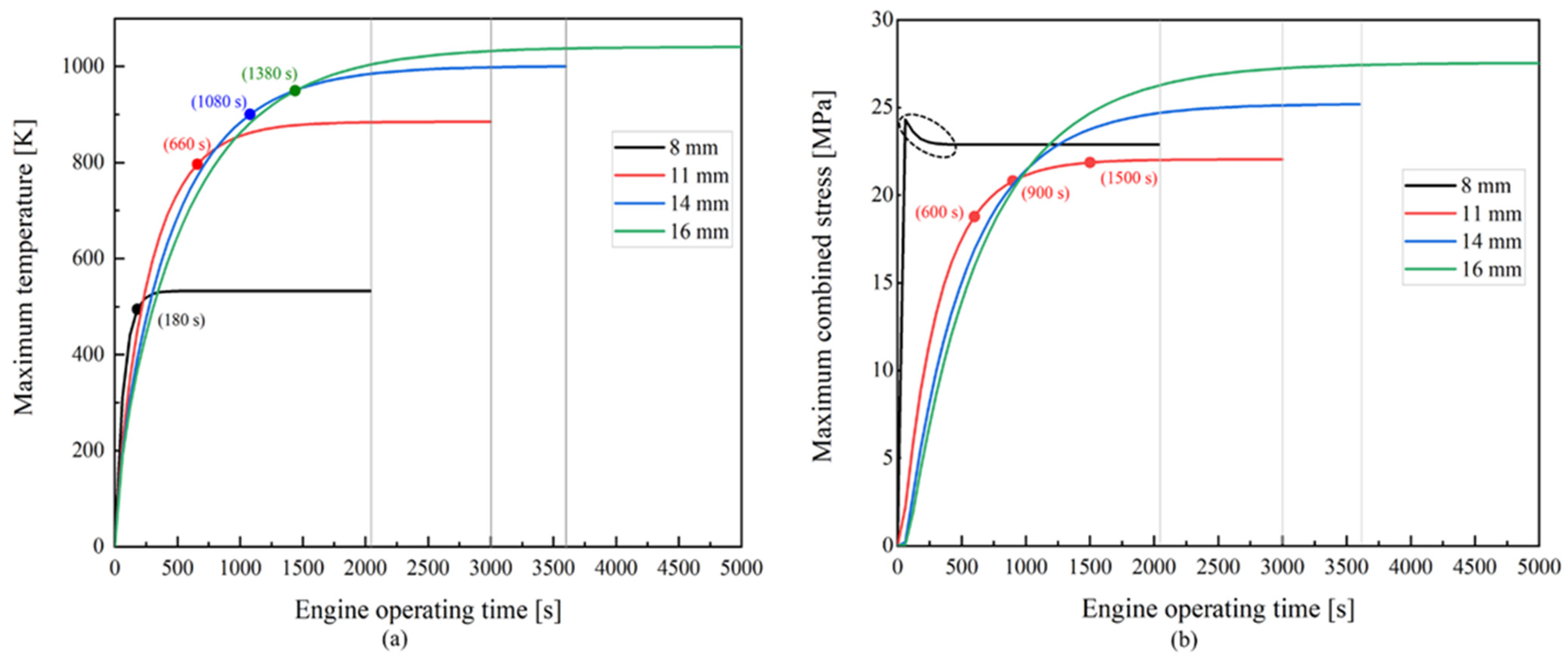
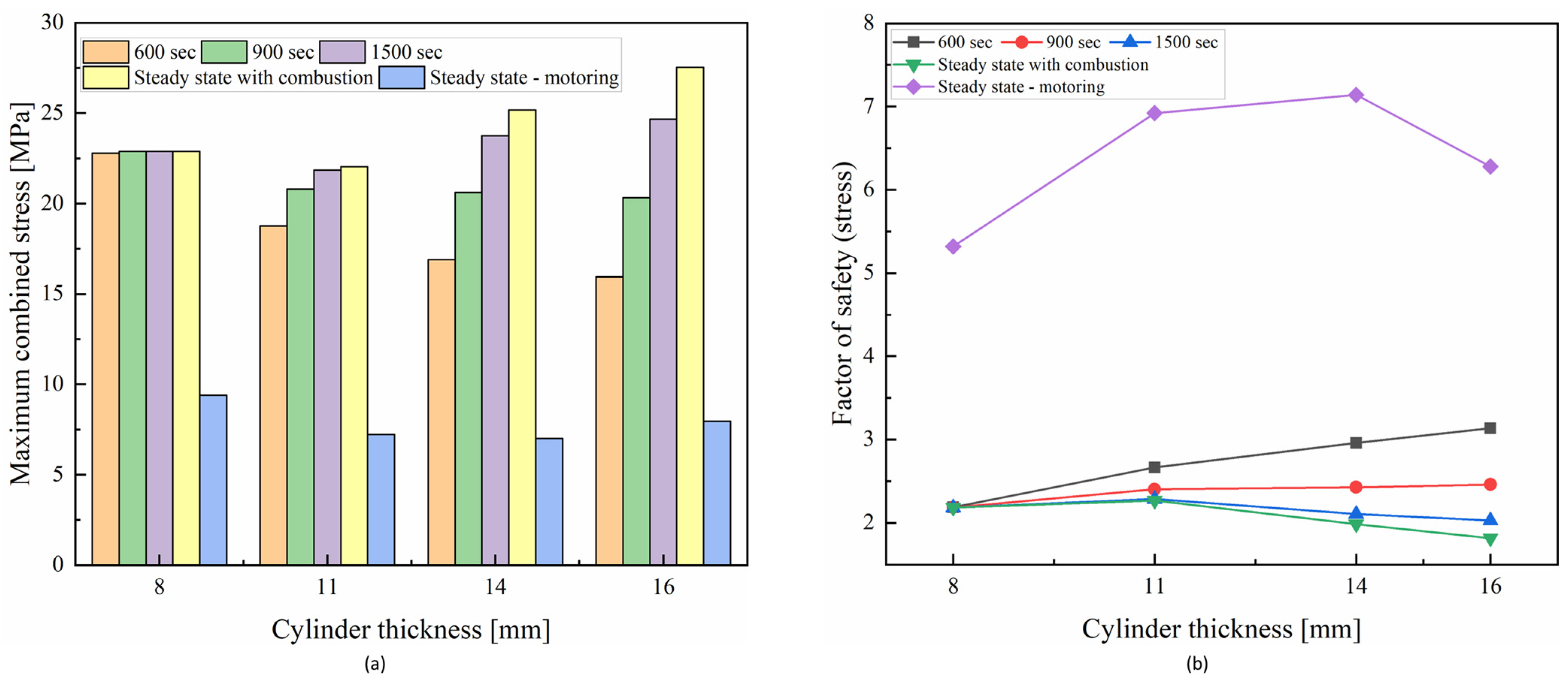
5.4. Effect of Different Engine Operating Times: Transient Analysis for the Quartz Cylinder
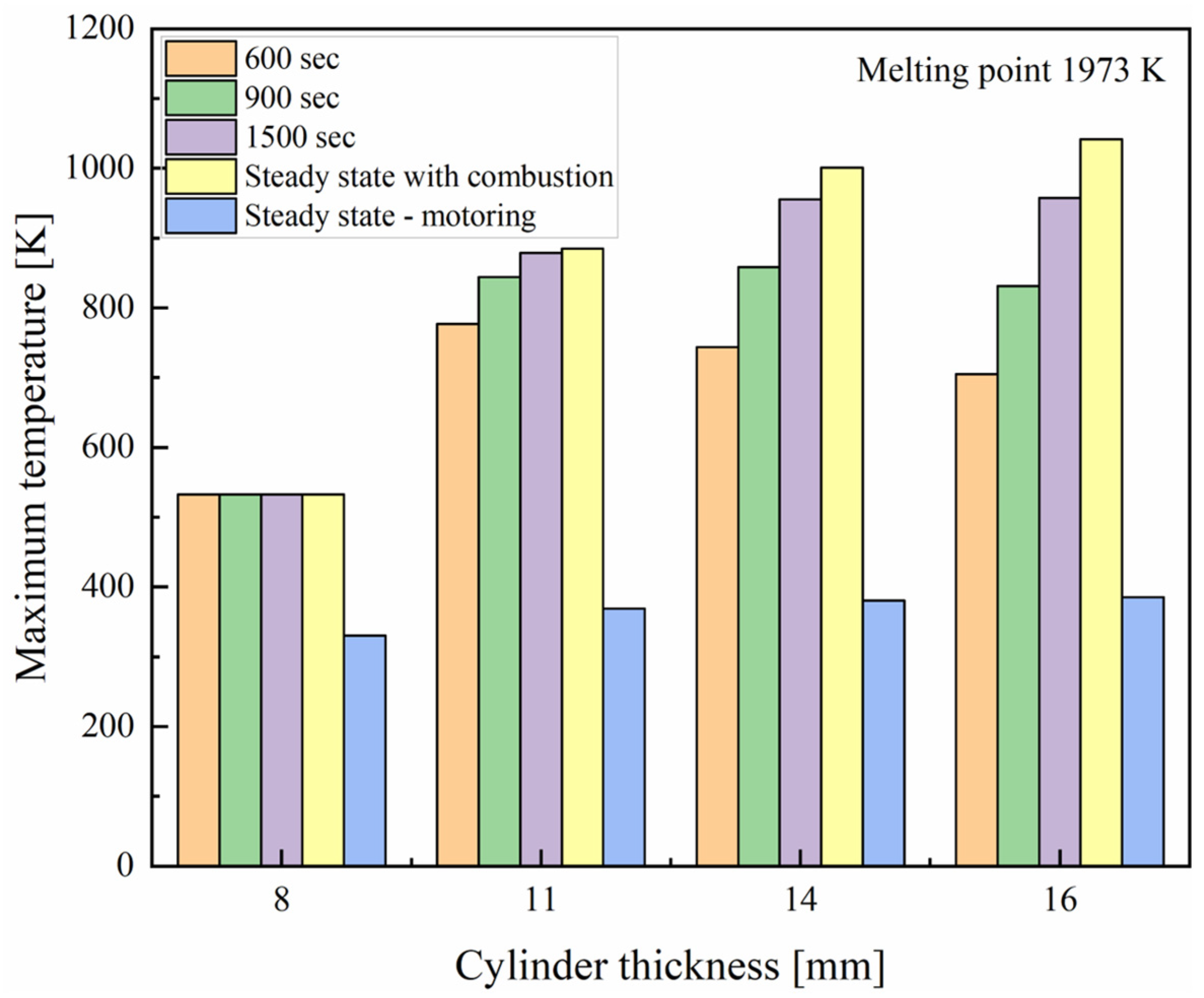
5.5. Selection of Optimum Thickness for the Quartz Cylinder and Piston Top
6. Conclusions
- For the various thicknesses considered of the quartz cylinder, the maximum temperature occurs at the top inner surface. These maximum temperatures are noted to be 532.7 K, 885 K, 1001 K and 1041 K for thicknesses of 8, 11, 14 and 16 mm, respectively. Also, the maximum temperature reduced in the transient analysis with early engine operating times. In the motoring case, the maximum temperature is found to be in the range of 330 K to 390 K for different thicknesses considered.
- In the case of combustion, the maximum combined stress within the 8 mm quartz cylinder thickness is 23.78 MPa, located on the inner top surface. In contrast, for all other thicknesses, the maximum combined stress is situated at the outer surface because of the dominant thermal stresses. The lowest combined stress observed was 22.04 MPa in the 11 mm thick quartz cylinder, attributed to the trade-off between thermal and mechanical stresses.
- Considering the case with combustion, the maximum combined stress within the 8 mm (thick) quartz cylinder is found to be 23.78 MPa, located at the inner top surface. In contrast, for all other thicknesses, the maximum combined stress is situated at the outer surface because of the dominant thermal stresses. The maximum combined stress (22.04 MPa) was lowest for the 11 mm thick cylinder compared to other thicknesses considered, attributed to the trade-off between thermal and mechanical stresses.
- For all the thicknesses of the quartz cylinder considered, there is no substantial variation in the maximum displacement at the inner surface.
- Lower combined stresses are reported during early engine operating times based on the transient study. As a result, a higher factor of safety occurs during lower operating times. Based on the steady-state and transient analyses, an 11 mm thickness was selected as the optimum thickness for the quartz cylinder.
- The maximum combined stress in the quartz piston top did not vary much with its thickness variation. The thickness was then calculated using Grashoff’s formula for the quartz piston top, and 8.5 mm was chosen as the optimum thickness in the present study.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Henriot, S.; Chaouche, A.; Chevé, E.; Duclos, J.M.; Leduc, P.; Ménégazzi, P.; Monnier, G.; Ranini, A. NSDI-3: A Small Bore GDI Engine; SAE: Warrendale, PA, USA, 1999. [Google Scholar]
- Cecere, G.; Irimescu, A.; Merola, S.S.; Rolando, L.; Millo, F. Lean Burn Flame Kernel Characterization for Different Spark Plug Designs and Orientations in an Optical GDI Engine. Energies 2022, 15, 3393. [Google Scholar] [CrossRef]
- Cho, K.; Grover, R.O., Jr.; Assanis, D.; Filipi, Z.; Szekely, G.; Najt, P.; Rask, R. Combining instantaneous temperature measurements and CFD for analysis of fuel impingement on the DISI engine piston top. J. Eng. Gas Turbines Power 2010, 132, 072805. [Google Scholar] [CrossRef]
- Jose, J.; Parsi, A.; Shridhara, S.; Mittal, M.; Ramesh, A. Effect of Fuel Injection Timing on the Mixture Preparation in a Small Gasoline Direct-Injection Engine; SAE: Warrendale, PA, USA, 2018. [Google Scholar]
- Kim, J.; Chung, J.; Kim, N.; Cho, S.; Lee, J.; Oh, S.; Song, C.; Min, K. Numerical investigation of soot emission sources in a direct-injection spark-ignition engine based on comprehensive breakup model validation. Int. J. Engine Res. 2023, 24, 217–239. [Google Scholar] [CrossRef]
- Nayek, S.; Mittal, M. Mixture Distribution in Spark Ignited Port Fuel Injection Engines: A Review. J. Eng. Gas Turbines Power 2023, 145, 70801. [Google Scholar]
- Jose, J.V.; Thakur, H.; Mittal, M.; Ramesh, A. A Computational Study on the Effect of Injector Location on the Performance of a Small Spark-Ignition Engine Modified to Operate under the Direct-Injection Mode; SAE: Warrendale, PA, USA, 2020. [Google Scholar]
- Jose, J.V.; Mittal, M.; Ramesh, A. Development of a small-bore gasoline direct-injection engine, and enhancement of its performance using multiple-injection strategies. SAE Int. J. Engines 2021, 14, 115–134. [Google Scholar] [CrossRef]
- Honda, T.; Kawamoto, M.; Katashiba, H.; Sumida, M.; Fukutomi, N.; Kawajiri, K. A Study of Mixture Formation and Combustion for Spray Guided DISI; SAE: Warrendale, PA, USA, 2004. [Google Scholar]
- El-Adawy, M.; Heikal, M.R.; Aziz, A.R.A.; Adam, I.K.; Ismael, M.A.; Babiker, M.E.; Baharom, M.B.; Firmansyah; Abidin, E.Z.Z. On the Application of Proper Orthogonal Decomposition (POD) for In-Cylinder Flow Analysis. Energies 2018, 11, 2261. [Google Scholar] [CrossRef]
- Mittal, M.; Mehta, P. Design Features of Optically Accessible Engines for Flow and Combustion Studies—A Review; SAE: Warrendale, PA, USA, 2018. [Google Scholar]
- Richman, R.M.; Reynolds, W.C. The Development of a Transparent Cylinder Engine for Piston Engine Fluid Mechanics Research; SAE: Warrendale, PA, USA, 1984. [Google Scholar]
- Bowditch, F.W. A New Tool for Combustion Research a Quartz Piston Engine; SAE: Warrendale, PA, USA, 1961. [Google Scholar]
- Nakanishi, K.; Hirano, T.; Inoue, T.; Ohigashi, S. The effects of charge dilution on combustion and its improvement—Flame photograph study. SAE Trans. 1975, 84, 352–364. [Google Scholar]
- Holtman, R.L.; McClure, P.B.; Detroit Diesel Allison, Indianapolis, Indiana. Private Communication, 1978.
- Bates, S.C. A transparent engine for flow and combustion visualization studies. SAE Trans. 1988, 97, 892–907. [Google Scholar]
- Lee, K.S.; Assanis, D.N. Thermo-mechanical analysis of optically accessible quartz cylinder under fired engine operation. Int. J. Automot. Technol. 2000, 1, 79–87. [Google Scholar]
- Lowe, A.S.H.; Morel, T. A new generation of tools for accurate thermo-mechanical finite element analyses of engine components. SAE Trans. 1992, 101, 1380–1395. [Google Scholar]
- Roy, S.; Ganesh, N.; Kumarasamy, A.; Viswanathan, P. Thermomechanical Analysis of a Cylindrical Liner. In The Advances in Engineering Design and Simulation: Select Proceedings of NIRC 2018; Springer: Singapore, 2020; pp. 33–40. [Google Scholar]
- Javanmardi, D.; Rezvani, M.A. Thermomechanical fracture failure analysis of a heavy-duty diesel engine cylinder liner through performance analysis and finite element modeling. SAE Int. J. Engines 2020, 13, 665–684. [Google Scholar] [CrossRef]
- Barbieri, S.G.; Giacopini, M.; Mangeruga, V.; Bianco, L.; Mastrandrea, L.N. A Simplified Methodology for the Analysis of the Cylinder Liner Bore Distortion: Finite Element Analyses and Experimental Validations; SAE: Warrendale, PA, USA, 2019. [Google Scholar]
- Liu, X.F.; Wang, Y.; Liu, W.H. Finite element analysis of thermo-mechanical conditions inside the piston of a diesel engine. Appl. Therm. Eng. 2017, 119, 312–318. [Google Scholar] [CrossRef]
- Shinde, G.; Mittal, M.; Lakshminarasimhan, V. A Study of Cycle-To-Cycle Flow Variations in a Small Spark-Ignition Engine at Low Throttle Opening; SAE: Warrendale, PA, USA, 2018. [Google Scholar]
- Alam, A.; Mittal, M.; Lakshminarasimhan, V. Analysis of In-Cylinder Flow and Cycle-To-Cycle Flow Variations in a Small Spark-Ignition Engine at Different Throttle Openings; SAE: Warrendale, PA, USA, 2020. [Google Scholar]
- Tsiogkas, V.D.; Chraniotis, A.; Kolokotronis, D.; Tourlidakis, A. In-Cylinder Flow Measurements in a Transparent Spark Ignition Engine; SAE: Warrendale, PA, USA, 2019. [Google Scholar]
- Ge, P.; Hung, D.L.S. Investigation of cycle-to-cycle variation of in-cylinder engine swirl flow fields using quadruple proper orthogonal decomposition. J. Eng. Gas Turbines Power 2017, 139, 72803. [Google Scholar] [CrossRef]
- Tornatore, C.; Sjöberg, M. Optical Investigation of a Partial Fuel Stratification Strategy to Stabilize Overall Lean Operation of a DISI Engine Fueled with Gasoline and E30. Energies 2021, 14, 396. [Google Scholar] [CrossRef]
- Misul, D.; Baratta, M.; Xu, J.; Fuerhapter, A.; Heindl, R. Experimental and CFD Investigation of Fuel Mixing in an Optical-Access Direct-Injection NG Engine and Correlation with Test Rig Combustion and Performance Data. Energies 2023, 16, 3004. [Google Scholar] [CrossRef]
- Zhu, C.; Chakrapani, V.; Wooldridge, M. An In-Cylinder Imaging Study of Pre-Chamber Spark-Plug Flame Development in a Single-Cylinder Direct-Injection Spark-Ignition Engine; SAE: Warrendale, PA, USA, 2023. [Google Scholar]
- Aronsson, U.; Chartier, C.; Horn, U.; Andersson, Ö.; Johansson, B.; Egnell, R. Heat Release Comparison between Optical and All-Metal HSDI Diesel Engines; SAE: Warrendale, PA, USA, 2008. [Google Scholar]
- ABAQUS, A. 6.14, Abaqus 6.14 Anal. User’s Guid; Dassault Systemes Simulia Corp.: Providence, RI, USA, 2014; Volume 14. [Google Scholar]
- Pourhamid, R.; Ahmadian, M.T.; Mahdavy Moghaddam, H.; Mohammadzadeh, A.R. Mechanical analysis of a functionally graded cylinder-piston under internal pressure due to a combustion engine using a cylindrical super element and considering thermal loading. Sci. Iran. 2015, 22, 493–503. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Introduction to Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Carreño, R. A Comprehensive Methodology to Analyse the Global Energy Balance in Reciprocating Internal Combustion Engines. Doctoral Thesis, Universitat Politècnica de València, Valencia, Spain, 2016. [Google Scholar]
- Stokes, J.; Lake, T.H.; Osborne, R.J. A Gasoline Engine Concept for Improved Fuel Economy—The Lean Boost System; SAE Technical Papers; SAE: Warrendale, PA, USA, 2000. [Google Scholar] [CrossRef]
- Nagar, P.; Miers, S. Friction between piston and cylinder of an IC engine: A review. In Proceedings of the SAE 2011 World Congress and Exhibition, Detroit, MI, USA, 12–14 April 2011. [Google Scholar] [CrossRef]
- Kennedy, M.; Hoppe, S.; Esser, J. Piston Ring Coating Reduces Gasoline Engine Friction. MTZ Worldw. 2012, 73, 40–43. [Google Scholar] [CrossRef]
- Mittal, M.; Schock, H.; Zhu, G. In-Cylinder Combustion Visualization of a Direct-Injection Spark-Ignition Engine with Different Operating Conditions and Fuels; SAE: Warrendale, PA, USA, 2012. [Google Scholar]
- Garg, S.; Mittal, M.; Sahu, S.; Lakshminarasimhan, V. Measurement of Fuel Distribution in a Small PFI Spark-Ignition Engine Using Tracer PLIF; SAE: Warrendale, PA, USA, 2020. [Google Scholar]
- Dudareva, N.Y.; Enikeev, R.D.; Ivanov, V.Y. Thermal Protection of Internal Combustion Engines Pistons. Procedia Eng. 2017, 206, 1382–1387. [Google Scholar] [CrossRef]
- Espadafor, F.J.; Villanueva, J.B.; García, M.T.; Trujillo, E.C. Analysis of a diesel generator cylinder failure. Eng. Fail. Anal. 2010, 17, 913–925. [Google Scholar] [CrossRef]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill Education: New York, NY, USA, 2018. [Google Scholar]
- Wulf, W. Integral methods for two-phase flow in hydraulic systems. Adv. Heat Transf. 1998, 31, 105–158. [Google Scholar]
- Spalding, D.B. Heat and Mass Transfer in Gasoline and Diesel Engines. International Symposium 1987. In Archives of Heat Transfer; Hemisphere Publishing Corporation: London, UK, 1988. [Google Scholar]
- Young, W.C.; Budynas, R.G. Elastic Stability; Springer: Dordrecht, The Netherlands, 1980; Volume 4, ISBN 007072542X. [Google Scholar]
- Bhandari, V.B. Design of Machine Elements, 3rd ed.; Denett & Company: Nagpur, India, 2020. [Google Scholar]




| Property | Value |
|---|---|
| Ultimate tensile strength (MPa) | 50 |
| Young’s modulus (MPa) | 70 × 103 |
| Poisson’s ratio (−) | 0.16 |
| Thermal expansion coefficient (/°C) | 0.6 × 10−6 |
| Thermal conductivity (mW/mm−K) | 1.4 |
| Density (ton/mm3) | 2.2 × 109 |
| Melting point (K) | 1973 |
| Particulars | Details |
|---|---|
| Bore | 62 mm |
| Stroke | 66 mm |
| Displacement | 200 cm3 |
| Compression ratio | 9.6:1 |
| Length of the quartz cylinder | 92 mm |
| Diameter of the quartz piston top | 50 mm |
| Engine speed and load | 3000 rpm and WOT |
| 1.148 kg/h | |
| ) | 44 MJ/kg |
| Thickness (mm) | Maximum Combined Stress (MPa) | ||
|---|---|---|---|
| at 600 s | at 900 s | at 1500 s | |
| 8 | 22.78 | 22.78 | 22.78 |
| 11 | 18.77 | 20.8 | 21.85 |
| 14 | 16.89 | 20.6 | 23.75 |
| 16 | 15.95 | 20.33 | 24.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velugula, R.; Thiruvallur loganathan, B.; Varadhaiyengar, L.; Asvathanarayanan, R.; Mittal, M. An Analysis of Mechanical and Thermal Stresses, Temperature and Displacement within the Transparent Cylinder and Piston Top of a Small Direct-Injection Spark-Ignition Optical Engine. Energies 2023, 16, 7400. https://doi.org/10.3390/en16217400
Velugula R, Thiruvallur loganathan B, Varadhaiyengar L, Asvathanarayanan R, Mittal M. An Analysis of Mechanical and Thermal Stresses, Temperature and Displacement within the Transparent Cylinder and Piston Top of a Small Direct-Injection Spark-Ignition Optical Engine. Energies. 2023; 16(21):7400. https://doi.org/10.3390/en16217400
Chicago/Turabian StyleVelugula, Ravi, Balasubramanian Thiruvallur loganathan, Lakshminarasimhan Varadhaiyengar, Ramesh Asvathanarayanan, and Mayank Mittal. 2023. "An Analysis of Mechanical and Thermal Stresses, Temperature and Displacement within the Transparent Cylinder and Piston Top of a Small Direct-Injection Spark-Ignition Optical Engine" Energies 16, no. 21: 7400. https://doi.org/10.3390/en16217400
APA StyleVelugula, R., Thiruvallur loganathan, B., Varadhaiyengar, L., Asvathanarayanan, R., & Mittal, M. (2023). An Analysis of Mechanical and Thermal Stresses, Temperature and Displacement within the Transparent Cylinder and Piston Top of a Small Direct-Injection Spark-Ignition Optical Engine. Energies, 16(21), 7400. https://doi.org/10.3390/en16217400






