Coupled Effects of Lorentz Force, Radiation, and Dissipation on the Dynamics of a Hybrid Nanofluid over an Exponential Stretching Sheet
Abstract
:1. Introduction
- What impact do the relevant parameters have on the flow profiles?
- What changes occur in the heat transfer rate due to the hybrid nanofluid?
- What are the impacts of the critical parameters on the physical quantities?
2. Mathematical Formulation
| Goud et al. [33] | Ishak et al. [36] | Bidin et al. [38] | Current Results | |||
|---|---|---|---|---|---|---|
| 0.0 | 0 | 1.0 | 0.954784 | 0.9548 | 0.9547 | 0.9548106 |
| 2.0 | 1.471462 | 1.4715 | 1.4714 | 1.4714540 | ||
| 3.0 | 1.869073 | 1.8691 | 1.8691 | 1.8690688 | ||
| 5.0 | 2.500111 | 2.5001 | 2.5001280 | |||
| 10.0 | 3.660346 | 3.6604 | 3.6603693 | |||
| 1.0 | 1.0 | 0.861097 | 0.8611 | 0.8615086 | ||
| 1.0 | 0.0 | 0.53117 | 0.5312 | 0 | 0.5313112 | |
| 1.0 | 0.450687 | 0.4505 | 0 | 0.4506955 |
3. Implementation of the Method
4. Validation of the Numerical Scheme
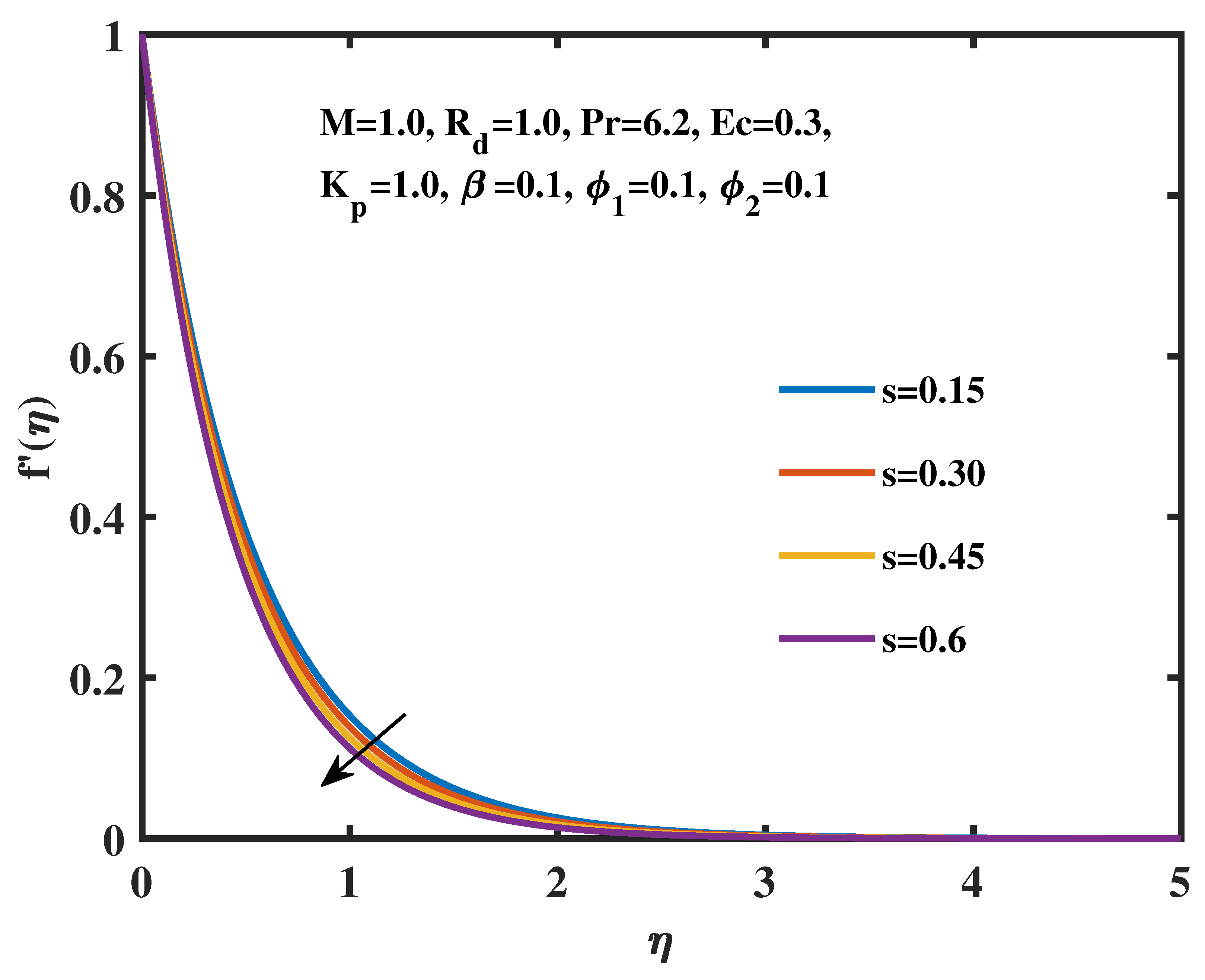
5. Results and Discussion
6. Conclusions
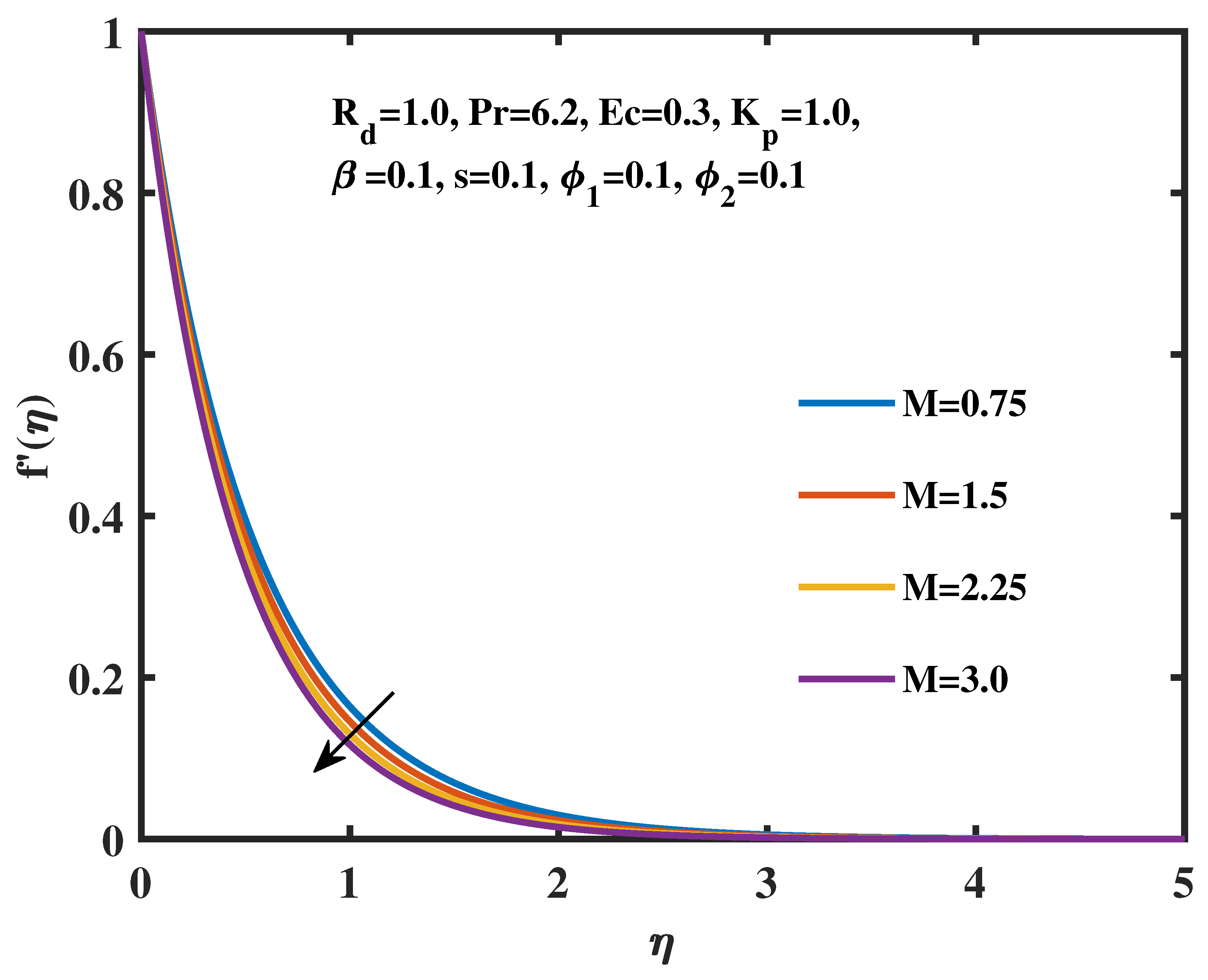
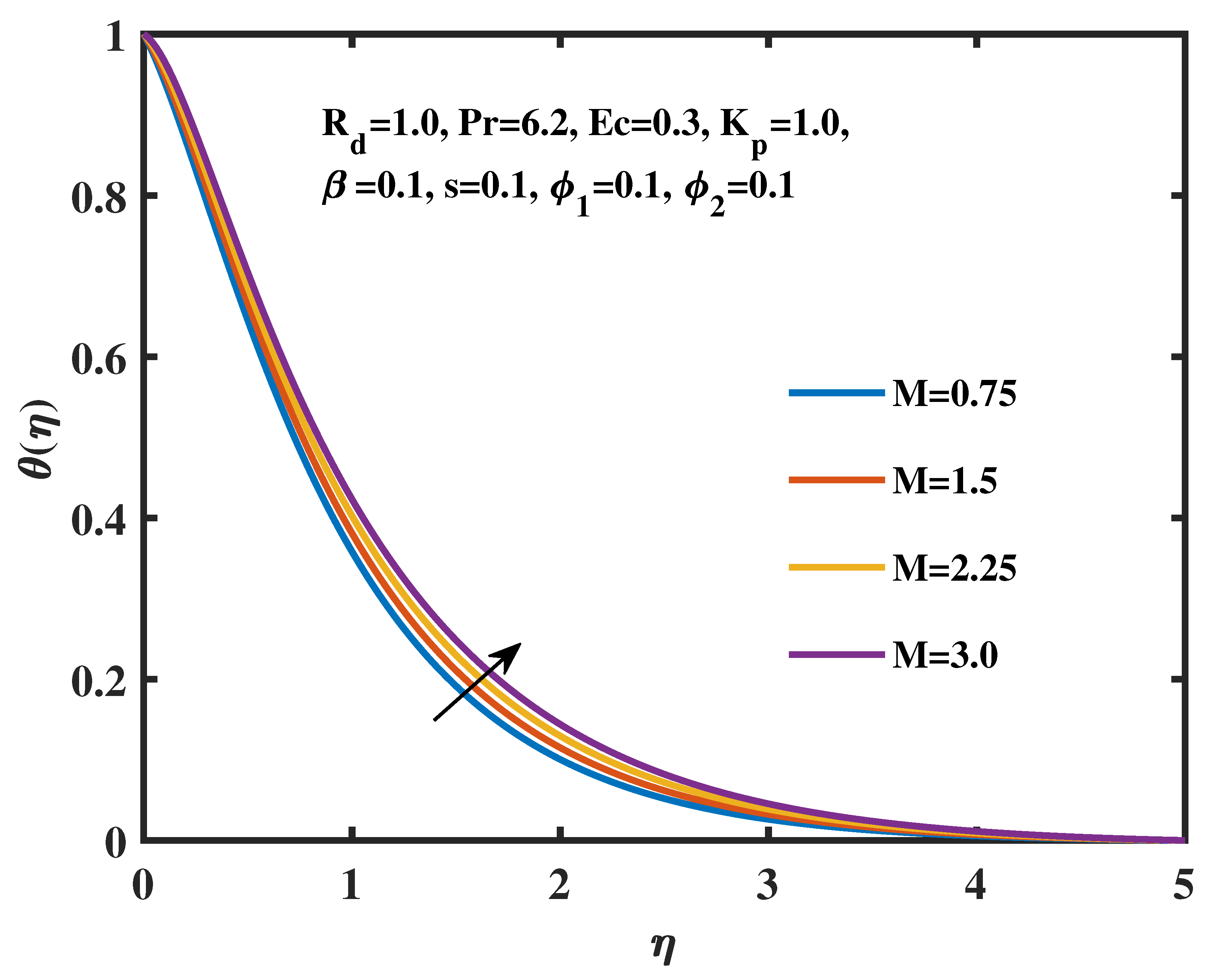
- The velocity profile is adversely affected by the magnetic field, whereas the temperature is positively impacted.
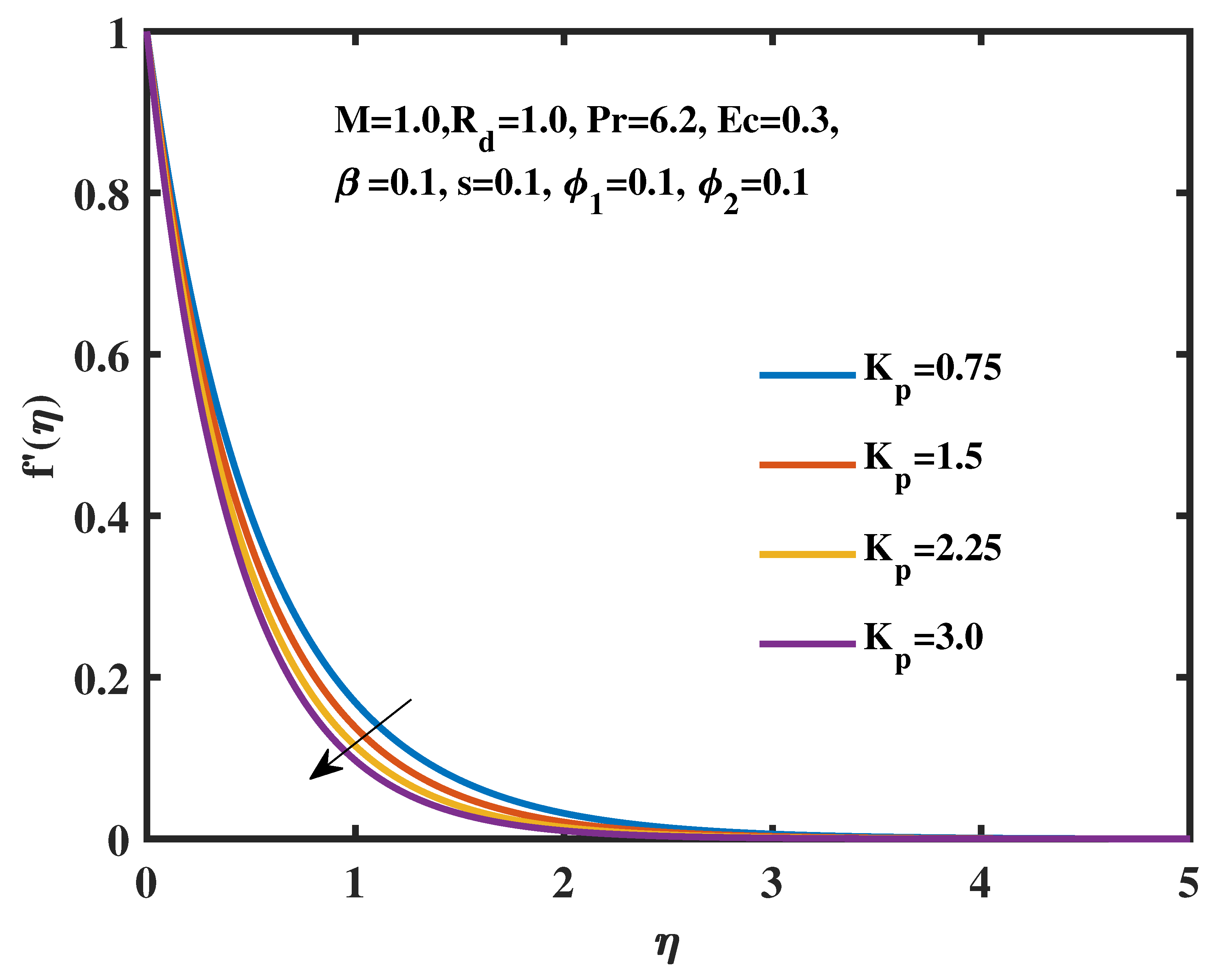
- The velocity profile is lowered by an increase in the porosity parameter, while the temperature is increased.
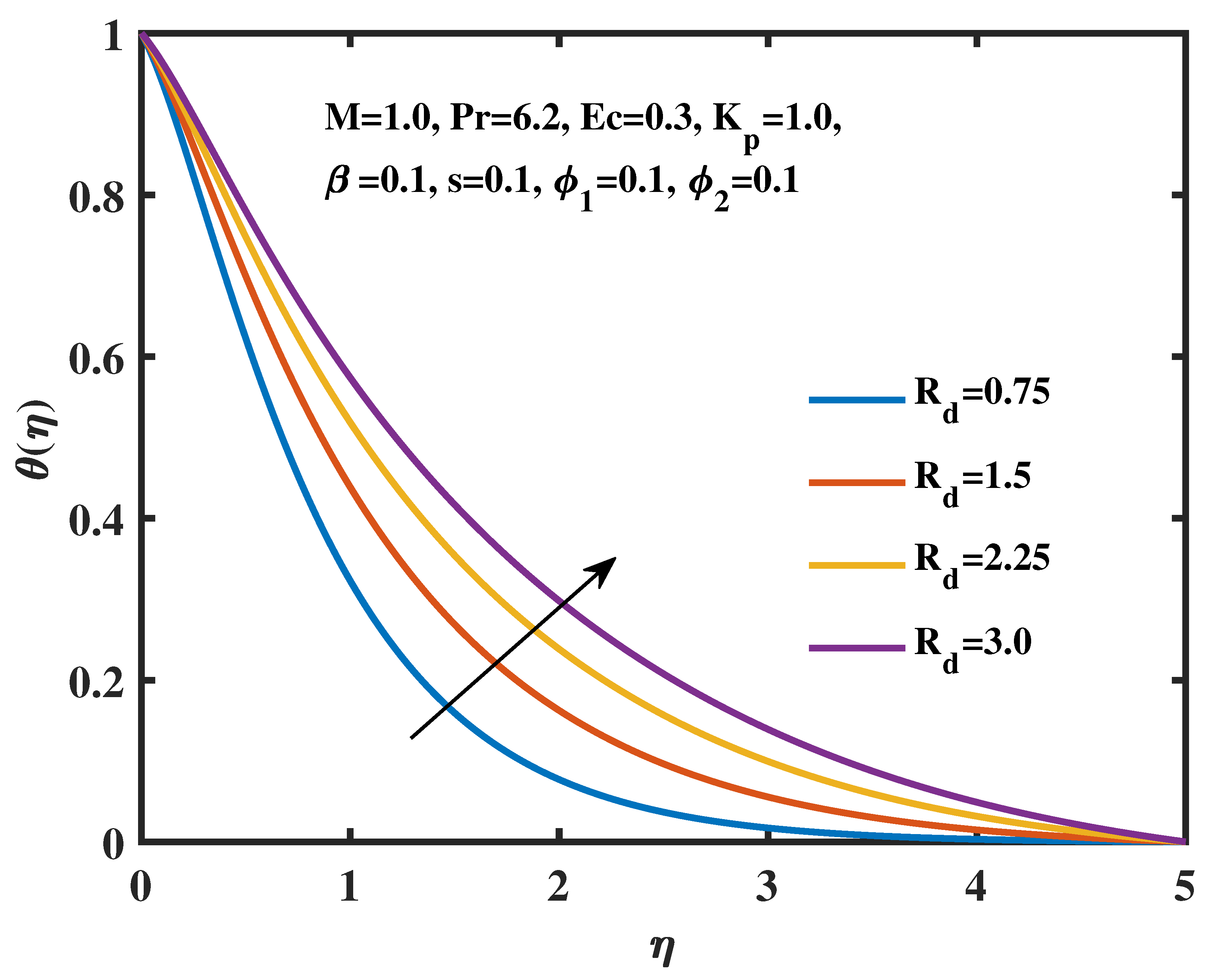
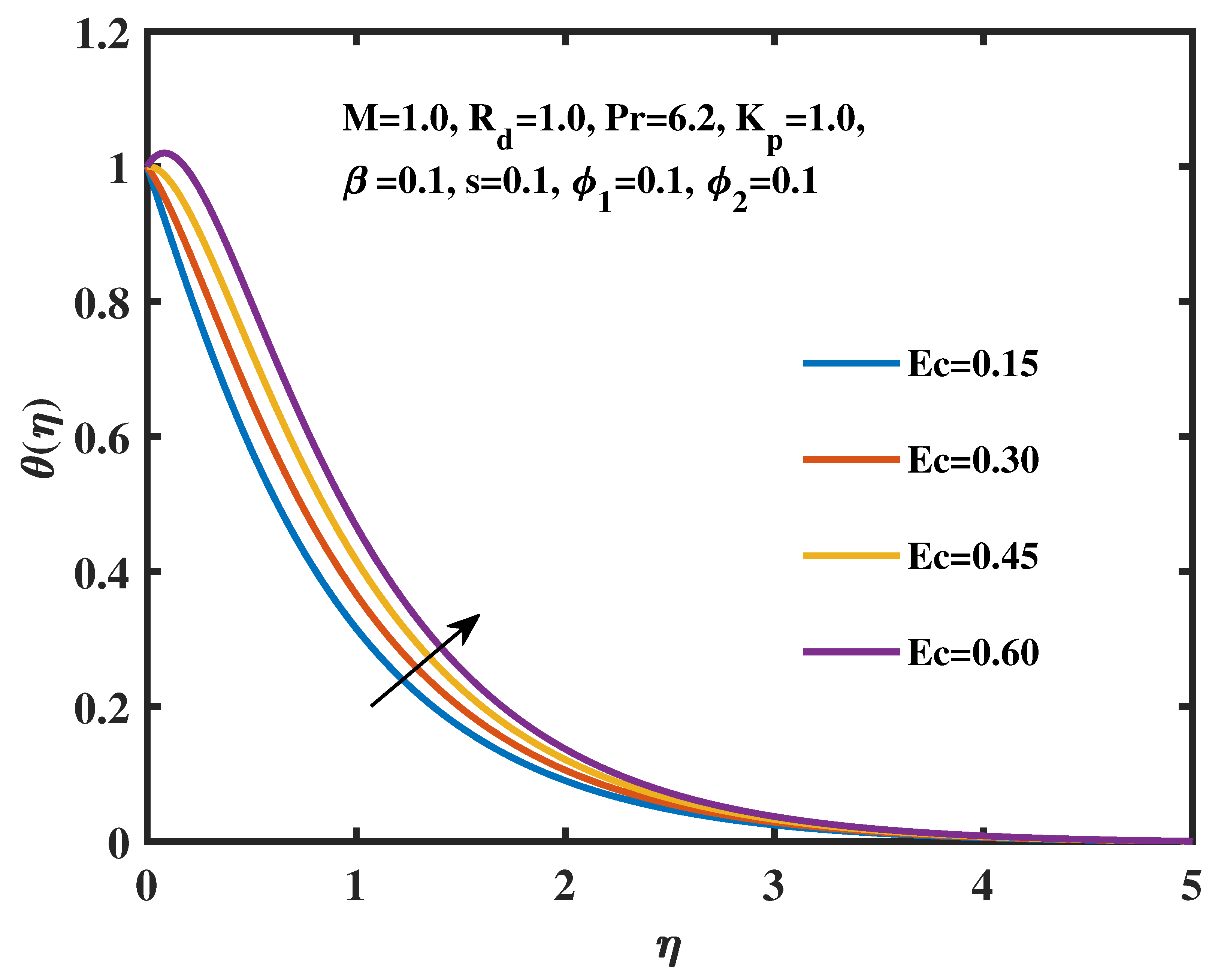
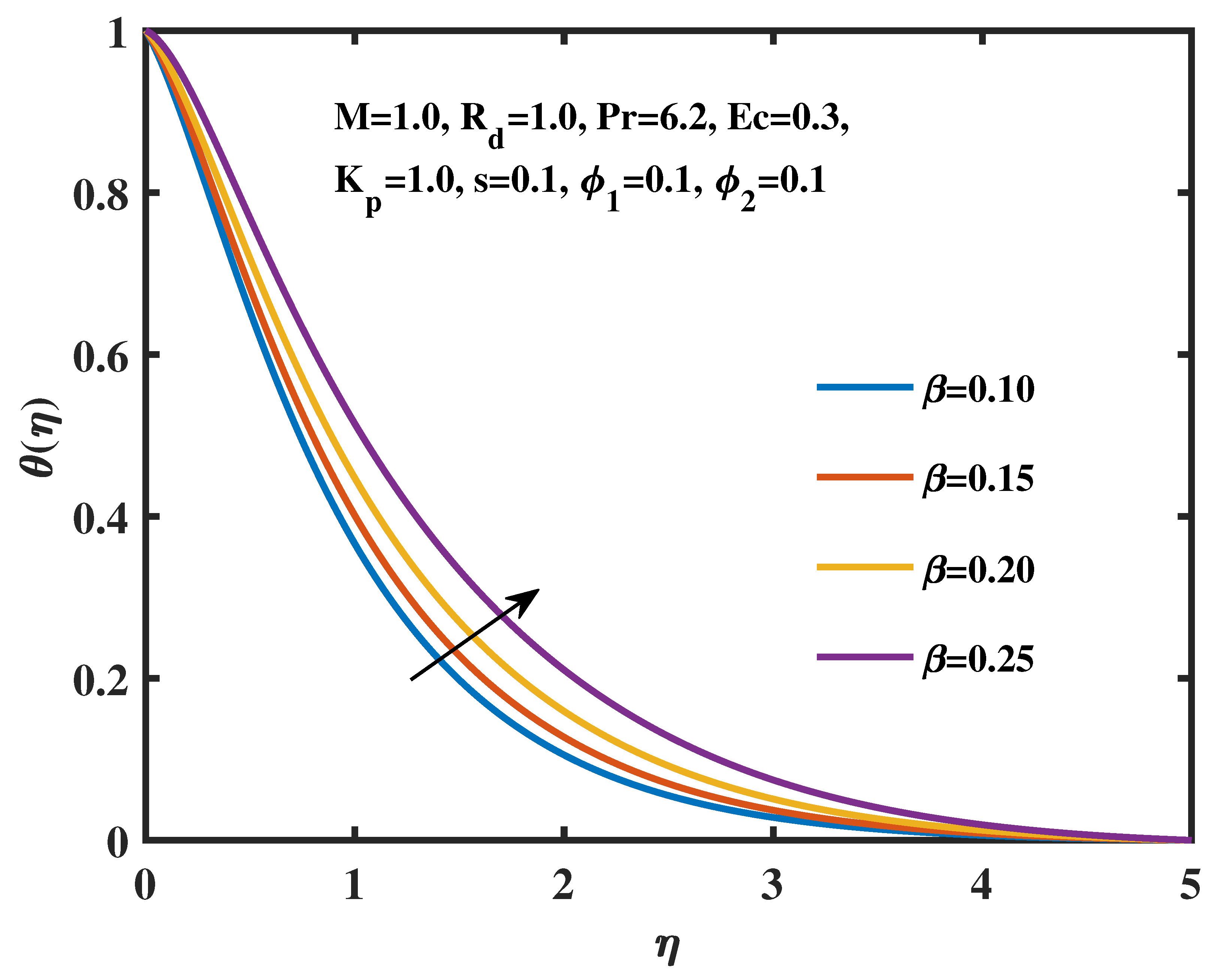
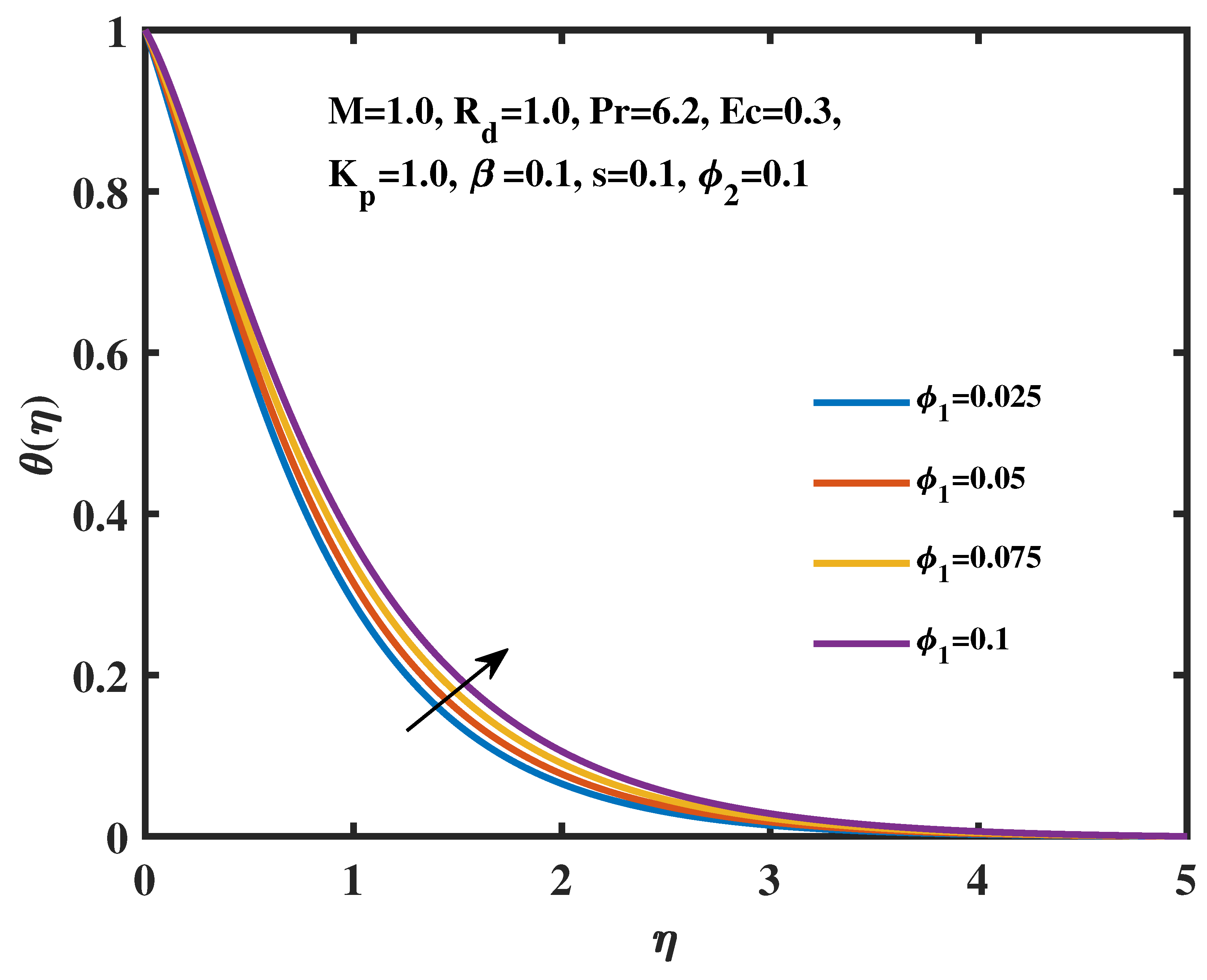
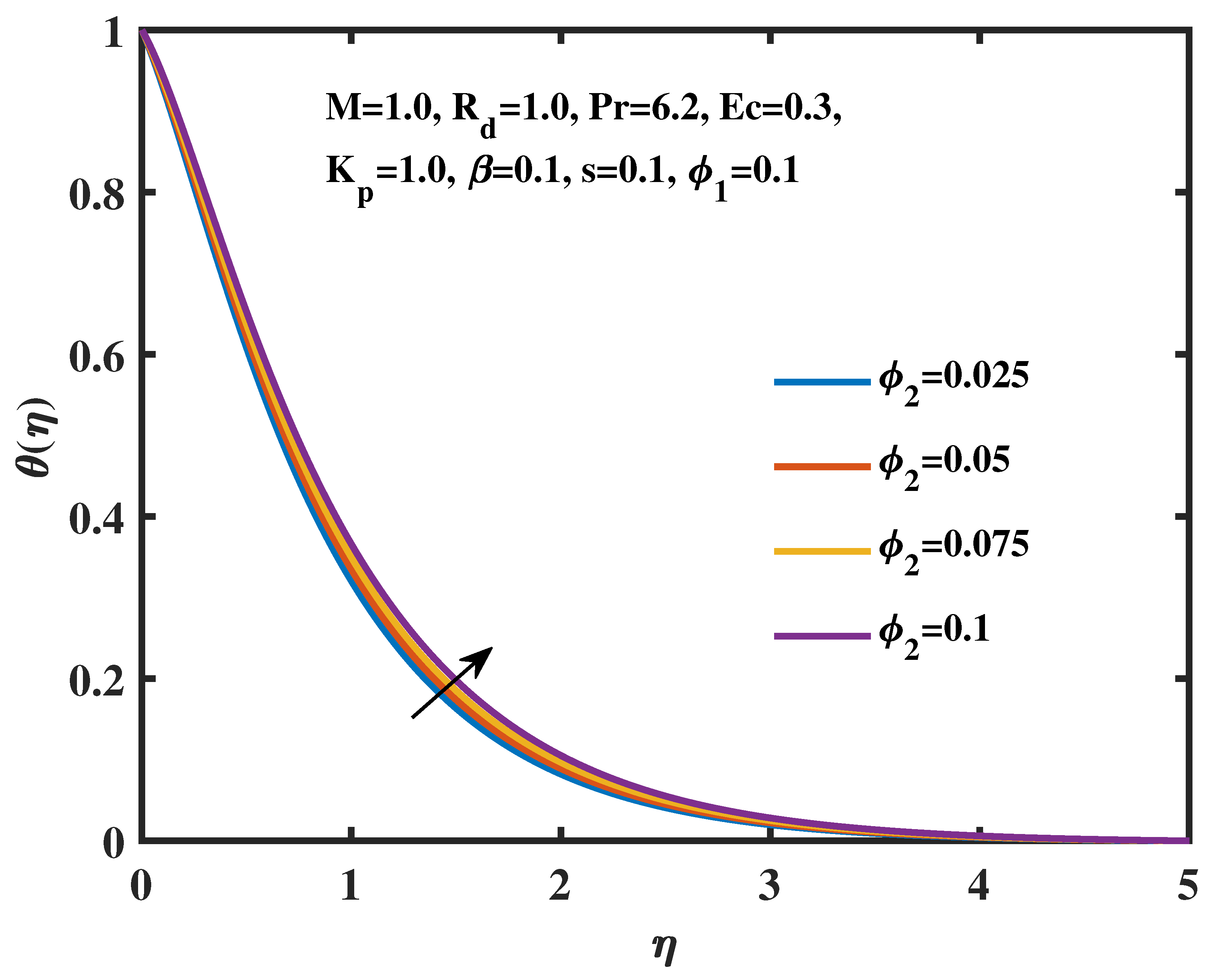
- The temperature profiles are proportional to the changes in the radiation parameter, magnetic field parameter, Eckert number, and volume fractions of TiO2 and Ag nanoparticles.
- The magnetic, suction, and porosity parameters are all inversely linked to the drag coefficient, as are the volume fractions of TiO2 and Ag nanoparticles.
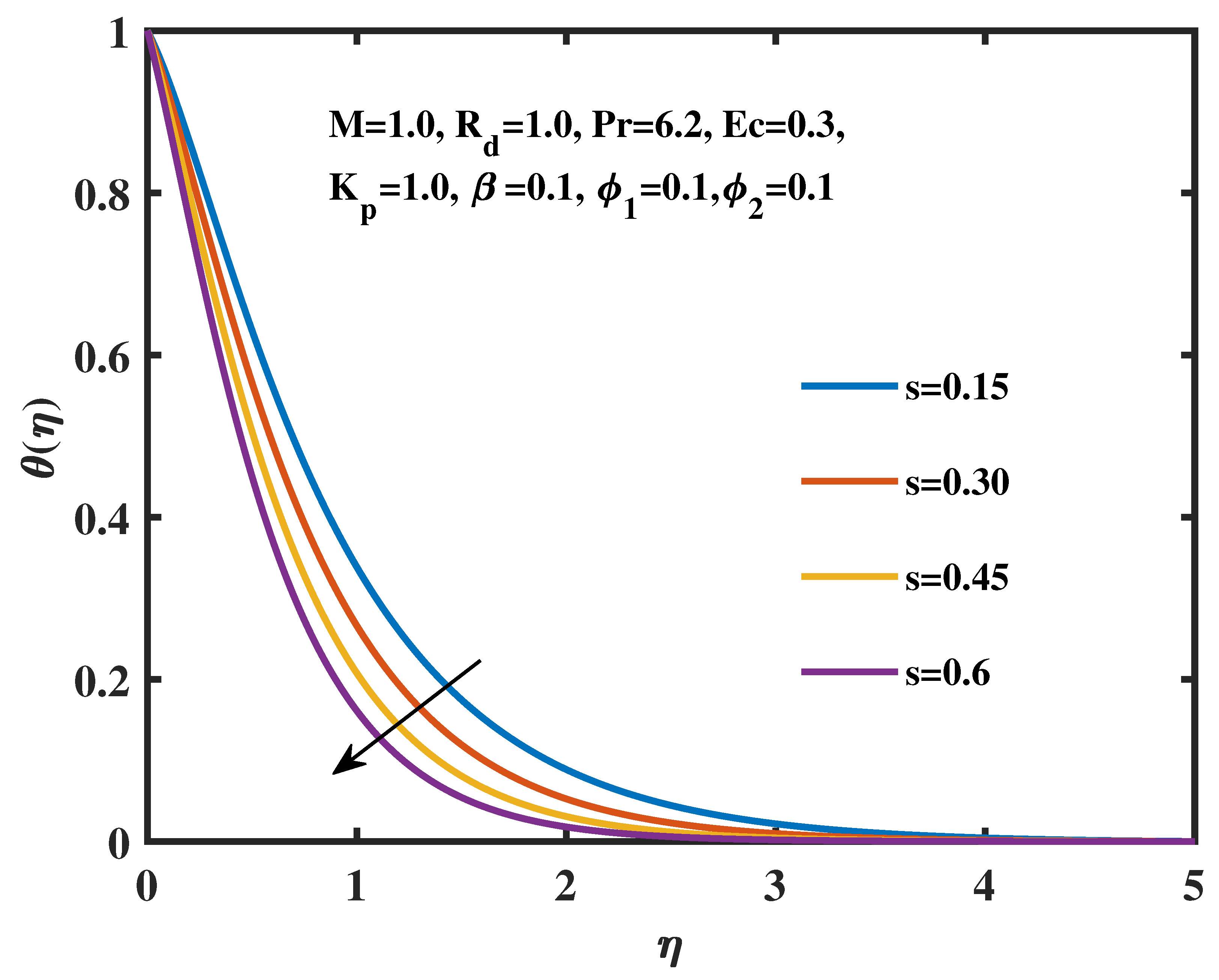
- The radiation parameter has a positive correlation with the heat transfer rate, while the magnetic parameter, heat source parameter, viscous dissipation parameter, and volume fractions of TiO2 and Ag nanoparticles all have negative correlations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Technical Report; Argonne National Lab: Argonne, IL, USA, 1995. [Google Scholar]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Qayyum, S.; Alsaedi, A. Entropy generation in flow with silver and copper nanoparticles. Colloids Surfaces A Physicochem. Eng. Asp. 2018, 539, 335–346. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Haq, R.U.; Khan, Z. Radiation effects on MHD stagnation point flow of nano fluid towards a stretching surface with convective boundary condition. Chin. J. Aeronaut. 2013, 26, 1389–1397. [Google Scholar] [CrossRef]
- Mustafa, I.; Javed, T.; Ghaffari, A. Heat transfer in MHD stagnation point flow of a ferrofluid over a stretchable rotating disk. J. Mol. Liq. 2016, 219, 526–532. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B.; Nandeppanavar, M.M. MHD stagnation point flow and heat transfer due to nanofluid towards a stretching sheet. Int. J. Heat Mass Transf. 2013, 56, 1–9. [Google Scholar] [CrossRef]
- Mathews, J.; Hymavathi, T. Magnetohydrodynamic stagnation point flow and heat transfer effects of Al2O3-Cu/water hybrid nanofluid over a porous stretching surface. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2023, 237, 1064–1072. [Google Scholar] [CrossRef]
- Javed, T.; Ghaffari, A.; Ahmad, H. Numerical study of unsteady MHD oblique stagnation point flow with heat transfer over an oscillating flat plate. Can. J. Phys. 2015, 93, 1138–1143. [Google Scholar] [CrossRef]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Devi, S.A. Numerical investigation of three-dimensional hybrid Cu-Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 2016, 94, 490–496. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N.; Pop, I. Magnetohydrodynamics (MHD) axisymmetric flow and heat transfer of a hybrid nanofluid past a radially permeable stretching/shrinking sheet with Joule heating. Chin. J. Phys. 2020, 64, 251–263. [Google Scholar] [CrossRef]
- Leong, K.Y.; Razali, I.; Ahmad, K.K.; Ong, H.C.; Ghazali, M.J.; Rahman, M.R.A. Thermal conductivity of an ethylene glycol/water-based nanofluid with copper-titanium dioxide nanoparticles: An experimental approach. Int. Commun. Heat Mass Transf. 2018, 90, 23–28. [Google Scholar] [CrossRef]
- Gul, T.; Saeed, A. Nonlinear mixed convection couple stress tri-hybrid nanofluids flow in a Darcy–Forchheimer porous medium over a nonlinear stretching surface. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Basit, A.; Asjad, M.I.; Akgül, A. Convective flow of a fractional second grade fluid containing different nanoparticles with Prabhakar fractional derivative subject to non-uniform velocity at the boundary. Math. Methods Appl. Sci. 2023, 46, 8148–8159. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.; Anusha, T.; Hatami, M. The MHD Newtonian hybrid nanofluid flow and mass transfer analysis due to super-linear stretching sheet embedded in porous medium. Sci. Rep. 2021, 11, 22518. [Google Scholar] [CrossRef] [PubMed]
- Kayalvizhi, J.; Vijaya Kumar, A. Entropy Analysis of EMHD Hybrid Nanofluid Stagnation Point Flow over a Porous Stretching Sheet with Melting Heat Transfer in the Presence of Thermal Radiation. Energies 2022, 15, 8317. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Liu, D.; Abid, M.; Imran, M.; Muhammad, T. Heat transfer analysis of hybrid nanofluid flow with thermal radiation through a stretching sheet: A comparative study. Int. Commun. Heat Mass Transf. 2022, 138, 106303. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D Appl. Phys. 1999, 32, 577. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A.; Farooq, M. Numerical simulation for melting heat transfer and radiation effects in stagnation point flow of carbon–water nanofluid. Comput. Methods Appl. Mech. Eng. 2017, 315, 1011–1024. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.; Ismail, A.M. MHD flow over exponential radiating stretching sheet using homotopy analysis method. J. King Saud Univ.-Eng. Sci. 2017, 29, 68–74. [Google Scholar] [CrossRef]
- Zaib, A.; Bhattacharyya, K.; Shafie, S. Unsteady boundary layer flow and heat transfer over an exponentially shrinking sheet with suction in a copper-water nanofluid. J. Cent. South Univ. 2015, 22, 4856–4863. [Google Scholar] [CrossRef]
- Abd El-Aziz, M. Viscous dissipation effect on mixed convection flow of a micropolar fluid over an exponentially stretching sheet. Can. J. Phys. 2009, 87, 359–368. [Google Scholar] [CrossRef]
- Dessie, H.; Kishan, N. MHD effects on heat transfer over stretching sheet embedded in porous medium with variable viscosity, viscous dissipation and heat source/sink. Ain Shams Eng. J. 2014, 5, 967–977. [Google Scholar] [CrossRef]
- Cortell, R. Effects of viscous dissipation and radiation on the thermal boundary layer over a nonlinearly stretching sheet. Phys. Lett. A 2008, 372, 631–636. [Google Scholar] [CrossRef]
- Rafique, K.; Mahmood, Z.; Alqahtani, H.; Eldin, S.M. Various nanoparticle shapes and quadratic velocity impacts on entropy generation and MHD flow over a stretching sheet with joule heating. Alex. Eng. J. 2023, 71, 147–159. [Google Scholar] [CrossRef]
- Alharbi, K.A.M.; Farooq, U.; Waqas, H.; Imran, M.; Noreen, S.; Akgül, A.; Baleanu, D.; El Din, S.M.; Abbas, K. Numerical solution of Maxwell-Sutterby nanofluid flow inside a stretching sheet with thermal radiation, exponential heat source/sink, and bioconvection. Int. J. Thermofluids 2023, 18, 100339. [Google Scholar] [CrossRef]
- Yirga, Y.; Tesfay, D. Heat and mass transfer in MHD flow of nanofluids through a porous media due to a permeable stretching sheet with viscous dissipation and chemical reaction effects. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2015, 9, 1–8. [Google Scholar]
- Hayat, T.; Abbas, Z.; Javed, T. Mixed convection flow of a micropolar fluid over a non-linearly stretching sheet. Phys. Lett. A 2008, 372, 637–647. [Google Scholar] [CrossRef]
- Haroun, N.A.; Mondal, S.; Sibanda, P. Hydromagnetic nanofluids flow through a porous medium with thermal radiation, chemical reaction and viscous dissipation using the spectral relaxation method. Int. J. Comput. Methods 2019, 16, 1840020. [Google Scholar] [CrossRef]
- Acharya, N.; Das, K.; Kumar Kundu, P. Ramification of variable thickness on MHD TiO2 and Ag nanofluid flow over a slendering stretching sheet using NDM. Eur. Phys. J. Plus 2016, 131, 303. [Google Scholar] [CrossRef]
- Goud, B.S.; Srilatha, P.; Bindu, P.; Krishna, Y.H. Radiation effect on MHD boundary layer flow due to an exponentially stretching sheet. Adv. Math. Sci. J. 2020, 9, 10755–10761. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow induced by an exponentially shrinking sheet. Chin. J. Phys. 2020, 68, 468–482. [Google Scholar] [CrossRef]
- Rosseland, S. Astrophysics and Atomic Theoretical Foundations; Springer: Berlin/Heidelberg, Germany, 1931. [Google Scholar]
- Ishak, A. MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malays. 2011, 40, 391–395. [Google Scholar]
- Bhattacharyya, K. Boundary layer flow and heat transfer over an exponentially shrinking sheet. Chin. Phys. Lett. 2011, 28, 074701. [Google Scholar] [CrossRef]
- Bidin, B.; Nazar, R. Numerical solution of the boundary layer flow over an exponentially stretching sheet with thermal radiation. Eur. J. Sci. Res. 2009, 33, 710–717. [Google Scholar]
- Versaci, M.; Jannelli, A.; Angiulli, G. Electrostatic micro-electro-mechanical-systems (MEMS) devices: A comparison among numerical techniques for recovering the membrane profile. IEEE Access 2020, 8, 125874–125886. [Google Scholar] [CrossRef]
- Mandal, I.C.; Mukhopadhyay, S. Heat transfer analysis for fluid flow over an exponentially stretching porous sheet with surface heat flux in porous medium. Ain Shams Eng. J. 2013, 4, 103–110. [Google Scholar] [CrossRef]
- Naramgari, S.; Sulochana, C. Dual solutions of radiative MHD nanofluid flow over an exponentially stretching sheet with heat generation/absorption. Appl. Nanosci. 2016, 6, 131–139. [Google Scholar] [CrossRef]


| Properties | Hybrid Nanofluid |
|---|---|
| Dynamic Viscosity | |
| Density | |
| Electrical Conductivity | |
| Specific Heat | |
| Thermal Conductivity | , where and |
| 0.5 | 1.0 | 0.1 | 0.1 | 0.1 | −3.2211 |
| 1.0 | 1.0 | 0.1 | 0.1 | 0.1 | −3.3551 |
| 1.5 | 1.0 | 0.1 | 0.1 | 0.1 | −3.4836 |
| 2.0 | 1.0 | 0.1 | 0.1 | 0.1 | −3.6073 |
| 1.0 | 0.5 | 0.1 | 0.1 | 0.1 | −3.1246 |
| 1.0 | 1.0 | 0.1 | 0.1 | 0.1 | −3.3551 |
| 1.0 | 1.5 | 0.1 | 0.1 | 0.1 | −3.5699 |
| 1.0 | 2.0 | 0.1 | 0.1 | 0.1 | −3.7719 |
| 1.0 | 1.0 | 0.1 | 0.1 | 0.1 | −3.3551 |
| 1.0 | 1.0 | 0.2 | 0.1 | 0.1 | −3.4634 |
| 1.0 | 1.0 | 0.3 | 0.1 | 0.1 | −3.5754 |
| 1.0 | 1.0 | 0.4 | 0.1 | 0.1 | −3.6911 |
| 1.0 | 1.0 | 0.1 | 0.01 | 0.1 | −2.5458 |
| 1.0 | 1.0 | 0.1 | 0.02 | 0.1 | −2.6292 |
| 1.0 | 1.0 | 0.1 | 0.03 | 0.1 | −2.7140 |
| 1.0 | 1.0 | 0.1 | 0.04 | 0.1 | −2.8003 |
| 1.0 | 1.0 | 0.1 | 0.1 | 0.01 | −2.8315 |
| 1.0 | 1.0 | 0.1 | 0.1 | 0.02 | −2.8848 |
| 1.0 | 1.0 | 0.1 | 0.1 | 0.03 | −2.9392 |
| 1.0 | 1.0 | 0.1 | 0.1 | 0.04 | −2.9947 |
| 0.5 | 0.3 | 1.0 | 0.1 | 0.1 | 0.1 | 1.3487 |
| 1.0 | 0.3 | 1.0 | 0.1 | 0.1 | 0.1 | 1.1466 |
| 1.5 | 0.3 | 1.0 | 0.1 | 0.1 | 0.1 | 0.9518 |
| 1.0 | 0.1 | 1.0 | 0.1 | 0.1 | 0.1 | 2.8107 |
| 1.0 | 0.2 | 1.0 | 0.1 | 0.1 | 0.1 | 1.9786 |
| 1.0 | 0.3 | 1.0 | 0.1 | 0.1 | 0.1 | 1.1466 |
| 1.0 | 0.3 | 0.5 | 0.1 | 0.1 | 0.1 | 0.9698 |
| 1.0 | 0.3 | 1.0 | 0.1 | 0.1 | 0.1 | 1.1466 |
| 1.0 | 0.3 | 1.5 | 0.1 | 0.1 | 0.1 | 1.2565 |
| 1.0 | 0.3 | 1.0 | 0.15 | 0.1 | 0.1 | 0.9012 |
| 1.0 | 0.3 | 1.0 | 0.20 | 0.1 | 0.1 | 0.5671 |
| 1.0 | 0.3 | 1.0 | 0.25 | 0.1 | 0.1 | −1.1570 |
| 1.0 | 0.3 | 1.0 | 0.1 | 0.01 | 0.1 | 1.8109 |
| 1.0 | 0.3 | 1.0 | 0.1 | 0.02 | 0.1 | 1.7405 |
| 1.0 | 0.3 | 1.0 | 0.1 | 0.03 | 0.1 | 1.6694 |
| 1.0 | 0.3 | 1.0 | 0.1 | 0.1 | 0.01 | 1.4423 |
| 1.0 | 0.3 | 1.0 | 0.1 | 0.1 | 0.02 | 1.4131 |
| 1.0 | 0.3 | 1.0 | 0.1 | 0.1 | 0.03 | 1.3831 |
| Properties | H2O | Ag | TiO2 |
|---|---|---|---|
| (kg/m3) | 997.1 | 10,500 | 4250 |
| (J/kgK) | 4179 | 235 | 686.2 |
| k (W/mK) | 0.613 | 429 | 8.9538 |
| (S/m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zahid, M.; Basit, A.; Ullah, T.; Ali, B.; Liśkiewicz, G. Coupled Effects of Lorentz Force, Radiation, and Dissipation on the Dynamics of a Hybrid Nanofluid over an Exponential Stretching Sheet. Energies 2023, 16, 7452. https://doi.org/10.3390/en16217452
Zahid M, Basit A, Ullah T, Ali B, Liśkiewicz G. Coupled Effects of Lorentz Force, Radiation, and Dissipation on the Dynamics of a Hybrid Nanofluid over an Exponential Stretching Sheet. Energies. 2023; 16(21):7452. https://doi.org/10.3390/en16217452
Chicago/Turabian StyleZahid, Muhammad, Abdul Basit, Tariq Ullah, Bagh Ali, and Grzegorz Liśkiewicz. 2023. "Coupled Effects of Lorentz Force, Radiation, and Dissipation on the Dynamics of a Hybrid Nanofluid over an Exponential Stretching Sheet" Energies 16, no. 21: 7452. https://doi.org/10.3390/en16217452
APA StyleZahid, M., Basit, A., Ullah, T., Ali, B., & Liśkiewicz, G. (2023). Coupled Effects of Lorentz Force, Radiation, and Dissipation on the Dynamics of a Hybrid Nanofluid over an Exponential Stretching Sheet. Energies, 16(21), 7452. https://doi.org/10.3390/en16217452








