Large Eddy Simulation of Flow Characteristics around Cylinders with Crosswise and Streamwise Arrangements in Ocean Energy
Abstract
:1. Introduction
2. Numerical Methods
2.1. Physical Model and Computational Domain
2.2. Numerical Methods
2.3. Grid Independence Tests
3. Results and Discussion
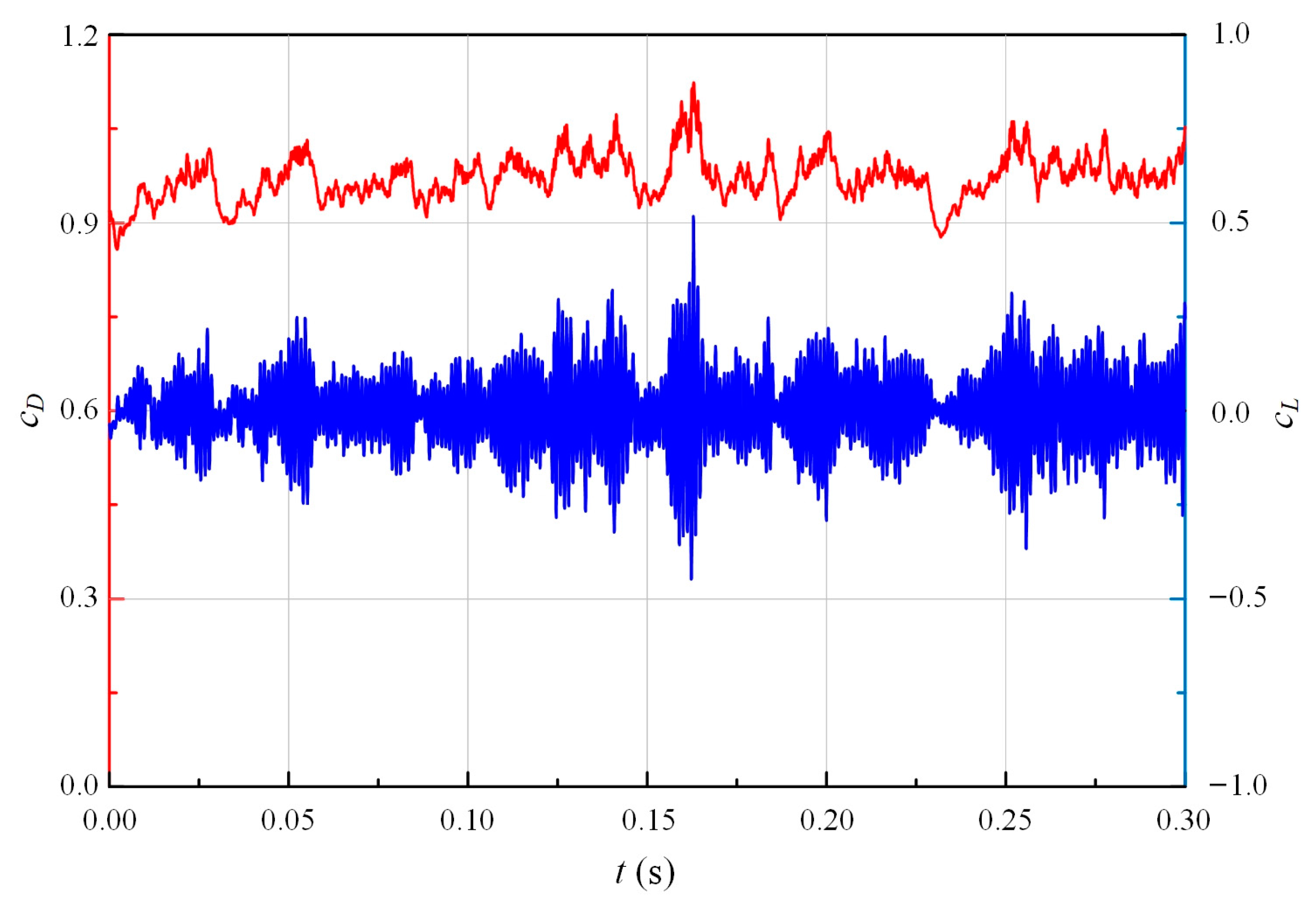
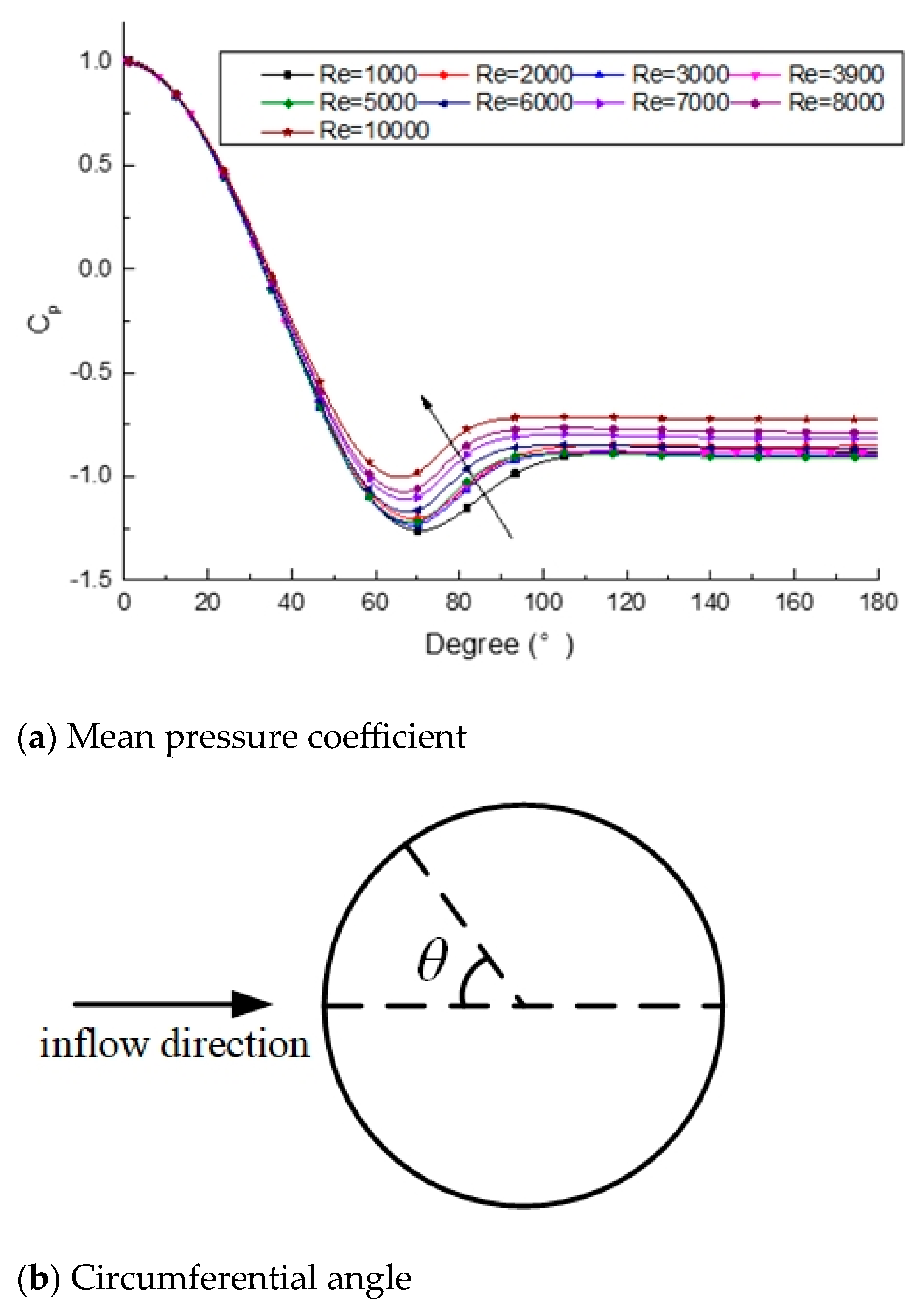
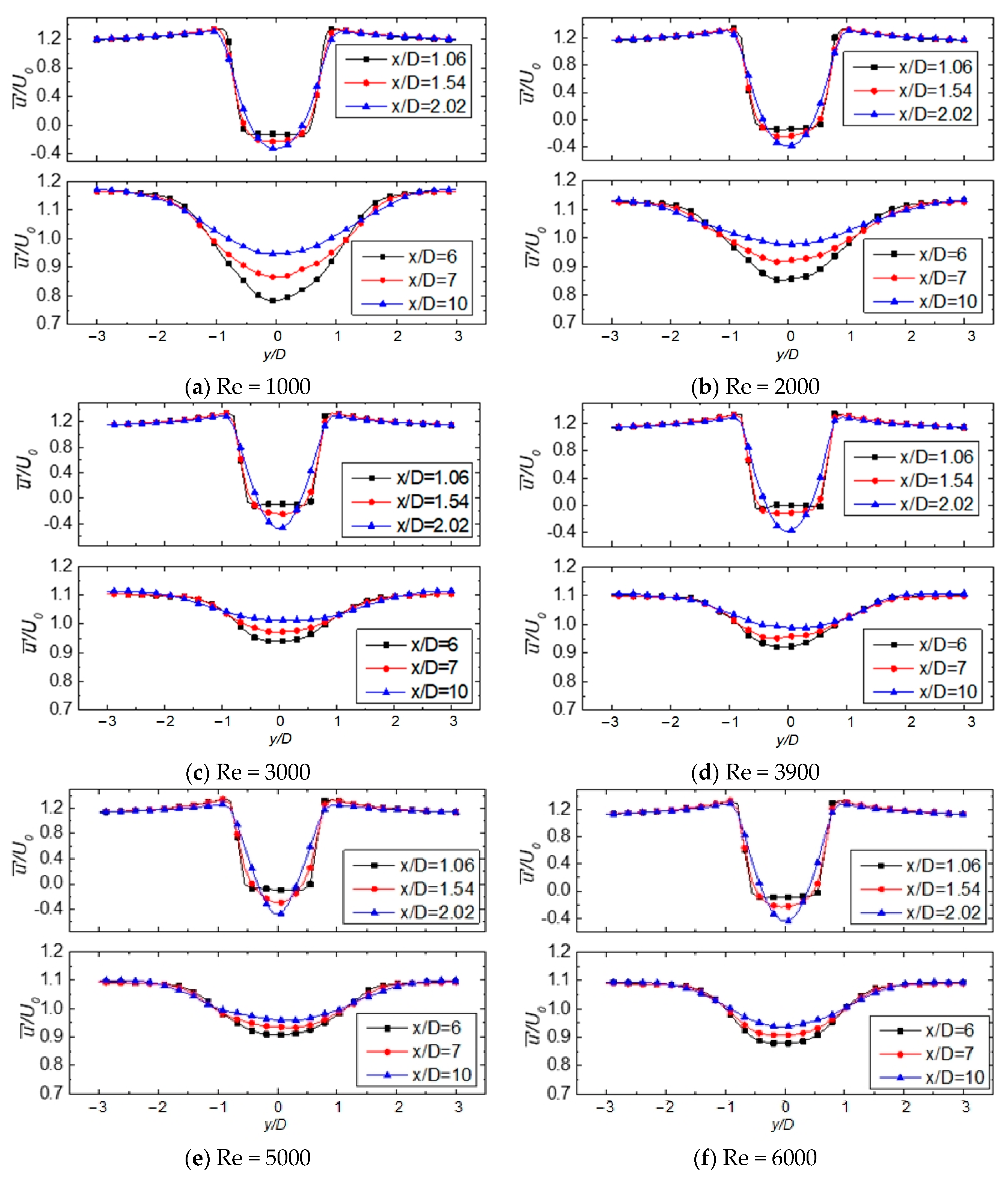
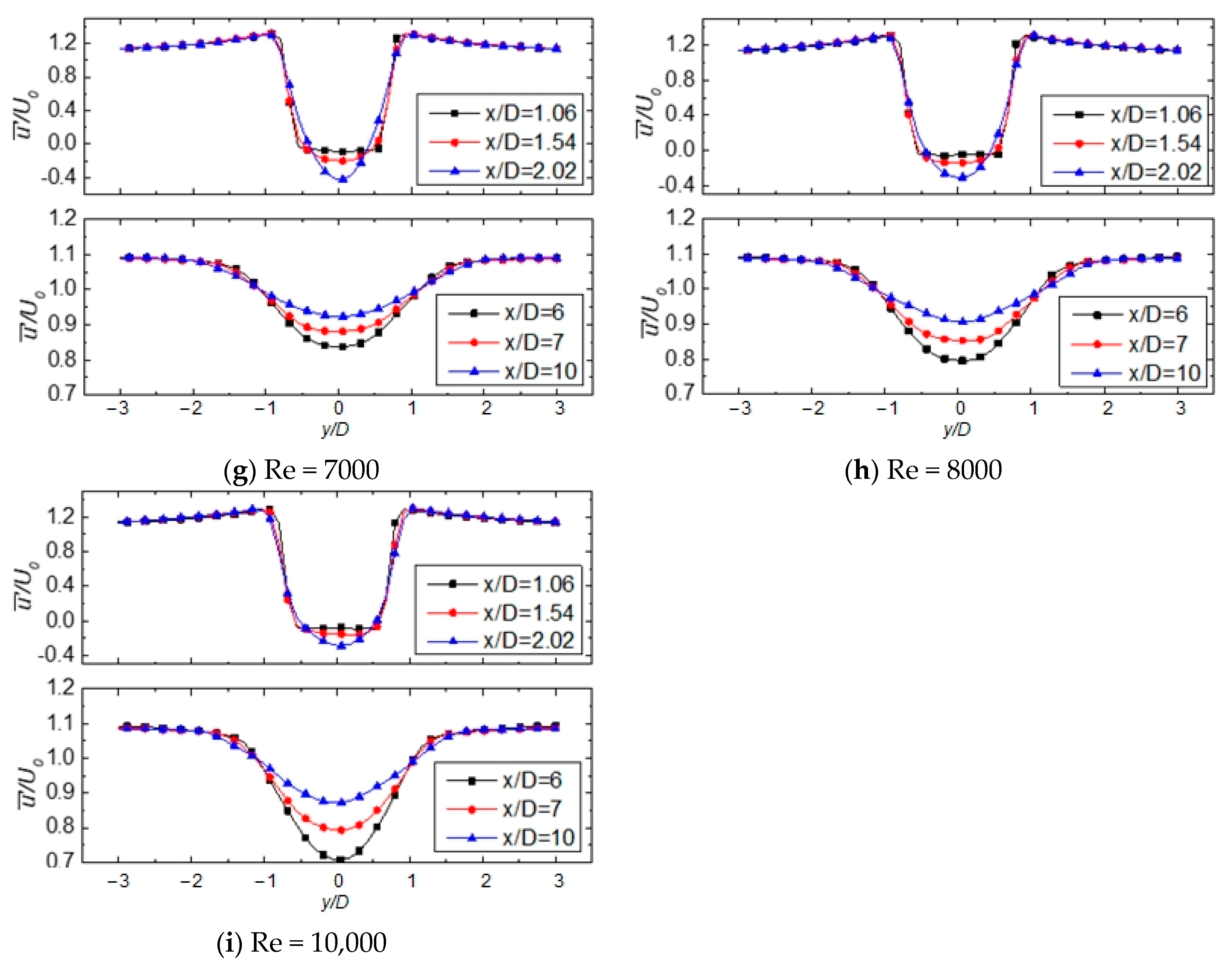
3.1. Single Cylinder
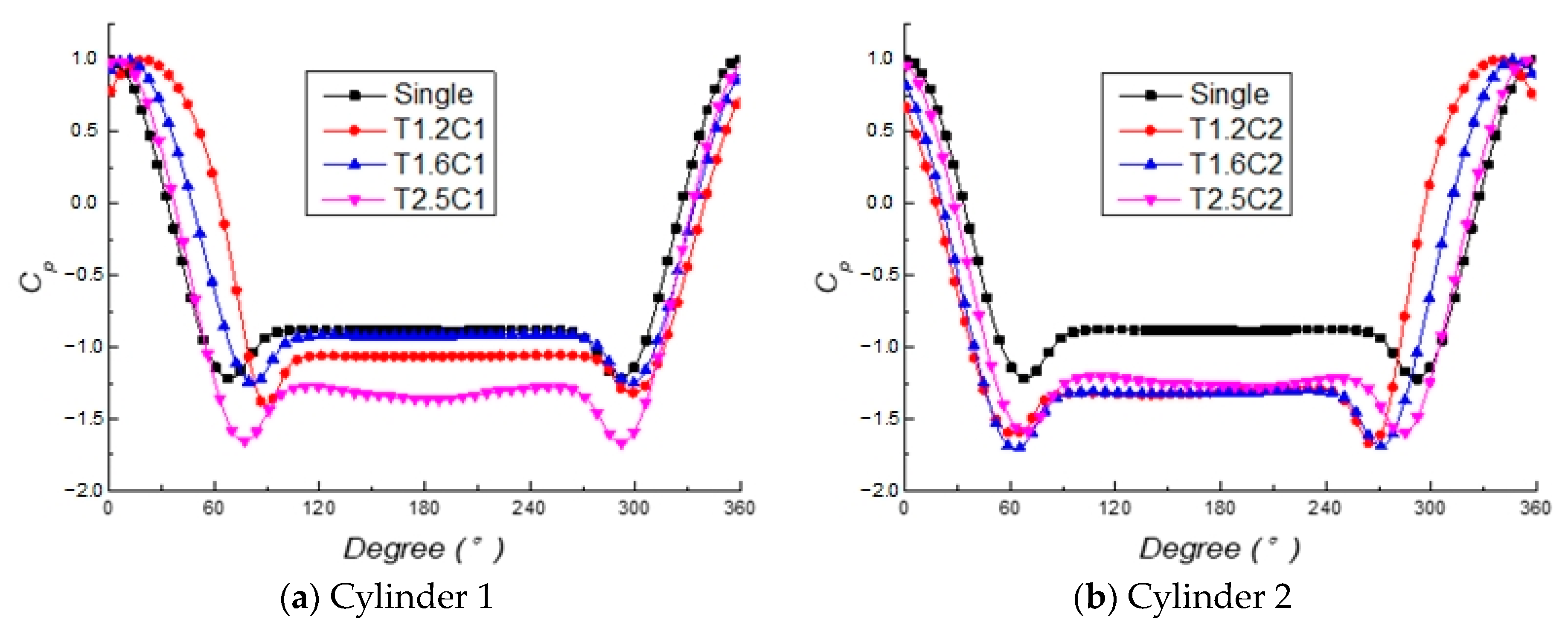
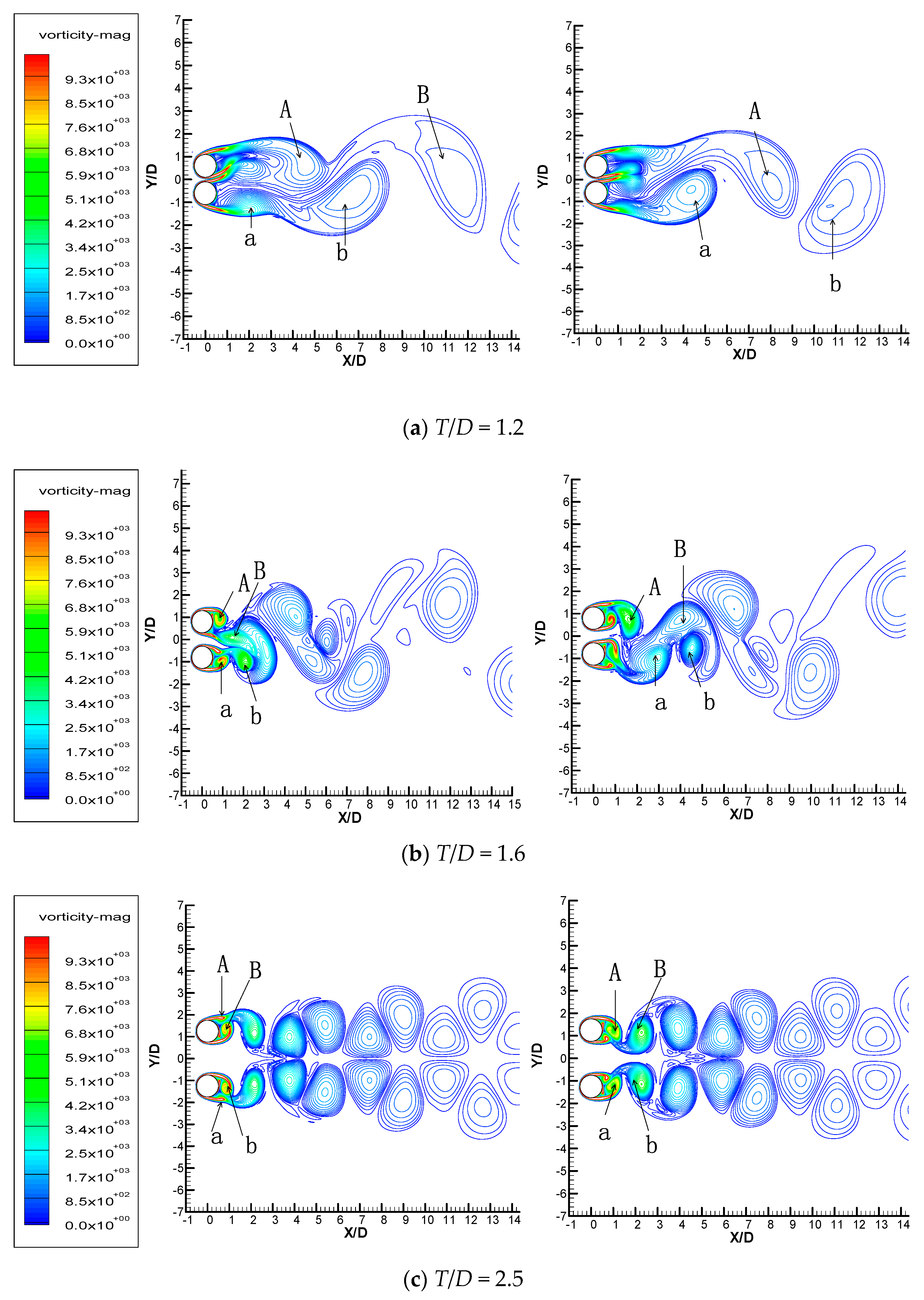
3.2. Crosswise Cylinders
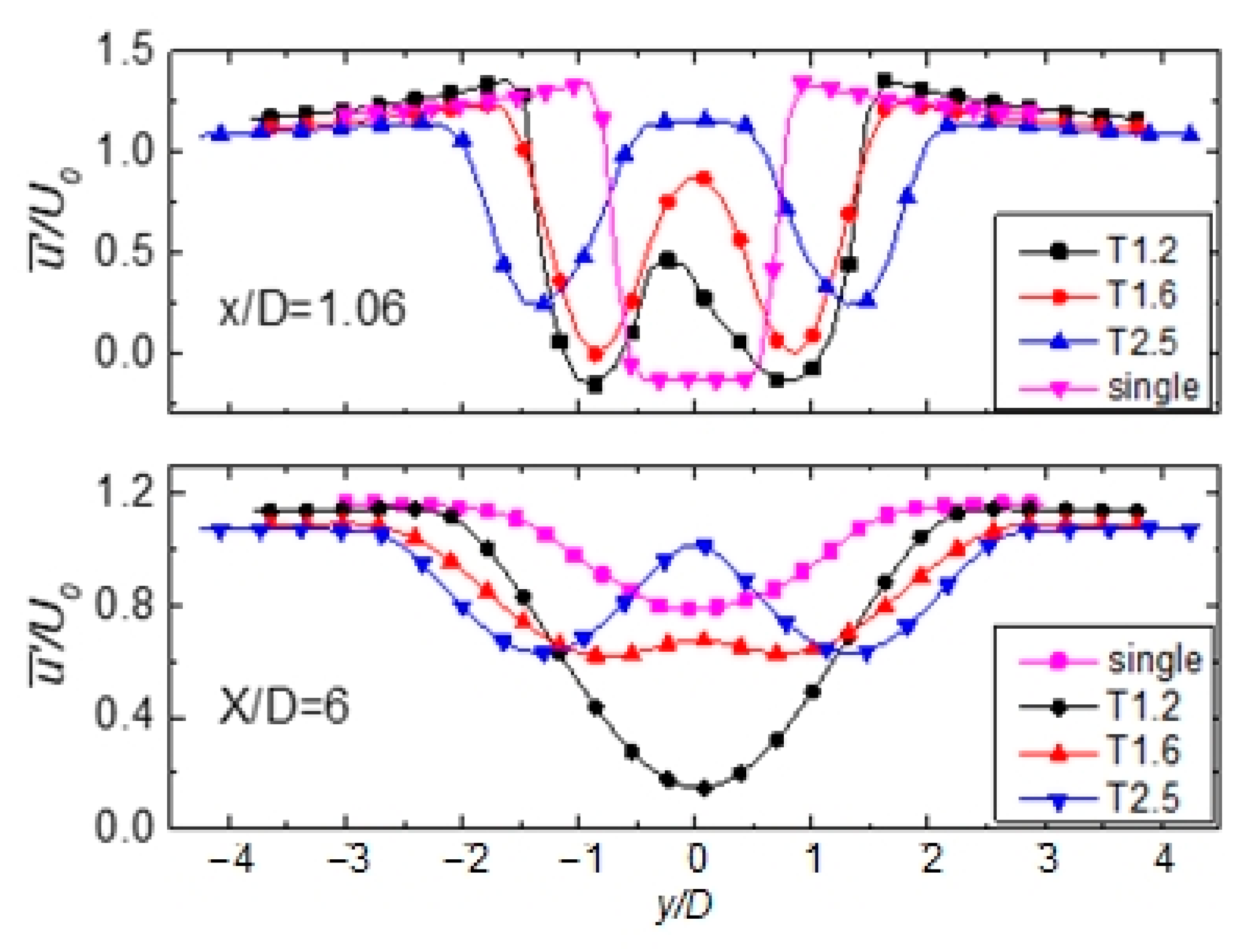
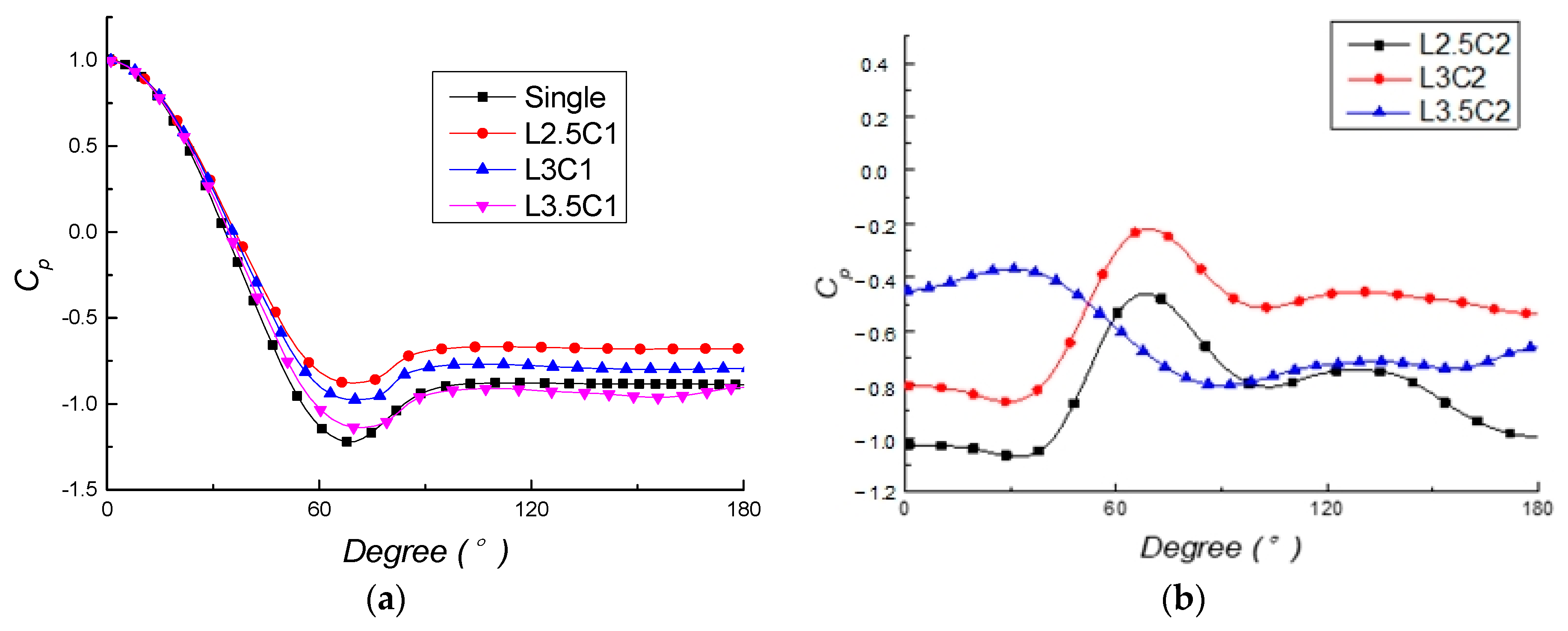
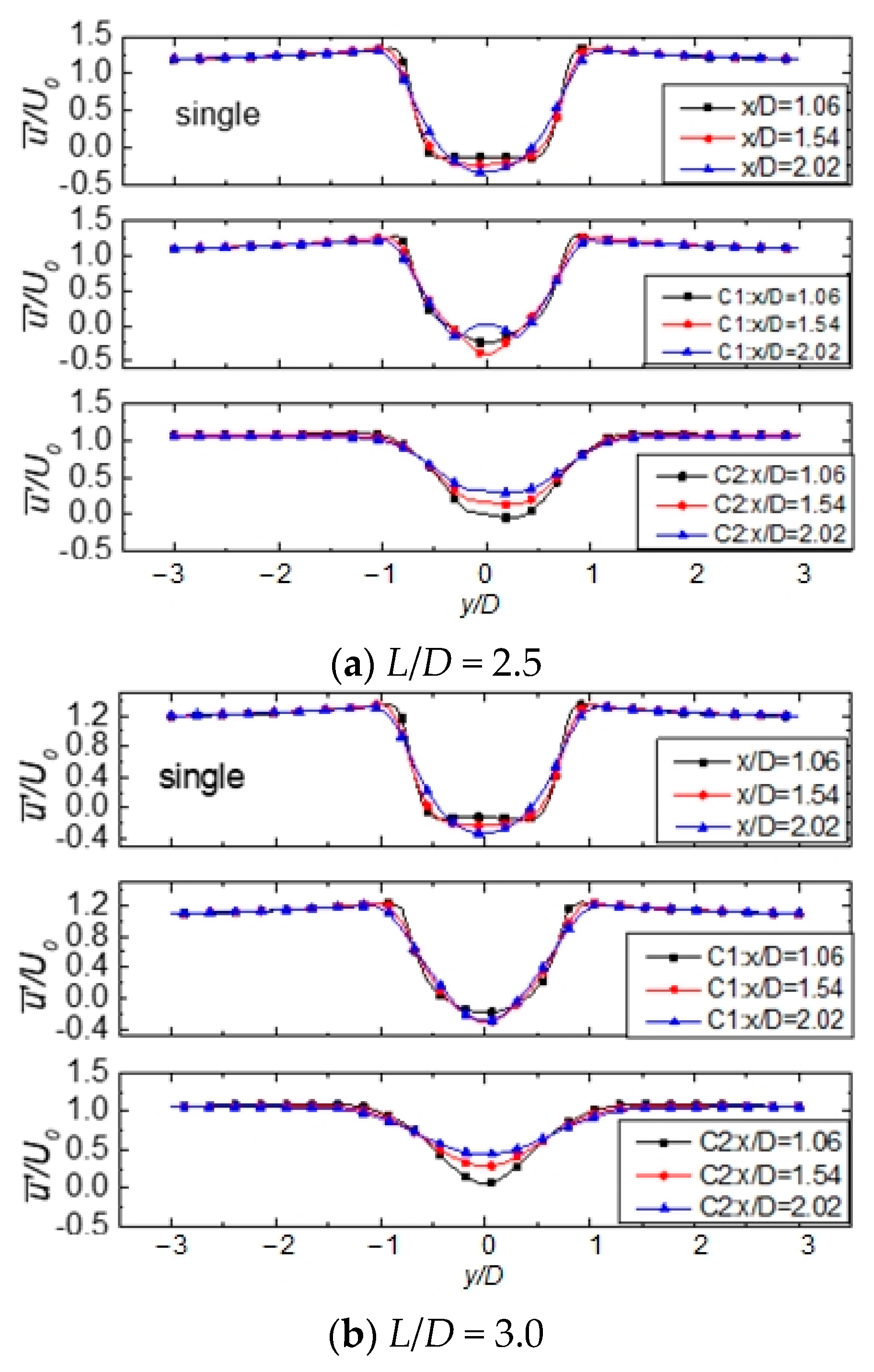
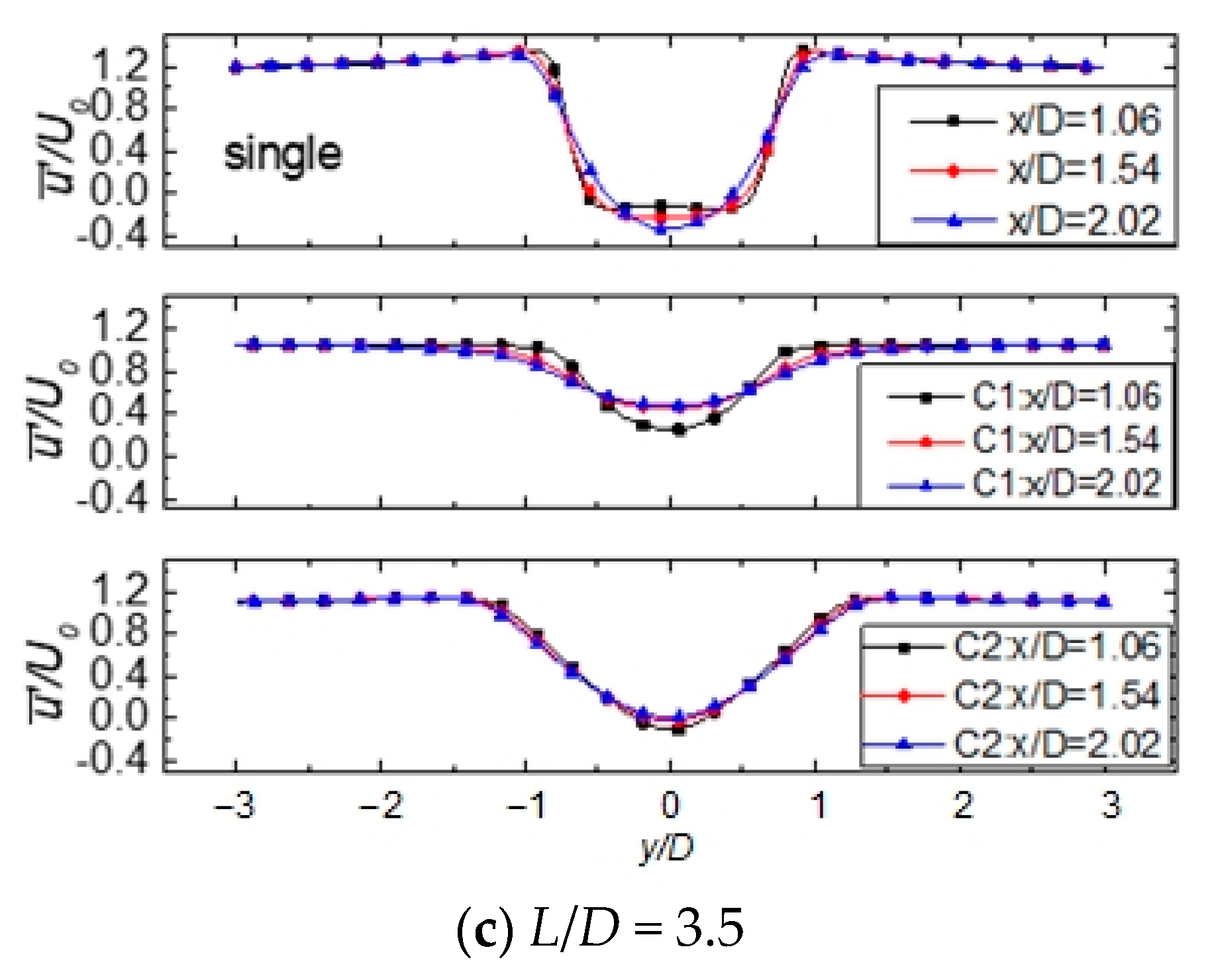
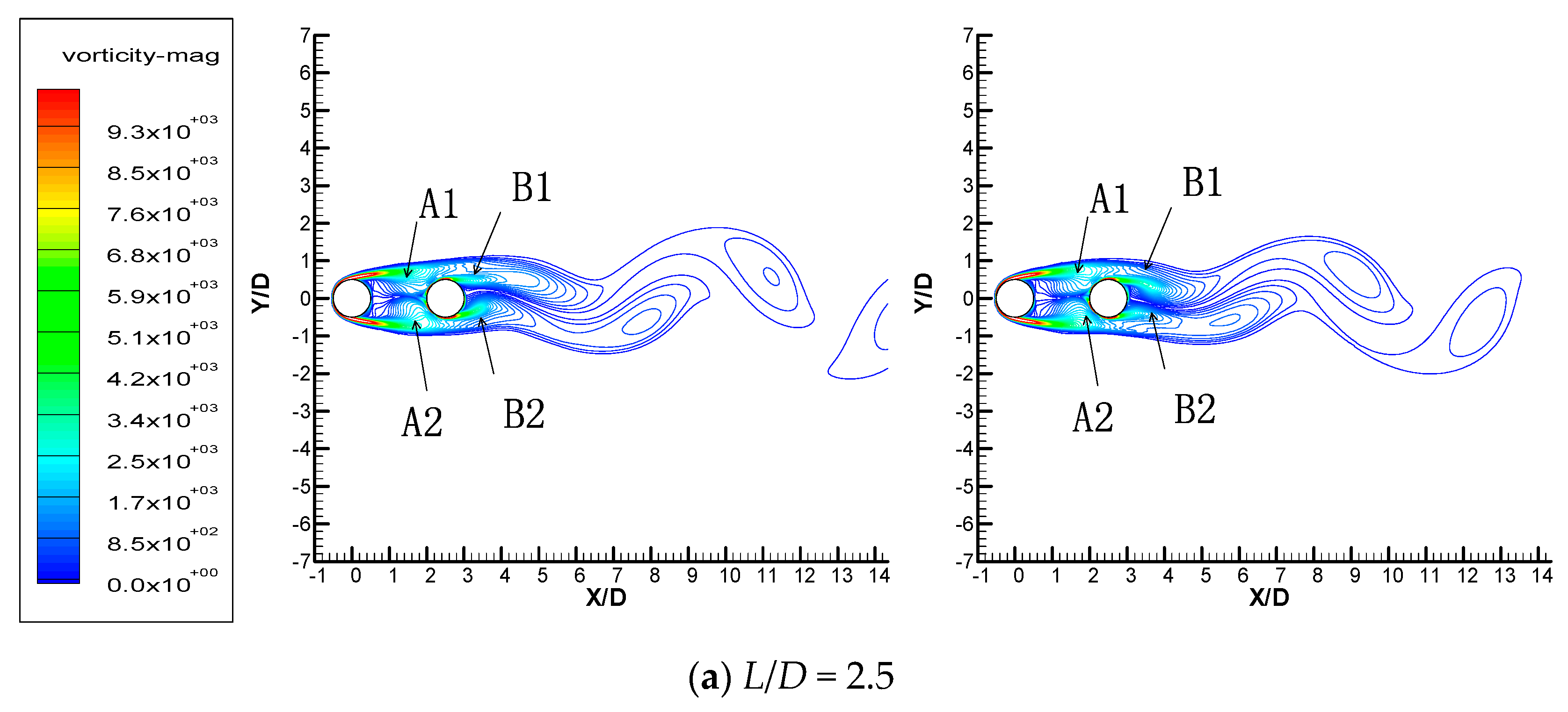
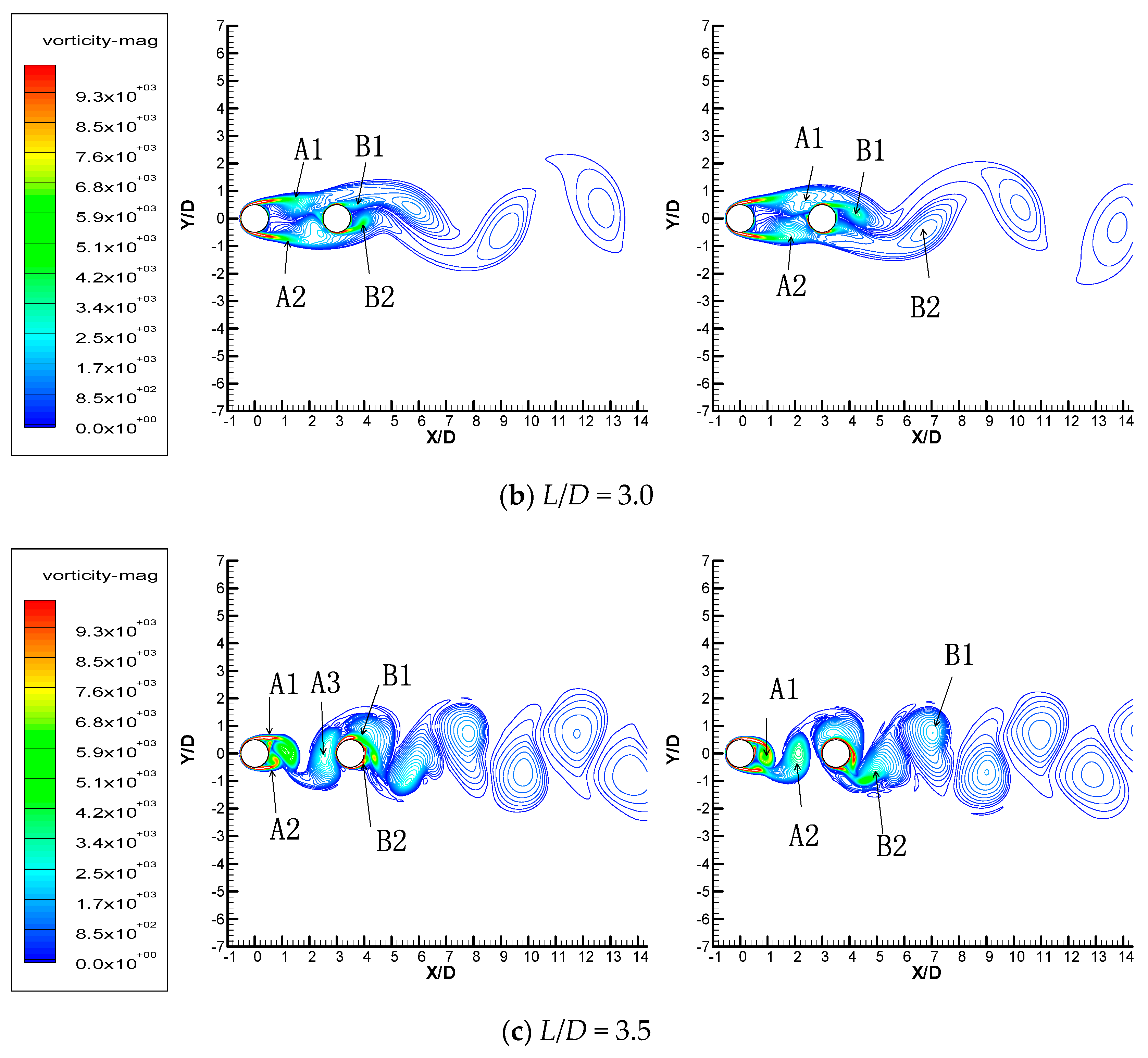
3.3. Streamwise Cylinders
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, Y.; Bao, J.; Liu, H.; Li, W.; Tu, L.; Zhang, D. Review of hydraulic transmission technologies for wave power generation. Renew. Sustain. Energy Rev. 2015, 50, 194–203. [Google Scholar] [CrossRef]
- Rehman, S.; Alhems, L.M.; Alam, M.; Wang, L.; Toor, Z. A review of energy extraction from wind and ocean: Technologies, merits, efficiencies, and cost. Ocean Eng. 2022, 267, 113192. [Google Scholar] [CrossRef]
- Heikkinen, H.; Lampinen, M.; Boling, J. Analytical study of the interaction between waves and cylindrical wave energy con-verters oscillating in two modes. Renew. Energy 2013, 50, 150–160. [Google Scholar] [CrossRef]
- Liu, H.X.; Zhang, W.C.; Zheng, X.B.; Zhang, L.; Zhang, X.W.; Cui, L. Wave energy conversion by cylinder array with a floating platform considering linear/nonlinear PTO damping. J. Mar. Sci. Technol. 2017, 22, 747–757. [Google Scholar] [CrossRef]
- Sung, H.G.; Baek, H.; Hong, S.; Choi, J.-S. Numerical study of vortex-induced vibration of pivoted cylinders. Ocean Eng. 2015, 93, 98–106. [Google Scholar] [CrossRef]
- Simpson, R.L. Junction flows. Annu. Rev. Fluids Mech. 2001, 33, 415–443. [Google Scholar] [CrossRef]
- Grandemange, M.; Gohlke, M.; Cadot, O. Turbulent wake past a three-dimensional blunt body. Part 1. Global modes and bi-stability. J. Fluid Mech. 2013, 722, 51–84. [Google Scholar] [CrossRef]
- Hourigan, K.; Thompson, M.; Tan, B. Self-sustained oscillations in flows around long blunt plates. J. Fluids Struct. 2001, 15, 387–398. [Google Scholar] [CrossRef]
- Gonçalves, R.; Franzini, G.; Rosetti, G.; Meneghini, J.; Fujarra, A. Flow around circular cylinders with very low aspect ratio. J. Fluids Struct. 2015, 54, 122–141. [Google Scholar] [CrossRef]
- Pinar, E.; Ozkan, G.M.; Durhasan, T.; Aksoy, M.M.; Akilli, H.; Sahin, B. Flow structure around perforated cylinders in shallow water. J. Fluids Struct. 2015, 55, 52–63. [Google Scholar] [CrossRef]
- Ong, L.; Wallace, J. The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 1996, 20, 441–453. [Google Scholar] [CrossRef]
- Wang, H.; Tan, L.; Liu, M.; Liu, X.; Zhu, B. Numerical Investigation on the Transition Flow around NLF Airfoil. Energies 2023, 16, 1826. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Liu, Y.; Xu, Y.; Cao, S. Large eddy simulation of cavitation vortex interaction and pressure fluctuation around hydrofoil ALE 15. Ocean Eng. 2018, 163, 264–274. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S. Cavitation–Vortex–Turbulence Interaction and One-Dimensional Model Prediction of Pressure for Hydrofoil ALE15 by Large Eddy Simulation. J. Fluids Eng. 2019, 141, 021103. [Google Scholar] [CrossRef]
- Lo, S.-C.; Hoffmann, K.A.; Dietiker, J.-F. Numerical Investigation of High Reynolds Number Flows over Square and Circular Cylinders. J. Thermophys. Heat Transf. 2005, 19, 72–80. [Google Scholar] [CrossRef]
- Breuer, M. Numerical and modeling influences on large eddy simulations for the flow past a circular cylinder. Int. J. Heat Fluid Flow 1998, 19, 512–521. [Google Scholar] [CrossRef]
- Lysenko, D.A.; Ertesv Aa GI, S.; Rian, K.E. Large-eddy simulation of the flow over a circular cylinder at Reynolds number 3900 using the OpenFOAM toolbox. Flow Turbul. Combust. 2012, 89, 491–518. [Google Scholar] [CrossRef]
- Kravchenko, A.G.; Moin, P. Numerical studies of flow over a circular cylinder at ReD=3900. Phys. Fluids 2000, 12, 403–417. [Google Scholar] [CrossRef]
- Ma, X.; Karamanos, G.-S.; Karniadakis, G.E. Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 2000, 410, 29–65. [Google Scholar] [CrossRef]
- Rodi, W. Large-Eddy Simulations of the Flow past Bluff Bodies: State-of-the Art. JSME Int. J. Ser. B 1998, 41, 361–374. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, C. Large eddy simulations of the flow past two side-by-side circular cylinders. Int. J. Comput. Fluid Dyn. 2008, 22, 393–404. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, J.; Meng, J. Large eddy simulation of flows past an array of square cylinders. J. Hydraul. Res. 2023, 61, 288–297. [Google Scholar] [CrossRef]
- Wang, X.; Gong, K.; Liu, H.; Zhang, J.-X.; Tan, S. Flow around four cylinders arranged in a square configuration. J. Fluids Struct. 2013, 43, 179–199. [Google Scholar] [CrossRef]
- Sewatkar, C.M.; Patel, R.; Sharma, A.; Agrawal, A. Flow around six in-line square cylinders. J. Fluid Mech. 2012, 710, 195–233. [Google Scholar] [CrossRef]
- Dubois, R.; Andrianne, T. Flow around tandem rough cylinders: Effects of spacing and flow regimes. J. Fluids Struct. 2021, 109, 103465. [Google Scholar] [CrossRef]
- Lam, K.; Gong, W.; So, R. Numerical simulation of cross-flow around four cylinders in an in-line square configuration. J. Fluids Struct. 2008, 24, 34–57. [Google Scholar] [CrossRef]
- Meneghini, J.; Saltara, F.; Siqueira, C.; Ferrari, J. Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. J. Fluids Struct. 2001, 15, 327–350. [Google Scholar] [CrossRef]
- Sharman, B.; Lien, F.S.; Davidson, L.; Norberg, C. Numerical predictions of low Reynolds number flows over two tandem circular cylinders. Int. J. Numer. Methods Fluids 2005, 47, 423–447. [Google Scholar] [CrossRef]
- Zhou, Y.; Yiu, M.W. Flow structure, momentum and heat transport in a two-tandem-cylinder wake. J. Fluid Mech. 2006, 548, 17–48. [Google Scholar] [CrossRef]
- Xu, S.J.; Zhou, Y.; So, R.M.C. Reynolds number effects on the flow structure behind two side-by-side cylinders. Phys. Fluids 2003, 15, 1214–1219. [Google Scholar] [CrossRef]
- Alam, M.; Moriya, M.; Sakamoto, H. Aerodynamic characteristics of two side-by-side circular cylinders and application of wavelet analysis on the switching phenomenon. J. Fluids Struct. 2003, 18, 325–346. [Google Scholar] [CrossRef]
- Sumner, D.; Wong, S.; Price, S.; Païdoussis, M. Fluid behaviour of side-by-side circular cylinders in steady cross-flow. J. Fluids Struct. 1999, 13, 309–338. [Google Scholar] [CrossRef]
- Chen, L.; Tu, J.; Yeoh, G. Numerical simulation of turbulent wake flows behind two side-by-side cylinders. J. Fluids Struct. 2003, 18, 387–403. [Google Scholar] [CrossRef]
- Qiu, X.; Bi, Z.-X.; Luo, J.-P.; Liu, Y.-L. Vortex shedding in the flow around two side-by-side circular cylinders of different diameters. J. Hydrodyn. 2017, 29, 470–478. [Google Scholar] [CrossRef]
- Palau-Salvador, G.; Stoesser, T.; Rodi, W. LES of the flow around two cylinders in tandem. J. Fluids Struct. 2008, 24, 1304–1312. [Google Scholar] [CrossRef]
- Prsic, M.A.; Ong, M.C.; Pettersen, B.; Myrhaug, D. Large Eddy simulations of flow around tandem circular cylinders in the vicinity of a plane wall. J. Mar. Sci. Technol. 2019, 24, 338–358. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, X.; You, Y. On the flow around two circular cylinders in tandem arrangement at high Reynolds numbers. Ocean Eng. 2019, 189, 106301. [Google Scholar] [CrossRef]
- Franke, J.; Frank, W. Large eddy simulation of the flow past a circular cylinder at ReD=3900. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 1191–1206. [Google Scholar] [CrossRef]
- Lesieur, M.; Metais, O. New trends in large-eddy simulations of turbulence. Annu. Rev. Fluid Mech. 1996, 28, 45–82. [Google Scholar] [CrossRef]
- Bose, S.T.; Park, G.I.; Davis, S.H.; Moin, P. Wall-Modeled Large-Eddy Simulation for Complex Turbulent Flows. Annu. Rev. Fluid Mech. 2018, 50, 535–561. [Google Scholar] [CrossRef]
- ANSYS Help, 17.0; ANSYS Inc.: Canonsburg, PA, USA, 2017.
- Du, X.; Lin, W.; Wu, G.; Daichin; Jiang, B. Effects of surface roughness on the wake-induced instabilities of two circular cylinders. J. Fluids Struct. 2019, 91, 102738. [Google Scholar] [CrossRef]
- de Moraes, P.G.; Pereira, L.A.A. Surface Roughness Effects on Flows Past Two Circular Cylinders in Tandem Arrangement at Co-Shedding Regime. Energies 2021, 14, 8237. [Google Scholar] [CrossRef]

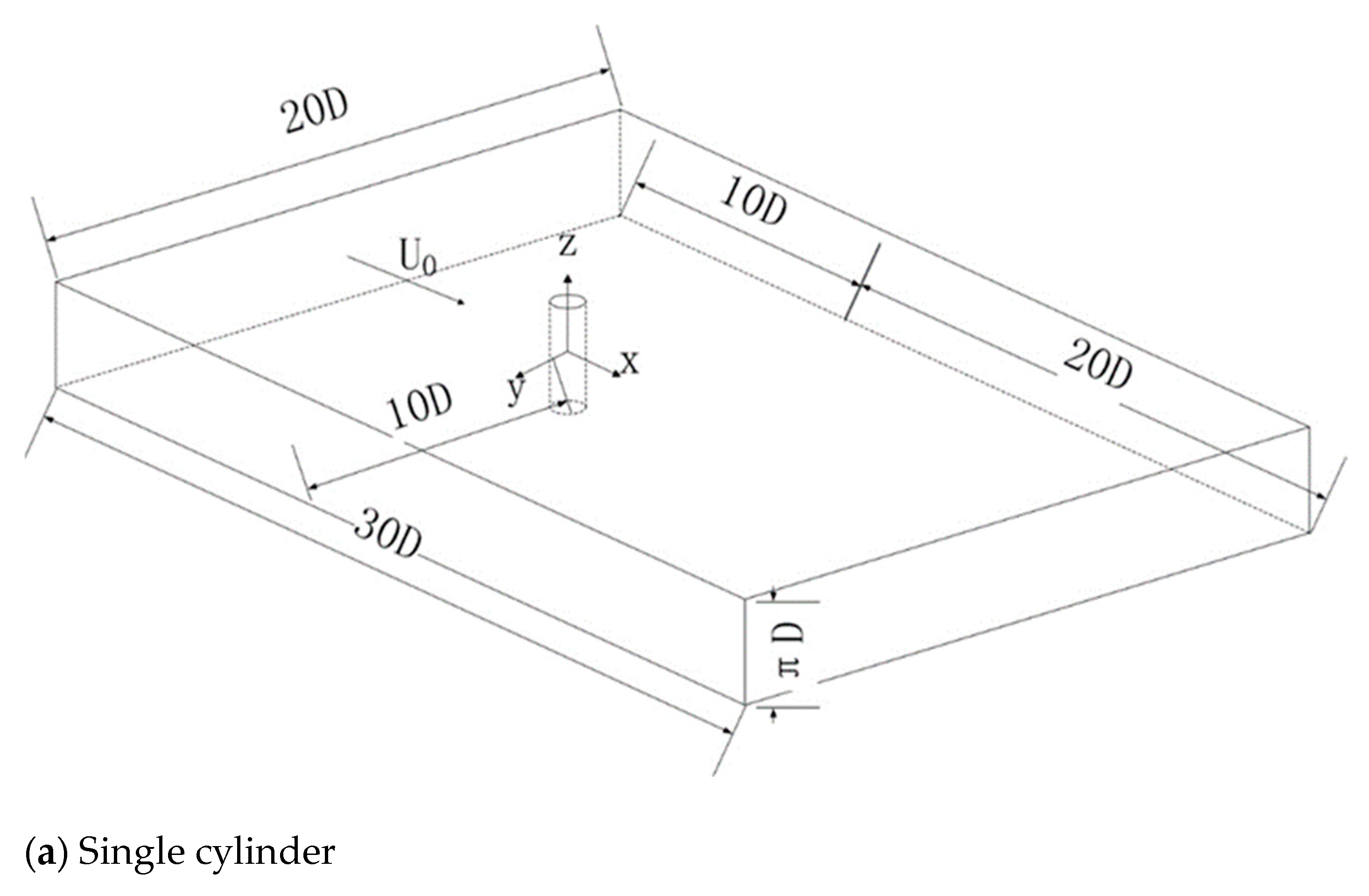
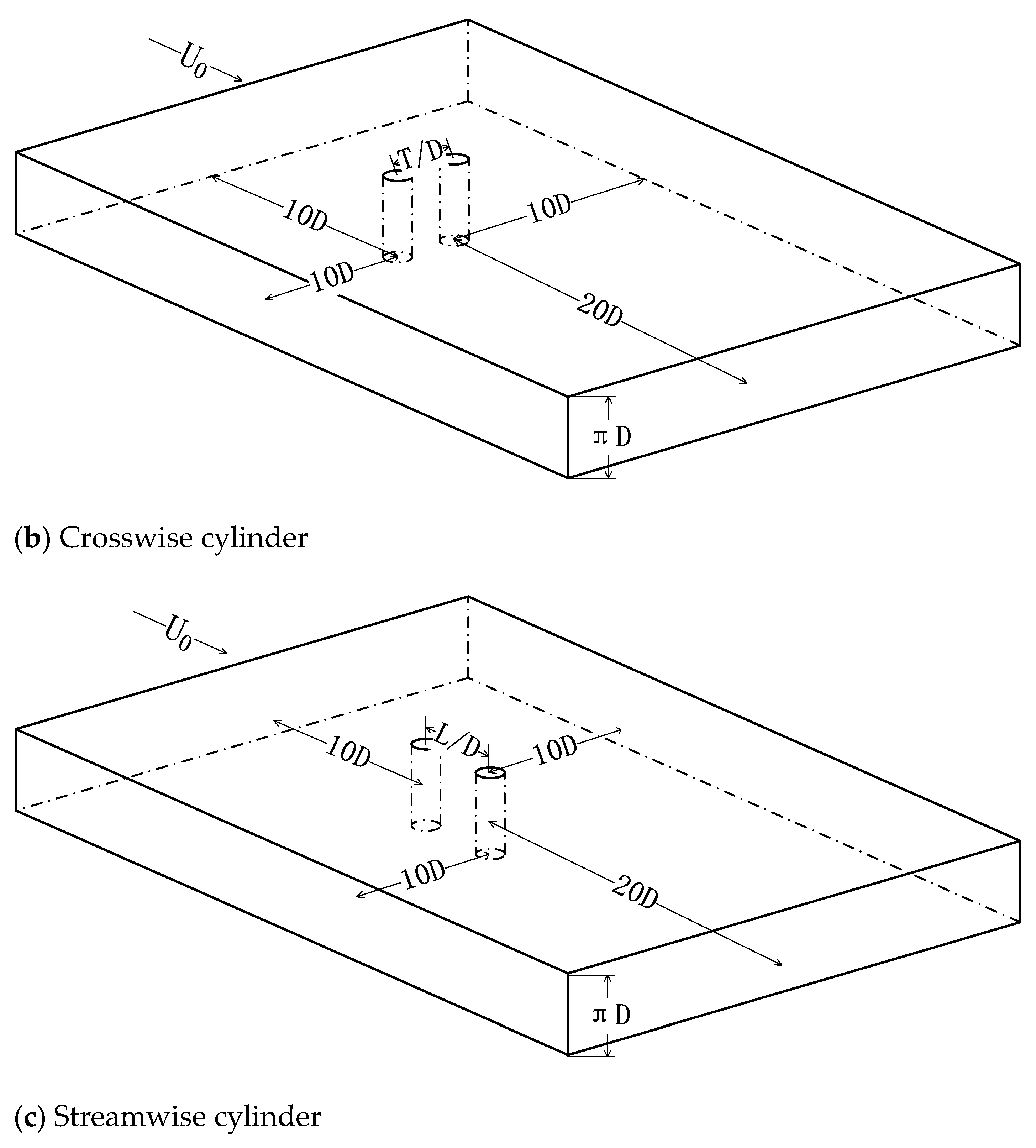

| Mesh | Mesh Distribution (r × θ × z) | Number of Mesh Cells | cD | Relative Error of cD | St | Relative Error of St |
|---|---|---|---|---|---|---|
| Mesh 1 | 50 × 120 × 35 | 0.78 × 106 | 0.977 | 1.31% | 0.189 | 12.06% |
| Mesh 2 | 70 × 120 × 48 | 1.82 × 106 | 0.981 | 0.81% | 0.201 | 6.77% |
| Mesh 3 | 90 × 200 × 58 | 2.80 × 106 | 0.978 | 1.17% | 0.209 | 2.99% |
| Mesh | Number of Mesh Cells | Cell Size of the First Layer | y+ | cD | Relative Error of cD | St | Relative Error of St |
|---|---|---|---|---|---|---|---|
| Mesh 2-1 | 1.82 × 106 | 0.01 | 8 | 0.982 | 0.81% | 0.200 | 6.77% |
| Mesh 2-2 | 1.82 × 106 | 0.005 | 5.6 | 0.965 | 2.56% | 0.204 | 5.26% |
| Mesh 2-3 | 1.82 × 106 | 0.001 | 1.5 | 0.971 | 1.88% | 0.215 | 0.14% |
| Mesh 2-4 | 1.82 × 106 | 0.0005 | 0.8 | 0.985 | 0.47% | 0.225 | 4.68% |
| Mesh 2-5 | 1.82 × 106 | 0.0001 | 0.5 | 1.017 | 2.73% | 0.231 | 7.44% |
| Δt (s) | cD | Relative Error of cD | St | Relative Error of St |
|---|---|---|---|---|
| 1 × 10−4 | 0.971 | 1.88% | 0.2153 | 0.14% |
| 5 × 10−5 | 1.017 | 2.72% | 0.2289 | 6.47% |
| 1 × 10−5 | 0.913 | 7.78% | 0.2209 | 2.76% |
| Case | Re | cD | St |
|---|---|---|---|
| 1 | 1000 | 1.210 | 0.210 |
| 2 | 2000 | 0.976 | 0.211 |
| 3 | 3000 | 0.983 | 0.214 |
| 4 | 3900 | 0.971 | 0.215 |
| 5 | 5000 | 0.974 | 0.196 |
| 6 | 6000 | 0.943 | 0.186 |
| 7 | 7000 | 0.916 | 0.175 |
| 8 | 8000 | 0.892 | 0.165 |
| 9 | 10,000 | 0.855 | 0.153 |
| Case | Re | θsep |
|---|---|---|
| 1 | 1000 | 92.25 |
| 2 | 2000 | 88.18 |
| 3 | 3000 | 86.40 |
| 4 | 3900 | 85.66 |
| 5 | 5000 | 84.74 |
| 6 | 6000 | 83.50 |
| 7 | 7000 | 82.46 |
| 8 | 8000 | 81.65 |
| 9 | 10,000 | 80.64 |
| Case | T/D | cD,s | St |
|---|---|---|---|
| Case Single | 0, single cylinder | 1.00 | 0.215 |
| Case T1.2 | 1.2 | 1.41 | 0.098 |
| Case T1.6 | 1.6 | 1.10 | 0.215 |
| Case T2.5 | 2.5 | 1.37 | 0.264 |
| Case | T/D | Cylinder 1 | Cylinder 2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| θsta | θses | θseo | |θses − θseo| | θsta | θses | θseo | |θses − θseo| | ||
| Single | 0 | 0 | 272 | 88 | |||||
| T1.2 | 1.2 | 19.31 | 284.98 | 100.84 | 184.14 | 338.21 | 74.89 | 250.47 | 175.58 |
| T1.6 | 1.6 | 9.81 | 278.3 | 98.02 | 180.28 | 347.24 | 81.56 | 255.27 | 173.71 |
| T2.5 | 2.5 | 4.64 | 273.79 | 95.77 | 178.02 | 355.14 | 86.46 | 264.11 | 177.65 |
| Case | L/D | cD,C1 | cD,C2 | St |
|---|---|---|---|---|
| Case Single | 0, single cylinder | 1.210 | 0.215 | |
| Case L2.5 | 2.5 | 0.917 | −0.080 | 0.136 |
| Case L3.0 | 3.0 | 0.915 | 0.168 | 0.126 |
| Case L3.5 | 3.5 | 1.370 | 0.307 | 0.2 |
| Case | L/D | Upstream Cylinder 1 | Downstream Cylinder 2 |
|---|---|---|---|
| θsep | θsep | ||
| Single | 0 | 88 | |
| L2.5 | 2.5 | 93.04 | 119.74 |
| L3.0 | 3.0 | 92.57 | 120.78 |
| L3.5 | 3.5 | 90.18 | 125.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, W.; Liu, M.; Huang, C.; Cheng, D.; Tan, L. Large Eddy Simulation of Flow Characteristics around Cylinders with Crosswise and Streamwise Arrangements in Ocean Energy. Energies 2023, 16, 7605. https://doi.org/10.3390/en16227605
Zhai W, Liu M, Huang C, Cheng D, Tan L. Large Eddy Simulation of Flow Characteristics around Cylinders with Crosswise and Streamwise Arrangements in Ocean Energy. Energies. 2023; 16(22):7605. https://doi.org/10.3390/en16227605
Chicago/Turabian StyleZhai, Weiming, Ming Liu, Changjiu Huang, Daoxi Cheng, and Lei Tan. 2023. "Large Eddy Simulation of Flow Characteristics around Cylinders with Crosswise and Streamwise Arrangements in Ocean Energy" Energies 16, no. 22: 7605. https://doi.org/10.3390/en16227605
APA StyleZhai, W., Liu, M., Huang, C., Cheng, D., & Tan, L. (2023). Large Eddy Simulation of Flow Characteristics around Cylinders with Crosswise and Streamwise Arrangements in Ocean Energy. Energies, 16(22), 7605. https://doi.org/10.3390/en16227605







