Impact of Material Solutions and a Passive Sports Hall’s Use on Thermal Comfort
Abstract
:1. Introduction
2. Materials and Methods
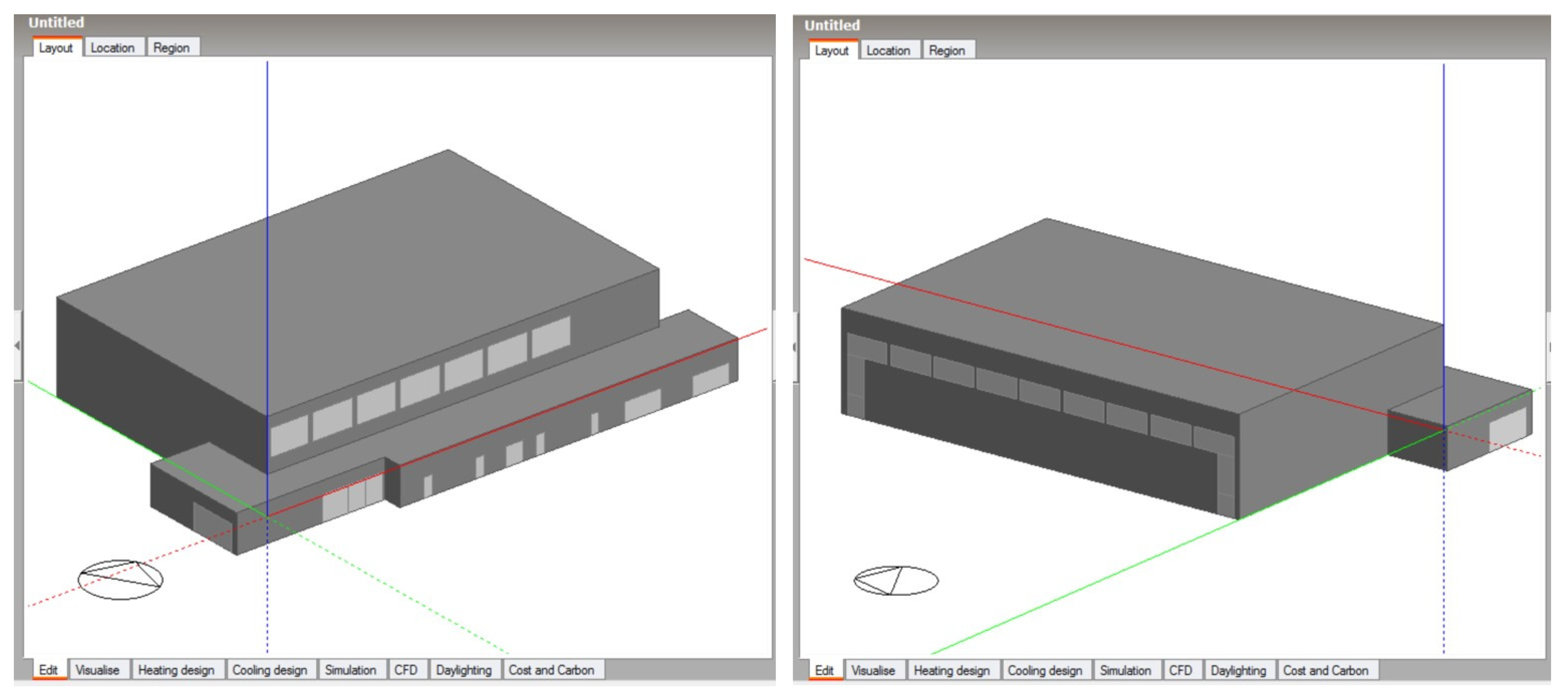
2.1. Passive Sports Hall
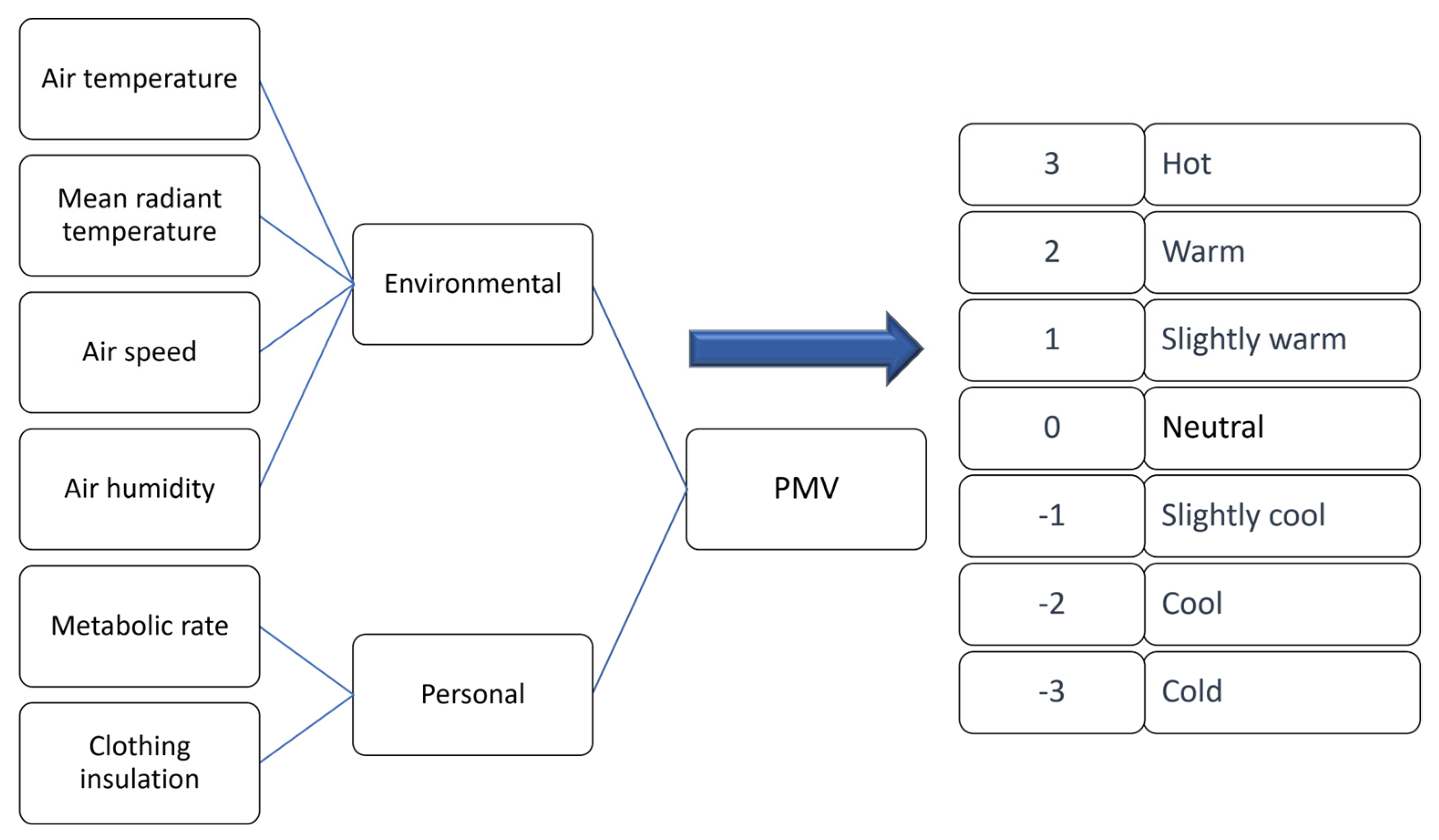
2.2. The Criterion for Ensuring Thermal Comfort
2.3. Simulation Model in Design Builder
- during a competition and with full stands—100%,
- 1/3 of the room used—20%,
- 2 or 3 spectator sectors occupied—40 or 60% of maximum capacity [32].
3. Results of Thermal Comfort Analysis
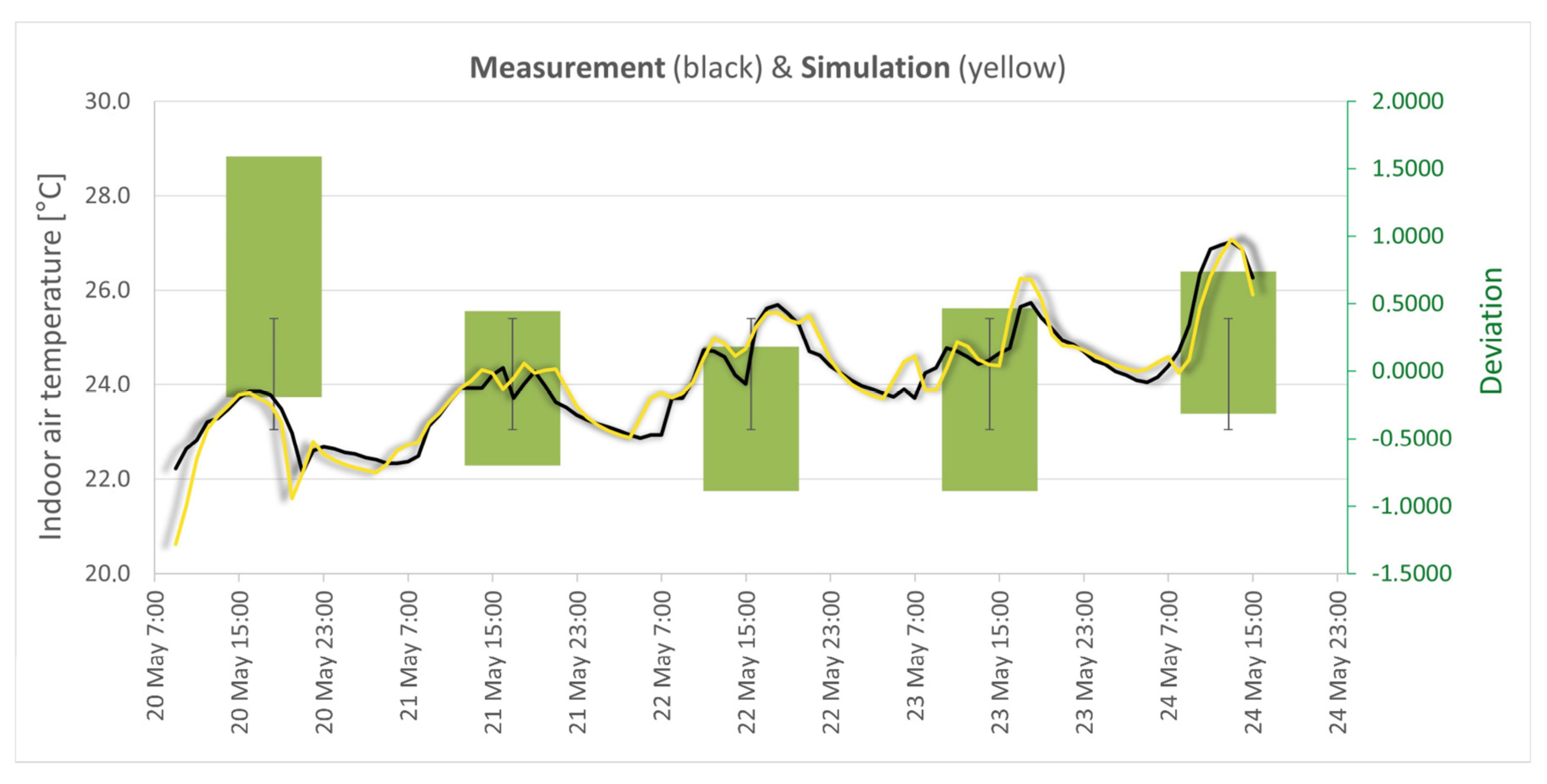
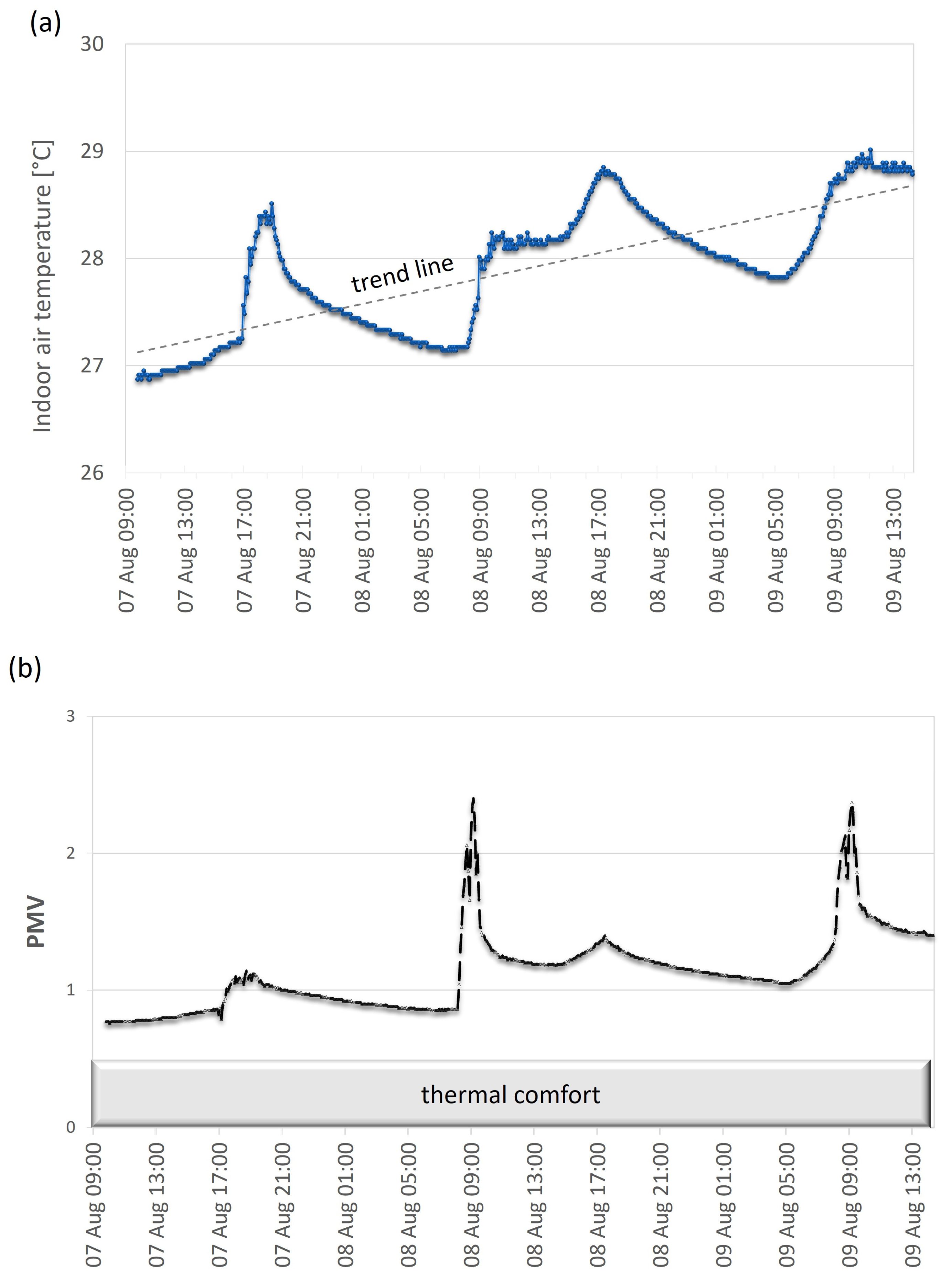
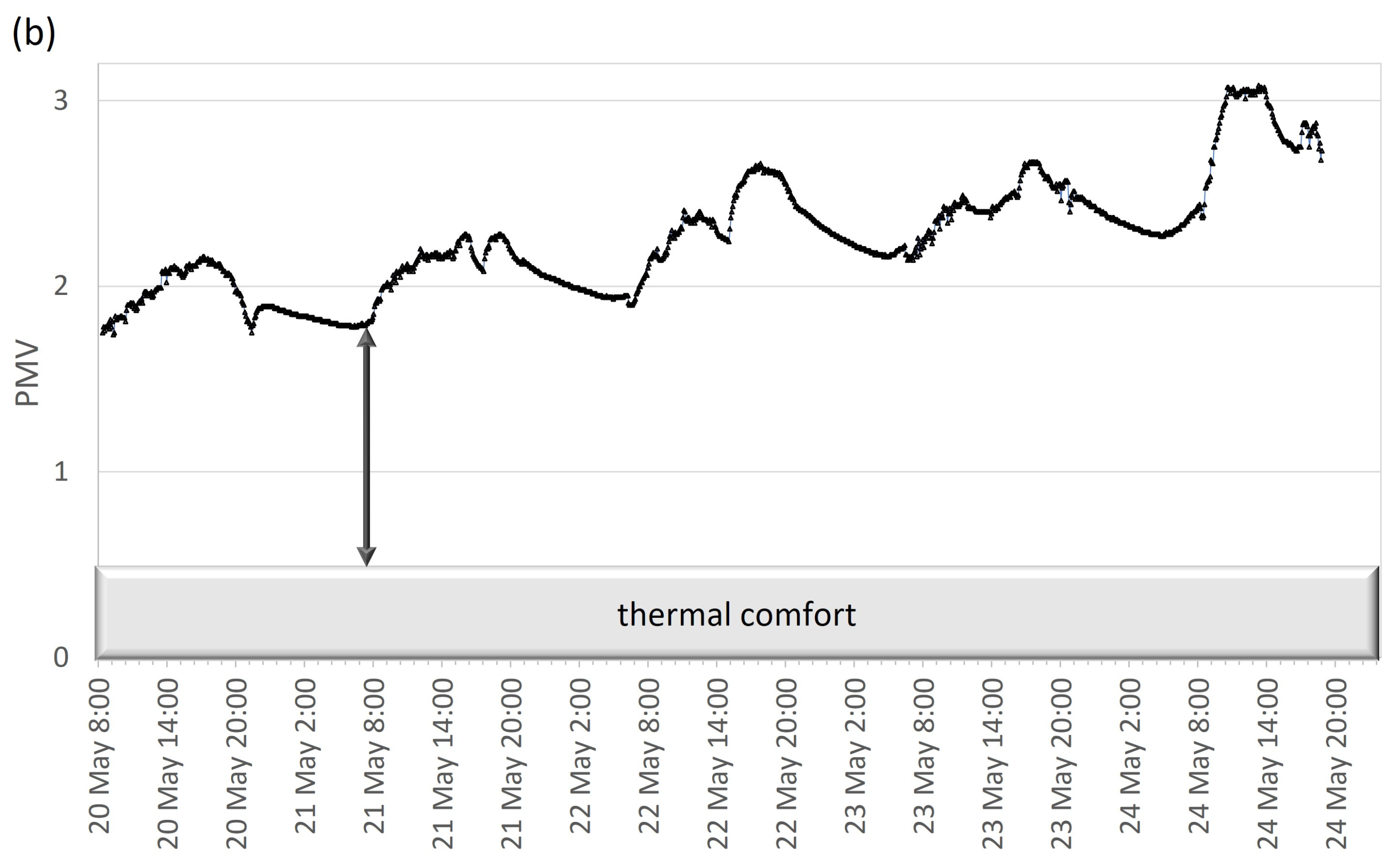
3.1. Experimental Analysis and Survey
3.2. Survey Results
- 9 men and 95 women—average physical activity,
- age of respondents: 19–23 years old,
- height of the respondents: 160–185 cm,
- clothing: light, shorts/leggings and t-shirts.
3.3. Simulation Variants and Results
- Tout—outdoor air temperature [°C],
- Tint—indoor air temperature [°C].
- Variant 1—external wall layering: external silicate plaster and adhesive layer reinforced with 1 cm thick mesh, thermal insulation—polystyrene Platinum 30 cm, plain concrete 25 cm (with parameters as in Table 5), internal mineral plaster 1 cm.
- Variant 2—aerated concrete in the construction layer with parameters as per Table 5.
- Variant 3—clinker bricks in the construction layer with parameters as in Table 5.
- Variant 4—solid bricks in the construction layer with parameters as in Table 5.
- Variant 5—natural stone in the construction layer with parameters as in Table 5.
- Variant 6—hollow silicate masonry units in the construction layer with parameters as in Table 5.
- Variant 7—solid silicate masonry units in the construction layer with parameters as in Table 5.
- Variant 8—reinforced concrete in the structural layer with parameters as in Table 5.
4. Discussion
5. Conclusions
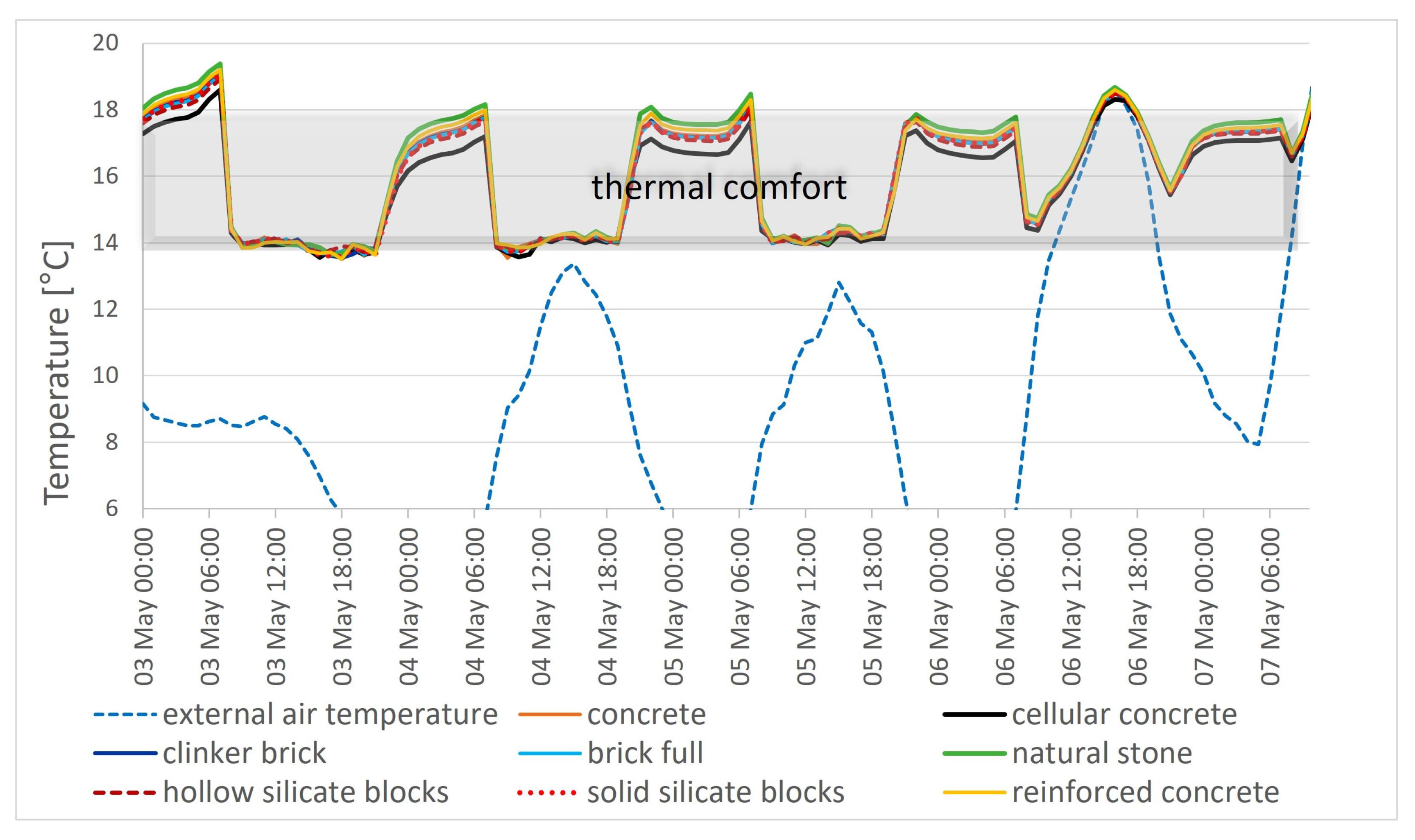
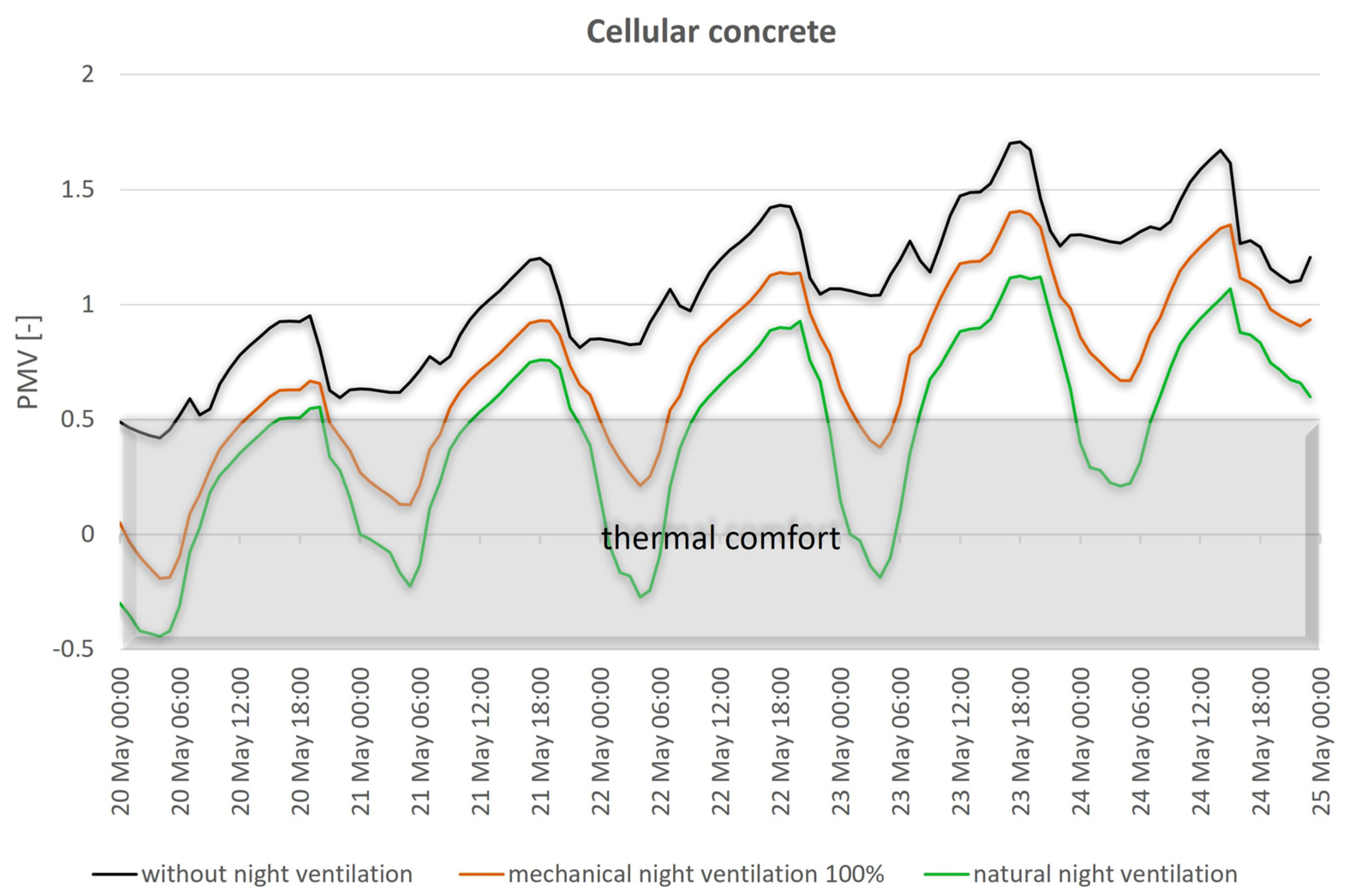
- Night-time cooling can have a large impact on protection against overheating in passive buildings during summer. Intensive natural ventilation is associated with the highest number of hours in the comfort range: 28.1–32.4% more hours compared to the variant without night-time ventilation. The use of mechanical ventilation, operating at night at maximum capacity, will result in an increase in the number of hours with air temperatures in the −0.5 < PMV < +0.5 range by only 14.1–21.3%.
- In the case where natural ventilation was used at night the maximum indoor air temperature during the day was lower by 2.4–3.3 °K, relative to the case where no night-time ventilation was used.
- With mechanical ventilation operating during the night at its design-recommended minimum level (20%), the maximum internal air temperature is only 0.4–0.6 K lower than without night ventilation. Mechanical ventilation operating at its maximum capacity can reduce maximum indoor temperature by 1.2–1.6 K.
- In the hall under study, the design of the ventilation system addressed the necessary hygienic air exchange resulting from the maximum number of users (maximum 0.75 ach). The design of the facility, taking into account thermal comfort, should allow much more intensive forced air exchange, even several exchanges during the hour [46].
- One important advantage of mechanical ventilation is its independence from external conditions, certainty of operation and adjustability. However, its significant cost and additional energy consumption is a downside.
- Natural ventilation depends directly on climatic conditions, poses problems of safety, protection from flooding, wind damage to windows, etc.
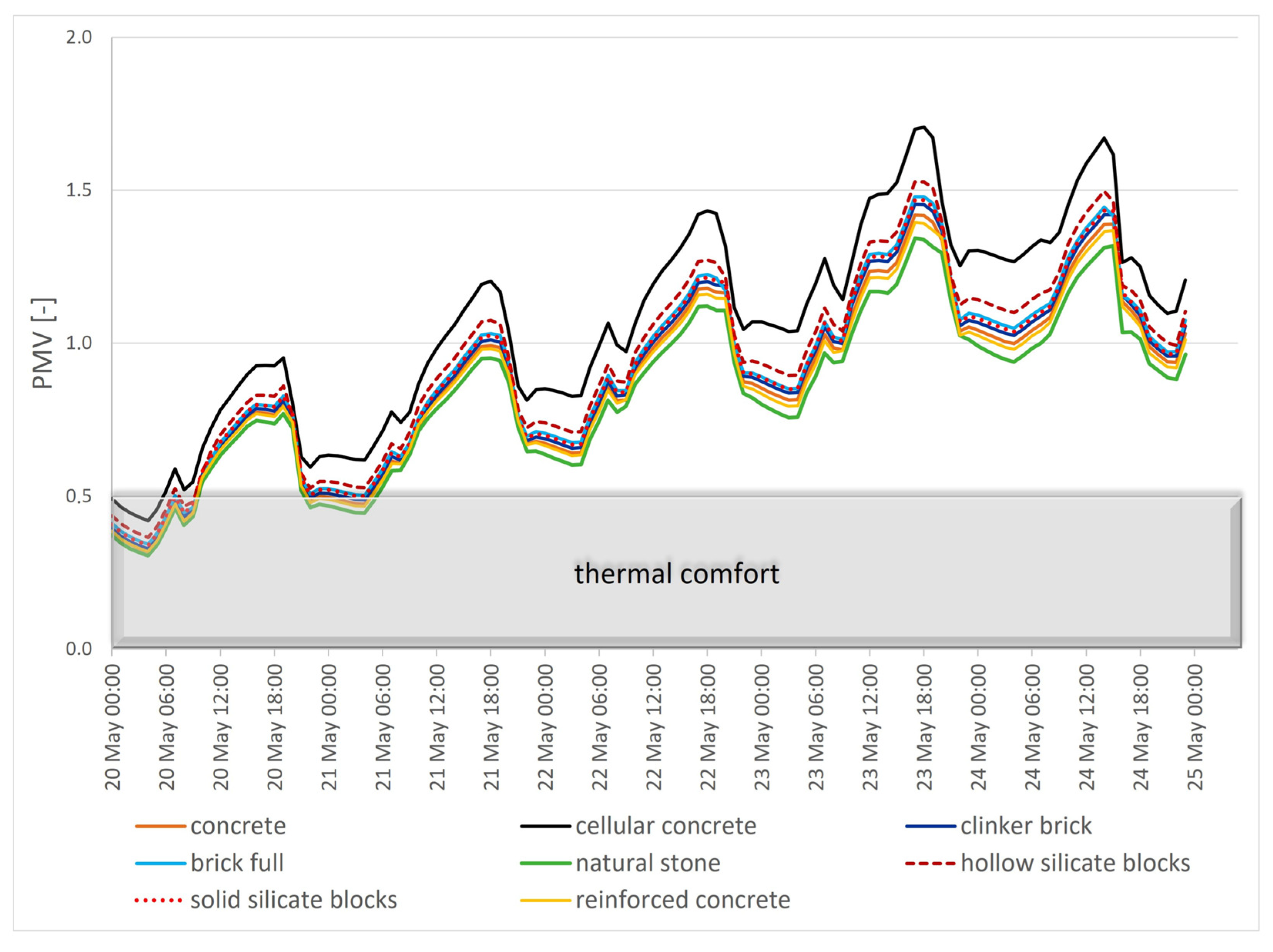
- In the case of a well-insulated sports hall with a very large volume, the thermal capacity of exterior wall materials has little effect on improving thermal conditions. It is not significant in shaping thermal comfort in summer. This is due to the low volume of wall materials in relation to the much greater volume of this building. In the case of residential or office buildings with small rooms, these proportions are different and the influence of the volume of the partitions can be much greater.
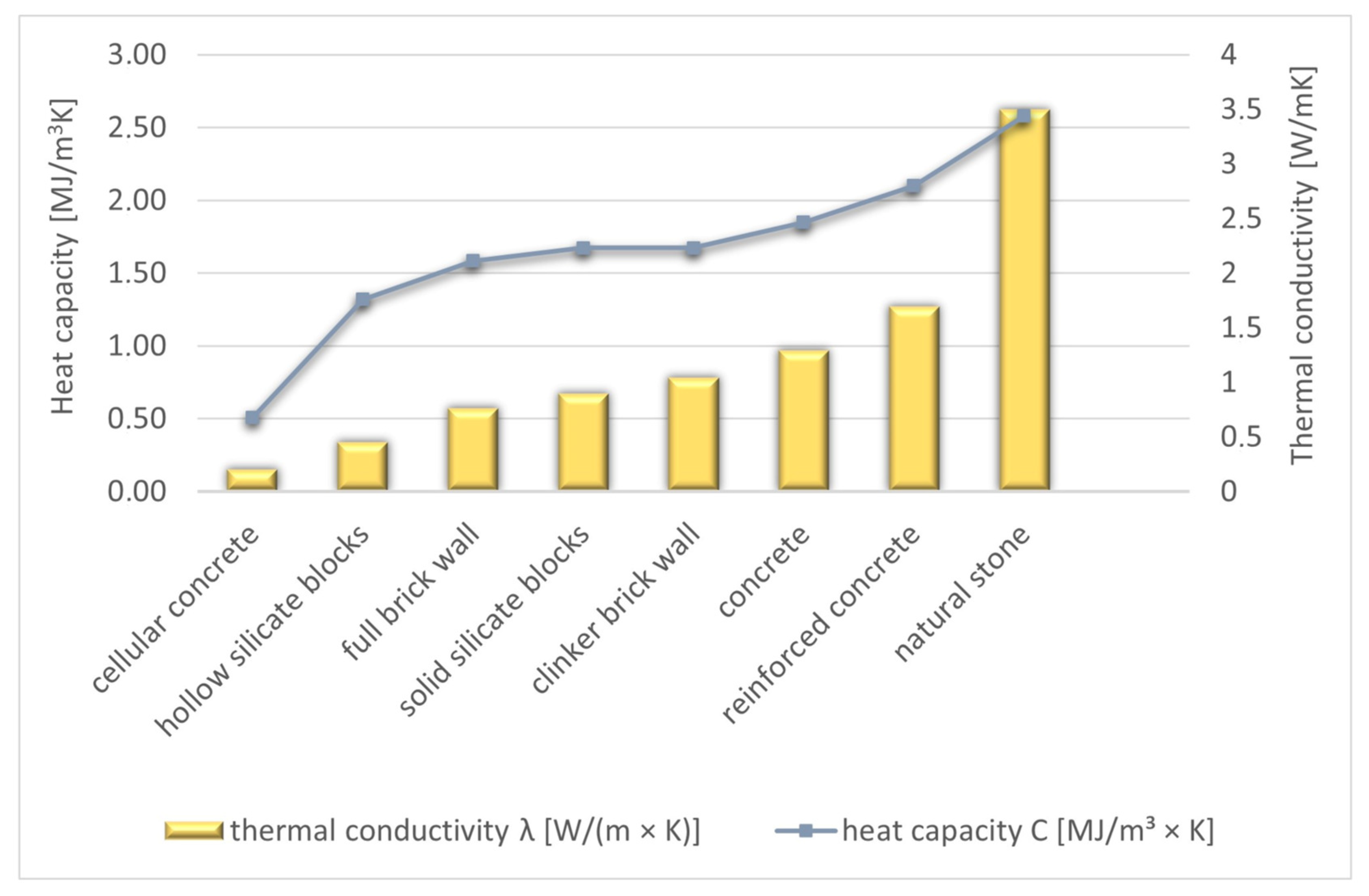
- Solid materials (natural stone, reinforced concrete), with high values of effusivity coefficient and temperature equalisation, allow slightly better results than lightweight materials with lower thermal conductivity.
- The high thermal capacity of the envelope reduces the occurrence of very high air temperature values inside the building, thus reducing overheating.
- The type of partition material is all the more important the greater the night-time air exchange rate.
- Opening windows at night results in a reduction in the daytime indoor air temperature (e.g., at 2 p.m.) by 2.2–3.3 K for lightweight cellular concrete and 2.0–2.5 K for natural stone compared to the alternative without night-time ventilation.
- The use of high thermal capacity materials in partitions usually promotes a reduction in project costs and provides better structural capabilities (carrying higher loads).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | |
| a | thermal diffusivity coefficient (temperature compensation coefficient) |
| cp | specific heat capacity [J/(kg × K)] |
| e | |
| PMV | Predicted Mean Vote |
| PPD | Predicted Percentage of Dissatisfied |
| Tint | indoor air temperature [°C] |
| Tout | outdoor air temperature [°C] |
| U | heat transfer coefficient W/m2K |
| Greek letters | |
| λ | thermal conductivity coefficient [W/mK] |
| ρ | density [kg/m3] |
References
- Kuczyński, T.; Staszczuk, A. Experimental study of the influence of thermal mass on thermal comfort and cooling energy demand in residential buildings. Energy 2020, 195, 116984. [Google Scholar] [CrossRef]
- Perino, M.; Serra, V. Switching from static to adaptable and dynamic building envelopes: A paradigm shift for the energy efficiency in buildings. J. Façade Des. Eng. 2015, 3, 143–163. [Google Scholar] [CrossRef]
- Stazi, F.; Bonfigli, C.; Tomassoni, E.; Di Perna, C.; Munafò, P. The effect of high thermal insulation on high thermal mass: Is the dynamic behaviour of traditional envelopes in Mediterranean climates still possible? Energy Build. 2015, 88, 367–383. [Google Scholar] [CrossRef]
- Givoni, B. Passive cooling of buildings by natural energies. Energy Build. 1979, 2, 279–285. [Google Scholar] [CrossRef]
- Holmes, M.; Hacker, J. Climate change, thermal comfort and energy: Meeting the design challenges of the 21st century. Energy Build. 2007, 39, 802–814. [Google Scholar] [CrossRef]
- Slee, B.; Parkinson, T.; Hyde, R. Quantifying useful thermal mass: How much thermal mass do you need? Archit. Sci. Rev. 2014, 57, 271–285. [Google Scholar] [CrossRef]
- Reynders, G.; Nuytten, T.; Saelens, D. Potential of structural thermal mass for demand-side management in dwellings. Build. Environ. 2013, 64, 187–199. [Google Scholar] [CrossRef]
- Dominkoviĉ, D.F.; Wahlroos, M.; Syri, S.; Schrøder Pedersen, A. Influence of different technologies on dynamic pricing in district heating systems: Comparative case studies. Energy 2018, 153, 136–148. [Google Scholar] [CrossRef]
- Gryś, S. Określanie czasu termicznego wymuszenia skokowego w celu wykrycia zmiany grubości pierwszej warstwy struktury dwuwarstwowej. In Proceedings of the XLVI Intercollegiated Conference of Metrologists MKM’2014 and 19th International Metrolog Seminar MSM’2014, Gdańsk, Poland, 13–16 September 2014. [Google Scholar]
- Minkina, W. Pomiary Termowizyjne—Przyrządy i Metody; Wydawnictwo Politechniki Częstochowskiej: Częstochowa, Poland, 2004; ISBN 83-7193-237-5. [Google Scholar]
- Dokka, T.H. Varmelagringseffekt Ved Bruk av Tunge Materialer i Bygninger (Effect of Thermal Storage by Use of Heavy Materials in Buildings); SINTEF Report STF 50 A05045; SINTEF: Trondheim, Norway, 2005; ISBN 8214035694. [Google Scholar]
- Gorgolewski, M. Framing Systems and Thermal Mass. Mod. Steel Constr. 2007, 47, 45. [Google Scholar]
- Hietamakai, J.; Kuoppala, M.; Kalema, T.; Taivalantti, K. Thermal Mass of Buildings—Central Researches and their Results; Report 2003:174; Tampere University of Technology, Institute of Energy and Process Engineering: Tampere, Finland, 2003. [Google Scholar]
- Johannenson, G. Possibility to Energy Efficient Houses by New Integrated Calculation Approach; ByggTeknik, No. 3: Stockholm, Sweden, 2006. [Google Scholar]
- Pilch, Z. Beton w Budynkach Efektywnych Energetycznie, Korzyści z Masy Termicznej; Stowarzyszenie Producentów Cementu: Kraków, Poland, 2007. [Google Scholar]
- Tasnuva, A. Investigating the Impact of Thermal Mass towards Energy Efficient Housing in Canada. Master’s Thesis, Rajshahi University of Engineering and Technology, Rajshahi, Bangladesh, 2007. [Google Scholar]
- Yinping, Z.; Kunping, L.; Qunli, Z.; Hongfa, D. Ideal thermophysical properties for free-cooling (or heating) buildings with constant thermal physical property material. Energy Build. 2006, 38, 1164–1170. [Google Scholar]
- Givoni, B. Effectiveness of mass and night ventilation in lowering the indoor daytime temperatures, Part I: 1993 experimental periods. Energy Build. 1998, 28, 25–32. [Google Scholar] [CrossRef]
- Thomas, J.M.; Algohary, S.; Hammad, F.; Soboyejo, W.O. Materials selection for thermal comfort in passive solar buildings. J. Mater. Sci. 2006, 41, 6897–6907. [Google Scholar] [CrossRef]
- Roberz, F.; Loonen, R.C.G.M.; Hoes, P.; Hensen, J.L.M. Ultra-lightweight concrete: Energy and comfort performance evaluation in relation to buildings with low and high thermal mass. Energy Build. 2017, 138, 432–442. [Google Scholar] [CrossRef]
- Guglielmini, G.; Magrini, U.; Nannei, E. The influence of the thermal inertia of building structures on comfort and energy consumption. J. Build. Phys. 1981, 5, 59–72. [Google Scholar] [CrossRef]
- Rehman, A.; Shuli Liu, M.; Shukla, A. A state of art review on the district heating systems. Renew. Sustain. Energy Rev. 2018, 96, 420–439. [Google Scholar]
- Romanchenko, D.; Kensby, J.; Odenberger, M.; Johnsson, F. Thermal energy storage in district heating: Centralised storage vs. storage in thermal inertia of buildings. Energy Convers. Manag. 2018, 162, 26–38. [Google Scholar] [CrossRef]
- Masy, G.; Georges, E.; Verhelst, C.; Lemort, V.; Andrĕ, P. Smart grid energy flexible buildings through the use of heat pumps and building thermal mass as energy storage in the Belgian context. Sci. Technol. Built Environ. 2015, 21, 800–811. [Google Scholar] [CrossRef]
- Gregory, K.; Moghtaderi, B.; Sugo, H.; Page, A. Effect of thermal mass on the thermal performance of various Australian residential constructions systems. Energy Build. 2008, 40, 459–465. [Google Scholar] [CrossRef]
- Berge, B. The Ecology of Building Materials; Oxford Architectural Press: Oxford, UK, 2001. [Google Scholar]
- Loonen, R.C.G.M.; Trčka, M.; Cóstola, D.; Hensen, J.L. Climate adaptive building shells: State-of-the-art and future challenges. Renew. Sustain. Energy Rev. 2013, 25, 483–493. [Google Scholar] [CrossRef]
- Belka, W. Concrete as Thermal Mass in Low Energy Buildings; Warsaw University of Technology: Warsaw, Poland, 2016. (In Polish) [Google Scholar]
- Golański, M. Building materials as thermal mass in Buildings. Przegląd Bud. 2011, 12, 88–93. (In Polish) [Google Scholar]
- Dudzińska, A. Ways of Shaping and Exploitation of Passive Public Utility Buildings Taking into Consideration the Requirements for Thermal Comfort. Ph.D. Thesis, Cracow University of Technology, Krakow, Poland, 2019. [Google Scholar]
- Architektura pasywna Pyszczek i Stelmach Sp., J. Hala Sportowa Uniwersytetu Rolniczego w Krakowie. Available online: http://architekturapasywna.pl/portfolio/centered-stack-2-2-2-4-2/ (accessed on 24 April 2023).
- Kisilewicz, T.; Dudzińska, A. Summer overheating of a passive sports hall building. Arch. Civ. Mech. Eng. 2015, 15, 1193–1201. [Google Scholar] [CrossRef]
- Dudzińska, A.; Kotowicz, A. Features of materials versus thermal comfort in a passive building. Procedia Eng. 2015, 108, 108–115. [Google Scholar] [CrossRef]
- PN-EN ISO 7730:2006; Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. ISO: Geneva, Switzerland, 2006.
- PN-EN ISO 7726: 2001; Ergonomics of the Thermal Environment—Instruments for Measuring Physical Quantities. ISO: Geneva, Switzerland, 2001.
- Fanger, P.O. Thermal Comfort; Arkady: Warsaw, Poland, 1974. [Google Scholar]
- PN-EN 16798-1:2019-06; Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings Addressing Indoor Air Quality, Thermal Environment, Lighting and Acoustics. European Committee for Standardization: Brussels, Belgium, 2019.
- PN-EN 12464-1:2012; Światło i Oświetlenie. Oświetlenie Miejsc Pracy, Część 1: Miejsca Pracy we Wnętrzach. PKN: Warsaw, Poland, 2012.
- PN-EN ISO 9972:2015-10; Cieplne Właściwości Użytkowe Budynków—Określanie Przepuszczalności Powietrznej Budynków—Metoda Pomiaru Ciśnieniowego z Użyciem Wentylatora. PKN: Warsaw, Poland, 2009.
- Jóźwiak, J.; Podgórski, J. Statystyka od Podstaw; PWE: Warsaw, Poland, 2009. [Google Scholar]
- Matysiak-Rakoczy, K. Budowa Domu z Silikatów—Bloczki Silikatowe, Cegły, Płytki. Available online: https://muratordom.pl/budowa/sciany-murowane/budowa-domu-z-silikatow-bloczki-silikatowe-aa-6Pfy-PK5J-Sg7E.html (accessed on 15 April 2023).
- EN ISO 10456; Materiały i Wyroby Budowlane—Tabele Wartości Projektowych, Określanie Deklarowanych i Projektowych Wartości Cieplnych. ISO: Geneva, Switzerland, 2009.
- EN ISO 6946:2017; Komponenty Budowlane i Elementy Budynku—Opór Cieplny i Współczynnik Przenikania Ciepła—Metody Obliczania. ISO: Geneva, Switzerland, 2017.
- PN-83/B-03430; Wentylacja w Budynkach Mieszkalnych Zamieszkania Zbiorowego i Użyteczności Publicznej—Wymagania (Uaktualniona 8 Lutego 2000 Roku PN-83/B-03430/Az3:2000). PKN: Warsaw, Poland, 2000.
- Dudzińska, A.; Kisilewicz, T. Alternative Ways of Cooling a Passive School Building in Order to Maintain Thermal Comfort in Summer. Energies 2020, 14, 70. [Google Scholar] [CrossRef]
- Dudzińska, A.; Kisilewicz, T. Efficiency of night ventilation in limiting the overheating of passive sports hall, MATBUD’2020–Scientific-Technical Conference: E-mobility. Sustain. Mater. Technol. 2020, 322, 01031. [Google Scholar] [CrossRef]
- Artmann, N.; Manz, H.; Heiselberg, P. Parameter study on performance of building cooling by night-time ventilation. Renew. Energy 2008, 33, 2589–2598. [Google Scholar] [CrossRef]









| Date | Hours | Number of Occupied Sectors | Approximate Number of People in the Room/h |
|---|---|---|---|
| 20 May | 11.00–14.00 | 2 | 50 |
| 14.00–16.30 | 1 | 25 | |
| 17.30–22.00 | 2 | 15 | |
| 21 May | 8.00–10.00 | 2 | 50 |
| 10.00–11.00 | 1 | 25 | |
| 11.00–15.30 | 2 | 50 | |
| 15.30–17.00 | 0 | 0 | |
| 17.00–18.00 | 1 | 25 | |
| 18.00–19.00 | 2 | 50 | |
| 19.00–20.00 | 1 | 10 | |
| 22 May | 8.30–10.00 | 1 | 25 |
| 10.00–11.00 | 2 | 30 | |
| 11.30–13.00 | 3 | 75 | |
| 13.00–14.30 | 1 | 25 | |
| 14.30–16.00 | 0 | 0 | |
| 16.00–18.00 | 2 | 30 | |
| 18.00–20.00 | 2 | 50 | |
| 20.00–22.00 | 1 | 15 | |
| 23 May | 8.00–11.00 | 1 | 25 |
| 11.00–12.00 | 2 | 30 | |
| 12.00–16.00 | 0 | 0 | |
| 16.00–19.00 | 3 | 50 | |
| 19.00–20.00 | 1 | 10 | |
| 20.00–22.00 | 3 | 75 | |
| 24 May | 9.00–15.00 | 3 | 50 |
| Date of Measurement | Windows on the Southeast Facade | Windows on the Northwest Facade |
|---|---|---|
| 20 May | tilted 7.00–21.00 | tilted 8.00–21.00 |
| 21 May | closed | closed |
| 22 May | tilted 14.00–20.00 | tilted 19.00–20.00 |
| 23 May | tilted 8.00–12.00 and 16.00–21.00 | tilted 19.00–22.00 |
| 24 May | tilted 8.00–20.00 | tilted 9.00–18.00 |
| Environmental Parameters (Average Values) | Unit | First Measurement Series | Second Measurement Series |
|---|---|---|---|
| Indoor air temperature ta | [°C] | 27.9 | 24.1 |
| Indoor air humidity | [%] | 58.28 | 50.85 |
| Radiation temperature tr | [°C] | 28.8 | 24.30 |
| PMV | [-] | 1.14 | 2.26 |
| PPD | [%] | 33.15 | 84.18 |
| Fanger Scale | How Would You Rate the Temperature in the Hall? | |
|---|---|---|
| Woman | Man | |
| +3 (hot) | 30 | - |
| +2 (warm) | 35 | 3 |
| +1 (quite warm) | 19 | 1 |
| 0 (neutral) | 11 | 5 |
| −1 (quite cool) | - | - |
| −2 (cool) | - | - |
| −3 (cold) | - | - |
| Construction Material | Density ρ [kg/m3] | Thermal Conductivity λ [W/(m × K)] | Specific Heat c [J/(kg × K)] | Thermal Capacity C [MJ/m3 × K] | Thermal Diffusivity (Temperature Compensation Coefficient) a [m2/s] | Material Effusivity e [(W × s1/2)/(m2 × K)] |
|---|---|---|---|---|---|---|
| Concrete | 2200 | 1.3 | 840 | 1.85 | 7.03 × 10−7 | 1549.97 |
| Aerated concrete | 600 | 0.21 | 840 | 0.50 | 4.17 × 10−7 | 325.33 |
| Clinker brick masonry | 1900 | 1.05 | 880 | 1.67 | 6.28 × 10−7 | 1324.99 |
| Solid brick masonry | 1800 | 0.77 | 880 | 1.58 | 4.86 × 10−7 | 1104.39 |
| Natural stone | 2800 | 3.5 | 920 | 2.58 | 1.36 × 10−6 | 3002.67 |
| Hollow-core silicate masonry units | 1500 | 0.46 | 880 | 1.32 | 3.48 × 10−7 | 779.23 |
| Silicate masonry units | 1900 | 0.9 | 880 | 1.67 | 5.38 × 10−7 | 1226.70 |
| Reinforced concrete | 2500 | 1.7 | 840 | 2.10 | 8.10 × 10−7 | 1889.44 |
| Day of the Week | Hours | Number of People in the Hall/h |
|---|---|---|
| Monday–Friday | 8:00 to 16:00 | 50 |
| 16:00 to 22:00 | 25 | |
| Saturday–Sunday | 9:00 to 20:00 | 50 |
| Construction Material | Indoor Air Temperature ta [°C] | Radiant Temperature tr [°C] | ||
|---|---|---|---|---|
| Average | Maximum | Average | Maximum | |
| Concrete | 19.8 | 26.0 | 20.8 | 25.7 |
| Aerated concrete | 20.0 | 27.2 | 21.0 | 27.0 |
| Clinker brick masonry | 19.8 | 26.1 | 20.8 | 25.8 |
| Solid brick masonry | 19.9 | 26.3 | 20.8 | 26.0 |
| Natural stone | 19.8 | 25.6 | 20.8 | 25.3 |
| Hollow-core silicate masonry units | 19.9 | 26.5 | 20.9 | 26.2 |
| Silicate masonry units | 19.9 | 26.2 | 20.8 | 25.9 |
| Reinforced concrete | 19.8 | 25.9 | 20.8 | 25.6 |
| Construction Material | Indoor Air Temperature ta [°C] | |
|---|---|---|
| Average | Maximum | |
| Concrete | 22.1 | 25.0 |
| Aerated concrete | 23.0 | 25.9 |
| Clinker brick masonry | 22.2 | 25.1 |
| Solid brick masonry | 22.3 | 25.2 |
| Natural stone | 21.9 | 24.6 |
| Hollow-core silicate masonry units | 22.5 | 25.4 |
| Silicate masonry units | 22.3 | 25.2 |
| Concrete | 22.1 | 24.9 |
| Number of Hours with Outdoor Air Temperature < 10 °C | Number of Hours with Outdoor Air Temperature within 10–15 °C | Number of Hours with Outdoor Air Temperature within 15–20 °C | Number of Hours with Outdoor Air Temperature within 20–25 °C | Number of Hours with Outdoor Air Temperature > 25 °C |
|---|---|---|---|---|
| 226 | 484 | 450 | 239 | 65 |
| Construction Material | Number of Hours with −0.5 < PMV< +0.5 | Number of Hours with PMV > 0.5 |
|---|---|---|
| Concrete | 684 | 780 |
| Aerated concrete | 669 | 782 |
| Clinker brick masonry | 681 | 783 |
| Solid brick masonry | 673 | 791 |
| Natural stone | 678 | 786 |
| Hollow-core silicate masonry units | 676 | 788 |
| Silicate masonry units | 675 | 789 |
| Concrete | 675 | 789 |
| Construction Material | Number of Hours with −0.5 < PMV < +0.5 | Number of Hours with PMV > 0.5 |
|---|---|---|
| Concrete | 17 | 103 |
| Aerated concrete | 6 | 114 |
| Clinker brick masonry | 14 | 106 |
| Solid brick masonry | 9 | 111 |
| Natural stone | 18 | 102 |
| Hollow-core silicate masonry units | 9 | 111 |
| Silicate masonry units | 11 | 109 |
| Concrete | 17 | 103 |
| Construction Material | Maximum Indoor Air Temperature [°C] | |||
|---|---|---|---|---|
| No Night-Time Cooling | With 20% Night-Time Cooling | With 100% Night-Time Cooling | Natural Night-Time Cross-Ventilation | |
| Concrete | 26.0 | 25.5 | 24.6 | 23.4 |
| Aerated concrete | 27.2 | 26.8 | 25.6 | 23.9 |
| Clinker brick masonry | 26.1 | 25.7 | 24.7 | 23.4 |
| Solid brick masonry | 26.3 | 25.8 | 24.7 | 23.5 |
| Natural stone | 25.6 | 25.2 | 24.4 | 23.2 |
| Hollow-core silicatemasonry units | 26.5 | 26.0 | 24.9 | 23.6 |
| Silicate masonry units | 26.2 | 25.7 | 24.7 | 23.4 |
| Concrete | 25.9 | 25.4 | 24.6 | 23.3 |
| Construction Material | Number of Hours with Conditions within the Thermal Comfort Range−0.5 < PMV < +0.5 | |||
|---|---|---|---|---|
| No Night-Time Cooling | With 20% Night-Time Cooling | With 100% Night-Time Cooling | Natural Night-Time Cross-Ventilation | |
| Concrete | 684 | 742 | 842 | 975 |
| Aerated concrete | 669 | 712 | 779 | 930 |
| Clinker brick masonry | 681 | 740 | 835 | 980 |
| Solid brick masonry | 673 | 733 | 825 | 966 |
| Natural stone | 678 | 740 | 862 | 992 |
| Hollow-core silicate masonry units | 676 | 728 | 811 | 952 |
| Silicate masonry units | 675 | 734 | 828 | 982 |
| Concrete | 675 | 741 | 847 | 998 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dudzińska, A.; Kisilewicz, T.; Panasiuk, E. Impact of Material Solutions and a Passive Sports Hall’s Use on Thermal Comfort. Energies 2023, 16, 7698. https://doi.org/10.3390/en16237698
Dudzińska A, Kisilewicz T, Panasiuk E. Impact of Material Solutions and a Passive Sports Hall’s Use on Thermal Comfort. Energies. 2023; 16(23):7698. https://doi.org/10.3390/en16237698
Chicago/Turabian StyleDudzińska, Anna, Tomasz Kisilewicz, and Ewelina Panasiuk. 2023. "Impact of Material Solutions and a Passive Sports Hall’s Use on Thermal Comfort" Energies 16, no. 23: 7698. https://doi.org/10.3390/en16237698
APA StyleDudzińska, A., Kisilewicz, T., & Panasiuk, E. (2023). Impact of Material Solutions and a Passive Sports Hall’s Use on Thermal Comfort. Energies, 16(23), 7698. https://doi.org/10.3390/en16237698






