New Reference Current Calculation Method of a Hybrid Power Filter Based on Customer Harmonic Emission
Abstract
:1. Introduction
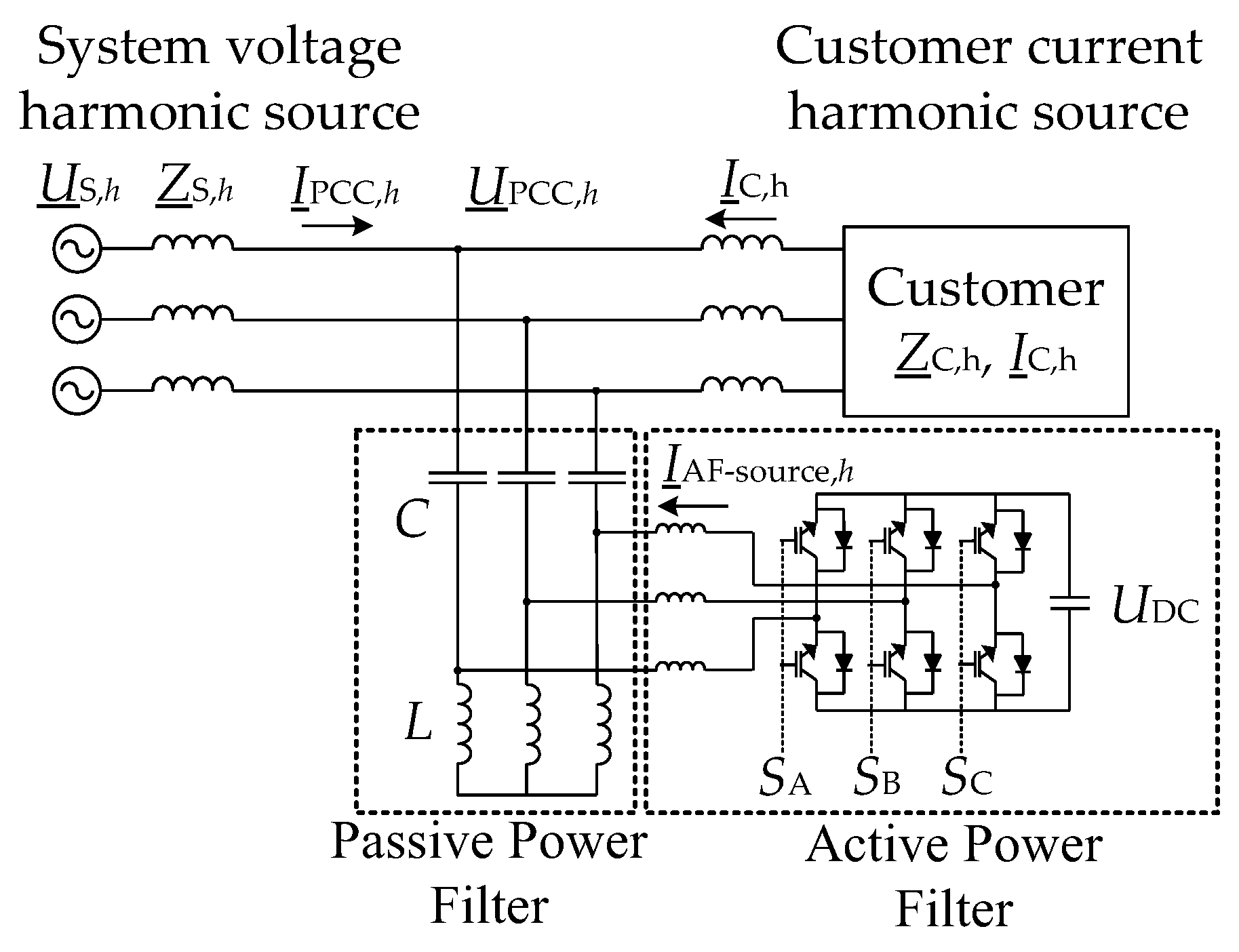
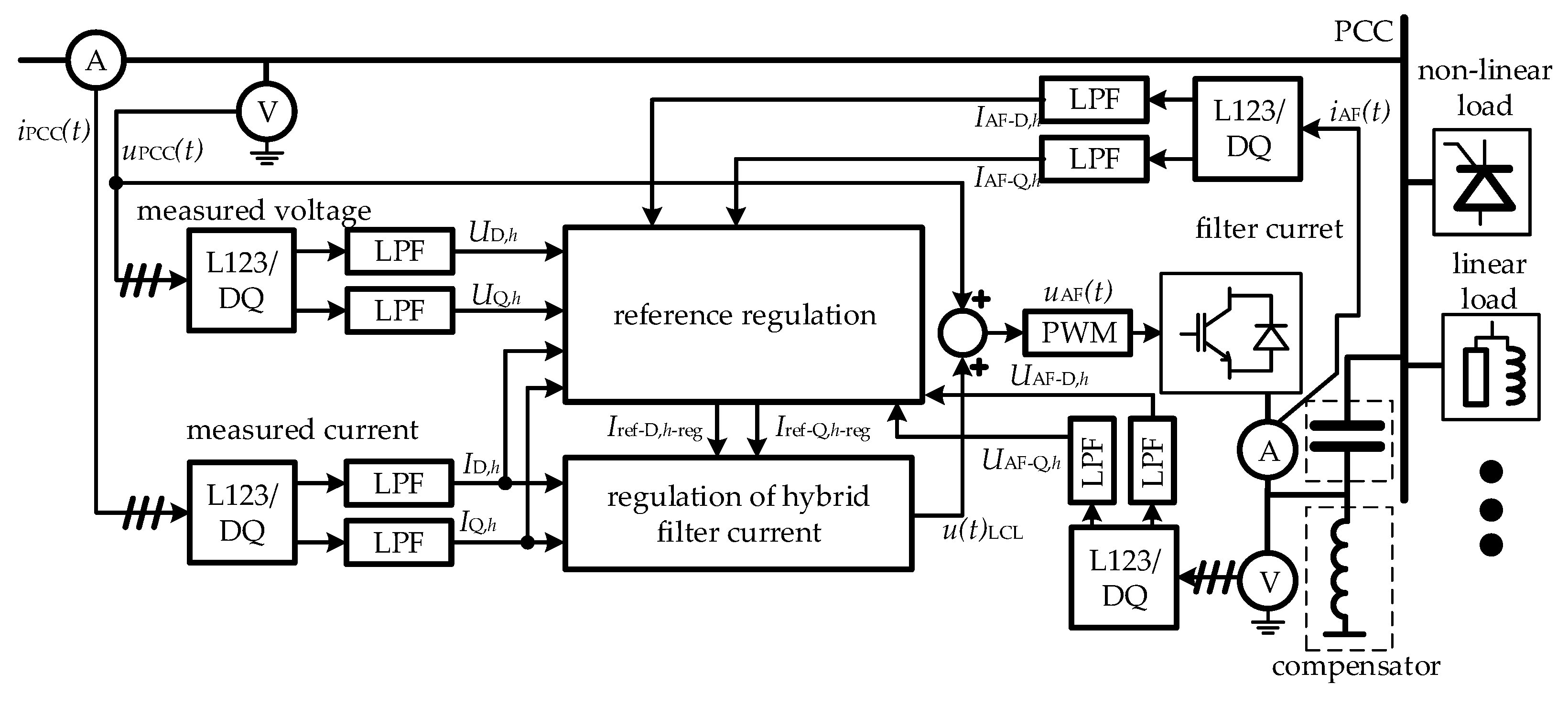
2. Hybrid Power Filter Topology
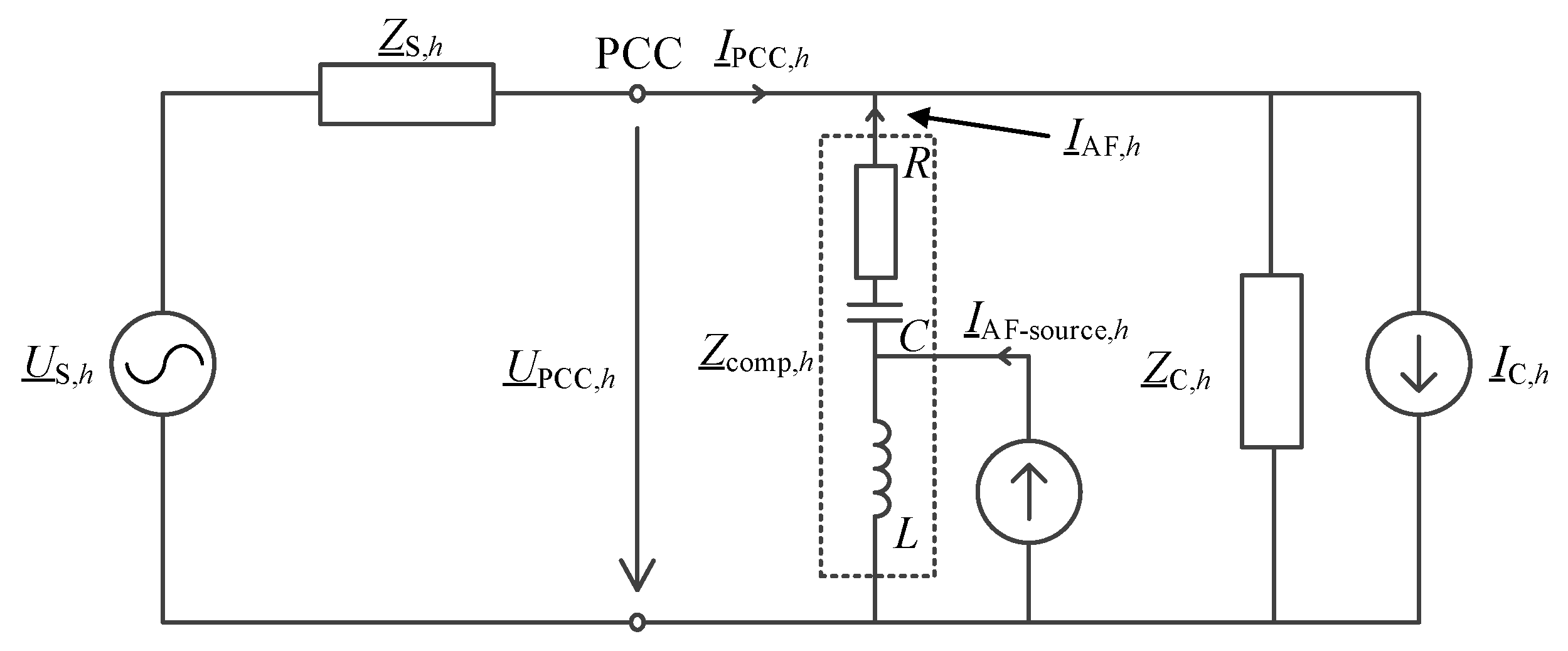
3. Reference Harmonic Impedances
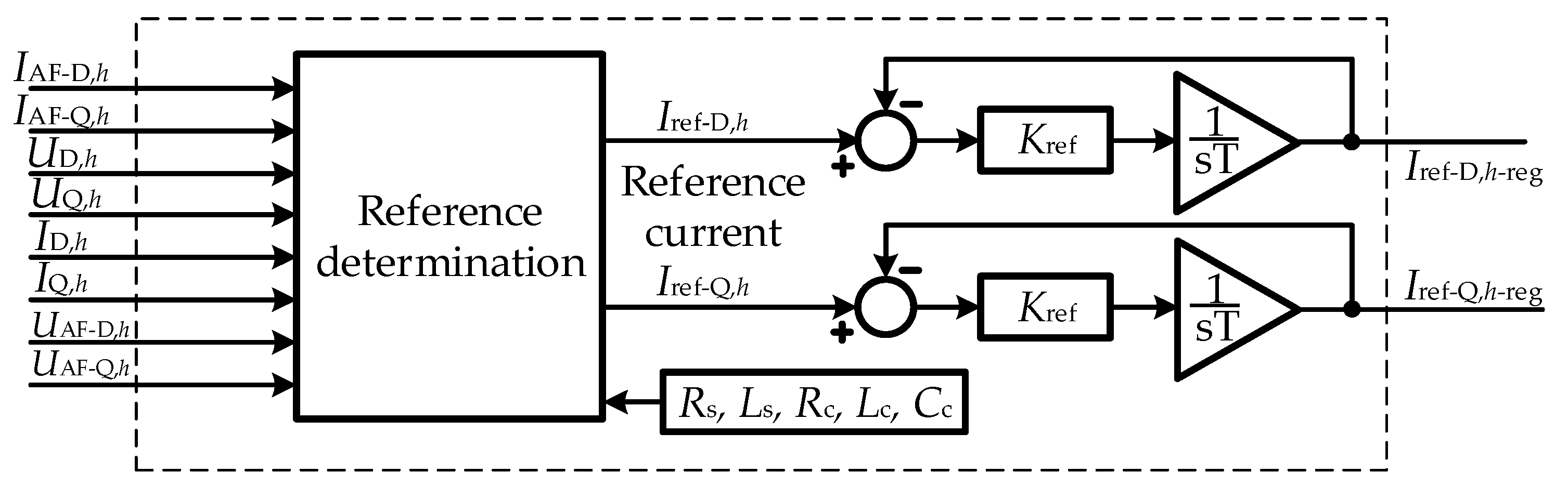
4. Reference Current Determination
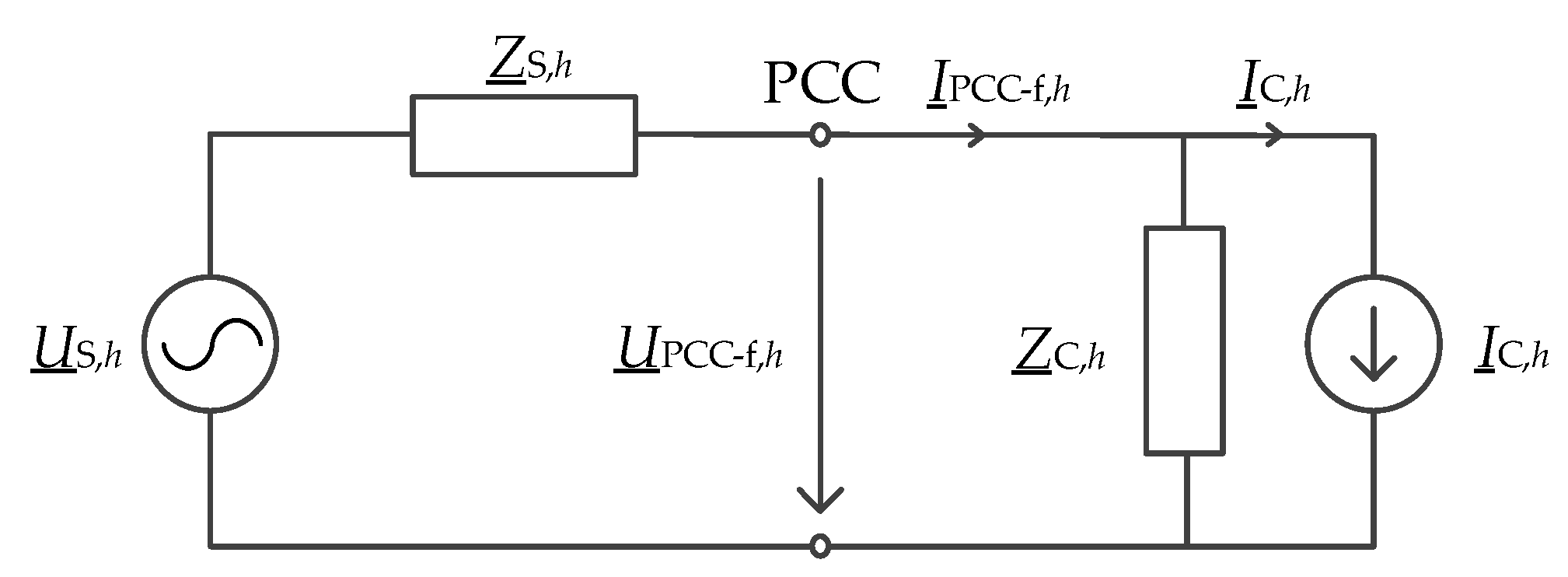
4.1. Harmonic Distortion without Hybrid Power Filter
4.2. Customer Harmonics Emissions and Hybrid Filter Current Reference
4.2.1. Hybrid Power Filter Current Reference
4.2.2. Evaluating Filtering Requirements
- −
- When a scalar value Iref-AF,h is negative, the HPF needs to filter the entire harmonic distortion at the PCC (IPCC-f,h).
- −
- On the other hand, a scalar value that is larger than the fictive harmonic distortion (IPCC-f,h) means that existing equipment, possibly from other customers, has already mitigated the distortion. Thus, further filtering by the HPF becomes unnecessary. This is mathematically represented by:
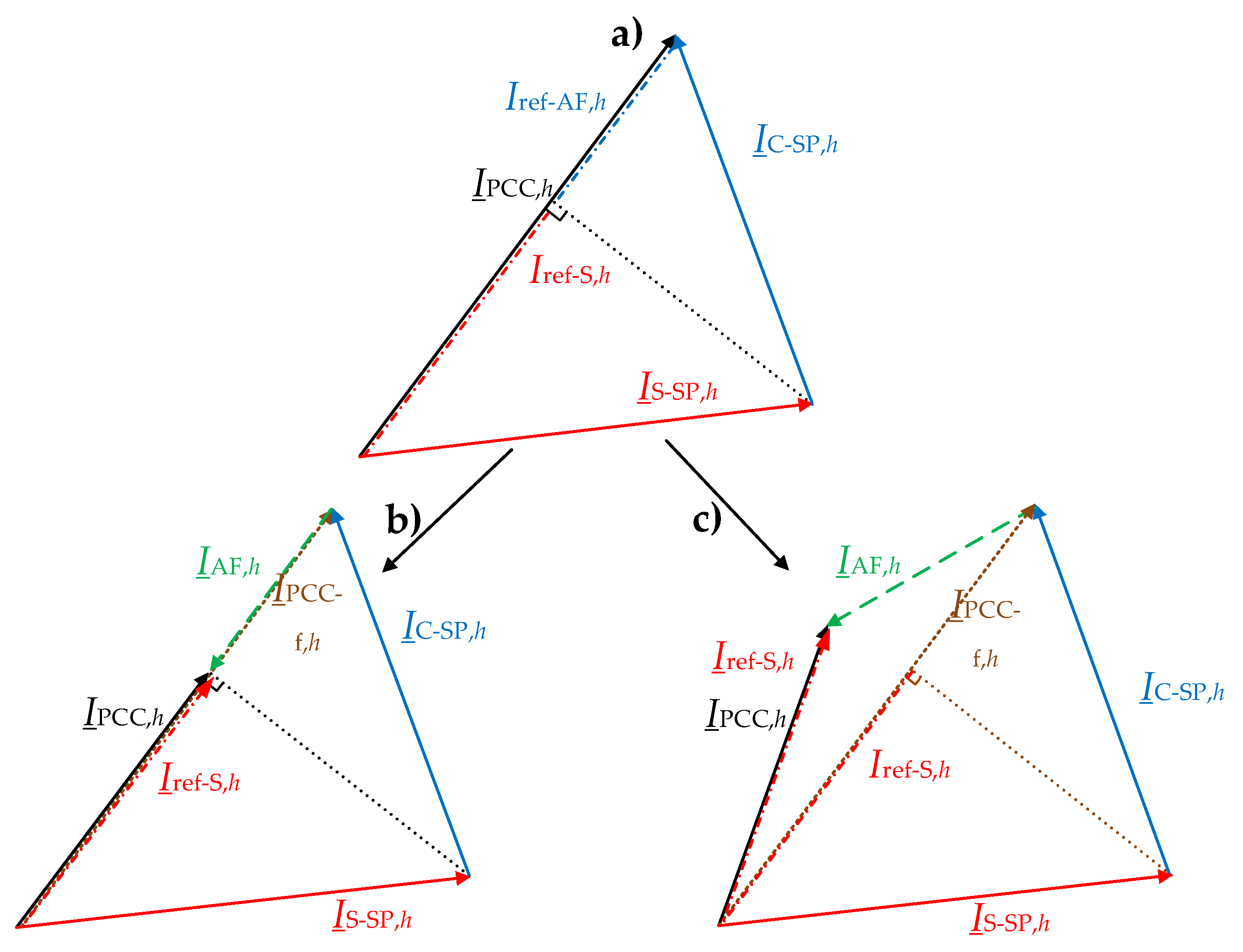
4.3. Phasor Diagram of the Hybrid Power Filter Current Reference Calculation
- −
- Red: representation of the system;
- −
- Blue: customer representation;
- −
- Black: measured harmonic current at the PCC;
- −
- Green: HPF current.
4.4. Reference Calculation Flowchart
5. Hybrid Power Filter Control Algorithm
5.1. Reference Control
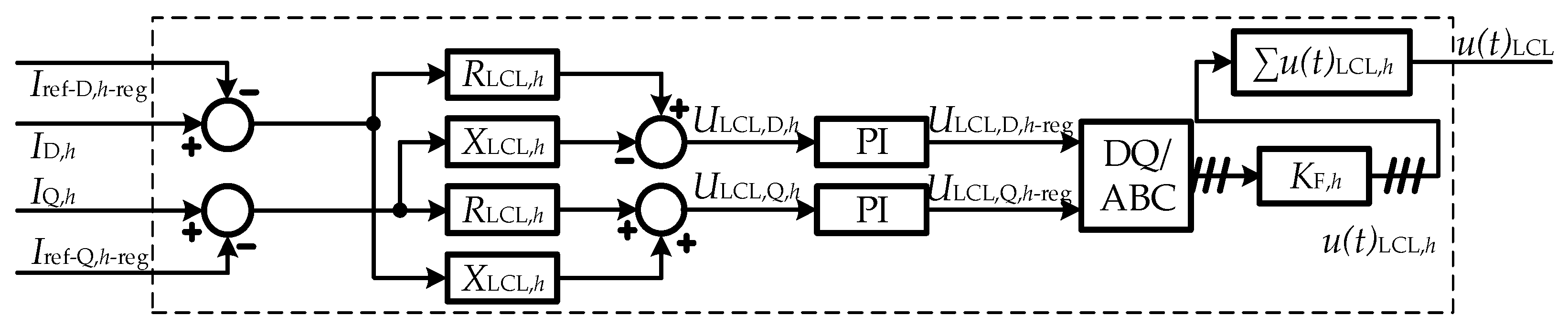
5.2. Main Current Control Block Diagram
- −
- Considering the purpose of use (filtering harmonics in a steady state), the speed of the controller is not of primary importance. We set the initial values of the proportional constant P and the integral constant I low.
- −
- We modeled the controller in the simulation program PSCAD, along with the model of the test system.
- −
- With simulations, we analyzed the behavior of the device with the initial constants and iteratively (trial-and-error approach) changed the constants in small steps to improve the following metrics: reducing overshoot, improving settling time, and ensuring stability.
- −
- For optimal stability, an extra step of measuring the voltage in the active part of the hybrid filter was implemented.
6. Hybrid Power Filter Performance Evaluation
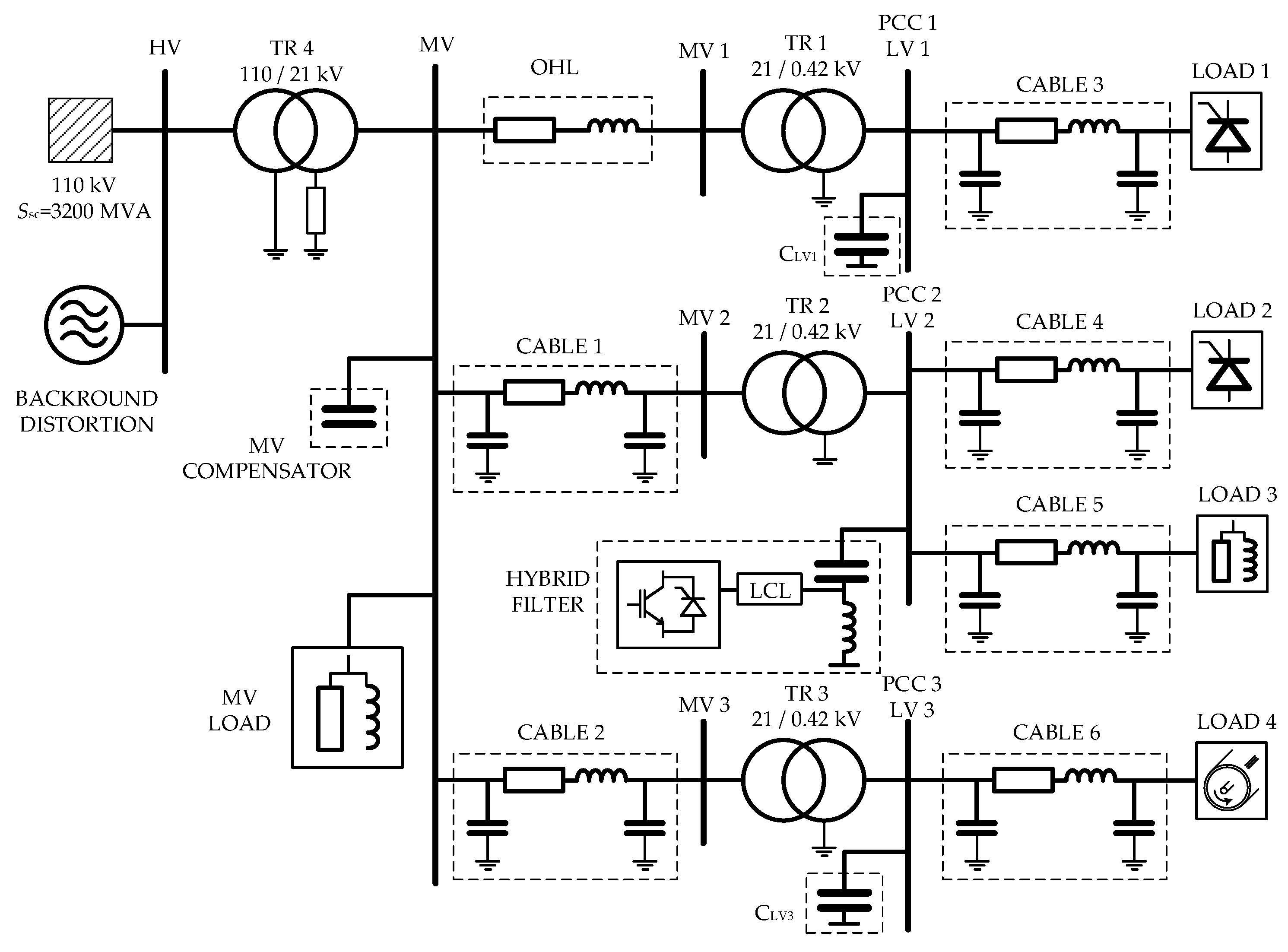
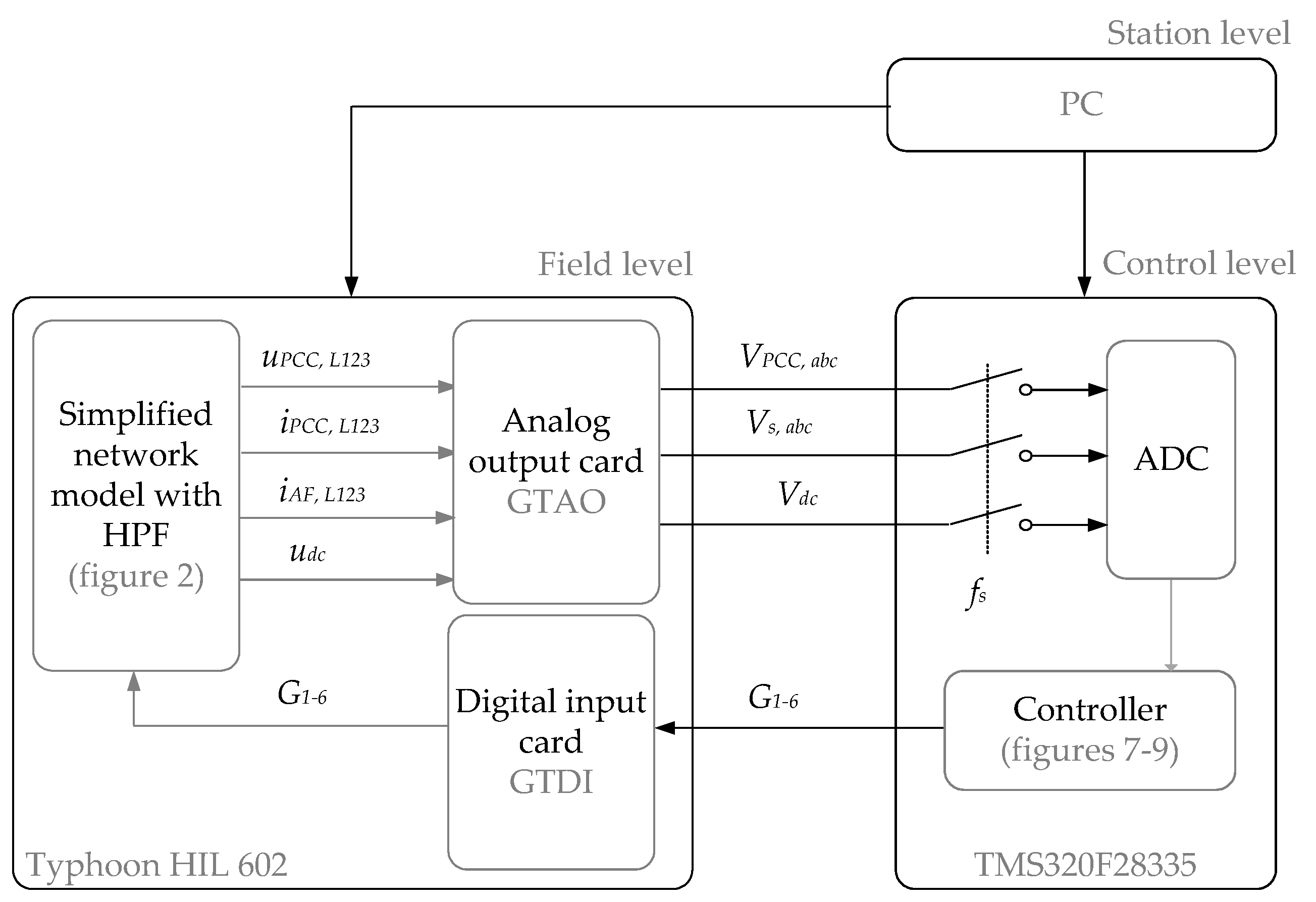
6.1. Introduction to the Test Environment
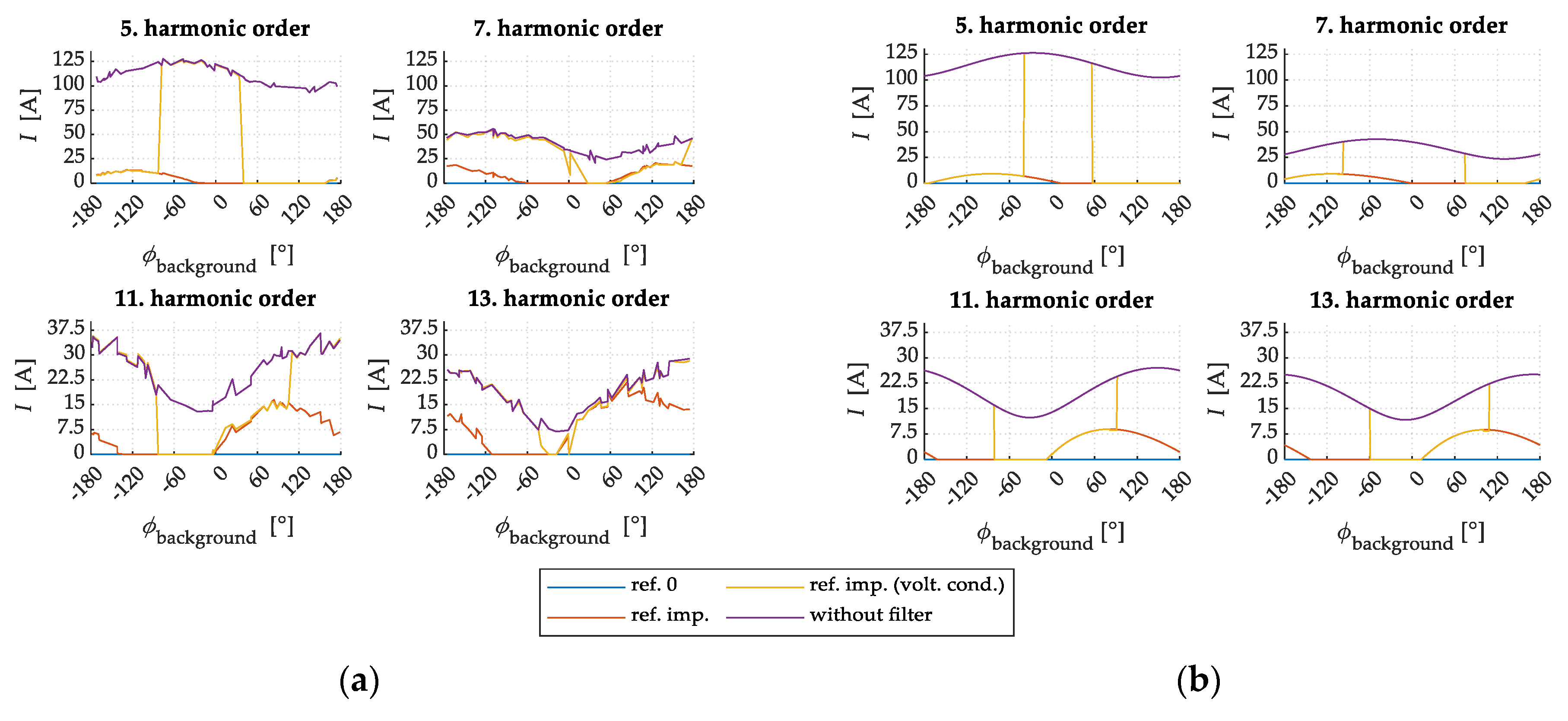
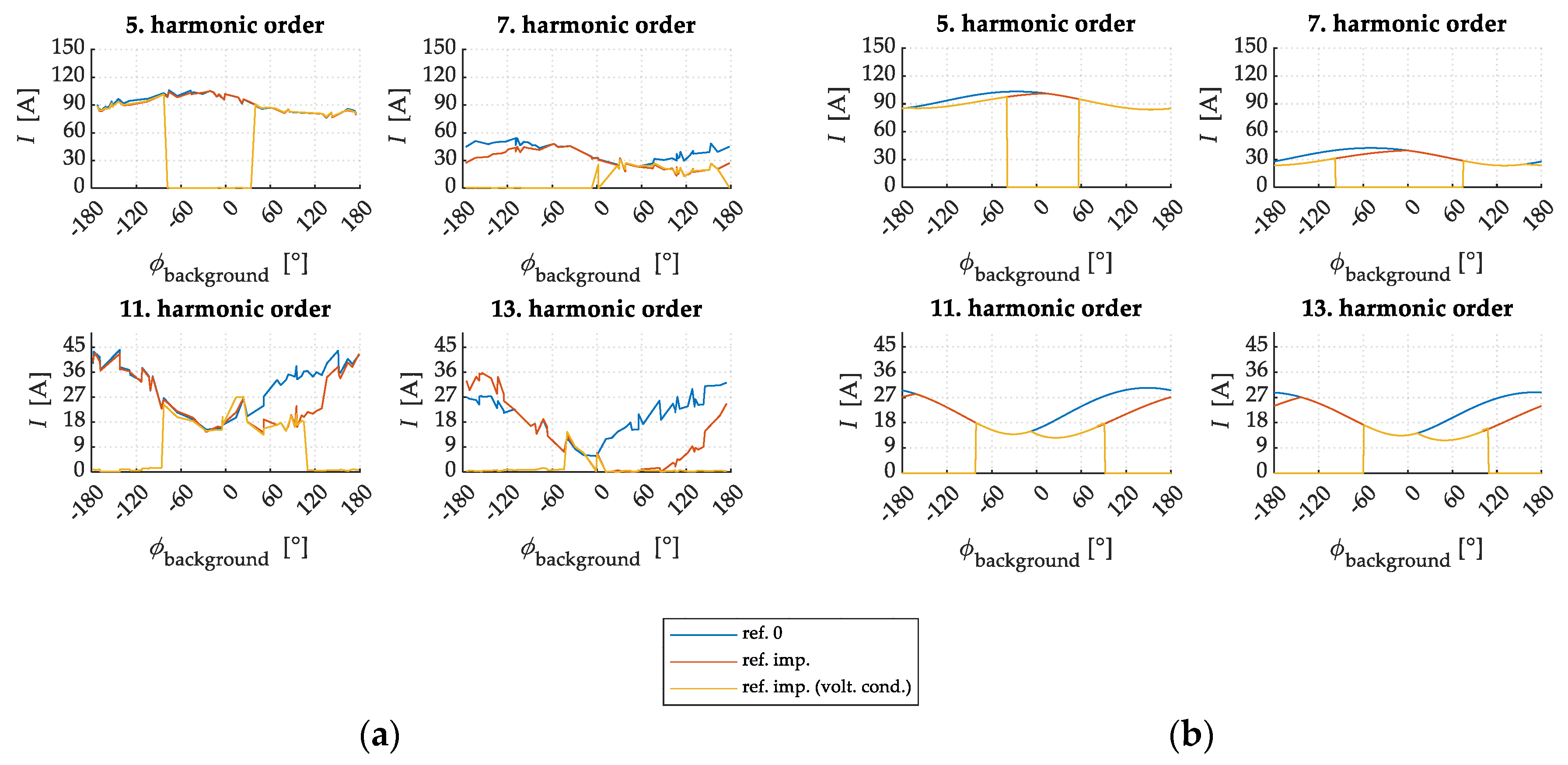
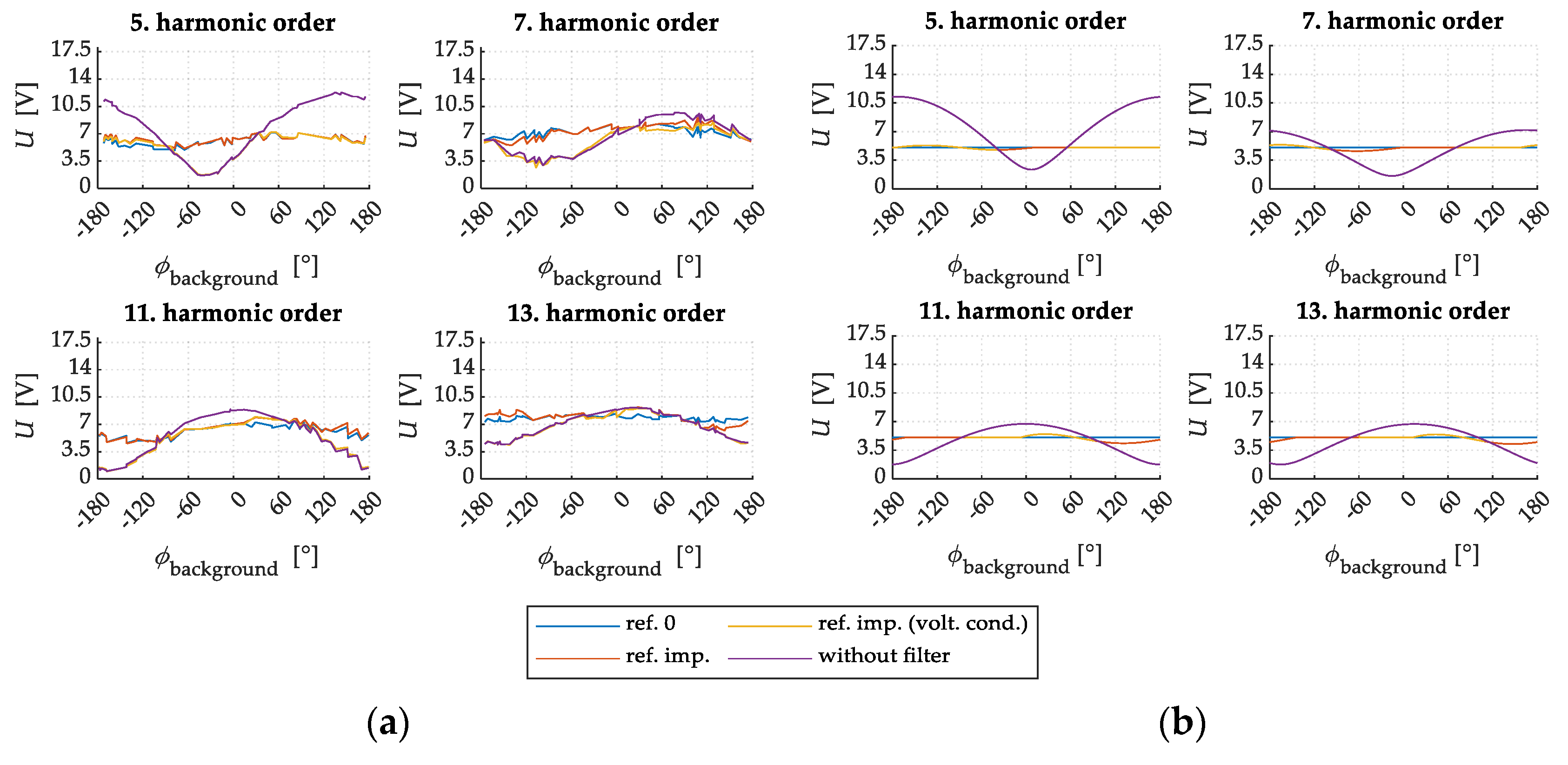
6.2. PSCAD Simulation Results
6.2.1. Filtering Performance Evaluation
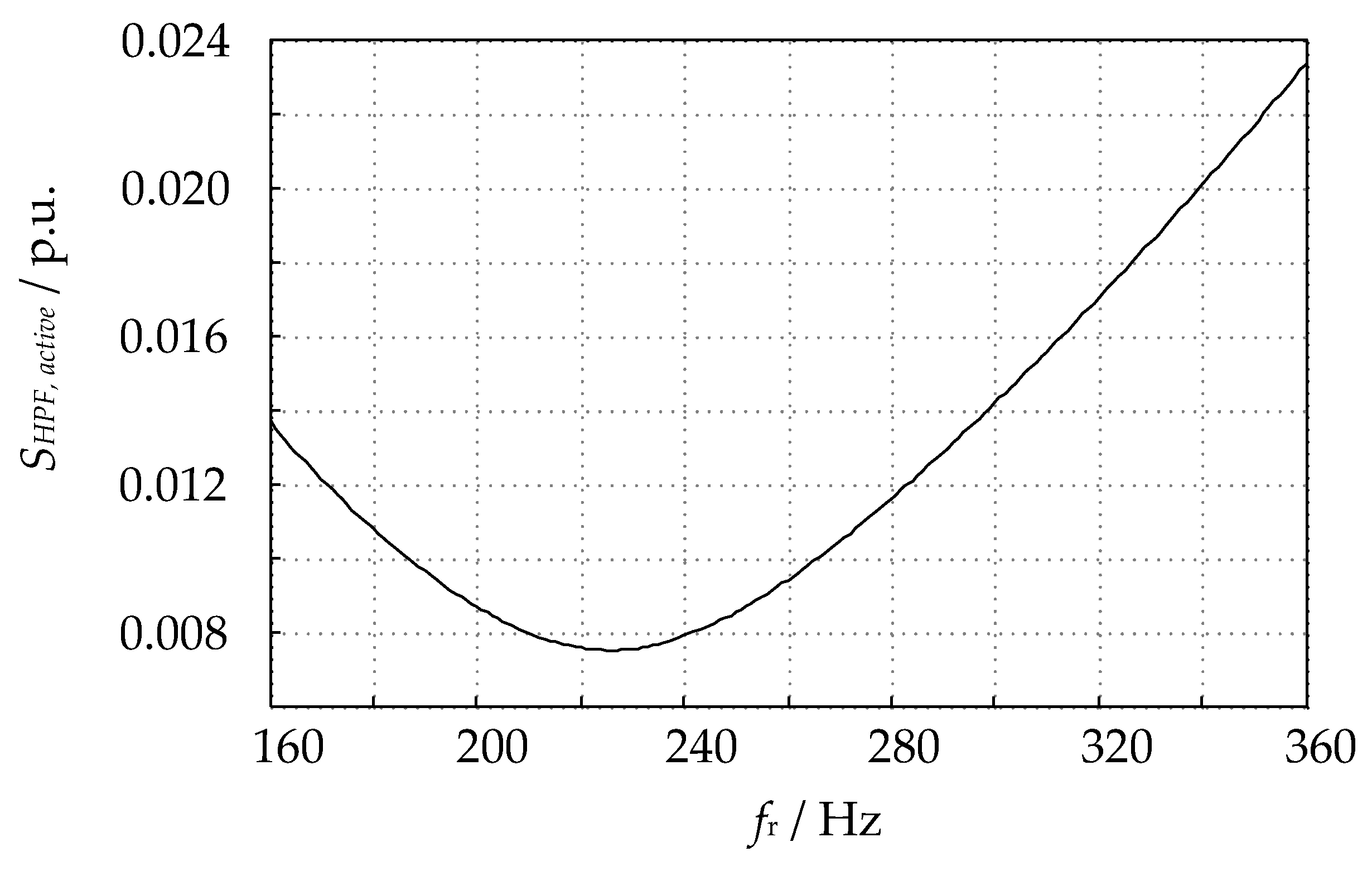
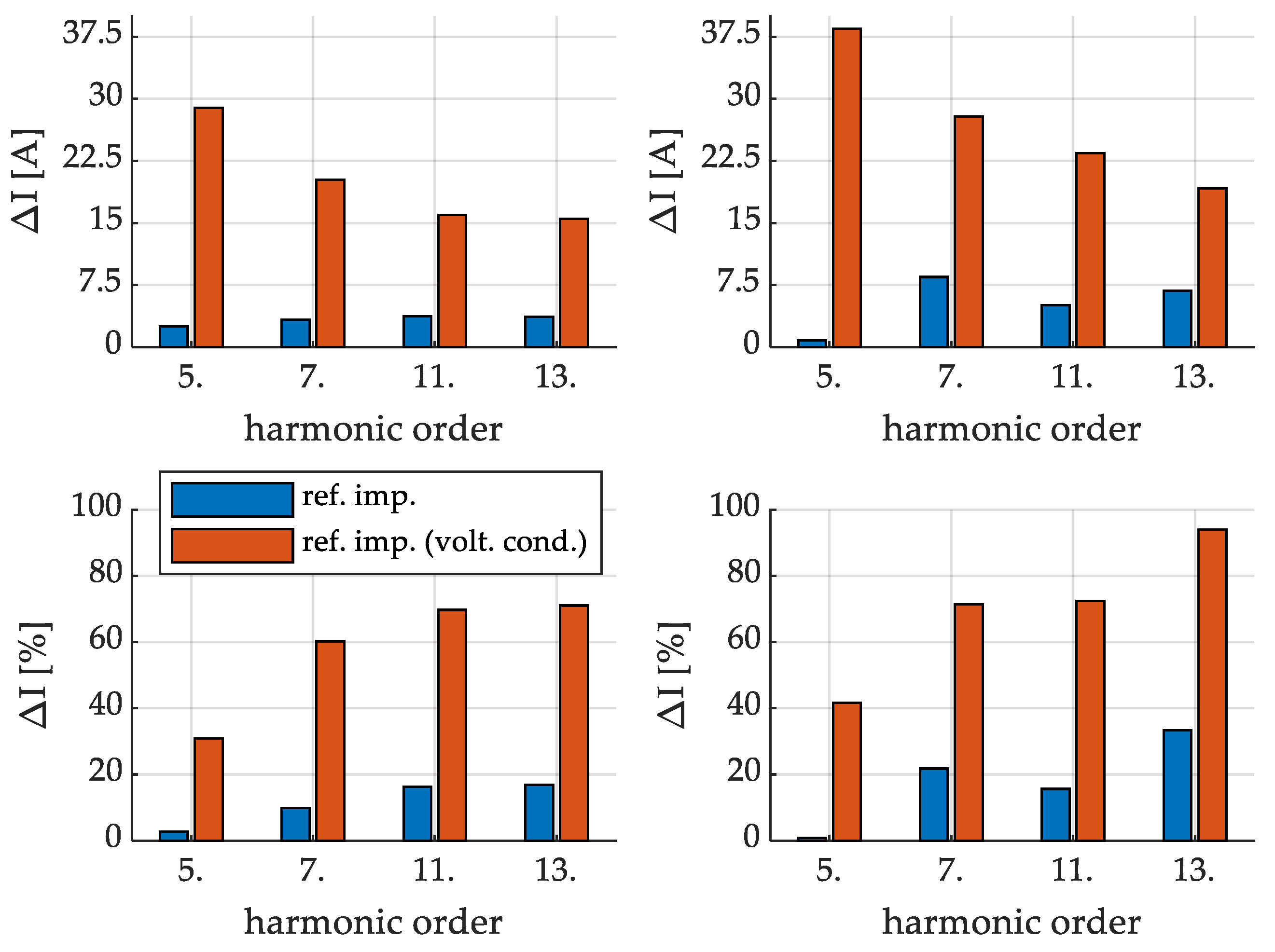
6.2.2. Assessing the Reduction in Required Current Ratings
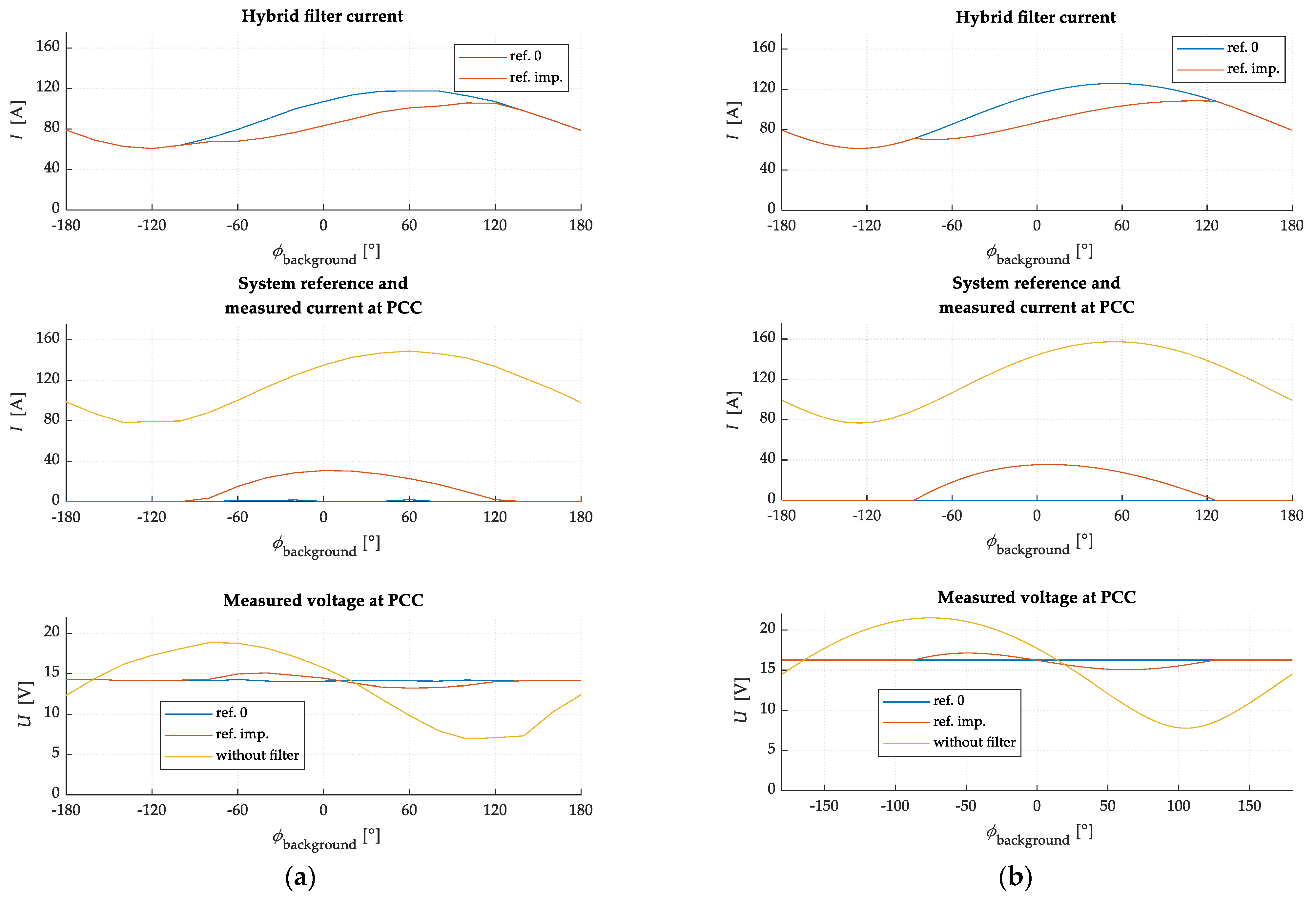
6.3. Controller-in-the-Loop Testing Results
7. Conclusions
- −
- Investigating some other control algorithms for the main current control loops of the HPF in combination with the proposed method for current reference calculation. Our initial focus will be on analyzing proportional-resonant (PR) controllers, which promise potential advantages, such as improved selectivity and transient performance, over the PI controllers currently in use.
- −
- Extended HIL testing on a real-time simulator, aiming for more accurate modeling of the HPF’s active part, currently modeled as an ideal source. Here, we were faced with equipment limitations that needed to be upgraded. Testing will expand to cover a wider range of harmonic distortions and various network topologies, including real network models and devices (nonlinear loads).
- −
- After HIL testing, our attention will move towards the development and laboratory testing of a hardware prototype of the device.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Acronyms
| Abbreviation | Definition |
| ADC | Analog-to-digital converter |
| AF | Active filter |
| CIG | Converter interfaced generation |
| CIL | Controller-in-the-loop |
| DSP | Digital signal processors |
| GTAO | Analog output card |
| GTDI | Digital input card |
| HIL | Hardware in the loop |
| HPF | Hybrid power filter |
| MV BNM | Medium-voltage benchmark model |
| PC | Personal computer |
| PCC | Point-of-common-coupling |
| PI | Proportional integral |
| THD | Total harmonic distortion |
References
- EN 50160; Voltage Characteristics of Electricity Supplied by Public Distribution Systems. IEC: Geneva, Switzerland, 2011.
- Padmanaban, S.; Sharmeela, C.; Holm-Nielsen, J.B.; Sivaraman, P. Power Quality in Modern Power Systems, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Bollen, M.H.J. Introduction to Power Quality. In Understanding Power Quality Problems: Voltage Sags and Interruptions; Wiley-IEEE Press: New York, NY, USA, 2000. [Google Scholar]
- Hernández-Mayoral, E.; Madrigal-Martínez, M.; Mina-Antonio, J.D.; Iracheta-Cortez, R.; Enríquez-Santiago, J.A.; Rodríguez-Rive, O.; Martínez-Reyes, G.; Mendoza-Santos, E. A Comprehensive Review on Power-Quality Issues, Optimization Techniques, and Control Strategies of Microgrid Based on Renewable Energy Sources. Sustainability 2023, 15, 9847. [Google Scholar] [CrossRef]
- Lee, T.-L.; Wang, Y.-C.; Li, J.-C.; Guerrero, J.M. Hybrid active filter with variable conductance for harmonic resonance suppression in industrial power systems. IEEE Trans. Ind. Electron. 2014, 62, 746–756. [Google Scholar] [CrossRef]
- Xue, G.; Chen, B.; Tian, C.; Yuan, J.; Zhou, Y.; Chen, G.; Luo, Y.; Chen, Y. A Novel Hybrid Active Power Filter with Multi-Coupled Coils. Electronics 2021, 10, 998. [Google Scholar] [CrossRef]
- Alasali, F.; Nusair, K.; Foudeh, H.; Holderbaum, W.; Vinayagam, A.; Aziz, A. Modern Optimal Controllers for Hybrid Active Power Filter to Minimize Harmonic Distortion. Electronics 2022, 11, 1453. [Google Scholar] [CrossRef]
- Dash, D.K.; Sadhu, P.K. A Review on the Use of Active Power Filter for Grid-Connected Renewable Energy Conversion Systems. Processes 2023, 11, 1467. [Google Scholar] [CrossRef]
- Fujita, H.; Akagi, H. A practical approach to harmonic compensation in power systems-series connection of passive and active filters. IEEE Trans. Ind. Appl. 1991, 27, 1020–1025. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Cheng, P.-T.; Divan, D.M. Hybrid Solutions for Improving Passive Filter Performance in High Power Applications. IEEE Trans. Ind. Appl. 1997, 33, 3. [Google Scholar] [CrossRef]
- Singh, B.; Verma, V. An Indirect Current Control of Hybrid Power Filter for Varying Loads. IEEE Trans. Power Deliv. 2005, 21, 178–184. [Google Scholar] [CrossRef]
- Inzunza, R.; Akagi, H. A 6.6-kV Transformerless Shunt Hybrid Active Filter for Installation on a Power Distribution System. IEEE Trans. Power Electron. 2005, 20, 893–900. [Google Scholar] [CrossRef]
- Peng, F.; Akagi, H.; Nabae, A. A New Approach to Harmonic Compensation in Power Systems-A Combined System of Shunt Passive and Series Active Filters. IEEE Trans. Ind. Appl. 1990, 26, 983–990. [Google Scholar] [CrossRef]
- Chen, Z.; Blaabjerg, F.; Pedersen, J. Hybrid Compensation Arrangement in Dispersed Generation Systems. IEEE Trans. Power Deliv. 2005, 20, 1719–1727. [Google Scholar] [CrossRef]
- Corasaniti, V.F.; Barbieri, M.B.; Arnera, P.L.; Valla, M.I. Hybrid Active Filter for Reactive and Harmonics Compensation in a Distribution Network. IEEE Trans. Ind. Electron. 2009, 56, 670–677. [Google Scholar] [CrossRef]
- Chen, L.; Xie, Y.; Zhang, Z. Comparison of Hybrid Active Power Filter topologies and principles. In Proceedings of the International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008. [Google Scholar]
- Shuai, Z.; Luo, A.; Zhu, W.; Fan, R.; Zhou, K. Study on a Novel Hybrid Active Power Filter Applied to a High-Voltage Grid. IEEE Trans. Power Deliv. 2009, 24, 2344–2352. [Google Scholar] [CrossRef]
- Luo, A.; Tang, C.; Shuai, Z.K.; Zhao, W.; Rong, F.; Zhou, K. A Novel Three-Phase Hybrid Active Power Filter with a Series Resonance Circuit Tuned at the Fundamental Frequency. IEEE Trans. Ind. Electron. 2009, 56, 2431–2440. [Google Scholar] [CrossRef]
- Srianthumrong, S.; Jintagosonwit, P. Implementation and Performance of an Anti-Resonance Hybrid Delta-Connected Capacitor Bank for Power Factor Correction. IEEE Trans. Power Electron. 2007, 22, 2543–2551. [Google Scholar] [CrossRef]
- Herman, L.; Papic, I.; Blazic, B. Comparison of circuit configuration and filtering performance between parallel and series hybrid active filter. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013. [Google Scholar]
- Akagi, H. Trends in Active Power Line Conditioners. IEEE Trans. Power Electron. 1994, 9, 263–268. [Google Scholar] [CrossRef]
- Sung, J.H.; Park, S.; Nam, K. New Hybrid Parallel Active Filter Configuration Minimizing Active Filter Size. IEE Proc. Electr. Power Appl 2006, 147, 93–98. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P.C. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IET Proc. Electr. Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef]
- Lascu, C.; Asiminoaei, L.; Boldea, I.; Blaabjerg, F. High Performance Current Controller for Selective Harmonic Compensation in Active Power Filters. IEEE Trans. Power Electron. 2007, 22, 1826–1835. [Google Scholar] [CrossRef]
- Bojoi, R.; Griva, G.; Bostan, V.; Guerriero, M.; Farina, F.; Profumo, F. Current Control Strategy for Power Conditioners Using Sinusoidal Signal Integrators in Synchronous Reference Frame. IEEE Trans. Power Electron. 2005, 20, 1402–1412. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Multiple Harmonics Control for Three-Phase Grid Converter Systems with the Use of PI-RES Current Controller in a Rotating Frame. IEEE Trans. Power Electron. 2006, 21, 836–841. [Google Scholar] [CrossRef]
- Bojoi, R.; Limongi, L.R.; Roiu, D.; Tenconi, A. Frequency-domain analysis of resonant current controllers for active power conditioners. In Proceedings of the IECON 2008—34th Annual Conference of IEEE Industrial Electronics Society, Orlando, FL, USA, 10–13 November 2008; pp. 3141–3148. [Google Scholar]
- Yepes, A.G.; Freijedo, F.D.; Doval-Gandoy, J.; López, Ó.; Malvar, J.; Fernandez-Comesaña, P. Effects of discretization methods on the performance of resonant controllers. IEEE Trans. Power Electron. 2010, 25, 1692–1712. [Google Scholar] [CrossRef]
- Miret, J.; Castilla, M.; Matas, J.; Guerrero, J.M.; Vasquez, J.C. Selective Harmonic-Compensation Control for Single-Phase Active Power Filter With High Harmonic Rejection. IEEE Trans. Ind. Electron. 2009, 56, 3117–3127. [Google Scholar] [CrossRef]
- Božiček, A.; Papič, I.; Blažič, B. Performance evaluation of the DSP-based improved time-optimal current controller for STAT-COM. Int. J. Electr. Power Energy Syst. 2017, 91, 209–221. [Google Scholar] [CrossRef]
- Herman, L.; Božiček, A.; Blažič, B.; Papič, I. Real-time simulations of a parallel hybrid active filter with hardware-in-the-loop. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 576–580. [Google Scholar]
- Bozicek, A.; Blazic, B.; Papic, I. Time-optimal operation of a predictive current controller for voltage source converters. In Proceedings of the 2011 International Conference on Power Engineering, Energy and Electrical Drives (POWERENG), Malaga, Spain, 11–13 May 2011; pp. 1–7. [Google Scholar]
- Špelko, A.; Blažič, B.; Papič, I.; Herman, L. Active Filter Reference Calculations Based on Customers’ Current Harmonic Emissions. Energies 2021, 14, 220. [Google Scholar] [CrossRef]
- Pfajfar, T.; Blazic, B.; Papic, I. Harmonic Contributions Evaluation with the Harmonic Current Vector Method. IEEE Trans. Power Deliv. 2007, 23, 425–433. [Google Scholar] [CrossRef]
- Spelko, A.; Blazic, B.; Papic, I.; Pourarab, M.; Meyer, J.; Xu, X.; Djokic, S.Z. CIGRE/CIRED JWG C4.42: Overview of common methods for assessment of harmonic contribution from customer installation. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 1–22 June 2017; pp. 1–6. [Google Scholar]
- Papic, I.; Matvoz, D.; Spelko, A.; Xu, W.; Wang, Y.; Mueller, D.; Miller, C.; Ribeiro, P.F.; Langella, R.; Testa, A. A Benchmark Test System to Evaluate Methods of Harmonic Contribution Determination. IEEE Trans. Power Deliv. 2018, 34, 23–31. [Google Scholar] [CrossRef]


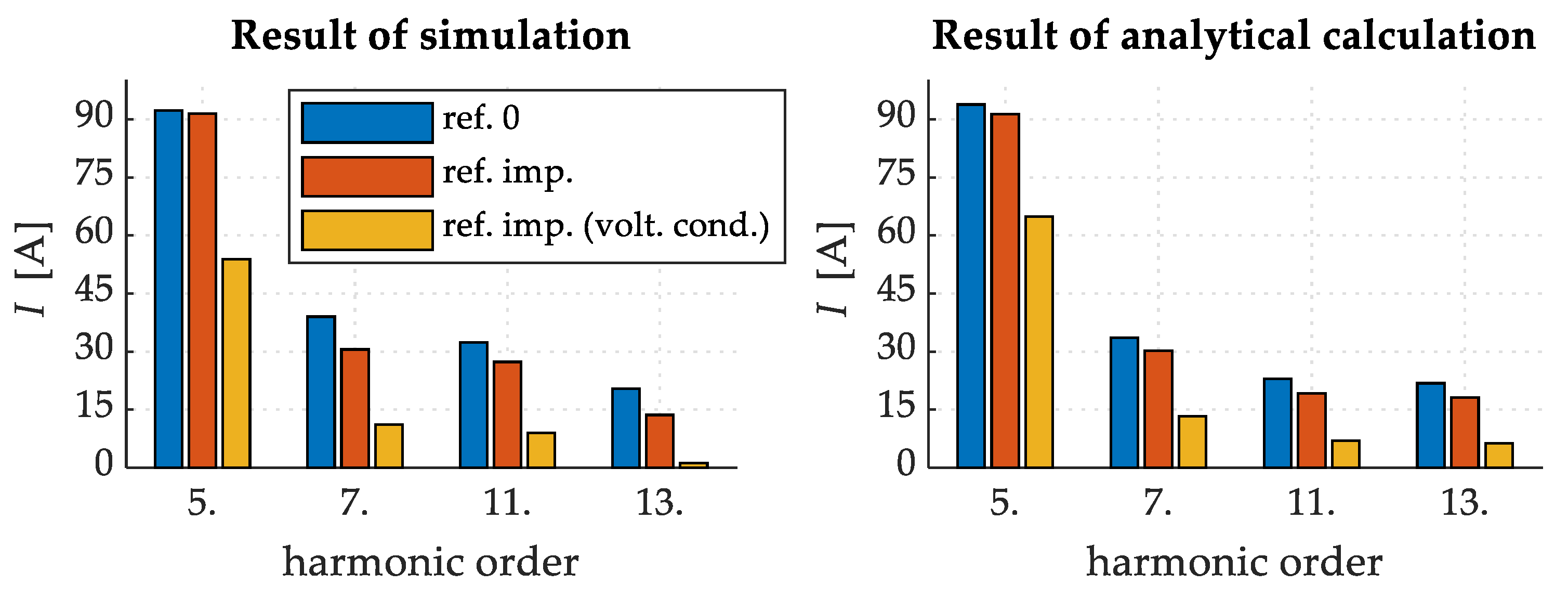
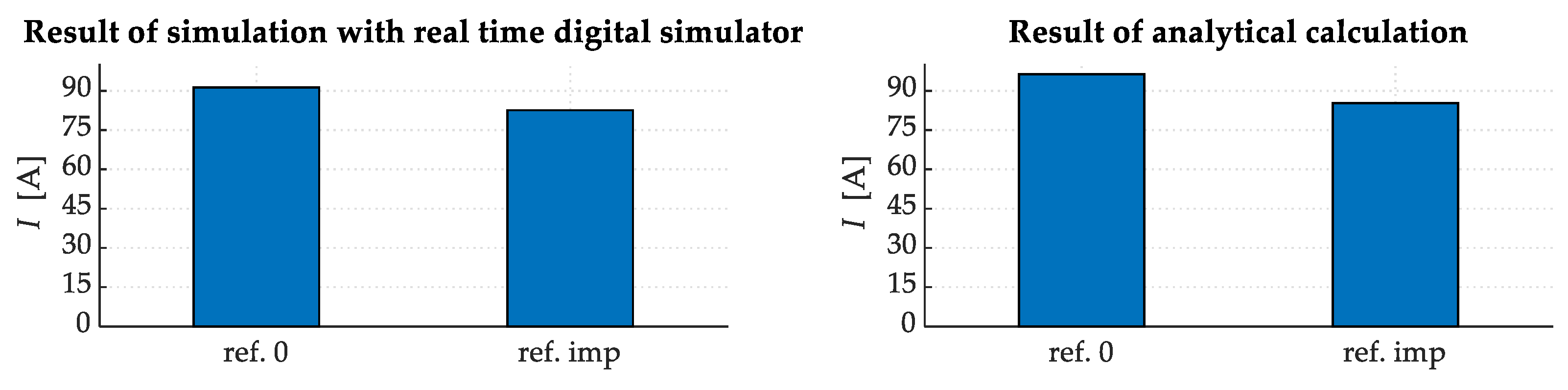
| Harm. Comp. | Results of Simulation | Results of Analytical Calculation | ||||
|---|---|---|---|---|---|---|
| Ref. 0 | Ref. Imp. | Ref. Imp. (Volt. Cond.) | Ref. 0 | Ref. Imp. | Ref. Imp. (Volt. Cond.) | |
| 5th | 92.34 | 9153 | 53.85 | 93.83 | 91.31 | 64.93 |
| 7th | 39.04 | 30.55 | 11.16 | 33.57 | 30.27 | 13.35 |
| 11th | 32.39 | 27.33 | 8.95 | 22.93 | 19.20 | 6.95 |
| 13th | 20.43 | 13.63 | 1.23 | 21.84 | 18.16 | 6.33 |
| Harm. Comp. | Results of Simulation | Results of Analytical Calculation | ||
|---|---|---|---|---|
| Ref. Imp. | Ref. Imp. (Volt. Cond.) | Ref. Imp. | Ref. Imp. (Volt. Cond.) | |
| 5th | 2.52 A | 28.90 A | 0.80 A | 38.48 A |
| 7th | 3.30 A | 20.22 A | 8.48 A | 27.88 A |
| 11th | 3.73 A | 15.96 A | 5.06 A | 23.44 A |
| 13th | 3.68 A | 15.51 A | 6.80 A | 19.20 A |
| Harm. Comp. | Results of Simulation | Results of Analytical Calculation | ||
|---|---|---|---|---|
| Ref. Imp. | Ref. Imp. (Volt. Cond.) | Ref. Imp. | Ref. Imp. (Volt. Cond.) | |
| 5th | 2.69% | 30.80% | 0.87% | 41.68% |
| 7th | 9.83% | 60.23% | 21.73% | 71.41% |
| 11th | 16.26% | 69.69% | 15.63% | 72.37% |
| 13th | 16.84% | 71.02% | 33.30% | 94.00% |
| Grid Impedance | HPF Passive Components | Equivalent Load | LCL-Filter |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herman, L.; Špelko, A. New Reference Current Calculation Method of a Hybrid Power Filter Based on Customer Harmonic Emission. Energies 2023, 16, 7876. https://doi.org/10.3390/en16237876
Herman L, Špelko A. New Reference Current Calculation Method of a Hybrid Power Filter Based on Customer Harmonic Emission. Energies. 2023; 16(23):7876. https://doi.org/10.3390/en16237876
Chicago/Turabian StyleHerman, Leopold, and Aljaž Špelko. 2023. "New Reference Current Calculation Method of a Hybrid Power Filter Based on Customer Harmonic Emission" Energies 16, no. 23: 7876. https://doi.org/10.3390/en16237876
APA StyleHerman, L., & Špelko, A. (2023). New Reference Current Calculation Method of a Hybrid Power Filter Based on Customer Harmonic Emission. Energies, 16(23), 7876. https://doi.org/10.3390/en16237876






