Durability and Damage Tolerance Analysis Approaches for Wind Turbine Blade Trailing Edge Life Prediction: A Technical Review
Abstract
:1. Introduction
1.1. Background
1.2. Scope of the Review Paper
1.3. Structure of the Review Paper and Some Useful Definitions
- Durability: Harris et al. [14] defines durability as "the ability of the structure to retain adequate properties (strength, stiffness, and environmental resistance) throughout its service life to the extent that any deterioration can be controlled and repaired, if there is a need, by economically acceptable maintenance practices. Structural durability affects the frequency and cost of inspection, replacement, repair, or other maintenance”. Another term often used in conjunction with durability is safe-life, when a fatigue analysis has demonstrated the structure can withstand all design loads during the design life [19]. The safe-life approach is the most commonly used methodology for wind turbine blade design [20].
- “As Designed” State: The “As designed” state refers to the state of a wind turbine blade design which is achieved after the completion of the detailed design phase. The process commences with the preliminary design, followed by a durability analysis, and an initial design life prediction. Once these steps are completed, the design moves forward with detailed designing, and eventually, the design is ready for manufacturing.
- Damage Tolerance: Padmaja et al. [21] define damage tolerance as “the ability of an aircraft structure to sustain anticipated loads (e.g., limit load) in the presence of fatigue, corrosion, or accidental damage until such damage is detected through inspections (or malfunctions) and repaired”. Two terms are often associated with the damage tolerance analysis methodology: fail-safe design and damage-tolerant design. A fail-safe design ensures a damaged structure can continue to withstand the design loads but with reduced margins of safety [19]. A damage-tolerant design extends the concept of fail-safe to encompass damage growth and residual strength analysis necessary to allow continued system operation [20]. Damage tolerance analysis can be applied during all phases of the system life cycle. During initial design, damage tolerance analysis can use assumed initial flaw sizes to support an initial life prediction. After the manufacturing phase, the damage tolerance analysis is updated to account for actual defects and flaws with a revised life prediction. During wind turbine operations, a periodic damage tolerance analysis update accounts for damage growth and identification of new damage resulting in a remaining useful life prediction.
- “As Built” State: The term “As built” refers to the state of a wind turbine blade, which is determined by inspecting its quality assurance results and documenting any manufacturing defects according to their location, type, and size. The process begins with the manufacturing of the first wind turbine blade and continues through a damage tolerance analysis that incorporates these defects in calculations and updates the design life prediction until the blade is tested and certified.
- “As Operated” State: The term “As operated” refers to the state of a wind turbine blade that incorporates all known manufacturing defects and any additional damage discovered during scheduled periodic maintenance or through online structural health monitoring. The process starts during wind turbine operations with periodic or online remote maintenance inspections to provide feedback and inform the damage tolerance analysis update that determines the remaining useful life prediction.
1.4. Assumption and Limitations of the Current Review
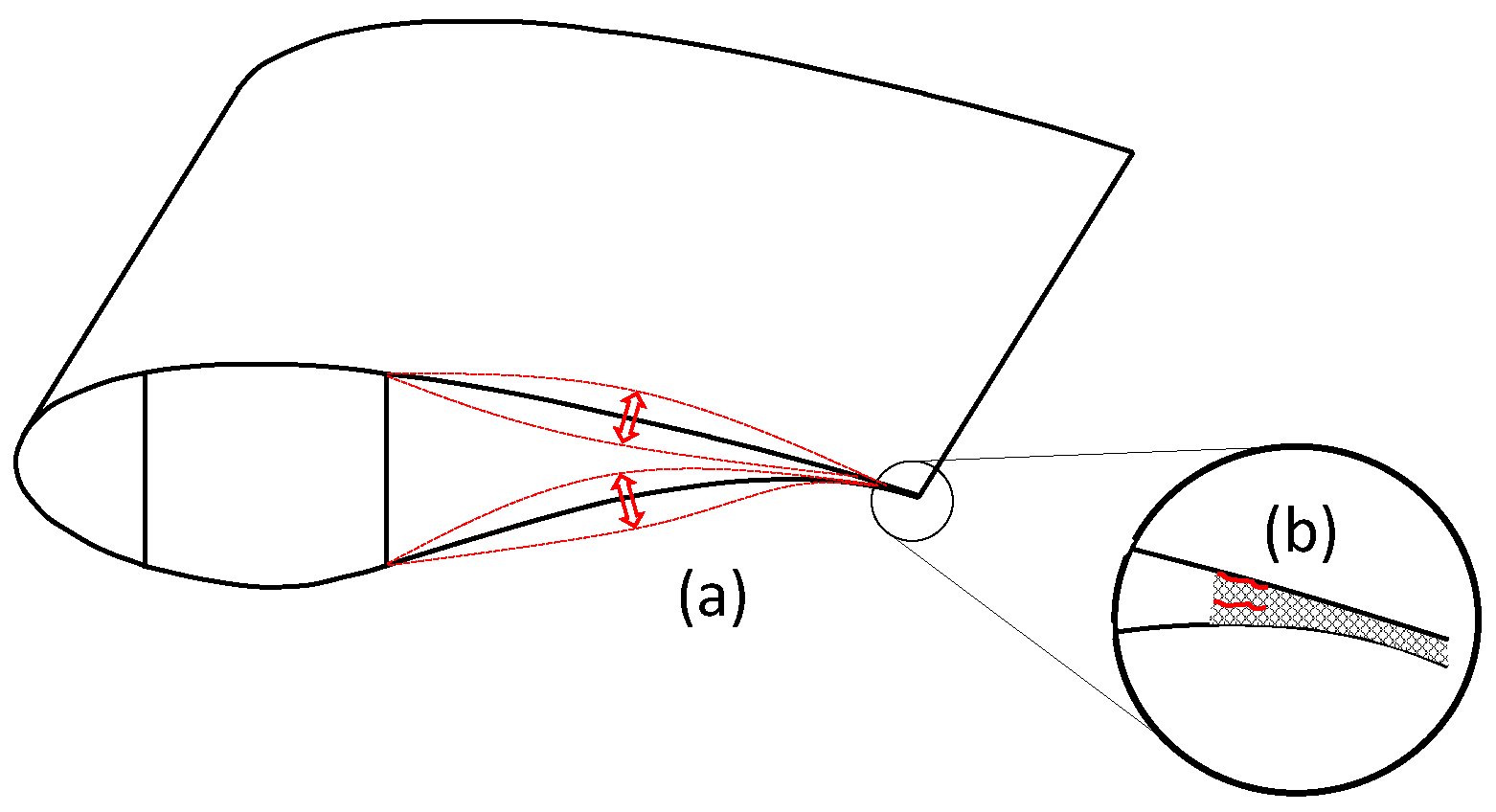
2. Problem Definition—Trailing Edge Failure
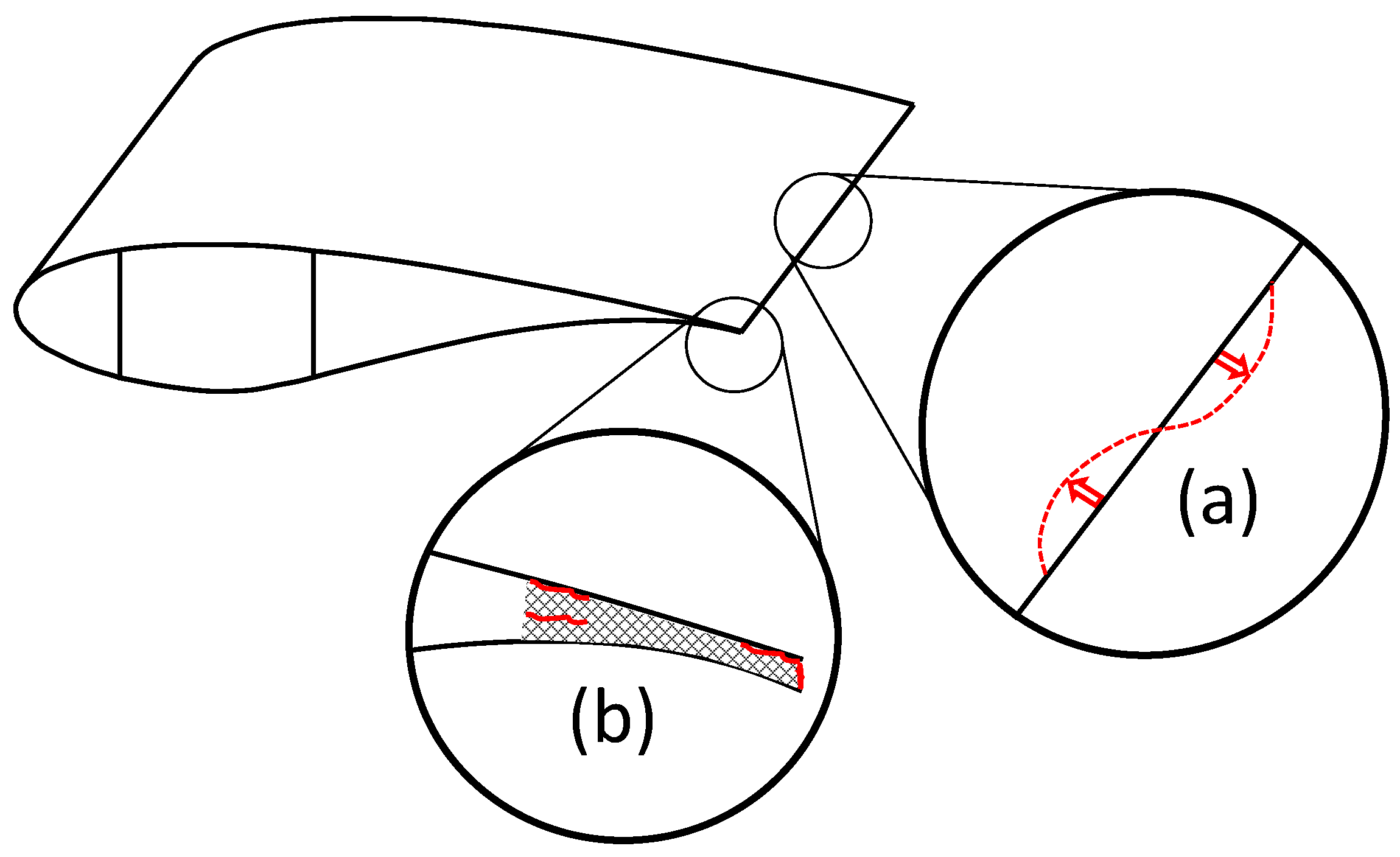
2.1. Ultimate Load Failure Modes
2.2. Fatigue Load Failure Modes
2.3. Other Failure Observations and Concerns
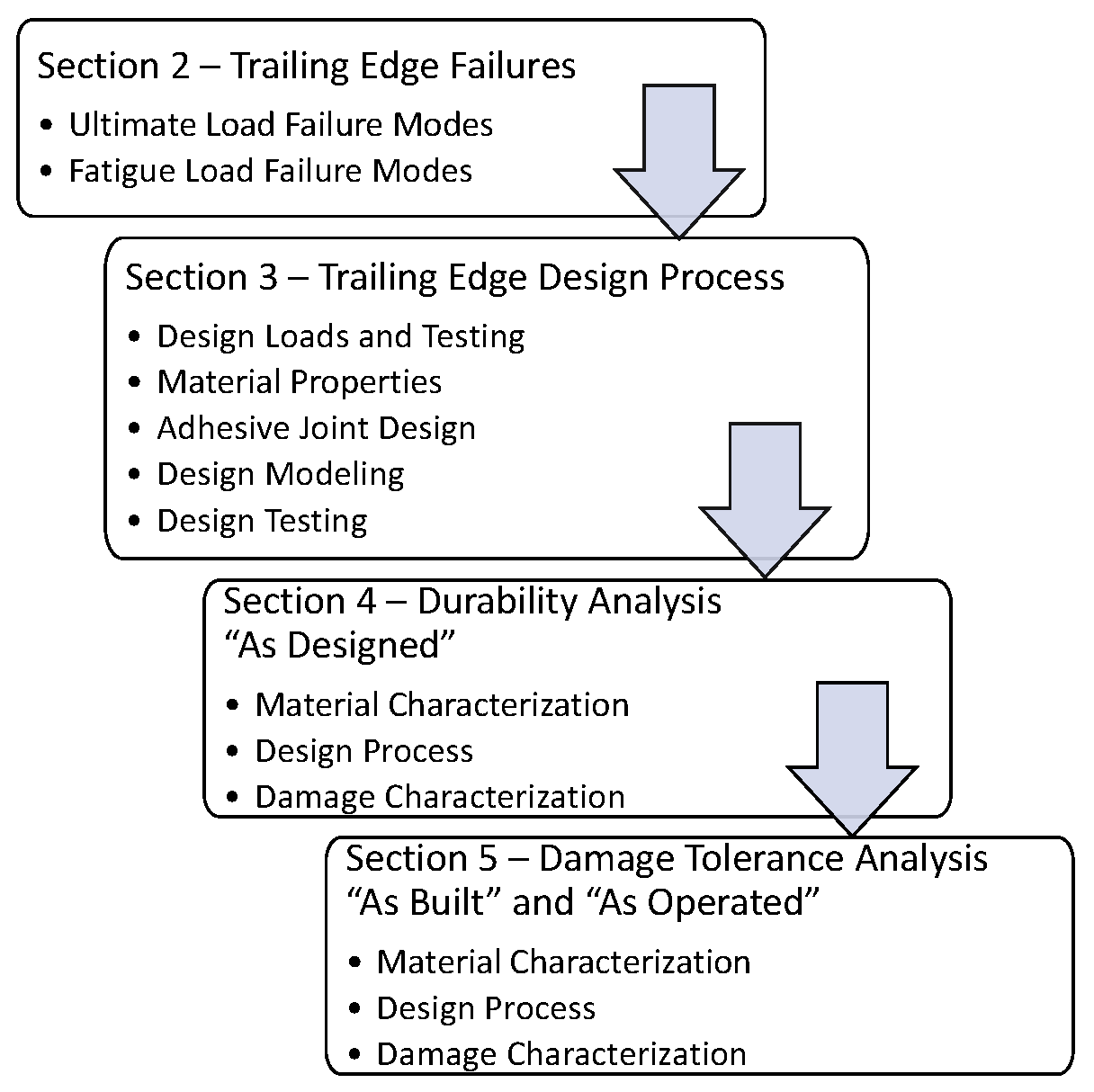
3. Trailing Edge Design Process
3.1. Design Loads and Testing Requirements
3.2. Materials and Properties
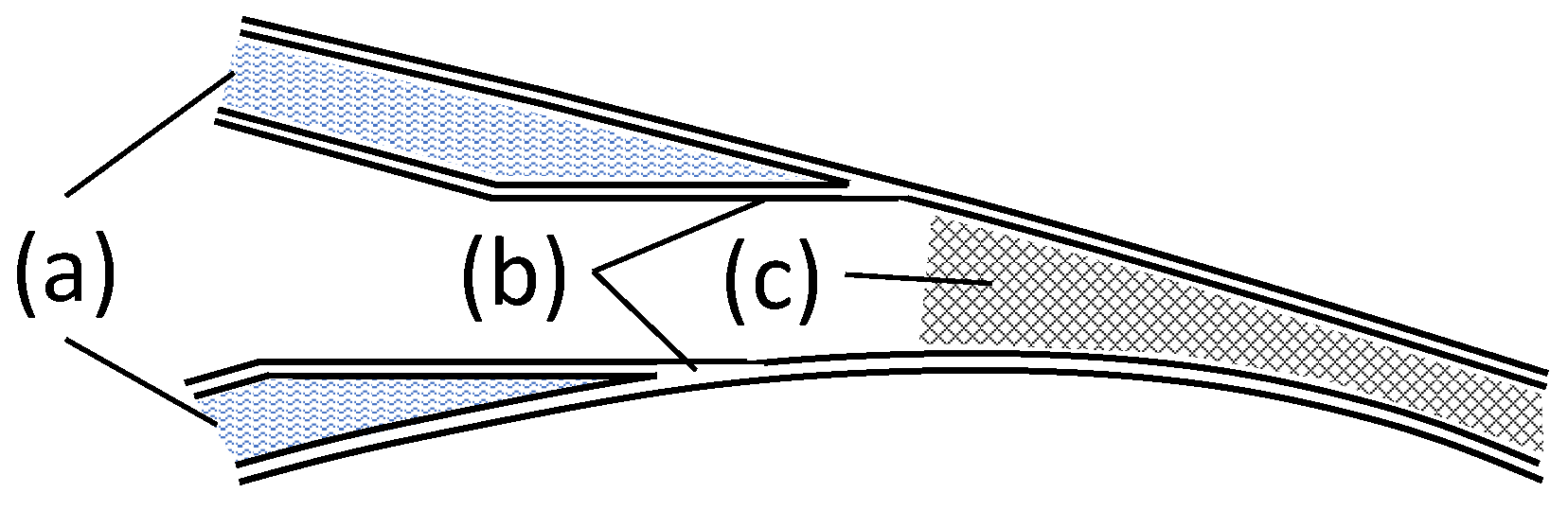
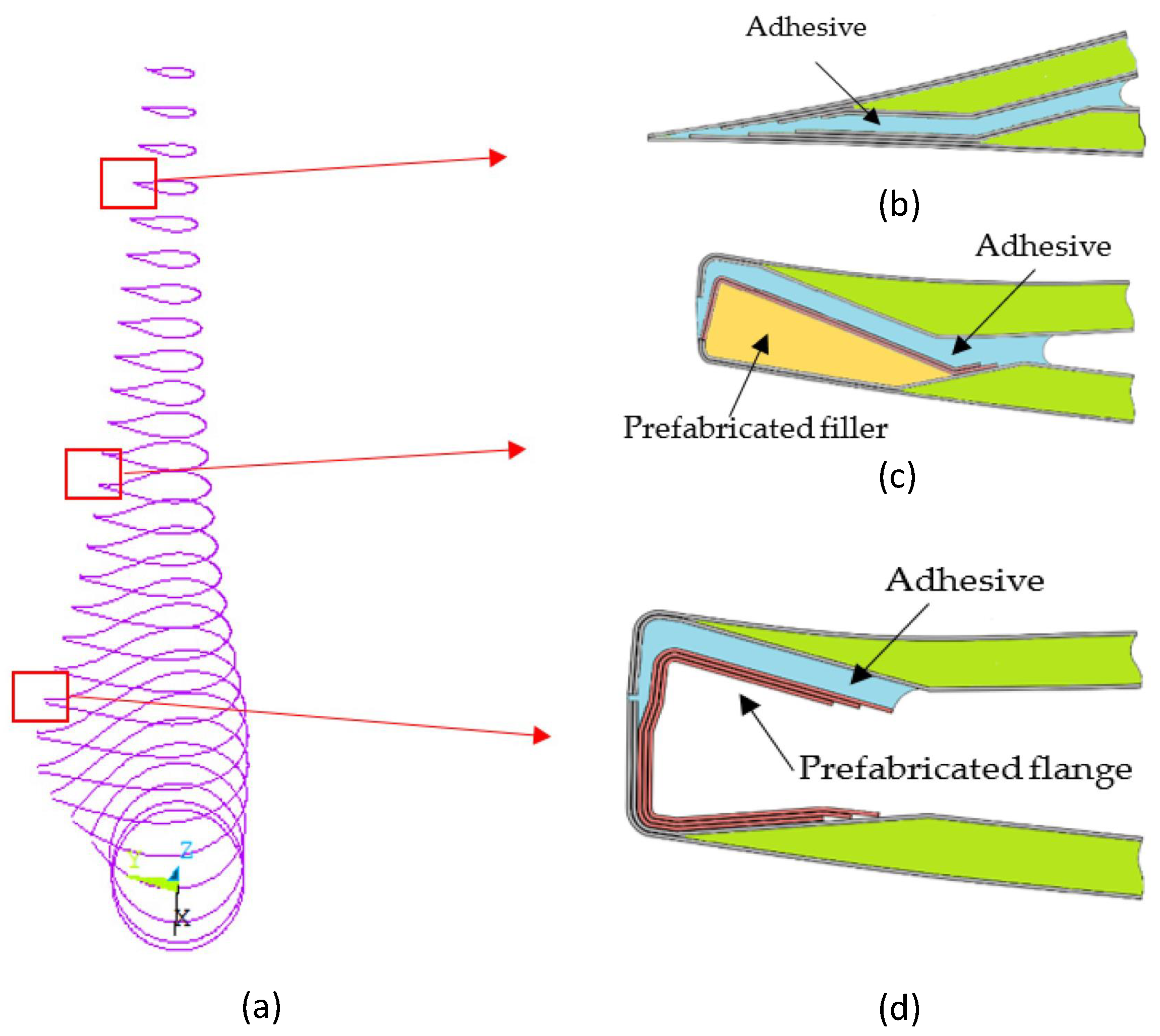
3.3. Trailing Edge Adhesive Joint Design
3.4. Trailing Edge Design Modeling
3.5. Trailing Edge Design Testing
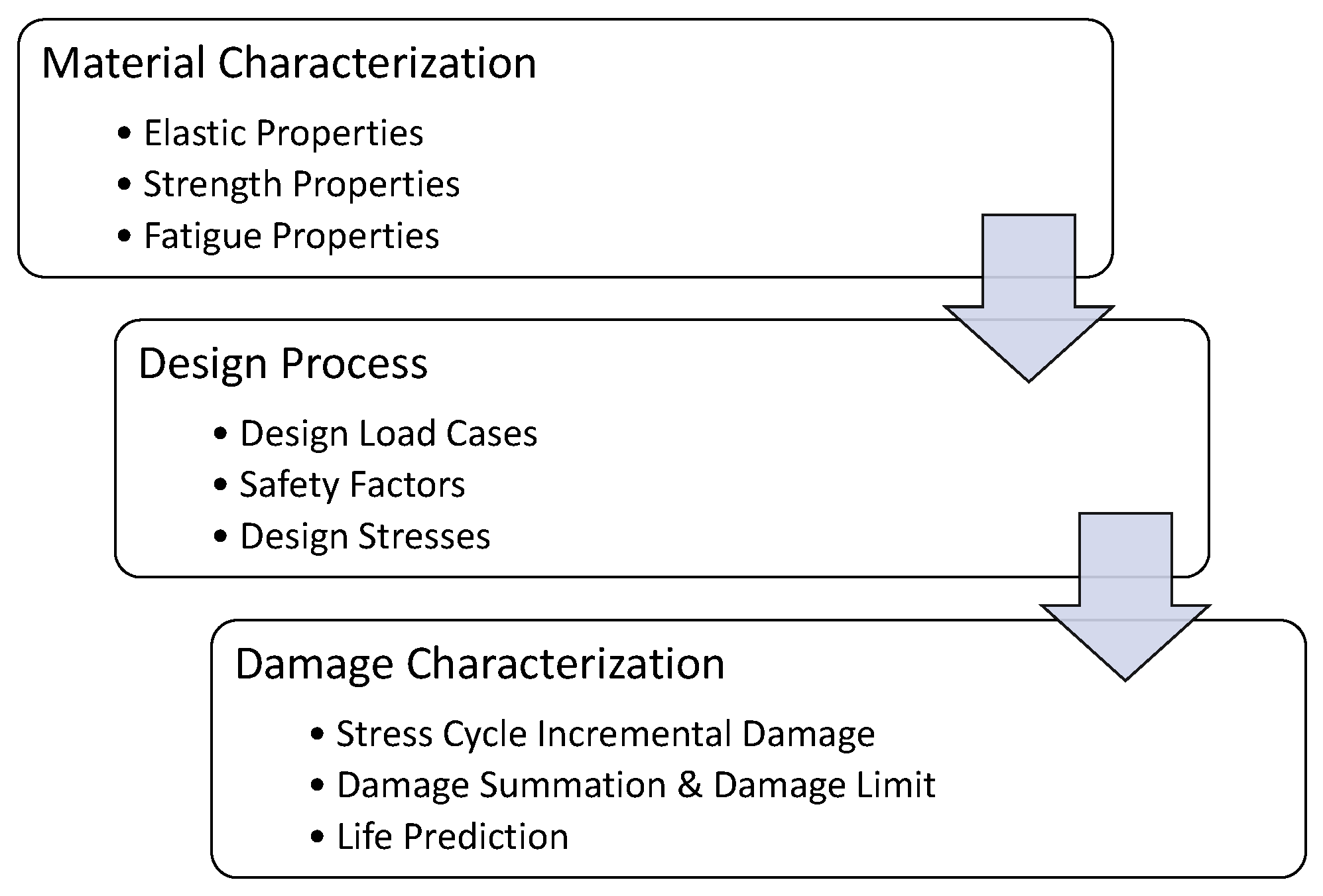
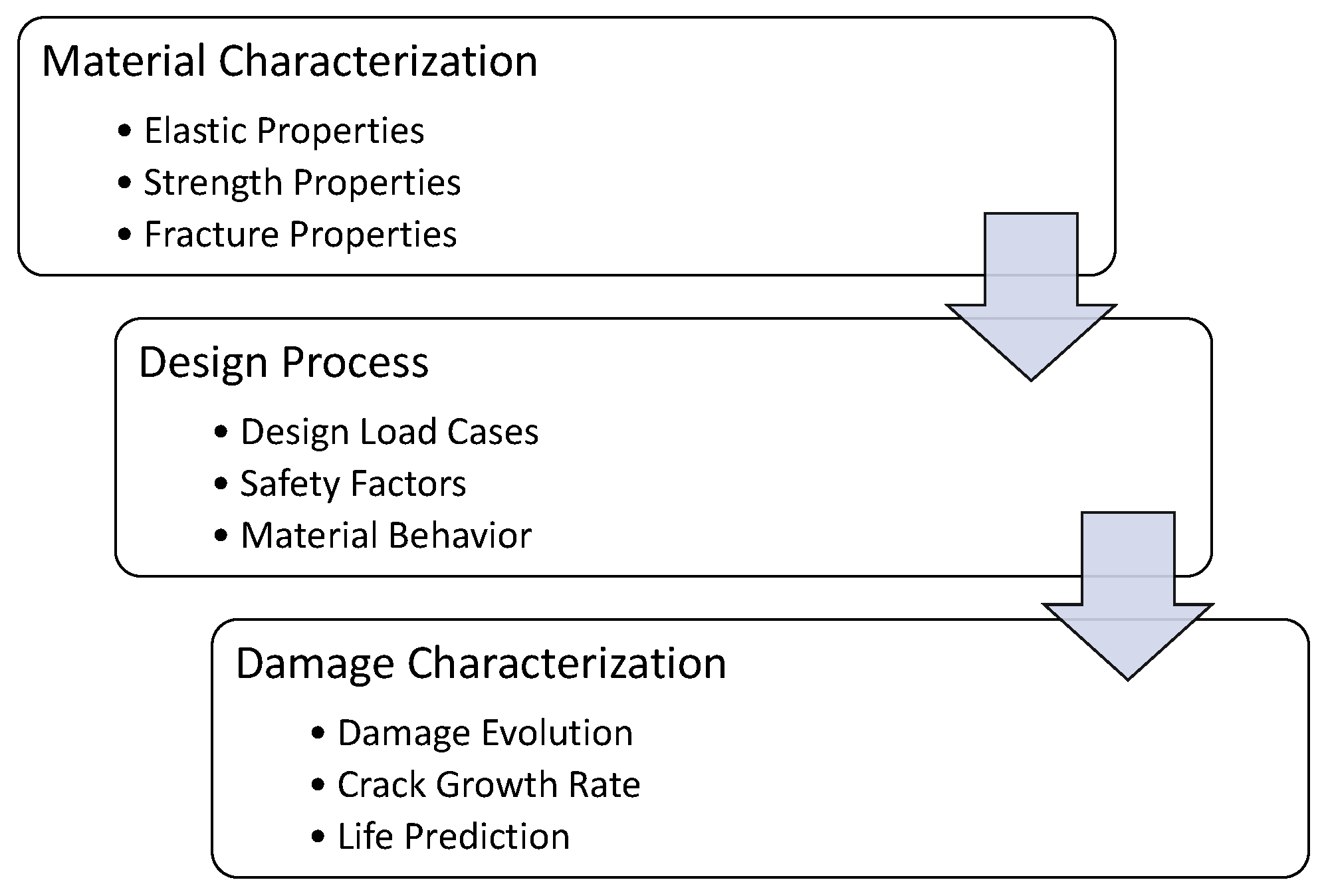
4. DADTA: Durability Analysis
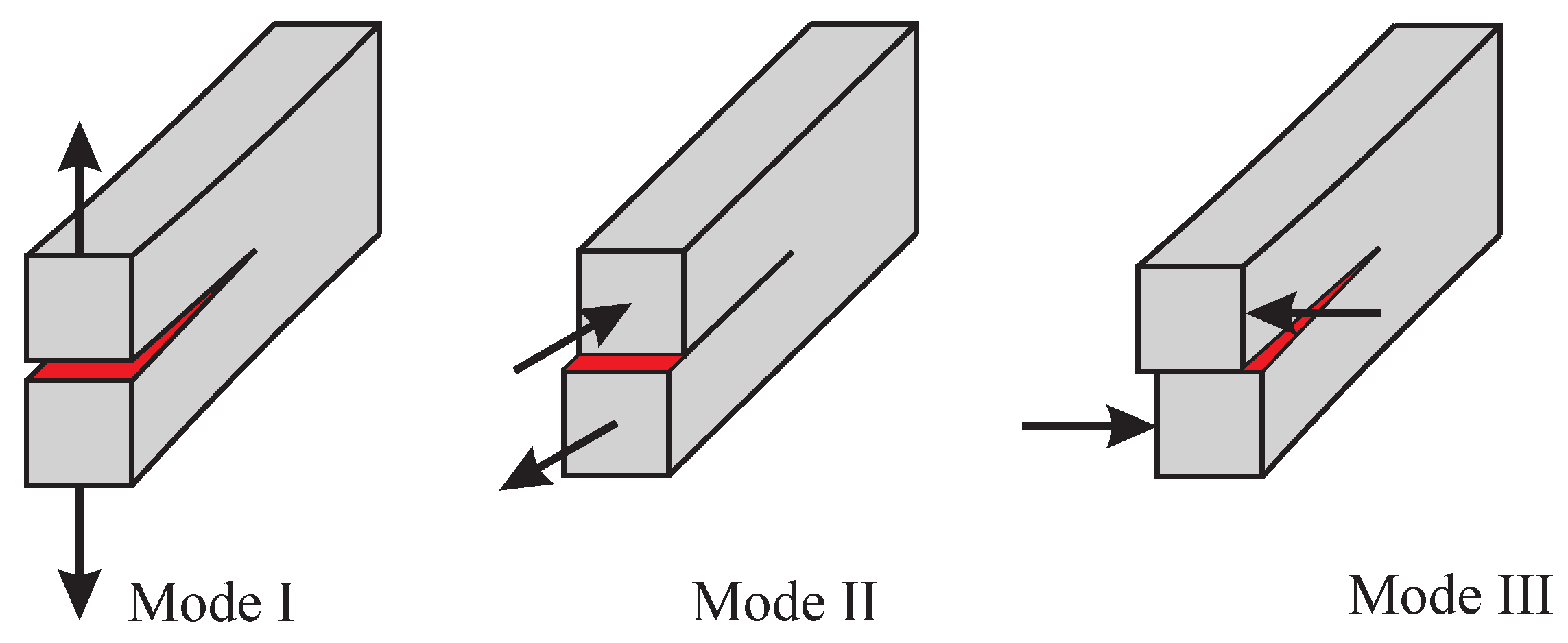
4.1. Materials Characterization
4.2. Design Process
4.2.1. Design Load Cases
4.2.2. Wind Loading Condition
4.2.3. Safety Factors
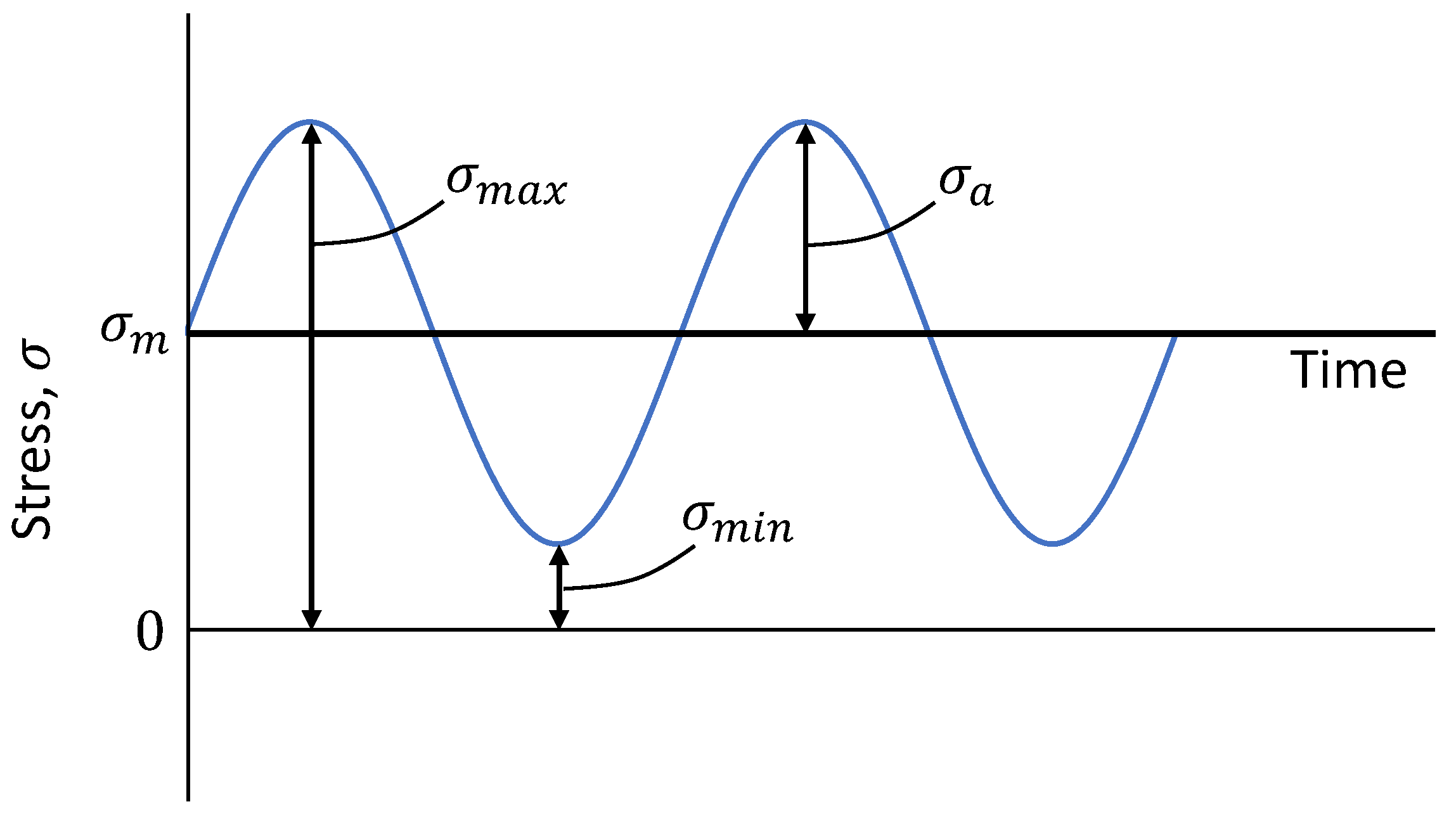
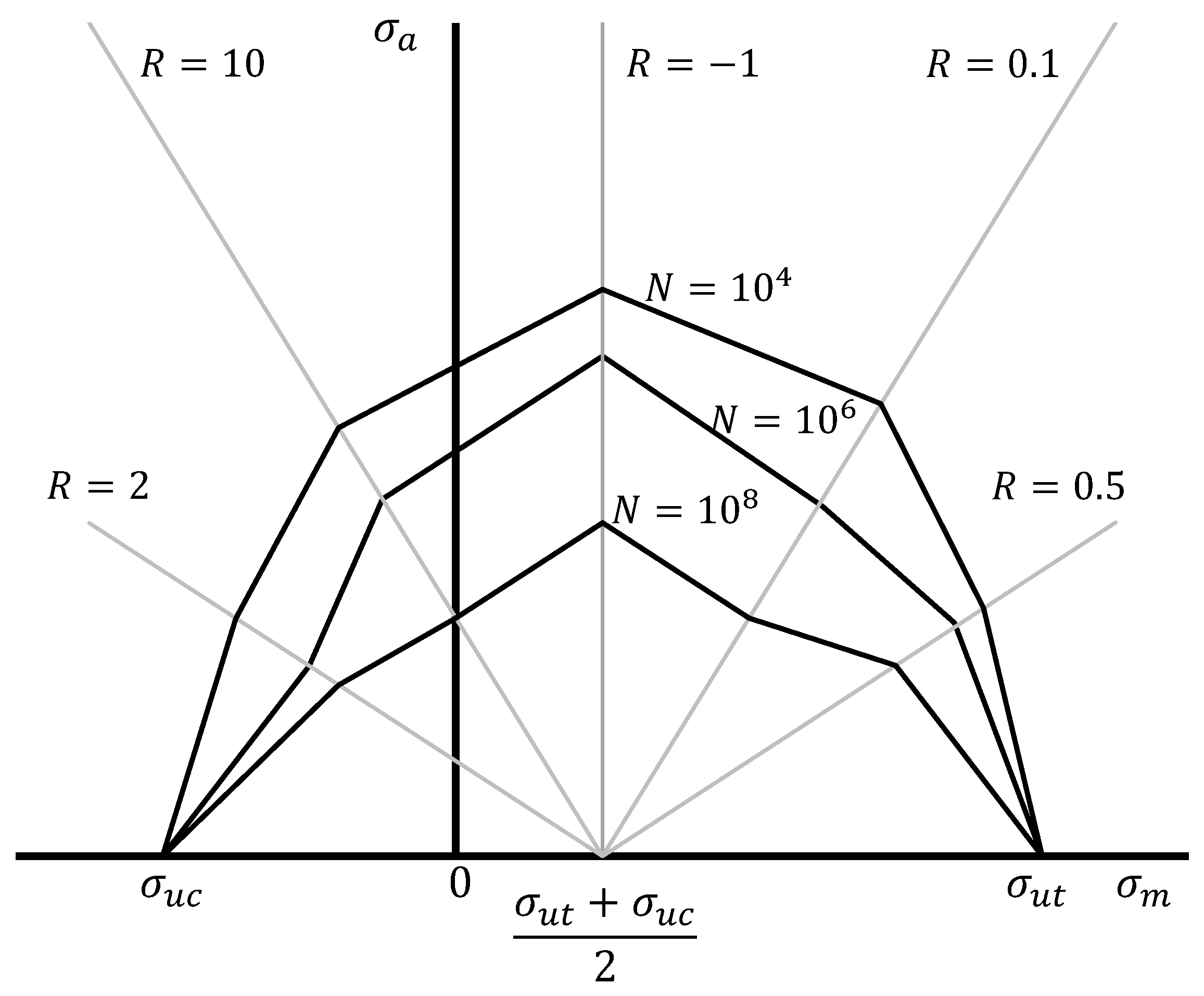
4.2.4. Design Stresses
4.3. Damage Characterization
4.3.1. Miner’s Rule
4.3.2. Life Prediction
4.3.3. Alternate Methodology, Tools, and Issues
5. DADTA: Damage Tolerance Analysis
5.1. As-Built Life Prediction
5.1.1. Material Characterization
5.1.2. Design Process
5.1.3. Damage Characterization
5.1.4. Alternate Methodology and Tools
5.2. As Operated Remaining Useful Life (RUL) Prediction
5.2.1. Damage Characterization
5.2.2. Damage Identification
5.2.3. Scheduled Maintenance Inspections
5.2.4. Remote Structural Health Monitoring
5.2.5. Remaining Useful Life Prediction
5.2.6. Alternate Methodology
6. Conclusions
- Trailing edge failure is common in both operational and test wind turbine blades, and occurs due to both structural overload and fatigue. Inspection of a limited set of operational blades indicates a variety of trailing edge cracks associated with fatigue. Various laboratory tests have confirmed trailing edge cracking and buckling failure due to ultimate and fatigue-loading conditions.
- Blade fatigue testing does not properly represent cyclic gravitational loads. Design standards only require single-axis fatigue testing to address flapwise loading. With dual-axis fatigue testing, edgewise loads attempt to include cyclic gravitational loads but fail to address the full impact of the breathing effect on the trailing edge.
- Gravitational loads cause trailing edge panel breathing. Wind turbine blade breathing eigenmodes have been reported in modal testing but have not correlated well to numerical simulations. Additionally, opening or breathing of trailing edge panels has clearly been reported and attributed to gravitational and torsional loading in various full-scale and subcomponent tests.
- Gravitational loads increase faster than aerodynamic loads with larger blade lengths, possibly leading to higher trailing edge failure rates. Basic scaling laws indicate that gravitational loads increase proportionally with the cube of the blade length, while aerodynamic loads increase with the square of the blade length. While the impact of gravitational loads can be reduced by optimizing the blade design to include carbon fiber in place of glass fiber, gravitational loads still increase more rapidly than aerodynamic loads and thereby will contribute to more trailing edge failures.
- Composite material properties are process-specific and must be determined for each intended design application. There are two major databases reporting composite fatigue material properties, but the results show differences. Design-specific material properties are dependent on the manufacturing process and sensitive to items such as postcure temperature.
- Three-dimensional modeling of full wind turbine blades is necessary to capture trailing edge buckling but two-dimensional cross-sectional modeling may be sufficient for trailing edge DADTA life prediction. Research has shown that the buckling of the trailing edge due to edgewise compressive loads can only be predicted using a 3D blade model but can be computationally expensive. A 2D subcomponent model can be used to properly represent the trailing edge constituents and obtain realistic responses, including the breathing effect. Therefore, the 2D model can examine the cyclic loading of the trailing edge joint and the resulting peel stresses necessary for a life prediction using DADTA.
- Durability analysis of Miner’s cumulative damage summation to unity should be used with caution for composite structures. Miner’s summation traditionally uses 1.0 as the cumulative damage limit, but research shows variance between composite blade materials that may lead to overly optimistic life predictions.
- The IEC wind turbine design standard relies on durability analysis life prediction and does not address the use of damage tolerance life prediction. While also including durability analysis, the DNV blade design standard additionally discusses, but does not mandate, use of damage tolerance analysis for life prediction.
- Damage tolerance analysis numerical modeling of composite structures using linear and nonlinear fracture mechanics is challenging due to complexities in composite material structures. The aerospace community has a long history of using damage tolerance analysis and has developed a deep understanding of metallic structures, but composite materials are more complex, with additional concerns at both the micro- and macrostructural levels.
7. Future Work
- Conducting a case study of DATDA effectiveness for an operational wind turbine blade. While case studies exist for the application of DADTA in the aerospace community, the literature does not include any DADTA case studies involving an operational wind turbine blade. Such a case study of an operational wind turbine blade will require participation from a wind turbine blade manufacturer and a wind turbine operator.
- Investigating the variance within the use of Miner’s accumulated damage value. The generally accepted use of a Miner’s accumulated damage value of 1.0 needs to be examined for wind turbine blade materials. An analysis of coupon tests has shown that using the value of 1.0 may be overly optimistic for some blade materials but not for others. Additional research is needed to examine the inconsistencies between materials and recommend appropriate accumulated damage values for use in the wind turbine blade industry.
- Increasing basic knowledge of fracture mechanics properties for wind turbine blade materials. The use of damage tolerance analysis for wind turbine blades is still considered a novel approach and requires additional foundational material characterization. Early investigations have focused on possible numerical approaches such as cohesive zone modeling and virtual crack closing techniques to predict properties but additional experimental research is needed for fracture mechanics material characterization of all blade materials to increase basic knowledge of properties such as SERR, crack resistance, and fracture toughness for a range of blade loading conditions, including various stress ratios.
- Improving the overall technology readiness level of CM and remote SHM systems. Research has been conducted for a wide range of possible sensors and has been investigated in the laboratory environment, achieving TRL 4. While successful for the initial two steps of determining the existence and location of the damage, most sensors cannot reliably conduct the last two steps to quantify the damage by type and severity fully. Therefore, the choice of sensors is difficult but can be tailored for different blade components, such as trailing edge joints and spar caps. Additional research is required to demonstrate CM and SHM concepts in the operational environment (TRL 7) with the goal of developing and qualifying commercial CM and SHM systems (TRL 8).
- Investigating the manufacturing and operational impact of embedded sensor systems for trailing edge adhesive joint damage identification and quantification. While CM and SHM concepts are promising to reduce overall wind turbine blade operations and maintenance costs, specific impacts to blade manufacturing processes and operational procedures have not been addressed. Additional research is needed to quantify and qualify the manufacturing and operational impact of embedded blade sensors.
- Reporting operational blade damage to inform research plans. Due to proprietary concerns, most operational wind turbine blade damage is not openly reported by manufacturers and system operators. This lack of reporting directly hinders the ability of the scientific community to address potential blade industry research needs adequately. Researchers must encourage wind turbine manufacturers and operators to publish blade damage inspection results.
- Modeling, predicting, and validating the breathing effect on the wind turbine blade trailing edge during design loading conditions (DLCs), including power production, start-up, shutdown, and parked (idling) operations. To date, wind turbine blade modal test results have not correlated well with numerical analysis. Additional research is needed to investigate this discrepancy using numerical analysis and experimental testing to validate the breathing effect on the trailing edge.
- Investigating the wind turbine blade trailing edge breathing effect on durability and damage tolerance life prediction. Current wind turbine blade fatigue testing does not account for dynamic cyclic gravitational loads, and therefore provides a possibly overly optimistic life prediction. Existing durability analysis has included gravitational loads but only in combined load cases. While some efforts have been made to examine damage tolerance remaining useful life prediction, more work is needed. Additional research is needed to isolate the breathing effect on the trailing edge durability and damage tolerance life prediction due to gravitational versus aerodynamic loads.
- Investigating mitigation techniques to minimize adverse impacts of the wind turbine trailing edge breathing effect. Research has been conducted to examine design improvements to mitigate trailing edge cyclic compressive load failures, but has not included trailing edge breathing due to cyclic gravitational loads. Additional research is needed to examine structural failures due to the breathing effect and to determine possible trailing edge design mitigation techniques.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sheng, S. Report on Wind Turbine Subsystem Reliability—A Survey of Various Databases (Presentation); Technical Report NREL/PR-5000-59111; National Renewable Energy Laboratory: Golden, CO, USA, 2013. [Google Scholar]
- Haselbach, P.U. Ultimate Strength of Wind Turbine Blades under Multiaxial Loading. Ph.D. Thesis, Technical University of Denmark, Department of Wind Energy, Roskilde, Denmark, 2015. [Google Scholar]
- Haselbach, P.U.; Branner, K. Initiation of trailing edge failure in full-scale wind turbine blade test. Eng. Fract. Mech. 2016, 162, 136–154. [Google Scholar] [CrossRef]
- Chou, J.S.; Chiu, C.K.; Huang, I.K.; Chi, K.N. Failure analysis of wind turbine blade under critical wind loads. Eng. Fail. Anal. 2013, 27, 99–118. [Google Scholar] [CrossRef]
- Reder, M.D.; Gonzalez, E.; Melero, J.J. Wind turbine failures-tackling current problems in failure data analysis. J. Phys. Conf. Ser. 2016, 753, 072027. [Google Scholar] [CrossRef]
- Rafiee, R.; Hashemi-Taheri, M.R. Failure analysis of a composite wind turbine blade at the adhesive joint of the trailing edge. Eng. Fail. Anal. 2021, 121, 105148. [Google Scholar] [CrossRef]
- IEC. Wind Turbines—Part 1: Design Requirements; Technical Report IEC 61400-1; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- ISO 2394:2015; General Principles on Reliability for Structures. International Standard: Geneva, Switzerland, 2015.
- Jacques, D. Sustaining Systems Engineering: The A-10 Example; Center for Systems Engineering Case Studies, Air Force Institute of Technology: Wright-Patterson AFB, OH, USA, 2008; pp. 1–20. [Google Scholar]
- Transport Airplane Directorate. Damage Tolerance and Fatigue Evaluation of Structure; Technical Report AC-25.571-1D; Federal Aviation Administration: Washington, DC, USA, 2011. [Google Scholar]
- Engineering & Force Management Division. Aircraft Structural Integrity Program and Air And Space Equipment Structural Management; Technical Report DAFI 63-140; Department of the Air Force: Washington, DC, USA, 2020. [Google Scholar]
- Engineering Directorate. Aircraft Structural Integrity Program (ASIP); Technical Report MIL-STD-1530D; Air Force Life Cycle Management Center: Wright-Patterson AFB, OH, USA, 2016. [Google Scholar]
- Ransom, J.; Glaessgen, E.; Raju, I.; Harris, C. Recent advances in durability and damage tolerance methodology at NASA Langley Research Center. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; p. 2377. [Google Scholar]
- Harris, C.E. Advanced Durability and Damage Tolerance Design and Analysis Methods for Composite Structures: Lessons Learned from NASA Technology Development Programs; Technical Report NASA/TM-2003-212420; Langley Research Center, National Aeronautics and Space Administration: Hampton, VA, USA, 2003. [Google Scholar]
- Jacques, D.; Strouble, D. A-10 Thunderbolt II (Warthog) Systems Engineering Case Study; Technical Report AFIT/SY; Center for Systems Engineering Case Studies, Air Force Institute of Technology: Wright-Patterson AFB, OH, USA, 2008. [Google Scholar]
- Lin, J. Durability and damage tolerance analysis methods for lightweight aircraft structures: Review and prospects. Int. J. Lightweight Mater. Manuf. 2022, 5, 224–250. [Google Scholar] [CrossRef]
- DVN. Rotor Blades for Wind Turbines; Technical Report DNVGL-ST-0376; Det Norske Veritas (DVN): Oslo, Norway, 2015. [Google Scholar]
- Burton, T.L.; Jenkins, N.; Bossanyi, E.; Sharpe, D.; Graham, M. Wind Energy Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Hayman, B. Approaches to damage assessment and damage tolerance for FRP sandwich structures. J. Sandw. Struct. Mater. 2007, 9, 571–596. [Google Scholar] [CrossRef]
- Lusty, A.F.; Cairns, D.A. Alternative Damage Tolerant Materials for Wind Turbine Blades: An Overview; Technical Report SAND2021-12461; Montana State University, Sandia National Lab: Albuquerque, NM, USA, 2021. [Google Scholar]
- Padmaja, R.K.; Bhargav, Y.; Subramanya, S. Fatigue and Damage Tolerance Analysis of Aircraft Structural Components; Technical Report; Cyient: East Hartford, CT, USA, 2017. [Google Scholar]
- Ataya, S.; Ahmed, M.M. Damages of wind turbine blade trailing edge: Forms, location, and root causes. Eng. Fail. Anal. 2013, 35, 480–488. [Google Scholar] [CrossRef]
- IEC. Wind Turbines—Part 23: Full-Scale Structural Testing of Rotor Blades; Technical Report IEC 61400-23; International Electrotechnical Commission: Geneva, Switzerland, 2014. [Google Scholar]
- Haselbach, P.U.; Branner, K. Effect of trailing edge damage on full-scale wind turbine blade failure. In Proceedings of the 20th International Conference on Composite Materials, Copenhagen, Danemark, 19–24 July 2015; pp. 19–24. [Google Scholar]
- Zhou, H.; Dou, H.; Qin, L.; Chen, Y.; Ni, Y.; Ko, J. A review of full-scale structural testing of wind turbine blades. Renew. Sustain. Energy Rev. 2014, 33, 177–187. [Google Scholar] [CrossRef]
- Chen, X.; Semenov, S.; McGugan, M.; Madsen, S.H.; Yeniceli, S.C.; Berring, P.; Branner, K. Fatigue testing of a 14.3 m composite blade embedded with artificial defects–damage growth and structural health monitoring. Compos. Part Appl. Sci. Manuf. 2021, 140, 106189. [Google Scholar] [CrossRef]
- Eder, M.A.; Branner, K.; Berring, P.; Belloni, F.; Toft, H.S.; Sørensen, J.D.; Corre, A.; Lindby, T.; Quispitupa, A.; Petersen, T.K. Experimental Blade Research: Phase 2; Technical Report E-0083; DTU Wind Energy, Technical University of Denmark: Roskilde, Denmark, 2015. [Google Scholar]
- Jørgensen, J. Adhesive Joints in Wind Turbine Blades. Ph.D. Thesis, Technical University of Denmark, Department of Wind Energy, Roskilde, Denmark, 2017. [Google Scholar]
- Mishnaevsky, L., Jr. Root causes and mechanisms of failure of wind turbine blades: Overview. Materials 2022, 15, 2959. [Google Scholar] [CrossRef]
- Nielsen, J.S.; Sørensen, J.D. Bayesian estimation of remaining useful life for wind turbine blades. Energies 2017, 10, 664. [Google Scholar] [CrossRef]
- Haselbach, P.U.; Eder, M.A.; Belloni, F. A comprehensive investigation of trailing edge damage in a wind turbine rotor blade. Wind Energy 2016, 19, 1871–1888. [Google Scholar] [CrossRef]
- Wu, H.; Qi, L.; Qian, J.; Cao, H.; Shi, K.; Xu, J. Experimental research on the compression failure of wind turbine blade trailing edge structure. J. Adhes. 2023, 99, 1488–1507. [Google Scholar] [CrossRef]
- Miao, X.Y.; Chen, X.; Lu, R.; Eder, M.A. Multi-site crack initiation in local details of composite adhesive joints. Compos. Part B Eng. 2022, 242, 110055. [Google Scholar] [CrossRef]
- Branner, K.; Berring, P.; Haselbach, P.U. Subcomponent testing of trailing edge panels in wind turbine blades. In Proceedings of the 17th European Conference on Composite Materials, Munich, Germany, 26–30 June 2016; pp. 26–30. [Google Scholar]
- Ghasemnejad, H.; Occhineri, L.; Swift-Hook, D. Post-buckling failure in multi-delaminated composite wind turbine blade materials. Mater. Des. 2011, 32, 5106–5112. [Google Scholar] [CrossRef]
- Chen, X. Experimental observation of fatigue degradation in a composite wind turbine blade. Compos. Struct. 2019, 212, 547–551. [Google Scholar] [CrossRef]
- Rosemeier, M.; Melcher, D.; Krimmer, A.; Wroblewski, W.; Antoniou, A. Validation of crack initiation model by means of cyclic full-scale blade test. J. Phys. Conf. Ser. 2022, 2265, 032045. [Google Scholar] [CrossRef]
- Rosemeier, M.; Krimmer, A.; Bardenhagen, A.; Antoniou, A. Tunneling crack initiation in trailing-edge bond lines of wind-turbine blades. AIAA J. 2019, 57, 5462–5474. [Google Scholar] [CrossRef]
- Kazacoks, R.; Jamieson, P. Evaluation of fatigue loads of horizontal up-scaled wind turbines. Energy Procedia 2015, 80, 13–20. [Google Scholar] [CrossRef]
- Cox, K.; Echtermeyer, A. Effects of composite fiber orientation on wind turbine blade buckling resistance. Wind Energy 2014, 17, 1925–1943. [Google Scholar] [CrossRef]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Natarajan, A.; Hansen, M.H. Description of the DTU 10 MW Reference Wind Turbine; Technical Report I-0092; DTU Wind Energy, Technical University of Denmark: Roskilde, Denmark, 2013. [Google Scholar]
- Fingersh, L.; Hand, M.; Laxson, A. Wind Turbine Design Cost and Scaling Model; Technical Report NREL/TP-500-40566; National Renewable Energy Laboratory: Golden, CO, USA, 2006. [Google Scholar]
- Loth, E.; Griffith, D.; Kaminski, M.; Qin, C.; Fingersh, L.J. Gravo-Aeroelastic Scaling for Extreme-Scale Wind Turbines; Technical Report SAND2017-5555C; Sandia National Laboratory: Albuquerque, NM, USA, 2017. [Google Scholar]
- Nettles, A.T. Allowables for structural composites. In Proceedings of the International Conference on Composites Engineering, Hilton Head, SC, USA, 8 August 2004; pp. 1–2. [Google Scholar]
- Sørensen, B.F.; Holmes, J.W.; Brøndsted, P.; Branner, K. Blade materials, testing methods and structural design. In Wind Power Generation and Wind Turbine Design; WIT Press: Southampton, UK, 2010; pp. 417–466. [Google Scholar]
- Ronold, K.O.; Echtermeyer, A.T. Estimation of fatigue curves for design of composite laminates. Compos. Part Appl. Sci. Manuf. 1996, 27, 485–491. [Google Scholar] [CrossRef]
- Ronold, K.O.; Echtermeyer, A.T. Using Tolerance Bounds for Estimation of Characteristic Fatigue Curves for Composites with Confidence. Safety 2021, 8, 1. [Google Scholar] [CrossRef]
- Chen, C.; Li, H.; Wang, T.; Wang, L. Influence of Structural Configurations on the Shear Fatigue Damage of the Blade Trailing-Edge Adhesive Joint. Appl. Sci. 2020, 10, 2715. [Google Scholar] [CrossRef]
- Mandell, J.F.; Samborsky, D.D. DOE/MSU Composite Material Fatigue Database: Test Methods, Materials, and Analysis; Technical Report SAND97-3002; Montana State University, Sandia National Lab: Albuquerque, NM, USA, 1997. [Google Scholar]
- Vallons, K. Databases for fatigue analysis in composite materials. In Fatigue of Textile Composites; Elsevier: Amsterdam, The Netherlands, 2015; pp. 75–82. [Google Scholar]
- De Smet, B.; Bach, P.W. Database FACT: Fatigue of Composites for Wind Turbines; Technical Report ECN-C-94-045; Energy Research Centre of the Netherlands: Petten, The Netherlands, 1994. [Google Scholar]
- Mandell, J.F.; Samborsky, D.D.; Sutherland, H.J. Effects of Materials Parameters and Design Details on the Fatigue of Composite Materials for Wind Turbine Blades; Technical Report SAND98-1997C; Sandia National Lab: Albuquerque, NM, USA, 1999. [Google Scholar]
- Zarouchas, D.; Nijssen, R. Mechanical behaviour of thick structural adhesives in wind turbine blades under multi-axial loading. J. Adhes. Sci. Technol. 2016, 30, 1413–1429. [Google Scholar] [CrossRef]
- Chen, X.; Eder, M.A. A critical review of damage and failure of composite wind turbine blade structures. In Proceedings of the IOP Conference Series: Materials Science and Engineering, 41st Risø International Symposium on Materials Science, Roskilde, Denmark, 7–10 September 2020; IOP Publishing: Bristol, UK, 2020; Volume 942, p. 012001. [Google Scholar]
- Jørgensen, J.B.; Sørensen, B.F.; Kildegaard, C. The effect of residual stresses on the formation of transverse cracks in adhesive joints for wind turbine blades. Int. J. Solids Struct. 2019, 163, 139–156. [Google Scholar] [CrossRef]
- ASTM. Standard Practice for Classifying Failure Modes in Fiber-Reinforced-Plastic (FRP) Joints; Technical Report D5573-99; American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2012. [Google Scholar]
- Haselbach, P.U.; Chen, X.; Berring, P. Place smart, load hard-structural reinforcement of the trailing edge regions of a wind turbine blade strengthening the buckling resistance. Compos. Struct. 2022, 300, 116068. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Huang, X.; Zhang, J.; Yuan, C. Initiation mechanism of transverse cracks in wind turbine blade trailing edge. Energy Eng. 2022, 119, 407–418. [Google Scholar] [CrossRef]
- Jørgensen, J.B.; Sørensen, B.F.; Kildegaard, C. Tunneling cracks in full scale wind turbine blade joints. Eng. Fract. Mech. 2018, 189, 361–376. [Google Scholar] [CrossRef]
- Gundlach, J.; Govers, Y. Experimental modal analysis of aeroelastic tailored rotor blades in different boundary conditions. J. Phys. Conf. Ser. 2019, 1356, 012023. [Google Scholar] [CrossRef]
- Foulds, D. Validation of Breathing Modes in Wind Turbine Blade Finite Element Models. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2021. [Google Scholar]
- Eder, M.A.; Bitsche, R.; Belloni, F. Effects of geometric non-linearity on energy release rates in a realistic wind turbine blade cross section. Compos. Struct. 2015, 132, 1075–1084. [Google Scholar] [CrossRef]
- Eder, M.A.; Bitsche, R. A qualitative analytical investigation of geometrically nonlinear effects in wind turbine blade cross sections. Thin-Walled Struct. 2015, 93, 1–9. [Google Scholar] [CrossRef]
- Chen, X.; Berring, P.; Madsen, S.H.; Branner, K.; Semenov, S. Understanding progressive failure mechanisms of a wind turbine blade trailing edge section through subcomponent tests and nonlinear FE analysis. Compos. Struct. 2019, 214, 422–438. [Google Scholar] [CrossRef]
- Chen, X.; Haselbach, P.U.; Branner, K.; Madsen, S.H. Effects of different material failures and surface contact on structural response of trailing edge sections in composite wind turbine blades. Compos. Struct. 2019, 226, 111306. [Google Scholar] [CrossRef]
- Sayer, F.; Antoniou, A.; van Wingerde, A. Investigation of structural bond lines in wind turbine blades by sub-component tests. Int. J. Adhes. Adhes. 2012, 37, 129–135. [Google Scholar] [CrossRef]
- Verma, A.S.; Vedvik, N.P.; Gao, Z.; Castro, S.G.; Teuwen, J.J. Bondline thickness effects on damage tolerance of adhesive joints subjected to localized impact damages: Application to leading edge of wind turbine blades. Materials 2021, 14, 7526. [Google Scholar] [CrossRef]
- Tomblin, J.S.; Yang, C.C.; Harter, P. Investigation of Thick Bondline Adhesive Joints; Technical Report DOT/FAA/AR-01/33; Wichita State University, Federal Aviation Administration, Office of Aviation Research: Washington, DC, USA, 2001. [Google Scholar]
- Budhe, S.; Banea, M.; De Barros, S.; Da Silva, L. An updated review of adhesively bonded joints in composite materials. Int. J. Adhes. Adhes. 2017, 72, 30–42. [Google Scholar] [CrossRef]
- Eder, M.A.; Bitsche, R.D. Fracture analysis of adhesive joints in wind turbine blades. Wind. Energy 2015, 18, 6. [Google Scholar] [CrossRef]
- Sørensen, B.F.; Jacobsen, T.K. Large-scale bridging in composites: R-curves and bridging laws. Compos. Part Appl. Sci. Manuf. 1998, 29, 1443–1451. [Google Scholar] [CrossRef]
- Sørensen, B.F.; Gamstedt, E.K.; Østergaard, R.C.; Goutianos, S. Micromechanical model of cross-over fibre bridging–Prediction of mixed mode bridging laws. Mech. Mater. 2008, 40, 220–234. [Google Scholar] [CrossRef]
- Sørensen, B.F.; Goutianos, S.; Jacobsen, T.K. Strength scaling of adhesive joints in polymer–matrix composites. Int. J. Solids Struct. 2009, 46, 741–761. [Google Scholar] [CrossRef]
- Dassault Systemes. ABAQUS Finite Element Analysis Software. 2023. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/ (accessed on 18 July 2023).
- ANSYS Inc. ANSYS Structural Analysis Software. 2023. Available online: https://www.ansys.com/ (accessed on 18 July 2023).
- Berg, J.C.; Resor, B.R. Numerical Manufacturing and Design Tool (NuMAD v2.0) for Wind Turbine Blades: User’s Guide; Technical Report SAND2012-7028; Sandia National Lab: Albuquerque, NM, USA, 2012. [Google Scholar]
- Haselbach, P.U. An advanced structural trailing edge modelling method for wind turbine blades. Compos. Struct. 2017, 180, 521–530. [Google Scholar] [CrossRef]
- Haselbach, P. Nonlinear Finite Element Analysis of Delamination Growth in Composite Wind Turbine Blades. Master’s Thesis, University Bremen, Bremen, Germany, 2013. [Google Scholar]
- Verma, A.S.; Vedvik, N.P.; Haselbach, P.U.; Gao, Z.; Jiang, Z. Comparison of numerical modelling techniques for impact investigation on a wind turbine blade. Compos. Struct. 2019, 209, 856–878. [Google Scholar] [CrossRef]
- Eder, M.A.; Bitsche, R.; Nielsen, M.; Branner, K. A practical approach to fracture analysis at the trailing edge of wind turbine rotor blades. Wind Energy 2014, 17, 483–497. [Google Scholar] [CrossRef]
- Rosemeier, M.; Gebauer, T.; Antoniou, A. A practical approach for the peel stress prediction in the trailing-edge adhesive joint of wind turbine blades. IOP Conf. Ser. Mater. Sci. Eng. 2020, 942, 012026. [Google Scholar] [CrossRef]
- Balzani, C.; Noever-Castelos, P.; Wentingmann, M. Finite Element Analysis and Failure Prediction of Adhesive Joints in Wind Turbine Rotor Blades. In Proceedings of the 6th European Conference on Computational Mechanics, Glasgow, UK, 11–15 June 2018; pp. 1–12. [Google Scholar]
- Bitsche, R. Modelling of Wind Turbine Blades with ABAQUS; Composites Seminar; Department of Wind Energy, Technical University of Denmark, DTU Risø Campus: Roskilde, Denmark, 2015; pp. 1–14. [Google Scholar]
- Blasques, J.P. User’s Manual for BECAS: A Cross Section Analysis Tool for Anisotropic and Inhomogeneous Beam Sections of Arbitrary Geometry; Technical Report RISØ-R 1785; Risø DTU—National Laboratory for Sustainable Energy, Technical University of Denmark: Roskilde, Denmark, 2012. [Google Scholar]
- Shokrieh, M.M.; Rafiee, R. Simulation of fatigue failure in a full composite wind turbine blade. Compos. Struct. 2006, 74, 332–342. [Google Scholar] [CrossRef]
- Castro, O.; Lennie, M.; Branner, K.; Pechlivanoglou, G.; Brøndsted, P.; Nayeri, C.N.; Paschereit, C.O. Comparing fatigue life estimations of composite wind turbine blades using different fatigue analysis tools. In Proceedings of the 20th International Conference on Composite Materials, Copenhagen, Danemark, 19–24 July 2015; pp. 19–24. [Google Scholar]
- Sayer, F.; Post, N.; Van Wingerde, A.; Busmann, H.; Kleiner, F.; Fleischmann, W.; Gansow, M. Testing of adhesive joints in the wind industry. In Proceedings of the European Wind Energy Conference and Exhibition, Marseille, France, 16–19 March 2009; Volume 2009, pp. 288–315. [Google Scholar]
- Sayer, F.; van Wingerde, A.; Busmann, H.; Knops, M.; Windbichler, R.; Kleiner, F.; Trusheim, M.; Henkel, A.; KGaA, C. Development of a new test methodology for adhesive joints in the wind industry. In Proceedings of the European Wind Energy Conference and Exhibition, Warsaw, Poland, 20–23 April 2010; pp. 20–23. [Google Scholar]
- Freebury, G.; Musial, W. Determining equivalent damage loading for full-scale wind turbine blade fatigue tests. In Proceedings of the 2000 ASME Wind Energy Symposium, Reno, NV, USA, 10–13 January 2000; p. 50. [Google Scholar]
- Rosemeier, M.; Basters, G.; Antoniou, A. Benefits of subcomponent over full-scale blade testing elaborated on a trailing-edge bond line design validation. Wind. Energy Sci. 2018, 3, 163–172. [Google Scholar] [CrossRef]
- Lahuerta, F.; Koorn, N.; Smissaert, D. Wind turbine blade trailing edge failure assessment with sub-component test on static and fatigue load conditions. Compos. Struct. 2018, 204, 755–766. [Google Scholar] [CrossRef]
- Echtermeyer, A.; Kensche, C.; Bach, P.; Poppen, M.; Lilholt, H.; Andersen, S.; Brøndsted, P. Method to predict fatigue lifetimes of GRP wind turbine blades and comparison with experiments. In Proceedings of the European Union Wind Energy Conference EUWEC’96, Göteborg, Sweden, 20–24 May 1996; FFA TN 1996-36. pp. 72–79. [Google Scholar]
- Sutherland, H.J. On the Fatigue Analysis of Wind Turbines; Technical Report SAND99-0089; Sandia National Lab: Albuquerque, NM, USA, 1999. [Google Scholar]
- Vassilopoulos, A.P.; Brondsted, P.; Nijssen, R.P. Chapter 8—Fatigue Life Prediction of Wind Turbine Blade Composite Materials. In Advances in Wind Turbine Blade Design and Materials; Woodhead Publishing Limited: Cambridge, UK, 2013; pp. 251–297. [Google Scholar]
- Nijssen, R.P.L. Fatigue Life Prediction and Strength Degradation of Wind Turbine Rotor Blade Composites; Technical Report SAND2006-7810P; Delft University of Technology, Sandia National Lab: Albuquerque, NM, USA, 2006. [Google Scholar]
- Curley, A.; Hadavinia, H.; Kinloch, A.; Taylor, A. Predicting the service-life of adhesively-bonded joints. Int. J. Fract. 2000, 103, 41–69. [Google Scholar] [CrossRef]
- Hu, W.; Choi, K.; Zhupanska, O.; Buchholz, J.H. Integrating variable wind load, aerodynamic, and structural analyses towards accurate fatigue life prediction in composite wind turbine blades. Struct. Multidiscip. Optim. 2016, 53, 375–394. [Google Scholar] [CrossRef]
- Ronold, K.O.; Wedel-Heinen, J.; Christensen, C.J. Calibration of partial safety factors for design of wind-turbine rotor blades against fatigue failure in flapwise bending. In Proceedings of the European Union Wind Energy Conference Göteborg, Göteborg, Sweden, 20–24 May 1996; pp. 129–136. [Google Scholar]
- McGugan, M.; Pereira, G.; Sørensen, B.F.; Toftegaard, H.; Branner, K. Damage tolerance and structural monitoring for wind turbine blades. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2015, 373, 20140077. [Google Scholar] [CrossRef]
- Holmes, J.W.; Sørensen, B.F.; Brøndsted, P. Reliability of wind turbine blades: An overview of materials testing. Proc. Wind Power Shanghai 2007, 35, 36. [Google Scholar]
- Kong, C.; Kim, T.; Han, D.; Sugiyama, Y. Investigation of fatigue life for a medium scale composite wind turbine blade. Int. J. Fatigue 2006, 28, 1382–1388. [Google Scholar] [CrossRef]
- Sutherland, H.; Mandell, J. Optimized Goodman Diagram for the Analysis of Fiberglass Composites Used in Wind Turbine Blades. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit. American Institute of Aeronautics and Astronautics, Reno, NV, USA, 10–13 January 2005; p. 196. [Google Scholar]
- Mandell, J.F.; Samborsky, D.D.; Cairns, D. Fatigue of Composite Materials and Substructures for Wind Turbine Blades; Technical Report SAND2002-0771; Montana State University, Sandia National Lab: Albuquerque, NM, USA, 2002. [Google Scholar]
- Marin, J.; Barroso, A.; Paris, F.; Canas, J. Study of fatigue damage in wind turbine blades. Eng. Fail. Anal. 2009, 16, 656–668. [Google Scholar] [CrossRef]
- Richards, P.W.; Griffith, D.T.; Hodges, D.H. Aeroelastic design of large wind turbine blades considering damage tolerance. Wind Energy 2017, 20, 159–170. [Google Scholar] [CrossRef]
- Tawade, S.V.; Todkar, S.B.; Hade, A.S. Fatigue life optimization of wind turbine blade. Int. J. Res. Eng. Technol. 2014, 3, 843–850. [Google Scholar]
- Veers, P.; Lange, C.; Winterstein, S. FAROW: A Tool for Fatigue and Reliability of Wind Turbines; Technical Report 930726-3; Sandia National Lab: Albuquerque, NM, USA, 1993. [Google Scholar]
- Kong, C.; Bang, J.; Sugiyama, Y. Structural investigation of composite wind turbine blade considering various load cases and fatigue life. Energy 2005, 30, 2101–2114. [Google Scholar] [CrossRef]
- Montesano, J.; Chu, H.; Singh, C.V. Development of a physics-based multi-scale progressive damage model for assessing the durability of wind turbine blades. Compos. Struct. 2016, 141, 50–62. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Lessard, L.B. Progressive fatigue damage modeling of composite materials, Part I: Modeling. J. Compos. Mater. 2000, 34, 1056–1080. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Lessard, L.B. Progressive fatigue damage modeling of composite materials, Part II: Material characterization and model verification. J. Compos. Mater. 2000, 34, 1081–1116. [Google Scholar] [CrossRef]
- Wahl, N.; Samborsky, D.; Mandell, J.; Cairns, D. Spectrum fatigue lifetime and residual strength for fiberglass laminates in tension. In Proceedings of the 20th 2001 ASME Wind Energy Symposium, Reno, NV, USA, 11–14 January 2001; p. 25. [Google Scholar]
- Abumeri, G.; Abdi, F. Advanced Composite Wind Turbine Blade Design Based on Durability and Damage Tolerance; Technical Report; AlphaSTAR Corporation: Long Beach, CA, USA, 2012. [Google Scholar]
- Noda, M.; Flay, R. A simulation model for wind turbine blade fatigue loads. J. Wind Eng. Ind. Aerodyn. 1999, 83, 527–540. [Google Scholar] [CrossRef]
- Castelos, P.N.; Balzani, C. The impact of geometric non-linearities on the fatigue analysis of trailing edge bond lines in wind turbine rotor blades. J. Phys. Conf. Ser. 2016, 749, 012009. [Google Scholar] [CrossRef]
- Kensche, C.W. Fatigue of composites for wind turbines. Int. J. Fatigue 2006, 28, 1363–1374. [Google Scholar] [CrossRef]
- Fan, X.; Sun, Q.; Kikuchi, M. Review of damage tolerant analysis of laminated composites. J. Solid Mech. 2010, 2, 275–289. [Google Scholar]
- Turon Travesa, A. Simulation of Delamination in Composites under Quasi-Static and Fatigue Loading Using Cohesive Zone Models. Ph.D. Thesis, Universitat de Girona, Girona, Spain, 2006. [Google Scholar]
- Mishnaevsky, L., Jr.; Branner, K.; Petersen, H.N.; Beauson, J.; McGugan, M.; Sørensen, B.F. Materials for wind turbine blades: An overview. Materials 2017, 10, 1285. [Google Scholar] [CrossRef]
- Höyland, J. Challenges for Large Wind Turbine Blades. Ph.D. Thesis, Norwegian University of Science and Technology, Department of Engineering Design and Materials, Trondheim, Norway, 2010. [Google Scholar]
- Baharvand, A. FEM Analysis of a Mode III Fracture Mechanics Test Specimens for Cohesive Law Determination of Fibre Composite. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
- Sørensen, B.F.; Horsewell, A.; Jørgensen, O.; Kumar, A.N.; Engbæk, P. Fracture resistance measurement method for in situ observation of crack mechanisms. J. Am. Ceram. Soc. 1998, 81, 661–669. [Google Scholar] [CrossRef]
- Jørgensen, J.; Thouless, M.; Sørensen, B.F.; Kildegaard, C. Determination of mode-I cohesive strength for interfaces. IOP Conf. Ser. Mater. Sci. Eng. 2016, 139, 012025. [Google Scholar] [CrossRef]
- Ji, Y.M.; Han, K. Fracture mechanics approach for failure of adhesive joints in wind turbine blades. Renew. Energy 2014, 65, 23–28. [Google Scholar] [CrossRef]
- Hua, Y.; Kasavajhala, A.R.M.; Gu, L. Elastic–plastic analysis and strength evaluation of adhesive joints in wind turbine blades. Compos. Part B Eng. 2013, 44, 650–656. [Google Scholar] [CrossRef]
- Richards, P.W.; Griffith, D.; Hodges, D.H. Operating Strategies and Design Recommendations for Mitigating Local Damage Effects in Offshore Turbine Blades; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2014. [Google Scholar]
- Sørensen, B.F.; Kirkegaard, P. Determination of mixed mode cohesive laws. Eng. Fract. Mech. 2006, 73, 2642–2661. [Google Scholar] [CrossRef]
- Sørensen, B.F.; Jørgensen, K.; Jacobsen, T.K.; Østergaard, R.C. DCB-specimen loaded with uneven bending moments. Int. J. Fract. 2006, 141, 163–176. [Google Scholar] [CrossRef]
- Samborsky, D.; Sears, A.; Mandell, J.; Agastra, P. Mixed mode static and fatigue crack growth in wind blade paste adhesives. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 19th AIAA/ASME/AHS Adaptive Structures Conference, Denver, CO, USA, 4–7 April 2011; p. 1755. [Google Scholar]
- Azari, S.; Papini, M.; Schroeder, J.; Spelt, J. Fatigue threshold behavior of adhesive joints. Int. J. Adhes. Adhes. 2010, 30, 145–159. [Google Scholar] [CrossRef]
- Kanchanomai, C.; Rattananon, S. Effects of loading rate and thickness on mixed-mode I/II fracture toughness of thermoset epoxy resin. J. Appl. Polym. Sci. 2008, 109, 2408–2416. [Google Scholar] [CrossRef]
- Sørensen, B.F. Cohesive law and notch sensitivity of adhesive joints. Acta Mater. 2002, 50, 1053–1061. [Google Scholar] [CrossRef]
- Sørensen, B.F.; Jacobsen, T.K. Joining structural parts of composite materials for large rotorblades. In Proceedings of the 27th Risø International Symposium on Materials Science, Polymer Composite Materials for Wind Power Turbines; Lilholt, H., Madsen, B., Andersen, T.L., Mikkelsen, L.P., Thygesen, A., Eds.; Risø National Laboratory: Roskilde, Denmark, 2006; pp. 69–82. [Google Scholar]
- Sørensen, B.F. Cohesive Laws for Assessment of Materials Failure: Theory, Experimental Methods and Application. Ph.D. Thesis, Technical University of Denmark, Risø DTU-National Laboratory for Sustainable Energy, Roskilde, Denmark, 2010. [Google Scholar]
- Sørensen, B.F.; Jacobsen, T.K. Characterizing delamination of fibre composites by mixed mode cohesive laws. Compos. Sci. Technol. 2009, 69, 445–456. [Google Scholar] [CrossRef]
- Krueger, R. Virtual crack closure technique: History, approach, and applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar] [CrossRef]
- Jørgensen, J.B.; Sørensen, B.F.; Kildegaard, C. The effect of buffer-layer on the steady-state energy release rate of a tunneling crack in a wind turbine blade joint. Compos. Struct. 2018, 188, 64–71. [Google Scholar] [CrossRef]
- Álvarez, D.; Blackman, B.; Guild, F.; Kinloch, A. Mode I fracture in adhesively-bonded joints: A mesh-size independent modelling approach using cohesive elements. Eng. Fract. Mech. 2014, 115, 73–95. [Google Scholar] [CrossRef]
- Lee, M.; Yeo, E.; Blacklock, M.; Janardhana, M.; Feih, S.; Wang, C.H. Predicting the strength of adhesively bonded joints of variable thickness using a cohesive element approach. Int. J. Adhes. Adhes. 2015, 58, 44–52. [Google Scholar] [CrossRef]
- Huang, Y.; Bu, Y.; Zhou, L.; Zhu, J.; Shi, H.; Xie, H.; Feng, X. Fatigue crack growth and propagation along the adhesive interface between fiber-reinforced composites. Eng. Fract. Mech. 2013, 110, 290–299. [Google Scholar] [CrossRef]
- Kanchanomai, C.; Thammaruechuc, A. Effects of stress ratio on fatigue crack growth of thermoset epoxy resin. Polym. Degrad. Stab. 2009, 94, 1772–1778. [Google Scholar] [CrossRef]
- Jørgensen, J.B.; Kildegaard, C.; Sørensen, B.F. Design of four-point SENB specimens with stable crack growth. Eng. Fract. Mech. 2018, 191, 168–186. [Google Scholar] [CrossRef]
- Jacobsen, T.; Sørensen, B.F. Mode I intra-laminar crack growth in composites—modelling of R-curves from measured bridging laws. Compos. Part Appl. Sci. Manuf. 2001, 32, 1–11. [Google Scholar] [CrossRef]
- Sørensen, B.F.; Gamstedt, E.K.; Jacobsen, T.K. Equivalence of J integral and stress intensity factor approaches for large scale bridging problems. Int. J. Fract. 2000, 104, 31–36. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Volume I: Introduction Fracture Mechanics. Fatigue Crack Propagation; Technical Report CT-93/69.I; US Department of Transportation, Research and Special Programs Administration, Volpe National Transportation System Center: Cambridge, MA, USA, 1993. [Google Scholar]
- Forman, R.; Shivakumar, V.; Cardinal, J.; Williams, L.; McKeighan, P. Fatigue Crack Growth Database for Damage Tolerance Analysis; Technical Report DOT/FAA/AR-05/15; US Department of Transportation, Federal Aviation Administration, Office of Aviation Research: Washington, DC, USA, 2005. [Google Scholar]
- Groves, R. 3.12 Inspection and Monitoring of Composite Aircraft Structures. In Reference Module in Materials Science and Materials Engineering: Comprehensive Composite Materials II; Elservier: Amsterdam, The Netherlands, 2018; pp. 300–311. [Google Scholar]
- Paquette, J.A.; Abnumeri, G.; Abdi, F. Durability and Reliability of Wind Turbine Composite Blades Using Robust Design Approach; Technical Report SAND2011-1916C; Sandia National Lab: Albuquerque, NM, USA, 2011. [Google Scholar]
- Valeti, B.; Pakzad, S.N. Estimation of remaining useful life of a fatigue damaged wind turbine blade with particle filters. In Dynamics of Civil Structures, Volume 2: Proceedings of the 36th IMAC, A Conference and Exposition on Structural Dynamics 2018; Springer International Publishing: Cham, Switzerland, 2019; pp. 319–328. [Google Scholar]
- Liu, M.; Gan, Y.; Hanaor, D.A.; Liu, B.; Chen, C. An improved semi-analytical solution for stress at round-tip notches. Eng. Fract. Mech. 2015, 149, 134–143. [Google Scholar] [CrossRef]
- Skinn, D.; Gallagher, J.P.; Berens, A.P.; Huber, P.; Smith, J. Damage Tolerant Design Handbook; Technical Report WL-TR-94-4054; Wright Laboratory, University of Dayton Research Institute: Dayton, OH, USA, 1994; Volume 3, Chapter 7. [Google Scholar]
- Anderson, B.; Hsu, C.; Carr, P.; Lo, J.; Yu, J.; Duong, C. Evaluation and Verification of Advanced Methods to Assess Multiple-Site Damage of Aircraft Structure; Technical Report DOT/FAA/AR-04/42 I; US Department of Transportation, Federal Aviation Administration, Office of Aviation Research: Washington, DC, USA, 2004. [Google Scholar]
- Boyd, K.; Jansen, D.; Krishnan, S.; Harter, J. Structural Integrity Analysis and Verification for Aircraft Structures. Volume 1; Technical Report WL-TR-95-3090; Wright Laboratory, Analytical Services and Materials: Hampton, VA, USA, 1996. [Google Scholar]
- King, C. Damage Tolerance vs Durability: Analysis for Sustainment of T-38 Aircraft; Technical Report HAFB 2014-09-04-WLD-100; Air Force Life Cycle Management Center, T-38 Structural Integrity and Analysis Section: Hill AFB, UT, USA, 2014. [Google Scholar]
- Katnam, K.; Comer, A.; Roy, D.; Da Silva, L.; Young, T. Composite repair in wind turbine blades: An overview. J. Adhes. 2015, 91, 113–139. [Google Scholar] [CrossRef]
- Shohag, M.A.S.; Hammel, E.C.; Olawale, D.O.; Okoli, O.I. Damage mitigation techniques in wind turbine blades: A review. Wind Eng. 2017, 41, 185–210. [Google Scholar] [CrossRef]
- Yang, B.; Sun, D. Testing, inspecting and monitoring technologies for wind turbine blades: A survey. Renew. Sustain. Energy Rev. 2013, 22, 515–526. [Google Scholar] [CrossRef]
- Beganovic, N.; Söffker, D. Structural health management utilization for lifetime prognosis and advanced control strategy deployment of wind turbines: An overview and outlook concerning actual methods, tools, and obtained results. Renew. Sustain. Energy Rev. 2016, 64, 68–83. [Google Scholar] [CrossRef]
- McGugan, M.; Mishnaevsky, L., Jr. Damage mechanism based approach to the structural health monitoring of wind turbine blades. Coatings 2020, 10, 1223. [Google Scholar] [CrossRef]
- Pereira, G.; Mikkelsen, L.P.; McGugan, M. Damage tolerant design and condition monitoring of composite material and bondlines in wind turbine blades: Failure and crack propagation. In Proceedings of the EWEA Offshore 2015 Conference. European Wind Energy Association (EWEA), Copenhagen, Denmark, 1–3 December 2015; pp. 1–9. [Google Scholar]
- Artigao, E.; Martín-Martínez, S.; Honrubia-Escribano, A.; Gómez-Lázaro, E. Wind turbine reliability: A comprehensive review towards effective condition monitoring development. Appl. Energy 2018, 228, 1569–1583. [Google Scholar] [CrossRef]
- Sørensen, B.F.; Lading, L.; Sendrup, P. Fundamentals for Remote Structural Health Monitoring of Wind Turbine Blades—A Preproject; Technical Report Risø-R-1336; Risø National Laboratory: Roskilde, Denmark, 2002. [Google Scholar]
- Myrent, N.J.; Barrett, N.C.; Adams, D.E.; Griffith, D.T. Structural Health and Prognostics Management for Offshore Wind Turbines: Sensitivity Analysis of Rotor Fault and Blade Damage with O&M Cost Modeling; Technical Report SAND2014-15588; Vanderbilt Laboratory for Systems Integrity and Reliability, Sandia National Lab: Albuquerque, NM, USA, 2014. [Google Scholar]
- Sierra-Pérez, J.; Torres-Arredondo, M.A.; Güemes, A. Damage and nonlinearities detection in wind turbine blades based on strain field pattern recognition. FBGs, OBR and strain gauges comparison. Compos. Struct. 2016, 135, 156–166. [Google Scholar] [CrossRef]
- Du, Y.; Zhou, S.; Jing, X.; Peng, Y.; Wu, H.; Kwok, N. Damage detection techniques for wind turbine blades: A review. Mech. Syst. Signal Process. 2020, 141, 106445. [Google Scholar] [CrossRef]
- Ciang, C.C.; Lee, J.R.; Bang, H.J. Structural health monitoring for a wind turbine system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19, 122001. [Google Scholar] [CrossRef]
- Rumsey, M.A.; Paquette, J.A. Structural health monitoring of wind turbine blades. In Proceedings of the Smart Sensor Phenomena, Technology, Networks, and Systems 2008, San Diego, CA, USA, 10–12 March 2008; Volume 6933, pp. 104–118. [Google Scholar]
- Schubel, P.; Crossley, R.; Boateng, E.; Hutchinson, J. Review of structural health and cure monitoring techniques for large wind turbine blades. Renew. Energy 2013, 51, 113–123. [Google Scholar] [CrossRef]
- Di Sante, R. Fibre optic sensors for structural health monitoring of aircraft composite structures: Recent advances and applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef]
- Solbes Ferri, I. Dynamic Continuous Fiber Optical Strain Sensing for Damage Diagnosis on Beam-Like Composite Structures. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2022. [Google Scholar]
- Pereira, G.F.; Mikkelsen, L.P.; McGugan, M. Crack detection in fibre reinforced plastic structures using embedded fibre bragg grating sensors: Theory, model development and experimental validation. PLoS ONE 2015, 10, e0141495. [Google Scholar] [CrossRef]
- Schroeder, K.; Ecke, W.; Apitz, J.; Lembke, E.; Lenschow, G. A fibre Bragg grating sensor system monitors operational load in a wind turbine rotor blade. Meas. Sci. Technol. 2006, 17, 1167. [Google Scholar] [CrossRef]
- Hill, K.O.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Light. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Taylor, S.G.; Farinholt, K.; Choi, M.; Jeong, H.; Jang, J.; Park, G.; Lee, J.R.; Todd, M.D. Incipient crack detection in a composite wind turbine rotor blade. J. Intell. Mater. Syst. Struct. 2014, 25, 613–620. [Google Scholar] [CrossRef]
- Shohag, M.A.; Ndebele, T.; Okoli, O. Real-time damage monitoring in trailing edge bondlines of wind turbine blades with triboluminescent sensors. Struct. Health Monit. 2019, 18, 1129–1140. [Google Scholar] [CrossRef]
- Antoniadou, I.; Dervilis, N.; Papatheou, E.; Maguire, A.; Worden, K. Aspects of structural health and condition monitoring of offshore wind turbines. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140075. [Google Scholar] [CrossRef]
- Griffith, D.T.; Yoder, N.C.; Resor, B.; White, J.; Paquette, J. Structural health and prognostics management for the enhancement of offshore wind turbine operations and maintenance strategies. Wind Energy 2014, 17, 1737–1751. [Google Scholar] [CrossRef]
- Griffith, D.T.; Yoder, N.; Resor, B.; White, J.; Paquette, J. Structural Health and Prognostics Management for Offshore Wind Turbines: An Initial Roadmap; Technical Report SAND2012-10109; Sandia National Lab: Albuquerque, NM, USA, 2012. [Google Scholar]
- Eleftheroglou, N.; Zarouchas, D.; Loutas, T.; Alderliesten, R.C.; Benedictus, R. Online remaining fatigue life prognosis for composite materials based on strain data and stochastic modeling. Key Eng. Mater. 2016, 713, 34–37. [Google Scholar] [CrossRef]



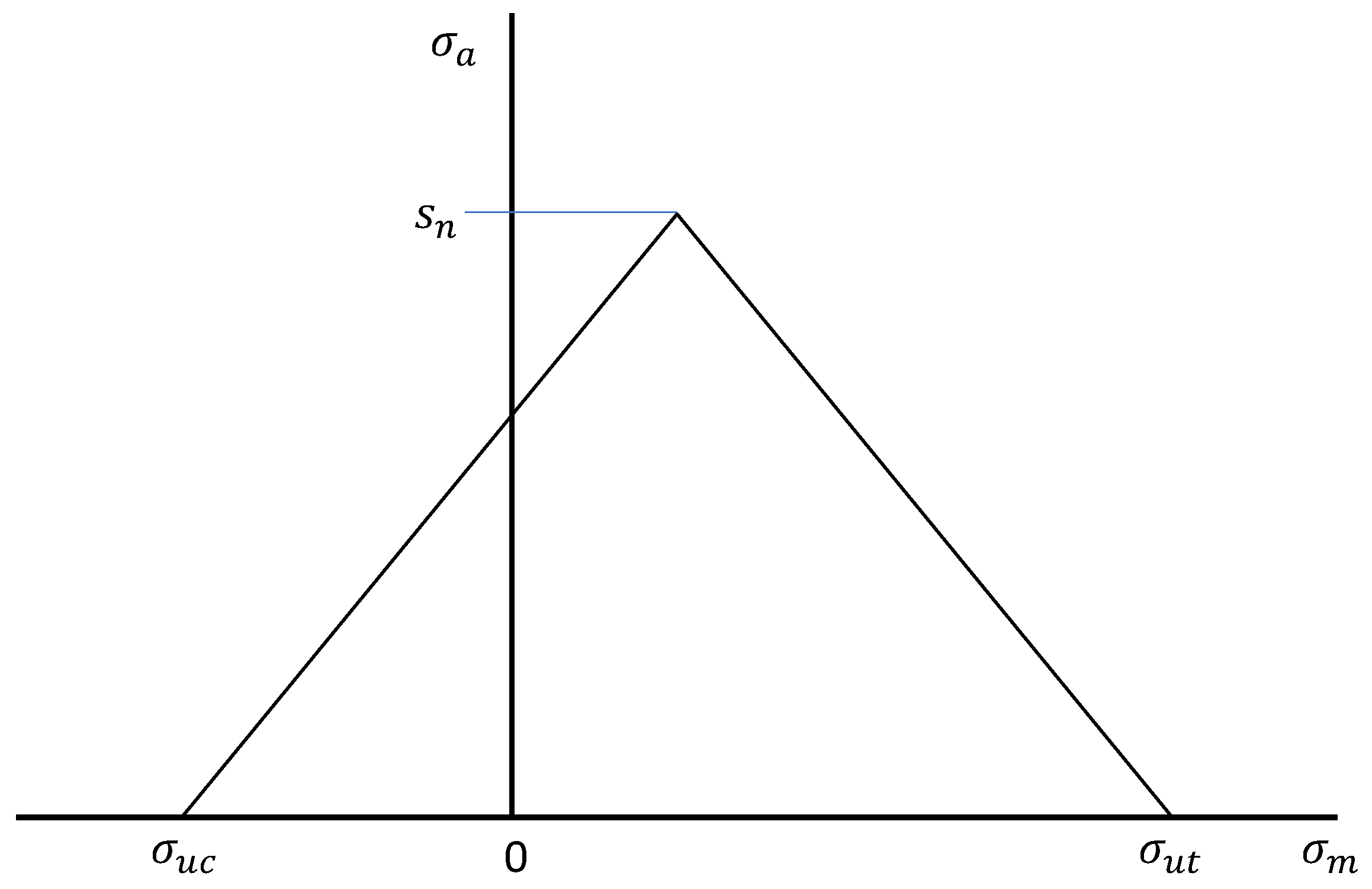

| Design Situation | Wind Condition | Design Load Case |
|---|---|---|
| Power production | Normal turbulence model (NTM) | 1.2 |
| Power production plus occurrence of fault | Normal turbulence model (NTM) | 2.4 |
| Start Up | Normal wind profile (NWP) model | 3.1 |
| Normal shut down | Normal wind profile (NWP) model | 4.1 |
| Parked | Normal turbulence model (NTM) | 6.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moroney, P.D.; Verma, A.S. Durability and Damage Tolerance Analysis Approaches for Wind Turbine Blade Trailing Edge Life Prediction: A Technical Review. Energies 2023, 16, 7934. https://doi.org/10.3390/en16247934
Moroney PD, Verma AS. Durability and Damage Tolerance Analysis Approaches for Wind Turbine Blade Trailing Edge Life Prediction: A Technical Review. Energies. 2023; 16(24):7934. https://doi.org/10.3390/en16247934
Chicago/Turabian StyleMoroney, Patrick D., and Amrit Shankar Verma. 2023. "Durability and Damage Tolerance Analysis Approaches for Wind Turbine Blade Trailing Edge Life Prediction: A Technical Review" Energies 16, no. 24: 7934. https://doi.org/10.3390/en16247934
APA StyleMoroney, P. D., & Verma, A. S. (2023). Durability and Damage Tolerance Analysis Approaches for Wind Turbine Blade Trailing Edge Life Prediction: A Technical Review. Energies, 16(24), 7934. https://doi.org/10.3390/en16247934






