The Efficiency Improvement of Track-Type Wireless Power Transmission Systems through Electromagnetic Finite Element Analysis
Abstract
:1. Introduction
2. The Magnetic Field Analysis of the WPT System Using FEA
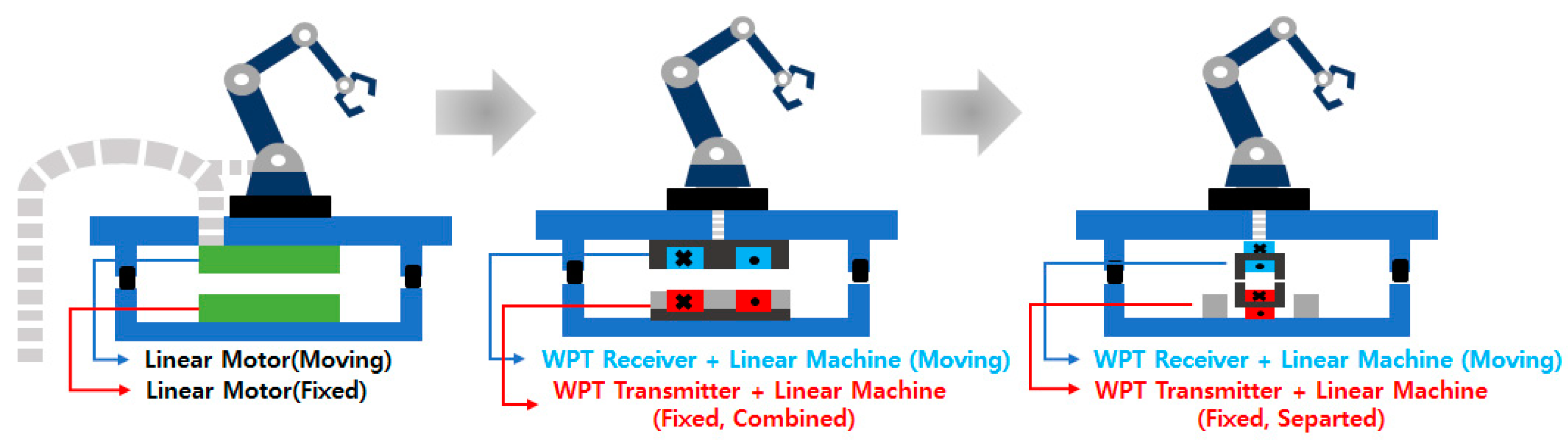
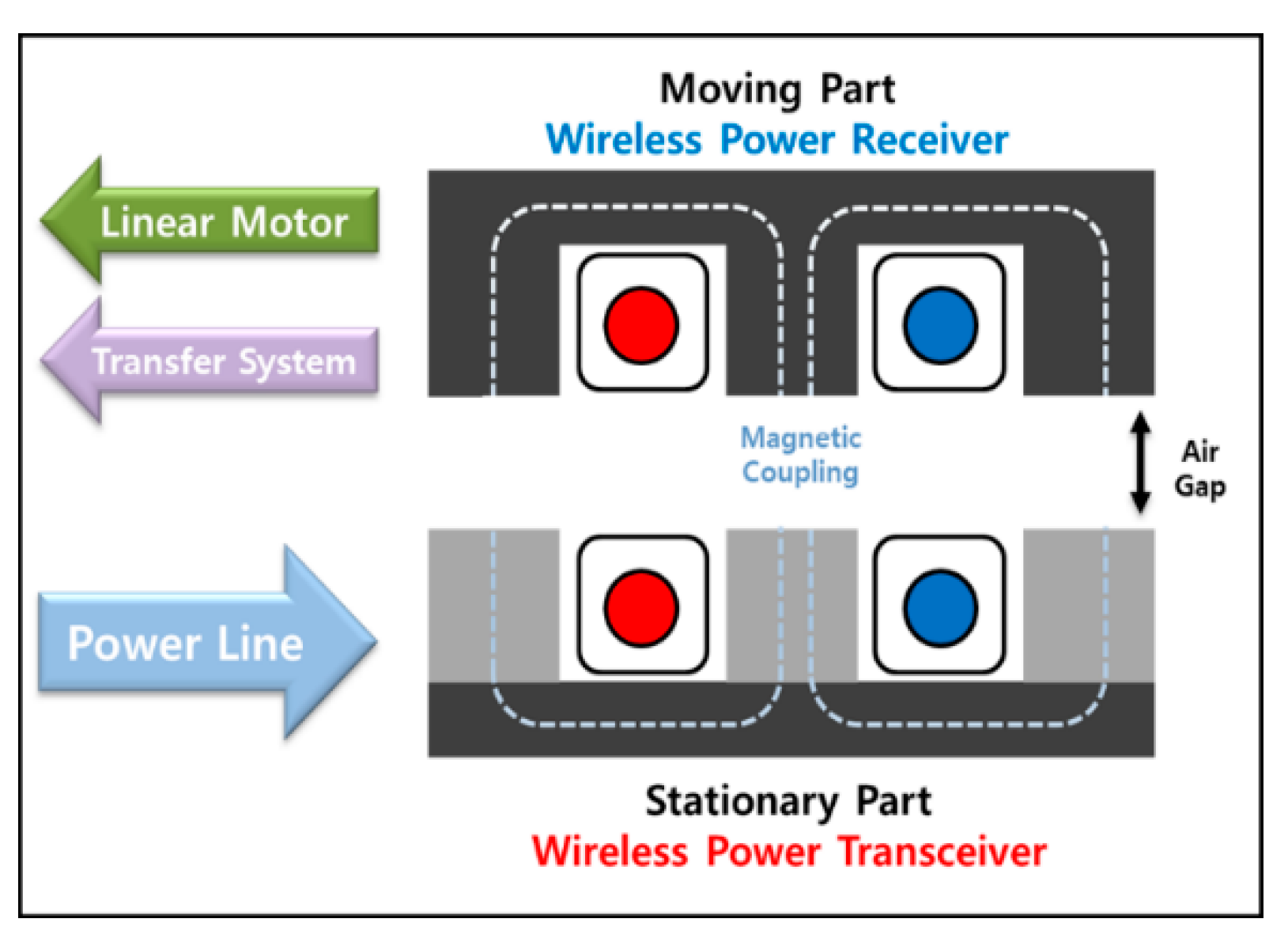
2.1. The Configuration of the WPT Model
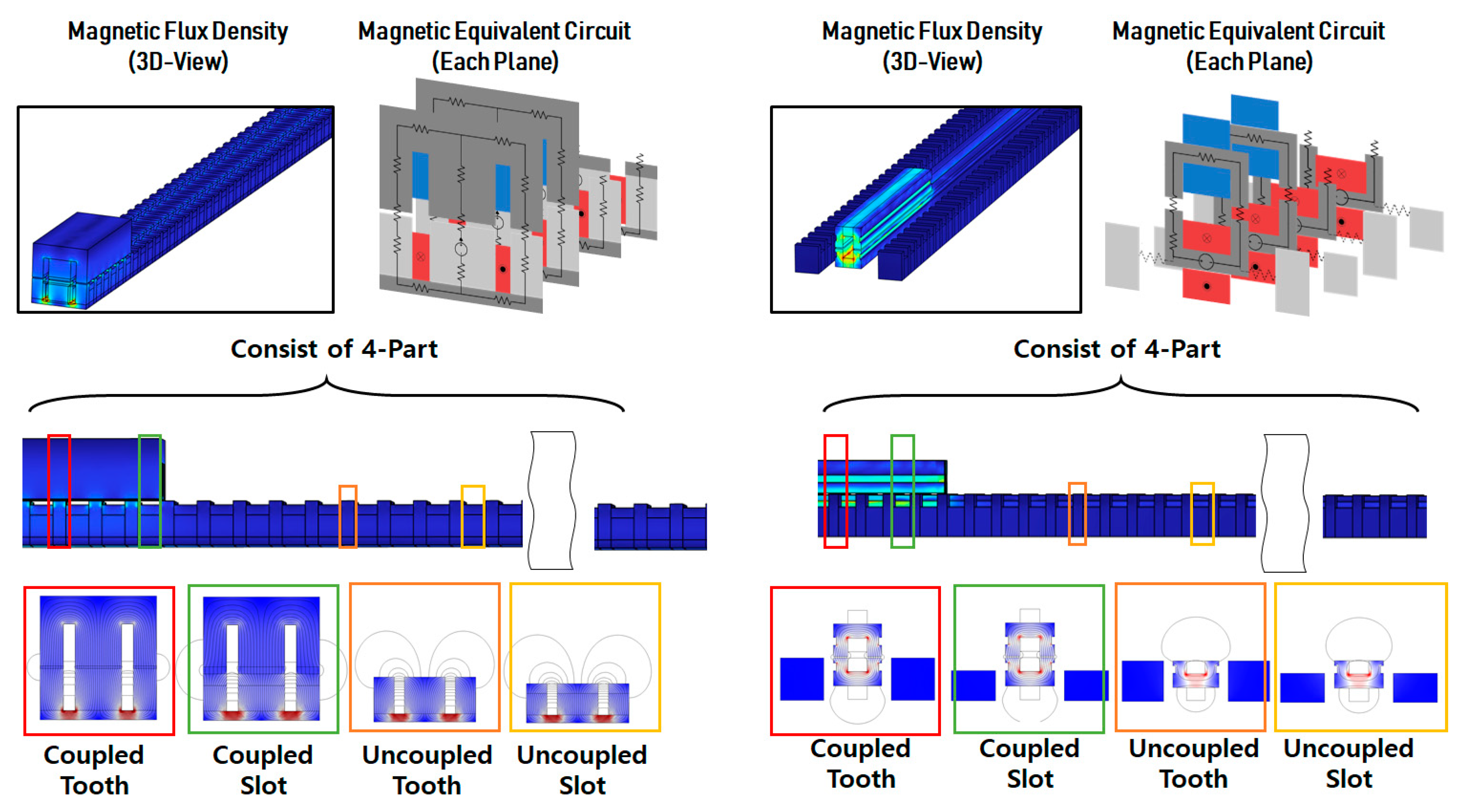
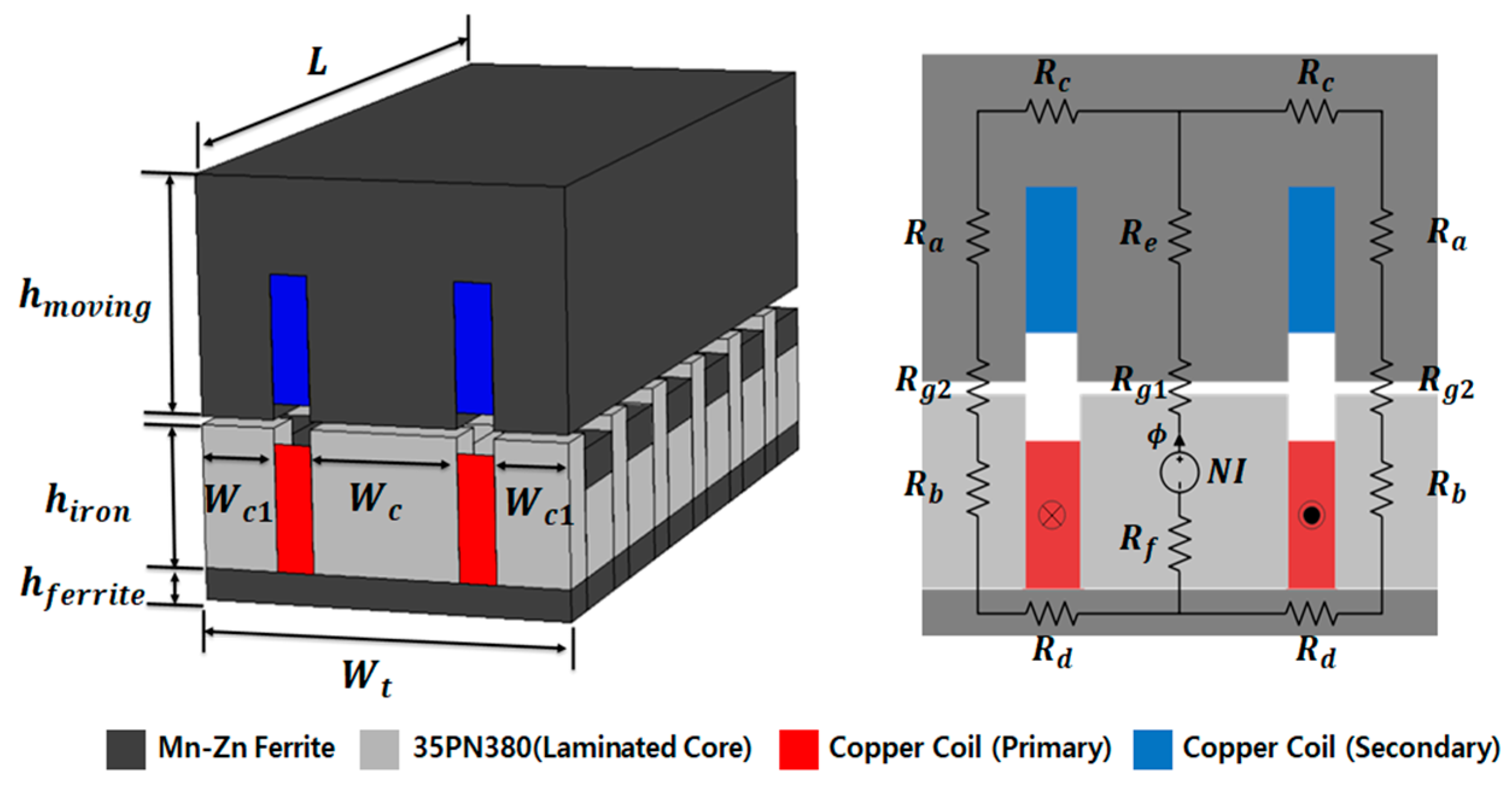
2.1.1. The Magnetic Equivalent Circuit Analysis of the Original Model
2.1.2. The Magnetic Equivalent Circuit Analysis of the Proposed Model
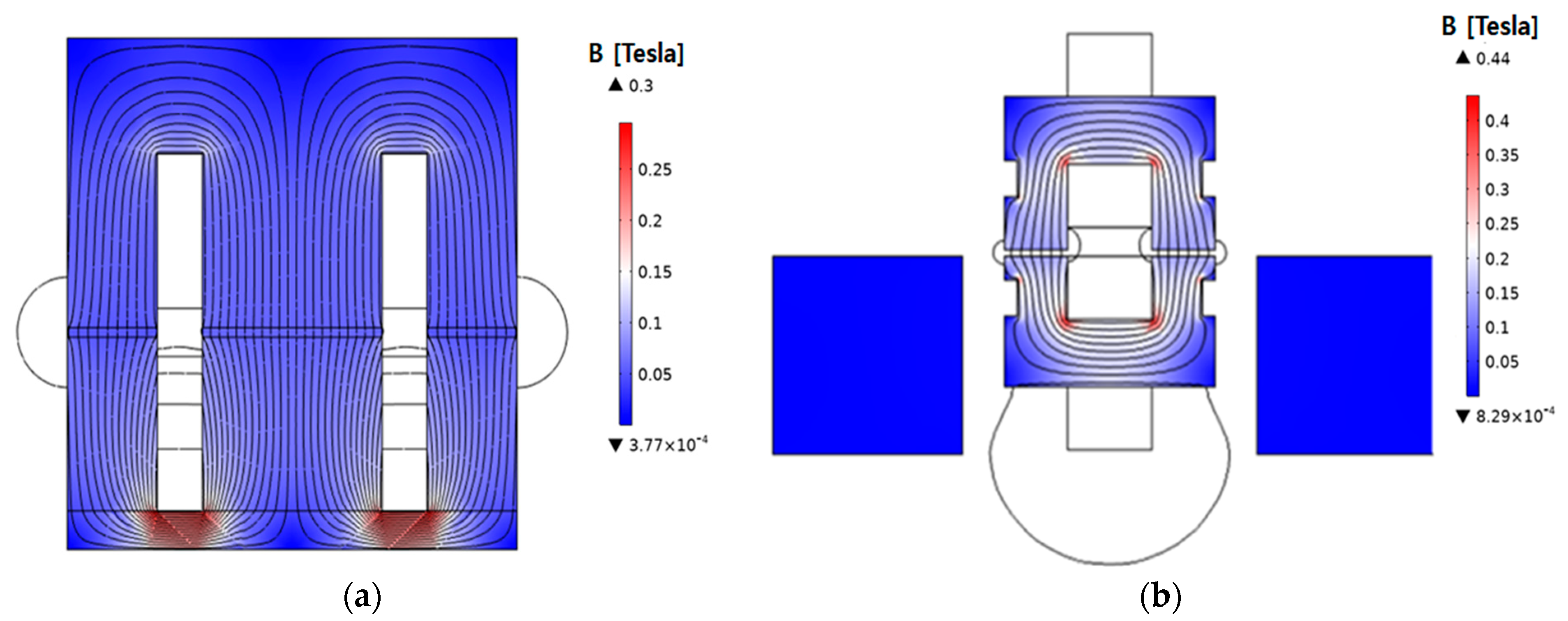
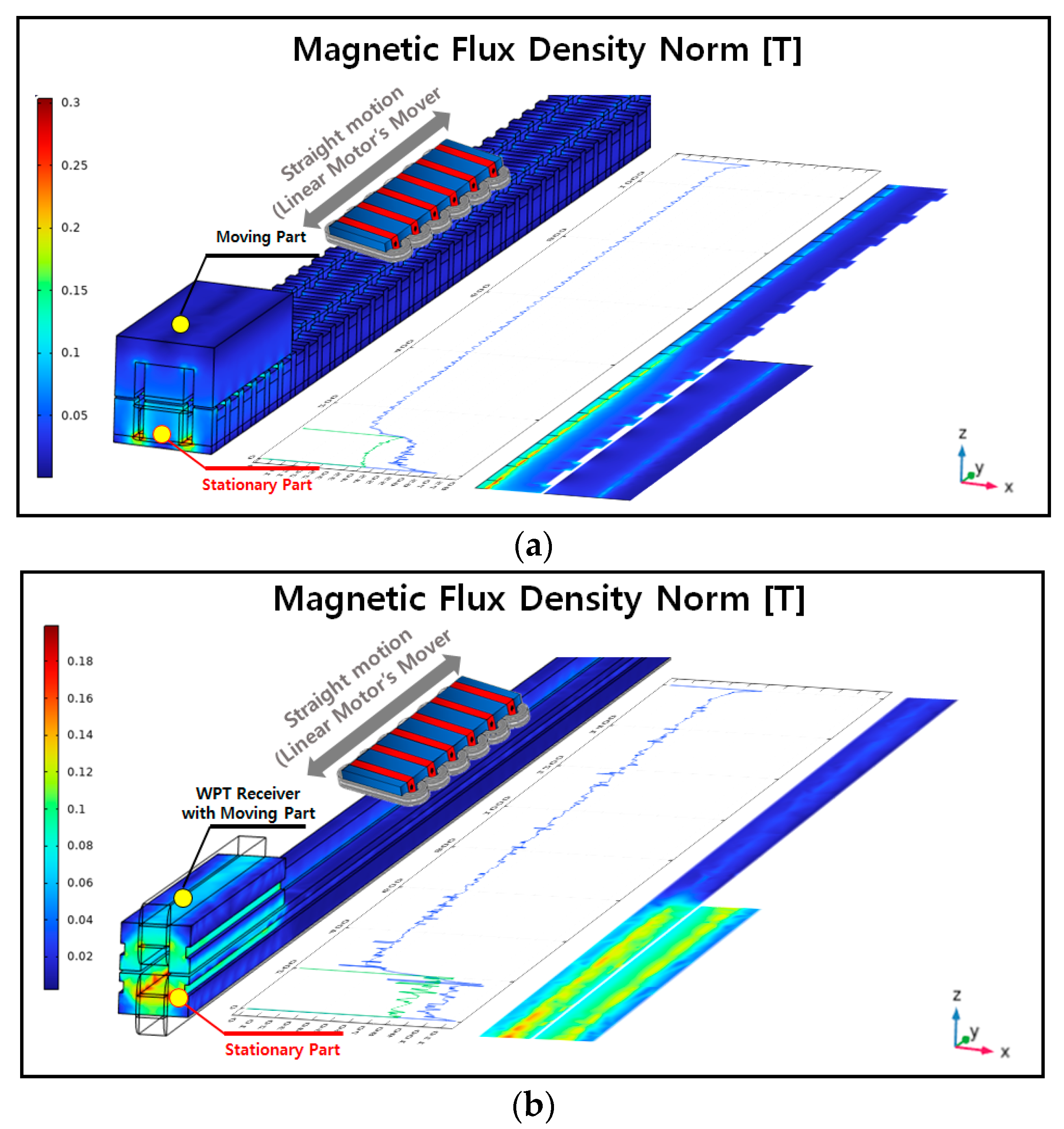
2.2. The FEM Analysis of Magnetic Coupling Characteristics
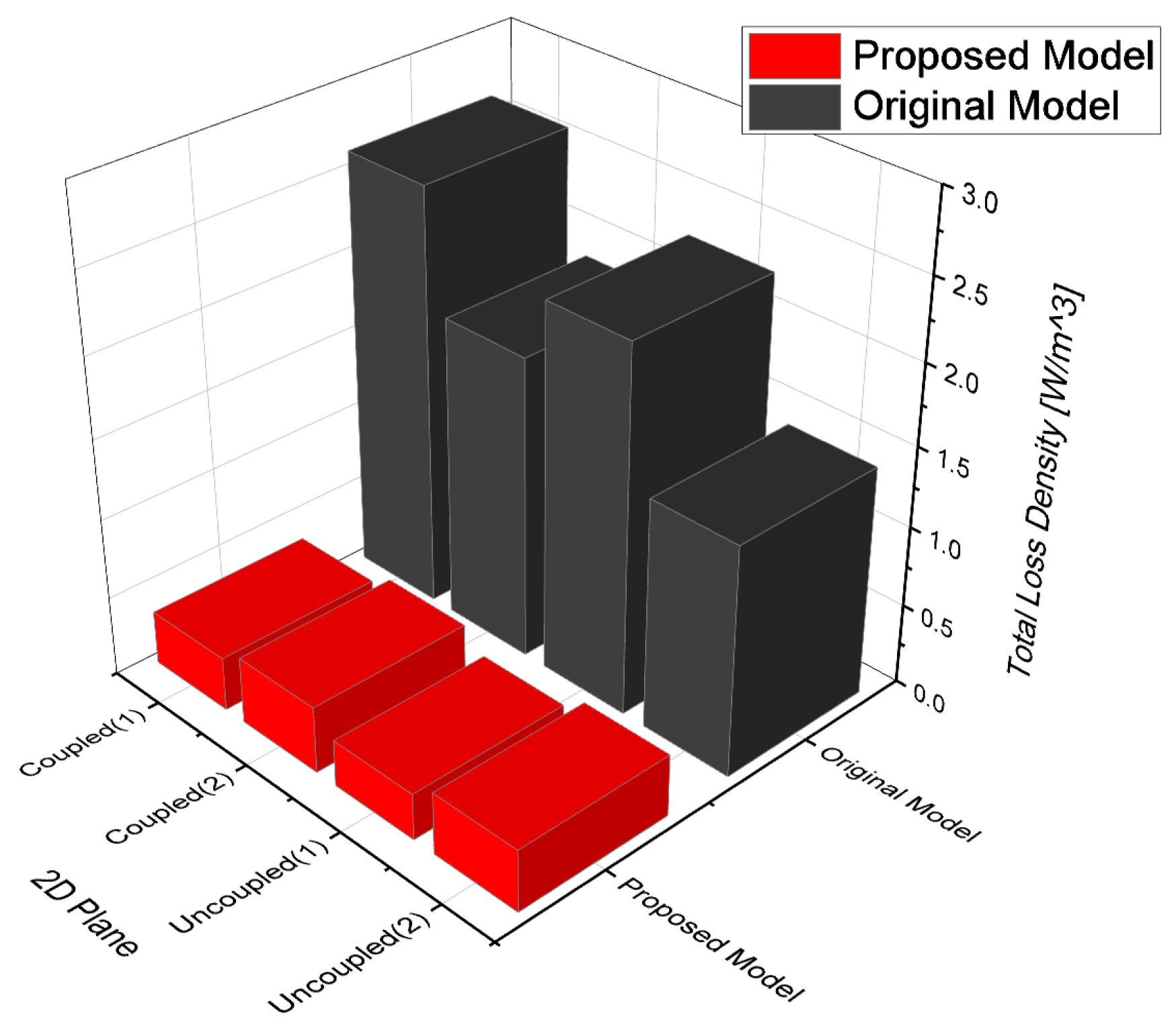
2.3. FEA for Core Loss Model Caculation
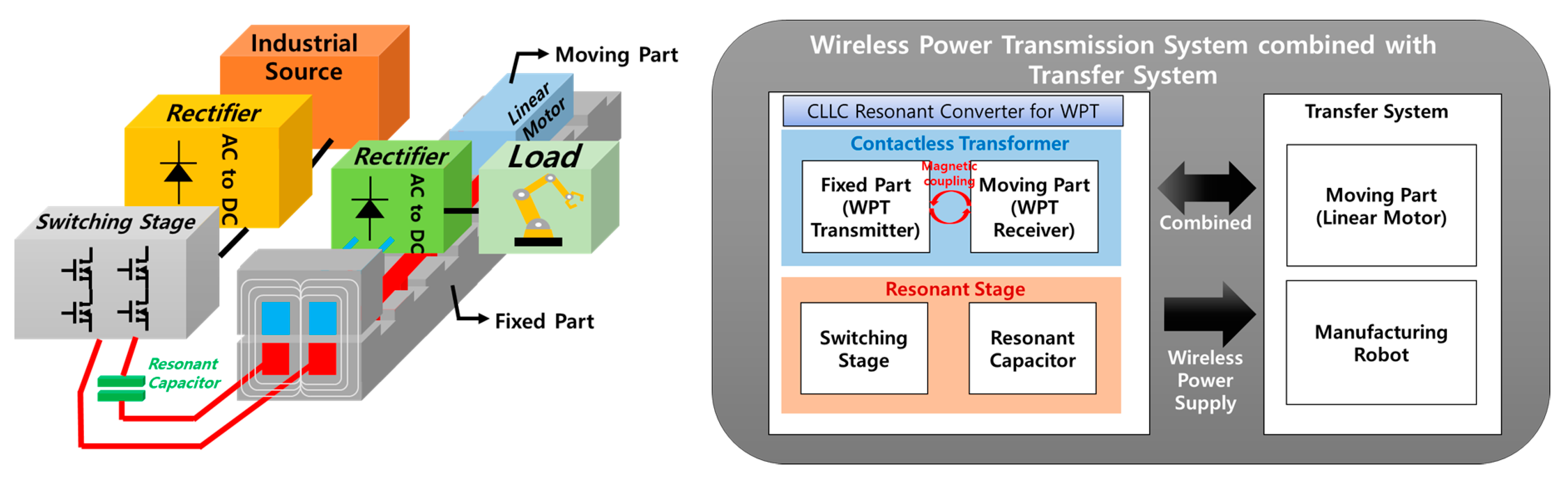
3. Power Converter System Characteristics and Experiment Result Analysis
3.1. Subsection Electrical System Structure and the Comparison of Excitation Current for Each Model
3.2. The First Harmonic Analysis of the CLLC Resonant Converter in the WPT System
3.3. Experiment and Simulation Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, W.; Liu, J.; Chen, S.; Zhang, L. Energy Shaping Control for Wireless Power Transfer System in Automatic Guided Vehicles. Energies 2020, 13, 2959. [Google Scholar] [CrossRef]
- Van Mulders, J.; Delabie, D.; Lecluyse, C.; Buyle, C.; Callebaut, G.; Van der Perre, L.; De Strycker, L. Wireless Power Transfer: Systems, Circuits, Standards, and Use Cases. Sensors 2022, 22, 5573. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.-S.; Huang, S.-J.; Wu, M.-J. Enhancement of Wireless Power Transfer for Automated Guided Vehicles Considering Disturbance Suppression. IEEE Access 2023, 11, 21508–21518. [Google Scholar] [CrossRef]
- Woo, H.; Park, J.-H.; Joo, C.; Ahn, H.; Kang, D.; Kim, T. Analysis of the Transformer Characteristics for an Integration System with a Wireless Power Transfer Device and Linear Motor. Energies 2021, 14, 6769. [Google Scholar] [CrossRef]
- Lee, J.Y.; Lee, I.J.; Kim, J.W.; Chang, J.H.; Kang, D.H.; Chung, S.U.; Hong, J.P. Contactless power transfer system combined with linear electric machine. In Proceedings of the 2007 International Conference on Electrical Machines and Systems (ICEMS), Seoul, Republic of Korea, 8–11 October 2007; pp. 1544–1548. [Google Scholar] [CrossRef]
- Joo, C.; Ahn, H.; Kim, T. A Study on the Design and Analysis of High Frequency Coil Shape for Contactless Power Transmission System Combined with Transfer System. J. Korea Ind. Inf. Syst. Res. 2021, 26, 41–54. [Google Scholar]
- Woo, H.; Park, J.-H.; Joo, C.; Ahn, H.; Kang, D.; Kim, T. Design of Wireless Power Transfer in Integration System of Wireless Power Transfer and Linear Motor; The Transactions of the Korean Institute of Electrical Engineers (KIEE): Seoul, Republic of Korea, 2020; pp. 40–44. [Google Scholar]
- Kang, J.; Ahn, J.; Kim, H.; Oh, S.; Lee, J.; Kim, C. A Study on the Levitation Force of Maglev Logistics Transport System Based on Magnetic Equivalent Circuits Considering the Fringing Effect; The Transaction of the Korean Institute of Electrical Engineers: Seoul, Republic of Korea, 2020; Volume 69P, pp. 243–247. [Google Scholar] [CrossRef]
- Bhatnagar, V.P. A Complete Course in ISC Physics; Pitambar Publishing: New Delhi, India, 1997; ISBN 978-81-209-0202-2. [Google Scholar]
- Veltman, A.; Pulle, D.W.J.; de Doncker, R.W. Fundamentals of Electrical Drivers, Power Systems; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-29409-4. [Google Scholar]
- Pavlek, M.; Donic, T. Simulation study of inductive heating of molybdenum sheet suited for rapid prototypes of rigid components of transport systems. ScienceDirect 2019, 40, 449–455. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the law of hysteresis. Proc. IEEE 1984, 72, 197–221. [Google Scholar] [CrossRef]
- Bertotti, G. General properties of power losses in soft ferromagnetic materials. IEEE Trans. Magn. 1988, 24, 621–630. [Google Scholar] [CrossRef]
- Westad, S. Loss Analysis in Laminated Iron Cores Using COMSOL Multiphysics and LiveLink for Matlab, NTNU. 2018. Available online: https://hdl.handle.net/11250/2574467 (accessed on 22 November 2018).
- Wick, M.; Jüttner, M.; Rucker, W.M. Harmonic balanced Jiles-Atherton hysteresis implementation for finite element simulation. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2017, 36, 1386–1395. [Google Scholar] [CrossRef]
- Wen, S.; Chen, F.; Xu, W.; Xiu, Z.; Xiu, L.; Yi, Y.; Xiao, J.; Jian, Y. Numerical Study of Electromagnetic Loss and Heat Transfer in an Oil-Immersed Transformer. Math. Probl. Eng. 2020, 2020, 6514650. [Google Scholar] [CrossRef]
- Deshmukh, S.; Iqbal, A.; Islam, S.; Khan, I.; Marzband, M.; Rahman, S.; Al-Wahedi, A.M. Review on classification of resonant converters for electric vehicle application. Energy Rep. 2022, 8, 1091–1113. [Google Scholar] [CrossRef]
- Kang, M.-H.; Joo, D.-M.; Woo, D.-G.; Lee, B.-K. Design of Resonant Network of SP topology for Wireless Power Transfer System. In Proceedings of the KIPE Conference 2015, Seoul, Republic of Korea, 1–5 June 2015; pp. 38–39. [Google Scholar]
- Jin, N.-Z.; Feng, Y.; Chen, Z.-Y.; Wu, X.-G. Bidirectional CLLLC Resonant Converter Based on Frequency-Conversion and Phase-Shift Hybrid Control. Electronics 2023, 12, 1605. [Google Scholar] [CrossRef]
- Shin, Y.; Ah, S. Principle of Power Transfer between Coils and the Method of Selecting Resonant Topologies in a Wireless Power Transfer System. J. Korean Inst. Electromagn. Eng. Sci. 2022, 33, 509–524. [Google Scholar] [CrossRef]



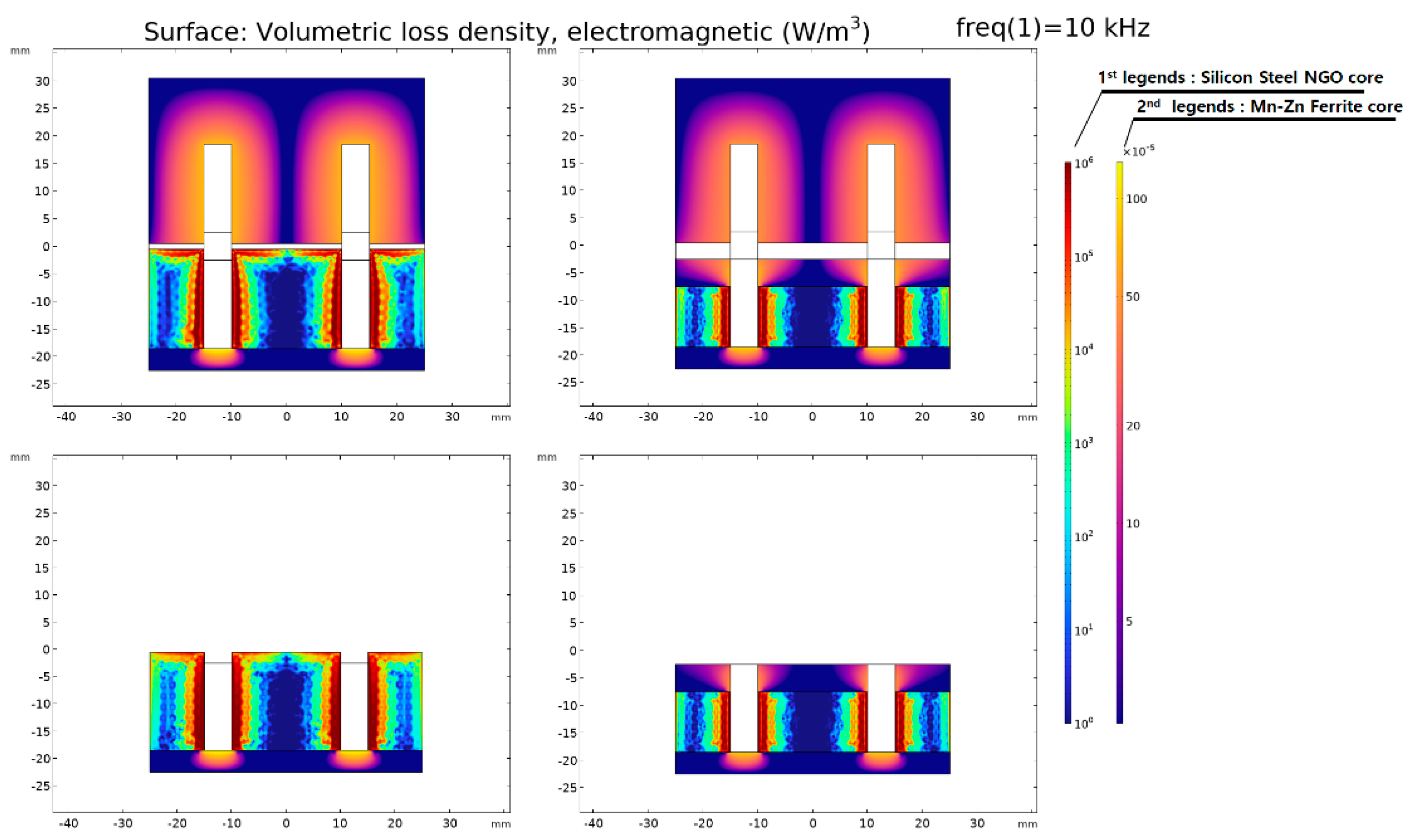


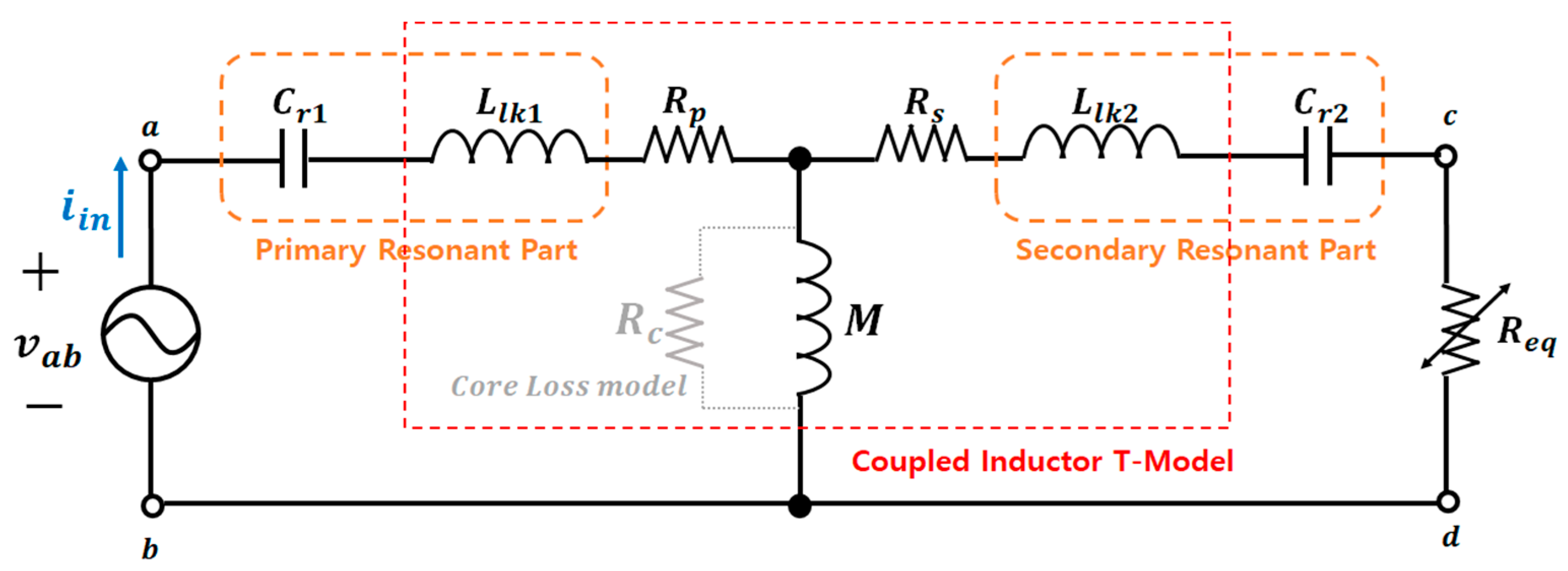


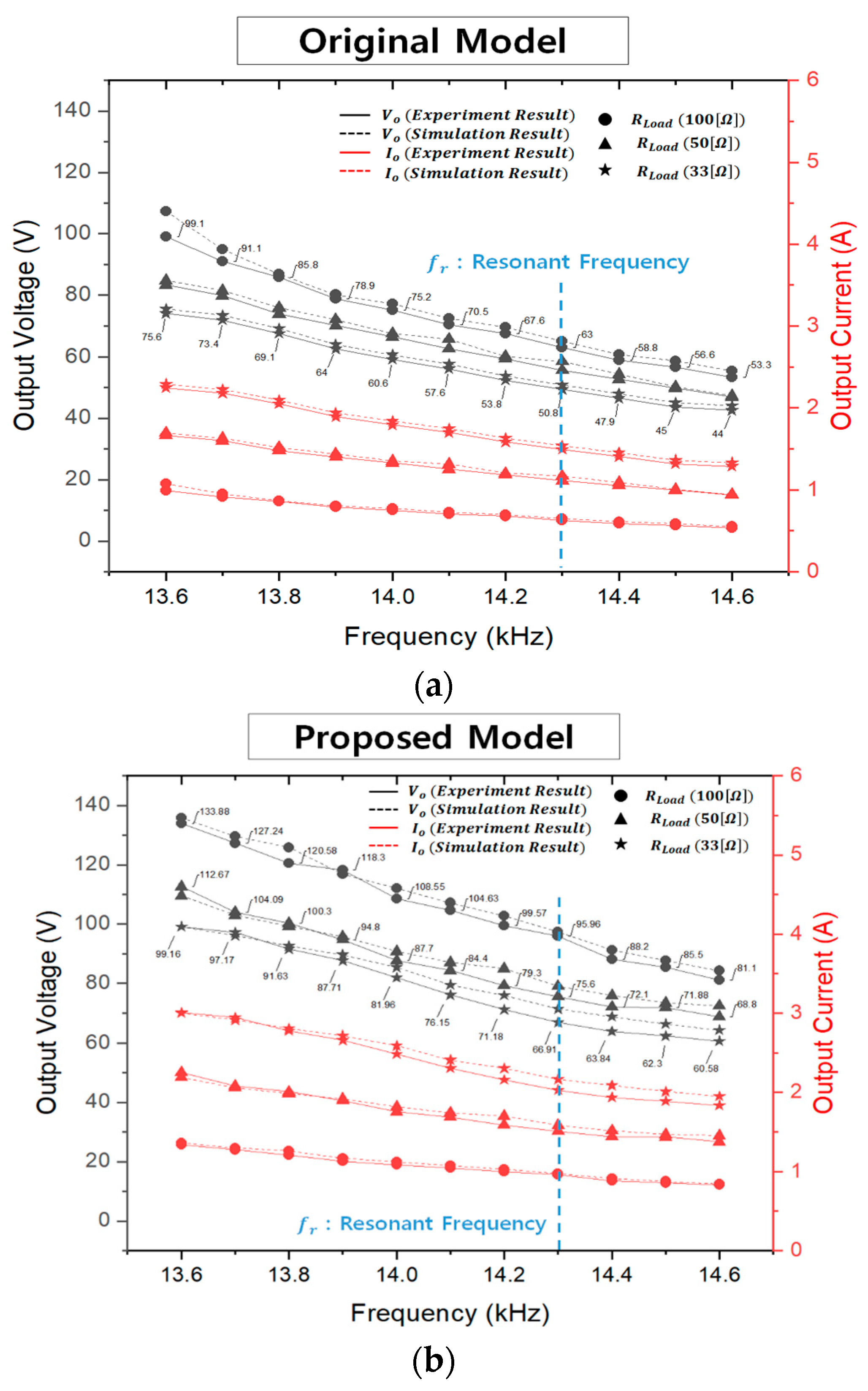

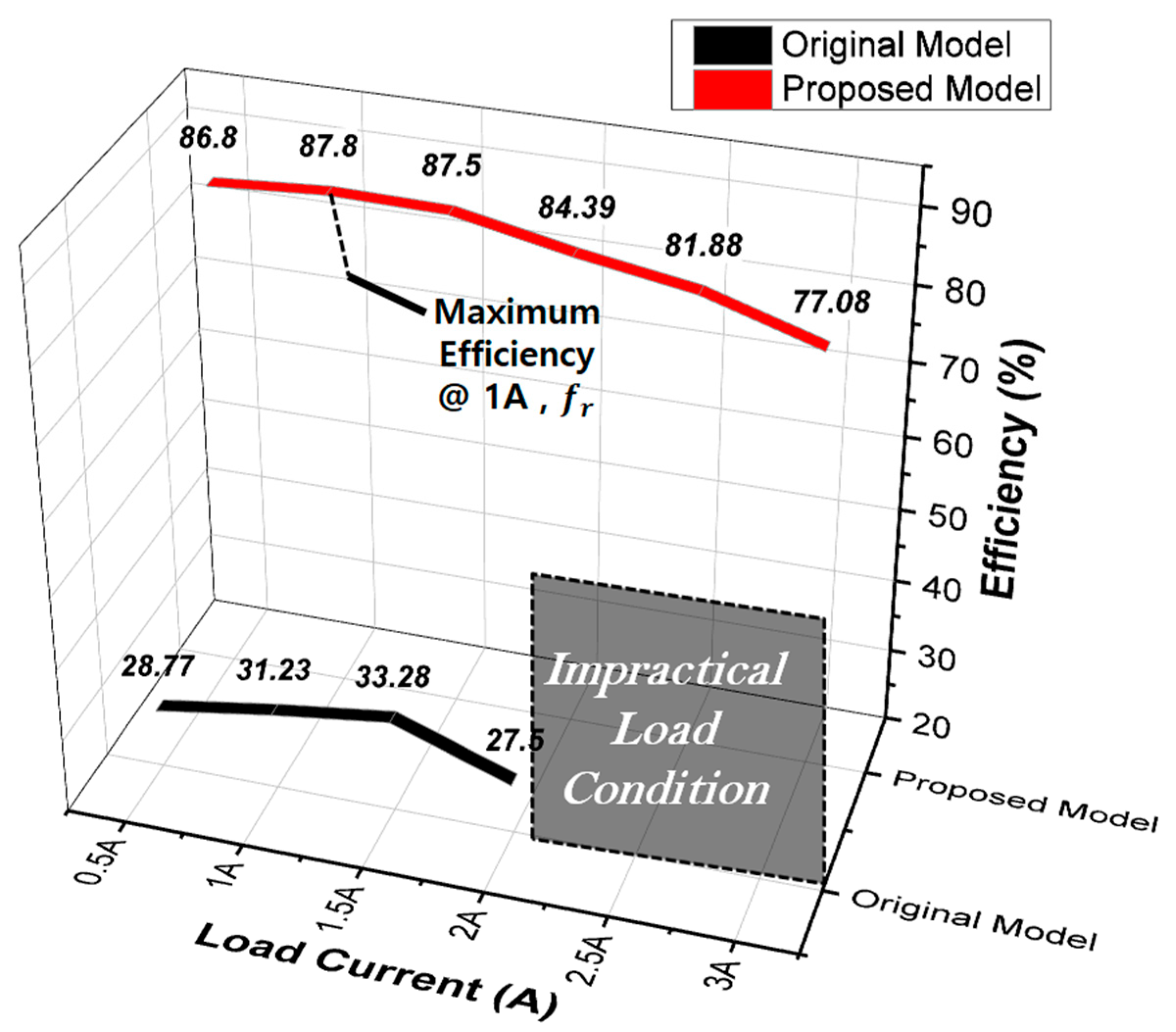
| Parameter | Description | Value |
|---|---|---|
| N1 | Number of Primary Turns | 19 |
| N2 | Number of Secondary Turns | 19 |
| Width of the Model | 50 | |
| Width of the E-core (center) | 20 | |
| Width of the E-core | 10 | |
| Height of the Stator (Iron) | 18 | |
| Height of the Stator (ferrite) | 4 | |
| Height of the Moving Core | 30 | |
| L | Length of the Moving Core | 108 |
| l | Length of the Stator Core | 1080 |
| Parameter | Description | Value |
|---|---|---|
| N1 | Number of Primary turns | 19 |
| N2 | Number of Secondary turns | 19 |
| Width of the Model | 25 | |
| Height of the Moving Core | 17 | |
| Height of the Stator Core | 14.5 | |
| L | Length of the Moving Core | 200 |
| Parameter | Original Model | Proposed Model |
|---|---|---|
| 8812 [kΩ] | 16,696 [kΩ] | |
| 10,762 [kΩ] | 9500 [kΩ] | |
| 26,014 [kΩ] | 67,684 [kΩ] | |
| 17,898 [kΩ] | 38,875 [kΩ] | |
| 149 [kΩ] | 236.8 [kΩ] |
| @ Io = 5 [A] Excitation Current | Original Model | Proposed Model | ||
|---|---|---|---|---|
| Tooth | Slot | Tooth | Slot | |
| 84.093 [mT] | 65.38 [mT] | 93.356 [mT] | 80.91 [mT] | |
| 49.861 [mT] | 32.5 [mT] | 84.726 [mT] | 68.1 [mT] | |
| 0.592 | 0.49 | 0.907 | 0.84 | |
| M | 300 [μH] | 500 [μH] | ||
| k | 0.3 | 0.5 | ||
| Original Model | Proposed Model | |||
|---|---|---|---|---|
| Simulated | Experimental | Simulated | Experimental | |
| L1 (mH) | 2.1 | 1.9 | 1.77 | 1.74 |
| L2 (mH) | 0.53 | 0.58 | 0.6 | 0.63 |
| M (mH) | 0.36 | 0.35 | 0.48 | 0.5 |
| Coil | Stator Core Part | Moving Core Part | ||
|---|---|---|---|---|
| Material | Copper | Silicon Steel NGO 35PN380 | Mn-Zn Alloy Powder Ferrite | |
| Electrical Conductivity [S/m] | 6 × 107 | 2.12765 | 1 × 10−12 | |
| Relative Permittivity | 1 | 1 | 1 | |
| Relative Permeability | 1 | 4092 @Linearity B-H | 7222 @Linearity B-H | |
| Total Volume | Original Model | 0.0002 | 0.00093 | 0.00014 |
| Proposed Model | 0.000256 | 0.00171 | 0.000063 | |
| Core Loss @ Io = 5 [A] & f = 10 [kHz] | ||
|---|---|---|
| Magnetically Coupled | Tooth (6.5 [mm]) | 15.72 |
| Slot (11.5 [mm]) | 18.9 | |
| Magnetically Uncoupled | Tooth (6.5 [mm]) | 174.04 |
| Slot (11.5 [mm]) | 109.44 | |
| Total Core Loss | ||
| 318.1 [W] | ||
| Core Loss @ Io = 5 [A] & f = 10 [kHz] | ||
|---|---|---|
| Magnetically Coupled | Tooth (6.5 [mm]) | 3.3765 |
| Slot (11.5 [mm]) | 4.1992 | |
| Magnetically Uncoupled | Tooth (6.5 [mm]) | 22.2512 |
| Slot (11.5 [mm]) | 29.64 | |
| Total Core Loss | ||
| 59.46 [W] | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joo, C.; Kim, T. The Efficiency Improvement of Track-Type Wireless Power Transmission Systems through Electromagnetic Finite Element Analysis. Energies 2023, 16, 8045. https://doi.org/10.3390/en16248045
Joo C, Kim T. The Efficiency Improvement of Track-Type Wireless Power Transmission Systems through Electromagnetic Finite Element Analysis. Energies. 2023; 16(24):8045. https://doi.org/10.3390/en16248045
Chicago/Turabian StyleJoo, Changdae, and Taekue Kim. 2023. "The Efficiency Improvement of Track-Type Wireless Power Transmission Systems through Electromagnetic Finite Element Analysis" Energies 16, no. 24: 8045. https://doi.org/10.3390/en16248045
APA StyleJoo, C., & Kim, T. (2023). The Efficiency Improvement of Track-Type Wireless Power Transmission Systems through Electromagnetic Finite Element Analysis. Energies, 16(24), 8045. https://doi.org/10.3390/en16248045






