Frictional Losses of Ring Pack in SI and HCCI Engine
Abstract
:1. Introduction
2. Piston Ring Pack Model
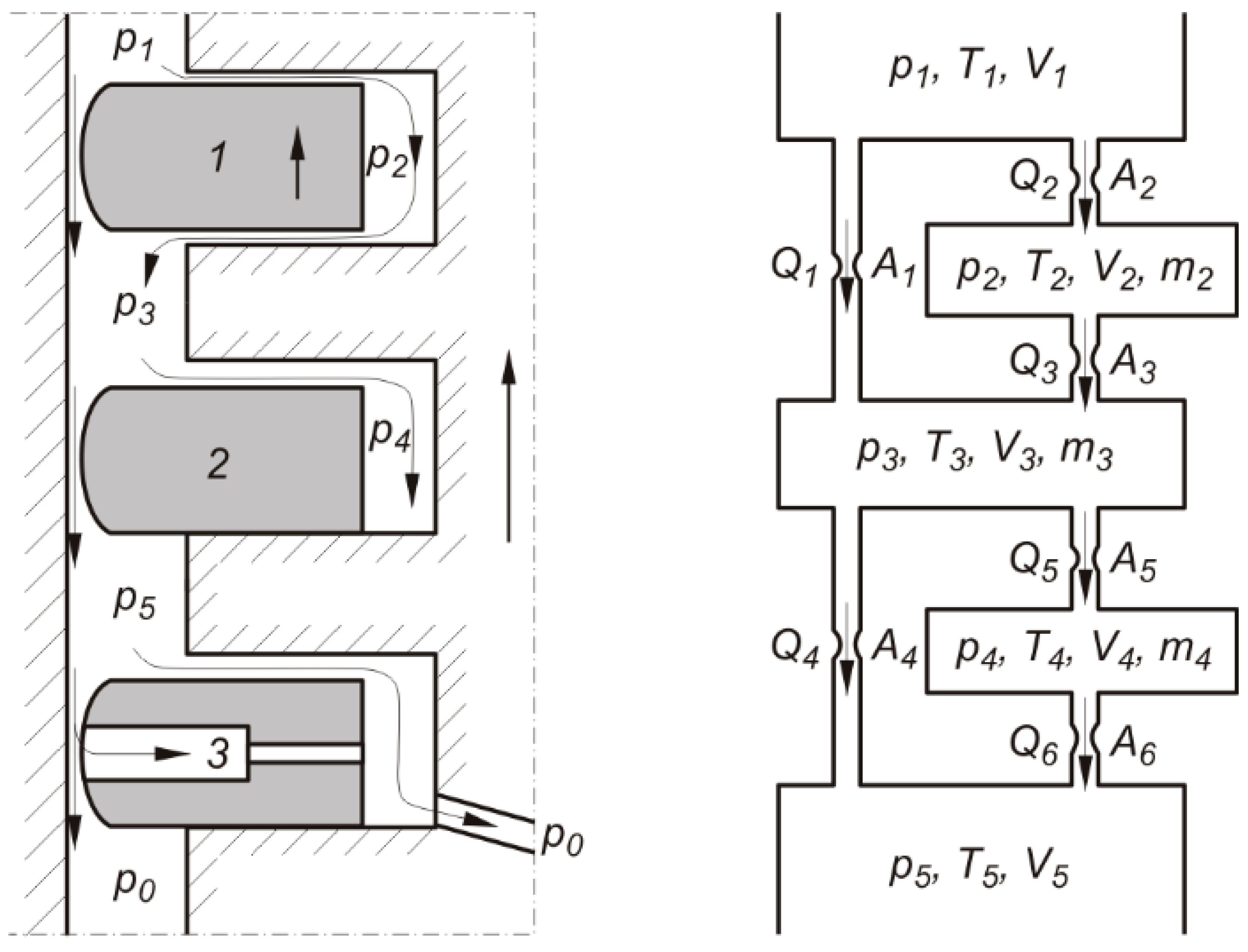
2.1. Gas Flow Model
2.2. Ring Dynamics Model
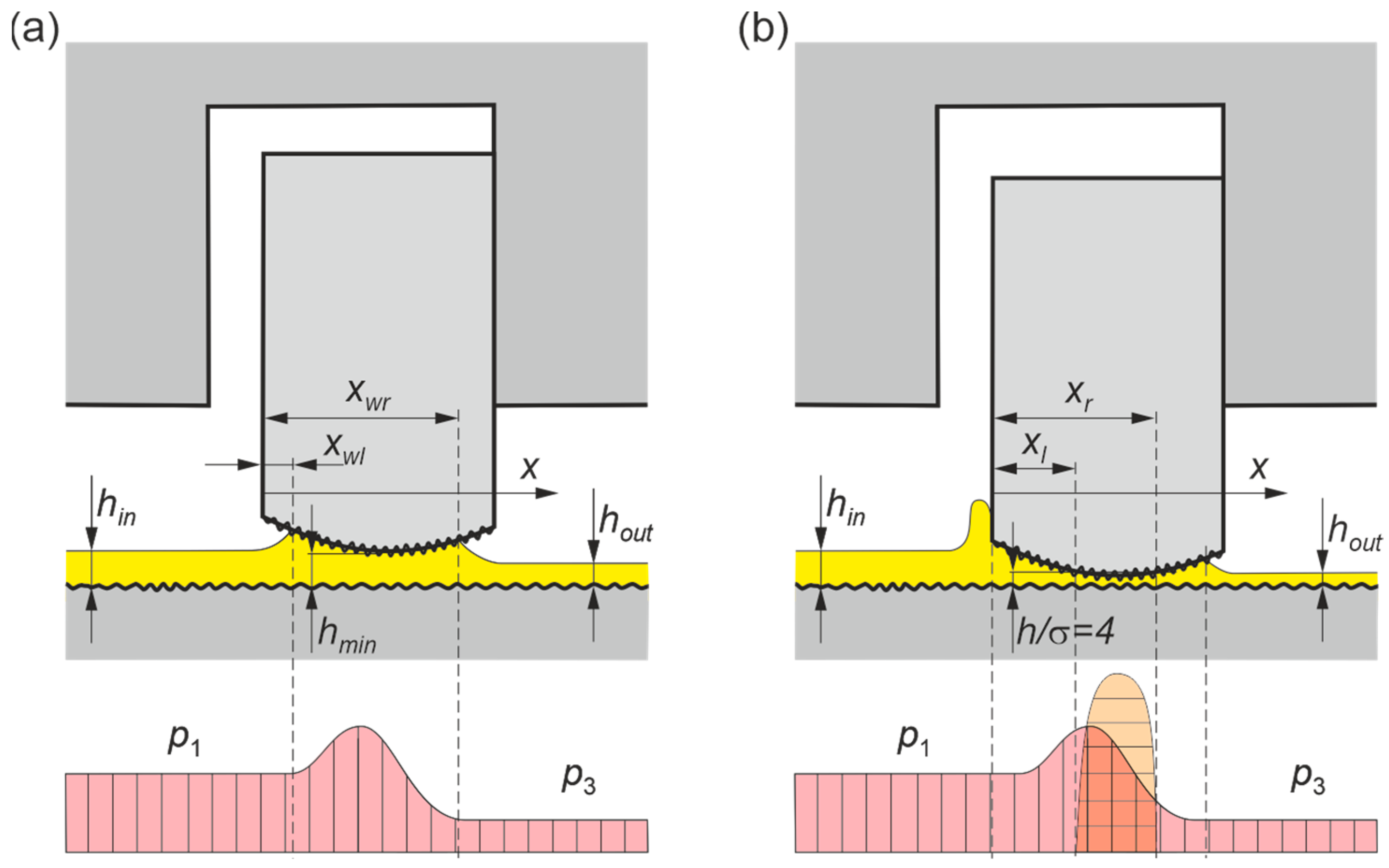
2.3. Mixed Lubrication Model
3. Object, Experiment and Simulations
3.1. Research Object
3.2. Test Stand and Measurements
3.3. Simulations
4. Results and Discussion
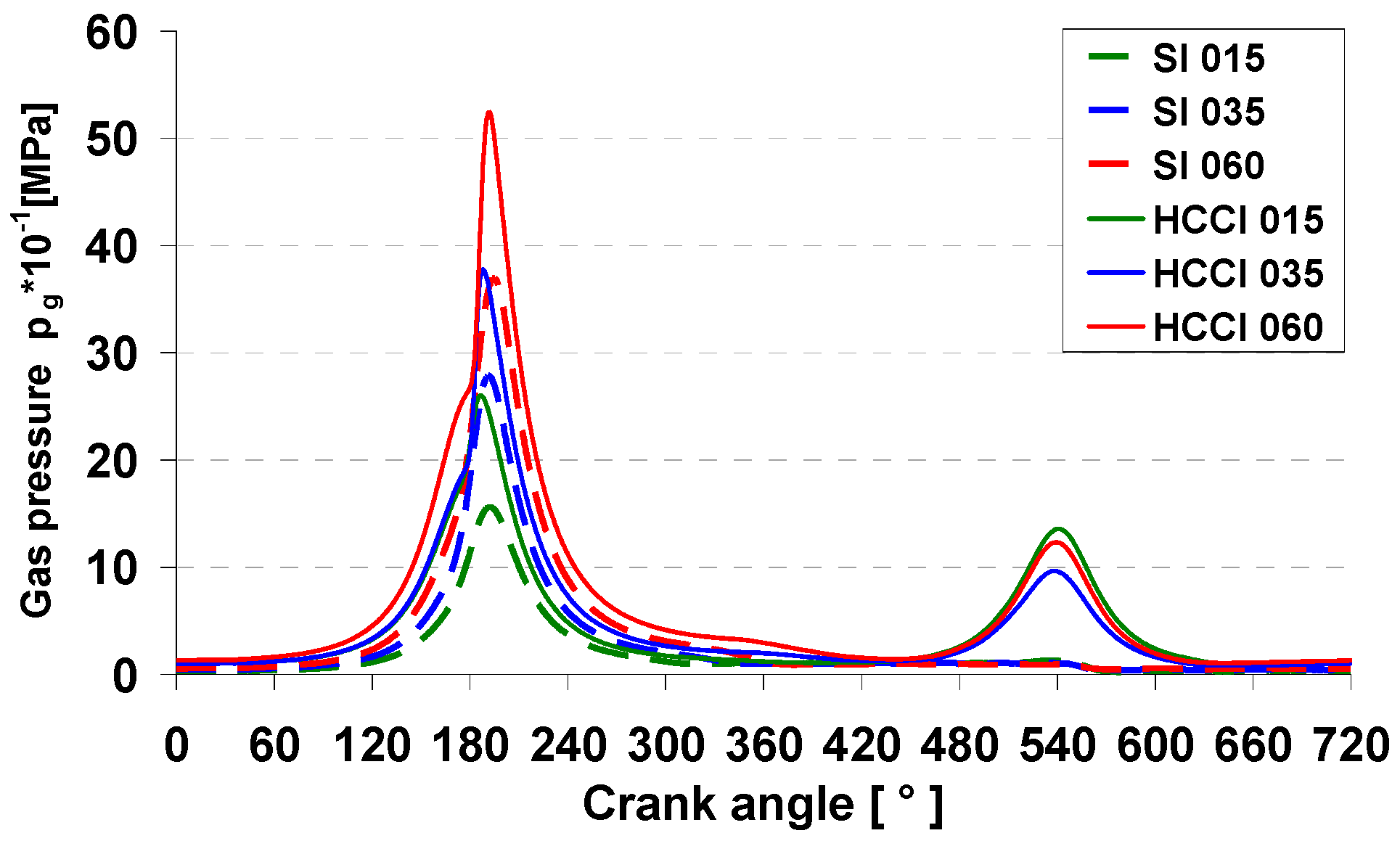
4.1. Pressure in the Combustion Chamber in SI and HCCI Modes
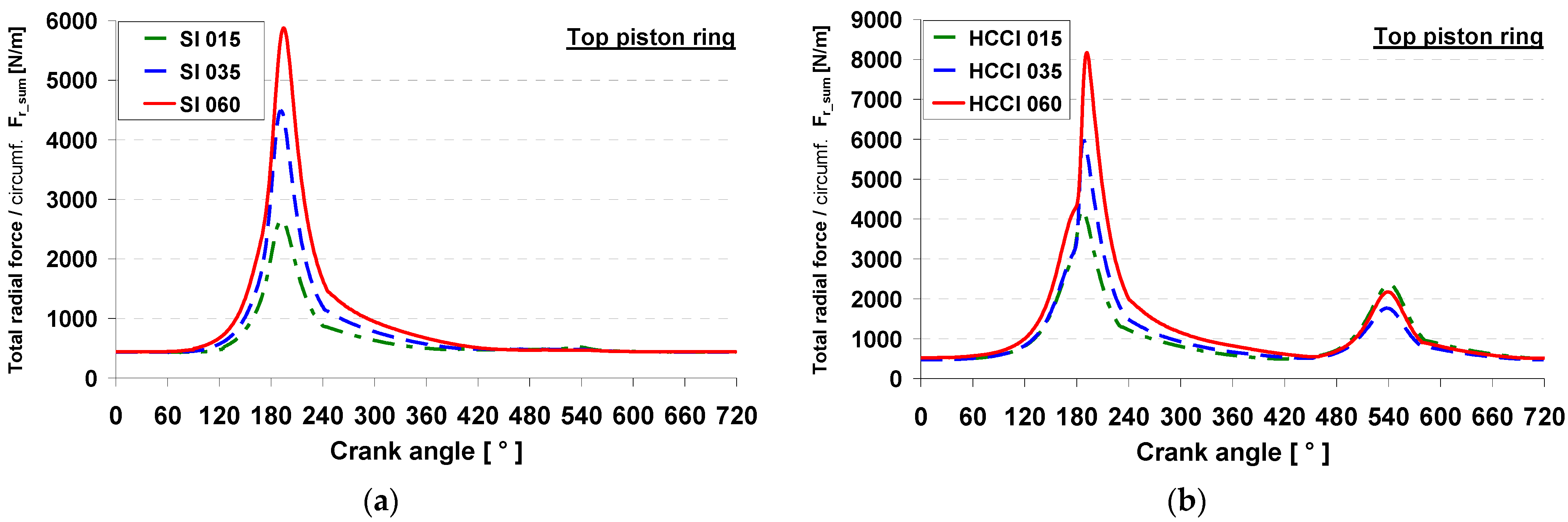
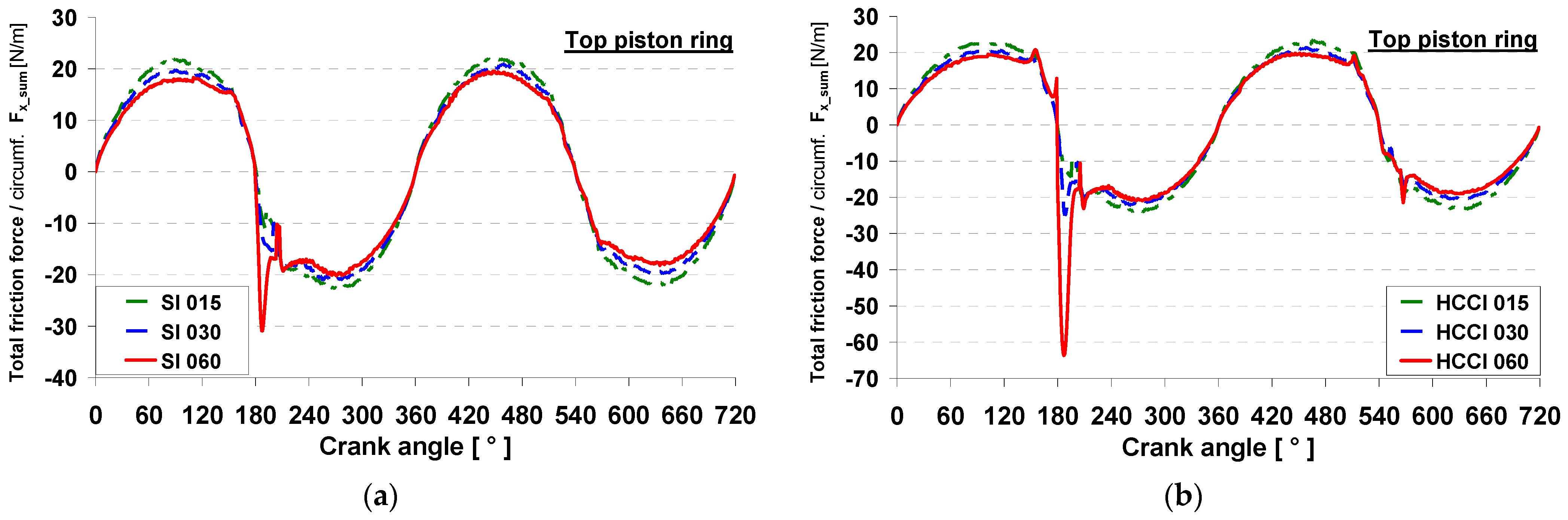
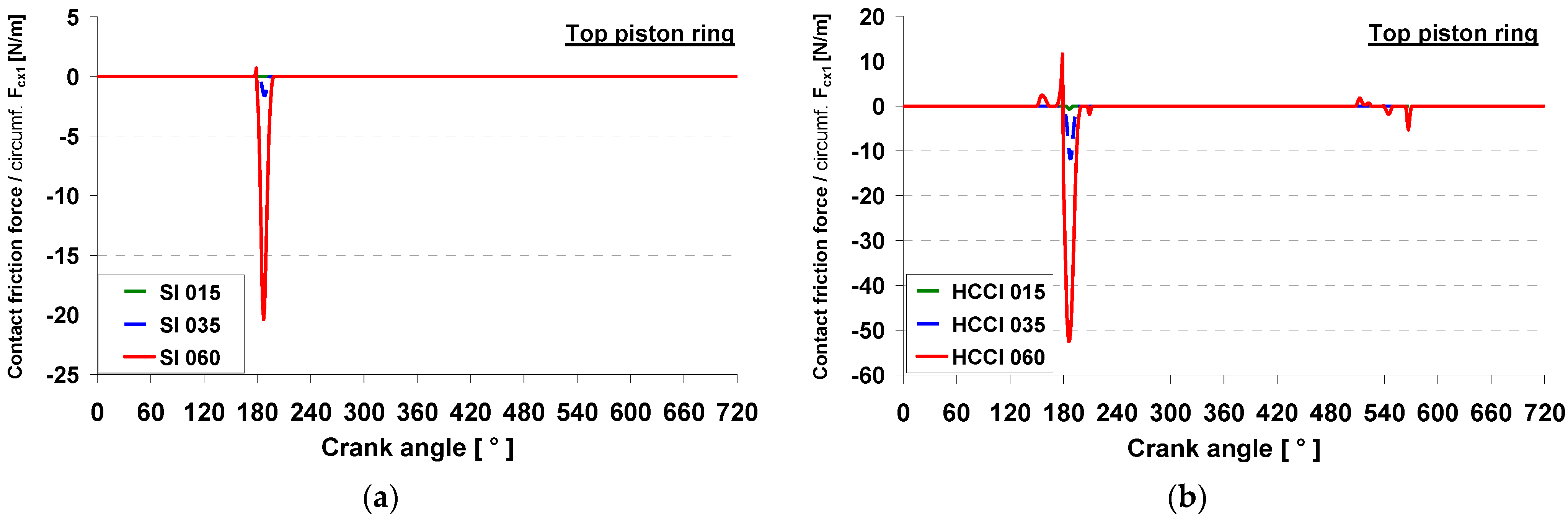
4.2. Top Ring Friction
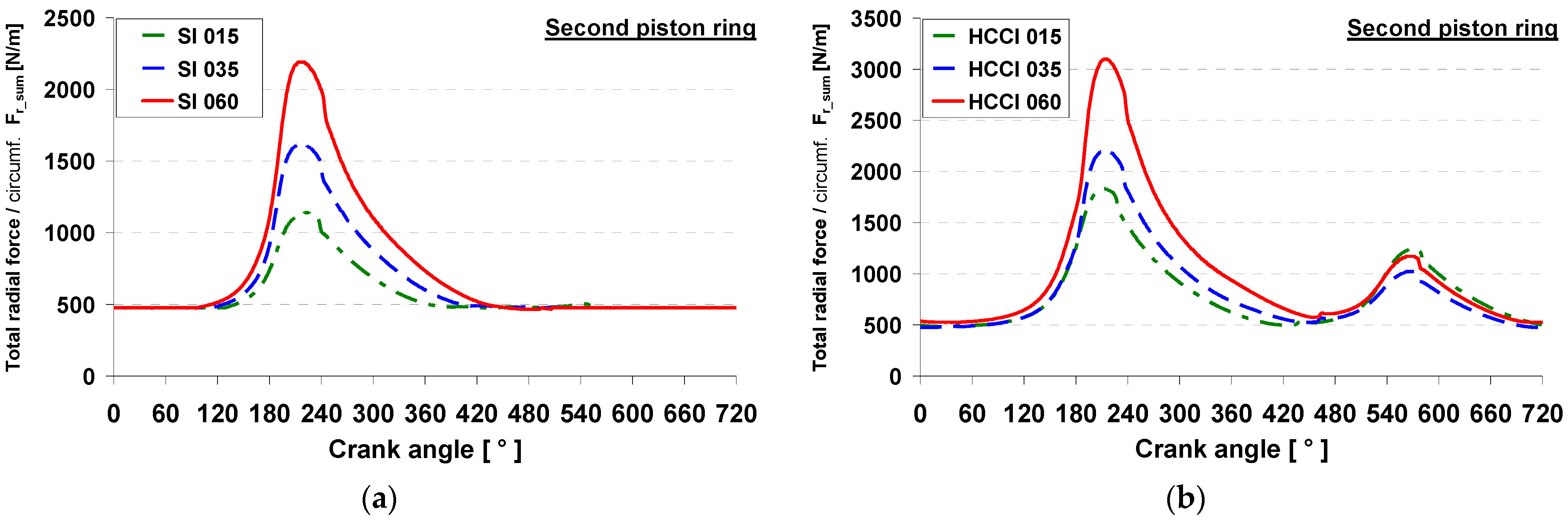
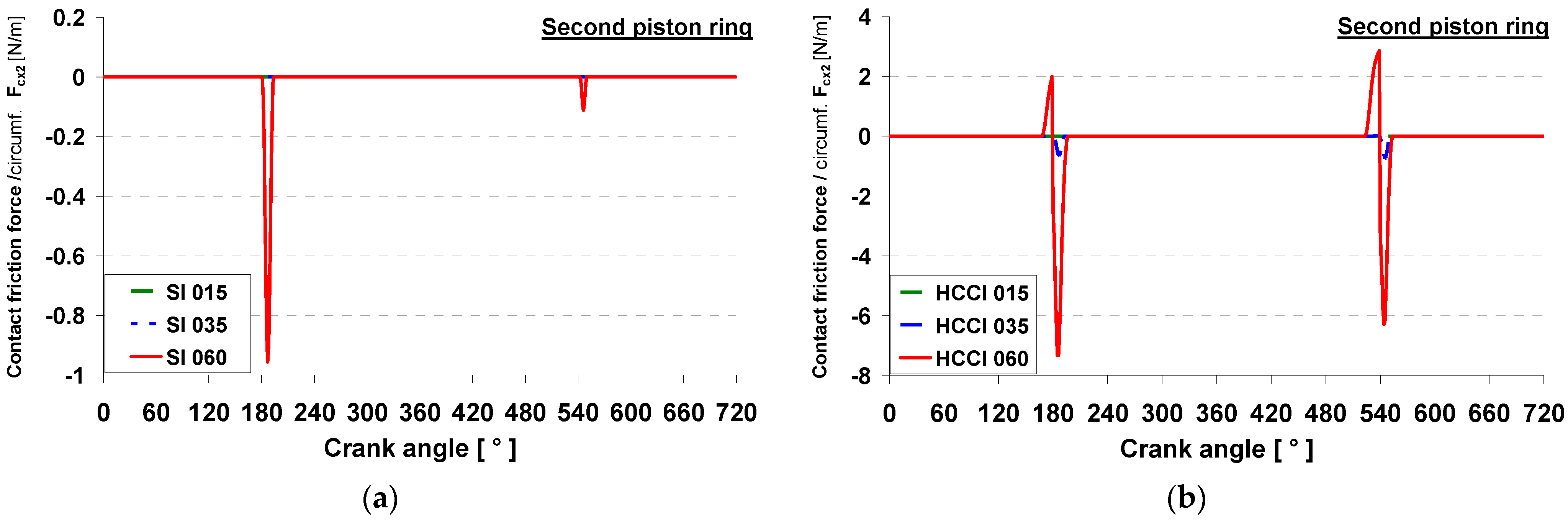
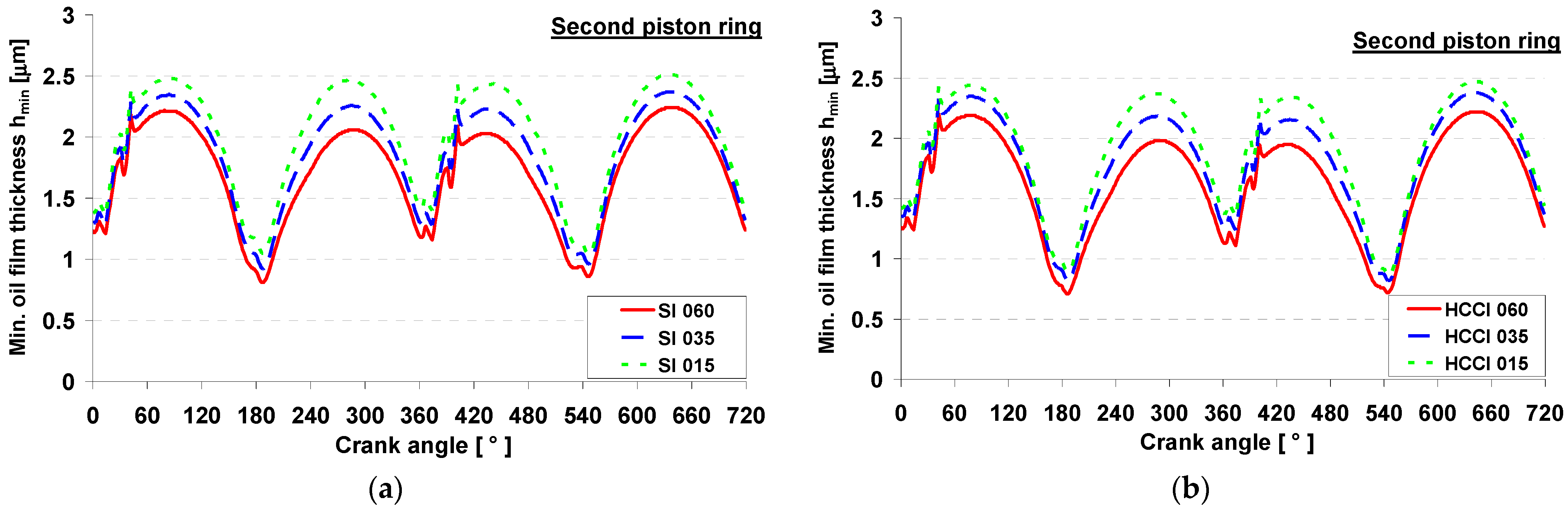
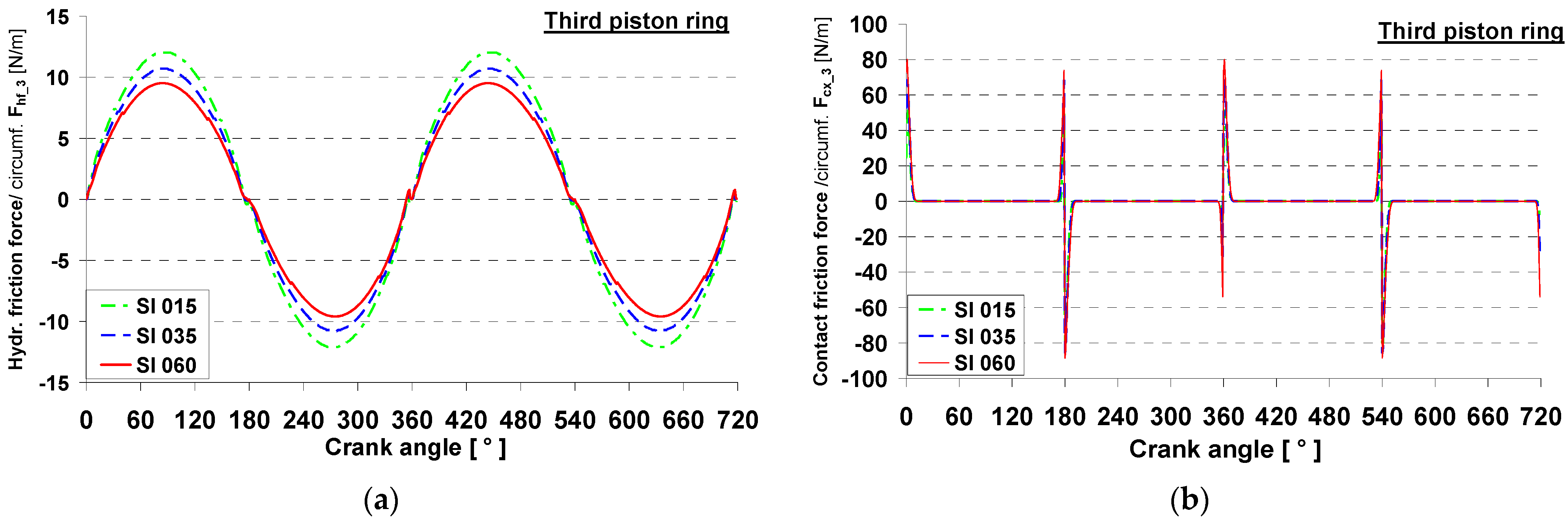
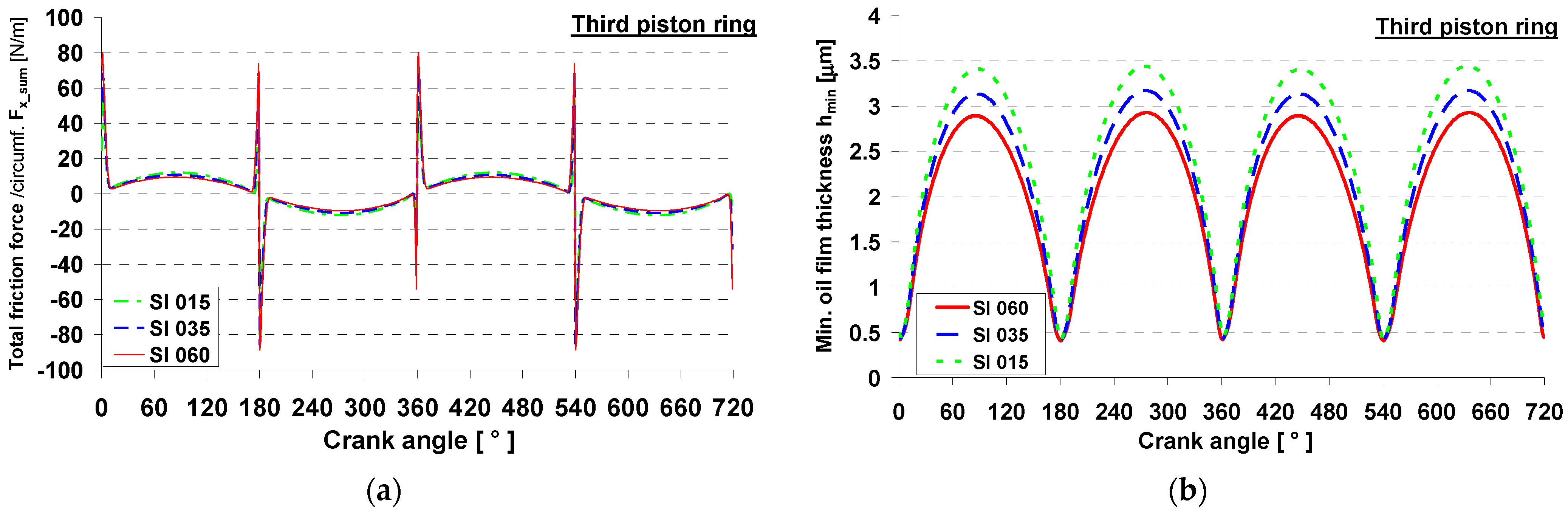
4.3. Second Ring Friction
4.4. Oil Ring Friction
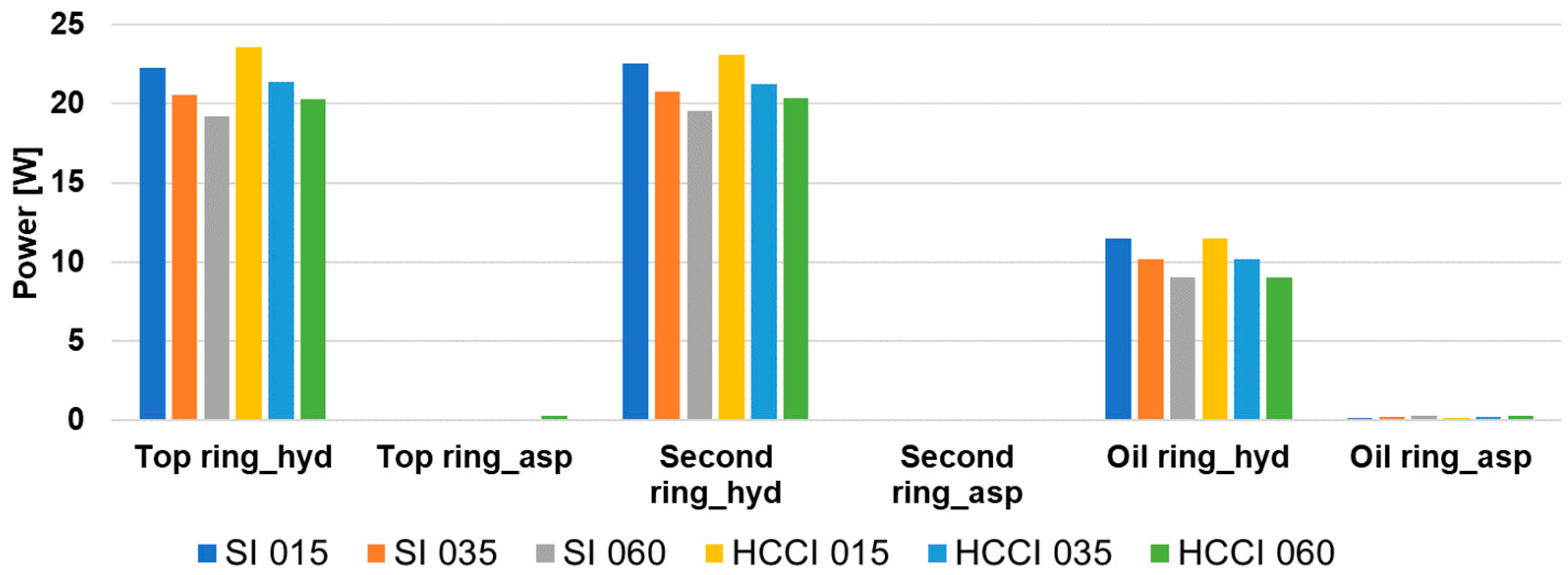
4.5. Energy Losess Due to Ring Friction
5. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Richardson, D.E. Review of power cylinder friction for diesel engines. J. Eng. Gas. Turb. Power 2000, 122, 506–519. [Google Scholar] [CrossRef]
- Gulwadi, S.D. Analysis of Tribological Performance of a Piston Ring Pack. Tribol. Trans. 2000, 43, 151–162. [Google Scholar] [CrossRef]
- Ma, Z.; Henein, N.A.; Bryzik, W. A Model for Wear and Friction in Cylinder Liners and Piston Rings. Tribol. Trans. 2006, 49, 315–327. [Google Scholar] [CrossRef]
- Livanos, G.A.; Kyrtatos, N.P. Friction model of a marine diesel engine piston assembly. Tribol. Int. 2007, 40, 1441–1453. [Google Scholar] [CrossRef]
- Tormos, B.; Martín, J.; Pla, B.; Jimenez-Reyes, A.J. A methodology to estimate mechanical losses and its distribution during a real driving cycle. Tribol. Int. 2020, 145, 106208. [Google Scholar] [CrossRef]
- Tian, T. Dynamic Behaviors of Piston Rings and Their Practical Impact—Part II: Oil Transport, Friction, and Wear of Ring/Liner Interface and the Effects of Piston and Ring Dynamics. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2002, 216, 229–247. [Google Scholar] [CrossRef]
- Novotny, P.; Pistek, V.; Drapal, L.; Svida, D.; Devera, T. Efficient approach for solution of the mechanical losses of the piston ring pack. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 1377–1388. [Google Scholar] [CrossRef]
- Koszalka, G.; Guzik, M. Mathematical model of piston ring sealing in combustion engine. Pol. Marit. Res. 2014, 21, 66–78. [Google Scholar] [CrossRef]
- Li, G.; Gu, F.; Wang, T.; Lu, X.; Zhang, L.; Zhang, C.; Ball, A. An Improved Lubrication Model between Piston Rings and Cylinder Liners with Consideration of Liner Dynamic Deformations. Energies 2017, 10, 2122. [Google Scholar] [CrossRef]
- Wolff, A. Simulation based study of the system piston-ring-cylinder of a marine two-stroke engine. Tribol. Trans. 2014, 57, 653–667. [Google Scholar] [CrossRef]
- Wolff, A. Influence of piston ring profiles and oil temperature distribution on cylinder liner lubrication of a marine two-stroke engine. Combust. Engines 2019, 178, 257–263. [Google Scholar] [CrossRef]
- Razavykia, A.; Delprete, C.; Brusa, E.; Hosseini, Y. The Effects of Oil Film Shape on Piston Ring and Liner Tribology under Mixed Lubrication. Am. J. Eng. Appl. Sci. 2021, 14, 436–447. [Google Scholar] [CrossRef]
- Bolander, N.W.; Steenwyk, B.D.; Sadeghi, F.; Gerber, G.R. Lubrication Regime Transitions at the Piston Ring—Cylinder Liner Interface. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2005, 219, 19–31. [Google Scholar] [CrossRef]
- Tamminen, J.; Sandström, C.-E.; Andersson, P. Influence of load on the tribological conditions in piston ring and cylinder liner contacts in a medium-speed diesel engine. Tribol. Int. 2006, 39, 1643–1652. [Google Scholar] [CrossRef]
- Soederfjaell, M.; Herbst, H.M.; Larsson, R.; Almqvist, A. Influence on friction from piston ring design, cylinder liner roughness and lubricant properties. Tribol. Int. 2017, 116, 272–284. [Google Scholar] [CrossRef]
- Tomanik, E.; Mansori, M.E.; Souza, R.; Profito, F. Effect of waviness and roughness on cylinder liner friction. Tribol. Int. 2018, 120, 547–555. [Google Scholar] [CrossRef]
- Chu, N.R.; Jackson, R.L.; Ghaednia, H.; Gangopadhyay, A. A Mixed Lubrication Model of Piston Rings on Cylinder Liner Contacts Considering Temperature-Dependent Shear Thinning and Elastic–Plastic Contact. Lubricants 2023, 11, 208. [Google Scholar] [CrossRef]
- Wolff, A. Numerical Analysis of the System Piston-Ring-Cylinder of an Automotive IC Engine. In Proceedings of the SAE Powertrains, Fuels & Lubricants Meeting, Kraków, Poland, 22–24 September 2020. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Tech. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication Between Rough Sliding Surfaces. J. Lubr. Tech. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Greenwood, J.; Tripp, J.H. The contact of Two Nominally Flat Rough Surfaces. Proc. Inst. Mech. Eng. 1971, 185, 625–633. [Google Scholar] [CrossRef]
- Bolander, N.W.; Sadeghi, F. Deterministic Modeling of Honed Cylinder Liner Friction. Tribol. Trans. 2007, 50, 248–256. [Google Scholar] [CrossRef]
- Koszalka, G. Predicting the durability of the piston-rings-cylinder assembly of a diesel engine using a piston ring pack model. Eksploat. I Niezawodn. Maint. Reliab. 2011, 51, 40–44. [Google Scholar]
- Vlădescu, S.-C.; Medina, S.; Olver, A.V.; Pegg, I.G.; Reddyhoff, T. Lubricant film thickness and friction force measurements in a laser surface textured reciprocating line contact simulating the piston ring-liner pairing. Tribol. Int. 2016, 98, 317–329. [Google Scholar] [CrossRef]
- Gu, C.; Wang, R.; Tian, T. Modeling the Fatigue Wear of the Cylinder Liner in Internal Combustion Engines during the Break-In Period and Its Impact on Piston Ring Lubrication. Lubricants 2019, 7, 89. [Google Scholar] [CrossRef]
- Li, W.; Yu, B.; Lv, Y.; Shen, Y.; Huang, R.; Du, F. Wear Behavior of CuSn Coated Piston Ring Sliding against Nodular Cast Iron Cylinder Liner under Heavy-Duty Conditions. Metals 2019, 9, 139. [Google Scholar] [CrossRef]
- Koszalka, G.; Krzeczek, P. Energy Losses Related to Ring Pack Wear in Gasoline Car Engine. Energies 2022, 15, 9570. [Google Scholar] [CrossRef]
- Tomanik, E.; Christinelli, W.; Souza, R.M.; Oliveira, V.L.; Ferreira, F.; Zhmud, B. Review of Graphene-Based Materials for Tribological Engineering Applications. Energies 2023, 4, 2764–2811. [Google Scholar] [CrossRef]
- Li, M.; Zhong, X.; Ahling, S.; Tian, T. An Investigation of Oil Supply Mechanisms to the Top of the Liner in Internal Combustion Engines. In Proceedings of the 2023 JSAE/SAE Powertrains, Energy and Lubricants International Meeting, Kyoto, Japan, 29 August–1 September 2023. [Google Scholar] [CrossRef]
- Taylor, R.I. Rough Surface Contact Modelling—A Review. Lubricants 2022, 10, 98. [Google Scholar] [CrossRef]
- Lin, P.; Barber, G.; Zou, Q.; Anderson, A.H.; Tung, S.; Quintana, A. Friction and Wear of Low-Phosphorus Engine Oils with Additional Molybdenum and Boron Compounds, Measured on a Reciprocating Lubricant Tester. Tribol. Trans. 2008, 51, 659–672. [Google Scholar] [CrossRef]
- Agarwal, A.K.; Singh, A.P.; Maurya, R.K. Evolution, challenges and path forward for low temperature combustion engines. Prog. Energy Comb. 2017, 61, 1–56. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H. Investigation of combustion, performance and emission characteristics of 2-stroke and 4-stroke spark ignition and CAI/HCCI operations in a DI gasoline. Appl. Energy 2014, 130, 244–255. [Google Scholar] [CrossRef]
- Hunicz, J.; Krzaczek, P. Detailed speciation of emissions from low-temperature combustion in a gasoline HCCI engine. Pol. J. Environ. Stud. 2016, 25, 137–145. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, B.V.S.; Sayyed, I.; Vedrantam, A.; Garg, A.; Bharti, S.; Shukla, M. State of the Art in Low-Temperature Combustion Technologies: HCCI, PCCI, and RCCI. In Advanced Combustion for Sustainable Transport. Energy, Environment, and Sustainability; Agarwal, A.K., Martínez, A.G., Kalwar, A., Valera, H., Eds.; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Kontarakis, G.; Collings, N.; Ma, T. Demonstration of HCCI using a single cylinder four-stroke SI engine with modified valve timing. SAE Tech. Pap. 2000, 109, 2057–2067. [Google Scholar] [CrossRef]
- Pachiannan, T.; Zhong, W.; Rajkumar, S.; He, Z.; Leng, X.; Wang, Q. A literature review of fuel effects on performance and emission characteristics of low-temperature combustion strategies. Appl. Energy 2019, 251, 113380. [Google Scholar] [CrossRef]
- Kale, A.V.; Krishnasamy, A. Experimental study on combustion, performance, and emission characteristics of a homogeneous charge compression ignition engine fuelled with multiple biofuel-gasoline blends. Energy 2023, 288, 129621. [Google Scholar] [CrossRef]
- Quintana, S.H.; Morales Rojas, A.D.; Bedoya, I.D. Experimental and Numerical Evaluation of an HCCI Engine Fueled with Biogas for Power Generation under Sub-Atmospheric Conditions. Energies 2023, 16, 6267. [Google Scholar] [CrossRef]
- Vasudev, A.; Mikulski, M.; Balakrishnan, P.R.; Storm, X.; Hunicz, J. Thermo-kinetic multi-zone modelling of low temperature combustion engines. Prog. Energy Comb. 2022, 91, 100998. [Google Scholar] [CrossRef]
- Han, L.; Duan, J.; Qian, D.; Gong, Y.; Wang, Y.; Xie, F.; Su, Y. Research on Homogeneous Charge Compression Ignition Combustion of Intake Port Exhaust Gas Recirculation Based on Cam Drive Hydraulic Variable Valve Actuation Mechanism. Energies 2022, 15, 438. [Google Scholar] [CrossRef]
- Hunicz, J.; Gęca, M.S.; Ratajczyk, E.; Andwari, A.M.; Yang, L.; Mikulski, M. An analytical approach to converting vibration signal to combustion characteristics of homogeneous charge compression ignition engines. Energ. Convers. Manag. 2023, 294, 117564. [Google Scholar] [CrossRef]
- Koszałka, G.; Hunicz, J. Comparative study of energy losses related to the ring pack operation in homogeneous charge compression ignition and spark ignition combustion. Energy 2021, 235, 121388. [Google Scholar] [CrossRef]
- Richardson, D.E.; Borman, G.L. Theoretical and Experimental Investigations of Oil Films for Application to Piston Ring Lubrication. In Proceedings of the International Fuels & Lubricants Meeting & Exposition, San Francisco, CA, USA, 19–22 October 1992. [Google Scholar] [CrossRef]
- Hunicz, J. An experimental study of combustion phasing control in CAI gasoline engine with in-cylinder fuel reforming. In Proceedings of the 10th International Conference on Engines & Vehicles, Napoli, Italy, 11–15 September 2011. [Google Scholar] [CrossRef]
- Hunicz, J.; Medina, A. Experimental study on detailed emissions speciation of an HCCI engine equipped with a three-way catalytic converter. Energy 2016, 117, 388–397. [Google Scholar] [CrossRef]
- Hunicz, J.; Mikulski, M.; Geca, M.S.; Rybak, A. An applicable approach to mitigate pressure rise rate in an HCCI engine with negative valve overlap. Appl. Energy 2020, 257, 114018. [Google Scholar] [CrossRef]
- Wolff, A.; Koszałka, G. Influence of engine load on piston ring pack operation of an automotive IC engine. Combust. Engines 2022, 190, 88–94. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Displacement, cm3 | 498.5 |
| Nominal diameter of bore, mm | 84 |
| Stroke, mm | 90 |
| Connecting rod length, mm | 215 |
| Compression ratio | 11.7:1 |
| No. of valves | 2 |
| Fuel injector | electromagnetic, single-stream, swirl-type |
| Parameter | Top Ring | Second Ring | Oil Ring |
|---|---|---|---|
| Total axial height, mm | 1.5 | 2.0 | 4.0 |
| Upper land axial height, mm | – | – | 1.0 |
| Lower land axial height, mm | – | – | 1.0 |
| Radial width, mm | 3.7 | 3.7 | 4.15 |
| Nominal ring end gap, mm | 0.5 | 0.45 | 0.4 |
| Radius of parabolic sliding surface, mm | 180 | 180 | 244 |
| Offset of parabolic sliding surface, mm | 0.75 | 1.5 | 2.0 |
| Elastic tension force Per unit of circumference, N/m | 476 | 526 | 1190 |
| Mass, g | 11.1 | 14.8 | 24.7 |
| Mode | IMEP [MPa] | IVO [deg] * | IVC [deg] * | EVO [deg] * | EVC [deg] * | IV Lift [mm] | EV Lift [mm] | MAP [kPa] | Excess Air Ratio [–] |
|---|---|---|---|---|---|---|---|---|---|
| SI | 0.167 | 540 | 40 | 321 | 540 | 9 | 9 | 32 | 1 |
| SI | 0.357 | 540 | 40 | 321 | 540 | 9 | 9 | 44 | 1 |
| SI | 0.595 | 540 | 40 | 321 | 540 | 9 | 9 | 55 | 1 |
| HCCI | 0.515 | 629 | 39 | 328 | 447 | 3.6 | 2.9 | 97 | 1.2 |
| HCCI | 0.342 | 625 | 35 | 341 | 460 | 3.6 | 2.9 | 95 | 1 |
| HCCI | 0.603 | 622 | 32 | 341 | 460 | 3.6 | 2.9 | 135 | 1 |
| Parameter | Cylinder Liner | Piston Rings |
|---|---|---|
| RMS roughness, µm | 0.22 | 0.044 |
| Elastic modulus, GPa | 113 | 150 |
| Poisson’s ratio | 0.26 | 0.25 |
| Combined Parameters | Cylinder Liner and Piston Rings | |
| Asperity density, m−2 | 1.1145 × 1012 | |
| Asperity radius, µm | 0.2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koszalka, G.; Wolff, A. Frictional Losses of Ring Pack in SI and HCCI Engine. Energies 2023, 16, 8096. https://doi.org/10.3390/en16248096
Koszalka G, Wolff A. Frictional Losses of Ring Pack in SI and HCCI Engine. Energies. 2023; 16(24):8096. https://doi.org/10.3390/en16248096
Chicago/Turabian StyleKoszalka, Grzegorz, and Andrzej Wolff. 2023. "Frictional Losses of Ring Pack in SI and HCCI Engine" Energies 16, no. 24: 8096. https://doi.org/10.3390/en16248096
APA StyleKoszalka, G., & Wolff, A. (2023). Frictional Losses of Ring Pack in SI and HCCI Engine. Energies, 16(24), 8096. https://doi.org/10.3390/en16248096






