Multi-Criteria Optimization of Energy and Water Consumption in Fruit- and Vegetable-Processing Plants in Poland

Abstract

Fruit and vegetable processing comes 6th in terms of energy consumption in the agri-food industry. At the same time, 88.4% of the industry’s final energy consumption structure is thermal energy, which depends heavily on electricity consumption. In addition, fruit and vegetable processing has a significant impact on the environment due to consumption of significant amounts of water. Reducing these three indicators simultaneously would increase the efficiency of the process while improving environmental protection. This paper proposes neural models of thermal energy, electricity and water consumption for selected major fruit- and vegetable-processing plants in Poland. These models were the basis for formulating a multi-criteria optimization task. Optimization of thermal energy, electricity and water consumption was carried out using genetic algorithms. The optimization results in the sense of Pareto can be the basis for the use of sustainable technology in selected fruit- and vegetable-processing plants.

1. Introduction

In Poland, fruit and vegetable processing comes 6th in terms of energy consumption in the agri-food industry, after the dairy, meat, fish, sugar and bakery sectors. At the same time, thermal energy accounts for 88.4% of the industry’s final energy consumption structure. Multi-directional processing of raw materials and their quality, variety of processes and operations, changeable operating conditions and non-simultaneous operation of equipment and seasonality of production contribute to high variability of consumption, especially of thermal energy [1,2,3,4,5]. Available publications [6,7,8,9,10] present selected cause–effect relationships in energy use but do not fully explain which factors influence energy and water consumption. Specific energy consumption rates for the same product may vary in individual cases. This is also due to differences in the technical equipment of the plants as well as the variety of methods used to establish these indicators. Detailed results of research on the determinants of fruit- and vegetable-processing energy intensity and water consumption are also discussed in publications by [11,12,13,14,15]. Gil et al. [16] also took into account aspects of production hygiene and related water consumption. The research is also justified due to the impact of fruit and vegetable industry plants on the environment [7,17] and the implementation of cleaner production principles [18]. The problem affects in particular African countries, where the demand for water, energy and food resources is increasing and communities have limited availability and affordability in these areas [19]. Optimization of water consumption in fruit and vegetable processing was achieved with the use of genetic algorithms [20]. The results obtained allow for the appropriate selection of the production structure to ensure the lowest water consumption. Attempts to simultaneously optimize the three criteria will therefore achieve even greater results. A publication [8,21] discusses attempts to describe the influence of various factors on the consumption of energy and water in agricultural production. However, their application is limited and they contribute only to a partial clarification of these poorly understood issues. Research in this area was also carried out by [22], and an analysis of energy and water consumption for sustainable paperboard production was undertaken by Man et al. [23]. The literature describes ranges of variation in specific heat consumption rates in agricultural processing companies but does not mention factors that may affect these values.

The aim of the work is to analyze the above issues leading to the construction of models of heat, electricity and water consumption in fruit- and vegetable-processing plants in Poland, which will become the basis for formulating an optimization task. The first part presents the current methodology for examining energy and water consumption in fruit- and vegetable-processing plants, which became the basis for creating a neural model. The complexity of the issue (many variables describing the three output variables, non-linear nature of the relationship) required a preliminary analysis of the data in order to select the most important predictors and the scope of research. A neural energy and water consumption model was used to describe the process. The use of neural networks is justified in such cases, as evidenced by similar studies [24,25]. The neural model was used to formulate the optimization task and then search for the optimal solution using genetic algorithms.

The following steps were carried out in the study.

• On the basis of empirical studies in fruit- and vegetable-processing plants, a dataset was collected on the basis of which three regression models of heat, electricity and water consumption were developed.
• The dataset was subjected to preliminary data analysis, excluding incomplete and outlier cases. The resulting 808 data cases were subjected to a non-hierarchical cluster analysis method, determining a set of 604 cases excluding cases with low values of independent variables (in such cases, the process is incomplete due to the limited volume of processed product and, in such a process, the use of equipment is inefficient).
• The dataset of 604 cases was subjected to an analysis of variance (ANOVA) to isolate the variables (predictors) that have the most significant impact on all three dependent variables (heat, electricity and water consumption).
• The extracted dataset and predictors were the basis for developing a neural model of the process describing heat, electricity and water consumption together.
• The neural model of heat, electricity and water consumption was the basis for formulating a multi-criteria optimization task.
• The solution of the optimization task was performed using genetic algorithms obtaining a set of optimal solutions in the Pareto sense.

2. Analysis of Fruit and Vegetable Processing

The materials and results of the measurements came from 16 fruit- and vegetable-processing plants researched during the summer. Fifty daily periods were analyzed at each site to obtain the necessary datasets. Figure 1 shows a generalized diagram of a fruit- and vegetable-processing plant.

Indicators W_e, W_c and W_w stand for specific consumption rates for electricity, heat and water, respectively, while A_e, A_c and A_w for the daily consumption of electricity, heat and water, while Z is the throughput of raw materials per day. The determinants of thermal energy consumption at the surveyed facilities can be divided into four groups. Group 1 is the general characteristics of the production facilities studied, described by the total installed capacity of the production facility’s electrical equipment P and the total volume of the facility’s premises V₂. Group 2 is the structure of installed electrical capacity described by P₁, P₂, P₃ and P₄, which respectively mean the installed capacity of: electrical equipment in the plant boiler room, hydrophore plant and water treatment plant, beverage and juice production lines, equipment used in storage, freezing and air conditioning (including ammonia compressors) and electrical equipment in the administrative and amenity buildings and plant lighting. Group 3 characterizes the structure of daily raw material processing or production and is described by Z₁, Z₂, Z₃, Z₄, Z₅ and Z₆ respectively denoting the daily production volume of: fruit concentrates, vegetable concentrates, beverages, frozen fruit, frozen vegetables and juices. Group 4 is the K₂ indicator, which determines the level of technical and technological equipment, organization of production processes and spatial development. Energy losses are described by the Qi index. Other variables adopted in the study that were found to be insignificant were not included. The correlation and strengths of the adopted independent variables on the selected dependent variables (daily consumption of energy carriers A_c and specific consumption rates for thermal energy W_c and water W_w) were established. Previous studies had analyzed cause-and-effect relationships that are a function of factors of low significance or that express trends assumed at the plant design stage. To explain the dependence of y on a number of independent variables (which are actual parameters observed in practice or functions of them), Formula (1) was adopted:

y = b₀ + b₁x₁ + b₂x₂ + … + b_kx_k

(1)

in which: y—explanatory variable (A_c or W_c), x—explanatory variables (e.g., P₁, P₂, K₂, V₁, Z₁, Z₂, Z₃). Application of the resulting empirical formulas when conditions (2) are met:

b₁x₁ + b₂x₂ + … +b_kx_k ≥ b₀ and x_i ≥ 0 for i = 1....k.

(2)

allows the problem in question to be explained to a large extent in the analyzed fruit and vegetable production facilities.

2.1. Thermal Energy Consumption

On the basis of the analyses, equations expressing the influence of the factors covered by the four adopted groups on thermal energy consumption are shown in

Table 1. Factors influencing the variability of heat energy consumption in the surveyed plants (SE—standard error).

Group of Independent Variables	Regression Equations	R2	SE	Independent Variables
				Designation, Dimension	Numerical Range
II	Ac = −260.8 + 0.74⋅P2 + 25.15⋅$\surd {\mathrm{P}}_1$	0.618	269.0	P1 [kW] P2 [kW]	41–1715 25–932
III	Ac = 200.5 + 3.6Z3 + 211.9⋅logZ1 + 443.0⋅logZ2	0.596	276.7	Z1 [kg] Z2 [kg] Z3 [kg]	(0.585–772.980) × 103 (2.920–8.640) × 103 (0.765–191.094) × 103
IV	Wc = −0.39 + 0.0014K2	0.845	8.9	K2 [m3/kg]	(307–307.692) × 10−3

. Only those regression equations for which the correlation coefficient R ˃ 0.75 were included. The average specific heat consumption of the analyzed plants, Wc, for the daily period varied considerably and was (0.2–45.7) × 10⁻³ [GJ/kg].

The lowest W_c rates were found in plants with a high share of refrigeration and freezing in the production technology. It can be seen from Table 1 that 61.8% of the variability in daily thermal energy consumption is attributed to Group 2 factors (installed capacity in the plant boiler house, hydrophore plant and water treatment plant and juice and beverage line). This is because the installed capacity of the electrical equipment in the boiler plant covered by P₁ is correlated with the size of the thermal equipment used to generate and use heat. Values Z₁ and Z₂ (production of fruit and vegetable concentrates) and Z₃ (production of beverages) included in Group 3 were responsible for 59.6% of the impact on daily thermal energy consumption. In this context, based on the work of Singh [26], we can analyze the example of a technological specific heat consumption rate (W_T) for the production of canned vegetables, which is 5.187 × 10⁻³ [GJ/kg]. Within the structure of this indicator, nearly 50% is accounted for by heat in steam and hot water consumed in the process. It should be noted that about 23% of the heat energy was losses, indicating the need for closed-loop circuits and waste heat recovery (Q_n in Figure 1). This is confirmed by detailed studies by Cuéllar and Webber [1]. Research on the energy intensity of production was also conducted by Gasparino et al. [27] and Sogut et al. [28]. Alvarez et al. [29] presented opportunities for implementing innovations in energy-efficient juice production. The production of frozen citrus concentrates required a thermal energy input of 8.234 × 10⁻³ [GJ/kg]. In this case, steam and hot water heat demand and direct heating oil consumption accounted for 83%. It should be noted that this rate was more than double the W_T technological specific electricity consumption rate. The application of the four groups of factors provides information on the combined influence of technical and technological factors, degree of mechanization of production operations, organizational and production factors and spatial development on thermal management.

The results obtained confirm the trend that the cubic capacity of both production and non-production rooms has a strong influence on heat consumption A_c and the level of specific thermal energy consumption W_c. The K₂ indicator in the equation (Table 1) is a function of the total volume of the plant and the daily throughput of raw materials. Due to the high degree of correlation (R = 0.916), it can be concluded that the equation obtained expresses the cause of the changes in specific thermal energy consumption in fruit- and vegetable-processing plants. Indeed, studies have shown that more than 84% of the variability in specific heat consumption is attributed to the K₂ indicator. In practice, this formula has been shown to be useful when K₂ is contained within the limits of (4000–30,000) × 10⁻³ [m³/kg] under established and fault-free operating conditions. The work [30] and WS Atkins International (1998) [31] show that in fruit- and vegetable-processing plants, the average specific heat energy consumption Wc for an annual period was 8.33 × 10⁻³ [GJ/kg] of processed raw materials, with a maximum value of 32.40 × 10⁻³ [GJ/kg] of raw material. Research [32] shows, for example, the technological specific thermal energy consumption rate WT for apple concentrate was 8.93 × 10⁻³ [GJ/kg] of product. For tomato concentrate, the corresponding value was 4.69 × 10⁻³ [GJ/kg]. The specific electricity consumption rate We was in the range of (22–1450) × 10⁻³ [kWh/kg].

2.2. Electric Energy Usage

On the basis of the analyses, empirical formulas expressing the influence of the factors covered by the four adopted groups on electricity consumption are shown in

Table 2. Factors affecting the volatility of electricity consumption in the surveyed plants (SE—standard error).

Group of Independent Variables	Regression Equations	R2	SE	Independent Variables
				Designation, Dimension	Numerical Range
I	Ae = 6806.04 + 0.0006⋅P2	0.635	23,360	P [kW]	413–14,237
II	Ae = −45,896.0 + 0.0013⋅$P_3^2$ + 29,020.5⋅log P4	0.708	20,920	P1 [kW] P2 [kW]	81–6566 35–3588
III	Ae = 8356.4 + 736.6⋅Z5 + 3468.1⋅$\surd Z_4+$ 13,703.4⋅logZ1 + 1.35⋅$Z_6^2$	0.630	23,560	Z1 [kg] Z4 [kg] Z5 [kg] Z6 [kg]	(0.6–773.0) × 103 (0.1–282.0) × 103 (0.7–155.6) × 103 (0.5–312.3) × 103
IV	We = 46.7 + 4.12 Km	0.942	420	Km [kW/kg]	(9–7929) × 10−3

. When Group 1 factors were used, only the impact of the total installed capacity was significant. More than 63% of the variability in daily electricity consumption Ae was attributed to the mentioned factor P. Group 2 factors are used to study the impact of installed capacity structure on electricity consumption. These factors show that 70.8% of the variation in daily electricity consumption is attributed to the installed capacity of ammonia compressors and equipment used in storage, freezing and air conditioning and, to a lesser extent, to consumers in administrative and amenities buildings. It is a starting point to clarifying the poorly recognized issues of electricity management at these plants. The two formulas obtained should be analyzed together due to the physical nature of the independent variables. Values Z₄ and Z₅ (production of frozen fruit and vegetables), Z₁ (production of fruit concentrates) and Z₆ (production of drinking juices) included in Group 3 factors were responsible for 63% of the impact on daily electricity consumption. In this context, based on the work of Singh [26], an example can be given of the technological specific consumption rate W_T for the production of canned vegetables, which is 200 [kJ/kg]. The production of frozen citrus concentrates required an electricity input of 4047 [kJ/kg]. The application of the four groups of factors provides information on the combined influence of technical and technological factors, degree of mechanization of production operations and organizational and production factors on electricity consumption.

The research shows that, again, the installed capacity P is significant, together with the utilization rate of the production facilities, as expressed by the K_m indicator. This indicator is also dependent on the volume of daily throughput of raw materials. Due to the vast range of variability of the K_m indicator, it can be considered that the resulting formula expresses the reason for changes in the specific consumption of electricity. Indeed, studies have shown that more than 94% of the variability in specific electricity consumption is attributed to the K_m indicator. In practice, this formula has been shown to be useful when K_m is less than 400 [kW/Mg], i.e., under conditions of established and fault-free operation and when the plant has more than 300 employees in the production area. Maximum throughput means the minimum K_m indicator. The work of Kubicki (1998) [29] and WS Atkins International (1998) [30] shows that in the fruit and vegetable industry, the average specific electricity consumption for an annual period was 720 × 10⁻³ [kWh/kg] of raw materials processed and at some plants producing apple concentrate this ratio may be three times lower. The sources mentioned also state that refrigeration is the most energy intensive, and that the plants analyzed did not pay attention to the need to minimize electricity consumption. The issue of manufacturing innovations leading to a reduction in electricity consumption was also addressed in publications [33,34,35,36].

2.3. Water Consumption

Group 2 and 3 factors did not have a significant impact on the explanation of specific water consumption. However, factors were responsible for the impact on daily water consumption Aw in the range of 47.6–54.3% (

Table 3. Factors affecting the variability of water consumption in fruit and vegetable industry plants (SE—standard error).

Group of Independent Variables	Regression Equations	R2	SE	Independent Variables
				Designation, Dimension	Numerical Range
II	Aw = 408.4 + 2.30⋅P1	0.543	1029	P1 [kW]	41–1715
III	Aw = 2180.0 + 66.6⋅logZ1 + 140.50⋅$\surd Z_3$ − 1420.0/Z5	0.476	1003	Z1 [kg] Z3 [kg] Z5 [kg]	(64.0–773) × 103 (11.1–191.1) × 103 (3.8–105.0) × 103
IV	Ww = 1.4 + 0.005K2	0.843	133.7	K2 [m3/kg]	(563–307,692) × 10−3

). Using Group 4 factors, it was found that 84.3% of the variation in specific water consumption Ww was explained by the influence of indicator K₂ (total plant volume per 1000 [kg] of raw material processed per day). There are significant ranges for the K₂ indicator. The first of these ranges is around approximately 30 [m³/kg]—to which the lower values of the specific water consumption Ww correspond. This refers to the operation of plants using near nominal production lines. The second range of variability of K₂ above 30 [m³/kg] is distinguished by increased values of specific water consumption rates Ww. This may concern plants at times of underutilized capacity. This phenomenon occurs, for example, during the start-up phase of production lines, in the event of a reduction in the supply of raw materials or semi-finished products or in the event of a breakdown. It is also due to the seasonality of production of the industry’s plants and the diversion of highly contaminated raw materials for processing.

Observations at the plants analyzed showed that significant water saving opportunities are associated with increasing the use of condensate (from water obtained from the concentration of fruit juices). Cuéllar and Webber [1] described the potential for reducing water consumption in the production of canned meat and vegetables from 15 × 10⁻³ to 7.5 × 10⁻³ [m³/kg]. An overview of the possibilities for reducing water consumption when blanching vegetables was described by Derden et al. [12]. It should be added that the results of the modeling of water consumption in fruit- and vegetable-processing plants by Trajer et al. [20] showed a definite impact of the production structure on the consumption.

3. Data Analysis

Assuming that the K₂ indicator is out of range of application, it can be considered that the most important factors influencing the variability of thermal energy and electricity consumption are: P, (x₁)—the installed capacity of the plant and the production structure for selected products, Z₄ and Z₅, (x₂)—production of frozen fruit and vegetables, Z₁ and Z₂, (x₃)—production of fruit and vegetable concentrates, Z₃ and Z₆, (x₄)—production of juices and beverages, Z₇, (x₆)—production of processed fruit and vegetables and Z₈, (x₅)—other products. The designations in brackets were adopted for further analysis. Similar factors are indicated by literature data from [6,7,8]. For the construction of the neural model of thermal energy, electricity and water consumption, the abovementioned independent variables were used, while the dependent variable Wc was the rate of specific heat consumption in the plant [GJ/kg], We—the rate of specific electricity consumption [kWh/kg] and W_w—the rate of specific water consumption in the plant [m³/kg].

The dataset was subjected to a preliminary data analysis omitting incomplete and outlier cases. The resulting 808 data instances were subjected to a non-hierarchical cluster analysis method using the expectation maximization (EM) algorithm [37], in order to identify similar groups of data characterizing the processing (Appendix A, Figure A1). Cluster 1, with 604 observations, refers to the cases with the largest values of the independent variables (except x₆—fruit and vegetable processing) and balanced values of the dependent variables W_w, W_c and W_e, signifying a process close to the full range of processing capabilities of the given plant. Cluster 2, with 145 observations, refers to cases with low values of the independent variables (except x₆—fruit and vegetable preparations) and high values of the dependent variables Ww, Wc and We. This is an incomplete process due to the limited volume of the processed product. In such a process, the use of equipment is inefficient, hence the high energy and water consumption. The analysis of variance (ANOVA) showed that the variable (x₆) has no effect on the dependent variables, the p-value being 0.840459 (Appendix A,

Table A1. Analysis of variance (ANOVA) for continuous variables, total number of training cases: 808.

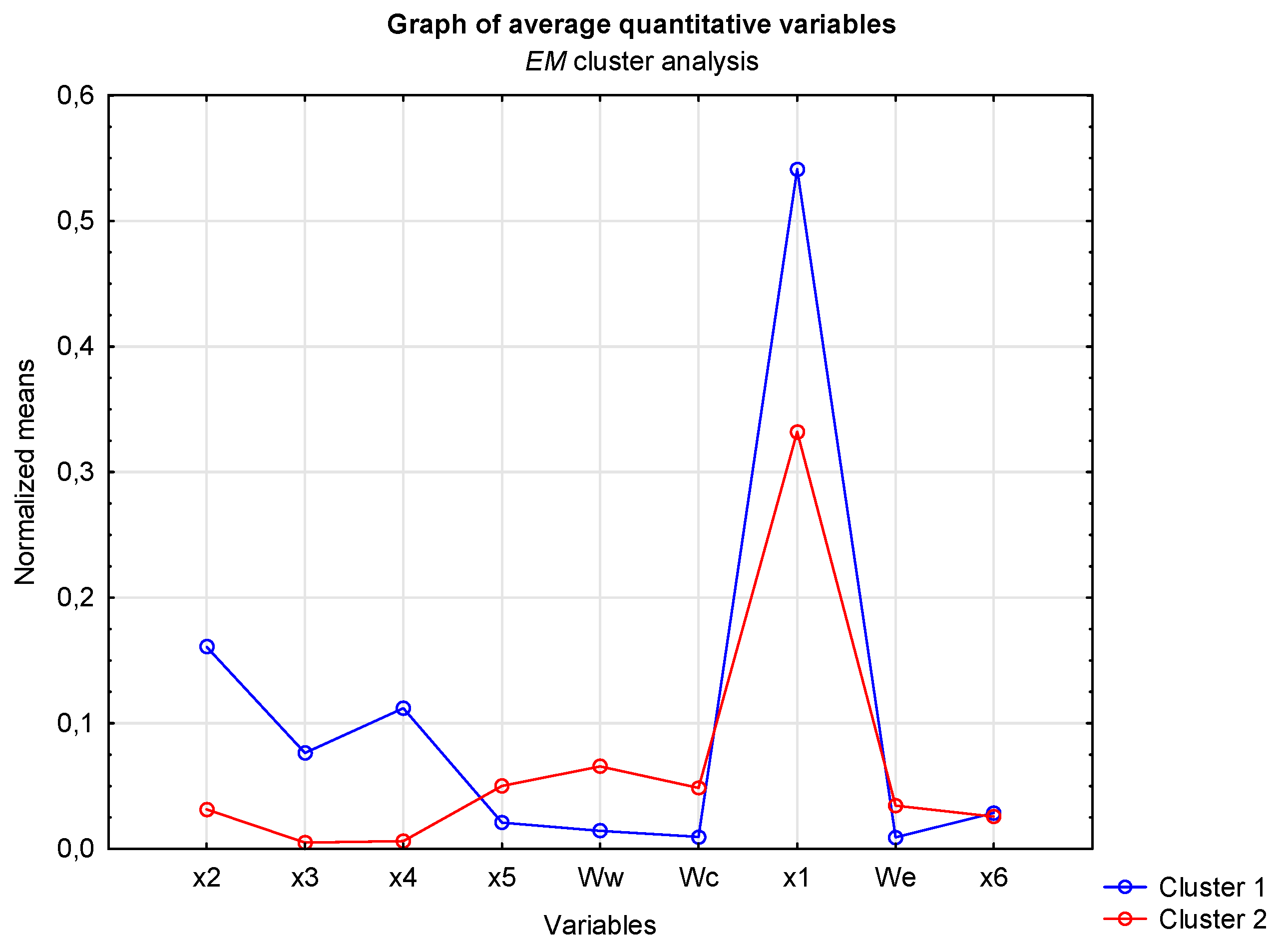
	ANOVA for Continuous Variables, Number of Clusters: 2, Total Number of Training Cases: 808
	Outgroup SS	df	Intragroup SS	df	F	p-Value
x2	1.943046 × 105	1	1.837805 × 106	806	85.2155	0.000000
x3	4.484888 × 105	1	7.026927 × 106	806	51.4424	0.000000
x4	1.628664 × 105	1	2.308415 × 106	806	56.8660	0.000000
x5	2.088467 × 103	1	8.127049 × 104	806	20.7124	0.000006
Ww	6.805427 × 105	1	5.072564 × 106	806	108.1341	0.000000
Wc	2.218745 × 104	1	1.817085 × 105	806	98.4163	0.000000
x1	1.323167 × 109	1	1.400941 × 1010	806	76.1255	0.000000
We	1.440855 × 108	1	1.963493 × 109	806	59.1461	0.000000
x6	3.956767 × 101	1	7.864680 × 105	806	0.0406	0.840459

). This variable was therefore omitted from the processing optimization. It is expedient to try to model and optimize the process described in cluster 1 in terms of water, heat and electricity consumption.

4. Modelling of ANN Architecture

Artificial neural networks (ANNs) were used to model the electricity consumption rate W_e, the water consumption rate W_w and the heat consumption rate W_c. The task of ANN was to map five input decision variables: total power (x₁), frozen products (x₂), concentrates (x₃), juices and beverages (x₄) and other products (x₅) for three output variables: W_e, W_w and W_c to obtain the smallest mean squared error (MSE) and the highest correlation coefficient R. Input and output parameter values were normalized from 0 to 1 (dividing by their maximum values: 14,237 × 10³, 282 × 10³, 772.98 × 10³, 773.312 × 10³, 37 × 10³ for the decision variables x₁, x₂, x₃, x₄, x₅, respectively, and 1413.23 × 10⁻³, 88.87 × 10⁻³, 17.59 × 10⁻³ for the indicators W_e, W_w and W_c, respectively. The input data (474 cases) were randomly divided into sets of learning (80%), testing (10%) and validation (10%) cases. The Neural Networks Toolbox R2018a [38] located in Matlab was used for learning data. The learning algorithm for the artificial neural networks was the Levenberg–Marquardt algorithm. In order to find the best relationships between the input and output parameters, different activation functions and the number of neurons in the hidden layers were tested (Appendix A,

Table A2. Characteristics of the tested artificial neural networks.

ID	Activate Function in the Hidden Layer	Number of Neurons in the Hidden Layer	Activate Function in the Output Layer	Statistical Analysis
				MSE	R
1	log-sigmoid	4		0.0168040	0.75844
2		9	pureline	0.0169810	0.70719
3		14		0.1732000	0.73911
4		4		0.0271820	0.63388
5		9	log-sigmoid	0.0072654	0.88576
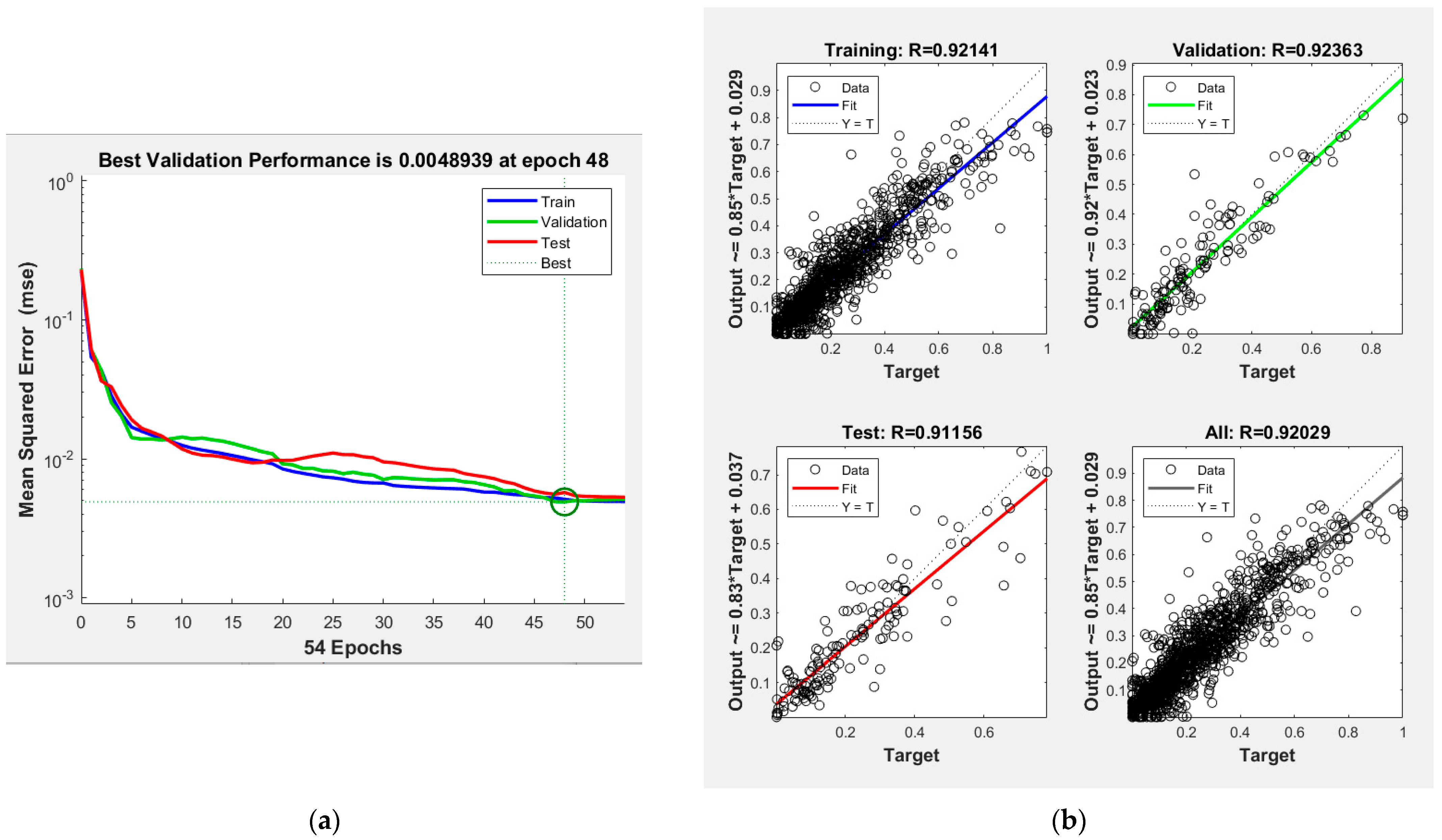
6		14		0.0048939	0.92363
7	tan-sigmoid	4		0.0160180	0.71191
8		9	pureline	0.0123480	0.74598
9		14		0.0062469	0.88769
10		4		0.0110210	0.77659
11		9	log-sigmoid	0.0086862	0.81746
12		14		0.0059845	0.90975

). Finally, for optimization, an ANN architecture multi-layer perceptron (MLP) 5:14:3 (Appendix A, Figure A3) was selected with five neurons in the input layer (x₁, x₂, x₃, x₄ and x₅), fourteen neurons in the hidden layer and three neurons in the output layer (W_e, W_w and W_c) with a logarithmic–sigmoidal activation function for the hidden and output layers (ID 6 in Appendix A, Table A2). The highest correlation coefficient R was 0.92 and the lowest mean squared error (MSE) 0.00489. The best fit was obtained after 48 epochs, for which the smallest MSE was 0.0048939 (Appendix A, Figure A2a). The correlation coefficients for the learning, validation and test data were, respectively: 0.92141, 0.92363 and 0.91156 (Appendix A, Figure A2b). The analysis of the sensitivity of the neural model shows that the production of juices and beverages and the power of devices installed in the plant have a more than twice greater impact on energy and water consumption than other independent variables.

5. Multi-Criteria Optimization of Fruit and Vegetable Processing

Optimization algorithms using linear and non-linear programming sometimes have difficulty finding global optima or, in the case of multi-objective optimization (MOO), a Pareto front. In multi-objective optimization, the definition of solution quality is much more complex than in single-objective optimization (SOO) problems. The main challenges in the MOO environment are: getting closer to the Pareto-optimal front and keeping the solution set as diverse as possible. The first task ensures that the resulting set of solutions is close to the optimum, while the second task ensures that a wide range of compromise solutions are obtained. Today, many engineering multi-objective optimization problems are solved using genetic algorithms (GAs). GAs are stochastic optimization methods, which are inspired by natural evolution [39]. Crossover and mutation are the key operators of the genetic algorithm. Crossover involves the random selection of genes from the chromosomes of a pair of parents. The probability of crossover is usually taken from a range of 0.5 to 0.8. A mutation parameter converts a random gene in a chromosome from 0 to 1 or vice versa. Mutation prevents premature convergence of the algorithm and the loss of valuable genetic information from the population. The probability of mutation is assumed to be between 0.005 and 0.50.

The objective function plays a main role in the genetic algorithm steps. The function should be well formulated because the main genetic operators perform their tasks based on the evaluation of the objective function. The function should be well formulated. Optimization of a multi-criteria genetic algorithm involves simultaneously minimizing or maximizing multiple objective functions (quality criterion) using constraints [40,41]. The basic steps of a multi-criteria genetic algorithm are described in the work [42,43]. In the present work, the objective functions W_e, W_c and W_w (Appendix A, Formulas (A1)–(A17)) were simultaneously minimized according to the constraints imposed on the decision variables: x₁, x₂, x₃, x₄ and x₅ (see limitations (3)).

$$\min \left(x\right)=\left\{\begin{array}{c}\min {\mathrm{W}}_{\mathrm{e}}=[\mathrm{k}\mathrm{W}\mathrm{h}/\mathrm{k}\mathrm{g}] \\ \min {\mathrm{W}}_{\mathrm{w}}=[{\mathrm{m}}^3/\mathrm{k}\mathrm{g}]\\ \min {\mathrm{W}}_{\mathrm{c}}=[\mathrm{G}\mathrm{J}/\mathrm{k}\mathrm{g}]\\ {412.5 \le x}_1\le \mathrm{14,237}\left[\mathrm{k}\mathrm{W}\right] \\ 0 \le x_2\le 282\times 1000 [\mathrm{kg}/\mathrm{day}] \\ 0 \le x_3\le 773\times 1000 [\mathrm{kg}/\mathrm{day}] \\ 0 \le x_4\le 312\times 1000 [\mathrm{kg}/\mathrm{day}] \\ 0 \le x_5\le 37\times 1000 [\mathrm{kg}/\mathrm{day}] \end{array}\right.$$

(3)

Multi-objective optimization was performed using a non-dominated sorting genetic algorithm (NSGA II), implemented in the Global Optimization Toolbox in Matlab R2018a. The following genetic parameters were used for optimization: crossover function was indirect, crossover probability of 0.8, migration was forward, mutation function was adapted, mutation probability of 0.15, number of generations of 300, Pareto front population fraction of 0.5, population size of 80 and selection function was tournament.

5.1. Pareto Solutions Using a Multi-Criteria Genetic Algorithm

Table 4. The Pareto optimal solution.

			Inputs			Outputs
ID	x1 [kW]	x2 × 103 [kg/Day]	x3 × 103 [kg/Day]	x4 × 103 [kg/Day]	x5 × 103 [kg/Day]	We × 10−3 [kWh/kg]	Ww × 10−3 [m3/kg]	Wc × 10−3 [GJ/kg]
1	3470	192	204	282	28	3.693	0.567	0.002
2	4422	160	231	180	20	2.405	0.777	0.005
3	4750	165	191	193	24	2.992	0.688	0.005
4	3928	162	211	182	21	2.045	1.120	0.008
5	3541	163	219	192	22	1.894	1.224	0.009
6	4334	155	216	177	23	1.732	1.355	0.013
7	3786	155	217	186	24	1.621	1.510	0.015
8	3627	159	214	196	25	1.588	1.610	0.017
9	3859	153	216	177	25	1.477	1.752	0.020
10	4113	152	210	180	26	1.433	1.873	0.024
11	3600	163	216	177	27	1.400	1.981	0.025
12	3742	154	202	179	26	1.356	2.151	0.028
13	3433	156	208	186	28	1.324	2.230	0.029
14	3650	151	203	175	27	1.288	2.392	0.033
15	3510	153	201	177	28	1.283	2.456	0.034
16	3514	151	199	173	28	1.274	2.579	0.036

shows the sixteen potential solutions (ID1–ID16) of the optimal set in the Pareto sense. It can be seen from Table 4 that daily electricity consumption is inversely proportional to daily water and heat consumption. Minimum solutions for the indicators W_e, W_w and W_c were found for parameters in the following ranges: from 3433 to 4750 [kW] for total power, from 151 × 10³ to 192 × 10³ [kg/day] for frozen products, from 191 × 10³ to 231 × 10³ [kg/day] for concentrates, from 173 × 10³ to 192 × 10³ [kg/day] for 282 × 10³ [kg/day] for juices and beverages and from 20 × 10³ to 28 × 10³ [kg/day] for other products. Figure 2 shows the Pareto curves created using a multi-criteria genetic algorithm.

The set of solutions consists of sixteen points forming a Pareto curve, whose boundaries are defined by the extreme points ID1 and ID16 (Table 4). Point ID16 in Figure 2 is the highest point on the Pareto curve with the lowest electricity consumption W_e = 1.274 × 10³ [kWh/kg], the highest heat consumption W_c = 0.036 × 10⁻³ [GJ/kg] and the highest water consumption W_w = 2.579 × 10⁻³ [m³/kg] (Table 4. ID = 16). For point ID16, the total installed capacity of the electrical equipment is x₁ = 3514 [kW], frozen products are x₂ = 151 × 10³ [kg/day], concentrates x₃ = 199 × 10³ [kg/day], juices and beverages x₄ = 173 × 10³ [kg/day] and other products x₅ = 28 × 10³ [kg/day]. The lowest point on the Pareto curve is ID1. For point ID = 1, the highest electricity consumption is W_e = 3.693 × 10⁻³ [kWh/kg], while the lowest water and heat consumption are, respectively: W_w = 0.567 × 10⁻³ [m³/kg] and W_c = 0.002 × 10⁻³ [GJ/kg]. For point ID = 1, the genetic algorithm found the following solutions: total power (x₁ = 3470 kW), frozen products (x₂ = 192 × 10³ [kg/day]), concentrates (x₃ = 204 × 10³ [kg/day]), juices and beverages (x₄ = 282 × 10³ [kg/day]) and other products (x₅ = 28 × 10³ [kg/day]). It can be seen from Figure 2 that electricity consumption is inversely proportional to water and heat consumption.

5.2. The Optimization Results

The points located on the curves (Figure 2a–c) are non-dominated solutions, since an improvement in the first objective function (W_e index) causes a simultaneous deterioration in the other objective functions (W_w and W_c indices) and vice versa. No single solution was found in which all the considered functions (minimum W_e, W_w and W_c) would simultaneously reach optimal values. An improvement in the W_e indicator (its minimization) causes a deterioration in the other two indicators W_e and W_c (their maximization). Thus, the We indicator is in constant conflict with the W_w and W_c parameters. In this case, the solution is the set of non-dominated solutions in the Pareto sense (Table 4). The choice of a particular solution depends on the requirements of the chosen plant and the preferences concerning the processing conditions.

The difference in values between the extreme points ID1 and ID6 of the solutions in the case of electricity consumption is three times, in water consumption it is about five times and the greatest difference in heat consumption is as much as eighteen times. There is no attempt in the literature at multi-criteria optimization of energy and water consumption in fruit and vegetable processing, which makes it impossible to compare it with other results. The method described is limited to the technology used. The procedure for a different technology would be analogous in all steps.

6. Conclusions

The knowledge obtained from this study allows us to understand the impact of the most important factors on energy and water consumption in fruit and vegetable processing in Poland and indicates the possibilities of using sustainable technologies in food production. To sum up, it can be said that:

• The power of the equipment installed in the plant and the production structure of selected products have the greatest impact on the consumption of energy and water in the processing of fruit and vegetables.
• The optimization results showed that with similar power of the installed devices, it is possible to use up to five times less thermal energy and several times less water consumption, but the processing structure needs to be selected appropriately.
• Sensitivity analysis of the neural model shows that the production of juices and beverages and the power of equipment installed in the plant have more than twice the impact on energy and water consumption than other independent variables.
• The results of Pareto optimization can be the basis for the use of sustainable technology in selected fruit- and vegetable-processing plants.
• Electricity consumption is inversely proportional to water and heat consumption in fruit and vegetable processing.

Further research should focus on analyzing the impact of the technology used on reducing energy and water consumption in processing. Focus should also be put on developing more efficient equipment and technology. The effort also needs to focus on solving the limitation in the availability of products for processing.