Thermodynamic Behavior and Energy Transformation Mechanism of the Multi-Period Evolution of Cavitation Bubbles Collapsing near a Rigid Wall: A Numerical Study

Abstract

The dynamic behavior and energy transformation mechanism of the multi-period evolution of bubbles collapsing near a wall have been essential considerations in bubble dynamics research. In this study, a compressible two-phase solver considering thermodynamics and phase transitions is developed on OpenFOAM (version v2112). This model is validated via comparison with analytical solutions and experimental results. The dynamics of the multi-period evolution of bubbles collapse process at different dimensionless stand-off distances (γ) were accurately reproduced. The results indicate that the shock wave emitted by the collapse of cavitation bubbles impacts the wall, causing the fluid temperature along the wall to increase. Moreover, the liquid jet has a dual effect on the wall temperature increase, depending on the initial stand-off distance between the bubble and the wall. When γ is small, the jet carries the low-temperature fluid to occupy the high-temperature region, and when γ is large, the jet carries the high-temperature fluid to occupy the low-temperature region. Compared with the mechanisms above of wall temperature increase, the collapse process of cavitation, when directly attached to the wall, increases the fluid temperature along the wall more significantly. Additionally, an energy transformation mechanism is proposed considering the internal bubble energy based on the analysis of the internal bubble energy and acoustic radiation energy with different γ values. Both the internal and acoustic radiation energy initially decreased and subsequently increased with increasing γ values. These findings provide deeper insights into the near-wall collapsing cavitation process mechanism.

1. Introduction

Cavitation erosion is damage to the surfaces of fluid devices caused by the cavitation process, involving the nucleation, growth, and collapse of the vapor and gas dissolved in a high-speed liquid flow. When a cavitation bubble collapses in the vicinity of a wall, a wall-oriented liquid jet is formed [1] and intense shock waves are emitted from the collapse site [2], which can cause considerable material damage and impact the operational efficiency and structural safety of hydraulic equipment such as turbines [3], hydrofoils [4,5], pumps [6], and propellers [7]. Additionally, when heat-sensitive material is exposed to a cavitation flow, repeated cavitation collapse can generate sufficient heat transfer and cause melting points on the surface, resulting in thermal damage. One of the primary causes of thermal damage is the thermodynamic effect resulting from cavitation; therefore, this phenomenon must be examined in depth.

In general, the causes of cavitation erosion involve complex hydrodynamic and thermodynamic mechanisms in which thermodynamic effects can exacerbate hydrodynamic phenomena. Hence, the study of the hydrodynamic and thermodynamic mechanisms of bubble collapse near walls, as well as the transformation and dissipation of various energies, is necessary to explore the mechanism through which thermal damage occurs. Numerous cavitation bubble experiments have been conducted to investigate such bubble dynamics. Laser generators [8,9,10] and electrical sparks [11] may be used to generate cavitation bubbles. High-speed cameras can then record their shape evolution, and sensors can monitor the flow-field temperatures and pressures. Ge et al. [12] investigated the unsteady cavitation characteristics and shedding dynamics of cavitating flows at different temperatures using a small-size Venturi-type test section. Their results show that there is a critical temperature of around 55 °C. Before this temperature, with increasing temperature, the average cavity length increased. They further confirmed that the critical temperature is 58 °C [13,14], the change in temperature will change the type of cavitation in the cavitating flow, and confirmed that the thermodynamic effects would significantly affect the dynamic behaviors of the cavity. Dular et al. [15] measured the temperature change in the fluid around cavitation bubbles using a high-speed thermal imager. Their results showed that the temperature of the surrounding liquid decreased by 3 and 4 K during the cavitation growth and collapse processes, respectively. However, the thermodynamic field within the bubble was not considered. Flint et al. [16] studied the sonoluminescence spectrum of ultrasonic cavitation bubbles with a spectroscopic probe, and the measured effective cavitation bubble temperature was 5075 ± 156 K. Liu et al. [17] investigated the influence of fluid temperature on the bubble collapse induced by a focused-laser-pulse near a rigid boundary. They found that the shock pressure generated by the liquid-jet increased with increasing fluid temperature and then decreased after reaching a peak value. This pressure decrease resulted from the thermodynamic effect of bubble collapse and the changing mechanical properties of the material of the wall at high temperatures. However, the thermodynamic field within the cavitation region was not considered. Using different measurement equipment in experimental studies can lead to different temperature results, and the infinitesimal time-scale of bubble oscillation, as well as the rapidly varying temperature and pressure during bubble oscillation, make it difficult to measure the pressure and temperature fields accurately. This is a considerable technical challenge when investigating the thermodynamic mechanisms of a single bubble. Therefore, high-precision numerical simulations are considered to be an effective approach to quantifying this effect and clarifying the mechanism of thermal damage during cavitation bubble collapse.

The Rayleigh–Plesset equation (R–P equation) has been widely used to describe the dynamics of a spherical bubble [18,19]. For non-spherical bubble collapse near rigid boundaries, complex fluid phenomena such as counter-jets and high-speed jets [20] are encountered. In these systems, the compressibility of the flow field cannot be ignored as it affects both the energy dissipation in the flow field [21,22] and the simulated shock waves [23]. Recently, extensive studies have been conducted to examine these complex phenomena by considering the compressible Naiver–Stokes (N–S) equations, phase equations, and interface capture models, such as the volume of fluid (VOF) and level set methods. Beig et al. [24] studied the effect of the initial distance and driving pressure on the maximum fluid temperature generated by collapsed bubbles along the wall and proposed two main influencing mechanisms, namely the temperature rise effect of shock waves and the effect of migration during cavitation bubble collapse. Yin et al. [25] investigated the heat transfer during the complete process, including the bubble growth, collapse, and rebound stages. They found that the pressure, velocity, and temperature peaked at the same time upon the collapse of the bubble. Phan et al. [26] simulated the cavitation in an underwater explosion and found that a smaller cavitation radius resulted in a thinner thermal boundary layer during the collapse stage, as well as the simultaneous appearance of high-velocity and abnormally high-temperature points, causing considerable damage to the structure. Furthermore, several studies [27,28,29,30,31] have considered phase transitions via simulations and found that vapor causes a much stronger collapse in experiments because of the phase transitions in this process.

Additionally, the physical quantities related to the study of thermal damage mechanisms should include the high temperatures along the wall and thermal properties such as the thermal conductivity and diffusivity of the wall. However, a single bubble does not cause thermal damage as insufficient heat can be transferred to the wall at this stage. Therefore, only the repeated collapse of many cavitation bubbles can transfer sufficient heat and cause thermal damage. Such damage occurs when the accumulated heat overcomes the van der Waals forces in the material. Hence, the total amount of transferred heat or energy is a physical quantity related to thermal damage, suggesting that the thermal damage mechanism should also be investigated from an energy perspective. The thermodynamic effect can be reflected in changes in the internal bubble energy, which includes the work due to the external pressure and the exchange of energy resulting from phase transitions, heat conduction, and chemical reactions [32]. Similarly, the dynamic mechanisms of a bubble can also be examined from an energy perspective, including the changes in various energies during the process of cavitation bubble collapse. The energy transformation and dissipation mechanisms can be examined based on the time histories of the energy components during multiple bubble oscillations, which not only further reflects the coupling effect of hydrodynamics and thermodynamics but also quantitatively reflects the thermal energy that is accumulated in the fluid.

Most existing studies concerning the mechanisms of bubble energy transformation have focused on the relationship between the potential energy, kinetic energy, and acoustic radiation energy during the bubble-collapse process. Schenke et al. [33] proposed an energy transfer relationship in which the bubble potential energy was converted into the flow-field kinetic energy before being converted into acoustic energy. Similar results were reported by Fortes–Patella et al. [34] and Zhang et al. [35]; these studies deepened our understanding of the mechanism of cavitation energy conversion. However, they ignored the internal energy, which plays a critical role in the bubble energy system. Several studies have proposed diverse internal energy formulas [36,37,38], but these formulas do not consider the effects of phase transitions and heat transfer. Consequently, analyzing the characteristics of internal energy remains challenging. Tinguely et al. [39] conducted a systematic experimental study on the energy distribution of the shock wave generated by the collapse of a bubble and its rebound stage. They proposed that the change in the internal energy over the entire period from bubble collapse to rebounding to its maximum radius was practically negligible. However, they did not consider the role of internal energy in the energy conversion mechanism. Shen et al. [40] proposed a formula that included pressure-based work, thermal conduction, and phase changes. Dehane et al. [32] further analyzed the influence of these three parameters on the internal energy during the process of bubble oscillation, which provided novel insights into the study of internal energy.

A comprehensive study of cavitation erosion requires the full representation of bubble clouds and the material response to such loadings. To achieve this, we first need to understand the mechanisms of heat transfer and energy dissipation at the single-bubble level. Using the open-source package OpenFOAM (version v2112), this study aims to develop a compressible two-phase model accounting for the phase transitions and thermal effects such that the hydrodynamic and thermodynamic mechanisms of multi-period evolution of bubble collapse may be investigated. We also explore the relationship between the internal and shock wave energies. Moreover, we focus only on the collapse phase to better research the effect of the distance between a bubble and the wall. The structure of this article is as follows. In Section 2, the mathematical formulation, numerical method, and verification of the solver are discussed. The simulation results at three typical stand-off distances are discussed in Section 3. In Section 4, an energy transformation mechanism is proposed and the relationship between the internal bubble and acoustic energies is analyzed. The main conclusions are summarized in Section 5.

2. Methods: Mathematical Formulation, Numerical Methods, and Verification

2.1. Governing Equations

In this study, we developed a compressible model considering the fluid viscosity, thermodynamic effects, and phase transition. Gravity could be neglected, given the short period of bubble oscillation and the small size of a single bubble. Moreover, the VOF method, widely applied in the literature [18,25,27], was used to capture the two-phase interface. The volume fraction (α) is introduced to describe the liquid (${\alpha }_l=1$) and vapor (${\alpha }_v=1$) states. The volume fraction can be estimated using the VOF method to satisfy ${\alpha }_l+{\alpha }_v=1$. The continuity and momentum equations can be expressed as follows:

$$\frac{\partial \rho }{\partial t}+\nabla ·\left(\rho \mathit{U}\right)=0,$$

(1)

$$\frac{\partial \rho \mathit{U}}{\partial t}+\nabla ·\left(\rho \mathit{U}\mathit{U}\right)=-\nabla p+2\nabla ·\left(\mu \mathit{D}\right)-\frac{2}{3}\nabla \left(\mu \nabla ·\mathit{U}\right)+\sigma \kappa \mathit{n},$$

(2)

where t denotes time; U denotes the mixture velocity; $p$ denotes the pressure; and $\rho$ and $\mu$ denote the mixture density and viscosity of the fluid, respectively. D denotes the deformation tensor and $\mathit{D}=\left[\nabla \mathit{U}+{\left(\nabla \mathit{U}\right)}^T\right]/2$. $\kappa$ denotes the interface curvature, σ = 0.07 is the tension coefficient of the interface, and $\mathit{n}$ represents the unit normal vector of the interface. The mixture density ($\rho$) and viscosity ($\mu$) can be obtained using the following equations:

$$\rho ={\alpha }_v{\rho }_v+{\alpha }_l{\rho }_l,$$

(3)

$$\mu ={\alpha }_v{\mu }_v+{\alpha }_l{\mu }_l.$$

(4)

in this study, the initial ${\rho }_v=0.017 \mathrm{kg}/{\mathrm{m}}^3$ and the initial ${\rho }_l=996.558 \mathrm{kg}/{\mathrm{m}}^3$; ${\mu }_v=9.919\times {10}^{-6} \mathrm{Pa}·\mathrm{s}$, and ${\mu }_l=8.538\times {10}^{-4} \mathrm{Pa}·\mathrm{s}$.

The mass equation can be written as follows:

$$\frac{\partial \left({\alpha }_i{\rho }_i\right)}{\partial t}+\nabla ·\left({\alpha }_i{\rho }_i\mathit{U}\right)=\mp \dot{m}\left(i=l,v\right),$$

(5)

where $\dot{m}={\dot{m}}^{+}-{\dot{m}}^{-}$ denotes the mass transfer rate, in which ${\dot{m}}^{+}$ and ${\dot{m}}^{-}$ are the rates of condensation and vaporization, respectively. The Schnerr–Sauer cavitation model, which has proven reliable in handling mass transport problems considering phase transitions [41], is introduced to better explain the effects of vaporization and condensation during the phase change process. In this model, the condensation and vaporization rates are expressed as follows:

$${\dot{m}}^{+}=C_c\frac{3{\rho }_l{\rho }_v}{\rho }{\alpha }_l\left(1-{\alpha }_l\right)\frac{1}{R_b}\sqrt{\frac{2\left(p_v-p\right)}{3p_l}} \left(p_v>p\right),$$

(6)

$${\dot{m}}^{-}=C_v\frac{3{\rho }_l{\rho }_v}{\rho }{\alpha }_l\left(1-{\alpha }_l-{\alpha }_{Nuc}\right)\frac{1}{R_b}\sqrt{\frac{2\left(p-p_v\right)}{3p_l}} \left(p_v<p\right),$$

(7)

where $C_c$ and $C_v$ are the coefficients of the condensation rate and vaporization, respectively; $R_b$ denotes the cavitation nuclei radius; $p_v$ denotes the saturation vapor; $p_l$ denotes the liquid pressure; and ${\alpha }_{Nuc}$ denotes the volume fraction of the nucleation site. $R_b$ and ${\alpha }_{Nuc}$ can be expressed as follows:

$$R_b={\left(\frac{1-{\alpha }_l-{\alpha }_{Nuc}}{{\alpha }_l}\frac{3}{4\pi }\frac{1}{n}\right)}^{\frac{1}{3}},$$

(8)

$${\alpha }_{Nuc}=\frac{\frac{n\pi {\left(d_{Nuc}\right)}^3}{6}}{1+\frac{n\pi {\left(d_{Nuc}\right)}^3}{6}},$$

(9)

where $d_{Nuc}$ and $n$ denote the nucleation site diameter and the number of nuclei per cubic meter, respectively. In this study, $C_c=1$, $C_v=1$, $d_{Nuc}=2.0\times {10}^{-6} \mathrm{m}$, and $n=1.6\times {10}^{13}{ \mathrm{m}}^{-3}$.

The saturation vapor ($p_v$) can be expressed as follows:

$$p_v=\exp \left(A+\frac{B}{T}+C\ln T+D{T}^E\right),$$

(10)

where $A=73.649$, $B=-7258.2$, $C=-7.3037$, $D=4.16536\times {10}^{-6}$, $E=2$, and $T$ is the temperature inside the bubble.

The energy equation can be expressed as follows [25,31]:

$$\begin{gathered} \left[\frac{\partial \left(\rho T\right)}{\partial t}+\nabla \left(\rho TU\right)\right]+\left(\frac{{\alpha }_l}{C_{pl}}+\frac{{\alpha }_v}{C_{pv}}\right)\left[\frac{\partial \left(\rho K\right)}{\partial t}+\nabla \left(\rho KU\right)\right]= \\ \left(\frac{{\alpha }_l}{C_{pl}}+\frac{{\alpha }_v}{C_{pv}}\right)\left[\frac{\partial P}{\partial t}+\nabla ·\left(\tau ·U\right)\right]+\left(\frac{{\alpha }_l{\lambda }_l}{C_{pl}}+\frac{{\alpha }_v{\lambda }_v}{C_{pv}}\right)\left({\nabla }^{2}T\right), \end{gathered}$$

(11)

where $C_{pl}$ and $C_{pv}$ denote the heat capacity of the liquid and vapor, respectively; $K=0.5\left|U^2\right|$ denotes the kinematic energy; $\tau$ denotes the shear stress; and ${\lambda }_l$ and ${\lambda }_v$ denote the thermal conductivities of the liquid and vapor phases, respectively. In this work, $C_{pl}=4181.097 \mathrm{J}/\left(\mathrm{kg}·\mathrm{K}\right)$, $C_{pv}=1913.953 \mathrm{J}/\left(\mathrm{kg}·\mathrm{K}\right)$, ${\lambda }_l=0.677 \mathrm{W}/\left(\mathrm{m}·\mathrm{K}\right)$, and ${\lambda }_v=0.020 \mathrm{W}/\left(\mathrm{m}·\mathrm{K}\right)$.

The equation of state (EOS) can be used to resolve the aforementioned motion equations, and in this study, different EOSs were used for each phase. The liquid phase can be modeled using the Tait equation, which describes the shock waves emitted during the bubble-collapse process [18] as follows:

$${\rho }_l={\rho }_0{\left(\frac{p+B}{p_0+B}\right)}^{1/\gamma },$$

(12)

where ${\rho }_0$ and $p_0$ denote the reference density and pressure, respectively; $B=3.3\times {10}^8$ is the model constant; and $\gamma =7.15$ is a fluid-specific parameter [30]. The EOS for the vapor phase can be expressed as follows:

$${\rho }_v=\frac{1}{RT}p,$$

(13)

where R denotes the gas constant.

Moreover, the potential association between the bubble internal energy and acoustic energy during bubble collapse is considered, and the potential energy can be defined as follows [42]:

$$E_{pot}=\frac{4}{3}\pi r^3\Delta p,$$

(14)

where $r$ denotes the bubble radius and $\mathsf{\Delta }p$ denotes the pressure difference between the two sides of the bubble interface.

The kinetic energy of the flow domain can be expressed as follows:

$$E_k={\displaystyle \int }\frac{1}{2}\rho U^{2}dV,$$

(15)

Moreover, the bubble internal energy can be defined as follows [32,40]:

$$\Delta E_i=-p\left(t\right)·\Delta V\left(t\right)+4\pi r^2\frac{\Delta t}{M_{H_{2}O}}\dot{m}{C}_{v,H2O}T+4\pi r^2\Delta t\lambda \frac{\left(T_{liq}-T\right)}{L_{th}},$$

(16)

where $p\left(t\right)$ denotes the internal bubble pressure; $\Delta V\left(t\right)$ denotes the volume difference; $M_{H_{2}O}$ denotes the molar mass of water; $C_{v,H2O}$ denotes the heat capacity of water; $T_{liq}$ denotes the temperature of the external bubble surface; and $L_{th}$ denotes the thickness of the thermal boundary layer, which can be obtained as follows:

$$L_{th}=min\left\{\frac{r}{\pi },\sqrt{\frac{r\chi }{\dot{R}}}\right\},$$

(17)

$$\chi =\frac{{\lambda }_{mix}}{C_p}.$$

(18)

where $\chi$ represents the bubble thermal diffusivity and ${\lambda }_{mix}$ represents the heat conductivity. The first term on the right-hand side of Equation (16) is the pressure work. The second term is the energy carried by the evaporating vapor from the surrounding liquid into the bubble and by the condensing vapor from the bubble into the liquid over the period $\Delta t$. The third term is the energy change due to thermal conduction.

The acoustic energy is expressed as follows [35]:

$$E_{wave}={\displaystyle \int }\frac{\mathsf{\Delta }{p}^2}{{\left(\rho c_l\right)}^2}dV,$$

(19)

where $c_l=1500 \mathrm{m}/\mathrm{s}$ denotes the speed of sound in the fluid.

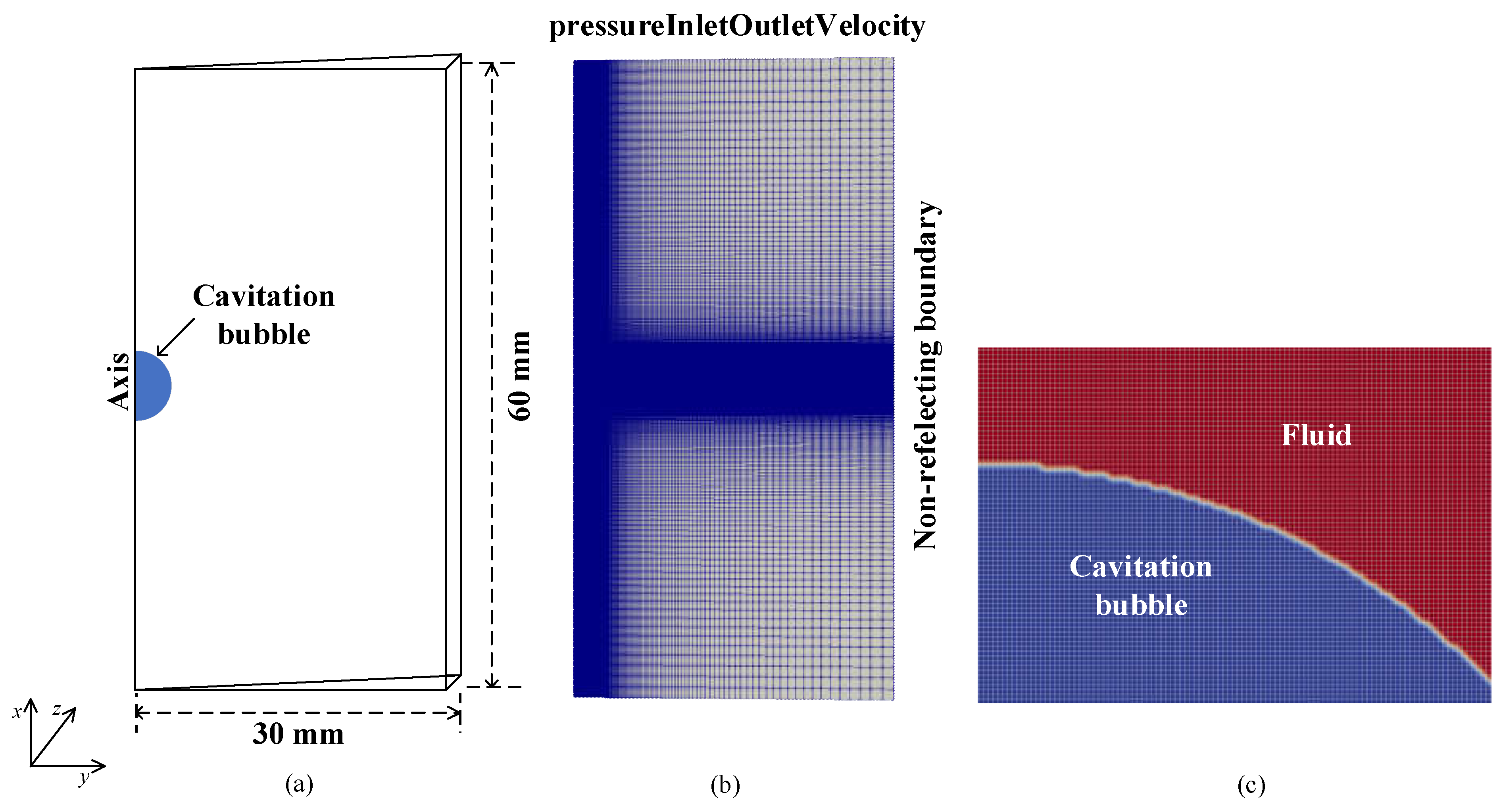
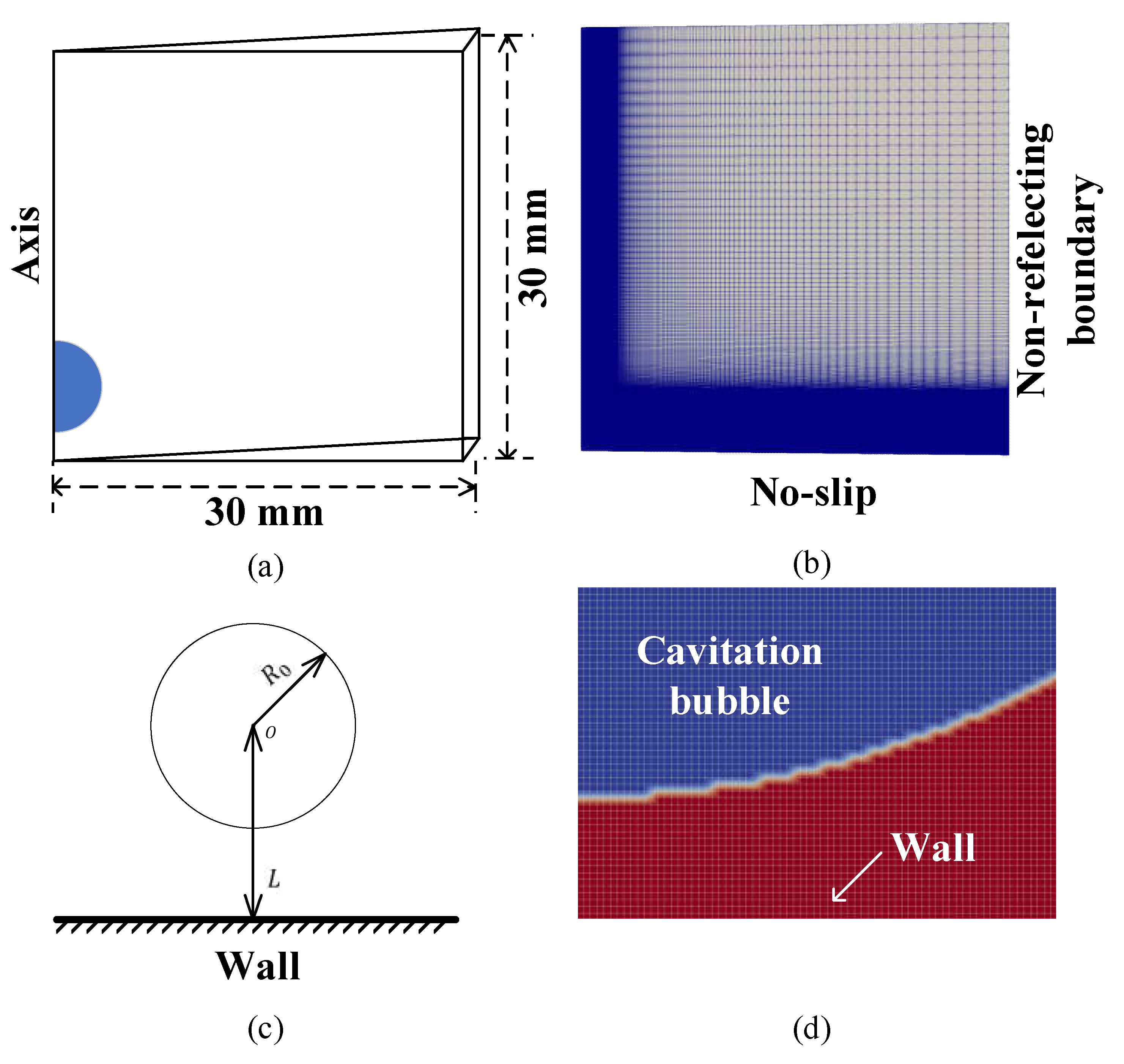
2.2. Numerical Setup

In this study, the finite volume method, which includes nonlinear compressibility effects in its calculation of aspherical bubble dynamics, has proven to result in an unproblematic variation in the bubble topology compared with the boundary integral method [18,43] and is applied to discretize the governing equations. The preconditioned bi-conjugate gradient (PBiCGStab) solver using a simplified diagonal-based incomplete LU (DILU) preconditioner is used to solve the temperature and velocity matrix, and the preconditioned conjugate gradient solver with a simplified diagonal-based incomplete Cholesky preconditioner is used to solve the pressure matrix. The pressure–velocity coupling is handled by the PIMPLE algorithm, which combines SIMPLE (the semi-implicit method for pressure-linked equations) and PISO (pressure implicit with splitting of operator).

In the present study, one outer SIMPLE loop was used for each time step, and three PISO loops were performed in one SIMPLE loop. The time derivatives use the first-order Euler implicit difference. The second-order Gaussian TVD scheme was applied for the spatial discretization to reduce the numerical diffusion. An adjustable time-step approach was employed, and to ensure that the maximum Courant number did not exceed 0.2, a sufficiently small time step was set. When the cavitation in the flow field disappears completely, the calculation is over.

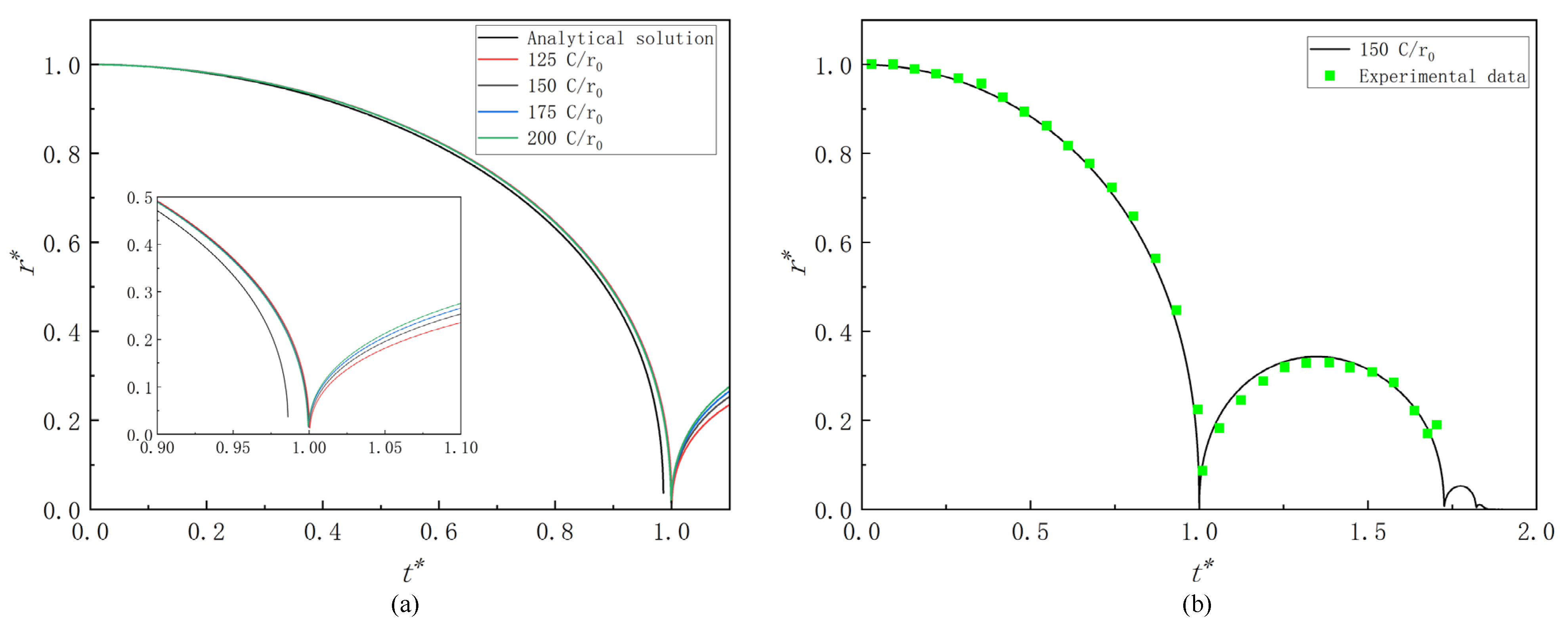
2.3. Model Validation

The simulations in this study are axisymmetric to reduce computational costs, and a wedge geometry ($30\times 60 \mathrm{mm}$) with a 5$°$ open-angle is applied, as shown in Figure 1a. The mesh is generated by using the OpenFOAM utility blockMesh, wherein the mesh of the area of bubble collapse is refined, thereby making the VOF method more accurate. The refinement region, which is sufficiently large to capture the behavior of collapsed bubble dynamics, is in the range of 0 to 4 mm in the x-direction and 0 to 2 mm in the y-direction, as shown in Figure 1b. Moreover, Figure 1c shows the mesh details around the bubble, where the blue area is the bubble area, the red area is the flow field area, and the thin white line is the mesh division line. In this work, the initial bubble radius $r_0$ is uniformly set to 0.747 mm. The spacing of the grids outside of the refinement area increases with a progression factor of 1.03. Additionally, the grid resolution parameter ($C/r_0$), which indicates the number of cells in the radial direction inside the initial bubble, is introduced to evaluate the mesh accuracy in the refinement area [30].

The accuracy of our model was verified by comparison with the analytical solution of a spherical bubble calculated using the simplified Rayleigh–Plesset equation. We assumed that the vapor bubble collapsed spherically in a free-flow field, as shown in Figure 1a. The boundary condition for the pressure field at the outer boundary of the computational domain is chosen to be waveTransmissive with the atmospheric pressure $p_{\infty }=101,325 \mathrm{Pa}$ and a relaxation length scale $lInf=0.0034 \mathrm{m}$. The boundary condition pressureInletOutletVelocity is used for the velocity $U$. The zeroGradient boundary condition is applied to ${\alpha }_l$ and $T$. Additionally, the wedge boundary condition is used in the front and back patches. The initial pressure inside the bubble is 3540 Pa and that in the liquid is 101,325 Pa. The initial temperature field is uniformly set to 300 K.

Figure 2a exhibits the time histories of the dimensionless radius $r^{*}$, where $r^{*}=r/r_0$, and the dimensionless time $t^{*}$, where $t^{*}=t/t_c$. Here, $t_c$ is the time when the bubble first reaches the minimum volume obtained using far-field cavitation bubble simulations. The results obtained under four different mesh resolutions are generally similar during the first bubble-collapse period, and the simulation results exhibit a good agreement with the analytical solution. However, there is a noticeable time delay in the final stages of collapse. This is because factors such as phase change and heat exchange are not considered by the simplified Rayleigh–Plesset equation. Given the slight delay differences obtained under the four mesh resolutions, as well as to balance the computational overhead and accuracy of the simulation results, a mesh resolution of $150C/r_0$ is used in this study.

The experimental results of Huang et al. [44] were selected as the reference for model validation. Figure 2b shows the evolution of the bubble radius over time. Here, the black line represents the simulation results and the green dots represent the experimental results. The numerical results are consistent with the experimental results. As the energy released by the acoustic waves of the bubble results from the first and second collapse cycles [21], our study focuses more on the first two cycles of the bubble dynamic behavior.

3. Results: Hydrodynamic and Thermodynamic of the Multi-Period Oscillation of Cavitation Bubble near the Wall

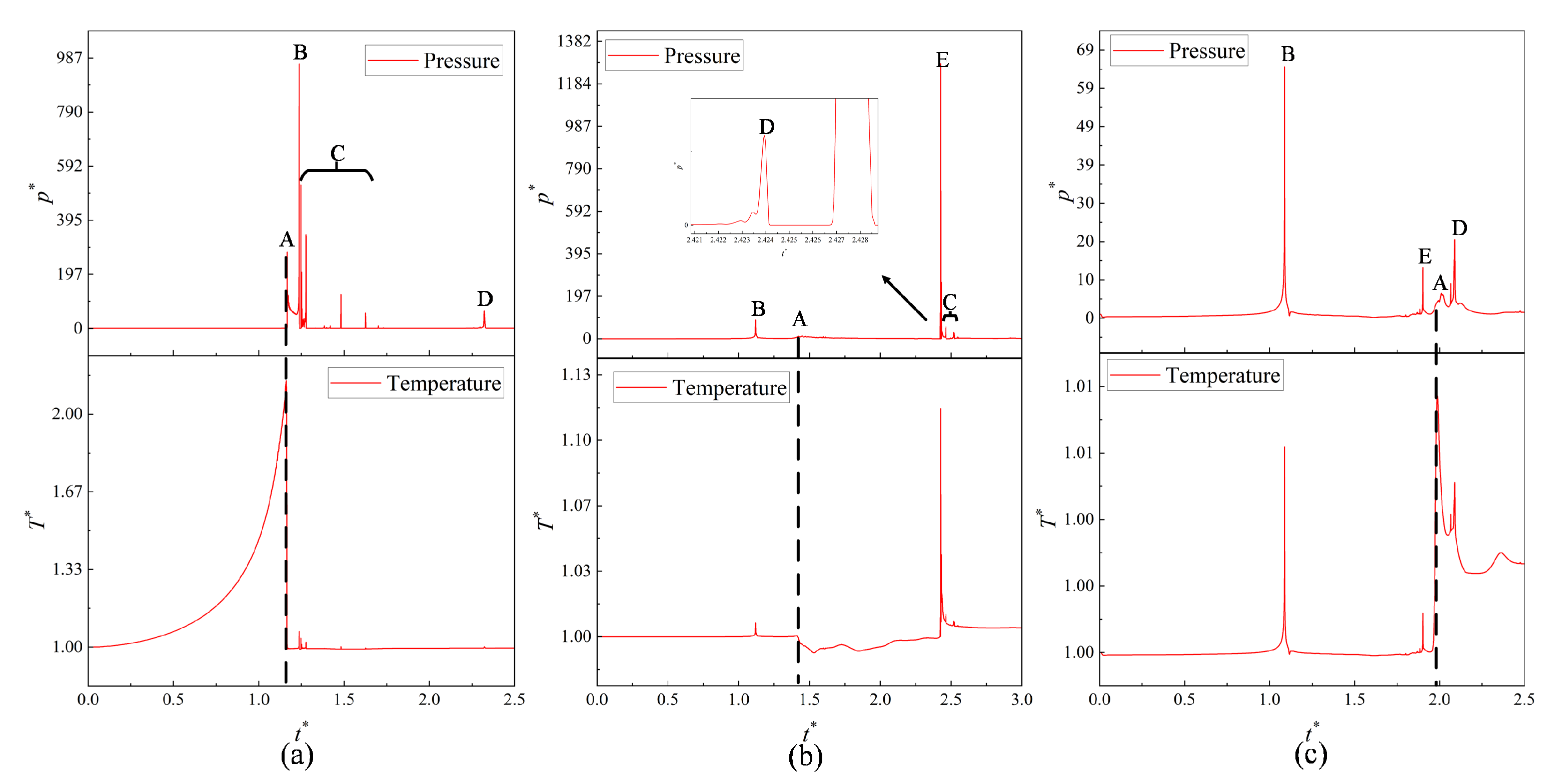
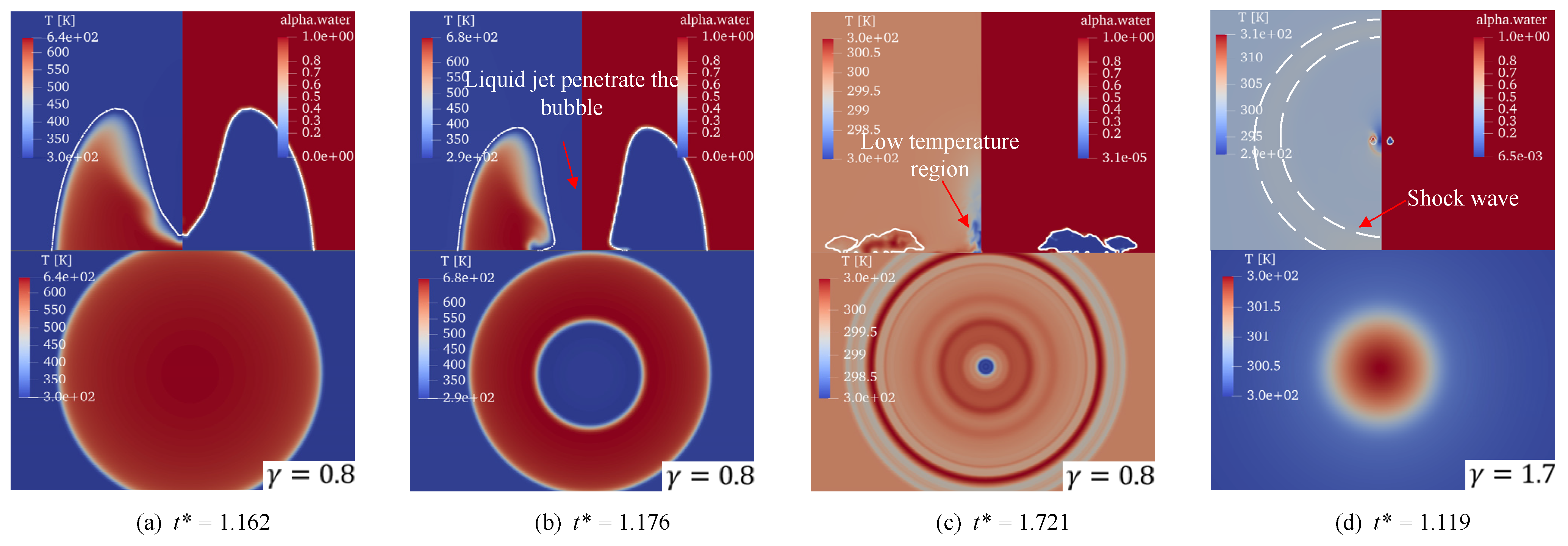
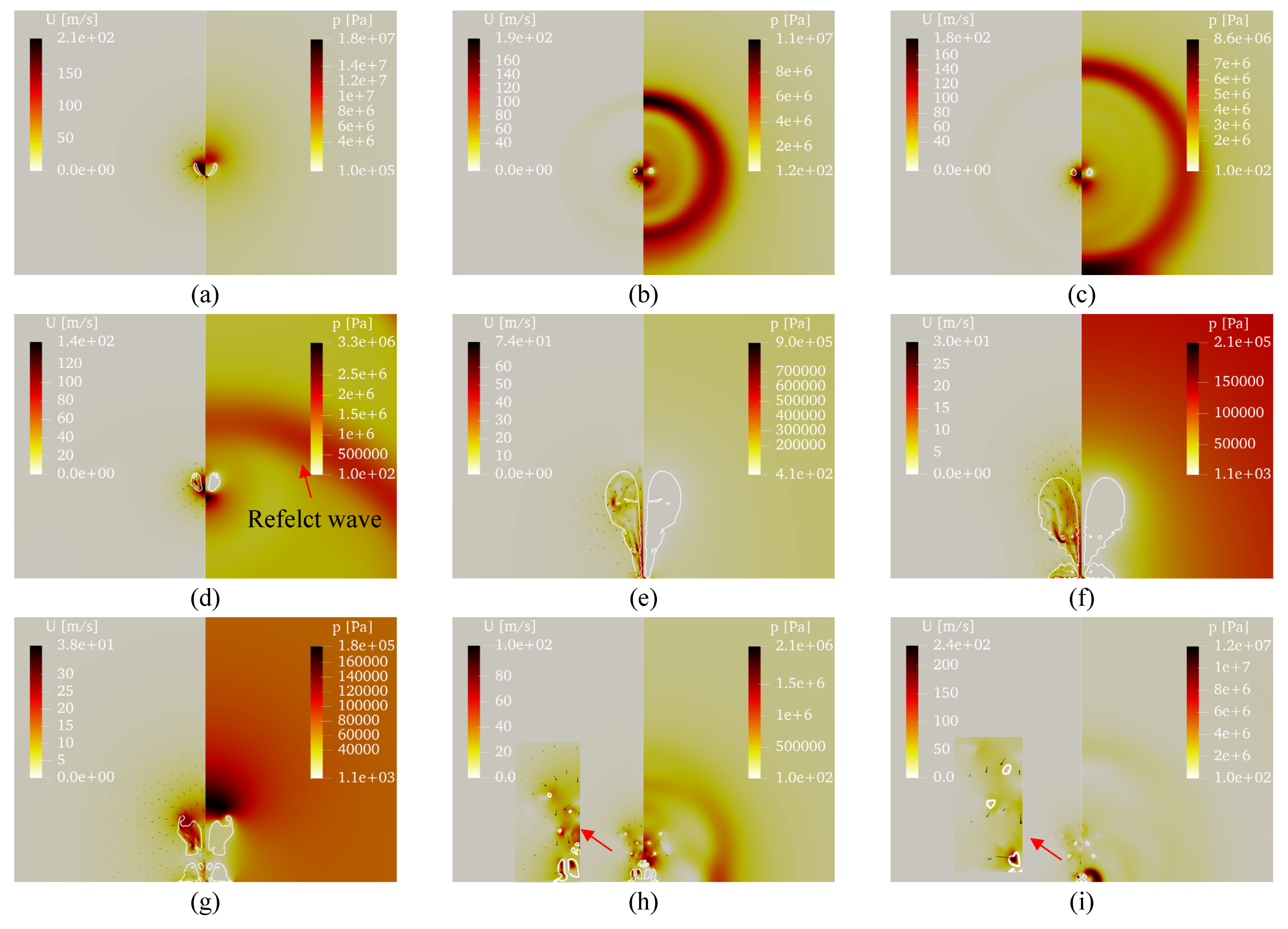
3.1. Small Stand-Off Distance, γ = 0.80

Figure 3 shows a schematic diagram of a cavitation bubble collapsing near a rigid wall. To better examine the effect of distance on bubble dynamics, we introduced the dimensionless distance $\gamma =L/r_0$, where $L$ denotes the initial distance between the center of the bubble and the wall, as shown in Figure 3c. The bubble–wall system and local refined mesh schematic diagram are shown in Figure 3a,b, respectively. Additionally, the mesh details are shown in Figure 3d. Here, the bottom is the wall. The boundary conditions are the same as in the far-field case except for the wall, which is set to a no-slip boundary condition. In simulations near the wall, the initial bubble radius is 0.747 mm, the pressure inside of the bubble is 3540 Pa, and the temperature within the bubble is 300 K. As for the liquid, the initial pressure ($p_0$) and temperature ($T_0$) are 101,325 Pa and 300 K, respectively. Owing to the non-spherical collapse of the cavitation process occurring near the wall, the equivalent radius can be expressed as follows:

$$R_e={\left(\frac{3V}{4\pi }\right)}^{\frac{1}{3}}$$

(20)

To better illustrate the hydrodynamic and thermodynamic mechanisms of cavitation oscillation, several figures are given in this study, as follows: Figure 4 shows the dynamic bubble behavior during the first and second oscillations with γ = 0.80, including the pressure (right-hand side) and velocity (left-hand side) fields, where the vapor–liquid interface is highlighted by the solid white line. The small arrow in the velocity field denotes the direction of the velocity and the size of the arrow indicates its magnitude. Figure 5 shows the temporal evolution of the pressure and fluid temperature at the wall center with three different γ values. Similarly, these results are dimensionless, in which $p^{*}=p/p_{w,0}$ and $T^{*}=T/T_0$ ($p_{w,0}$ denotes the initial pressure on the wall). As shown in this figure, multiple pressure peaks, referred to as A to E, are identified by combining the pressure and velocity contours. The temperature distribution (left-hand side) and bubble shape (right-hand side) at several typical moments and the fluid temperature field at the wall (bottom) are shown in Figure 6.

During the initial stage of cavitation oscillation, the bubble begins to collapse as the ambient pressure is much higher than the pressure inside the vapor bubble, as shown in Figure 4a. Figure 4b shows a high-pressure area appearing above the bubble, resulting in a jet directed toward the wall, which continues to impinge the bubble and creates a concave area, as shown in Figure 4c. During the collapse stage, the bubble margin continuously works on the compressible vapor within it, and the heat exchange between the high-temperature bubble and low-temperature fluid is relatively small such that the temperature in the bubble increases rapidly [45], causing the fluid temperature near the wall to rise, as shown in Figure 6a. Subsequently, the liquid jet penetrates the bubble and contacts the wall, as indicated in Figure 4c, leading to a low-temperature jet outside of the cavitation region occupying the high-temperature area (Figure 6b). A cliff-like decrease in the fluid temperature occurs at the center of the wall, and the pressure peak A is formed by the jet impacting the wall, as shown in Figure 5a. Figure 4d shows that a high-pressure area is created because of the liquid jet, and the shape of the bubble becomes annular. Furthermore, the impact of the jet on the wall also causes a splash phenomenon [46] wherein the direction of the splash flow is opposite to that of the liquid jet, which further splits the bubble and lengthens the duration of the pressure peak. Two shock waves can then be identified from the first collapse of the cavitation and the subsequent collapse of the tiny cavitation region, as shown in Figure 4e. These two shock waves cause different pressure peaks, denoted as B and C. As depicted in Figure 4f, the bubble rebounds and spreads annularly along the wall because of the radial flow, which is contributed by the redirection of the jet contacting the wall, and it further changes the temperature distribution of the fluid as well as that of the wall. Meanwhile, the generation of a splash flow lowers the temperature of the jet impingement area (Figure 6c). Figure 4g,h show the rebounding cavitation bubble’s further movement, resulting in a shock wave propagating outward while the bubble collapses to its minimum volume. The shock wave produces a pressure peak D when it contacts the wall, as shown in Figure 4i. Although the dynamic behavior of the tiny bubble splitting from the main bubble can be identified in the above descriptions, the effects of this tiny bubble are neglected because of the complexity of this system as the main goal of this study concerns the dynamics of a multi-period collapsing bubble.

3.2. Medium Stand-Off Distance, γ = 1.70

To further explore the effect of distance on the bubble multi-period collapse dynamics, a simulation using γ = 1.70 was conducted, and the pressure and velocity fields are exhibited in Figure 7. Similar to the γ = 0.80 results, Figure 7a shows a high-pressure area appearing above the bubble that drives the liquid into the bubble. After the bubble collapses to its minimum volume, two high-pressure regions appear above and below, as shown in Figure 7b. Figure 7c,d show the reflected wave produced by the shock wave hitting the wall and bouncing off. Moreover, from Figure 5b, the temperature peaks occur simultaneously with the pressure peaks. Combined with Figure 6d, it is shown that the propagation of the shock wave removes some of the heat inside of the bubble after it has collapsed, thereby affecting the temperature distribution inside of the fluid field, which demonstrates the function of the shock wave in raising the temperature along the wall [24]. Then, the liquid jet drives the bubble, which is still in the rebound stage, to impact the wall, as shown in Figure 7e. The impingement of the liquid jet reduces the fluid temperature near the wall. Similarly, the radial flow makes the lower half of the bubble move along the wall, and coupled with the effect of the splash flow, the bouncing bubble is split into upper and lower parts of different sizes, as shown in Figure 7f. In this study, the bubble that has split and closed is referred to as the split bubble. Due to the attenuation of the wall effect, the upper bubble contracts faster, finally collapsing to its minimum volume. Simultaneously, many tiny bubbles start to collapse, as shown in Figure 7g,h. Figure 7i shows that the lower bubble has finally collapsed to its minimum volume and a shock wave has been emitted. Owing to the smaller distance between the collapsing position and the wall, the pressure peak E created by the shock wave from the split bubble collapse is higher than that of the others, as shown in Figure 5b.

3.3. Large Stand-Off Distance, γ = 2.50

When γ increases to 2.50, the bubble dynamics differ to a certain extent from those described earlier, and the pressure and velocity fields are depicted in Figure 8. Figure 8a–c show the high-pressure region above the bubble, the high-pressure region above and below the bubble after the collapse, and the reflected wave after the shock wave impacts the wall, respectively. During the rebound stage, because of the effects of the liquid jet, the bubble protrudes in the lower half, as shown in Figure 8d. Furthermore, as the jet continues to move toward the wall, the protrusion is broken because of the difference between the lower and upper velocities, as shown in Figure 8e. However, based on Figure 5c, the impact of the jet increases the fluid temperature near the wall, which differs from the above-described two cases. This phenomenon shows that the liquid jet has a dual role in increasing fluid temperature along the wall, which depends on the initial distance between the cavitation bubble and the wall itself. Figure 8f,g show that the bubble is then divided into two parts, wherein the part near the wall is trapped by the jet and moves towards the wall until its collapses to the minimum volume and then disappears in the fluid, while the part far from the wall is still in the contraction stage. Figure 8h shows the shock wave emitted by the larger bubble during the collapse. Next, the bubbles rebound again, as shown in Figure 8i. The pressure peaks at the center of the wall caused by the shock waves and liquid jet are identified and indicated, as shown in Figure 5c.

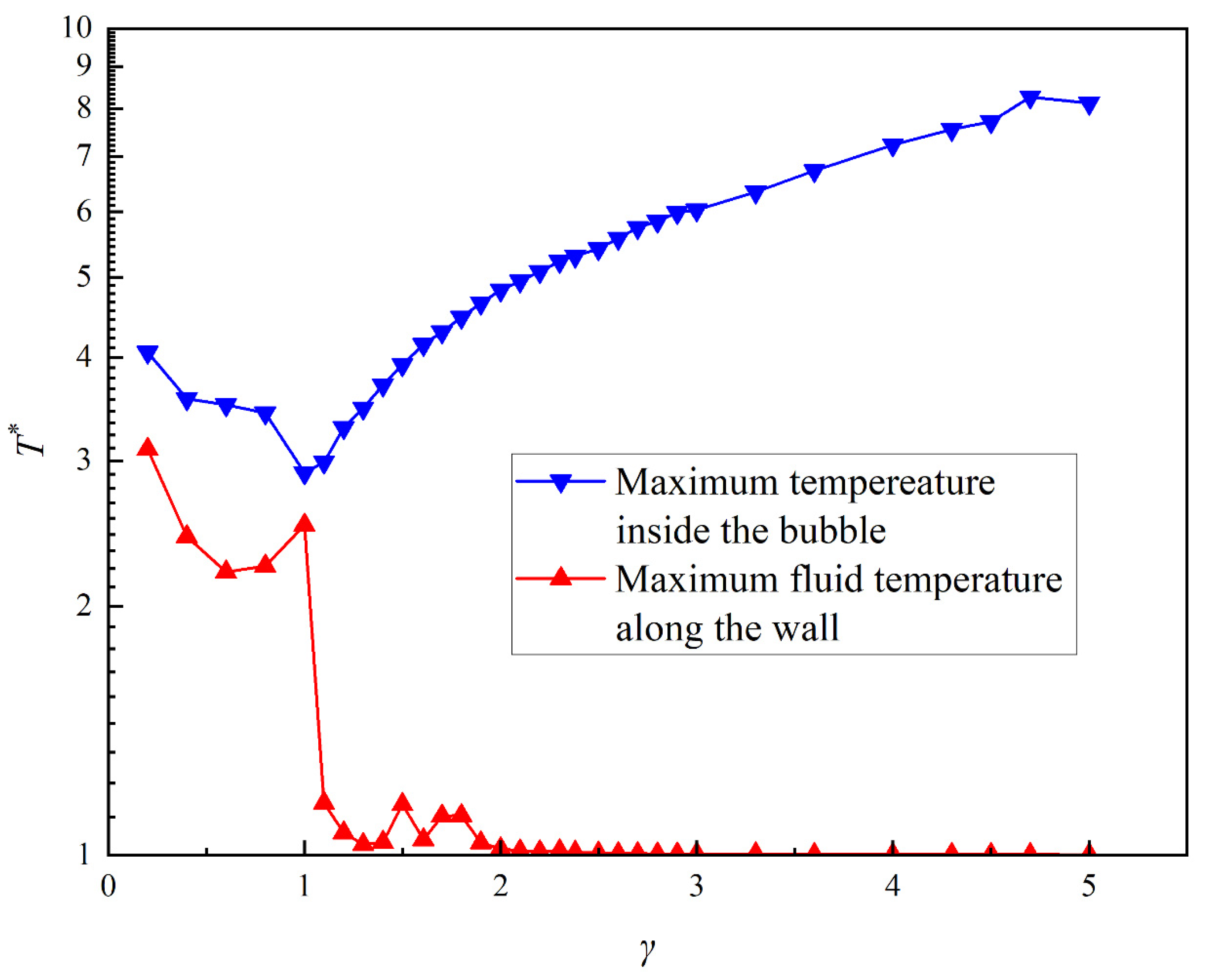
3.4. Effect of the Stand-Off Distance on Bubble Hydrodynamics and Thermodynamics

As mentioned earlier, γ has a major influence on the bubble hydrodynamics and thermodynamics, and the influence of γ on the maximum temperature and the maximum fluid temperature along the wall is shown in Figure 9. For a bubble that is in direct contact with a solid wall (γ < 1.0), as γ decreases, the liquid jet hits the wall directly, increasing the pressure and creating a shock wave that further accelerates the collapse of the bubble [24]. Consequently, the bubble collapses more violently, and the temperature within the bubble becomes higher. The maximum fluid temperature along the wall increases with an increase in the maximum temperature within the bubble; a typical example is shown in Figure 4. For a bubble near the wall that is not in direct contact with it (γ ≥ 1.0), the wall effect on the bubble is weakened due to the increase in γ, resulting in a reduced non-spherical collapse and a stronger energy focus [47]. Consequently, a higher temperature inside the bubble is achieved. However, the maximum fluid temperature along the wall decreases sharply under these conditions, and it no longer increases with the maximum temperature inside the bubble as the bubble no longer contacts the wall directly. At a certain distance, the split bubble driven by the liquid jet collapses on the wall, causing the maximum fluid temperature along the wall to increase.

We further studied the relationship between the shock wave and its resulting maximum pressure and fluid temperature at the center of the wall via simulations for different initial γ values, as shown in Figure 10. As the liquid jet does not carry heat, the fluid temperature change caused by the jet contacting the wall is not considered here. A comparison of Figure 10a,b reveals a strong correlation between the pressure and temperature peaks, wherein a more intense shock wave that reaches the wall results in higher pressure and temperature peaks. To better illustrate this relationship, four stages can be identified in Figure 10, referred to as Stages Ι, ΙΙ, ΙΙΙ, and ΙV.

During Stage Ι (0 < γ ≤ 1.0), as depicted in Figure 9, more energy is dissipated in the first cycle, causing the pressure peak generated by the first collapse of the bubble to be much higher than that of the others. At a close stand-off distance, the liquid jet arrives before the first collapse, and there is a good correlation between the temperature and pressure peaks of the shock wave. Additionally, the pressure peaks formed by the liquid jet impinging upon the wall are also higher than those of the second bubble collapse.

During Stage ΙΙ (1.0 < γ< 1.7), the liquid jet pierces the upper and lower surfaces of the cavitation region and impacts the wall with a considerably reduced impact force, as is evident from the reduced pressure peaks. Due to the bubble moving toward the wall during the collapse stage, the bubble contacts the wall in the rebound stage, resulting in pressure peaks from the second collapse being higher than the other pressure peaks.

During Stage ΙΙΙ (1.7 ≤ γ < 2.5), the phenomenon of split bubbles begins to appear. Under the action of the liquid jet, a split bubble can be located close to the wall. Therefore, the pressure peak from the collapse of a split bubble is greater than those of the other conditions. However, as γ increases, the volume of the split bubble decreases rapidly, resulting in a rapid decrease in these pressure peaks. The temperature peaks resulting from the second collapse exhibit irregularities due to the dual role of the liquid jet on the aforementioned temperature field, as well as the short time interval between the jet impinging upon the wall and the second collapsing shock wave impacting the wall.

During Stage ΙV (2.5 ≤ γ), the jet no longer impacts the wall, and as the second collapse of the bubble occurs away from the wall itself, the pressure peaks caused by the first and second collapses are similar. When γ = 3.0, the shock wave from the split bubble collapse does not damage the wall owing to the large distance. Furthermore, the temperature and pressure peaks are similar.

The above analysis concerns the impact of the shock waves and liquid jets on the wall during the collapse of a multi-period cavitation bubble. First, it was found that both the impact of the shock wave produced at collapse and the liquid jet may cause damage to the wall, as is evident from the pressure peak curve, as shown in Figure 10a. The heat carried by the shock wave also increases the fluid temperature at the wall, while the liquid jet has a dual impact on the temperature changes at the wall. When γ is small, the jet carries the low-temperature fluid to occupy the high-temperature region, but when γ is large, the jet carries the high-temperature fluid to occupy the low-temperature region. Comparing the impacts of these two effects, the direct heating effect resulting from cavitation collapse on the wall is more severe; when the jet contacts the heated wall surface, it may cause hot spots. Moreover, when γ is small, the radial flow caused by the jet, as shown in Figure 4, promotes the annular movement of the bubble on the wall, further changing the temperature distribution on the wall.

4. Discussion: Energy Considerations during the Collapsing of Bubbles

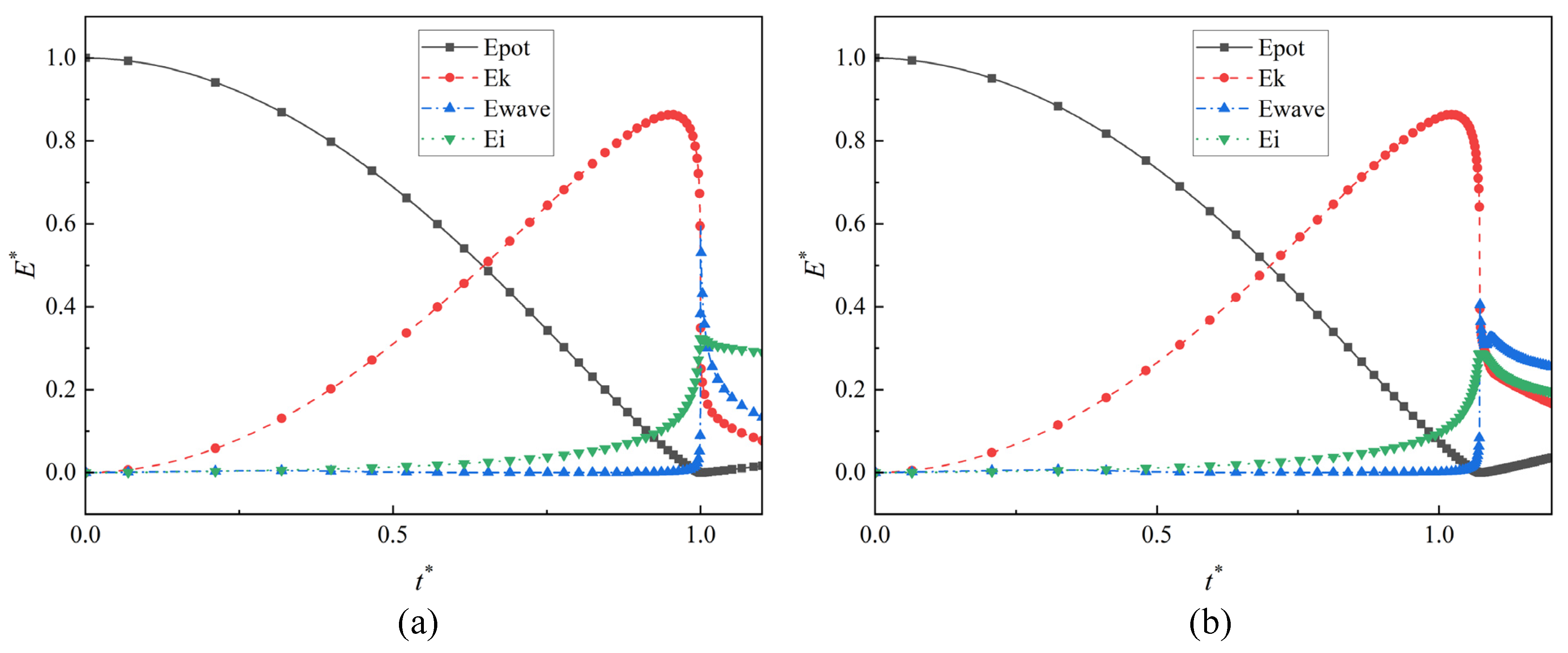
4.1. Transformation of Energy during the Collapsing of Bubbles

Figure 11 shows the histories of the energy components of the bubble system calculated using the proposed model. The potential, kinetic, acoustic, and internal energies of the bubble are shown. Figure 11a shows the far-field cavitation bubble-collapse process, whereas Figure 11b shows the case of bubble collapse when γ = 2.5, wherein all energies are normalized as $E^{*}=E^{*}/E_{pot,0}$, where $E_{pot,0}$ denotes the initial bubble potential energy. Combined with the dynamic bubble characteristics of the cases mentioned above, the energy transformation mechanism during the bubble collapse can be determined. During the bubble contraction stage, the initial potential energy of the bubble is continuously converted into the kinetic energy of the surrounding flow and the internal energy of the bubble. At the end of the contraction stage, a high-pressure area is formed near the bubble, and the kinetic energy of the surrounding flow accumulates in this region [33]. The kinetic energy decreases before the bubble collapses to its minimum volume. When the bubble collapses to its minimum volume, the bubble potential energy reaches its minimum value and the internal energy reaches its maximum value. Subsequently, most of the kinetic energy accumulated in the surrounding flow and the internal energy of the bubble are converted into acoustic wave energy and released. The remaining kinetic energy enters the next bubble cycle and repeats the pattern of the first cycle. Comparing Figure 11a,b, the energy transformation of the bubble collapse near the wall occurs later than the collapse in the far field. This is attributable to the delay caused by the wall during the collapse process of the cavitation bubble. For the same reason, the acoustic and internal energy generated by the bubble-collapse process in the far-field region is greater than those observed during bubble collapse occurring near the wall. This is detailed in the following sections.

4.2. Internal Energy

Figure 12 shows plots of the histories of the internal energy calculated using Equation (16), where Figure 12a shows the far-field cavitation bubble collapse and Figure 12b shows the case of bubble collapse when γ = 2.5. The three components of internal energy (i.e., the pressure work, phase change energy, and heat exchange) are represented using different colors. The internal energy is normalized as $\Delta E_i^{*}=\Delta E_i/E_{pot,0}$. Evidently, during the shrinking stage of the cavitation bubble, the surface of the bubble that is driven by external pressure continuously works on the compressible vapor within it, causing an increase in the temperature inside of the bubble. Because of the temperature difference between the bubble and ambient fluid, the bubble transfers heat to the surrounding fluid. After the bubble collapses to its minimum volume, the energy inside of the bubble is rapidly released in the form of a shock wave, which carries away heat, as described earlier, causing a decrease in the temperature within the bubble. Subsequently, the bubble begins to rebound under the influence of pressure as the internal pressure of the collapsed bubble is higher than the pressure of the surrounding fluid, which further reduces the temperature within the bubble. When the temperature is lower than that of the surrounding liquid, the surrounding liquid in turn transfers heat to the bubble. As the collapse of a bubble is more intense in the far-field region, more heat is exchanged from the surroundings to the bubble, as shown in Figure 12. After the bubble rebounds to its maximum volume, a new cycle begins. Considering the energy exchange resulting from the phase transition, the value of this term is insignificant both in the far-field region and the region near the wall compared with the other terms. This is because of the consideration of a single bubble in this study, and the region where the phase change occurs is located only at the interface between the bubble and liquid. Moreover, by comparing Figure 12a,b, it is evident that the order of magnitude of the energies in these systems is not the same and that in Figure 12a is much higher than in Figure 12b. This is because the collapsed bubble near the wall presents a more non-spherical and weaker energy focus, resulting in the collapse intensity not being as violent as that of the far-field case.

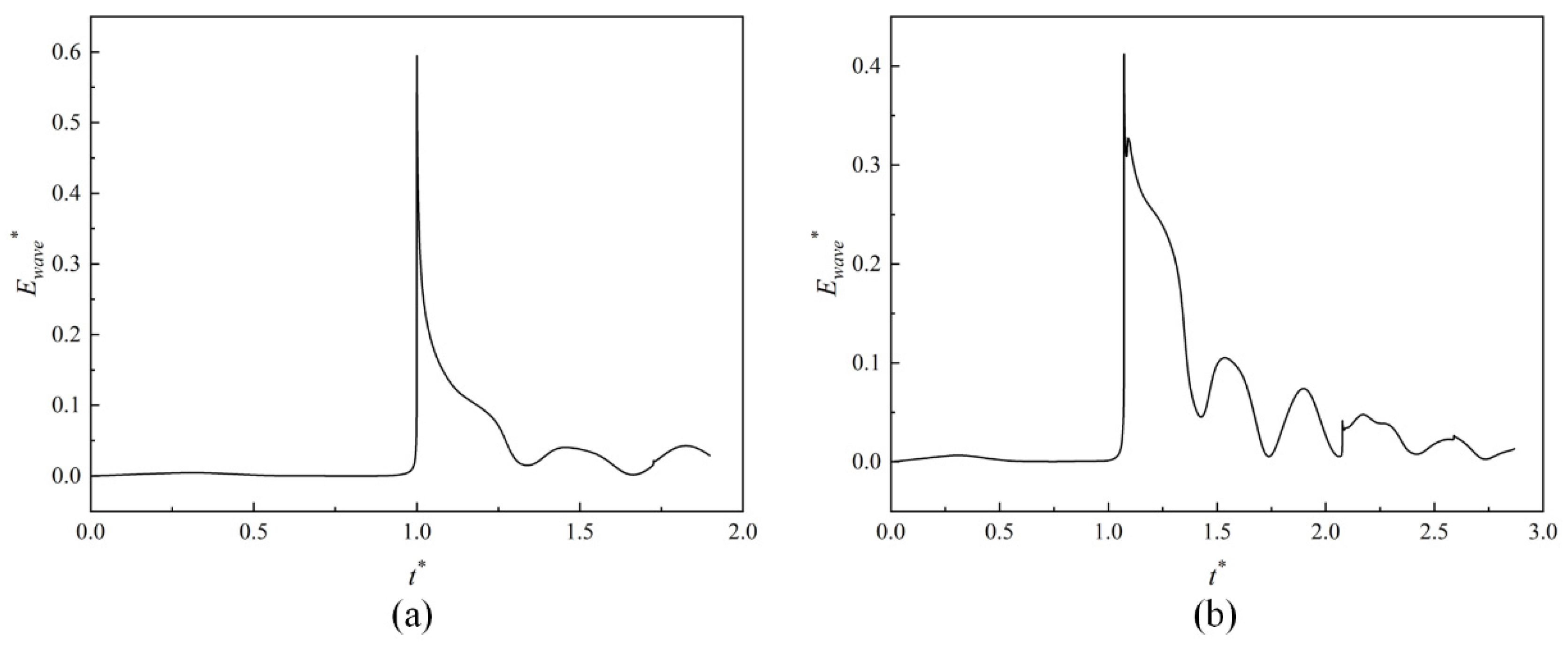
4.3. Acoustic Radiation Energy

Figure 13 shows the temporal evolution of the acoustic energy calculated using Equation (19). The far-field bubble collapse is shown in Figure 13a, and the near-wall bubble collapse is shown in Figure 13b. The peak of the far-field case is much higher than that near the wall, indicating that more initial potential energy is transformed into acoustic energy after the first bubble cycle in the far-field case, and the acoustic energy is then dissipated through the emitted shock wave. Consequently, the small initial potential energy exhibited upon entering the rebound stage results in a small bubble maximum rebound radius. Moreover, the acoustic energy curve near the wall has a softer downward trend that exhibits more fluctuations, as the presence of the wall both delays the collapse of the cavitation and reflects the shock wave, as mentioned earlier.

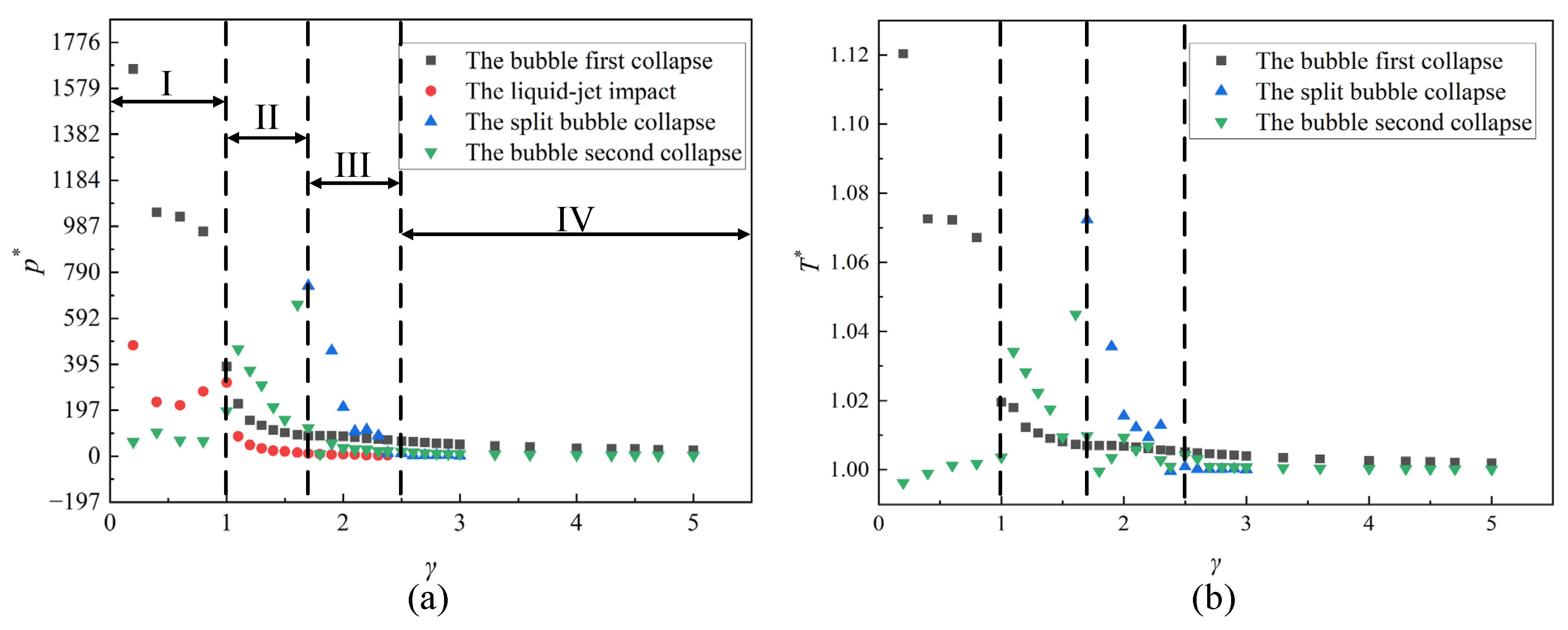
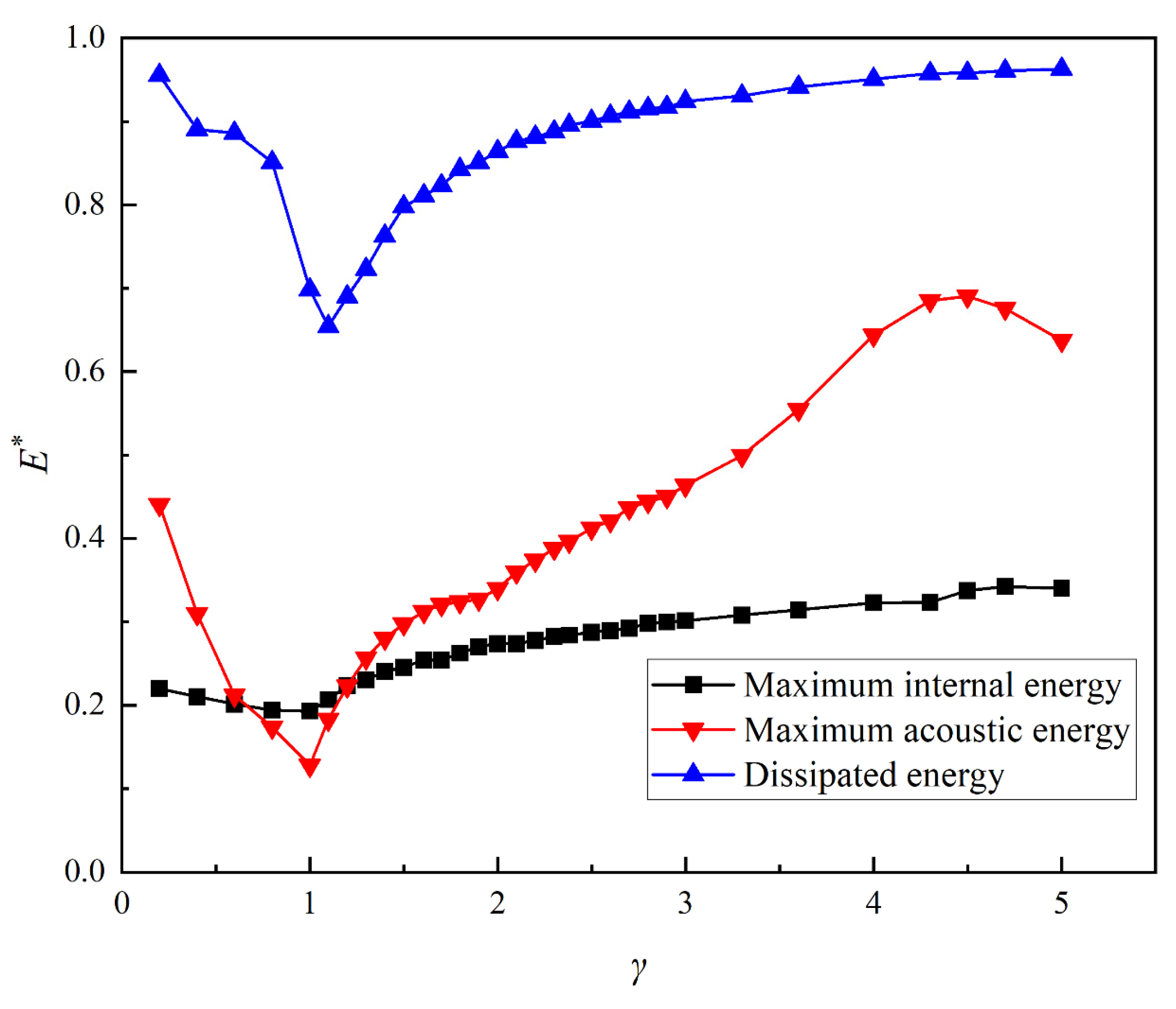
4.4. Influence of Different Stand-Off Distances on the Energy

The relationship between γ, the maximum internal energy, maximum acoustic energy, and dissipated energy can be further compared, as shown in Figure 14. Here, the maximum internal energy is obtained from the time integration before the bubble rebounds, the maximum acoustic energy refers to the acoustic energy emitted after the first bubble collapse, and the dissipated energy is calculated from the initial potential energy minus the maximum potential energy after the bubble rebounds. All three energies tend to decrease initially before increasing with increasing γ. When γ = 4.5, the maximum acoustic energy reaches its peak. There is a close correlation between the maximum internal energy and the maximum acoustic energy, wherein the larger the value of the maximum internal energy, the larger the value of the maximum acoustic energy.

Compared with Figure 9, the dissipated energy is proportional to the maximum temperature inside the bubble. A previous study obtained similar conclusions [19]. Additionally, by comparing the dissipated and maximum acoustic energies, it is observed that not all energy dissipated by the bubble is finally converted into acoustic energy. Acoustic energy dissipation is only a component of the total dissipated bubble energy, as the liquid jet that generates a shock wave removes some acoustic energy, and the viscosity-related shear flow enhances the energy loss. Moreover, some tiny bubbles may disappear directly into the liquid without continuing to collapse [21], which is a process that requires further investigation.

5. Conclusions

In this study, a compressible two-phase solver on OpenFOAM (version v2112) accounting for phase transitions and thermal effects was developed to examine bubble hydrodynamic and thermodynamic behaviors near a wall, as well as the energy transformation mechanism during bubble collapse. In particular, the internal bubble energy and acoustic energy were investigated. This system was validated by comparing the simulation results with analytical solutions and experiments involving the collapse of a single bubble. Furthermore, the bubble dynamics and energy were analyzed and discussed using different γ values. The main conclusions obtained from this study are as follows:

The impact of the shock wave increased the fluid temperature along the wall, whereas the impact of the liquid jet had a dual effect that depended on the initial stand-off distance between the cavitation bubble and the wall. When γ was small, the jet carried the low-temperature fluid to high-temperature regions, and when γ was large, the jet carried the high-temperature fluid to low-temperature regions. Additionally, compared with the aforementioned two mechanisms of elevated temperatures along the wall, the collapse of a cavitation bubble in contact with the wall increased the temperature of the fluid along the wall conspicuously.

The dynamics of bubble collapse near the wall with different γ values differed. Four stages were identified based on the pressure and temperature peaks at the center of the wall. Stage Ι (0 < γ ≤ 1.0) resulted in more energy loss in the first cycle, and the pressure peak generated by the first collapse process is higher than the others. Additionally, the pressure and temperature peaks produced by the shock wave agreed well under these conditions, and the maximum temperature inside the bubble decreased as γ increased. In Stage ΙΙ (1.0 < γ < 1.7), the pressure peak caused by the liquid jet was reduced as the jet had to penetrate the upper and lower surfaces of the bubble. The pressure and temperature peaks generated by the shock wave from the first and second bubble-collapse processes both decreased with increasing γ. In Stage ΙΙΙ (1.7 ≤ γ < 2.5), the phenomenon of the split bubble first appeared, and the pressure peaks caused by the split bubble dominated this process. Owing to the effect of the liquid jet, the temperature peak generated by the second collapse process of the bubble was disordered. In Stage ΙV (2.5 ≤ γ), the jet no longer contacted the wall, and the pressure peaks from the first and second bubble-collapse processes were similar. When 3.0 < γ, the shock wave from the split bubble collapsed and did not reach the wall.

A novel energy transformation mechanism considering the internal bubble energy was proposed, and the time-varying curves of the internal bubble energy and acoustic energy were quantitatively analyzed. The influence of γ on the energy was further examined, and the results revealed that the internal bubble energy and acoustic energy were closely related. The more internal energy the cavitation bubble converted during the energy transformation process, the more energy was dissipated through acoustic energy.

This study primarily focused on single bubbles. In the future, we will investigate the hydrodynamic behavior and thermodynamic effect of the collapse of multiple cavitation bubbles near a rigid boundary, as the interaction between bubbles is an important consideration in cavitation bubble research.