Testing and Modeling of Vehicle Li-Ion Battery Module with Prismatic Cells under Abuse Conditions
Abstract
:1. Introduction
2. Battery Module
3. Experimental Procedure
4. Numerical Model
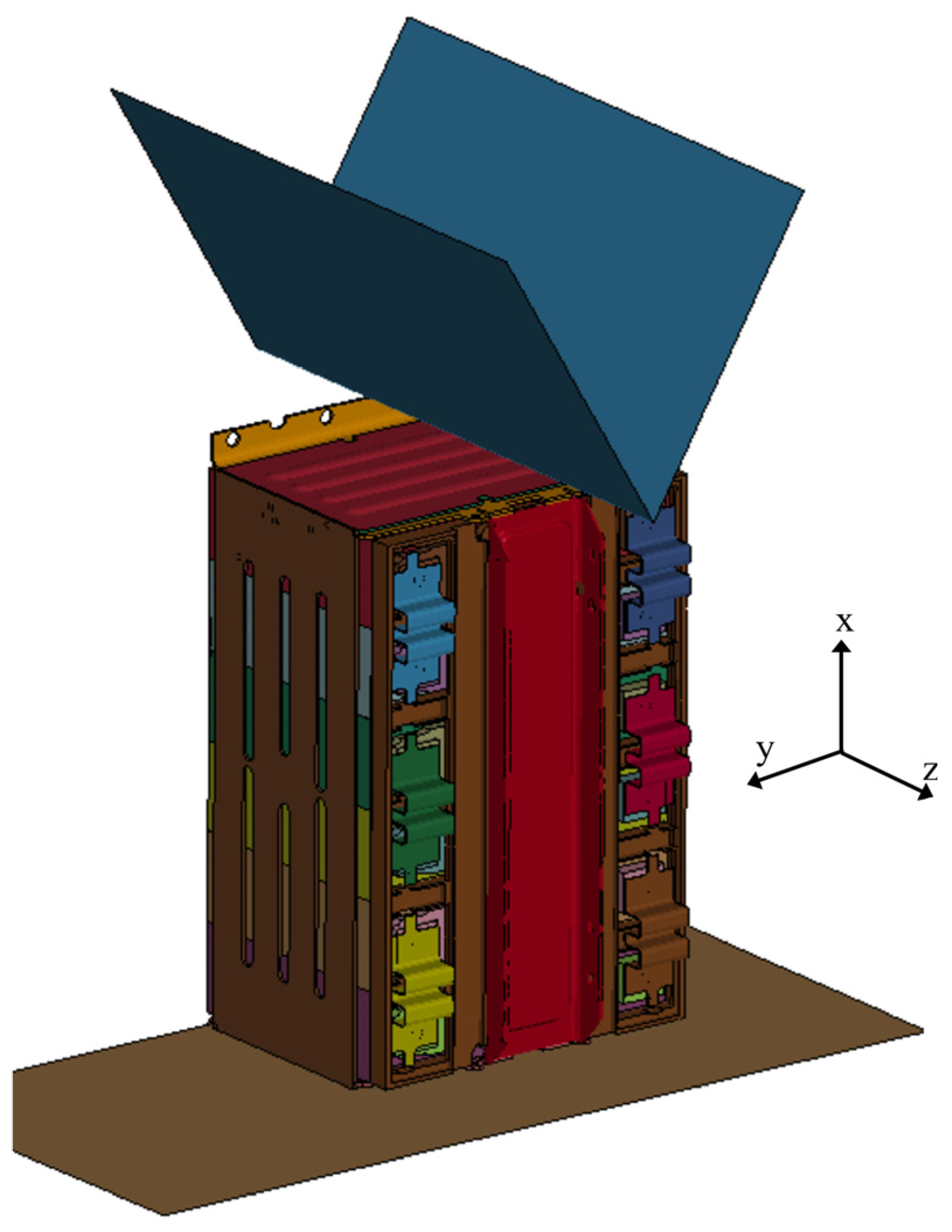
4.1. Parts Geometry Modeling
4.2. Boundary Conditions and Contacts
4.3. Material Models
5. Experimental Results and Numerical Model Comparison
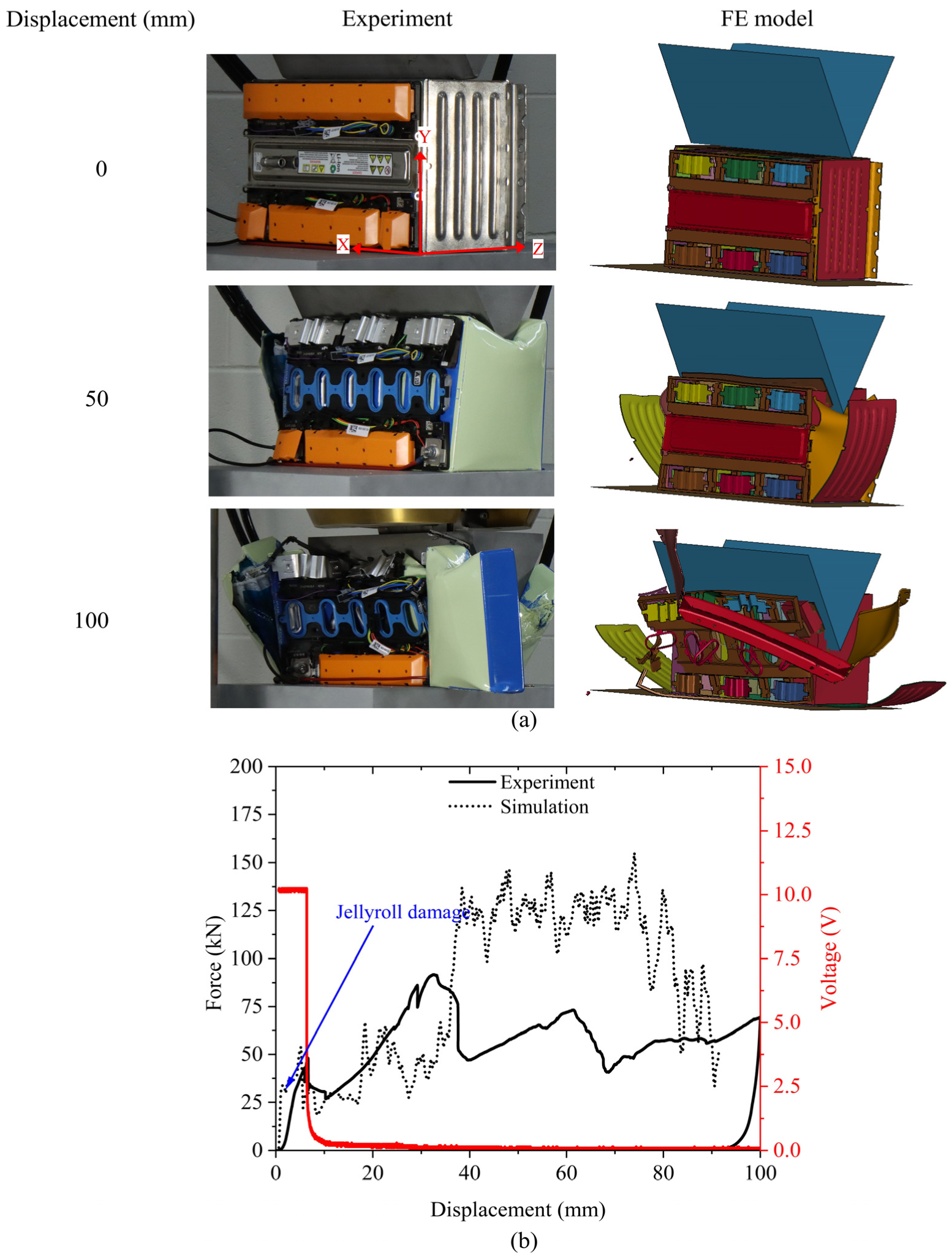
5.1. Case 1
5.2. Case 2
5.3. Case 3
5.4. Case 1H
6. Discussion
6.1. Energy Absorption of Individual Parts
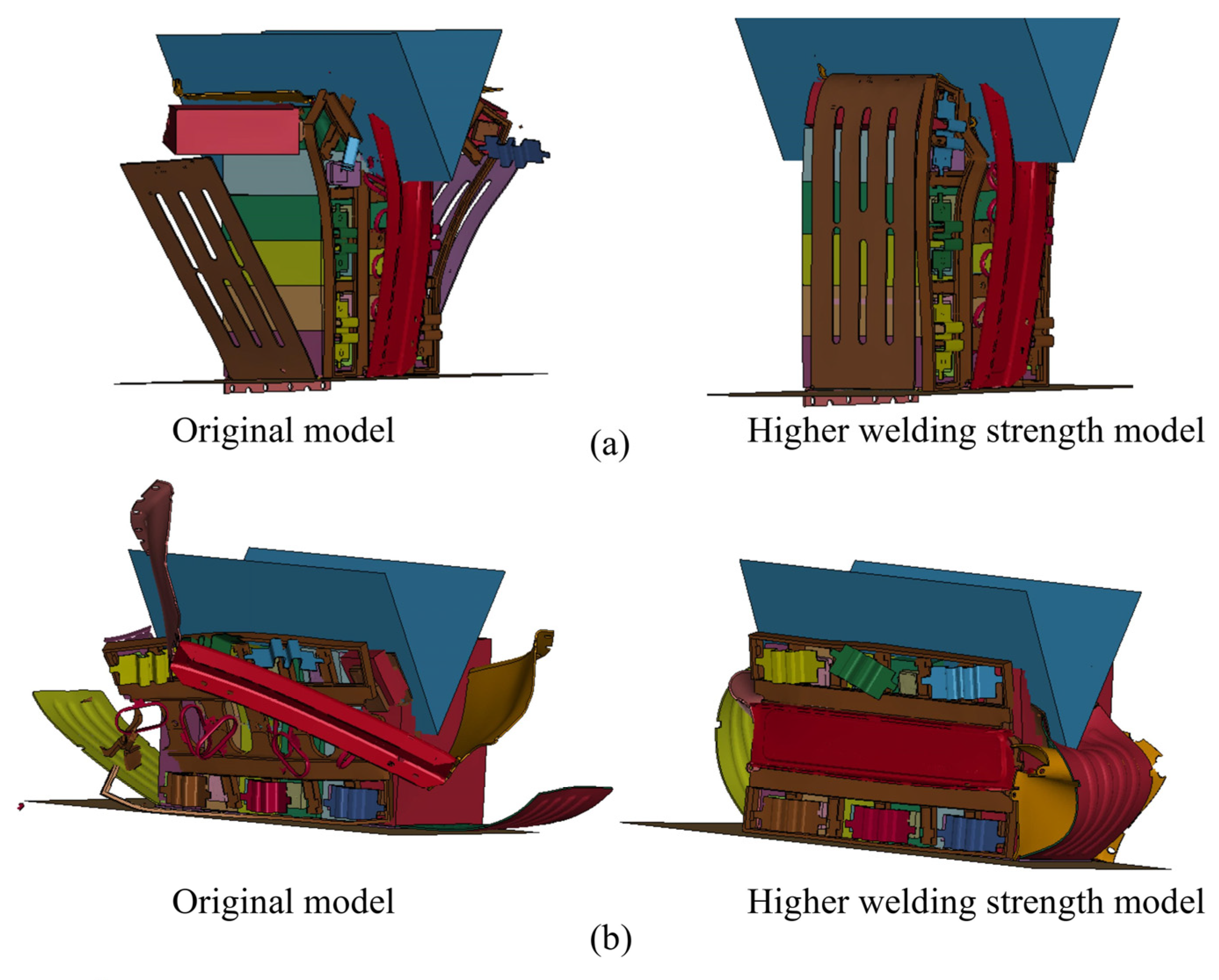
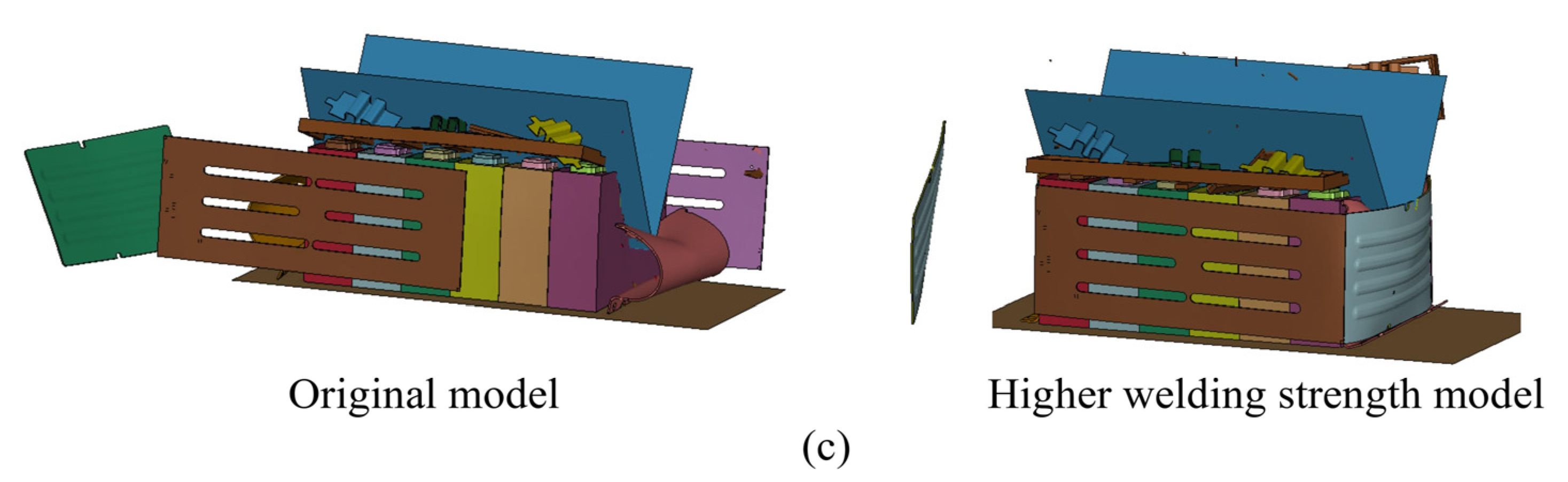
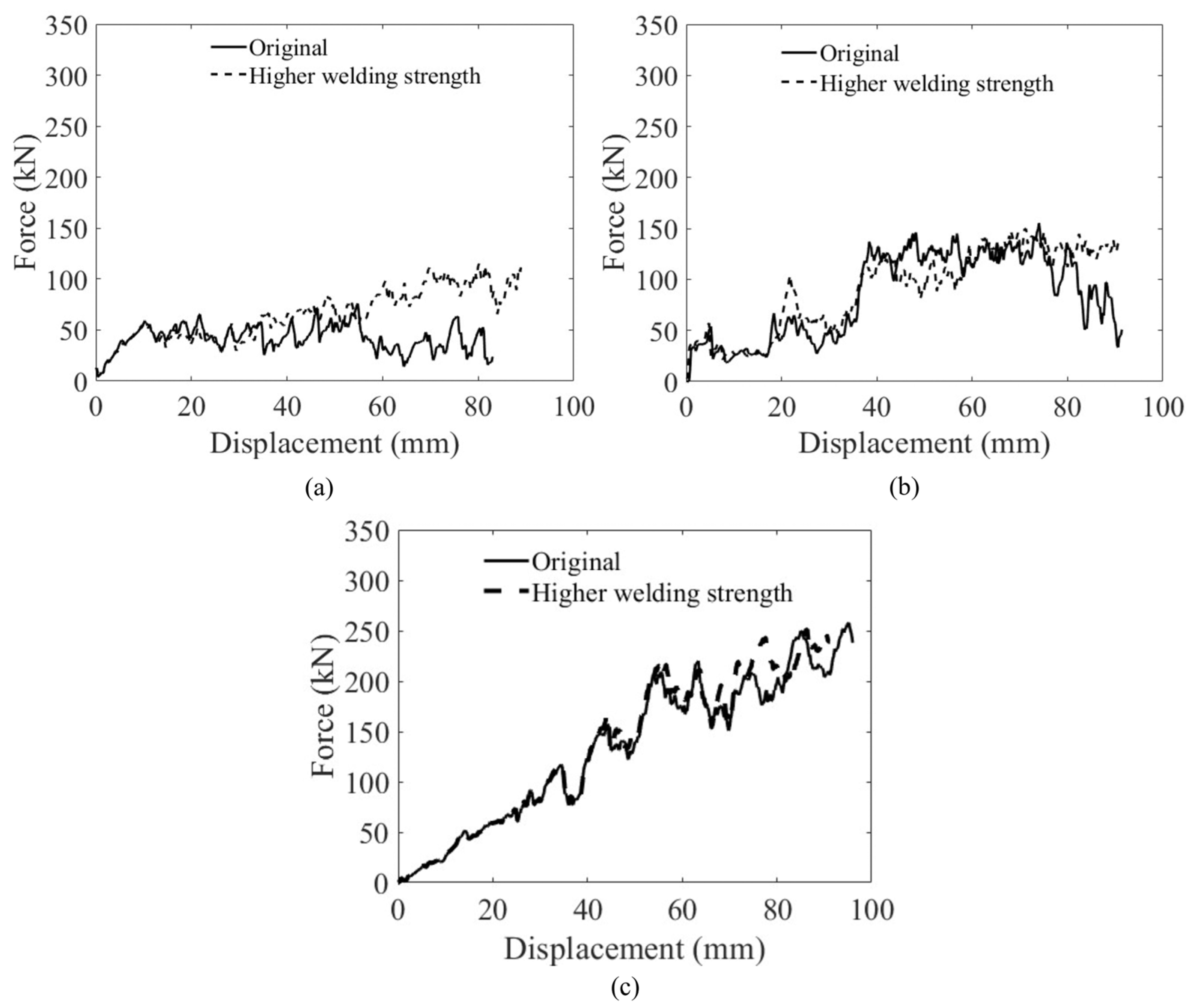
6.2. Effect of Welding Strength
6.3. Summary and Safety Design Consideration
- Indentation along y and z directions could cause immediate large voltage drop because all of the cells can be subjected to deformation nearly simultaneously. As observed during the experiment, Case 2, bulging of the cells can be facilitated due to generation of gases at low voltage within the cells. This can become a source of fire during a crash.
- The presence of a sidewall mounting bracket and side plates provides protection for impact along x direction compared to y direction. The effective thickness of the stainless-steel plates between the wedge and cells along x direction is 2.3 mm. However, the side plates between the wedge and cells along y direction are merely 0.7 mm thick. Better energy absorption might be observed by increasing their thickness.
- As discussed in Section 5.2, improving the weld-failure strain connecting the stainless-steel side plates can improve the energy absorbed by the protective structure, but does not bring much change regarding initiation of short-circuiting.
- Replacing the monolithic cover plate with sandwich structures with two metal face sheets and a low-density core material like foam could improve the safety of the battery module. The sandwich cover plates could significantly reduce the peak impact force and delay the short circuit. A detailed discussion on this design can be seen in Zhu and Logakannan [28].
7. Outlook
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, B.; Jia, Y.; Yuan, C.; Wang, L.; Gao, X.; Yin, S.; Xu, J. Safety Issues and Mechanisms of Lithium-Ion Battery Cell upon Mechanical Abusive Loading: A Review. Energy Storage Mater. 2020, 24, 85–112. [Google Scholar] [CrossRef]
- Sahraei, E.; Hill, R.; Wierzbicki, T. Calibration and Finite Element Simulation of Pouch Lithium-Ion Batteries for Mechanical Integrity. J. Power Sources 2012, 201, 307–321. [Google Scholar] [CrossRef]
- Wang, H.; Kumar, A.; Simunovic, S.; Allu, S.; Kalnaus, S.; Turner, J.A.; Helmers, J.C.; Rules, E.T.; Winchester, C.S.; Gorney, P. Progressive Mechanical Indentation of Large-Format Li-Ion Cells. J. Power Sources 2017, 341, 156–164. [Google Scholar] [CrossRef] [Green Version]
- Chung, S.H.; Tancogne-Dejean, T.; Zhu, J.; Luo, H.; Wierzbicki, T. Failure in Lithium-Ion Batteries under Transverse Indentation Loading. J. Power Sources 2018, 389, 148–159. [Google Scholar] [CrossRef]
- Zhu, J.; Luo, H.; Li, W.; Gao, T.; Xia, Y.; Wierzbicki, T. Mechanism of Strengthening of Battery Resistance under Dynamic Loading. Int. J. Impact Eng. 2019, 131, 78–84. [Google Scholar] [CrossRef]
- Kisters, T.; Kuder, J.; Töpel, A.; Langkemper, R.; Nau, S.; Schopferer, S. Strain-Rate Dependence of the Failure Behavior of Lithium-Ion Pouch Cells under Impact Loading. J. Energy Storage 2021, 41, 102901. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Grolleau, V.; Mohr, D. Strain Rate Dependent Plasticity of Lithium-Ion Pouch Cells: Experiments and Simulations. Int. J. Impact Eng. 2022, 159, 104048. [Google Scholar] [CrossRef]
- Zhu, F.; Zhou, R.; Sypeck, D.; Deng, J.; Bae, C. Failure Behavior of Prismatic Li-Ion Battery Cells under Abuse Loading Condition–A Combined Experimental and Computational Study. J. Energy Storage 2022, 48, 103969. [Google Scholar] [CrossRef]
- Deng, J.; Smith, I.; Bae, C.; Rairigh, P.; Miller, T.; Surampudi, B.; L’Eplattenier, P.; Caldichoury, I. Impact Modeling and Testing of Pouch and Prismatic Cells. J. Electrochem. Soc. 2020, 167, 090550. [Google Scholar] [CrossRef]
- Kotter, P.; Kisters, T.; Schleicher, A. Dynamic Impact Tests to Characterize the Crashworthiness of Large-Format Lithium-Ion Cells. J. Energy Storage 2019, 26, 100948. [Google Scholar] [CrossRef]
- Chen, X.; Wang, T.; Zhang, Y.; Ji, H.; Ji, Y.; Yuan, Q. Dynamic Mechanical Behavior of Prismatic Lithium-ion Battery upon Impact. Int. J. Energy Res. 2019, 43, 7421–7432. [Google Scholar] [CrossRef]
- Kalnaus, S.; Wang, Y.; Turner, J.A. Mechanical Behavior and Failure Mechanisms of Li-Ion Battery Separators. J. Power Sources 2017, 348, 255–263. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Wang, L.; Guan, J.; Yin, S. Coupled Effect of Strain Rate and Solvent on Dynamic Mechanical Behaviors of Separators in Lithium Ion Batteries. Mater. Des. 2016, 95, 319–328. [Google Scholar] [CrossRef]
- Zhu, J.; Li, W.; Wierzbicki, T.; Xia, Y.; Harding, J. Deformation and Failure of Lithium-Ion Batteries Treated as a Discrete Layered Structure. Int. J. Plast. 2019, 121, 293–311. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, J.; Cao, L.; Wu, Z.; Santhanagopalan, S. Constitutive Behavior and Progressive Mechanical Failure of Electrodes in Lithium-Ion Batteries. J. Power Sources 2017, 357, 126–137. [Google Scholar] [CrossRef]
- Duan, X.; Wang, H.; Jia, Y.; Wang, L.; Liu, B.; Xu, J. A Multiphysics Understanding of Internal Short Circuit Mechanisms in Lithium-Ion Batteries upon Mechanical Stress Abuse. Energy Storage Mater. 2022, 45, 667–679. [Google Scholar] [CrossRef]
- Lee, D.-C.; Kim, C.-W. Two-Way Nonlinear Mechanical-Electrochemical-Thermal Coupled Analysis Method to Predict Thermal Runaway of Lithium-Ion Battery Cells Caused by Quasi-Static Indentation. J. Power Sources 2020, 475, 228678. [Google Scholar] [CrossRef]
- Zhou, M.; Hu, L.; Chen, S.; Zhao, X. Different Mechanical-Electrochemical Coupled Failure Mechanism and Safety Evaluation of Lithium-Ion Pouch Cells under Dynamic and Quasi-Static Mechanical Abuse. J. Power Sources 2021, 497, 229897. [Google Scholar] [CrossRef]
- Yiding, L.; Wenwei, W.; Cheng, L.; Xiaoguang, Y.; Fenghao, Z. Multi-Physics Safety Model Based on Structure Damage for Lithium-Ion Battery under Mechanical Abuse. J. Clean. Prod. 2020, 277, 124094. [Google Scholar] [CrossRef]
- Zhu, J.; Wierzbicki, T.; Li, W. A Review of Safety-Focused Mechanical Modeling of Commercial Lithium-Ion Batteries. J. Power Sources 2018, 378, 153–168. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, G.; Zhou, Q.; Shi, X.; Shi, F. Failure Behaviours of 100% SOC Lithium-Ion Battery Modules under Different Impact Loading Conditions. Eng. Fail. Anal. 2017, 82, 149–160. [Google Scholar] [CrossRef]
- Kalnaus, S.; Wang, H.; Watkins, T.R.; Simunovic, S.; Sengupta, A. Features of Mechanical Behavior of EV Battery Modules under High Deformation Rate. Extrem. Mech. Lett. 2019, 32, 100550. [Google Scholar] [CrossRef]
- Zhu, F.; Du, X.; Lei, J.; Audisio, L.; Sypeck, D. Experimental Study on the Crushing Behaviour of Lithium-Ion Battery Modules. Int. J. Crashworthiness 2021, 26, 598–607. [Google Scholar] [CrossRef]
- Deng, J.; Smith, I.; Bae, C.; Rairigh, P.; Miller, T.; Surampudi, B. Communication—Impact Behaviors of Pouch and Prismatic Battery Modules. J. Electrochem. Soc. 2021, 168, 020520. [Google Scholar] [CrossRef]
- Deng, J.; Bae, C.; Miller, T.; L’Eplattenier, P.; Bateau-Meyer, S. Accelerate Battery Safety Simulations Using Composite Tshell Elements. J. Electrochem. Soc. 2018, 165, A3067–A3076. [Google Scholar] [CrossRef]
- Logakannan, K.P.; Zhu, F.; Speck, D.; Deng, J.; Kim, S. Dynamic Indentation of Prismatic Li-Ion Battery Cells. Proc. Mater. Today Proc. 2022; under review. [Google Scholar]
- Jia, S.; Tan, Q.; Ye, J.; Zhu, Z.; Jiang, Z. Experiments on Dynamic Mechanical Properties of Austenitic Stainless Steel S30408 and S31608. J. Constr. Steel Res. 2021, 179, 106556. [Google Scholar] [CrossRef]
- Zhu, F.; Logakannan, K. Crash Safety Design for Lithium-Ion Vehicle Battery Module with Machine Learning. SAE Int. J. Adv. Curr. Prac. Mobil. 2022, 4, 1667–1677. [Google Scholar] [CrossRef]






| Case | Wedge Indentation Orientation | Wedge Edge Orientation | Actuator Speed (mm/s) | Initial Photograph |
|---|---|---|---|---|
| 1 | x | parallel to z | 0.05 |  |
| 2 | y | parallel to x | 0.05 |  |
| 3 | z | parallel to x | 0.05 |  |
| 1H | x | parallel to z | 50 |  |
| Part Number | Part Name | Material Model | Element Type | Element Size (mm) | Number of Elements |
|---|---|---|---|---|---|
| 1 | C-section beam | MAT_024 | Tetra | 0.021~5.04 | 66,641 |
| 2 | Sidewall mounting brackets | MAT_024 | Hex | 0.513~2.68 | 14,813 |
| 3 | Side plates | MAT_024 | Hex | 0.102~2.81 | 29,112 |
| 4 | Cell covers | MAT_099 | Hex | 0.377~21.58 | 17,988 |
| 5 | Jellyrolls | MAT_063 | Hex | 1.45~12.21 | 58,488 |
| 6 | Plastic parts | MAT_024 | Hex | 0.01~2.71 | 65,781 |
| 7 | Bus bars | MAT_024 | Hex | 0.6~1.88 | 4428 |
| Stainless Steel | Plastic | Enclosure Material |
|---|---|---|
| Young’s modulus = 180 GPa Poisson’s ratio = 0.28 Yield strength = 250 MPa Tangent modulus = 5 GPa For dynamic loading: C = 0.9/ms P = 4.6 | Young’s modulus = 7 GPa Poisson’s ratio = 0.35 Yield strength = 40 MPa Tangent modulus = 0.15 GPa | Young’s modulus = 52 GPa Poisson’s ratio = 0.33 A = 0.12 GPa B = 0.156 GPa C = 0 n = 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Logakannan, K.P.; Zhu, F.; Sypeck, D.; Xu, S.; Deng, J.; Kim, S. Testing and Modeling of Vehicle Li-Ion Battery Module with Prismatic Cells under Abuse Conditions. Energies 2023, 16, 1055. https://doi.org/10.3390/en16031055
Logakannan KP, Zhu F, Sypeck D, Xu S, Deng J, Kim S. Testing and Modeling of Vehicle Li-Ion Battery Module with Prismatic Cells under Abuse Conditions. Energies. 2023; 16(3):1055. https://doi.org/10.3390/en16031055
Chicago/Turabian StyleLogakannan, Krishna Prasath, Feng Zhu, David Sypeck, Sida Xu, Jie Deng, and Sangyeon Kim. 2023. "Testing and Modeling of Vehicle Li-Ion Battery Module with Prismatic Cells under Abuse Conditions" Energies 16, no. 3: 1055. https://doi.org/10.3390/en16031055
APA StyleLogakannan, K. P., Zhu, F., Sypeck, D., Xu, S., Deng, J., & Kim, S. (2023). Testing and Modeling of Vehicle Li-Ion Battery Module with Prismatic Cells under Abuse Conditions. Energies, 16(3), 1055. https://doi.org/10.3390/en16031055








