High-Precision Switched Capacitor Device with an Energy Estimation Circuit
Abstract
:1. Introduction
2. Switched Capacitor Device
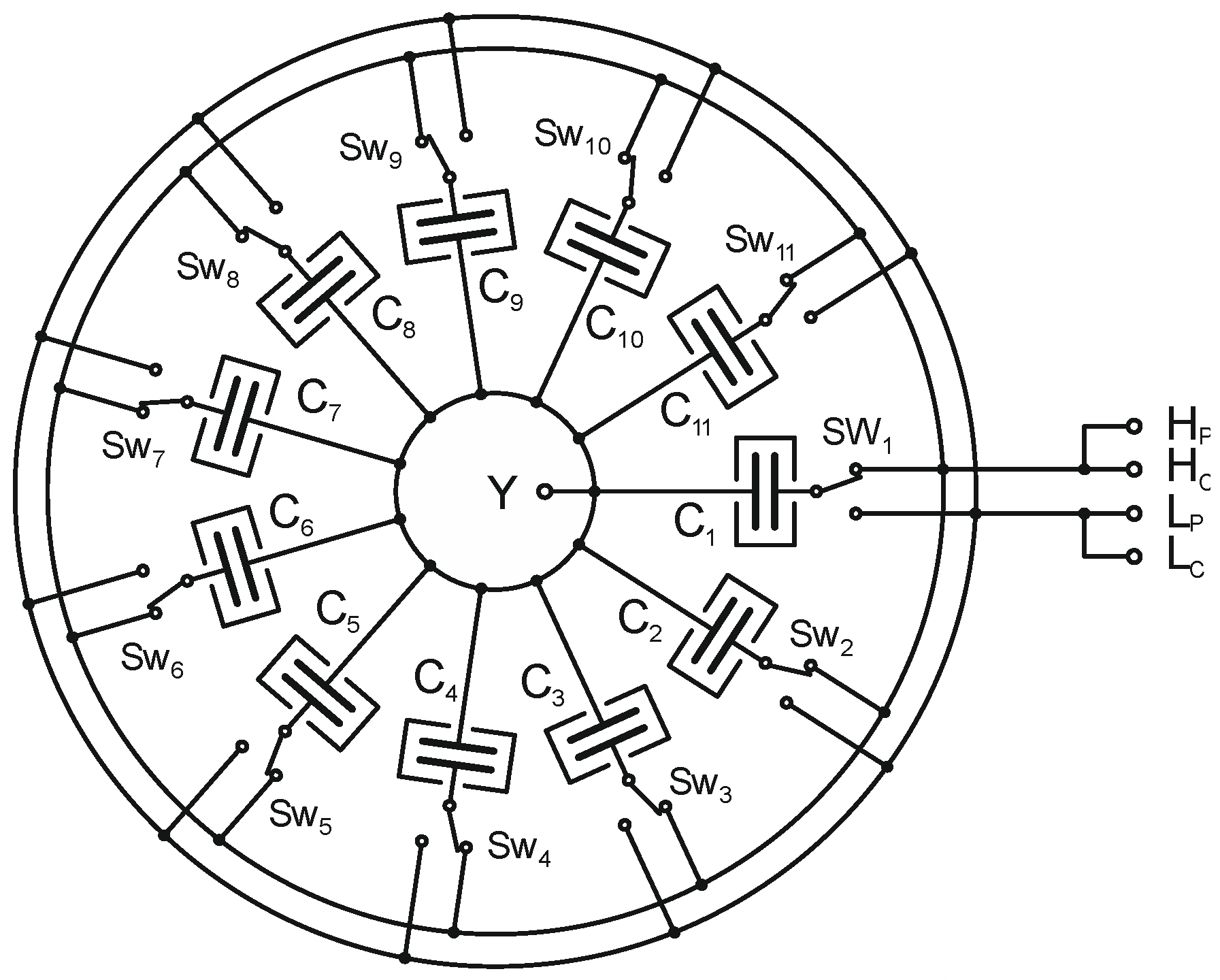
2.1. Device Concept
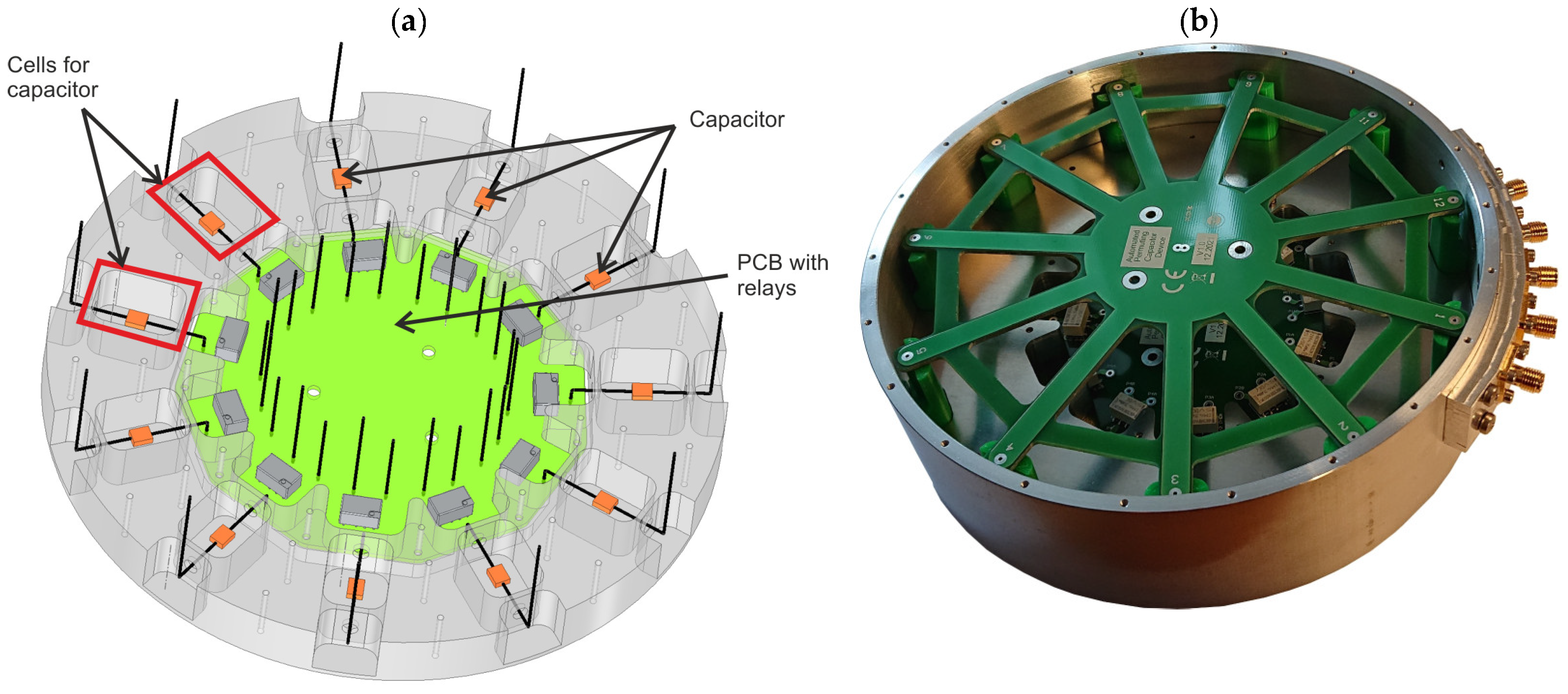
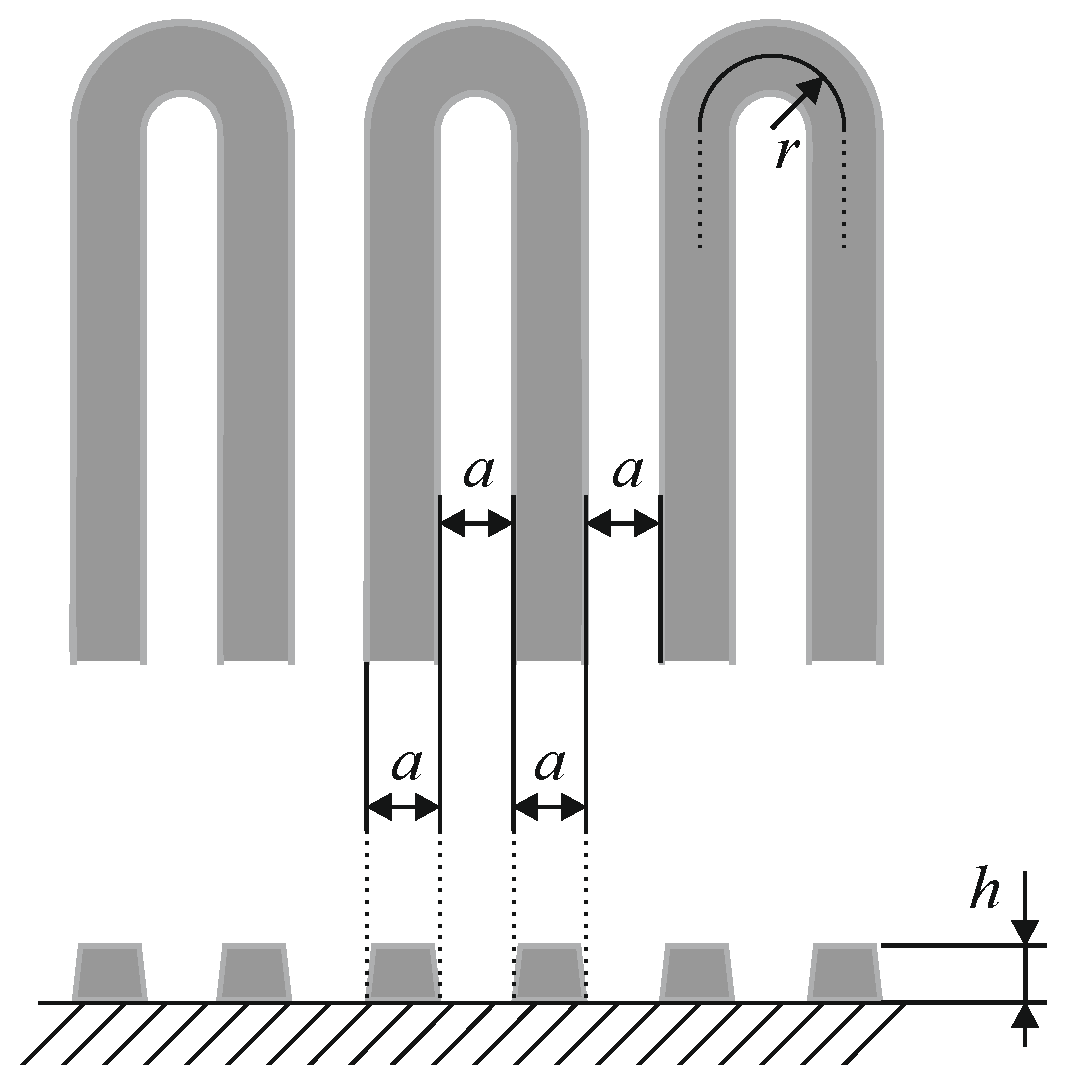
2.2. Construction of the SCM
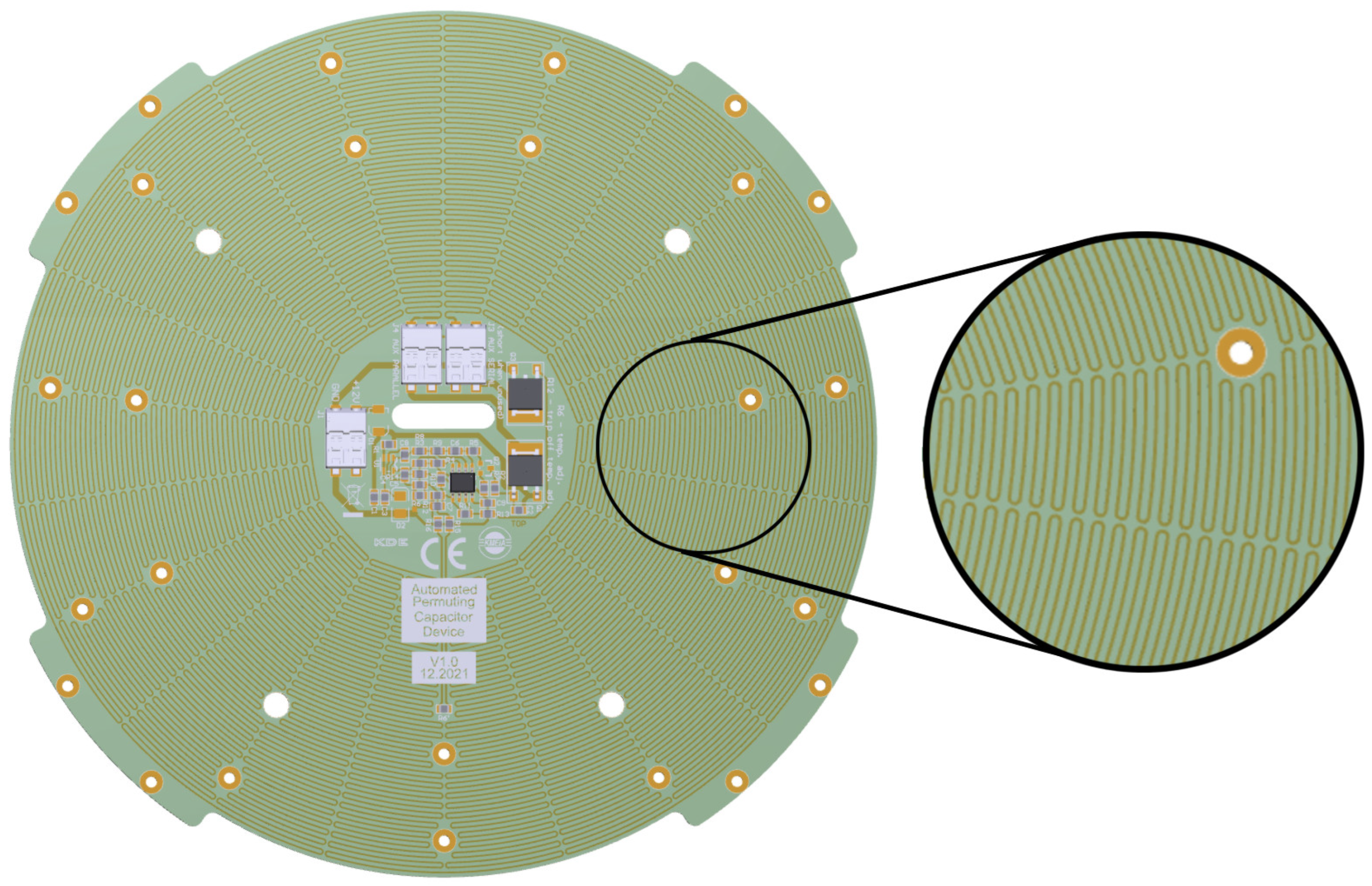
2.3. Relay Controller
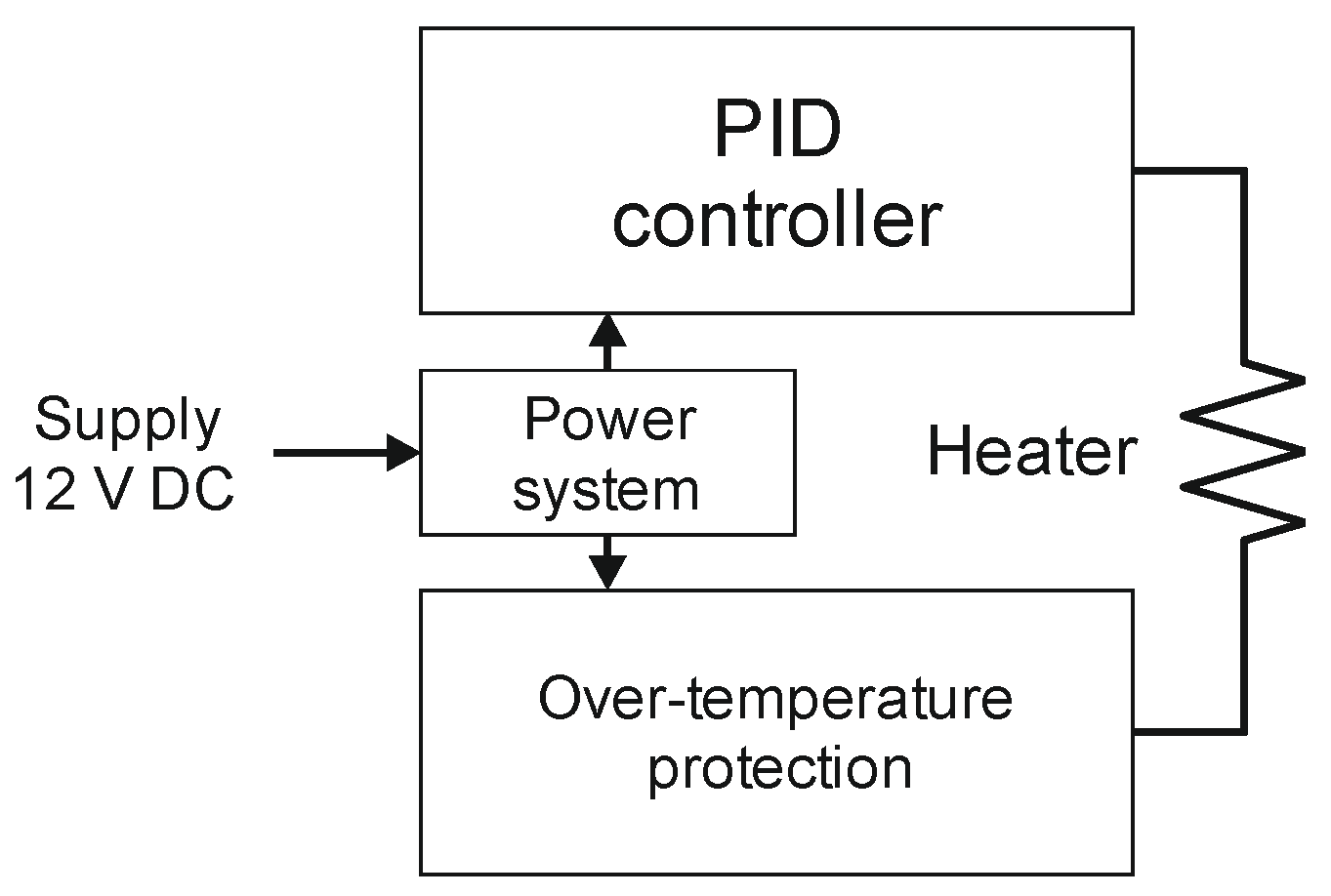
2.4. The Temperature-Stabilization System
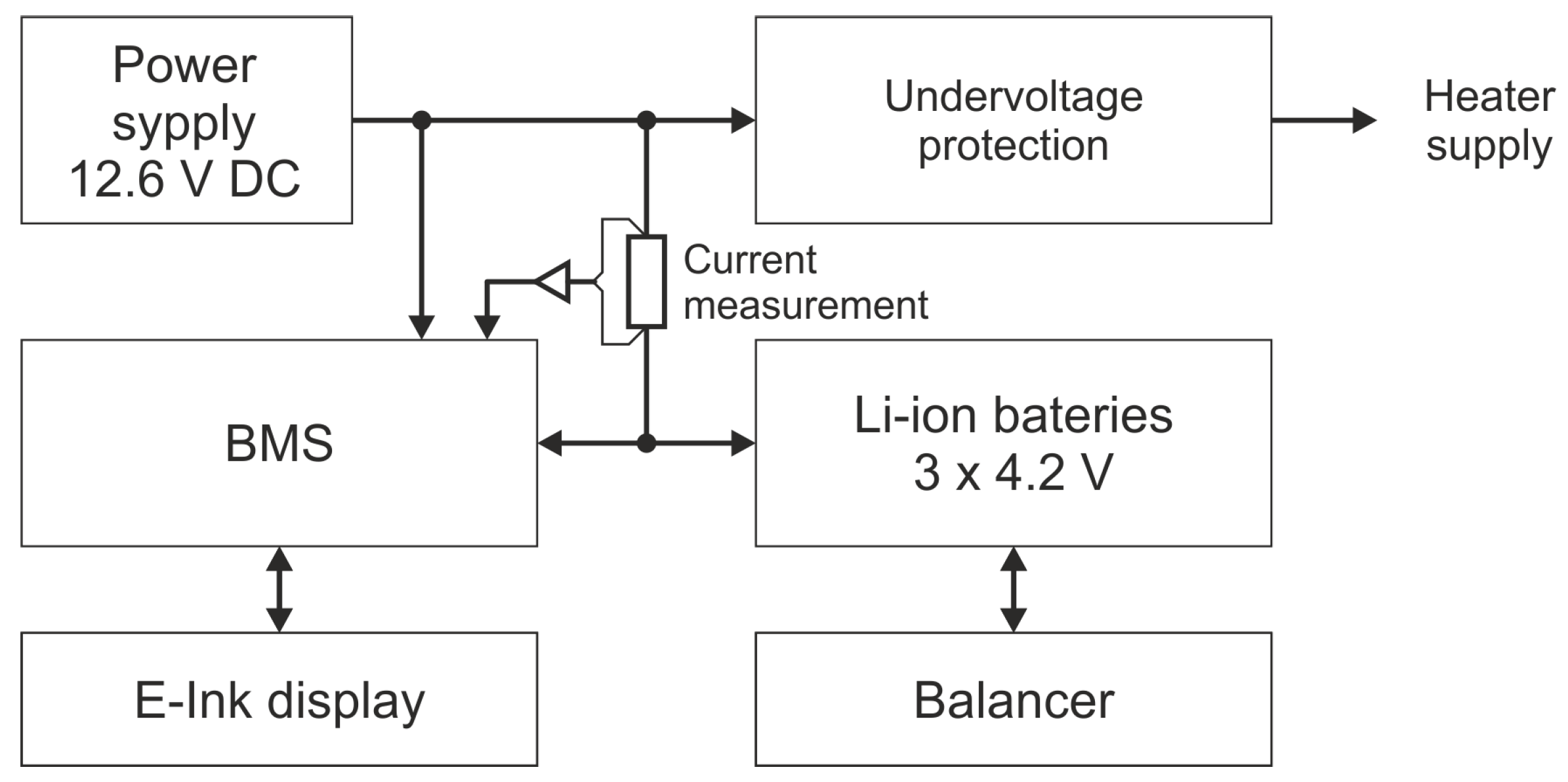
2.5. Power Supply—BMS and Power Setup
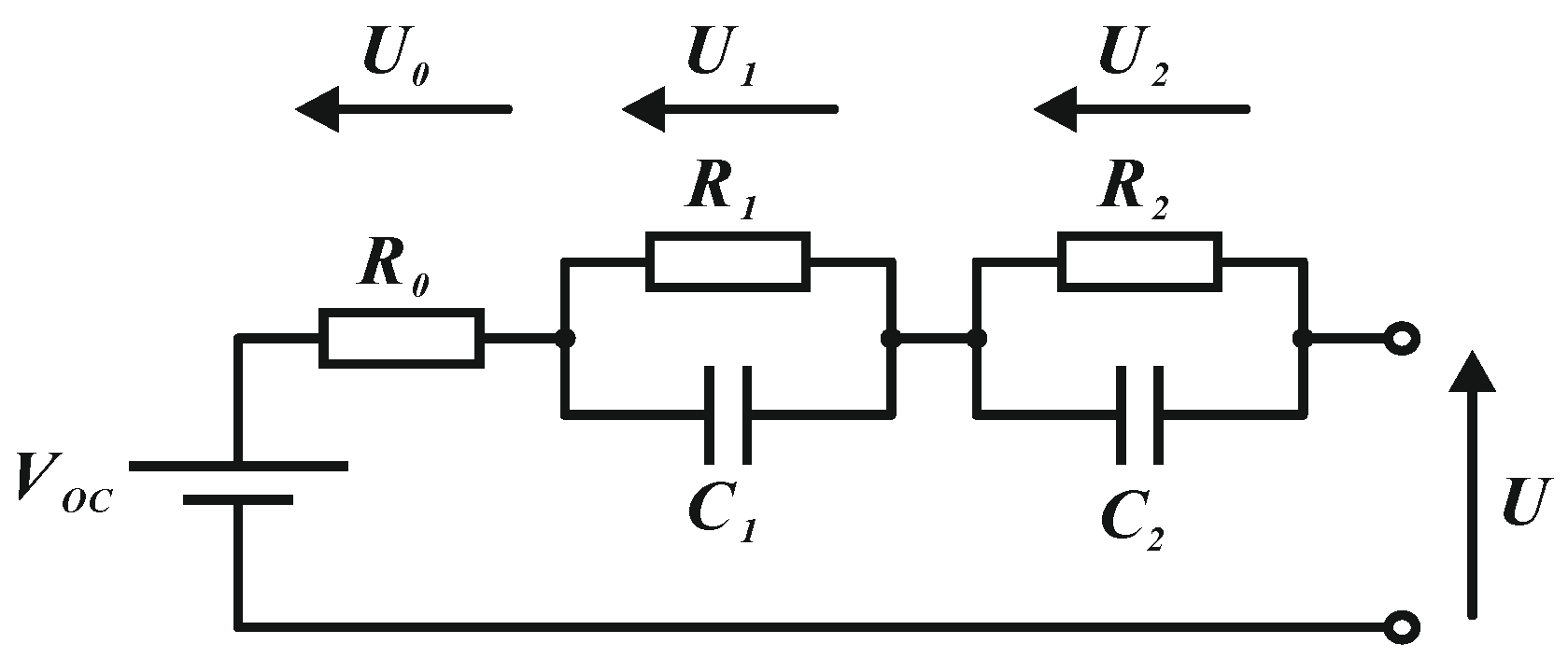
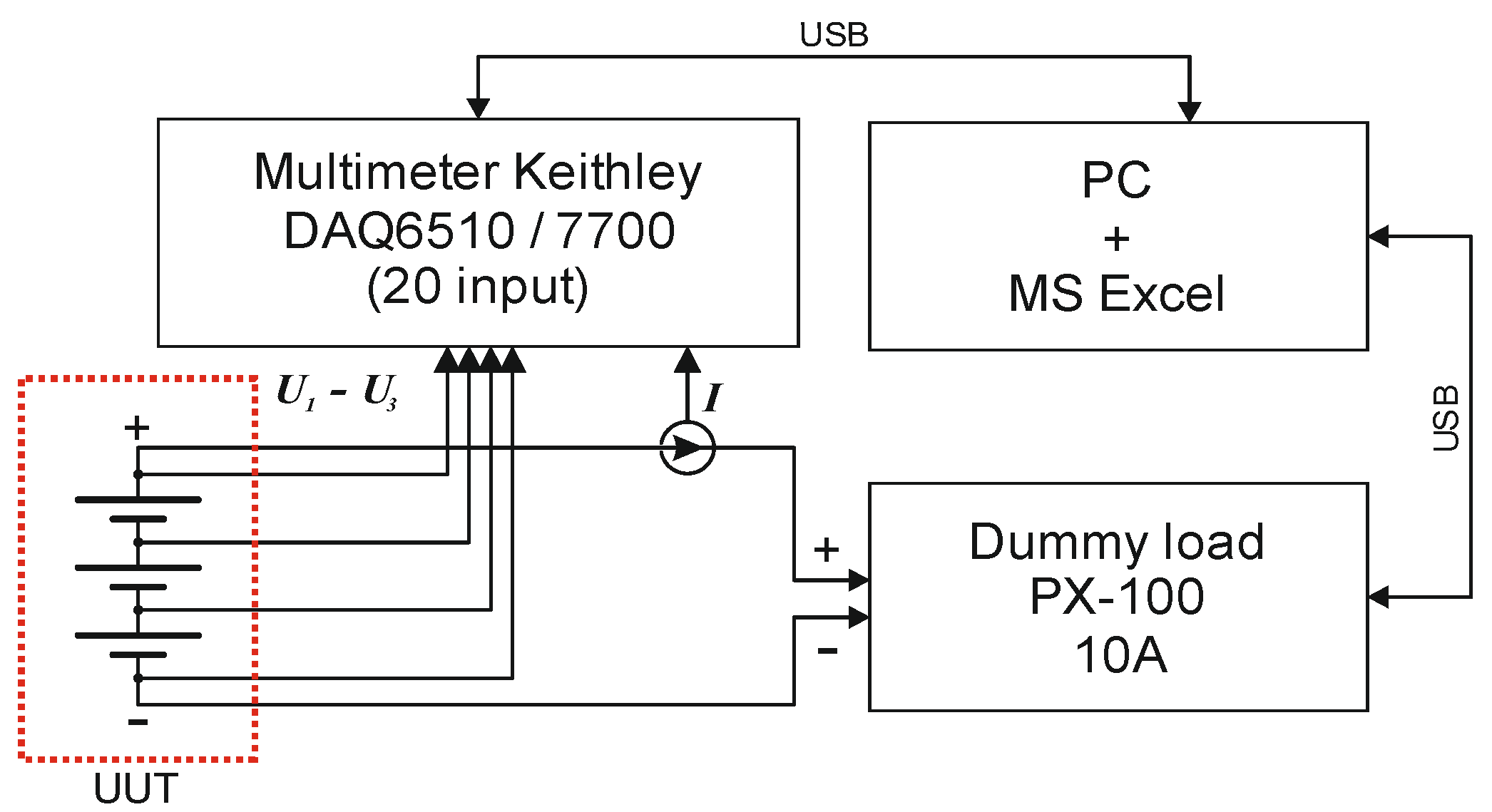
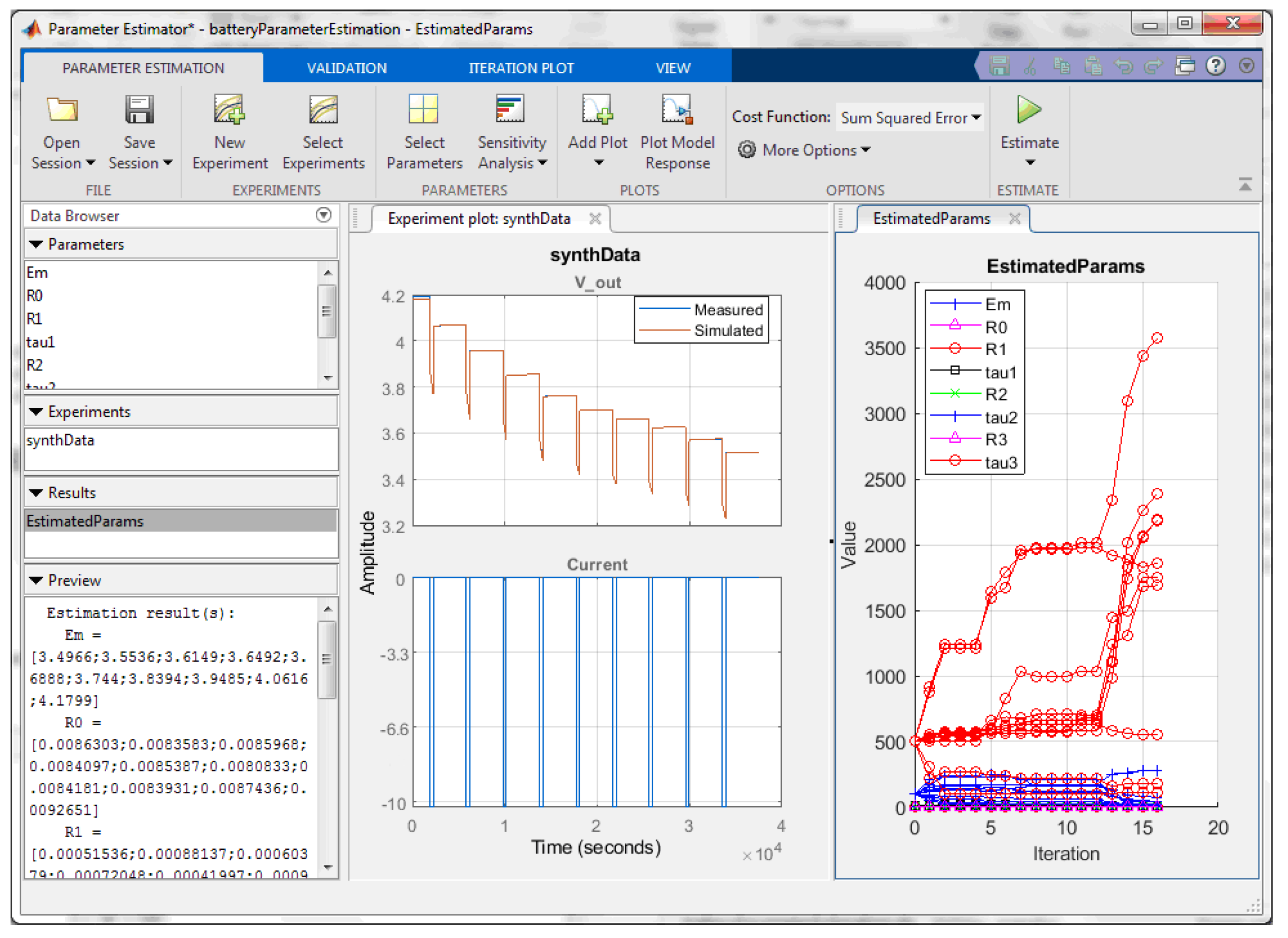
Battery Energy Estimation Algorithm
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Overney, F.; Flowers-Jacobs, N.E.; Jeanneret, B.; Rüfenacht, A.; Fox, A.E.; Dresselhaus, P.D.; Benz, S.P. Dual Josephson impedance bridge: Towards a universal bridge for impedance metrology. Metrologia 2020, 57, 065014. [Google Scholar] [CrossRef]
- Overney, F.; Flowers-Jacobs, N.E.; Jeanneret, B.; Rüfenacht, A.; Fox, A.E.; Underwood, J.M.; Koffman, A.D.; Benz, S.P. Josephson-based full digital bridge for high-accuracy impedance comparisons. Metrologia 2016, 53, 1045–1053. [Google Scholar] [CrossRef]
- Callegaro, L.; D’Elia, V.; Kampik, M.; Kim, D.B.; Ortolano, M.; Pourdanesh, F. Ngoc Thanh Mai Tran, Experiences with a two terminal-pair digital impedance bridge. IEEE Trans. Instrum. Meas. 2015, 64, 1460–1465. [Google Scholar] [CrossRef] [Green Version]
- Miroslaw, M.; Kaczmarek, J.; Rybski, R. Characterization of PXI-Based Generators for Impedance Measurement Setups. IEEE Trans. Instrum. Meas. 2019, 68, 1806–1813. [Google Scholar] [CrossRef]
- Kučera, J.; Kováč, J. A reconfigurable four terminal-pair digitally assisted and fully digital impedance ratio bridge. IEEE Trans. Instrum. Meas. 2018, 67, 1199–1206. [Google Scholar] [CrossRef]
- Ortolano, M.; Palafox, L.; Kucera, J.; Callegaro, L.; D’Elia, V.; Marzano, M.; Overney, F.; Gulmez, G. An international comparison of phase angle standards between the novel impedance bridges of CMI, INRIM and METAS. Metrologia 2018, 55, 499–512. [Google Scholar] [CrossRef] [Green Version]
- Mašláň, S.; Šíra, M.; Skalická, T.; Bergsten, T. Four-Terminal Pair Digital Sampling Impedance Bridge up to 1 MHz. IEEE Trans. Instrum. Meas. 2019, 68, 1860–1869. [Google Scholar] [CrossRef]
- Overney, F.; Jeanneret, B. RLC Bridge based on an Automated Synchronous Sampling System. IEEE Trans. Instrum. Meas. 2011, 60, 2393–2398. [Google Scholar] [CrossRef]
- Musioł, K.; Kampik, M.; Koszarny, M. A new sampling based four-terminal-pair digital impedance bridge. Meas. Sens. 2021, 18, 100307. [Google Scholar] [CrossRef]
- Musioł, K.; Kampik, M. Metrological triangles in impedance comparisons. Measurement 2019, 148, 106908. [Google Scholar] [CrossRef]
- Musioł, K.; Kampik, M. Investigations of the high-performance source of digitally synthesized sinusoidal voltage for primary impedance metrology. Measurement 2021, 168, 108308. [Google Scholar]
- Awan, S.; Kibble, B.; Schurr, J. Coaxial Electrical Circuits for Interference-Free Measurements (Electrical Measurement); IET: Edison, NJ, USA, 2010. [Google Scholar]
- Rybski, R.; Kaczmarek, J.; Koziol, M. A PXI-Based Calibration System for Low-Value AC Resistors. IEEE Trans. Instrum. Meas. 2018, 67, 905–911. [Google Scholar] [CrossRef]
- Rybski, R.; Kaczmarek, J.; Koziol, M. A High-Resolution PXI Digitizer for a Low-Value-Resistor Calibration System. IEEE Trans. Instrum. Meas. 2013, 62, 1783–1788. [Google Scholar] [CrossRef]
- Musioł, K.; Kampik, M. Calibration of PXI Data Acquisition Cards Used for Primary Impedance Metrology; Measurement systems in theory and practice; University of Zielona Góra: Zielna Góra, Poland, 2020; pp. 159–171. [Google Scholar]
- Ortolano, M.; Marzano, M.; D’Elia, V.; Tran, N.T.M.; Rybski, R.; Kaczmarek, J.; Koziol, M.; Musiol, K.; Christensen, A.E.; Callegaro, L.; et al. A Comprehensive Analysis of Error Sources in Electronic Fully Digital Impedance Bridges. IEEE Trans. Instrum. Meas. 2020, 70, 1–14. [Google Scholar] [CrossRef]
- Ortolano, M.; Marzano, M.; D’Elia, V.; Tran, N.T.M.; Rybski, R.; Kaczmarek, J.; Kozioł, M.; Musioł, K.; Christensen, A.; Pokatilov, A.; et al. Error sources in electronic fully-digital impedance bridges. In Proceedings of the 2020 Conference on Precision Electromagnetic Measurements (CPEM), Denver, CO, USA, 24–28 August 2020; pp. 1–2. [Google Scholar]
- Hsu, J.; Gong, J.; Huang, C. An automated permuting capacitor device for calibration of IVDs. IEEE Trans. Instrum. Meas. 2014, 63, 2271–2278. [Google Scholar] [CrossRef]
- Waltrip, B. A Programmable Capacitor for Inductance Measurements. IEEE Trans. Instrum. Meas. 2017, 66, 1572–1578. [Google Scholar] [CrossRef]
- Cutkosky, R.D.; Shields, J.Q. The Precision Measurement of Transformer Ratios. IRE Trans. Instrum. 1960, 9, 243–250. [Google Scholar] [CrossRef]
- Tran, N.T.M.; D’Elia, V.; Callegaro, L.; Ortolano, M. A Capacitance Build-up Method to Determine LCR Meter Errors and Capacitance Transfer. IEEE Trans. Instrum. Meas. 2020, 69, 5727–5735. [Google Scholar] [CrossRef]
- Musioł, K. Experimental Study of Digitizers Used in High-Precision Impedance Measurements. Energies 2022, 15, 4051. [Google Scholar] [CrossRef]
- IET Labs. 1482 Specification. Available online: https://www.ietlabs.com/pdf/Datasheets/1482.pdf (accessed on 28 September 2022).
- Guo, Y.; Zhao, Z.; Huang, L. SoC Estimation of Lithium Battery Based on AEKF Algorithm. In Proceedings of the 8th International Conference on Applied Energy, ICAE2016, Beijing, China, 8–11 October 2016. [Google Scholar]
- Pang, H.; Zhang, F. Experimental Data-Driven Parameter Identification and State of Charge Estimation for a Li-Ion Battery Equivalent Circuit Model. Energies 2018, 11, 1033. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- Charkhgard, M.; Farrokhi, M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF. IEEE Trans. Ind. Electron. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- Taborelli, C.; Onori, S. State of charge estimation using extended Kalman filters for battery management system. In Proceedings of the IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014; pp. 1–8. [Google Scholar]




| Item | Capacitance C pF | Dissipation Factor tgδ × 10−5 |
|---|---|---|
| 1 | 101.40 | 5.5 |
| 2 | 101.40 | 5.4 |
| 3 | 101.40 | 5.2 |
| 4 | 101.42 | 5.6 |
| 5 | 101.43 | 5.1 |
| 6 | 101.43 | 5.7 |
| 7 | 101.44 | 6.1 |
| 8 | 101.45 | 5.5 |
| 9 | 101.46 | 5.8 |
| 10 | 101.47 | 6.0 |
| 11 | 101.48 | 5.7 |
| Length of the Meander (mm) | Path Width a (mm) | Projected (Desired) Resistance (Ω) | Measured (Real) Resistance (Ω) | Relative Error of the Resistance (%) |
|---|---|---|---|---|
| 10,611.4 | 0.254 | 20.4 | 27.1 | 33% |
| 14,045.2 | 0.18 | 38.0 | 54.5 | 43% |
| 19,774.5 | 0.31 | 31.1 | 42.8 | 38% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musioł, K.; Dudzik, K.; Kampik, M. High-Precision Switched Capacitor Device with an Energy Estimation Circuit. Energies 2023, 16, 1086. https://doi.org/10.3390/en16031086
Musioł K, Dudzik K, Kampik M. High-Precision Switched Capacitor Device with an Energy Estimation Circuit. Energies. 2023; 16(3):1086. https://doi.org/10.3390/en16031086
Chicago/Turabian StyleMusioł, Krzysztof, Kordian Dudzik, and Marian Kampik. 2023. "High-Precision Switched Capacitor Device with an Energy Estimation Circuit" Energies 16, no. 3: 1086. https://doi.org/10.3390/en16031086
APA StyleMusioł, K., Dudzik, K., & Kampik, M. (2023). High-Precision Switched Capacitor Device with an Energy Estimation Circuit. Energies, 16(3), 1086. https://doi.org/10.3390/en16031086







