The Flow of a Thermo Nanofluid Thin Film Inside an Unsteady Stretching Sheet with a Heat Flux Effect
Abstract
:1. Introduction
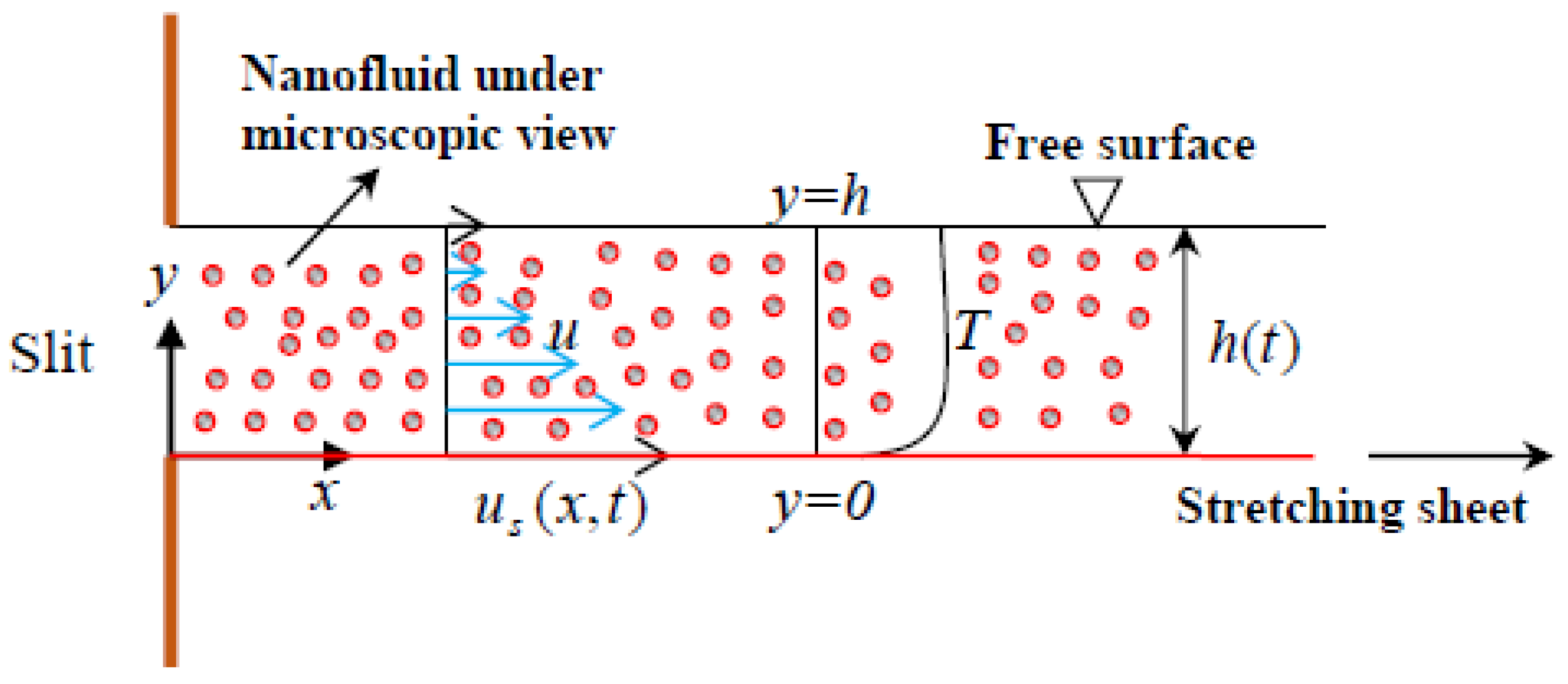
2. Flow Analysis
3. Engineering and Industrial Quantities
4. Methodology
- when
- when
5. Validation of the Numerical Solution
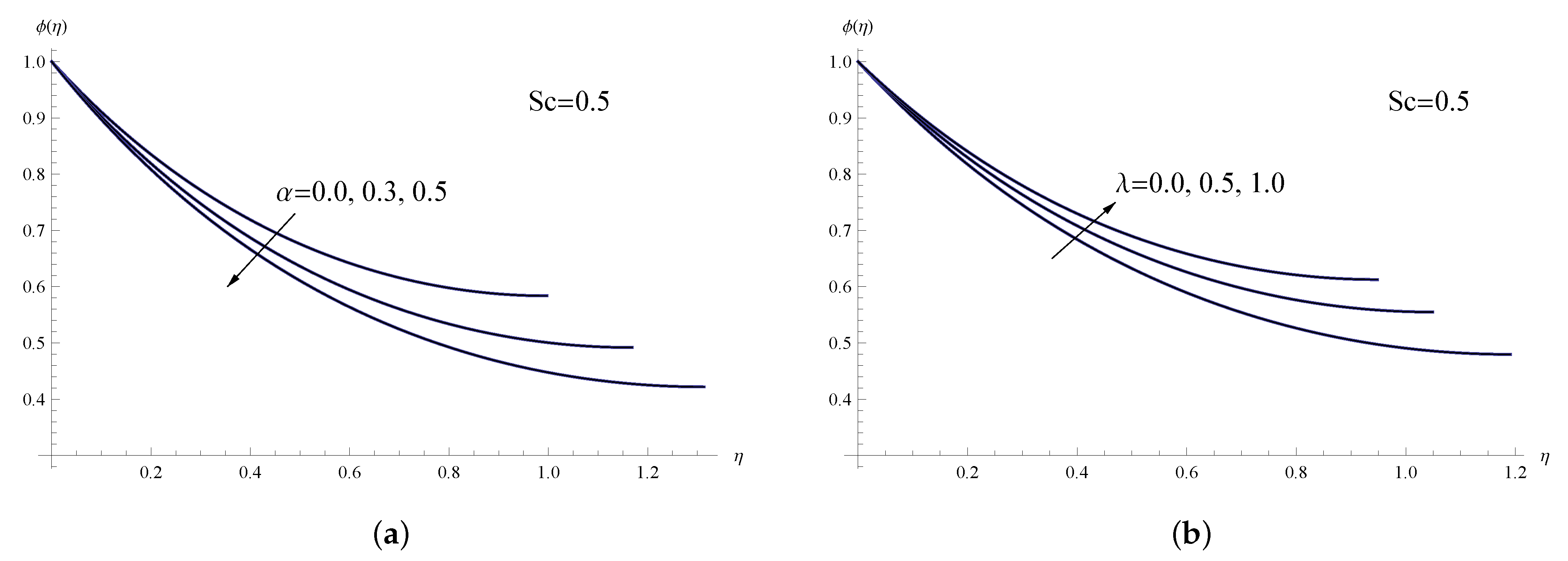
6. Interpretation of Numerical Results
7. Conclusions
- It is possible to greatly improve the nanofluid thin film’s thickness by using higher viscoelastic parameter values and lower unsteadiness and porous parameter values.
- The local skin-friction coefficient, heat transfer rate, and nanofluid temperature all increase as the porous parameter is increased, but the Sherwood number exhibits the opposite tendency.
- It is feasible to successfully accomplish the best nanoparticle arrangement within the viscoelastic nanofluid liquid thin film by raising the porous parameter and the thermophoresis parameter, and decreasing the Brownian motion parameter.
- The skin-friction coefficient, the rate of surface heat transfer, and the rate of mass transfer can all be significantly enhanced by employing higher values of the unsteadiness parameter and the viscoelastic parameter.
- As the thermal conductivity parameter and the thermal radiation increase, the temperature distribution and sheet temperature are both reduced.
- Improvements in the thermal conductivity and radiation parameters cause the local Nusselt and Sherwood numbers to rise, but increases in the thermophoresis parameter cause the former two to decrease.
- It is possible to use this kind of problem to enhance the industrial technology’s mass and heat-transmission mechanism.
- In the future, we intend to expand on this research by analyzing how variable mass flux and variable density affect the flow properties through porous media regulated by the modified Darcy law.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | is a constant () |
| b | is a constant () |
| C | concentration () |
| concentration at slit () | |
| reference concentration () | |
| nanofluid concentration along the sheet () | |
| specific heat () | |
| local skin friction coefficient | |
| coefficient of thermophoresis diffusion () | |
| coefficient of Brownian diffusion () | |
| f | dimensionless stream function |
| h | film thickness (m) |
| k | permeability of porous medium () |
| coefficient of mean absorption () | |
| Brownian motion parameter | |
| local Nusselt number | |
| thermophoresis parameter | |
| Prandtl number | |
| radiative heat flux () | |
| variable heat flux () | |
| R | radiation parameter |
| local Reynolds number | |
| S | unsteadiness parameter |
| Schmidt number | |
| local Sherwood number | |
| t | time (s) |
| T | nanofluid temperature (K) |
| temperature at slit (K) | |
| reference temperature (K) | |
| u | velocity component in the direction () |
| fluid velocity at the sheet () | |
| v | velocity component in the direction () |
| Cartesian coordinates (m) | |
| Greek symbols | |
| Stefan–Boltzmann constant () | |
| density of nanofluid () | |
| kinematic viscosity () | |
| thermal conductivity parameter | |
| heat capacity of nanoparticles in relation to heat capacity of basic fluid () | |
| the thermal conductivity at the slit () | |
| thermal conductivity () | |
| the local viscoelastic parameter | |
| material parameter of the viscoelastic fluid () | |
| coefficient of viscosity () | |
| dimensionless concentration | |
| dimensionless temperature | |
| similarity variable | |
| the porous parameter | |
| the dimensionless film thickness | |
| Superscripts | |
| ′ | differentiation with respect to |
References
- Andersson, H.I.; Aarseth, J.B.; Braud, N.; Dandapat, B.S. Flow of a power-law fluid film on an unsteady stretching surface. J. Non-Newtonian Fluid Mech. 1996, 62, 1–8. [Google Scholar] [CrossRef]
- Wang, C.; Pop, I. Analysis of the flow of a power-law fluid film on an unsteady stretching surface by means of homotopy analysis method. J. Non-Newtonian Fluid Mech. 2006, 138, 161–172. [Google Scholar] [CrossRef]
- Abbas, Z.; Hayat, T.; Sajid, M.; Asghar, S. Unsteady flow of a second grade fluid film over an unsteady stretching sheet. Math. Comput. Model. 2008, 48, 518–526. [Google Scholar] [CrossRef]
- Wang, C.Y. Liquid film on an unsteady stretching surface. Q. Appl. Math. 1990, 48, 601–610. [Google Scholar] [CrossRef] [Green Version]
- Choi, U.S. Enhancing thermal conductivity of fluids with nanoparticles. ASME FED 1995, 231, 99–103. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Mass Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D.; Farooq, U. Mixed convective flow of Maxwell nanofluid past a porous vertical stretched surface—An optimal solution. Results Phys. 2016, 6, 1072–1079. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.; Azam, M.; Alshomrani, A.S. On unsteady heat and mass transfer in Carreau nanofluid flow over expanding or contracting cylinder with convective surface conditions. J. Mol. Liq. 2017, 231, 474–484. [Google Scholar] [CrossRef]
- Sharma, K.; Gupta, S. Viscous dissipation and thermal radiation effects in MHD flow of Jeffrey nanofluid through impermeable surface with heat generation/absorption. Nonlinear Eng. 2017, 6, 153–166. [Google Scholar] [CrossRef]
- Patel, H.R.; Mittal, A.S.; Darji, R.R. MHD flow of micropolar nanofluid over a stretching/shrinking sheet considering radiation. Int. Commun. Heat Mass Transf. 2019, 108, 104322. [Google Scholar] [CrossRef]
- Alali, E.; Megahed, A.M. MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon. Nanotechnol. Rev. 2022, 11, 463–472. [Google Scholar] [CrossRef]
- Yousef, N.S.; Megahed, A.M.; Ghoneim, N.I.; Elsafi, M.; Fares, E. Chemical reaction impact on MHD dissipative Casson-Williamson nanofluid flow over a slippery stretching sheet through porous medium. Alex. Eng. J. 2022, 61, 10161–10170. [Google Scholar] [CrossRef]
- Areshi, M.; Alrihieli, H.; Alali, E.; Megahed, A.M. Temperature distribution in the flow of a viscous incompressible non-Newtonian Williamson nanofluid saturated by gyrotactic microorganisms. Mathematics 2022, 10, 1256. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Dero, S.; Khan, I.; Baleanu, D.; Nisar, K.S. Magnetized Flow of Cu + Al2O3 + H2O Hybrid Nanofluid in Porous Medium: Analysis of Duality and Stability. Symmetry 2020, 12, 1513. [Google Scholar] [CrossRef]
- Alrehili, M. Development for cooling operations through a model of nanofluid flow with variable heat flux and thermal radiation. Processes 2022, 10, 2650. [Google Scholar] [CrossRef]
- Alrihieli, H.; Alrehili, M.; Megahed, A.M. Radiative MHD nanofluid flow due to a linearly stretching sheet with convective heating and viscous dissipation. Mathematics 2022, 10, 4743. [Google Scholar] [CrossRef]
- Farooq, M.; Khan, M.I.; Waqas, M.; Hayat, T.; Alsaedi, A.; Khan, M.I. MHD stagnation point flow of viscoelastic nanofluid with non-linear radiation effects. J. Mol. Liq. 2016, 221, 1097–1103. [Google Scholar] [CrossRef]
- Hayat, T.; Waqas, M.; Shehzad, S.A.; Alsaedi, A. Mixed convection flow of viscoelastic nanofluid by a cylinder with variable thermal conductivity and heat source/sink. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 214–234. [Google Scholar] [CrossRef]
- Macha, M.; Kishan, N. Boundary layer flow of viscoelastic nanofluid over a wedge in the presence of buoyancy force effects. Comput. Therm. Sci. Int. J. 2017, 9, 257–267. [Google Scholar]
- Liu, I.-C.; Megahed, A.M.; Wang, H.-H. Heat transfer in a liquid film due to an unsteady stretching surface with variable heat flux. ASME J. Appl. Mech. 2013, 80, 041003. [Google Scholar] [CrossRef]
- Liu, I.-C.; Wang, H.-H.; Umavathi, J.C. Effect of viscous dissipation, internai heat source/sink, and thermal radiation on a hydromagnetic liquid fiim over an unsteady stretching sheet. J. Heat Transf. 2013, 135, 031701. [Google Scholar] [CrossRef]
- Megahed, A.M. Flow and heat transfer of a non-Newtonian power-law fluid over a non-linearly stretching vertical surface with heat flux and thermal radiation. Meccanica 2015, 50, 1693–1700. [Google Scholar] [CrossRef]
- Nourhan, I.G.; Megahed, A.M. Hydromagnetic nanofluid film flow over a stretching sheet with prescribed heat flux and viscous dissipation. Fluid Dyn. Mater. Process. 2022, 18, 1373–1388. [Google Scholar]
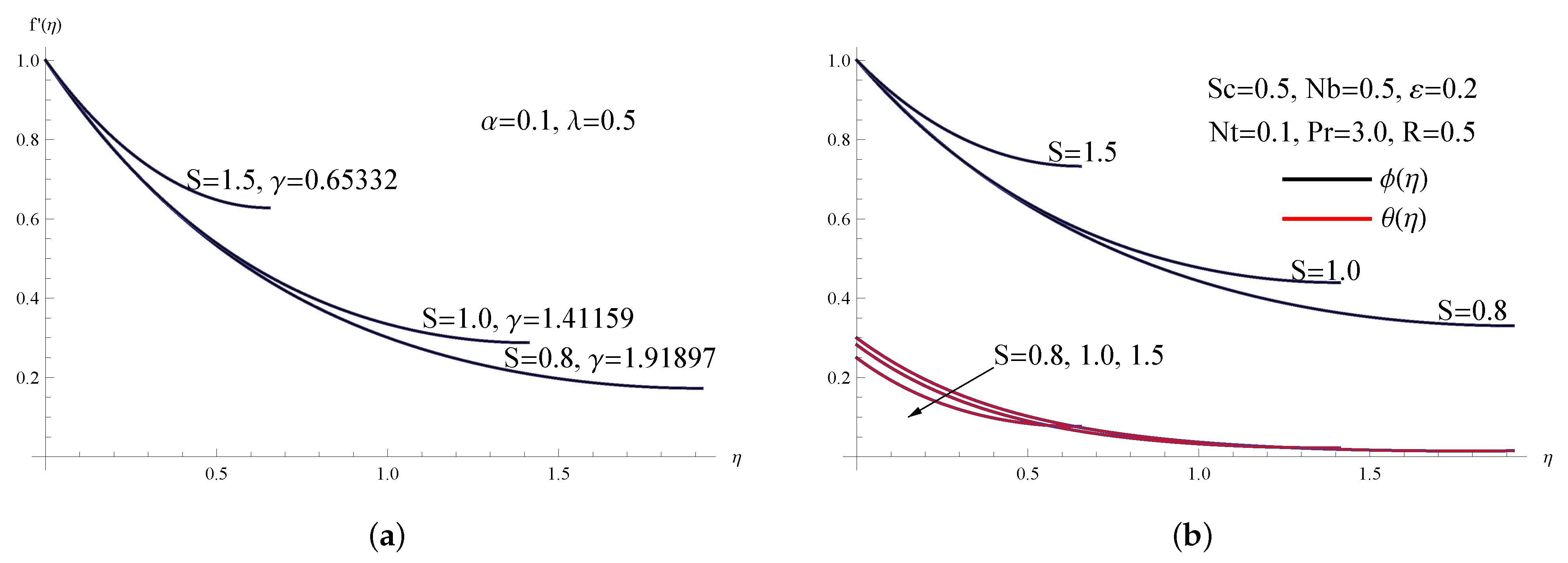
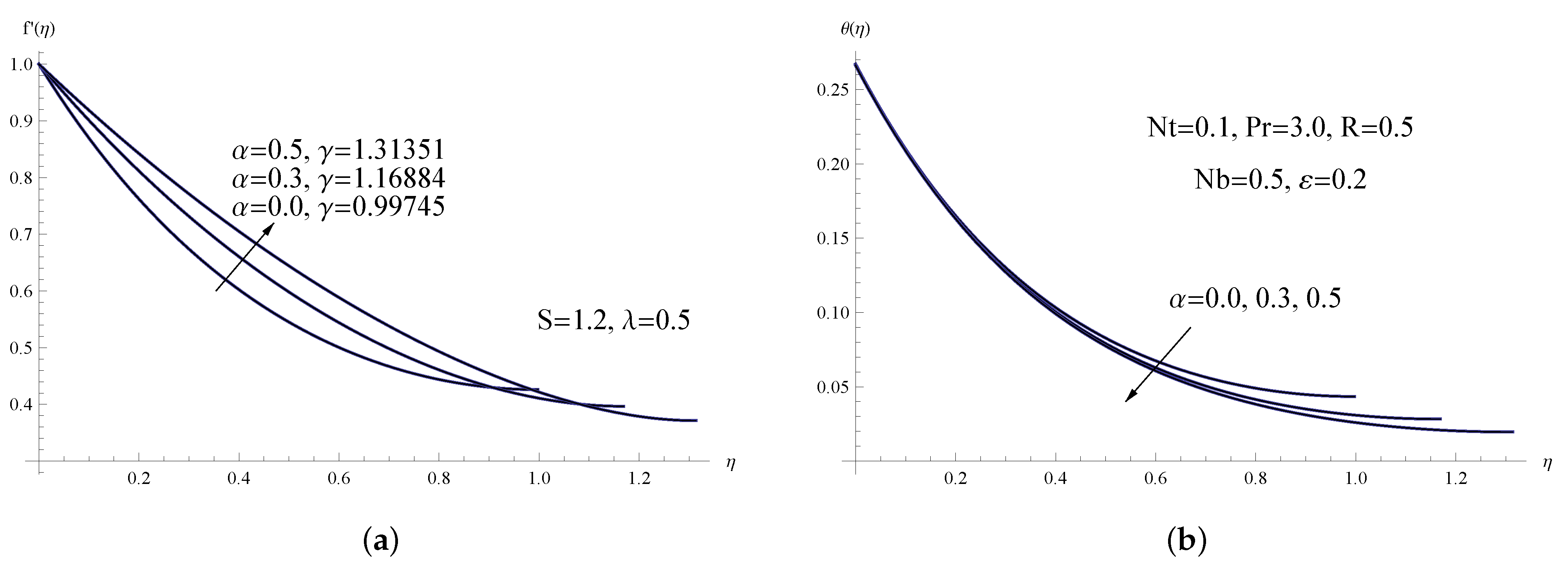

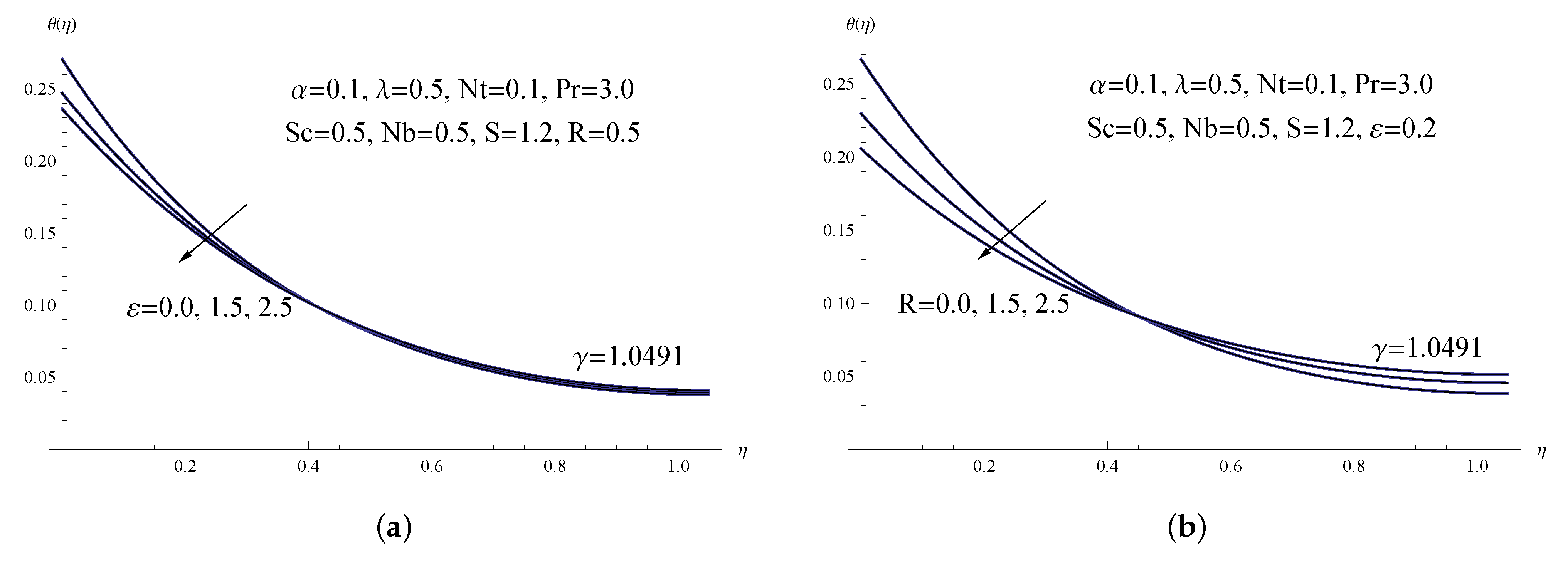
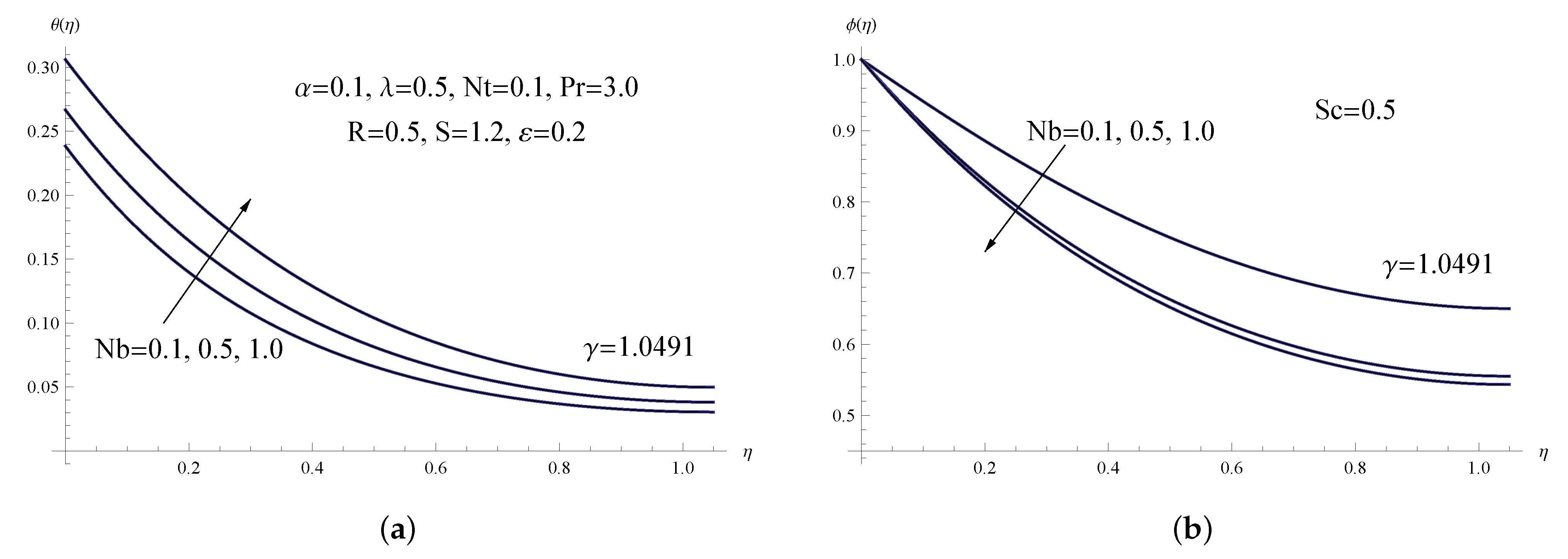
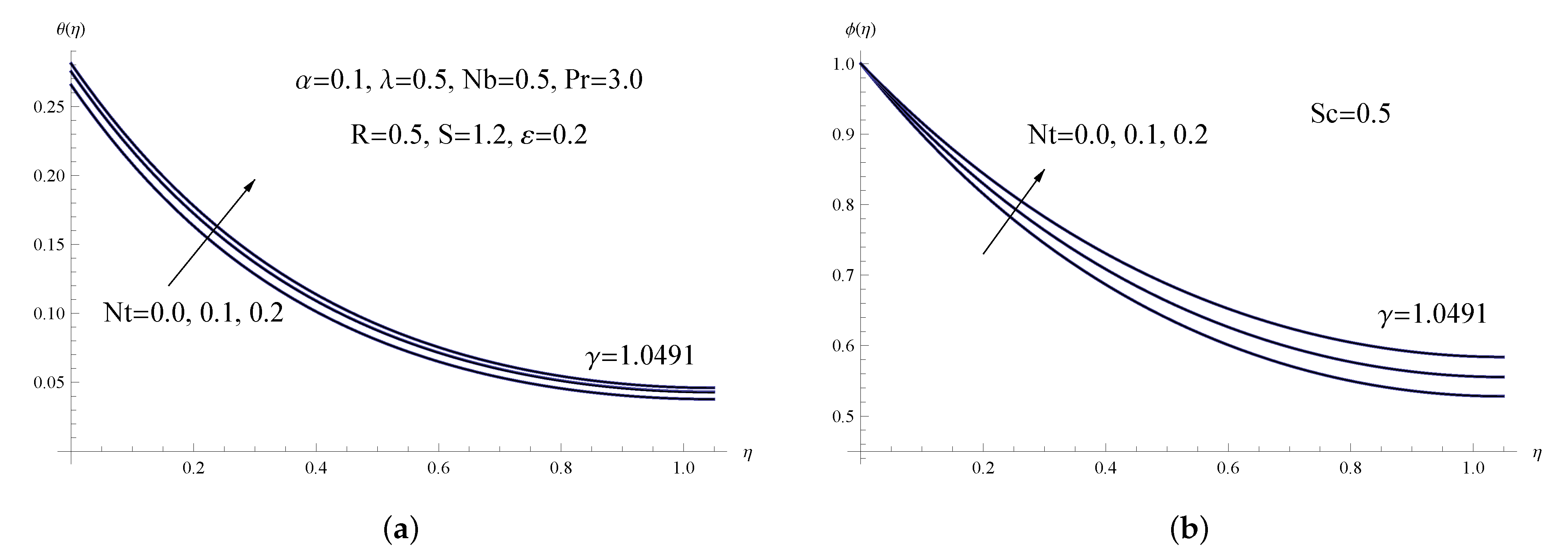
| S | Liu et al. [21] | Present Results | ||
|---|---|---|---|---|
| 0.4 | 4.981454 | 1.134096 | 4.98144987 | 1.13409589 |
| 0.8 | 2.151994 | 1.245806 | 2.15199394 | 1.24580568 |
| 1.2 | 1.127781 | 1.279172 | 1.12777819 | 1.27917195 |
| 1.6 | 0.576173 | 1.114938 | 0.57616859 | 1.11493776 |
| S | R | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.8 | 0.1 | 0.5 | 0.2 | 0.5 | 0.5 | 0.1 | 1.56398 | 3.339711 | 0.99554 |
| 1.0 | 0.1 | 0.5 | 0.2 | 0.5 | 0.5 | 0.1 | 1.62151 | 3.543831 | 1.01335 |
| 1.5 | 0.1 | 0.5 | 0.2 | 0.5 | 0.5 | 0.1 | 1.85604 | 4.011625 | 1.18829 |
| 1.2 | 0.0 | 0.5 | 0.2 | 0.5 | 0.5 | 0.1 | 1.43108 | 3.744241 | 0.96981 |
| 1.2 | 0.3 | 0.5 | 0.2 | 0.5 | 0.5 | 0.1 | 1.91377 | 3.755142 | 1.05311 |
| 1.2 | 0.5 | 0.5 | 0.2 | 0.5 | 0.5 | 0.1 | 2.01324 | 3.758601 | 1.10675 |
| 1.2 | 0.1 | 0.0 | 0.2 | 0.5 | 0.5 | 0.1 | 1.46275 | 3.744262 | 1.05908 |
| 1.2 | 0.1 | 0.5 | 0.2 | 0.5 | 0.5 | 0.1 | 1.65017 | 3.634431 | 0.99810 |
| 1.2 | 0.1 | 1.0 | 0.2 | 0.5 | 0.5 | 0.1 | 1.81997 | 3.774517 | 0.94273 |
| 1.2 | 0.1 | 0.5 | 0.0 | 0.5 | 0.5 | 0.1 | 1.65017 | 3.696661 | 0.99356 |
| 1.2 | 0.1 | 0.5 | 1.5 | 0.5 | 0.5 | 0.1 | 1.65017 | 4.046820 | 1.01457 |
| 1.2 | 0.1 | 0.5 | 2.5 | 0.5 | 0.5 | 0.1 | 1.65017 | 4.237523 | 1.10507 |
| 1.2 | 0.1 | 0.5 | 0.2 | 0.0 | 0.5 | 0.1 | 1.65017 | 3.749153 | 0.99747 |
| 1.2 | 0.1 | 0.5 | 0.2 | 1.5 | 0.5 | 0.1 | 1.65017 | 4.355022 | 1.02115 |
| 1.2 | 0.1 | 0.5 | 0.2 | 2.5 | 0.5 | 0.1 | 1.65017 | 4.863840 | 1.03684 |
| 1.2 | 0.1 | 0.5 | 0.2 | 0.5 | 0.1 | 0.1 | 1.65017 | 4.194981 | 0.59368 |
| 1.2 | 0.1 | 0.5 | 0.2 | 0.5 | 0.5 | 0.1 | 1.65017 | 3.634431 | 0.99810 |
| 1.2 | 0.1 | 0.5 | 0.2 | 0.5 | 1.0 | 0.1 | 1.65017 | 3.267371 | 1.04801 |
| 1.2 | 0.1 | 0.5 | 0.2 | 0.5 | 0.5 | 0.0 | 1.65017 | 3.766812 | 1.09521 |
| 1.2 | 0.1 | 0.5 | 0.2 | 0.5 | 0.5 | 0.1 | 1.65017 | 3.634431 | 0.99810 |
| 1.2 | 0.1 | 0.5 | 0.2 | 0.5 | 0.5 | 0.2 | 1.65017 | 3.559033 | 0.90139 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrehili, M. The Flow of a Thermo Nanofluid Thin Film Inside an Unsteady Stretching Sheet with a Heat Flux Effect. Energies 2023, 16, 1160. https://doi.org/10.3390/en16031160
Alrehili M. The Flow of a Thermo Nanofluid Thin Film Inside an Unsteady Stretching Sheet with a Heat Flux Effect. Energies. 2023; 16(3):1160. https://doi.org/10.3390/en16031160
Chicago/Turabian StyleAlrehili, Mohammed. 2023. "The Flow of a Thermo Nanofluid Thin Film Inside an Unsteady Stretching Sheet with a Heat Flux Effect" Energies 16, no. 3: 1160. https://doi.org/10.3390/en16031160
APA StyleAlrehili, M. (2023). The Flow of a Thermo Nanofluid Thin Film Inside an Unsteady Stretching Sheet with a Heat Flux Effect. Energies, 16(3), 1160. https://doi.org/10.3390/en16031160





