High Voltage Electric Pulse Drilling: A Study of Variables through Simulation and Experimental Tests
Abstract
:1. Introduction
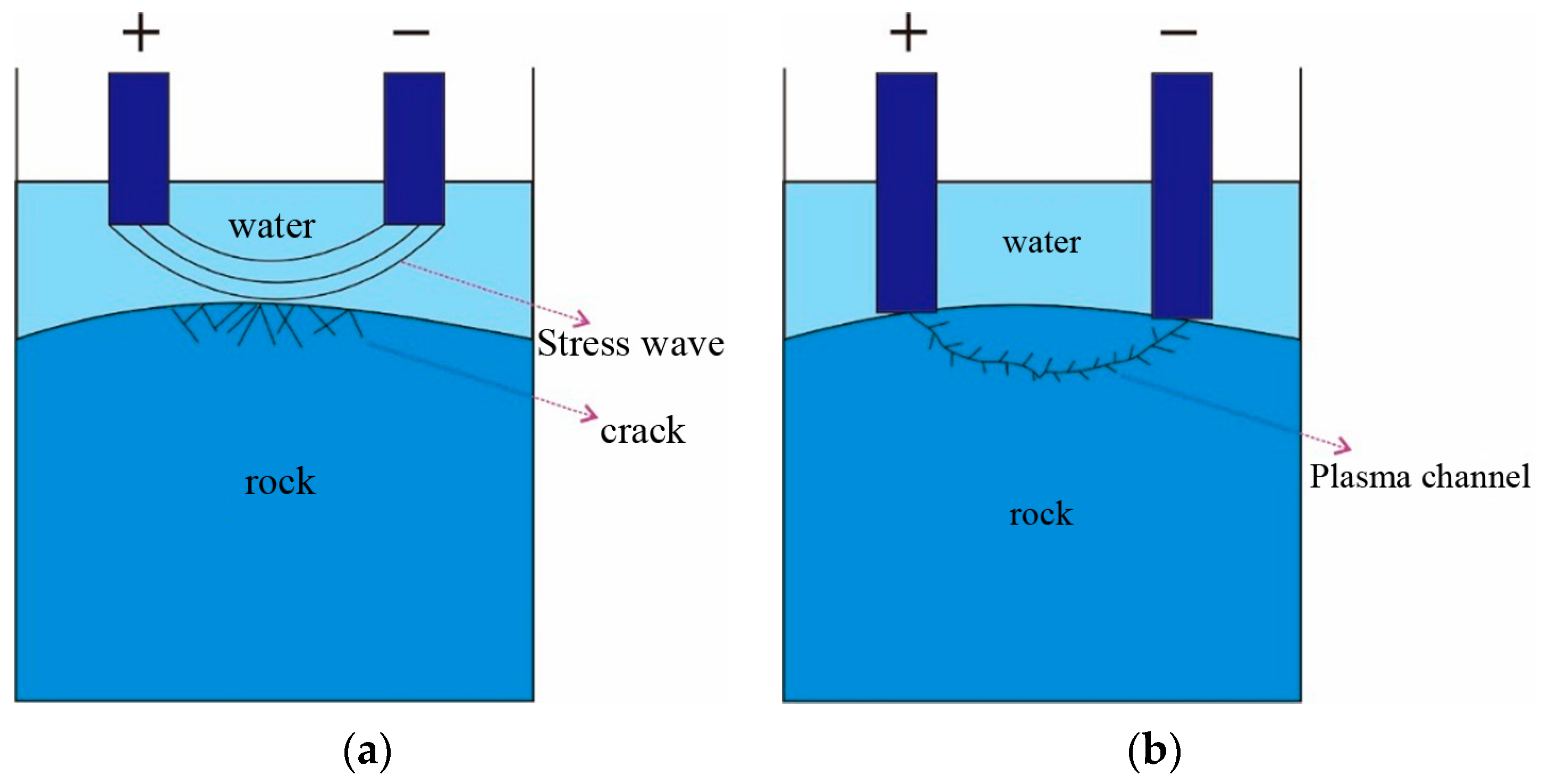
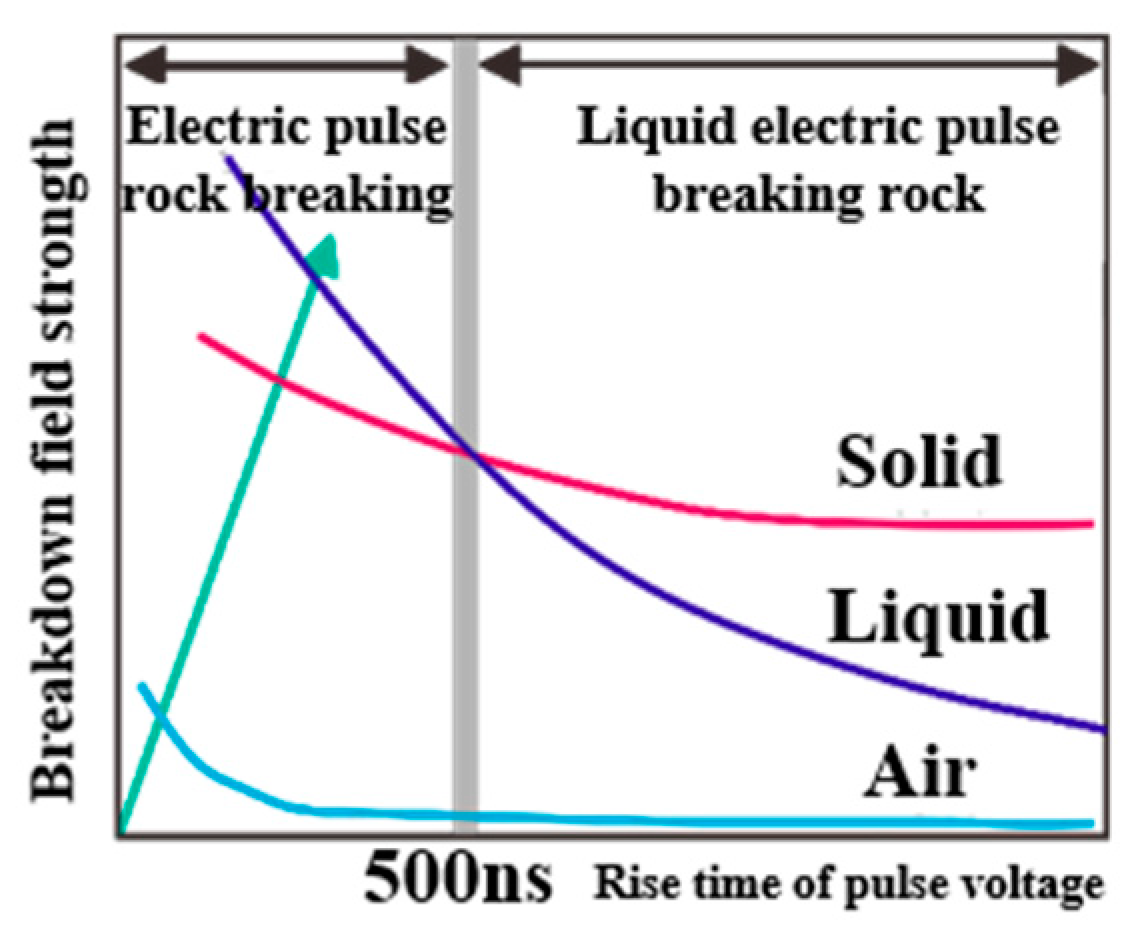
2. Theoretical Background of Rock Breaking Process by HVEP
3. Simulation of HVERB
- (1)
- The geometric model and mesh generation model are shown in Figure 7. Since the influence of bubbles is considered in the simulation, the bubbles are magnified to make the bubble boundary contact with the rock boundary in a larger area. Here, the rock is set as a rectangle of 20 mm × 10 mm, and the bubble radius is 3 mm. At the same time, because the quality of the mesh is the key to determining whether the subsequent simulation can converge and whether the convergence result is accurate, and because the model is relatively simple and the number of iterations is less, the model is ultra-refined mesh generation, as shown in Figure 8. It can be seen from the figure that COMSOL Multiphysics software can refine the boundary mesh of the contact between rock and bubble, which meets the requirements of mesh generation.
- (2)
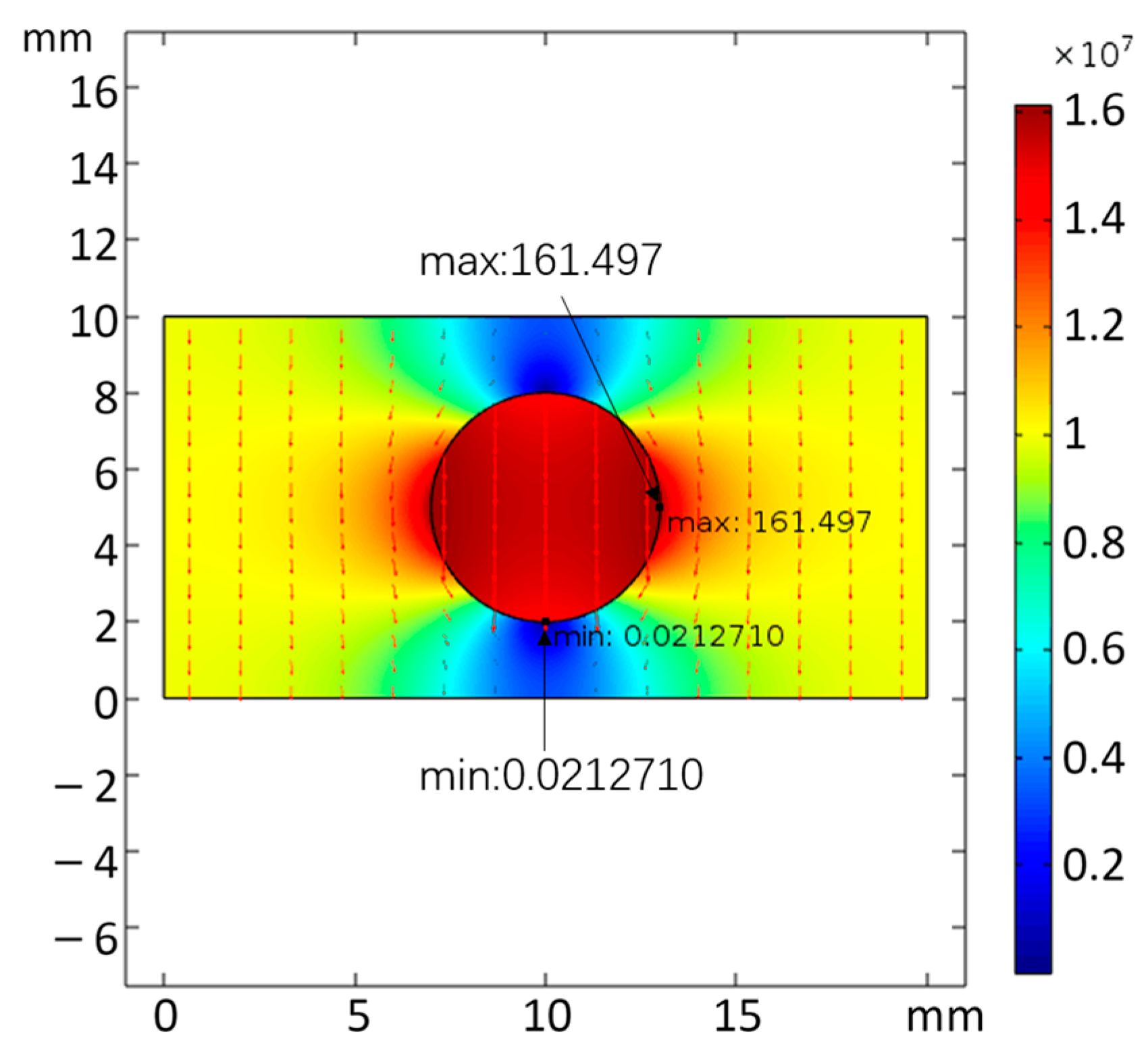
- The simulation results of the model are shown in Figure 9. The EFS is 100 kV/cm which is far from the bubble, while the maximum EFS near the bubble is 161.497 kV/cm. At the same time, the EFS at the upper and lower boundaries of the bubble become lower, and the EFS near the bubble boundary is close to zero. The EFS around the bubble forms a clear difference, and the uniformity of the electric field inside the rock decreases. Under such EFS distribution, the rock breakdown becomes easier.
- (3)
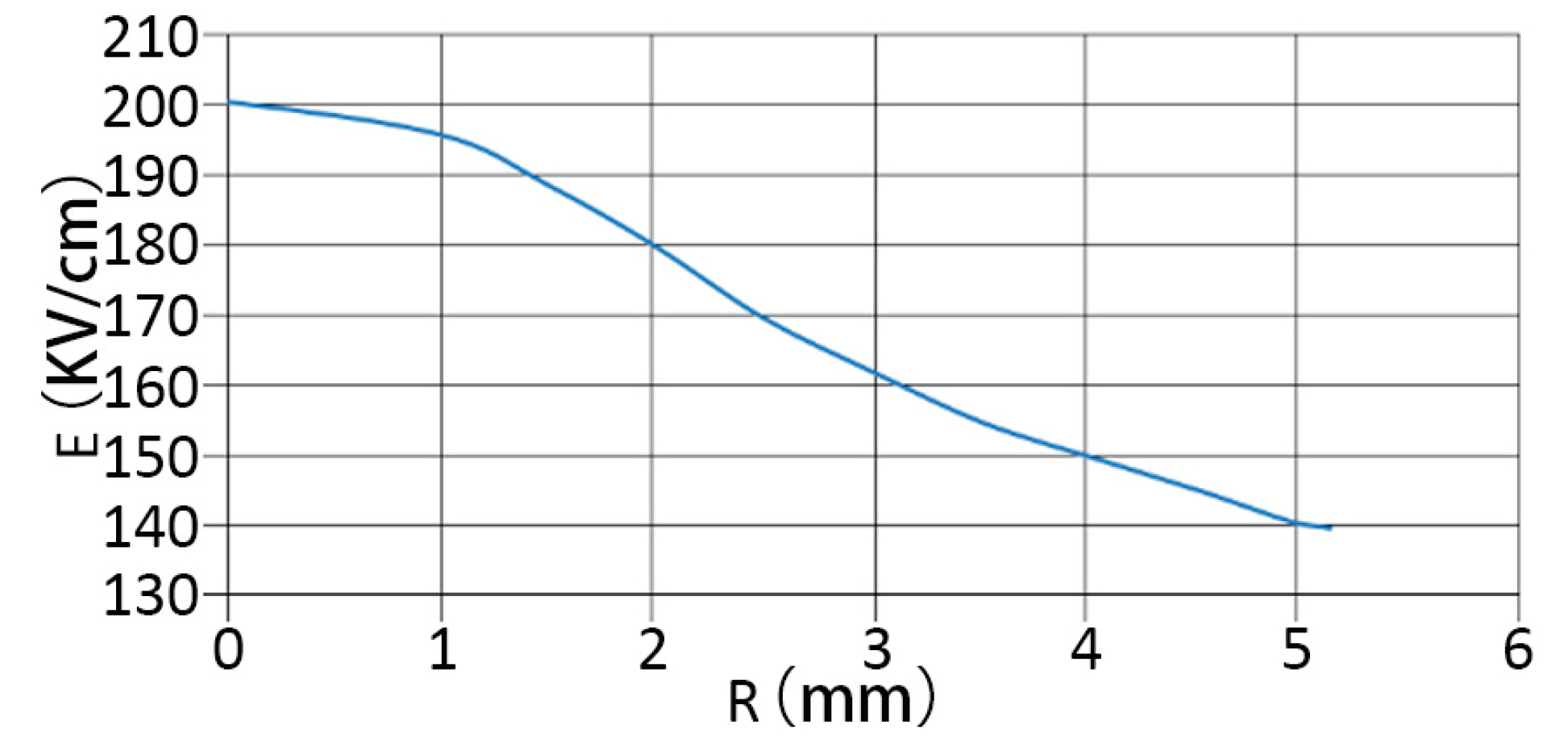
- By changing the radius of the middle bubble to adjust the area of the bubble, the influence of the bubble size on the EFS of rock is analyzed, as shown in Table 1. The fitting curve is shown in Figure 10. With the decrease in the bubble area, the influence on the EFS inside the rock becomes larger. However, from the comparison between Figure 9 and Figure 11, it can be seen that due to the smaller volume of the bubble, the contact between the bubble and the rock boundary becomes smaller, which leads to a smaller range of its influence on the EFS inside the rock. According to the average EFS inside the bubble and inside the rock, with the increase of the bubble volume, the influence range of the bubble on the EFS inside the rock increases, the average EFS inside the rock decreases, and the difference between the maximum and minimum EFS decreases. Therefore, in the interior of rocks, more tiny and disordered bubbles have a greater influence on the uniformity and maximum of EFS than a single big bubble.
- (4)
- Using the analytical model of a 2 mm bubble, to explore the effect of distance between the bubble and electric potential on rock EFS. By changing the distance between the bubble center and the high electric potential, the maximum and minimum EFS results of the rock are obtained. As shown in Table 2, as the distance between the bubble and the electric potential boundary increases, the influence of the bubble on the EFS of the rock increases. However, combined with Table 2, comparing the influence of the bubble volume on the EFS of the rock, it can be seen that the influence of the distance between the bubble and the electric potential boundary is relatively small.
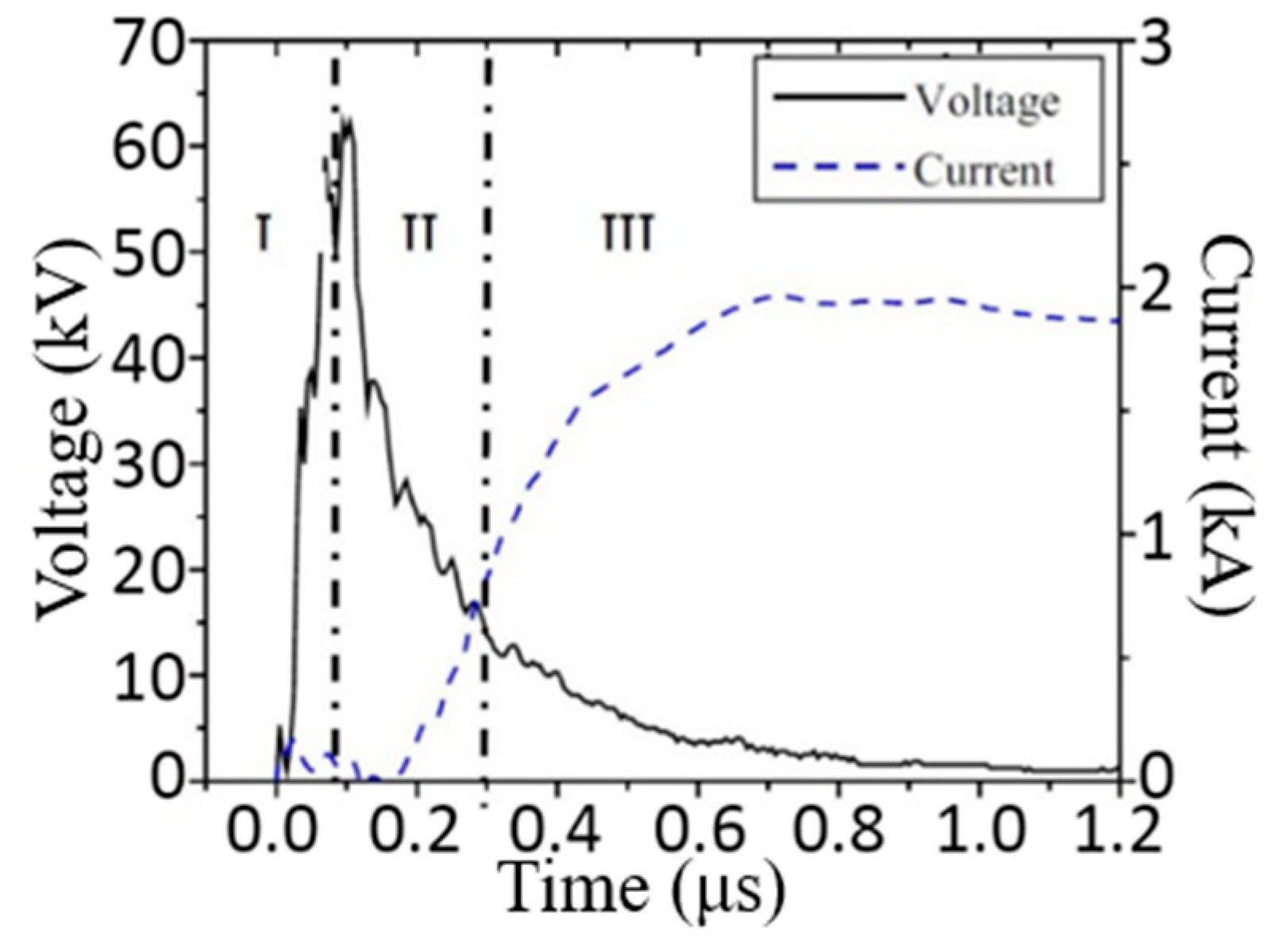
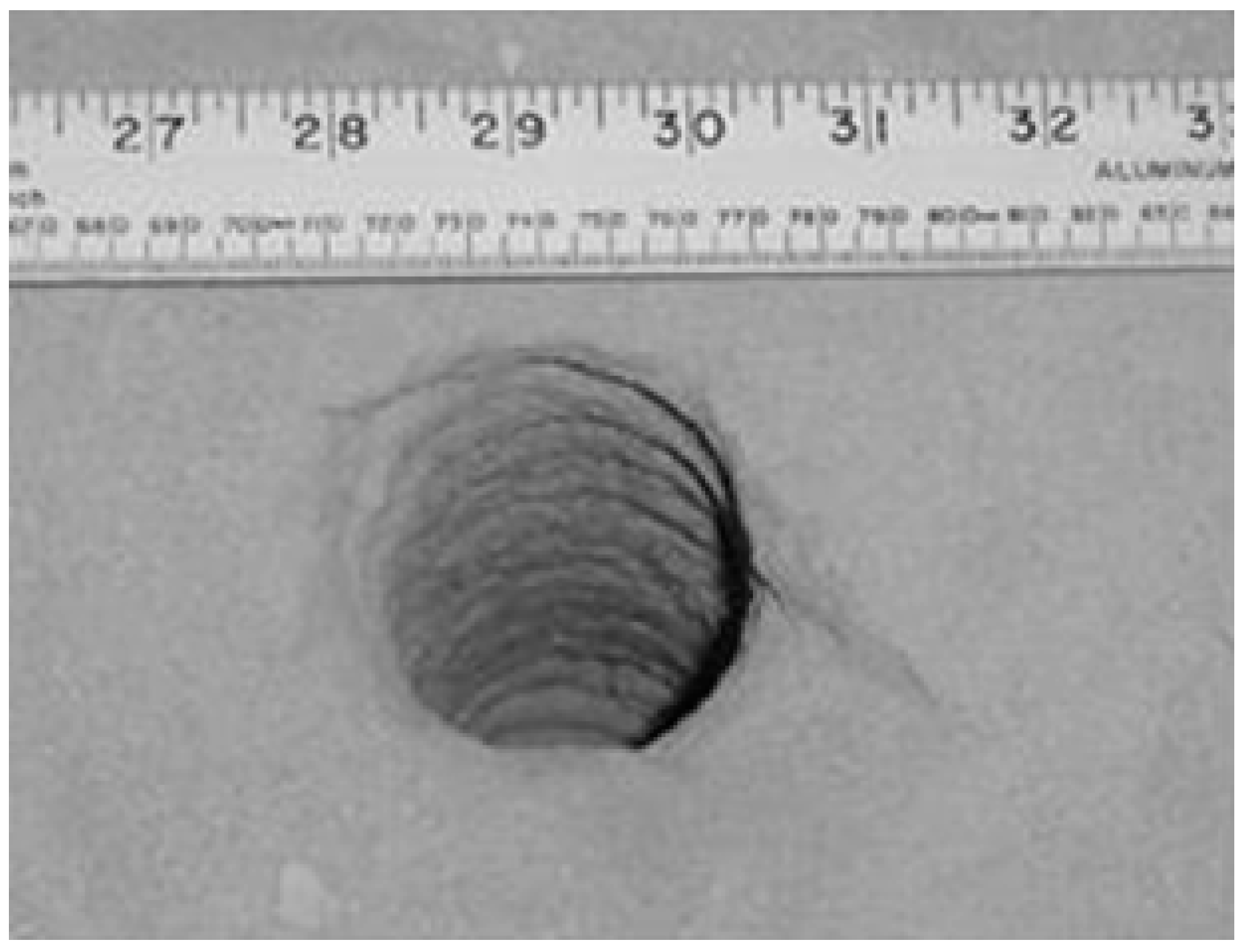
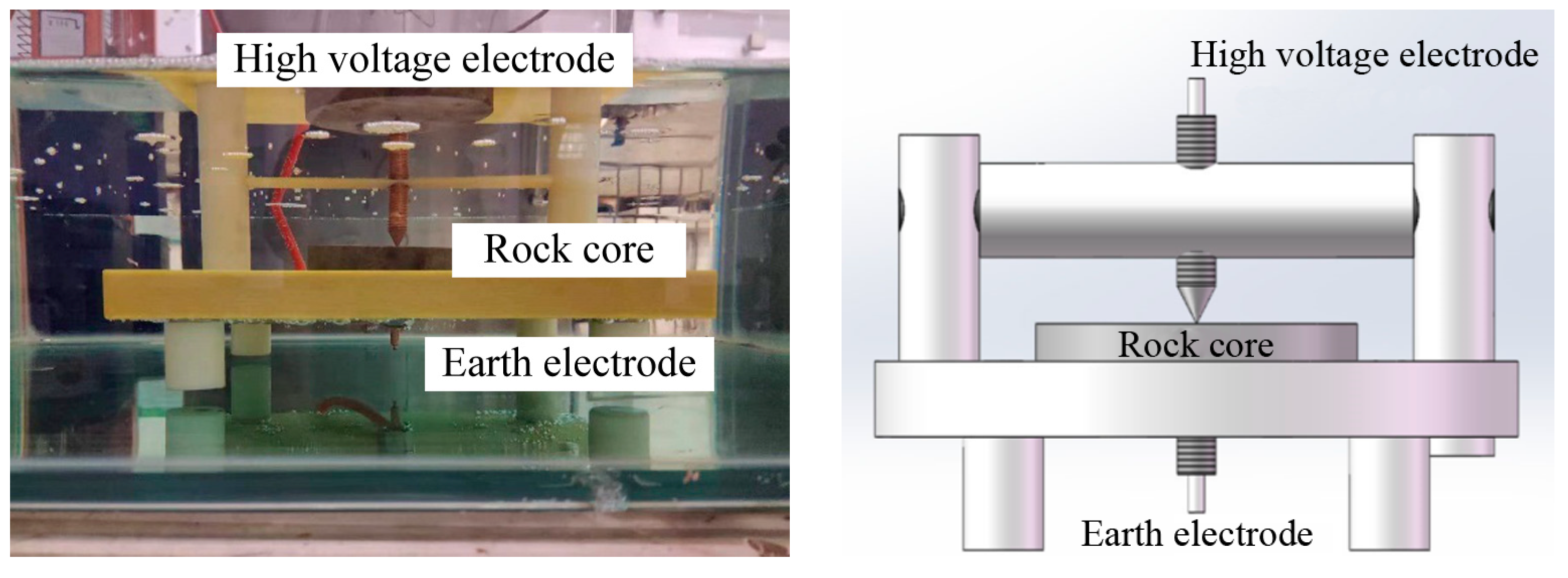
4. Experimental Study on Rock Breaking of a High-Voltage Electric Pulse Generator
5. Conclusions
- (1)
- Through the simulation analysis of the influence of bubbles on the electric breakdown of rock, the influence of bubble volume, the distance between bubbles and electric potential on the EFS of rock, and the distribution of EFS around bubbles are obtained. Finally, the disordered distribution of bubbles in rock contributes to the breaking of rock.
- (2)
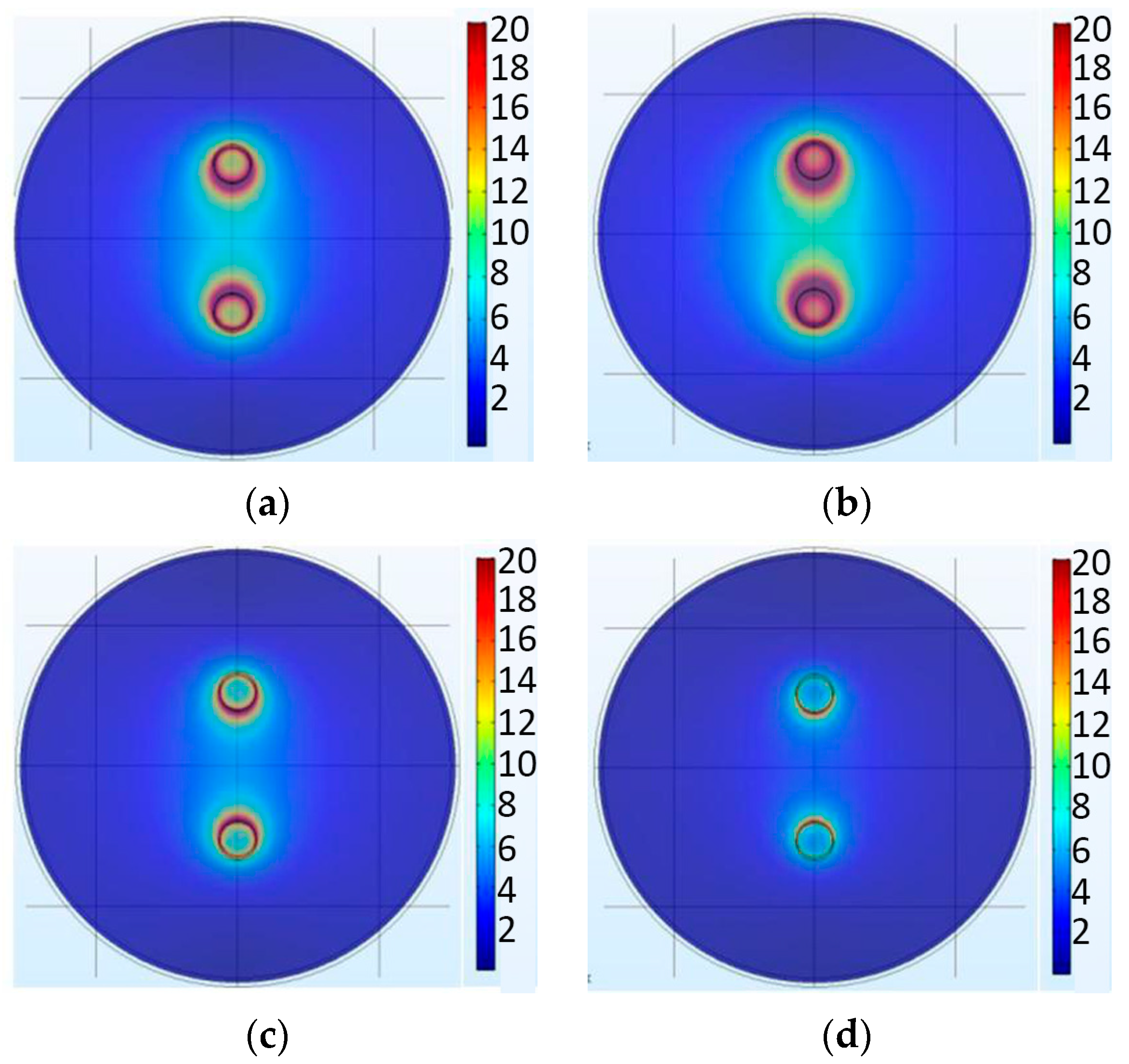
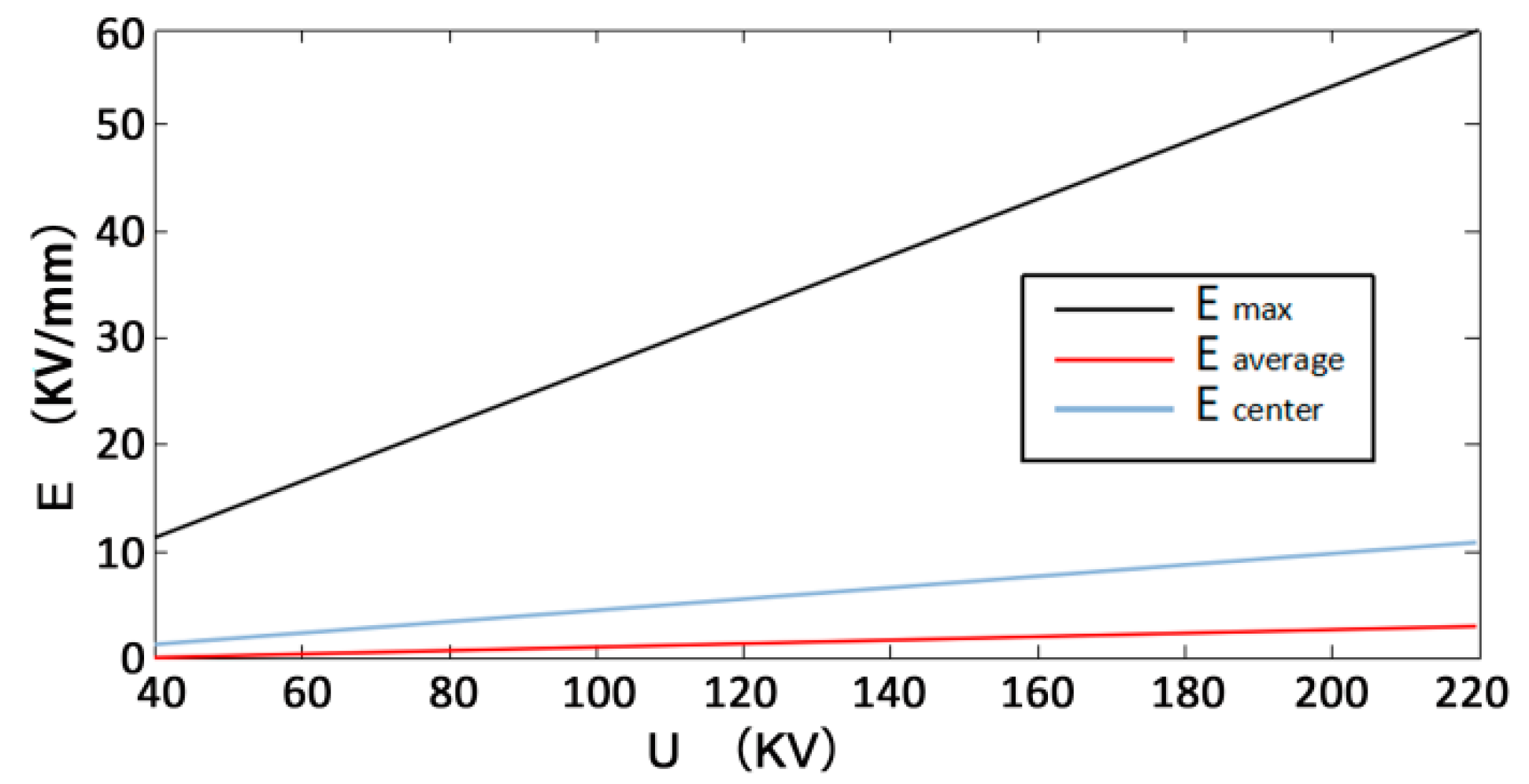
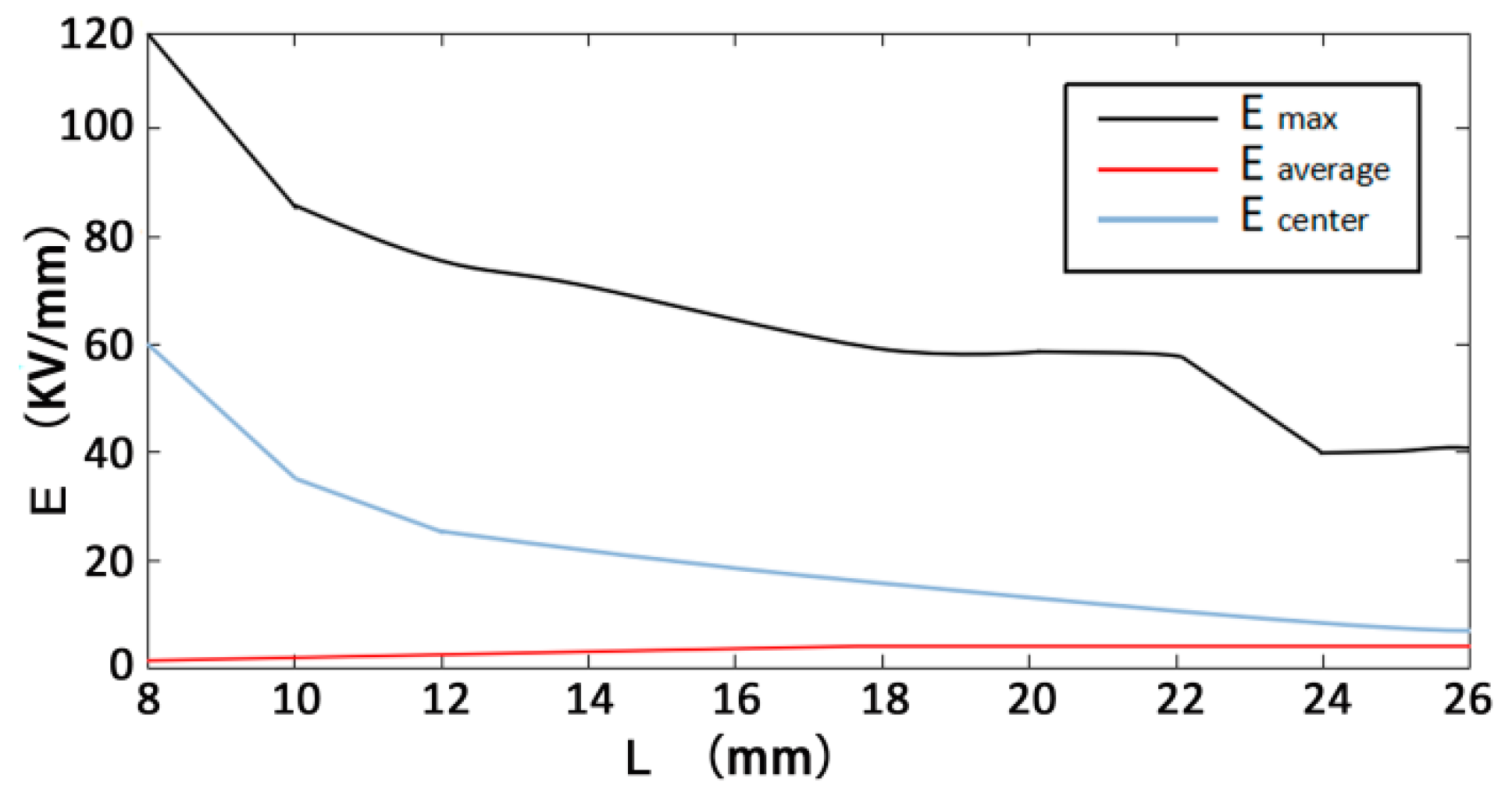
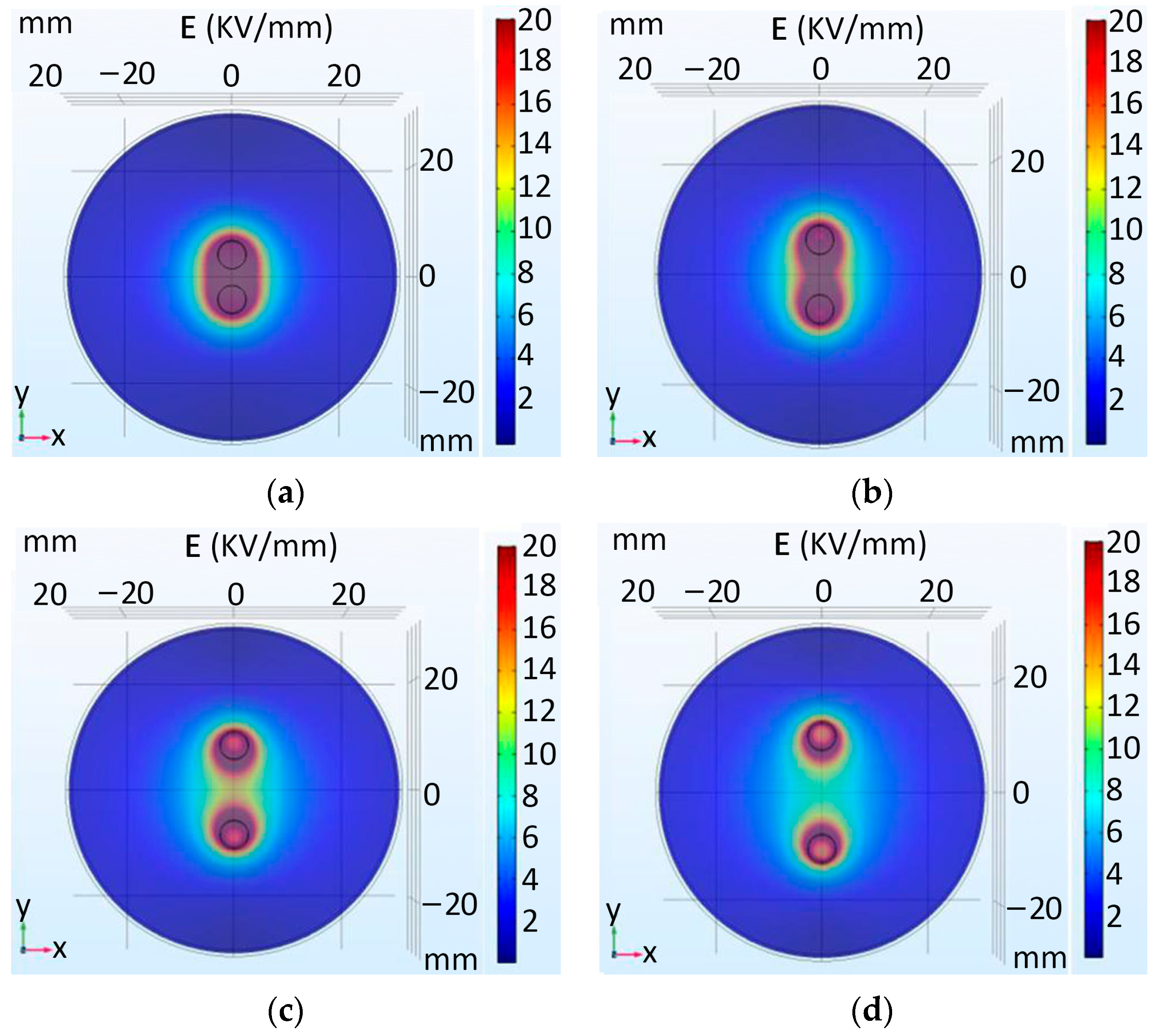
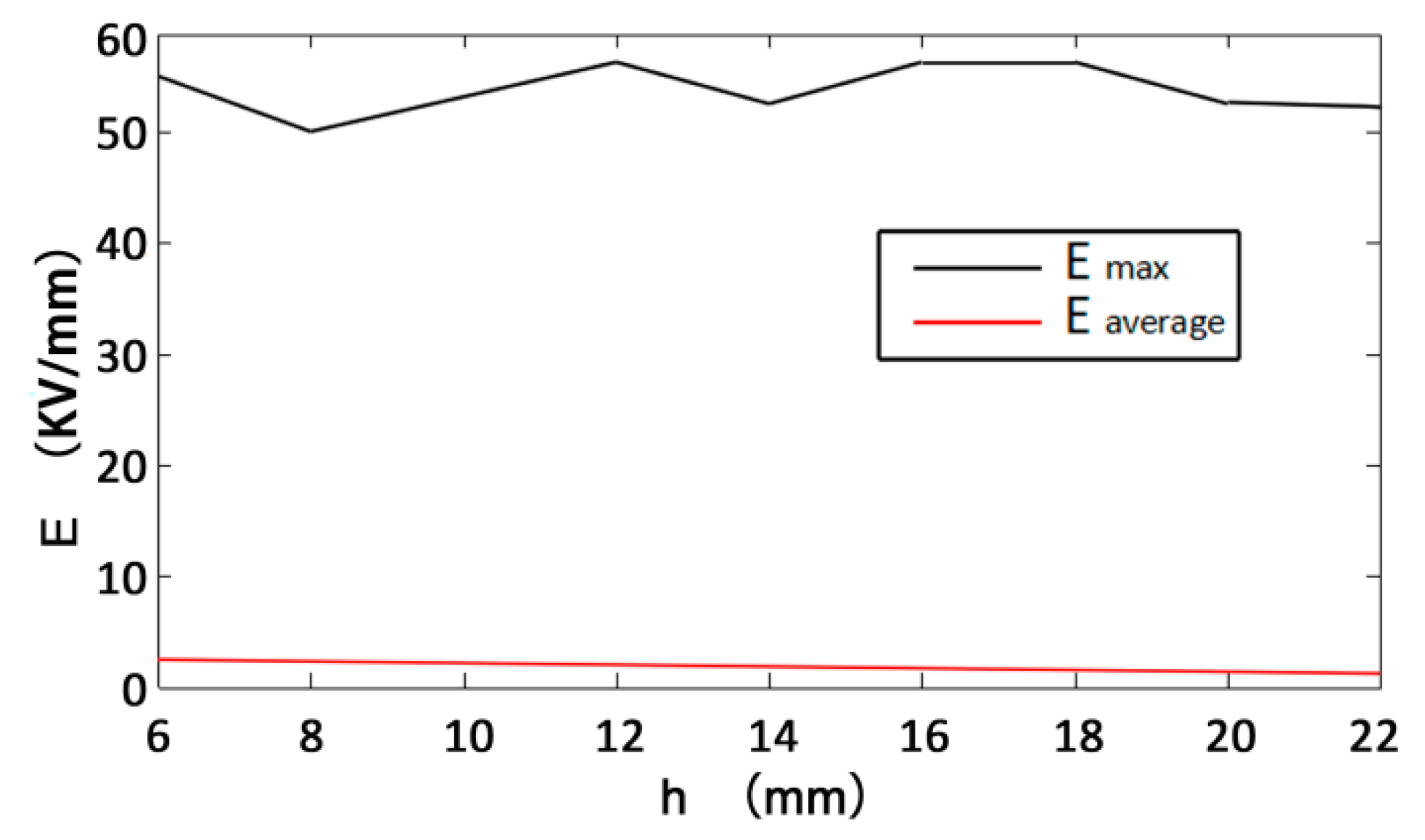
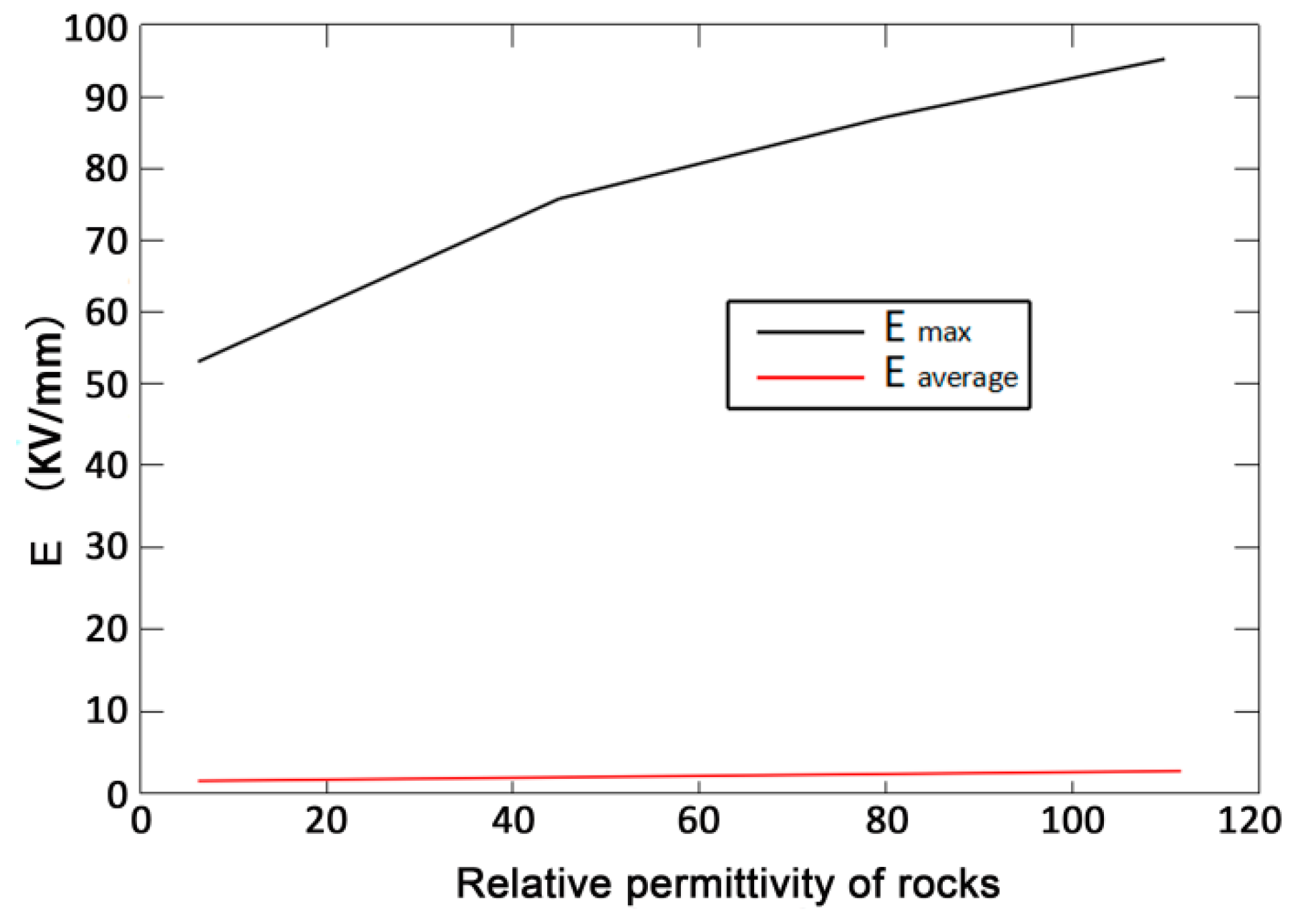
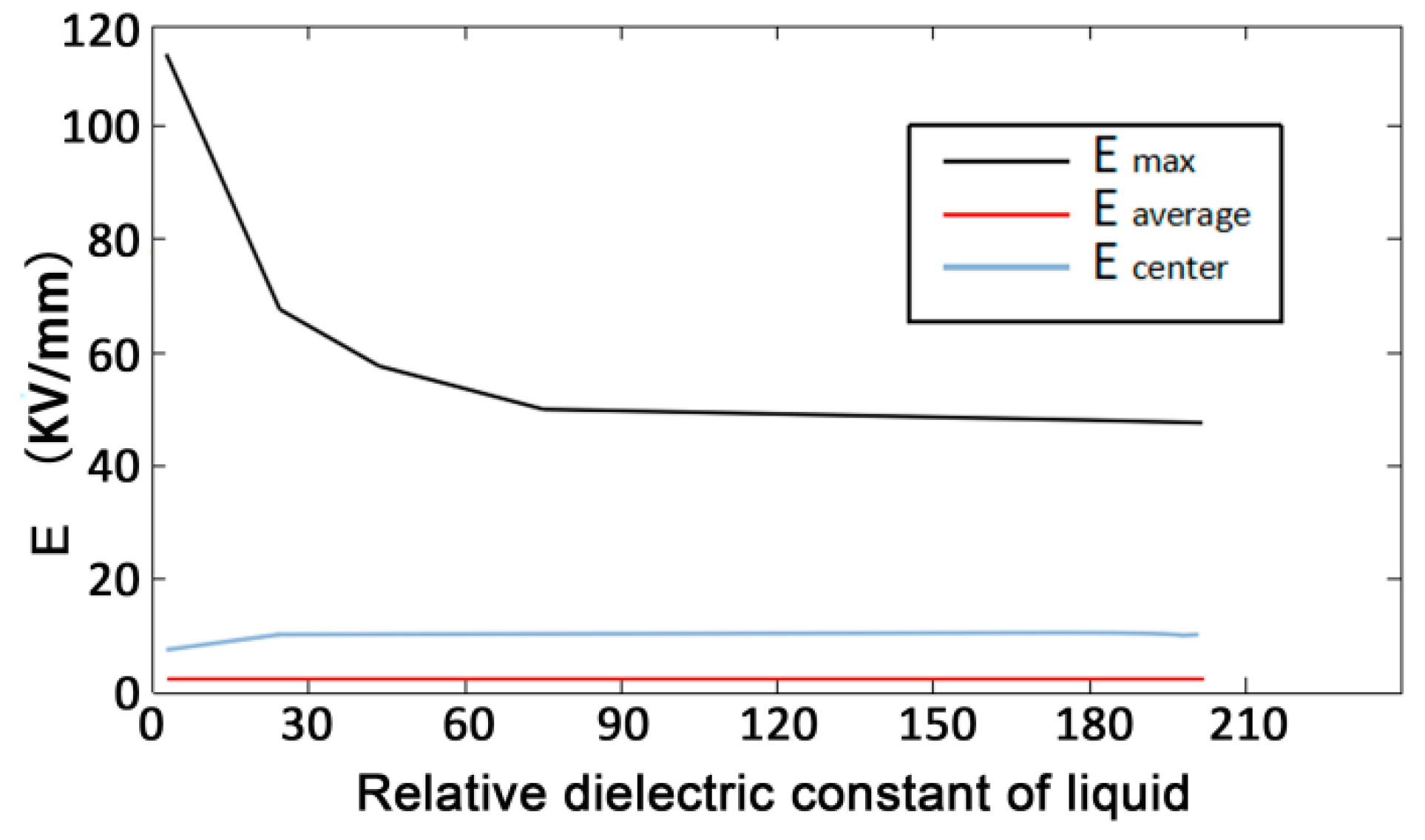
- Through the simulation and analysis of different electrode voltages, electrode spacing, rock thickness, and liquid material in rock breakdown, the law of their influence on rock breaking by HVEP is obtained. The results show that the higher the electrode voltage is, the smaller the electrode spacing is, and the lower the dielectric constant of liquid material is, the better the crushing effect of rock is; the thickness of rock has little effect on the electric breakdown of rock.
- (3)
- Explore the influence of plasma channel expansion and explosion on the interior of rock through relevant theories of explosion mechanics and rock mechanics, establish a mathematical model for the rock-breaking process, and analyze the rock-breaking process and force of rock. It is calculated that the pressure generated by the energy in the plasma channel of the rock is far greater than the tensile strength of the rock. In the process of high-voltage electric pulse rock breaking, the rock breaking is due to the work done by the plasma channel to overcome the tensile strength of the rock.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nian, T.; Wang, G.; Cang, D.; Tan, C.; Tan, Y.; Zhang, F. The diagnostic criteria of borehole electrical imaging log for volcanic reservoir interpretation: An example from the Yingcheng Formation in the Xujiaweizi Depression, Songliao Basin, China. J. Petrol. Sci. Eng. 2022, 208, 109713. [Google Scholar] [CrossRef]
- Liu, Z.; Pan, Z.; Li, S.; Zhang, L.; Wang, F.; Han, L.; Zhang, J.; Ma, Y.; Li, H.; Li, W. Study on the effect of cemented natural fractures on hydraulic fracture propagation in volcanic reservoirs. Energy 2022, 241, 122845. [Google Scholar] [CrossRef]
- Feng, Y.; Bian, W.; Gu, G.; Huang, Y.; Qiu, J.; Sun, A.; Wang, P. A drilling data-constrained seismic mapping method for intermediate-mafic volcanic facies. Petrol. Explor. Dev. 2016, 43, 251–260. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, H.; Chen, H.; Du, S.; Li, C. Quantitative characterization of fracture-pore distribution and effects on production capacity of weathered volcanic crust reservoirs: Insights from volcanic gas reservoirs of the Dixi area, Junggar Basin, Western China. Mar. Petrol. Geol. 2022, 140, 105651. [Google Scholar] [CrossRef]
- Zhang, Z.C. Rock Fragmentation by Pulsed Highvoltage Discharge and Drilling Equipment Development; Zhejiang University: Hangzhou, China, 2013. [Google Scholar]
- Schiegg, H.O.; Rødland, A.; Zhu, G.; Yuen, D.A. Electro-pulse-boring (EPB): Novel super-deep drilling technology for low cost electricity. J. Earth Sci. 2015, 26, 37–46. [Google Scholar] [CrossRef]
- Song, B.-P.; Zhang, M.-Y.; Fan, Y.; Jiang, L.; Kang, J.; Gou, T.-T.; Zhang, C.-L.; Yang, N.; Zhang, G.-J.; Zhou, X. Recycling experimental investigation on end of life photovoltaic panels by application of high voltage fragmentation. Waste Manag. 2020, 101, 180–187. [Google Scholar] [CrossRef]
- Duan, C.; Han, J.; Zhao, S.; Gao, Z.; Qiao, J.; Yan, G. The stripping effect of using high voltage electrical pulses breakage for waste printed circuit boards. Waste Manag. 2018, 77, 603–610. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, F.; Du, C.; Yang, X. Effects of confining pressure on crater blasting in rock-like materials under electric explosion load. Int. J. Impact Eng. 2020, 139, 103534. [Google Scholar] [CrossRef]
- Peng, J.; Wang, X.; Zhang, F.; Yang, X.; Gao, J. Influences of the burden on the fracture behaviour of rocks by using electric explosion of wires. Theor. Appl. Fract. Mech. 2022, 118, 103270. [Google Scholar] [CrossRef]
- Fujita, T.; Yoshimi, I.; Shibayama, A.; Miyazaki, T.; Abe, K.; Sato, M.; Yen, W.T.; Svoboda, J. Crushing and liberation of materials by electrical disintegration. EJMP&EP 2001, 1, 113–122. [Google Scholar]
- Sperner, B.; Jonckheere, R.; Pfänder, J.A. Testing the influence of high-voltage mineral liberation on grain size, shape and yield, and on fission track and 40Ar/39Ar dating. Chem. Geol. 2014, 371, 83–95. [Google Scholar] [CrossRef]
- Boev, S.; Vajov, V.; Levchenko, B.; Jgun, D.; Muratov, V.; Peltsman, S.; Adam, A.; Uemura, K. Electropulse technology of material destruction and boring. In Digest of Technical Papers, Proceedings of the 11th IEEE International Pulsed Power Conference, Baltimore, MD, USA, 29 June–2 July 1997; IEEE: Piscataway, NJ, USA, 1997; Volume 1, pp. 220–225. [Google Scholar]
- Andres, U. Development and prospects of mineral liberation by electrical pulses. Int. J. Miner. Process. 2010, 97, 31–38. [Google Scholar] [CrossRef]
- Burkin, V.V.; Kuznetsova, N.S.; Lopatin, V.V. Dynamics of electro burst in solids: I. Power characteristics of electro burst. J. Phys. D Appl. Phys. 2009, 42, 185204. [Google Scholar] [CrossRef]
- Andres, U.; Timoshkin, I.; Jirestig, J.; Stallknecht, H. Liberation of valuable inclusions in ores and slags by electrical pulses. Powder Technol. 2001, 114, 40–50. [Google Scholar] [CrossRef]
- Andres, U.; Timoshkin, I.; Soloviev, M. Energy consumption and liberation of minerals in explosive electrical breakdown of ores. Miner. Process. Extr. Metall. 2001, 110, 149–157. [Google Scholar] [CrossRef]
- Lisitsyn, I.V.; Inoue, H.; Nishizawa, I.; Katsuki, S.; Akiyama, H. Breakdown and destruction of heterogeneous solid dielectrics by high voltage pulses. J. Appl. Phys. 1998, 84, 6262–6267. [Google Scholar] [CrossRef]
- Inoue, H.; Lisitsyn, I.; Akiyama, H.; Nishizawa, I. Drilling of hard rocks by pulsed power. IEEE Electr. Insul. Mag. 2000, 16, 19–25. [Google Scholar] [CrossRef]
- Burkin, V.V.; Kuznetsova, N.S.; Lopatin, V.V. Dynamics of electro burst in solids: II. Characteristics of wave process. J. Phys. D Appl. Phys. 2009, 42, 235209. [Google Scholar] [CrossRef]
- Van der Wielen, K.P.; Pascoe, R.; Weh, A.; Wall, F.; Rollinson, G. The influence of equipment settings and rock properties on high voltage breakage. Miner. Eng. 2013, 46, 100–111. [Google Scholar] [CrossRef]
- Timoshkin, I.V.; Mackersie, J.W.; MacGregor, S.J. Plasma channel microhole drilling technology. In Digest of Technical Papers, Proceedings of the 14th IEEE International Pulsed Power Conference, Dallas, TX, USA, 15–18 June 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 2, pp. 1336–1339. [Google Scholar]
- Cho, S.H.; Cheong, S.S.; Yokota, M.; Kaneko, K. The dynamic fracture process in rocks under high-voltage pulse fragmentation. Rock Mech. Rock Eng. 2016, 49, 3841–3853. [Google Scholar] [CrossRef]
- Cho, S.H.; Kaneko, K. Influence of the applied pressure waveform on the dynamic fracture processes in rock. Int. J. Rock Mech. Min. 2004, 41, 771–784. [Google Scholar] [CrossRef]
- Kusaiynov, K.; Nussupbekov, B.R.; Shuyushbayeva, N.N.; Tanasheva, N.K.; Shaimerdenova, K.M.; Khassenov, A.K. On electric-pulse well drilling and breaking of solids. Tech. Phys. 2017, 62, 867–870. [Google Scholar] [CrossRef]
- Kovalchuk, B.M.; Kharlov, A.V.; Vizir, V.A.; Kumpyak, V.V.; Zorin, V.B.; Kiselev, V.N. High-voltage pulsed generator for dynamic fragmentation of rocks. Rev. Sci. Instrum. 2010, 81, 103506. [Google Scholar] [CrossRef] [Green Version]
- Mehta, G.; Somani, M.; Babu, T.N.; Watts, T. Contact stress analysis on composite spur gear using finite element method. Mater. Today Proc. 2018, 5, 13585–13592. [Google Scholar] [CrossRef]







| Radus (mm) | Averagefield Strength in Bubble (kV/cm) | Average Field Strength in Rock (kV/cm) | Maximum EFS (kV/cm) | Minimum EFS (kV/cm) |
|---|---|---|---|---|
| 0 | / | 100 | 100 | 100 |
| 0.5 | 198.36 | 99.711 | 198.991 | 0.562990 |
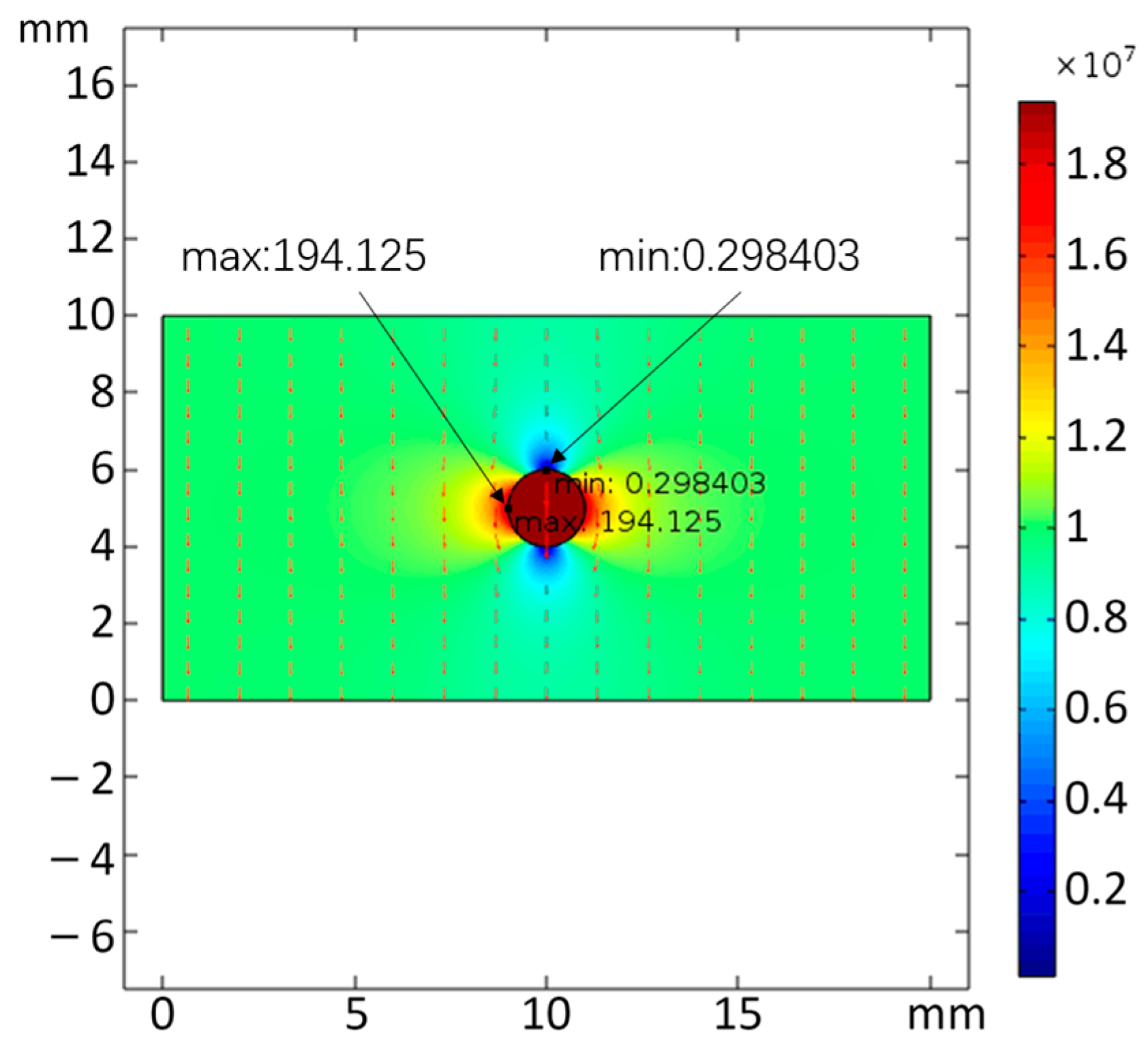
| 1 | 193.63 | 98.877 | 194.125 | 0.298403 |
| 1.5 | 186.22 | 97.595 | 187.372 | 0.716550 |
| 2 | 176.75 | 96.012 | 178.825 | 0.149587 |
| 2.5 | 165.93 | 94.316 | 170.046 | 0.225034 |
| 3 | 154.46 | 92.724 | 161.497 | 0.021227 |
| 3.5 | 142.98 | 91.485 | 154.22 | 0.009392 |
| 4 | 132.06 | 90.896 | 148.21 | 0.003924 |
| 4.5 | 122.10 | 91.329 | 143.38 | 0.001834 |
| 5 | 113.27 | 93.255 | 139.473 | 0.000001 |
| Distance (mm) | Maximum EFS (KV/cm) | Minimum EFS (KV/cm) |
|---|---|---|
| 2.5 | 175.285 | 0.161014 |
| 3 | 176.612 | 0.515544 |
| 3.5 | 177.537 | 0.185995 |
| 4 | 178.234 | 0.274461 |
| 4.5 | 178.646 | 0.450939 |
| 5 | 178.825 | 0.149587 |
| 5.5 | 178.653 | 0.156543 |
| 6 | 178.224 | 0.132506 |
| 6.5 | 177.619 | 0.128387 |
| 7 | 176.628 | 0.129468 |
| 7.5 | 175.310 | 0.086176 |
| Rock Types | Relative Permittivity |
|---|---|
| silicate | 6 |
| Granite | 7 |
| Pyrite | 45 |
| quartz | 80 |
| chalcopyrite | 110 |
| Insulating Liquid Material | Dielectric Constant |
|---|---|
| Salt solution | 201 |
| Water | 81 |
| Deionized water | 45 |
| methanol | 25.7 |
| Transformer oil | 2.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Wang, G.; Pan, X.; Li, Y.; He, J.; Qi, Y.; Yang, J. High Voltage Electric Pulse Drilling: A Study of Variables through Simulation and Experimental Tests. Energies 2023, 16, 1174. https://doi.org/10.3390/en16031174
Zhang Q, Wang G, Pan X, Li Y, He J, Qi Y, Yang J. High Voltage Electric Pulse Drilling: A Study of Variables through Simulation and Experimental Tests. Energies. 2023; 16(3):1174. https://doi.org/10.3390/en16031174
Chicago/Turabian StyleZhang, Qingyu, Guanglin Wang, Xudong Pan, Yuefeng Li, Jianqi He, Yue Qi, and Juesuan Yang. 2023. "High Voltage Electric Pulse Drilling: A Study of Variables through Simulation and Experimental Tests" Energies 16, no. 3: 1174. https://doi.org/10.3390/en16031174
APA StyleZhang, Q., Wang, G., Pan, X., Li, Y., He, J., Qi, Y., & Yang, J. (2023). High Voltage Electric Pulse Drilling: A Study of Variables through Simulation and Experimental Tests. Energies, 16(3), 1174. https://doi.org/10.3390/en16031174






