What Else Do the Deep Learning Techniques Tell Us about Voltage Dips Validity? Regional-Level Assessments with the New QuEEN System Based on Real Network Configurations
Abstract
:1. Introduction
2. Voltage Dips Monitoring: The QuEEN System
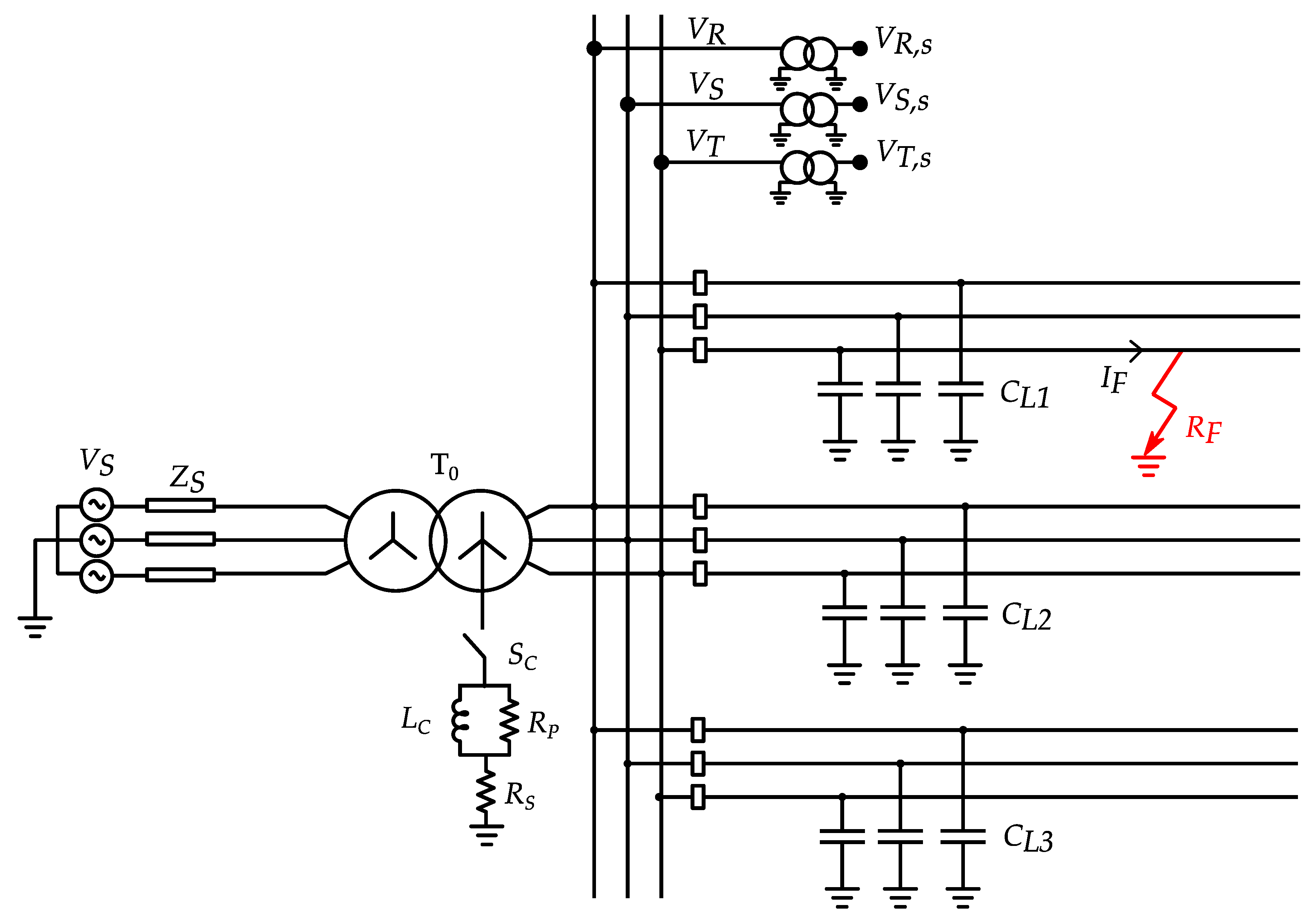
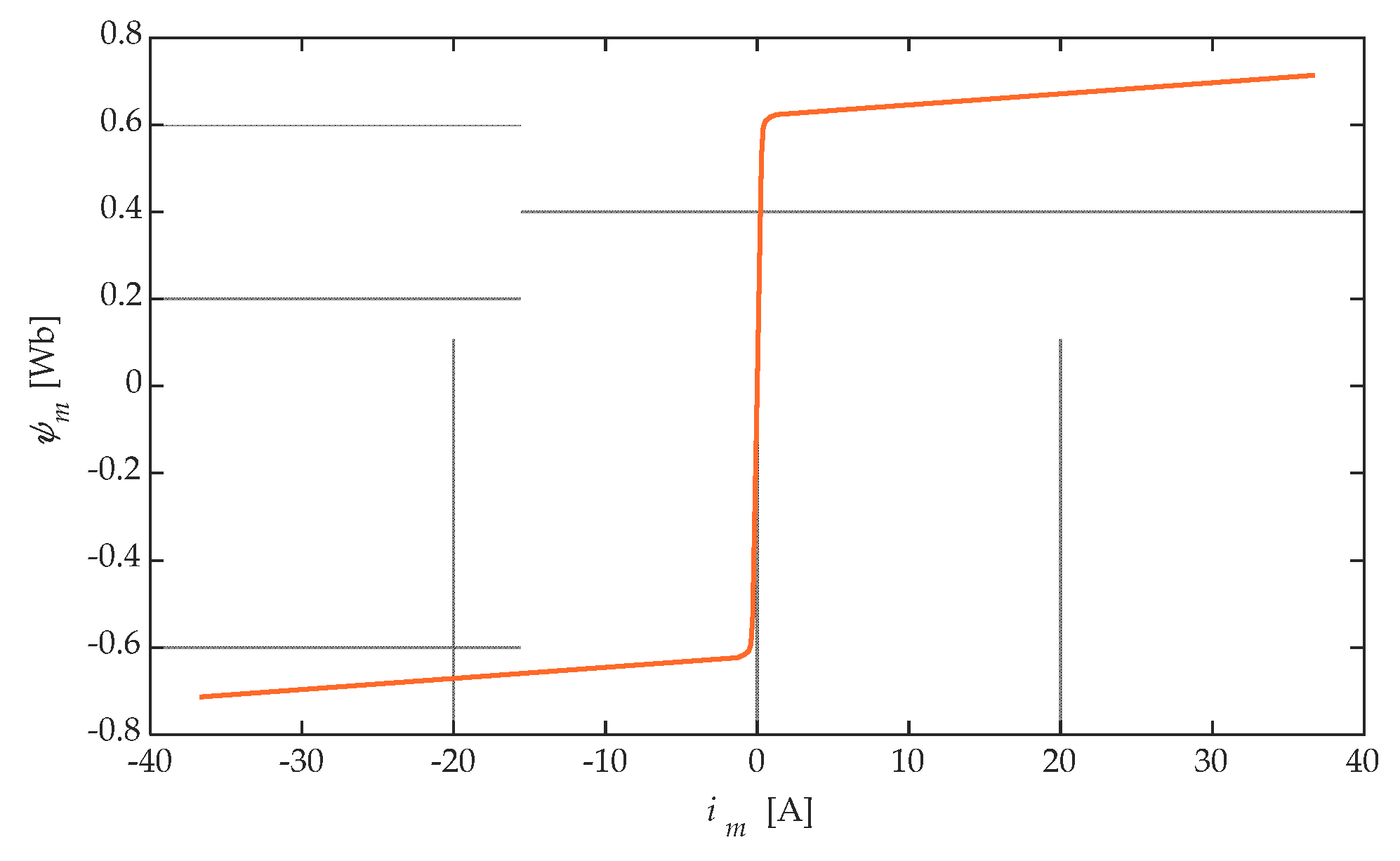
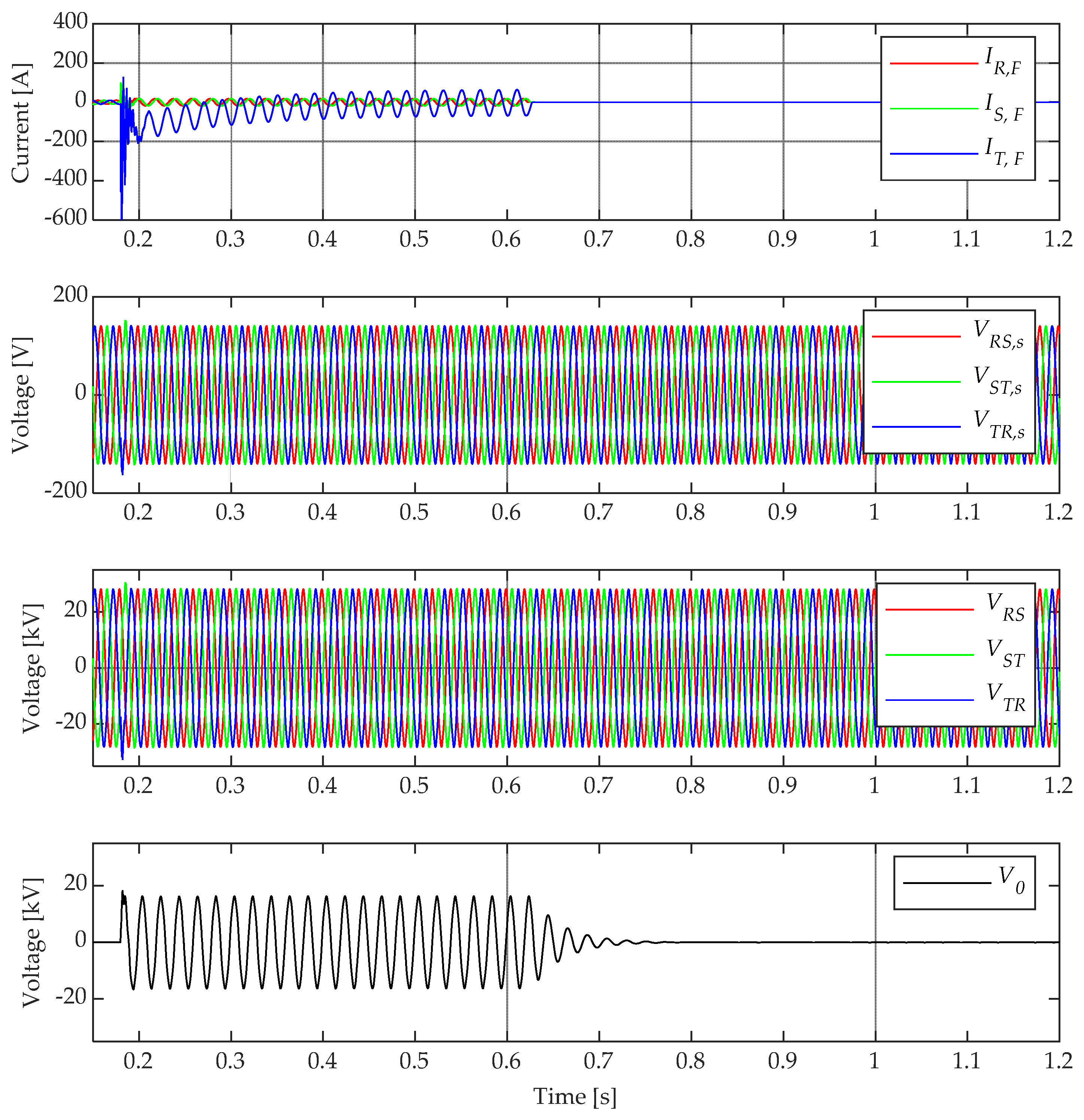
3. Voltage Dips Validity in Isolated and Compensated Network
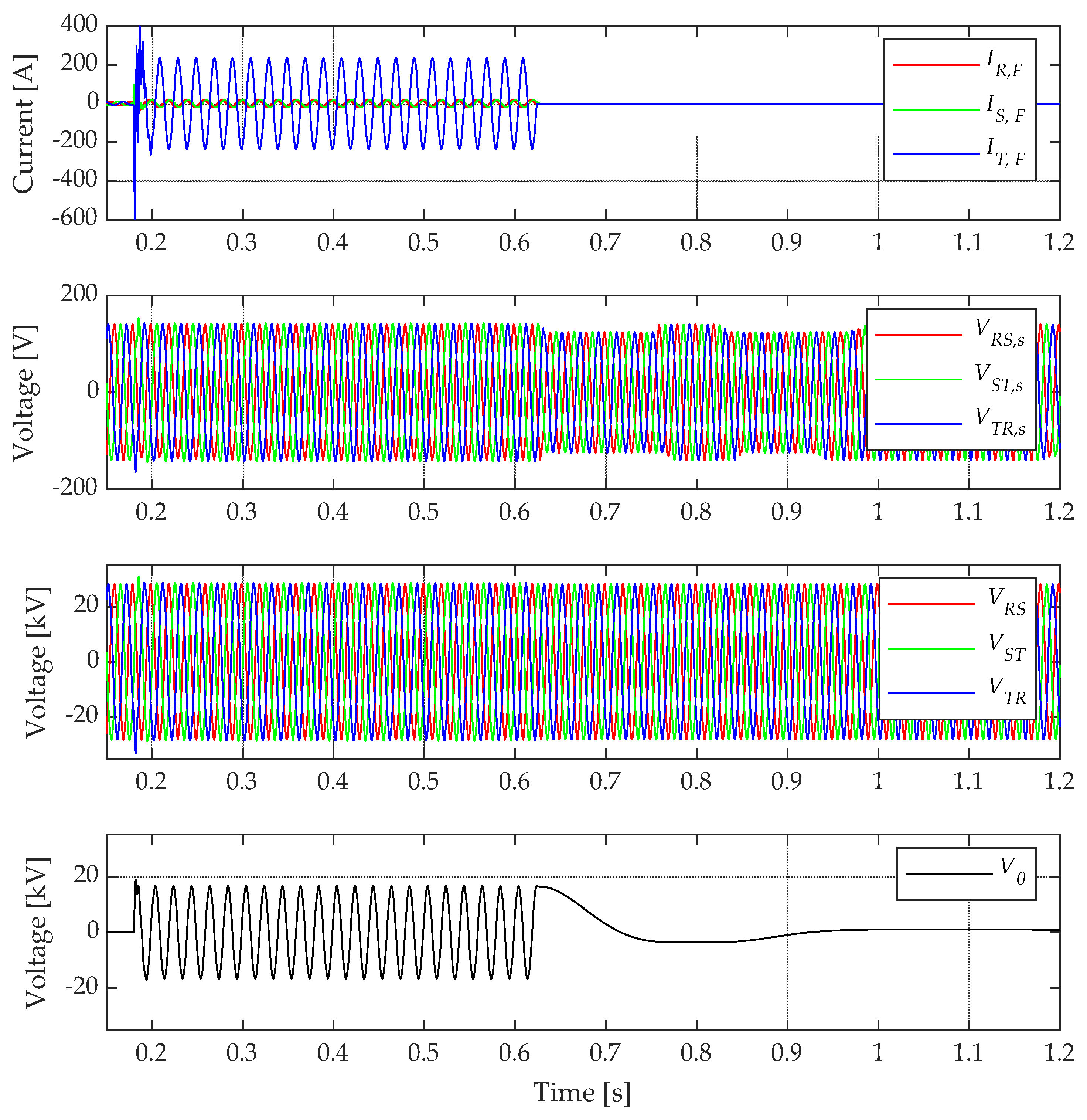
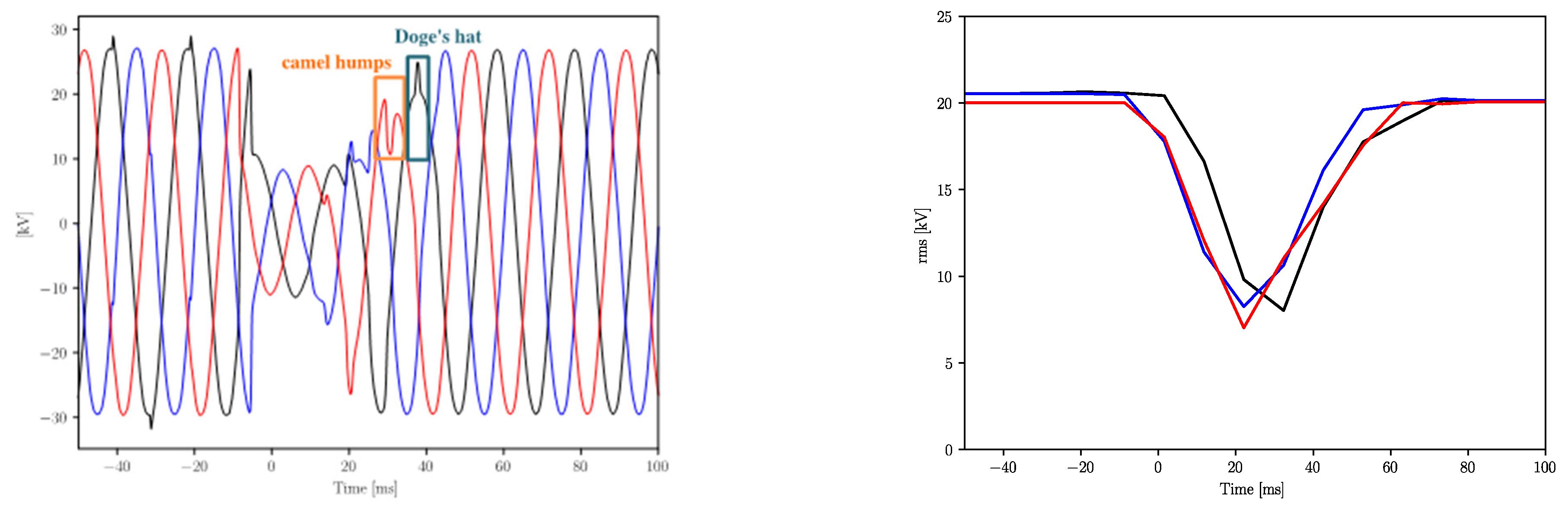
Extinction of a Single Phase-to-Ground Fault
- Case 1: SC closed—compensated neutral (CN) system;
- Case 2: SC open—isolated neutral (IN) system.
- Faulted line currents (IR, F, IS, F, IT, F);
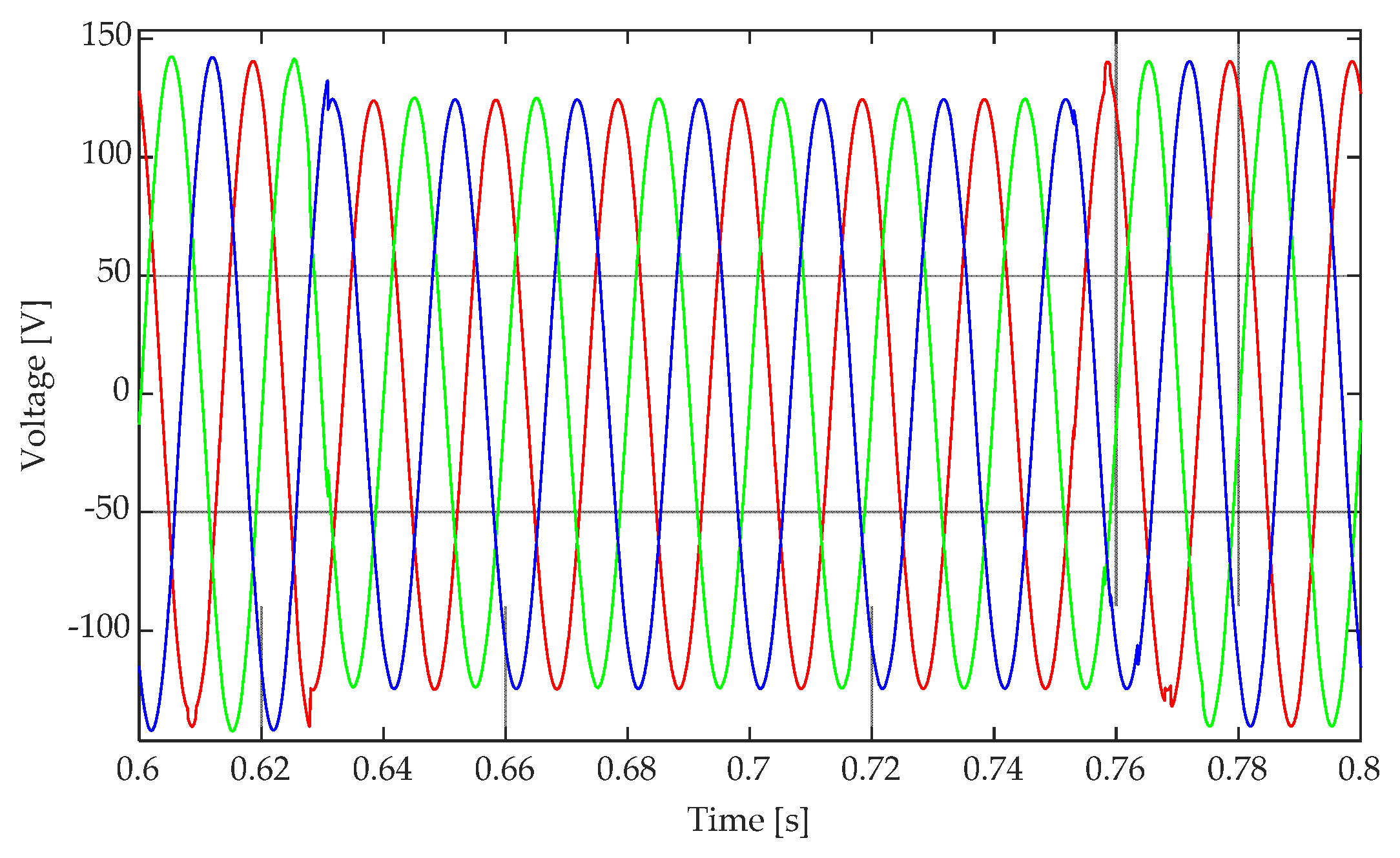
- Line-to-line voltages (VRS, s, VST, s, VTR, s) computed from the VTs secondary side phase to ground voltages (VR, s, VS, s, VT, s);
- Line-to-line voltages at MV busbar (VRS, VST, VTR);
- Homopolar voltage (V0).
4. Voltage Dip Validity Assessment: Current and New Criteria
4.1. 2nd Harmonic Criterion
- the occurrence of an exceeding of the second harmonic threshold (fixed at a given percentage of the effective value);
- the occurrence of a minimum number of consecutive overruns of the second harmonic threshold.
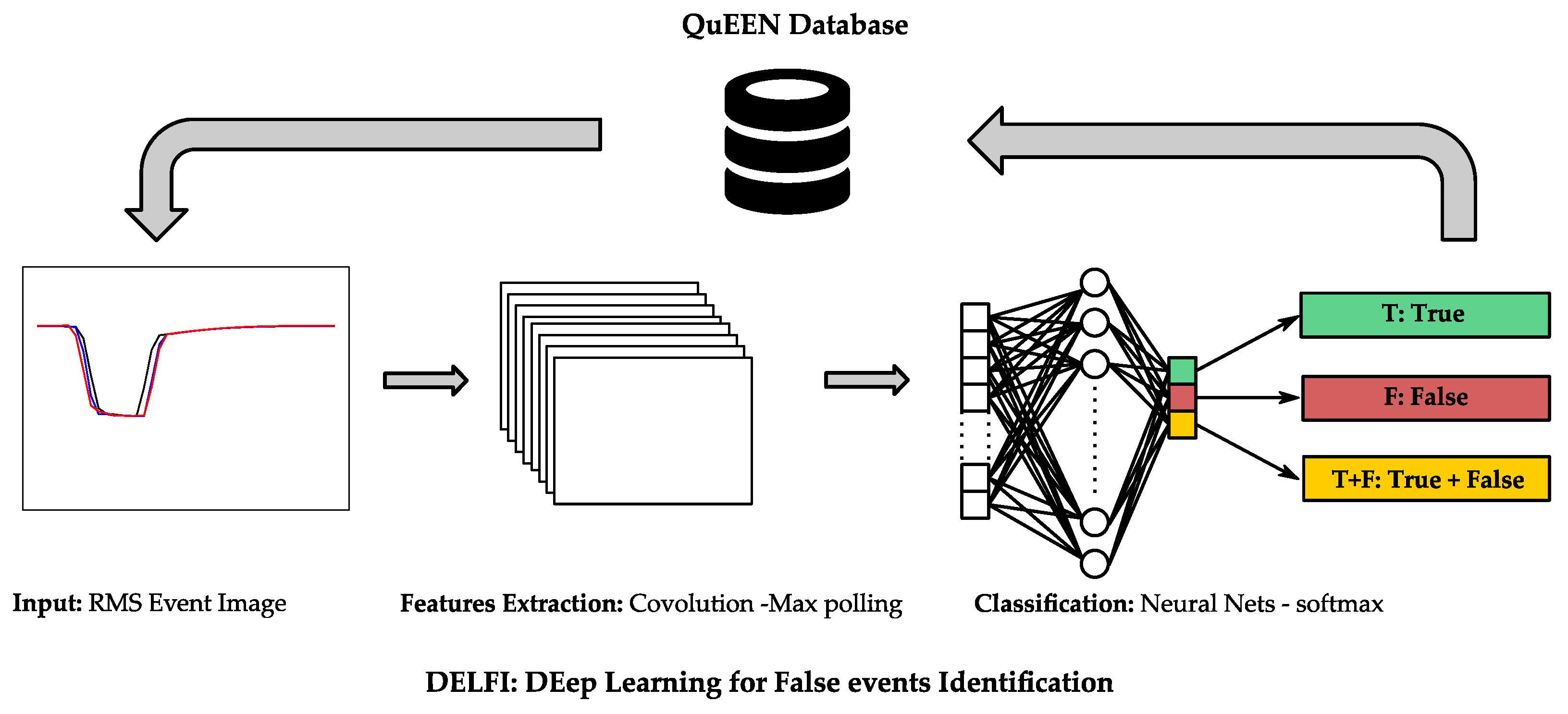
4.2. DELFI—Deep Learning for False Events Identification
5. Comparison of Criteria for Validity Assessment
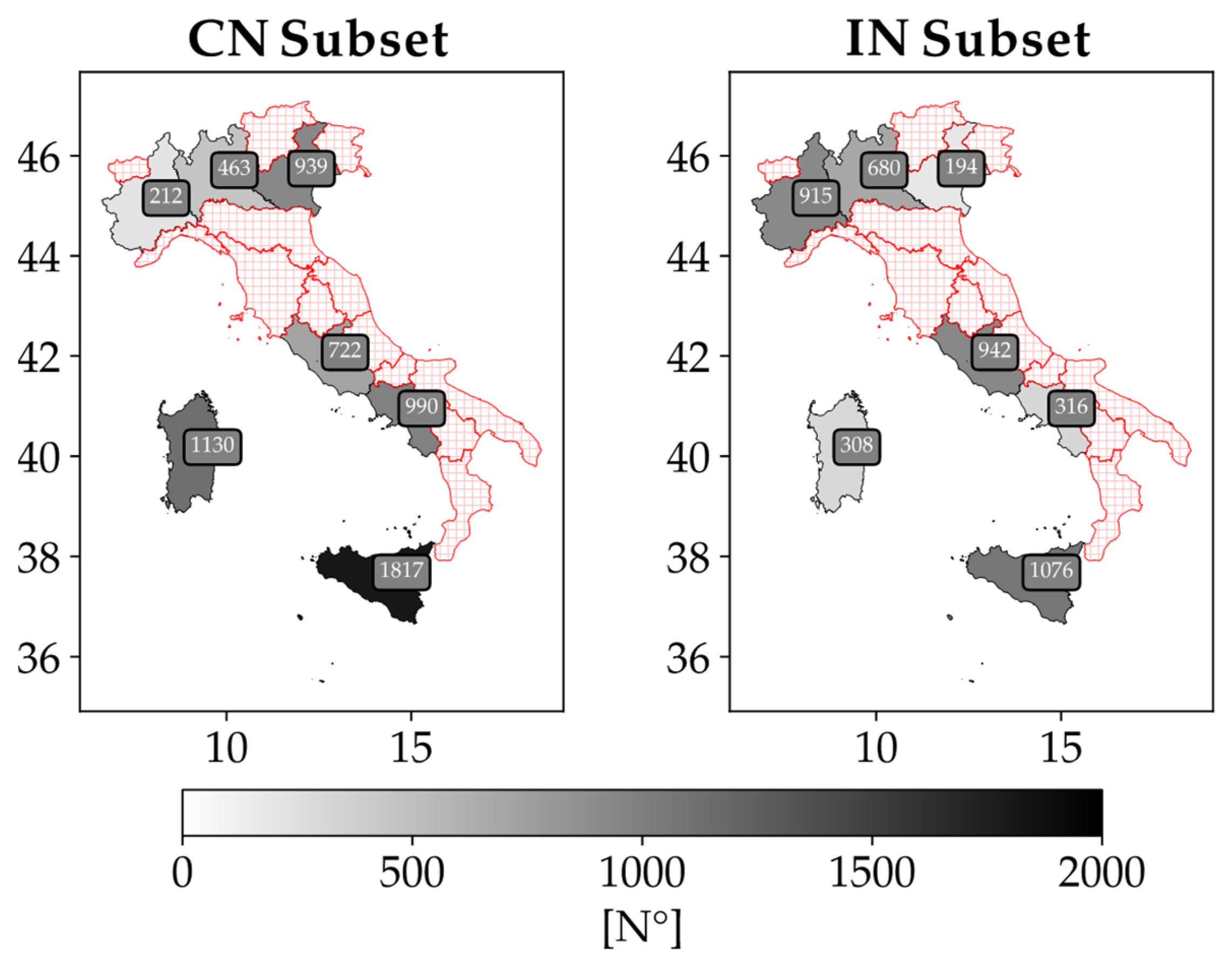
- Overall Set: 10,704 events;
- Compensated Neutral Subset: 6273 events;
- Isolated Neutral Subset: 4431 events.
- Global analysis: all data are grouped, respectively for each defined subset;
- Sensibility analysis: the subsets are analyzed considering duration and residual voltage;
- Regional analysis: subsets are considered among the seven chosen regions.
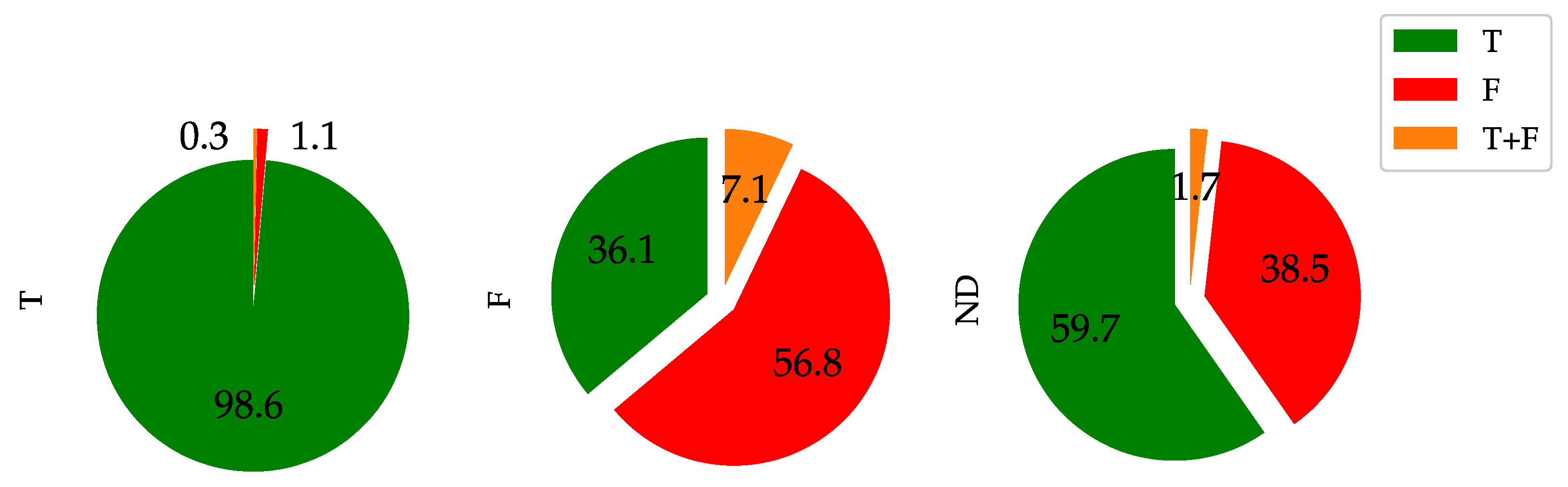
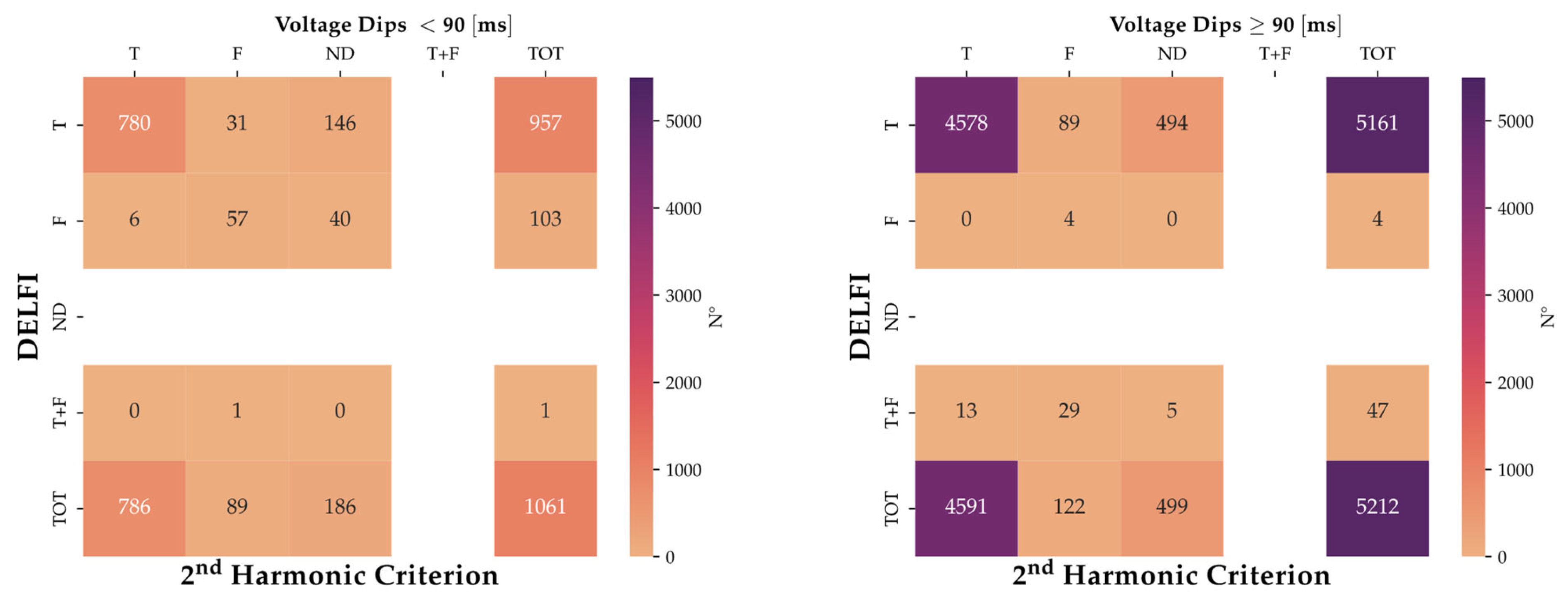
5.1. Global Analysis
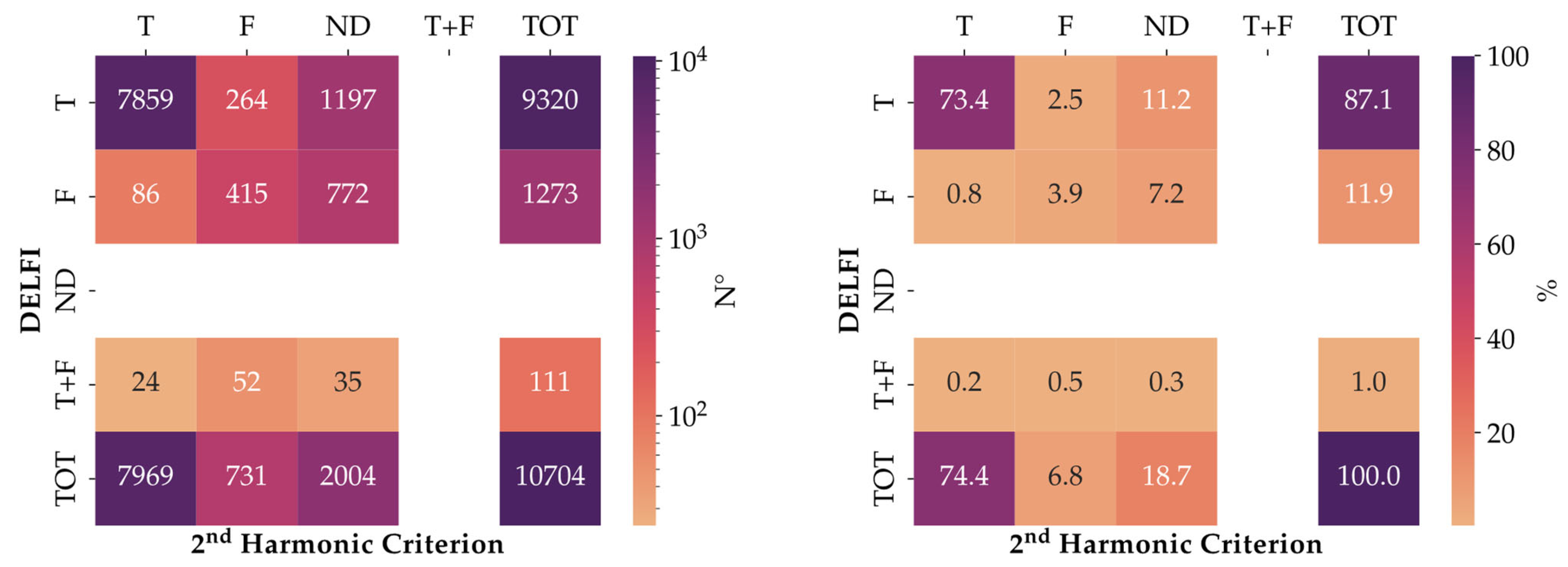
- T, F, ND for the 2nd Harmonic Criterion classifier;
- T, F, T + F for the DELFI classifier.
- DELFI results are in the rows;
- the columns refer to the outcomes of the 2nd Harmonic Criterion.
- (T, ND): the recorded values for the CN and IN Subsets are, respectively 10.2% and 12.6%, namely a considerable number of events, classified as ND by the 2nd Harmonic Criterion but readmitted as T by the DELFI classifier (respectively 640 and 557 voltage dips). This means that the DELFI classifier readmits into class T a not negligible number of ND events for both subsets;
- (F, ND): the recorded value is 0.6% for the CN Subset, namely 40 events, while the same cell reaches 16.5% or 732 events for the IN Subset. This disparity is a consistent result since, theoretically, the F events are not foreseen for the CN Subset and hence the new criterion acts coherently with the expected electrical characteristics of the network;
- (T, F): the number of events classified as F by the 2nd Harmonic Criterion and readmitted as T by DELFI is not negligeable for both the CN and IN Subsets with 1.9% (120 events) and 3.2% (144 events), respectively.
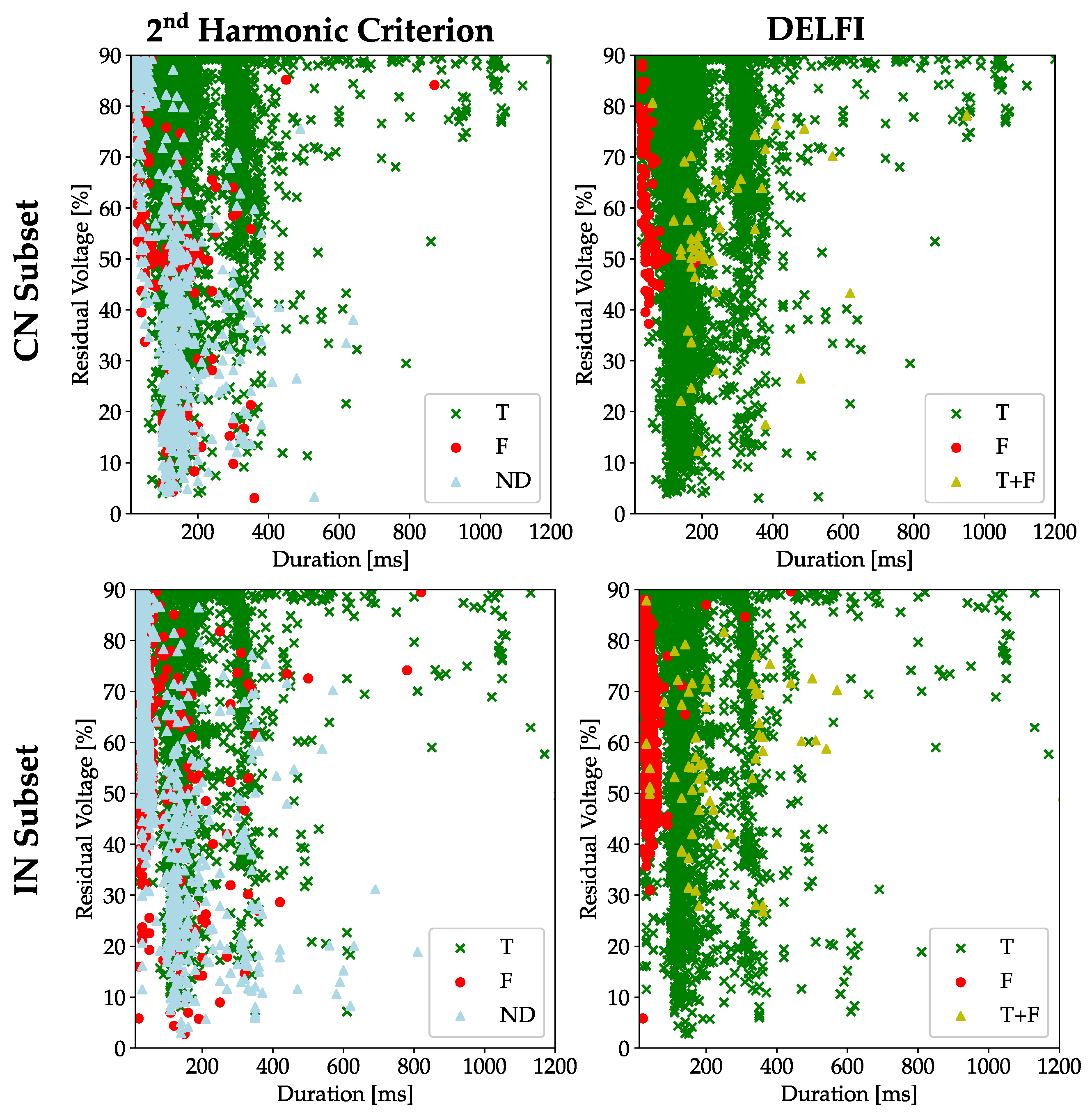
5.2. Sensibility Analysis: Duration and Residual Voltage
- events with duration < 90 ms;
- events with duration ≥ 90 ms.
5.3. Regional Analysis
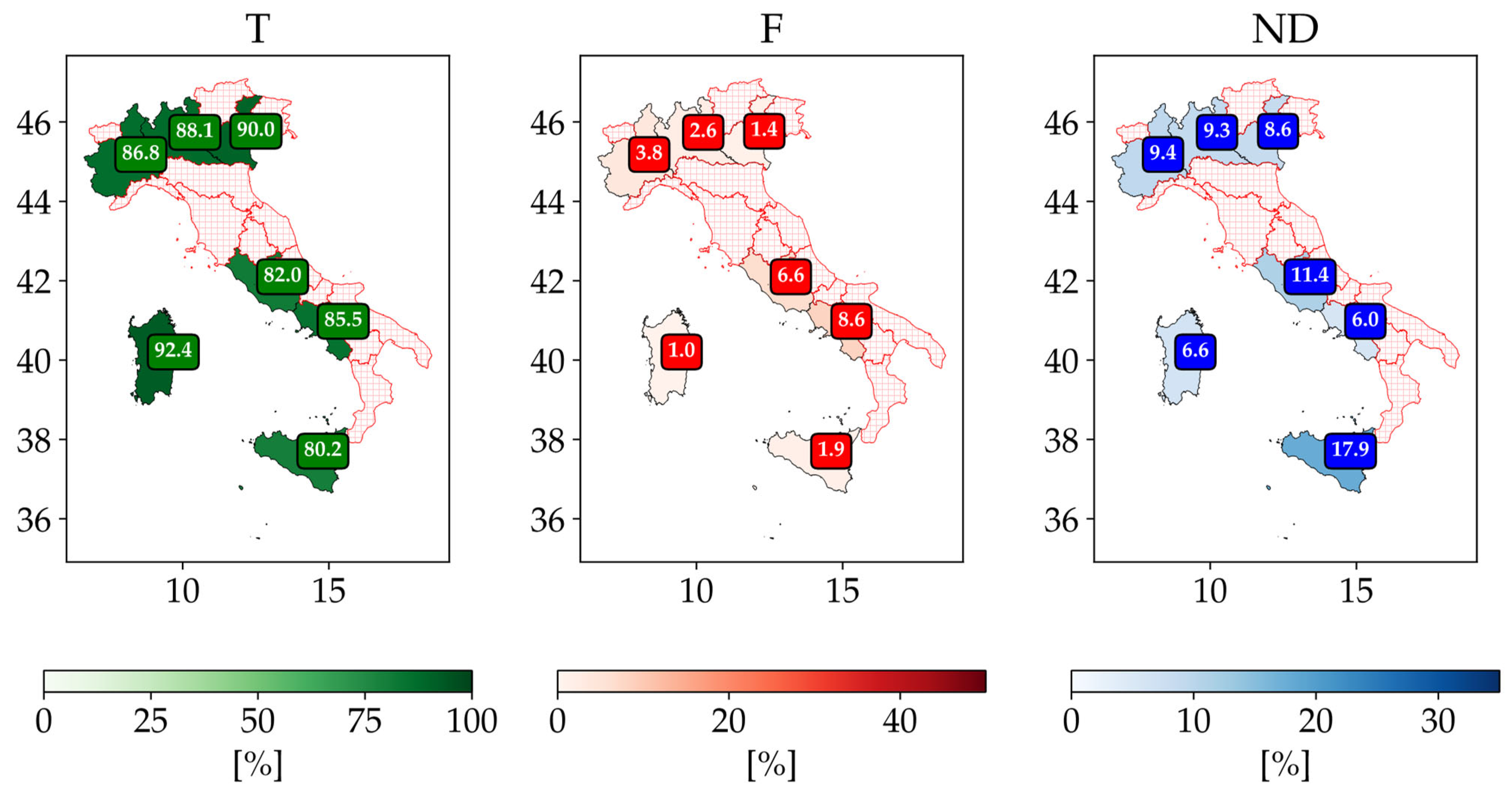
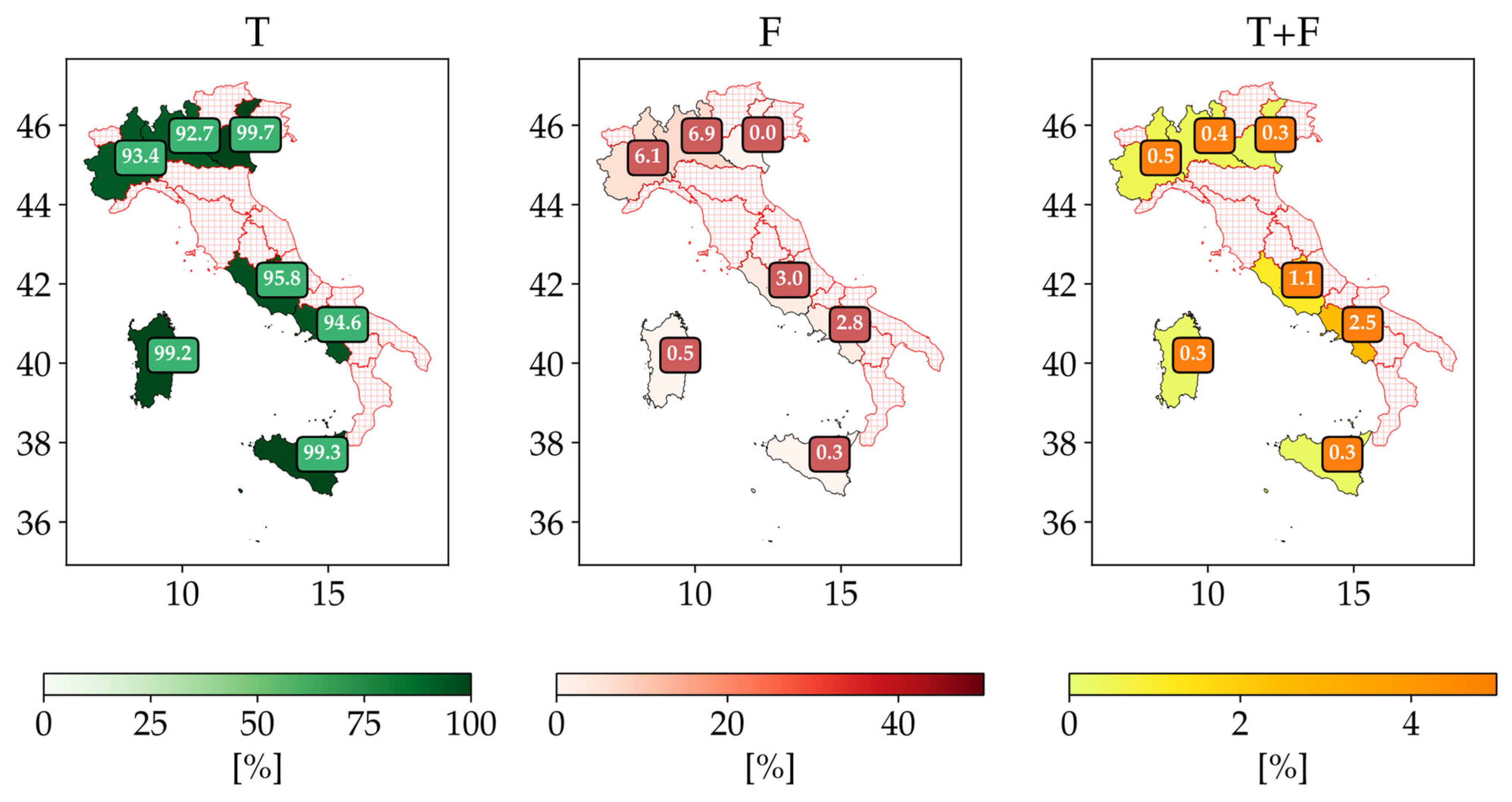
- the T label rate ranges from 80.2% in Sicilia up to 92.4% in Sardegna;
- considering F events, the highest ratios are recorded for Lazio and Campania with 6.6% and 8.6%, respectively;
- finally, for the ND label rate, high values are recorded for Sicilia (17.9%), Lazio (11.4%), Piemonte (9.4%) and Lombardia (9.3%).
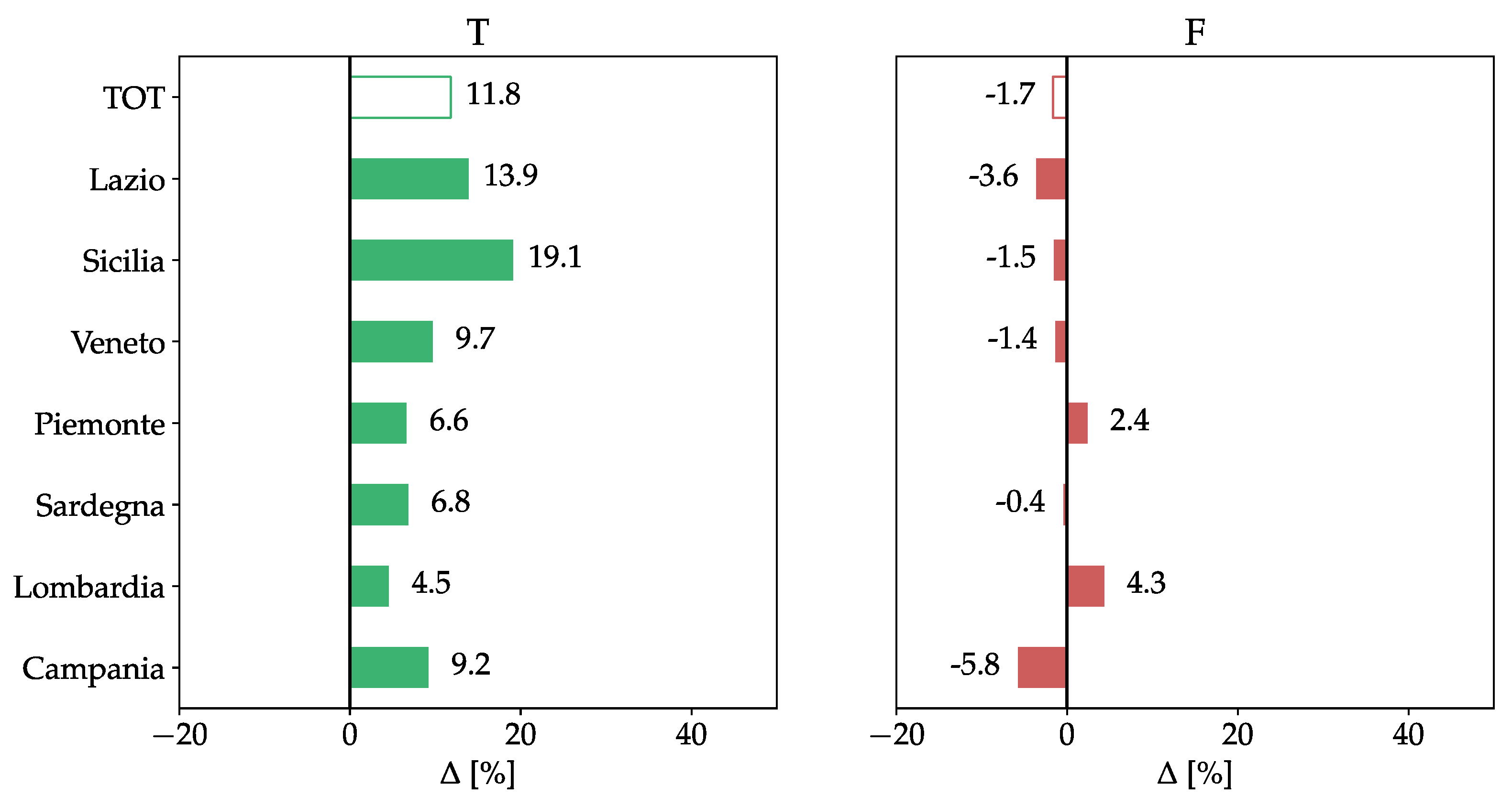
- there is a significant increase in the T rate for all regions, going from 92.7% in Lombardia up to the 99.2% reached in Sardegna;
- consistent with what has been highlighted for class T, class F rate decreases in percentage for almost all regions except for Piemonte and Lombardia. This means that most of the ND events are reclassified as T in each region so that the increase of the T class compared to the F class is significantly larger. This is in accordance with what is expected from the network characteristics.
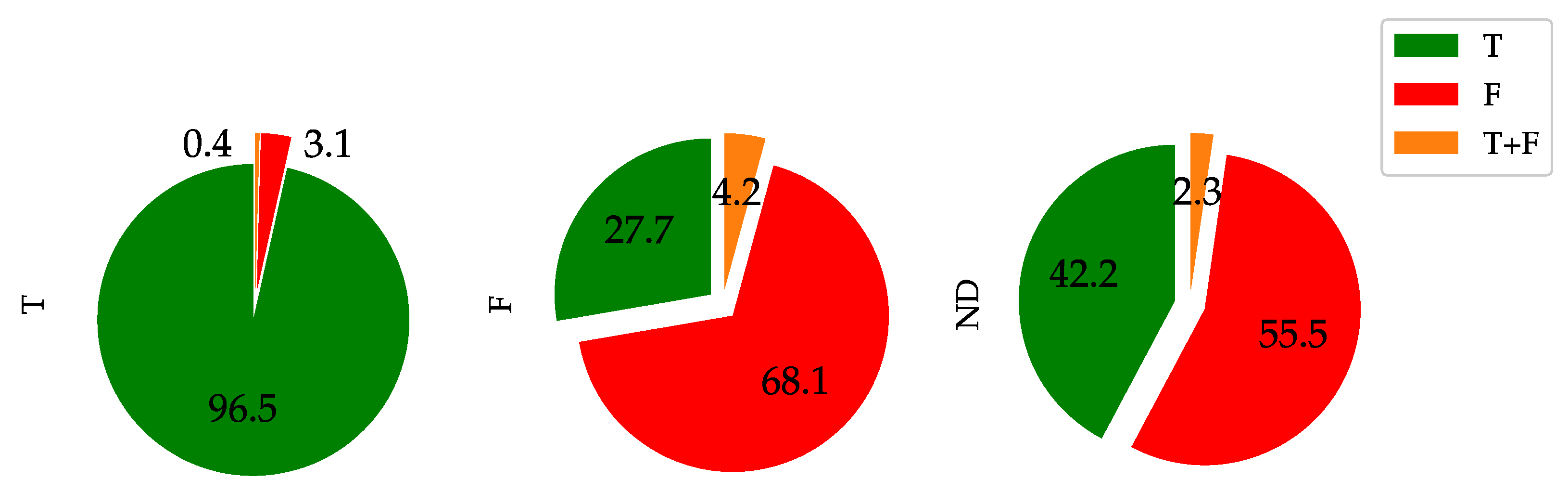
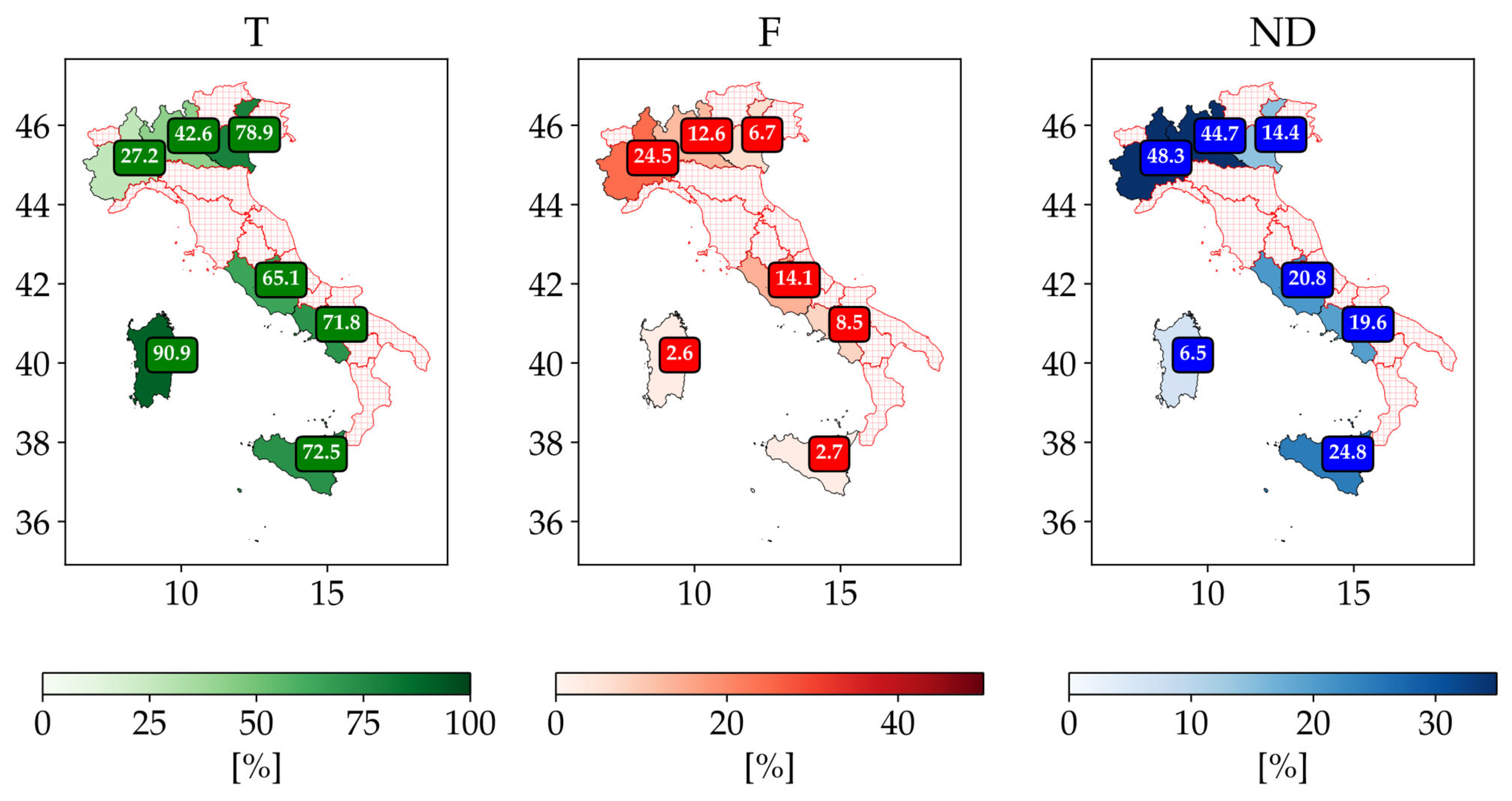
- the T events ratio shows a considerable variation, ranging from 27.2% in Piemonte to 90.9% in Sardegna. Additionally, noteworthy is the 42.6% recorded in Lombardia;
- considering F events, the regional distribution is very irregular as the maximum values is reached by Piemonte with 24.5% while the minimum value 2.6% is recorded in Sardegna;
- finally, also for ND events, the regional distribution is uneven and with considerably higher values than the CN Subset: the highest values are recorded in Piemonte at 48.3% and Lombardia at 44.7% while Sicilia, Lazio and Campania have slightly lower values, with 25%, 21% and 20%, respectively. However, they are still higher than those of the CN Subset.
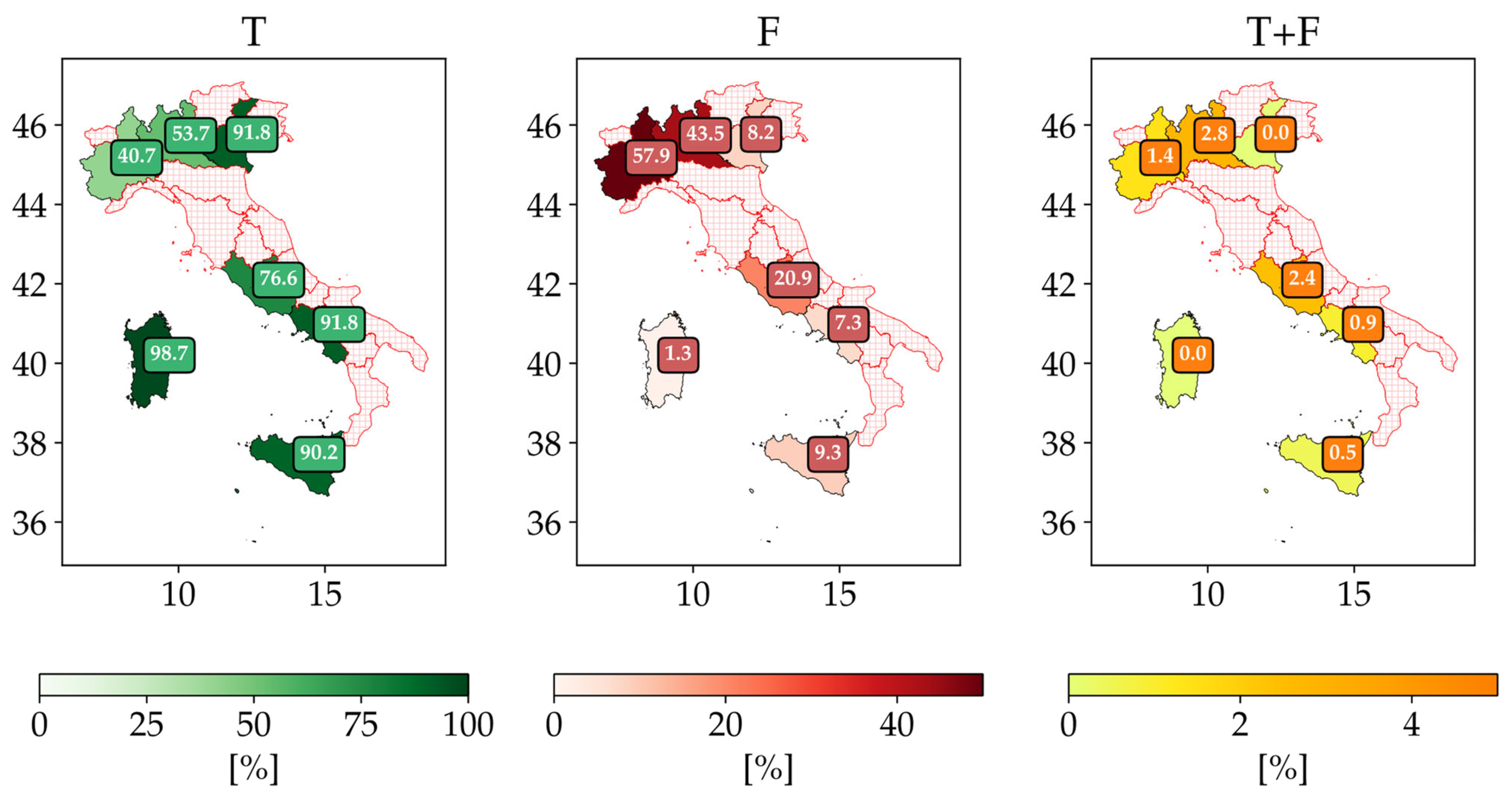
- for the T class, a global increase is achieved. Four regions have reached a T rate above 90% (Veneto, Campania, Sicilia and Sardegna), while Lombardia and Piemonte show considerably lower values with, respectively 53.7% and 40.7%;
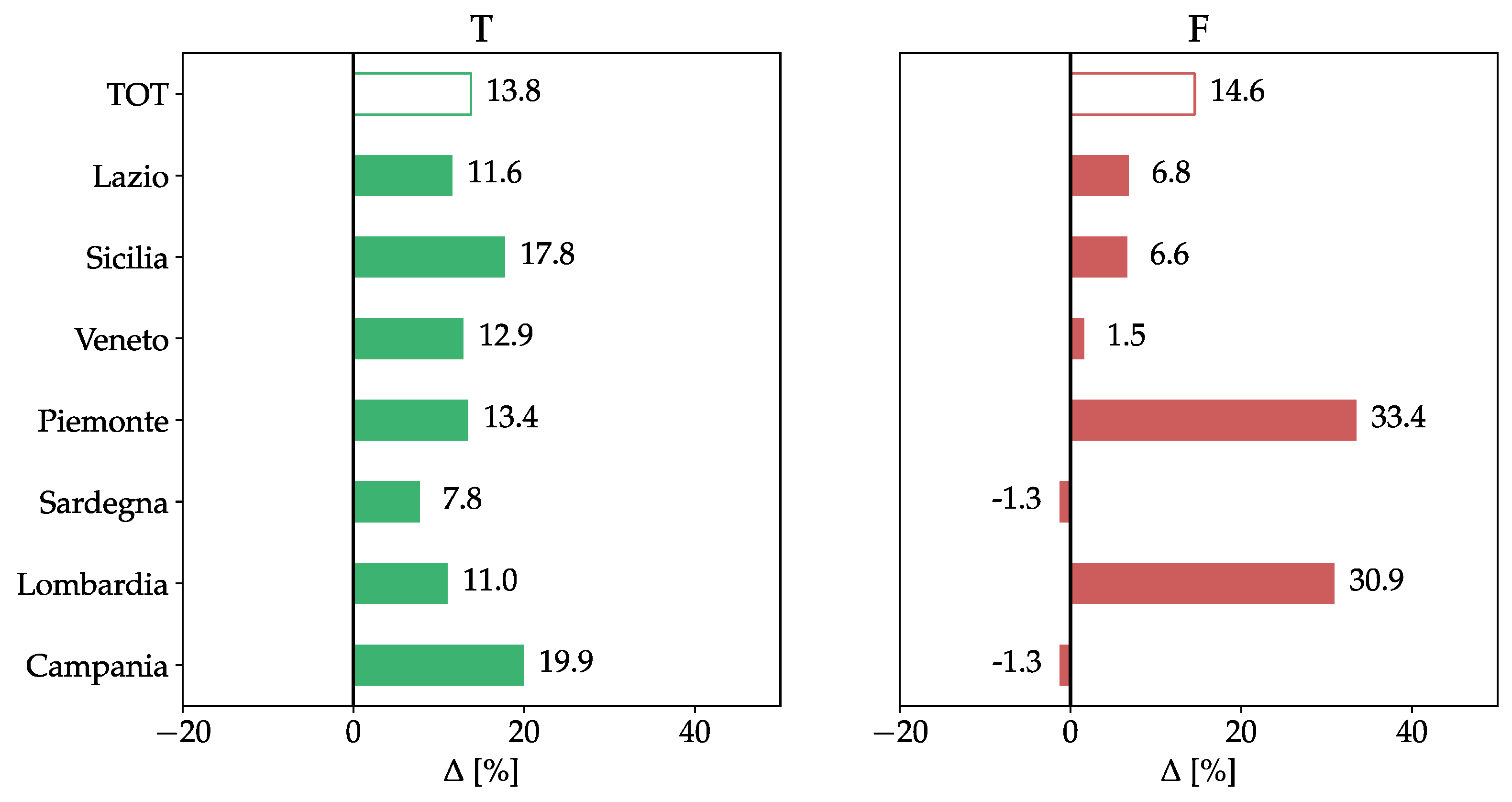
- focusing on F events, the adoption of the new criterion in Lombardia and Piemonte outcomes is relevant: an increase of 31% and 33%, respectively, was recorded, while Lazio and Sicilia recorded an increase of about 7%. On the other hand, Sardegna and Campania showed a reduction in the F rate of −1.3%.
- Piemonte and Lombardia (~50% of F events) which seem to be characterized by a high number of single phase-to-ground faults compared to polyphase ones;
- Veneto, Campania, Sardegna and Sicily (<10% of F events) which show a low number of single-phase to ground faults compared to polyphase ones;
- Lazio (20% of F events), which seems to have been affected by an intermediate number of single-phase to ground faults compared to polyphase ones.
5.4. New QuEEN Website Tables
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bollen, M.H.J.; Das, R.; Djokic, S.; Ciufo, P.; Meyer, J.; Rönnberg, S.K.; Zavodam, F. Power Quality Concerns in Implementing Smart Distribution-Grid Applications. IEEE Trans. Smart Grid 2017, 8, 391–399. [Google Scholar] [CrossRef] [Green Version]
- Bollen, M.H.J. Understanding Power Quality Problems: Voltage Sags and Interruptions; IEEE Press: New York, NY, USA, 1999. [Google Scholar]
- CIGRE/CIRED JWG C4.112. Guidelines For Power Quality Monitoring—Measurement Locations, Processing and Presentation of Data. proceeding of the International Conference on Renewable Energies and Power Quality (ICREPQ’14), Cordoba, Spain, 8–10 April 2014. [Google Scholar]
- Kattmann, C.; Rudion, K.; Tenbohlen, S. Detailed power quality measurement of electric vehicle charging infrastructure. CIRED—Open Access Proc. J. 2017, 2017, 581–584. [Google Scholar] [CrossRef] [Green Version]
- Mottola, F.; Proto, D.; Varilone, P.; Verde, P. Planning of Distributed Energy Storage Systems in μGrids Accounting for Voltage Dips. Energies 2020, 13, 401. [Google Scholar] [CrossRef] [Green Version]
- Meyer, J.; Blanco, A.; Rönnberg, S.; Bollen, M.; Smith, J. CIGRE C4/C6.29: Survey of utilities experiences on power quality issues related to solar power. CIRED—Open Access Proc. J. 2017, 1, 539–543. [Google Scholar] [CrossRef]
- Ray, K.; Mohanty, S.R.; Kishor, N. Classification of power quality disturbances due to environmental characteristics in distributed generation system. IEEE Trans. Sustain. Energy 2013, 4, 302–313. [Google Scholar] [CrossRef]
- EN50160: 2010; Voltage Characteristics of Electricity Supplied by Public Electricity Networks. CENELEC: Brussels, Belgium, 2010.
- IEEE Std 1564–2014; IEEE Guide for Voltage Sag Indices. IEEE: Piscataway, NJ, USA, 2014; pp. 1–59.
- Joint Working Group Cigre/Cired C4.110. Voltage Dip Immunity of Equipment and Installations; Report 412; Cigré: Paris, France, 2010. [Google Scholar]
- De Santis, M.; Di Stasio, L.; Noce, C.; Verde, P.; Varilone, P. Initial Results of an Extensive, Long-Term Study of the Forecasting of Voltage Sags. Energies 2021, 14, 1264. [Google Scholar] [CrossRef]
- D’Orazio, L.; Corsi, N.; Riva, S. Analysis of voltage dips on Italian distribution network. In Proceedings of the 2021 AEIT International Annual Conference (AEIT), Milan, Italy, 4–8 October 2021; pp. 1–6. [Google Scholar]
- Šipoš, M.; Klaić, Z.; Nyarko, E.K.; Fekete, K. Determining the Optimal Location and Number of Voltage Dip Monitoring Devices Using the Binary Bat Algorithm. Energies 2021, 14, 255. [Google Scholar] [CrossRef]
- Patra, J.; Pal, N. A Mathematical Approach of Voltage Sag Analysis Incorporating Bivariate Probability Distribution in a Meshed System. Energies 2022, 15, 7592. [Google Scholar] [CrossRef]
- Yalman, Y.; Uyanık, T.; Atlı, İ.; Tan, A.; Bayındır, K.Ç.; Karal, Ö.; Golestan, S.; Guerrero, J.M. Prediction of Voltage Sag Relative Location with Data-Driven Algorithms in Distribution Grid. Energies 2022, 15, 6641. [Google Scholar] [CrossRef]
- Guo, X.; Li, Y.; Wang, S.; Cao, Y.; Zhang, M.; Zhou, Y.; Yosuke, N. A Comprehensive Weight-Based Severity Evaluation Method of Voltage Sag in Distribution Networks. Energies 2021, 14, 6434. [Google Scholar] [CrossRef]
- Milanovic, J.V.; Gupta, C.P. Probabilistic Assessment of Financial Losses due to Interruptions and Voltage Sags—Part I: The Methodology. IEEE Trans. Power Deliv. 2006, 21, 918–924. [Google Scholar] [CrossRef]
- Milanovic, J.V.; Gupta, C.P. Probabilistic Assessment of Financial Losses due to Interruptions and Voltage Sags—Part II: Practical Implementation. IEEE Trans. Power Deliv. 2006, 21, 925–932. [Google Scholar] [CrossRef]
- Celli, G.; Pilo, F.; Pisano, G.; Soma, G.G. Including voltage dips mitigation in cost-benefit analysis of storages. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Motoki, É.M.; Filho, J.M.d.C.; da Silveira, P.M.; Pereira, N.B.; de Souza, P.V.G. Cost of Industrial Process Shutdowns Due to Voltage Sag and Short Interruption. Energies 2021, 14, 2874. [Google Scholar] [CrossRef]
- Chiumeo, R.; Cucchietti, F.; Griffa, G.; Tenti, L. The power quality of the distribution networks and its impact on the telecommunication next generation access network. REPQJ 2014, 12, 396–400. [Google Scholar] [CrossRef]
- Chiumeo, R.; de Nigris, M.; Garbero, L.; Porrino, A.; Tenti, L. The Italian power quality monitoring system of the MV network results of the measurements of voltage dips after 3 years campaign. In Proceedings of the 20th International Conference and Exhibition on Electricity Distribution (CIRED 2009), Prague, Czech Republic, 8–11 June 2009. paper 0737. [Google Scholar] [CrossRef] [Green Version]
- Chiumeo, R.; de Nigris, M.; Gandolfi, C.; Garbero, L.; Tenti, L.; Carpaneto, E. Implementation of a New Method for an Improved Voltage Dips Evaluation by the Italian Power Quality Monitoring System in Presence of VT Saturation Effects. REPQJ 2010, 1, 519–523. [Google Scholar] [CrossRef]
- Chiumeo, R.; Garbero, L.; Malegori, F.; Tenti, L. Feasible methods to evaluate voltage dips origin. REPQJ 2015, 1, 357–361. [Google Scholar] [CrossRef]
- Turović, R.; Dragan, D.; Gojić, G.; Petrović, V.B.; Gajić, D.B.; Stanisavljević, A.M.; Katić, V.A. An End-to-End Deep Learning Method for Voltage Sag Classification. Energies 2022, 15, 2898. [Google Scholar] [CrossRef]
- Mei, F.; Ren, Y.; Wu, Q.; Zhang, C.; Pan, Y.; Sha, H.; Zheng, J. Online Recognition Method for Voltage Sags Based on a Deep Belief Network. Energies 2019, 12, 43. [Google Scholar] [CrossRef]
- Balouji, E.; Gu, I.Y.H.; Bollen, M.H.J.; Bagheri, A.; Nazari, M. A LSTM-based deep learning method with application to voltage dip classification. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Tenti, L.; Chiumeo, R.; Zanoni, M.; Shadmehr, H. Deep Learning to Assess Voltage Dips Validity. In Proceedings of the 2020 AEIT International Annual Conference (AEIT), Catania, Italy, 23–25 September 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Zanoni, M.; Chiumeo, R.; Tenti, L.; Volta, M. Automated Tool Based on Deep Learning to Assess Voltage Dips Validity: Integration in the QuEEN MV network Monitoring System. REPQJ 2021, 14, 409–413. [Google Scholar] [CrossRef]
- Shadmehr, H.; Chiumeo, R.; Tenti, L. Self-tuning kalman filter and machine learning algorithms for voltage dips upstream or downstream origin detection. REPQJ 2016, 19, 235–240. [Google Scholar] [CrossRef]
- Zanoni, M.; Chiumeo, R.; Tenti, L.; Volta, M. FExWaveS application for voltage dips origin assessment: Optimization of the tool in views of its integration into the QuEEN monitoring system. In Proceedings of the 2021 AEIT International Annual Conference (AEIT), Milan, Italy; 2021; pp. 1–6. [Google Scholar]
- Zanoni, M.; Chiumeo, R.; Tenti, L.; Volta, M. Advanced Machine Learning Functionalities in the Medium Voltage Distributed Monitoring System QuEEN: A Macro-Regional Voltage Dips Severity Analysis. Energies 2021, 14, 7949. [Google Scholar] [CrossRef]
- Zanoni, M.; Chiumeo, R.; Tenti, L.; Volta, M. Highlighting of local Power Quality states with the new QuEEN system, enhanced with Deep Learning and Machine Learning algorithms. In Proceedings of the 2022 AEIT International Annual Conference (AEIT), Rome, Italy, 3–5 October 2022. [Google Scholar] [CrossRef]
- IEC 61000-4-30; Electromagnetic Compatibility (EMC)—Part 4-30: Testing and Measurement Techniques—Power Quality Measurement Methods. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2015.
- QuEEN—RSE (Qualità dell’Energia Elettrica) Home Page. Available online: http://queen.rse-web.it/ (accessed on 14 December 2022).
- CEER. 5th CEER Benchmarking Report on the Quality of Electricity Supply 2011; Annex to Chapter 3 on Voltage Quality data; CEER: Brussels, Belgium, 2012; pp. 136–139. [Google Scholar]
- AEEGSI. Resolution 29 December 2011, 198/2011. Available online: https://www.arera.it/it/docs/11/198-11arg.htm (accessed on 14 December 2022).
- ARERA. Resolution 23 December 2019, 566/2019/R/EEL. Available online: https://www.arera.it/it/docs/19/566-19.htm (accessed on 14 December 2022).
- Voltage Quality Indicators in Distribution Networks. 2021. Available online: https://www.arera.it/it/elettricita/qualitatensione.htm (accessed on 14 December 2022).

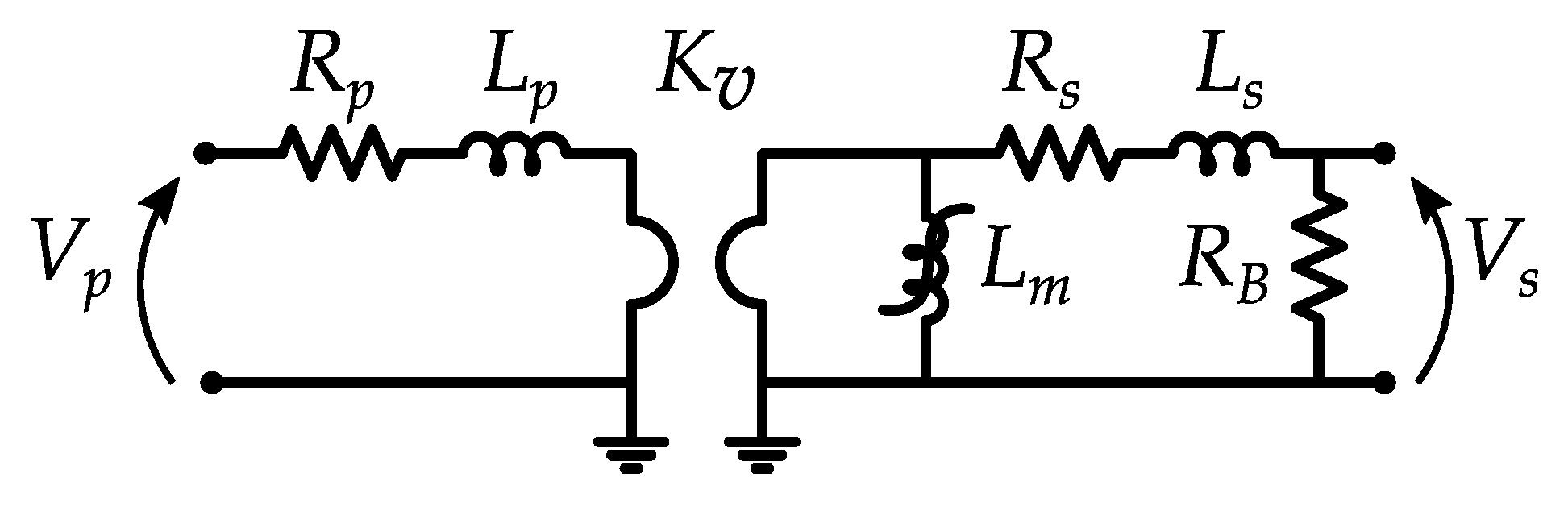


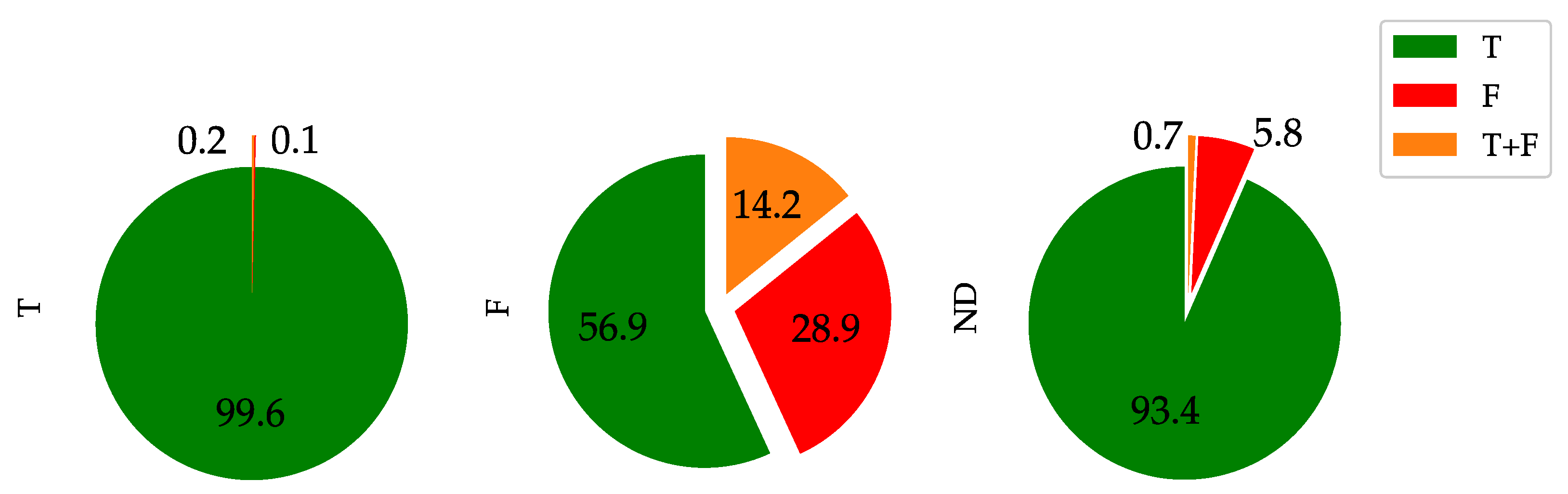


| Parameter | Value |
|---|---|
| Rp | 2667 Ω |
| Lp | 12.75 H |
| Kv | 20 kV/√3/100 V/√3 |
| Rs | 0.067 Ω |
| Ls | 0.32 mH |
| RB | 66.67 Ω |
| Parameter | Value |
|---|---|
| CNN number of Layers | 1 |
| Number of Kernel Matrices | 63 |
| Mini-Batch Size | 33 |
| Learning Rate | 1.2 × 10−5 |
| Max-Epoch | 20 |
| Italian Region | Number of Events |
|---|---|
| Piemonte | 1127 |
| Lombardia | 1143 |
| Veneto | 1133 |
| Lazio | 1664 |
| Campania | 1306 |
| Sardegna | 1438 |
| Sicilia | 2893 |
| Validity Criterion | Dataset | Criterion Labels | |||
|---|---|---|---|---|---|
| T [%] | F [%] | ND [%] | T + F [%] | ||
| 2nd Harmonic Criterion | Overall Set | 74.4% | 6.8% | 18.7% | - |
| CN Subset | 85.7% | 3.4% | 10.9% | - | |
| IN Subset | 58.5% | 11.7% | 29.8% | - | |
| DELFI | Overall Set | 87.1% | 11.9% | - | 1% |
| CN Subset | 97.5% | 1.7% | - | 0.8% | |
| IN Subset | 72.3% | 26.3% | - | 1.4% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zanoni, M.; Chiumeo, R.; Tenti, L.; Volta, M. What Else Do the Deep Learning Techniques Tell Us about Voltage Dips Validity? Regional-Level Assessments with the New QuEEN System Based on Real Network Configurations. Energies 2023, 16, 1189. https://doi.org/10.3390/en16031189
Zanoni M, Chiumeo R, Tenti L, Volta M. What Else Do the Deep Learning Techniques Tell Us about Voltage Dips Validity? Regional-Level Assessments with the New QuEEN System Based on Real Network Configurations. Energies. 2023; 16(3):1189. https://doi.org/10.3390/en16031189
Chicago/Turabian StyleZanoni, Michele, Riccardo Chiumeo, Liliana Tenti, and Massimo Volta. 2023. "What Else Do the Deep Learning Techniques Tell Us about Voltage Dips Validity? Regional-Level Assessments with the New QuEEN System Based on Real Network Configurations" Energies 16, no. 3: 1189. https://doi.org/10.3390/en16031189









