Next Article in Journal
Recent Trends, Opportunities and Challenges in Sustainable Management of Rice Straw Waste Biomass for Green Biorefinery
Next Article in Special Issue
Advanced Method of Variable Refrigerant Flow (VRF) Systems Designing to Forecast Onsite Operation—Part 2: Phenomenological Simulation to Recoup Refrigeration Energy
Previous Article in Journal
Modulus Estimation of Composites with High Porosity, High Particle Volume Fraction, and Particle Eigenstrain: Application to the LIB Active Layer with a Bridged-Particle Mesostructure
Previous Article in Special Issue
Advanced Method of Variable Refrigerant Flow (VRF) Systems Designing to Forecast On-Site Operation—Part 1: General Approaches and Criteria
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 16
Issue 3
10.3390/en16031425
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Evaluation of Numerical Methods for Predicting the Energy Performance of Windows

by
Anatoliy M. Pavlenko
* and
Karolina Sadko
Department of Building Physics and Renewable Energy, Kielce University of Technology, al. Tysiąclecia Państwa Polskiego 7, 25-314 Kielce, Poland
*
Author to whom correspondence should be addressed.
Energies 2023, 16(3), 1425; https://doi.org/10.3390/en16031425
Submission received: 14 December 2022 / Revised: 15 January 2023 / Accepted: 26 January 2023 / Published: 1 February 2023
(This article belongs to the Special Issue Latest Research of Building Heat and Mass Transfer)
Browse Figures
Versions Notes

Abstract

:
Windows are important structural components that determine the energy efficiency of buildings. A significant parameter in windows technology is the overall heat transfer coefficient, U. This paper analyzes the methods of numerical determination of the U-value, including for windows that use passive technologies to improve thermal performance. The analysis was intended to evaluate the heat flux and temperature distribution across glazed surfaces and the accuracy of traditional approaches to the determination of heat loss through window structures. The results were obtained using the heat flux measurement method described in the international standard ISO 9869-1:2014. The paper shows that the non-uniformity of the heat flux density on a window surface can be as high as 60%, which in turn generates an error in the calculations based on stationary heat transfer conditions.

1. Introduction

The methods of calculation of heat transfer through building structures are based on parameters that depend on variable weather conditions: outdoor air temperature, solar radiation intensity, and wind velocity. The rate of heat exchange for walls can be controlled by changing the thickness of the walls or increasing the thickness of the layer of insulating material, this approach is not possible with the glass components of windows [1]. Increasing the number of window panes can only reduce the heat transfer to a certain level, but causes the overall thickness of the window, its weight, and its cost to increase significantly, while decreasing its light transmittance [2]. Therefore, windows constitute the weakest parts of the enclosing structures of buildings and are characterized by the lowest energy efficiency among all building components [3,4], generating up to 60% of the total heat loss through building partitions [5]. In this context, it is important to estimate the impact of all factors on heat transfer by conduction, convection in the gas layer filling the gap between the panes, and thermal radiation through windows that constitute components of enclosing structures. Heat transfer can be controlled by increasing the thermal resistance of the gas layer between the panes, reducing the level of thermal radiation, and controlling solar radiation.
Reduction of conduction and convection in the gas layer filling the gap between panes can be achieved by using multi-pane windows [6,7,8,9], optimizing the gap width between the panes [10,11,12,13], filling the gap with an inert gas [14,15,16] or an aerogel [17,18], evacuating the gap [19,20], or using special roller shutters or blinds in the space between the panes to limit the convection movements of the gaseous medium [20,21,22,23,24,25]. Proper selection of the glass material can reduce the component of solar heat gain in the summer, as well as the heat losses in the winter, which are related to the impact of solar radiation [26,27,28,29]. Therefore, the heat transfer due to thermal and solar radiation can be minimized by using special low-emissivity coatings [30,31,32,33], solar control films [34,35,36], external roller blinds [37,38], specialized curtains [39], smart window techniques (e.g., electrochromic [40], thermochromic [41], or photochromic [42] glazing), or double-skin facades [43,44,45,46,47,48]. Moreover, windows are characterized by high instantaneous efficiency, while being susceptible to changes in atmospheric conditions due to their low heat capacity. Some of the solutions causing an increase in windows energy efficiency involve the use of phase change materials [49,50,51,52], as well as glazing units with electric heating [53,54] or with a heat exchanger [55,56].
In this paper, a review of the mathematical models of heat transfer in different window systems is presented, considering the one-, two-, or three-dimensional approach, the diversity of the applied temperature boundary conditions, and the impact of incident solar radiation or an additional heat source.

2. Review of Publications Dedicated to Numerical Investigations of Heat Transfer through Windows

A study of the literature on windows heat transfer indicates many different approaches to numerical simulation. This is due to the variety of possible geometric configurations, types, and orientations, as well as to the diversity of the heat transfer modes (natural or forced convection, with or without consideration of thermal radiation and incident solar radiation) [57,58,59]. Table 1 shows overview of the topically relevant numerical investigations of heat transfer in windows. It provides information on the window type, the kind of dimensional simulation (one-, two-, or three-dimensional), the fluid dynamics condition (steady or transient), the classification of fluid flow (laminar or turbulent), the aim of the study, the mathematical modeling approach with the parameters considered, and whether the thermal radiation and incident solar radiation were or were not taken into account.

2.1. Window Heat Transfer Modelling without Taking into Account Thermal and Solar Radiation

A numerical determination of the optimum air-layer thickness for double-pane windows for different climates was proposed in paper [10]. The mathematical model of two-dimensional flow was based on vorticity-transport, stream function, and energy equations, in which the compressibility work and the viscous dissipation conditions were neglected. Conduction through the panes and thermal radiation were not taken into account. It can be concluded that heat loss through a double-pane window can be considerably minimized by optimizing the width of the air layer.
Similar investigation in order to determine optimum gap width for four different cities of Turkey with various climate conditions was carried out by Aydın [12]. The impacts of thermal and solar radiation were not taken into account due to the fact that panes were assumed to be kept as isothermal surfaces. Using the relevant values for each city, the temperature difference, the Prandtl, Rayleigh, and Nusselt numbers were obtained. The impact of gap width on the average Nusselt number at the inner pane, for temperature differences corresponding to the various climate conditions, is given in Figure 1.
Figure 1 indicates that for smaller values of air layer thickness, average Nusselt number was equal to around 1, which indicated that the heat transfer occurred through convection and conduction at the same level. Heat flux decreased considerably with the increasing air layer thickness up to L = 10 mm due to the fact that conduction dominated over convection. The thermal conductivity of air is low, thus the air layer between the panes acted as an insulation material. For gap widths of more than 15 mm, Nu increased as a result of an intensified convection mechanism. The decline in the heat transfer with the L increasing due to the conduction was balanced by the intensified natural convection. Beyond L = 20 mm, Nu increased significantly with increasing L due to the fact that convection dominated over conduction. Summing up, selection of the optimal distance between the panes at which the air layer worked as insulation, while not causing increased convection, is a very important parameter determining the heat transfer in windows.
In paper [13], Aydın extended his previous research to include more realistic boundary conditions. Conduction through the panes and constant temperature for the outer window surfaces were taken into account, while thermal radiation was still disregarded. It was showed that the convection assumptions for the outer surfaces of the glass panes led to lower heat exchange values than those determined with the assumption of a constant temperature. Assuming a constant temperature of external surfaces affected the convection resistances of external and internal air were ignored.
De Giorgi et al. investigated reduction or suppression of convective motions in a double-pane window with transparent fins within the gap [60]. The first investigated window geometry was a standard double-pane window. An array of 30 equally-spaced horizontal fins spaced 16 mm from each other was placed in the gap of the second window. The third geometry was obtained by placing fins in the gap, arranged to create a spiral labyrinth pattern. The temperature boundary conditions were imposed on the internal and external surfaces of the panes and radiative heat transfer was not taken into account. The proposed three-dimensional model for each of the three geometries was determined using the commercial software CFD Fluent. It was shown that the presence of fins delayed the onset of convection and each additional internal fin reduced the convective heat transfer for both low and high Rayleigh numbers.

2.2. Window Heat Transfer Modelling including Thermal Radiation and Excluding Incident Solar Radiation

Karabay and Arıcı studied the optimal number of panes for various climatic regions [6]. A numerical investigation was carried out to determine heat transfer coefficients in single, double-, triple-, and quadruple-pane windows, which are shown in Figure 2.
Figure 2 indicates that the U-value significantly decreased with an increase in the number of panes compared with a single-pane window. For a double-pane window, it was a decrease by 47%, for a triple-pane window—by 70%, and for a quadruple-pane window, by 78%. In each of the cases studied, the radiative coefficient to convective coefficient ratio was approximately two, which indicates that radiation was the dominant heat transfer mechanism. In addition, as the number of panes increased, the value of the radiative coefficient decreased because the central panes installed in triple- and quadruple-pane windows acted as a screen.
The impact of outdoor temperature changes on the U-value of double- and triple-pane windows in cold climate zones was presented in paper [61]. Calculations were conducted according to the standard EN 673 [85], except the Nusselt number, which was determined according to ISO 15099 [86]. The impact of changes in the outdoor temperature and the gap width on the U-value for a double-pane window filled with air is shown in Figure 3.
As can be seen from Figure 3, with a decrease in the outdoor temperature, the U−value decreased for a small width of the gap between the panes from L = 10 mm to L = 14 mm. The U−value increased slightly for larger gap widths, up to 2%. Thus, for an air-filled double-pane window without low-e coatings, the increase in the convection in the gap as the external air temperature decreased was compensated by a decrease in the radiative heat transfer and partly by a decrease in the thermal conductivity of the air in the gap. However, the use of low-e coatings and filling the gap between the panes with inert gas caused changes in thermal transmittance. The impact of changes in the outdoor temperature and the gap width on the overall heat transfer coefficient for a triple-pane window filled with argon is shown in Figure 4.
Figure 4 indicates that the distance between the panes had a different impact on the increase in the overall heat transfer coefficient as the external air temperature decreased. If the gap width was 10 mm, the overall heat transfer coefficient even slightly decreased as the outdoor temperature decreased due to the heat exchange by conduction with a negligible convection. While the distances between the glass panes were L = 12 mm and L = 14 mm, the U−value slightly increased. A significant increase in the U−value was noticed when the gap widths were from 16 mm to 25 mm, due to the domination of convection over conduction.
The above investigation show that the air gap width L depends on the temperature difference on the glass surfaces (Tint and Text). Therefore, its optimal value from the point of view of convective heat transfer, determined by modelling, can be achieved only for certain ranges of ΔT = Tint–Text values. This aspect will also be discussed in the third part of the paper.
The impact of the Rayleigh number, the aspect ratio, and the blind geometry on the convective heat transfer in a double-pane window with an enclosed pleated blind was determined in paper [21]. The conjugate conduction in the cloth blind was included, while the impact of long-wave radiation was not taken into account. In addition, a simplified one-dimensional model of the coupled convective and radiative heat transfer was also presented in order to calculate the overall heat transfer coefficient of the window. The radiation heat exchange between the glazing and the blind was calculated using a simple grey, diffuse, two-surface model. It was shown that the overall heat transfer coefficient from the one-dimensional model was within 3.1% of the value predicted by a fully conjugate CFD solution, which took the impact of radiation into account.
The overall heat transfer coefficient for a double-pane was predicted using a CFD code in paper [11]. Isothermal boundary conditions were applied, and thus the radiative heat transfer was decoupled from the convective heat transfer in the model. The radiative heat transfer coefficient was evaluated using the simple analytical method [87]. The CFD flow model consisted of the governing equations for mass, momentum, and heat transfer, as well as turbulence. Buoyant flow in a double-pane window could range from laminar to turbulent regimes, thus the renormalization group turbulence k–ε model was used [88,89]. It was concluded that the overall heat transfer coefficient varied depending on the width of the gap and the inner surface temperature, as shown in Figure 5.
Figure 5 shows that for the value of gap width from L = 5 mm to L = 20 mm the increase in the thermal resistance was significant due to the thermal conductivity, because the air layer worked as an insulating layer. Moreover, an increase in the gap width resulted in a decrease in the view factor, and thus a decrease in the radiative heat transfer coefficient. However, above L = 25 mm, the U value remained at an approximately constant level due to the intensified convection.
Arıcı et al. investigated the impact of the number of panes, the gap width, and the temperature difference on the fluid flow and heat transfer in double-, triple-, and quadruple-pane windows [7]. The flow of an air in the gap was assumed to be laminar and unsteady. The radiative heat transfer was determined using the S2S radiation model. The stream lines in tested windows for gap width of 21 mm are given in Figure 6.
As shown in Figure 6, an increase in the number of panes resulted in a considerable decrease in the magnitude of the velocity in the air medium. Air ascended along the inner pane and descended along the outer pane, which created a primary circulation. In addition, multicellular secondary circulations occurred in the gaps of double- and triple- pane windows, which caused shortcuts between the hot and cold panes. The magnitude of the velocities was lower, and the number of multicellular circulations was higher in the gaps of the triple-pane window compared with the double-pane window due to a lower temperature gradient. The multicellular circulations disappeared in the gaps of the quadruple-pane window, which resulted a linear temperature profile. It was found that the airflow changed when the Rayleigh number was greater than 6800.
Basok et al. came to similar conclusions in paper [90]. The numerical investigation resulted in determination of the critical Rayleigh number, at which a multicellular flow occurred, in a range from 6070 to 6740. A similar result was established in paper [91] for Ra = 6228 and for the aspect ratio of 40. The Rayleigh number exceeds approximately 6300, which caused a degradation of the linearity of the temperature profiles due to the formation of the multicellular circulations.
Arıcı et al. studied the flow and the conjugate heat transfer in multiple-pane windows with respect to five different emissivity values [30]. The use of low-emission coatings result in a change in the primary long-wave emissivity ε (λ > 3 μm) from about 0.84 to less than 0.1. The transient governing equations for mass, momentum, and energy were solved using the commercial CFD code. The results showed that the overall heat transfer coefficient of the windows decreased significantly with the decrease in emissivity. For example, for a triple-pane window filled with argon, with the gap width of L = 6 mm, the U value decreased from 2.3 W/m2K to 1.4 W/m2K when the emissivity changed from 1 to 0.25. The impact of emissivity on the U-value was more significant for larger gap widths. For the gap width of L = 12 mm, in the same window, the U-value was equal to 1.95 W/m2K for ε = 1 and decreased to 0.85 W/m2K for ε = 0.25.

2.3. Window Heat Transfer Modelling in Conditions of Exposure to Incident Solar Radiation

The solar radiation incident on the window panes is partly transmitted, reflected, and absorbed within the glass material, which resulted in heat transfer inward, as well as outward. The ability to transmit radiant heat is an essential factor of heat transfer through a transparent window’s elements, thus the impact of solar radiation should be taken into account in mathematical modelling [92].
Evaluation of the pseudo-transient thermal performance of a double-pane window with and without solar control coating was performed by Xamán et al. [34]. The impact of the incident solar radiation and the changes in air temperature in the room and outside were analyzed as a function of time (every 5 s). The surface thermal radiation model was determined using the net radiation method [93,94]. The results showed that the application of a solar control coating reduced the heat gain by approximately 54%.
Pal et al. developed a mathematical model to determinate the amount of global radiation on window glazing and the corresponding pane surface temperature over the diurnal cycle [66]. The optical and thermal properties of a window were analyzed to evaluate the performance of the glazing in increasing the temperature of a building interior. Various types of convection were taken into account depending on the outdoor conditions. The natural convection was considered in the winter, along with the forced convection in the summer due to the forced circulation of the air by a ceiling fan inside a building. The total or global radiation on any tilted surface was calculated as a sum of beam radiation on a horizontal surface, the isotropic and circumpolar diffusion on a horizontal surface, the horizontal brightening on a horizontal surface, and the component reflected from the ground. The temperature on the surfaces of window panes, the solar heat gains, and the heat fluxes determined in the simulation in the ambient conditions of summer and winter are shown in Figure 7.
As can be seen from Figure 8, the temperature on the surface of window panes, the solar heat gains, and the heat fluxes (both from convection and thermal radiation) changed with time throughout the day. The maximum solar gains in summer reached about 430 W and in winter about 300 W, along with a reaching the maximum values of heat fluxes in the middle of the day, when a significant increase in the global solar radiation was observed.
A numerical investigation of the distinctive features of a triple-pane window that have an impact on a rise in the thermal resistance was conducted by Basok et al. [72]. A fourth kind boundary condition, taking into account the presence of radiant heat fluxes between the pane surfaces, was assigned on the pane surfaces facing the gap. For the numerical calculation of a system of governing equations, the control-volume method was used [95]. The temperature fields, velocity, and pressure in the panes and in the gas medium between panes. The distributions of the dimensionless vertical velocity and of the dimensionless temperature through the window in its horizontal cross-section are shown in Figure 8.
Figure 7 indicates that in both gaps between the panes, ascending-descending free-convective motion occurred in the gas medium. The central pane in a triple-pane window prevented the development of free convective flows in the gap. In the outer gap, the maximum vertical velocity was Vmax = 0.03 and in the inner gap was Vmax = 0.0245. The low values of velocity indicated that the convection in the gaps significantly affected the heat transfer. Moreover, it was shown that the dimensionless temperature distribution was almost linear, as in the case of conduction. The temperature change across the thickness of the panes was small (~0.4 °C). The convective heat flux increased with a decrease in the exterior surface temperature (at a constant value of interior temperature). The Rayleigh number increased from 3.07 × 109 to 7.25 × 109 for a window filled with air, and from 3.65 × 109 to 8.64 × 109 for a window filled with argon, as the temperature of the outer pane decreased from 0 to −20 °C. In addition, the outer pane temperature affected the thermal resistance. From τout = −20 °C to τout = 0 °C, the thermal resistance of an air-filled window varied from 0.34 m2K/W to 0.32 m2K/W, and of an argon-filled window varied from 0.39 m2K/W to 0.36 m2K/W. The thermal resistance of a double-pane window was equal to R = 0.19 mK/W, which was 1.7 times lower than the thermal resistance of a triple-pane window. The features indicated caused an increase in the thermal resistance of a triple-pane window compared to a double-pane window.
Ismail et al. developed mathematical model of heat transfer in conditions of exposure to incident solar radiation across a single-pane window [96]. The model was two-dimensional and transient due to the change in the incident solar radiation and the outdoor temperature with time, according to the geographical and weather conditions. The energy equation included a source term to account for the solar radiation absorbed through the glass pane. The total heat gain, the solar heat gain, and the shading coefficient were analyzed for different thicknesses of the glass pane varying from 3 to 8 mm. It was concluded that, in the absence of incident solar radiation, i.e., on cloudy days and during the night, the heat gain is exclusively due to the temperature difference between the internal and external environments.
A new method for the evaluation of solar heat gains through glazed surfaces to obtain the thermal energy requirements of buildings was proposed in [97]. The model considered that the entering energy was partly absorbed by the surfaces of the cavity and partly dispersed outwards, through the same window surfaces. The authors developed the effective entering solar radiation absorption coefficient corresponding to the optical and geometrical properties of the indoor environment and the transmission coefficient of the diffuse radiation of transparent surfaces.
In advanced window structures, the absorbed radiation can be extracted by other means, such as conversion to electricity and natural airflow, in order to improve heat recovery or reduce losses. Ventilated windows can use cavity airflow to heat up the air between the panes, creating buoyancy forces that induces upward flow of air [98,99].
Ismail et al. investigated modelling for a ventilated double-pane window in paper [63]. The window consisted of two parallel panes forming a gap in which the flow and initial heating of the air stream occurred. The calculations assumed a transient regime due to the incident solar radiation and the internal ambient temperature changed over time. The source term in the energy equation was used to calculate the solar radiation absorbed by the glass panes forming the channel. According to the results, the difference between the solar heat gain for different gap widths was insignificant because the optical transmittance of the systems was almost the same, regardless of the distance between the panes.
The same authors developed mathematical models of heat transfer in a ventilated double-pane windows in forced air flow conditions [74] and in a ventilated double-pane window filled with an absorbing gas [100,101]. Complex boundary conditions, such as variable heat flow and variable outdoor temperature, were assumed on the outer panes due to the incident solar radiation. It was concluded that the impact of an increase in the mass flow rate on the thermal performance of the ventilated window caused a reduction of the mean solar heat gain coefficient and the shading coefficient.
The heat transfer and the total heat gain coefficient of a double-pane window filled with an absorbing gas and exposed to solar radiation in a hot climate were compared for both a single-pane window and a naturally ventilated double-pane window in paper [64]. The mathematical models were two-dimensional and transient. An upward airflow in the gap between the panes was induced by the incident solar radiation and the temperature difference between the external and internal environment, which caused non-symmetric heating of the panes. Figure 9 shows the total heat gain for different values of the gap width of a ventilated double-pane window in solar radiation = 600 W/m2.
As can be seen from Figure 9, for gap width L = 20 mm and larger, the values of the total heat gain remained nearly unchanged, regardless of the distance between the panes. It was assumed that that the optical transmittance of the windows was nearly the same.
Lago et al. presented a numerical investigation of the thermal performance of a ventilated double-pane window with a solar reflective film [77]. The variability of radiation and outside temperature depending on the solar time (which was determined by the passage of time from a position of the Sun in the sky) was estimated for a specific month using climatic and geographical parameters. It was found that the use of a solar reflective film in a ventilated double-pane window reduced the solar energy penetrating towards the internal environment by almost 65% in comparison with a traditional double-pane window.
Michaux et al. developed a pseudo-three-dimensional model of the thermal performance of a triple-pane air-supply window, in comparison with conventional double- and triple-pane closed windows [102]. Nodal model included convection in the gaseous medium filling the gap between the panes, conduction through the glass panes and the frame and at the inner and outer window’s surfaces, and the short- and long wave radiation. The tested airflow window provided a preheating of fresh outdoor air by heat loss recovery and absorbed solar heat. It was concluded that for the air flow rate of 15 m3/h, the SHGC of the air-flow window was approximately 20% and 30% higher compared with a double- and triple-pane window, respectively.
Zhang et al. proposed an opening triple-exhaust window with two air cavities, one of which acted as a ventilation duct [103]. It was concluded that, compared with conventional double- and triple-pane windows, a triple exhaust window reduces the heat gains in the summer period by 73.5% and 71.9%. In paper [104], the authors concluded that the use of an exhaust window with triple glazing can reduce over 25% and 50% of the annual accumulated cooling and heating loads, respectively.
Basok et al. carried out research on the processes of heat exchange through an energy-saving double-pane window with electric heating [82]. The inner surface of the inner pane and the inner surface of the outer pane were covered with a low-e coating, while the inner surface of the inner pane was electrically heated. The energy equation contained a source term for electric heating power. The boundary conditions of the fourth type were applied for the inner surfaces of the panes facing the gap, taking into account the heat exchange by thermal radiation. According to the results, 83–85% of the heat emitted by a window was transmitted inside the room and 15–17% to the outside environment.
A two-dimensional mathematical model of heat transfer in a double-pane window integrated with a see-through a-Si photovoltaic cells was presented in paper [83]. This advanced window system can generate electricity while allowing daylight to freely penetrate inside. The temperature distribution and the flow field of the buoyancy forces that induced a natural convective airflow in the gap between the panes were analyzed numerically for different Rayleigh numbers. The results provided accurate heat transfer variables that are necessary for predicting the PV conversion efficiency.
Regulation of the temperature depending on the change in the environmental parameters or on the electric current passing through an active layer on the pane surface can be achieved by use of smart glass. Smart glass makes use of chromogenic technologies to change the optical properties in response to external stimuli. Smart window types and their operation mechanisms are shown in Table 2.
The impact of innovative phase-change materials on the energy efficiency of windows was investigated by Lichołai and Musiał [84]. The aim of the study was to define two complex heat transfer resistances between the external glazing and the PCM accumulator, as well as between the PCM accumulator and the internal glazing. The proposed model determined the one-dimensional heat flow in a window connected to the heat accumulator and the two-dimensional heat flow and storage in a phase-change accumulator. The investigation resulted in evidence of an improvement in the thermal resistance of windows with a phase-change heat accumulator, which was confirmed by both the temperature and the heat flux density recorded on the inner surface of the panes.
The use of a phase change material for initial heating or cooling of the supplied air in a ventilated window was investigated in paper [112]. The results indicated that the proposed window ensured an increase in the inlet air temperature by 2 °C for 12 h in a day (heating mode) and maintained the inlet air temperature on average 1.4 °C lower for 7 h in a day, compared to a conventional window.
Nourozi et al. presented the thermal properties of an innovative energy-active window (EAW) [55]. It can utilize low-grade energy, such as waste heat in a sealed air loop between the window panes, in order to provide higher window surface temperatures in winter. The proposed EAW consisted of a double-slot glazing configuration and a closed air loop. An up flow of heated air to the slots was provided by a built-in heat exchanger combined with a fan underneath the window. The thermal performance of the EAW was compared with a those of a conventional triple-pane window in order to determine the U-value and select the appropriate Nusselt number correlations. The air flow between the panes was caused by an integrated fan underneath the window; therefore, the heat transfer occurred by natural, forced, and mixed convection. The Nusselt numbers for the convection occurring between symmetrically heated parallel panes was adapted for use in the EAW due to the different pane surface temperatures resulting from the up flow of warm air and a large temperature difference between the inside and the outside. Therefore, the constant values of 7.54 and 7.55 in the Nusselet number were changed to four so as to more correctly consider the effects of asymmetrically heated boundaries. The results showed that the Nusselt number for the parallel panes with asymmetric surface temperatures was approximately 1.9 times lower than that for symmetrically heated surfaces. The U-value of the EAW was significantly depended on the supply air temperature, thus in order to provide the U-value under 0.65 W/m2K, the supply air temperature must be above the indoor temperature.

3. Material and Methods

As can be seen, many investigations studied the modelling of heat transfer processes taking place through window structures. The authors of the above publications proposed various solutions that ensured a good agreement between the simulation results and the practical measurements of the overall heat transfer coefficient for specific conditions, despite the simplifications adopted in the mathematical models. Those approaches can be verified using the proposed models. In our review paper, a different approach was proposed, based on a practical assessment of the thermal transmission through windows. A detailed study of heat transfer processes was not the aim of this paper and will be the subject of another research paper. The major goal of this study is to demonstrate that even the best agreement of simulation results does not reflect the real distribution of heat flows. It is due to fact that the nature of heat transfer inside window cavities significantly depends on the local thermal conditions inside and outside the window, which also change in the glazing area.
Thermal tests of windows in a climate chamber were carried out in order to verify the proposed average heat transfer coefficients, as shown in Figure 10 and Figure 11. The temperature, humidity, and air velocity were changed depending on the conditions set in the chamber. The steady state of the microclimate in the chamber on the internal and external sides, calibration of the heating part of the chamber, and measurement of temperature and wind speed were taken into account during the test. The studied windows were mounted in a climate chamber in order to determine the temperature variability and the amount of the heat flux in the cross-section. Figure 10 shows the general external installation of the climatic chamber.
The tested windows were triple-pane windows with the gap width of L = 18 mm, filled with argon, with a low-ecoating with ε = 0.17. The tested window systems also included conventional triple-pane windows, with the gap width of L = 18 mm, filled with air, with emissivity of ε = 0.84, whose thermal parameters served as a basis for comparison. Thermocouples with the measured temperature range of −30 °C to +40 °C and accuracy 0.1 °C were installed between the panes of each tested window. The thermocouples were located in the lower, central, and upper part of the internal gap and one thermocouple was located in the central part of the external gap, in order to measure the temperature distribution. The density of the heat flux was measured by using FHF04 foil heat flux sensors (Hukseflux) with sensitivity of Φi = 10.84 μV/(W/m2). They were attached on the glass surfaces, which made it possible determine the local values of the tested parameters. FHF04 measured heat flux from conduction, radiation, and convection over a temperature range from −70 to +120 °C. The LI19 heat flux density data-logger (Hukseflux) was used to display and store the measured minimum, maximum and average heat flux along with the date and time. Its calibration uncertainty is 0.1%. Moreover, the digital TM-947SD four-channels thermometer with data-logger (Lutron), with resolution of 0.1 °C, was used in order to store the measured temperature of gas layer between the panes from K-type thermocouples. Figure 11 shows the studied windows with thermocouples installed in the climatic chamber.
The aim of the experimental tests was to measure the temperature and the heat flux density in the windows. The tests in the climate chamber were carried out for the constant internal temperature Tin = 20 °C and 50% humidity, and for four external temperatures Tout = −10 °C; −5 °C; 0 °C, and +5 °C. The thermocouple and heat flux recorder has the function of automatic saving of the measured parameters, which are then exported to Microsoft Excel tables. The measurements were carried out in accordance with ISO 9869-1:2014.

4. Results and Discussion

Table 3 shows the different approaches to mathematical modeling of thermal transmission through windows.
Modelling of heat exchange processes through windows involves making a number of assumptions that simplify the solution of the governing equations. This fact indicates a discrepancy between the calculated and experimental data. The fact that the data obtained varies greatly in different parts of the windows is a significant problem. For example, convection may occur in the middle of a window, but there may be no convection closer to the edges of the window or in its lower part. As a consequence, the densities of heat fluxes on the window surfaces are different and the temperature distribution shown for the solution of some models may be practically ideal only for a part of the window. If the data was average for the local values of heat fluxes over the entire surface of the window, the error can be significant. The results of measurements obtained in our study are shown in Figure 12.
The heat flux density for different types of windows of the same height was:
  • − for a triple-pane window filled with air: 1.29 W/m2, 1.72 W/m2, and 1.86 W/m2;
  • − for a triple-pane window filled with argon: 1.1 W/m2, 1.2 W/m2, and 1.65 W/m2; and
  • − for a window with a low-emission coating: 1.34 W/m2, 1.42 W/m2, and 1.68 W/m2.
Another aspect of the modelling problem is the lack of consideration of the conditions of heat exchange with the surrounding air. The coefficient of convective heat transfer from the window surface changes along with the change in humidity and wind speed. Thus, the simulation error will be even greater. Our measurements show that with an increase in wind speed from 0 to 8 m/s, the local heat flux values increased by 40%, and thus the thermal resistance of the window decreased. As a rule, this was not taken into account in cited mathematical models.
Finally, the third feature that is also not evaluated in the models, is the location of the window relative to the wall. Figure 13 indicates the impact of the location of a window on the temperature fields around the window. As can be seen from Figure 13, the location affected the convective air movements taking place along the window surface and the thermal properties of the window itself.
To summarise, a change in the position of the window affects the temperature distribution in the wall, the intensity of convective air movement on the inner surface of the window, and the intensity of heat exchange through the window. It results in uneven temperature fields and speed of convective air movement inside the windows, and the presence of micro convection and multicellular secondary circulations in the gaps between the panes (which was also considered by some authors). These features were not taken into account in the cited papers and it seems that it is difficult to include them in mathematical models. However, these three aspects have a significant impact on the accuracy of the mathematical predictions of the thermal resistance of windows.

5. Conclusions

The results suggest that the conjugate heat transfer and fluid flow within windows is far from being fully understood, thus further research is needed. On the other hand, the mathematical models developed so far do not allow for such comprehensive research. The current approach to modeling for standard windows seems to be redundant. The aforementioned parameters should be included in the models of modern window designs in which the phenomenon of forced convection occurs or in which an additional heat source causing convection movements is used. Accurate characterization of the thermal properties, including thermal transmittance (U-value), is of key importance for the development of new generation window designs.
Another important parameter is the width of the gap between the panes, which was pointed out by almost all cited authors. In general, it depends on the temperature difference on the glass surfaces and on the thermal conditions, thus significantly affecting the thermal transmittance. It was established that the optimal value was of 18 mm in our tested windows, according to results in the literature review.
Moreover, our experimental tests of windows carried out in a climate chamber show significant differences in the values of heat flux density in different parts of windows. A discrepancy between the average values for different types of windows was identified. These discrepancies amounted to 36% for the upper part and 21% for the lower part of a window compared to the values in the central part.
The inconsistency in the data with respect to width remains almost the same for all windows. The error would range from 17 to 54% if the U-values for the entire window were averaged and compared with the calculated data, However, the experiments did not take into account radiation, which introduces even greater errors in the calculations, especially for windows with low-e coatings.
It can be concluded that modeling the processes of heat exchange through windows can be effective for certain strictly defined conditions. However, even in this case, significant errors were obtained in determining the level of heat transfer intensity. In this regard, the task of developing new active window designs in which it would be advisable to use appropriate mathematical models to assess energy performance looks more promising.

Author Contributions

Conceptualization, A.M.P.; Methodology, A.M.P.; Software, A.M.P.; Validation, K.S.; Formal analysis, A.M.P.; Investigation, A.M.P.; Data curation, A.M.P.; Writing—original draft preparation, A.M.P. and K.S.; Writing—review and editing, A.M.P.; Visualization, A.M.P.; Supervision, A.M.P.; Project administration, A.M.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

PrPrandtl number
RaRayleigh number
NuNusselt number

Abbreviation

ADIalternating direction implicite
CFDcomputational fluid dynamics
CWcumulative wavenumber model
DOdiscrete ordinates radiation model
EAWenergy-active window
PCMphase change materials
RANSReynolds averaged Navier–Stokes
RTEradiative transport equation
S2Ssurface-to-surface
SHGCsolar heat gain coefficient
SORsuccessive over-relaxation
SSTshear stress transport
TDM a tridiagonal matrix algorithm

References

  1. Basok, B.I.; Nakorchevskii, A.I.; Goncharuk, S.M.; Kuzhel, L.N. Experimental Investigations of Heat Transfer Through Multiple Glass Units with Account for the Action of Exterior Factors. J. Eng. Phys. Thermophys. 2017, 90, 88–94. [Google Scholar] [CrossRef]
  2. Cuce, E.; Riffat, S.B. A state-of-the-art review on innovative glazing technologies. Renew. Sustain. Energy Rev. 2015, 41, 695–714. [Google Scholar] [CrossRef]
  3. Jelle, B.P.; Hynd, A.; Gustavsen, A.; Arasteh, D.; Goudey, H.; Hart, R. Fenestration of today and tomorrow: A state-of-the-art review and future research opportunities. Sol. Energy Mater. Sol. Cells 2012, 96, 1–28. [Google Scholar] [CrossRef]
  4. Wang, Y.; Shukla, A.; Liu, S. A state of art review on methodologies for heat transfer and energy flow characteristics of the active building envelopes. Renew. Sustain. Energy Rev. 2017, 78, 102–1116. [Google Scholar] [CrossRef]
  5. Tian, Z.; Zhang, X.; Jin, X.; Zhou, X.; Shi, X. Towards adoption of building energy simulation and optimization for passive building design: A survey and a review. Energy Build. 2018, 158, 1306–1316. [Google Scholar] [CrossRef]
  6. Karabay, H.; Arıcı, M. Multiple pane window applications in various climatic regions of Turkey. Energy Build. 2012, 45, 67–71. [Google Scholar] [CrossRef]
  7. Arıcı, M.; Karabay, H.; Kan, M. Flow and heat transfer in double, triple and quadruple pane windows. Energy Build. 2015, 86, 394–402. [Google Scholar] [CrossRef]
  8. Gorantla, K.; Shaik, S.; Setty, A.B.T.P. Effects of single, double, triple and quadruple window glazing of various glass materials on heat gain in green energy buildings. Mater. Energy Environ. Eng. 2017, 5, 45–50. [Google Scholar] [CrossRef]
  9. No, S.T.; Seo, J.S. Analysis of Window Components Affecting U-Value Using Thermal Transmittance Test Results and Multiple Linear Regression Analysis. Adv. Civ. Eng. 2018, 2018, 1780809. [Google Scholar] [CrossRef]
  10. Arıcı, M.; Karabay, H. Determination of optimum thickness of double-glazed windows for the climatic regions of Turkey. Energy Build. 2010, 42, 1773–1778. [Google Scholar] [CrossRef]
  11. Gan, G. Thermal transmittance of multiple glazing: Computational fluid dynamics prediction. Appl. Therm. Eng. 2001, 21, 1583–1592. [Google Scholar] [CrossRef]
  12. Aydın, O. Determination of optimum air-layer thickness in double-pane windows. Energy Build. 2000, 32, 303–308. [Google Scholar] [CrossRef]
  13. Aydın, O. Conjugate heat transfer analysis of double pane windows. Build. Environ. 2006, 41, 109–116. [Google Scholar] [CrossRef]
  14. Aguilar-Santana, J.L.; Velasco-Carrasco, M.; Riffat, S. Thermal Transmittance (U-value) Evaluation of Innovative Window Technologies. Future Cities Environ. 2020, 6, 12. [Google Scholar] [CrossRef]
  15. Park, S.; Song, S.-Y. Evaluation of Alternatives for Improving the Thermal Resistance of Window Glazing Edges. Energies 2019, 12, 244. [Google Scholar] [CrossRef]
  16. Cuce, E. Accurate and reliable U-value assessment of argon-filled double glazed windows: A numerical and experimental investigation. Energy Build. 2018, 171, 100–106. [Google Scholar] [CrossRef]
  17. Buratti, C.; Moretti, E.; Zinzi, M. High Energy-Efficient Windows with Silica Aerogel for Building Refurbishment: Experimental Characterization and Preliminary Simulations in Different Climate Conditions. Buildings 2017, 7, 8. [Google Scholar] [CrossRef]
  18. Gao, T.; Ihara, T.; Grynning, S.; Jelle, B.P.; Gunnarshaug Lien, A. Perspective of aerogel glazings in energy efficient buildings. Build. Environ. 2016, 95, 405–413. [Google Scholar] [CrossRef]
  19. Eames, P. Vacuum glazing: Current performance and future prospects. Vacuum 2008, 82, 717–722. [Google Scholar] [CrossRef]
  20. Fang, Y.; Eames, P.C.; Norton, B.; Hyde, T.J.; Zhao, J.; Wang, J.; Huang, Y. Low emittance coatings and the thermal performance of vacuum glazing. Sol. Energy 2007, 81, 8–12. [Google Scholar] [CrossRef]
  21. Dalal, R.; Naylor, D.; Roeleveld, D. A CFD study of convection in a double glazed window with an enclosed pleated blind. Energy Build. 2009, 41, 1256–1262. [Google Scholar] [CrossRef]
  22. Collins, M.; Tasnim, S.; Wright, J. Numerical analysis of convective heat transfer in fenestration with between-the-glass louvered shades. Build Env. 2009, 44, 2185–2192. [Google Scholar] [CrossRef]
  23. Pavlenko, A.M.; Koshlak, H. Application of thermal and cavitation effects for heat and mass transfer process intensification in multicomponent liquid media. Energies 2021, 14, 7996. [Google Scholar] [CrossRef]
  24. Koshlak, H.; Pavlenko, A. Method of formation of thermophysical properties of porous materials. Rocz. Ochr. Srodowiska 2019, 21, 1253–1262. [Google Scholar]
  25. Silva, T.; Vicente, R.; Amaral, C.; Figueiredo, A. Thermal performance of a window shutter containing PCM: Numerical validation and experimental analysis. Appl. Energy 2016, 179, 64–84. [Google Scholar] [CrossRef]
  26. Souviron, J.; van Moeseke, G.; Khan, A.Z. Analysing the environmental impact of windows: A review. Build. Environ. 2019, 161, 106268. [Google Scholar] [CrossRef]
  27. Garlisi, C.; Trepci, E.; Li, X.; Al Sakkaf, R.; Al-Ali, K.; Nogueira, R.P.; Zheng, L.; Azar, E.; Palmisano, G. Multilayer thin film structures for multifunctional glass: Self-cleaning, antireflective and energy-saving properties. Appl. Energy 2020, 264, 114697. [Google Scholar] [CrossRef]
  28. Jørgensen, J.D.; Nielsen, J.H.; Giuliani, L. Thermal resistance of framed windows: Experimental study on the influence of frame shading width. Saf. Sci. 2022, 149, 105683. [Google Scholar] [CrossRef]
  29. Marinoski, d.l.; Güths, S.; Pereira, F.O.R.; Lamberts, R. Improvement of a measurement system for solar heat gain through fenestrations. Energy Build. 2007, 39, 478–487. [Google Scholar] [CrossRef]
  30. Arıcı, M.; Kan, M. An investigation of flow and conjugate heat transfer in multiple pane windows with respect to gap width, emissivity and gas filling. Renew. Energy 2015, 75, 249–256. [Google Scholar] [CrossRef]
  31. Jelle, B.P.; Kalnæs, S.E.; Gao, T. Low-emissivity materials for building applications: A state-of-the-art review and future research perspectives. Energy Build. 2015, 96, 329–356. [Google Scholar] [CrossRef] [Green Version]
  32. Pavlenko, A.; Usenko, B.; Koshlak, A. Thermal conductivity of the gas in small space. Metall. Min. Ind. 2014, 6, 20–24. [Google Scholar]
  33. Chaiyapinunt, S.; Phueakphongsuriya, B.; Mongkornsaksit, K.; Khomporn, N. Performance rating of glass windows and glass windows with films in aspect of thermal comfort and heat transmission. Energy Build. 2004, 37, 725–738. [Google Scholar] [CrossRef]
  34. Xamán, J.; Jiménez-Xamán, C.; Álvarez, G.; Zavala, I.; Hernández-Pérez, I.; Aguilar, J.O. Thermal performance of a double pane window with a solar control coating for warm climate of Mexico. Appl. Therm. Eng. 2016, 106, 257–265. [Google Scholar] [CrossRef]
  35. Pereira, J.; Gomes, M.G.; Rodrigues, A.M.; Almeida, M. Thermal, luminous and energy performance of solar control films in single-glazed windows: Use of energy performance criteria to support decision making. Energy Build. 2019, 198, 431–443. [Google Scholar] [CrossRef]
  36. Teixeira, H.; Gomes, M.G.; Rodrigues, A.M.; Pereira, J. Thermal and visual comfort, energy use and environmental performance of glazing systems with solar control films. Build. Env. 2019, 168, 106474. [Google Scholar] [CrossRef]
  37. Bavaresco, M.V.; Ghisi, E. Influence of user interaction with internal blinds on the energy efficiency of office buildings. Energy Build. 2018, 166, 538–549. [Google Scholar] [CrossRef]
  38. Jain, S.; Garg, V. A review of open loop control strategies for shades, blinds and integrated lighting by use of real-time daylight prediction methods. Build. Environ 2018, 135, 352–364. [Google Scholar] [CrossRef]
  39. Bedon, C.; Zhang, X.; Santos, F.; Honfi, D.; Lange, D. Performance of structural glass facades under extreme loads—Design methods, existing research, current issues and trends. Constr. Build. Mater. 2018, 163, 921–937. [Google Scholar] [CrossRef]
  40. Lahmar, I.; Cannavale, A.; Martellotta, F.; Zemmouri, N. The Impact of Building Orientation and Window-to-Wall Ratio on the Performance of Electrochromic Glazing in Hot Arid Climates: A Parametric Assessment. Buildings 2022, 12, 724. [Google Scholar] [CrossRef]
  41. Ji, C.; Wu, Z.; Wu, X.; Wang, J.; Jiang, Y. Al-doped VO2 films as smart window coatings: Reduced phase transition temperature and improved thermochromic performance. Sol. Energy Mater. Sol. Cells 2018, 176, 174–180. [Google Scholar] [CrossRef]
  42. Wu, Y.; Krishnan, P.; Zhang, M.H.; Yu, L.E. Using photocatalytic coating to maintain solar reflectance and lower cooling energy consumption of buildings. Energy Build. 2018, 164, 176–186. [Google Scholar] [CrossRef]
  43. Fallahi, A.; Haghighat, F.; Elsadi, H. Energy performance assessment of double-skin façade with thermal mass. Energy Build. 2010, 42, 1499–1509. [Google Scholar] [CrossRef]
  44. Regmi, G.; Velumani, S. Radio frequency (RF) sputtered ZrO2-ZnO-TiO2 coating: An example of multifunctional benefits for thin film solar cells on the flexible substrate. Solar Energy 2023, 249, 301–311. [Google Scholar] [CrossRef]
  45. Zanghirella, F.; Perino, M.; Serra, V. A numerical model to evaluate the thermal behaviour of active transparent façades. Energy Build. 2011, 43, 1123–1138. [Google Scholar] [CrossRef]
  46. Koo, S.Y.; Park, S.; Song, J.-H.; Song, S.-Y. Effect of Surface Thermal Resistance on the Simulation Accuracy of the Condensation Risk Assessment for a High-Performance Window. Energies 2018, 11, 382. [Google Scholar] [CrossRef]
  47. Zhao, X.; Mofid, S.A.; Al Hulayel, M.R.; Saxe, G.W.; Jelle, B.P.; Yang, R. Reduced-scale hot box method for thermal characterization of window insulation materials. Appl. Therm. Eng. 2019, 160, 114026. [Google Scholar] [CrossRef]
  48. Ghadimi, M.; Ghadamian, H.; Hamidi, A.; Fazelpour, F.; Behghadam, M. Analysis of free and forced convection in airflow windows using numerical simulation of heat transfer. Int. J. Energy Environ. Eng. 2012, 3, 14. [Google Scholar] [CrossRef]
  49. Vigna, I.; Bianco, L.; Goia, F.; Serra, V. Phase Change Materials in Transparent Building Envelopes: A Strengths, Weakness, Opportunities and Threats (SWOT) Analysis. Energies 2018, 11, 111. [Google Scholar] [CrossRef]
  50. Li, S.; Zou, K.; Sun, G.; Zhang, X. Simulation research on the dynamic thermal performance of a novel triple-glazed window filled with PCM. Sustain. Cities Soc. 2018, 40, 266–273. [Google Scholar] [CrossRef]
  51. Wei, L.; Li, G.; Ruan, S.-T.; Qi, H. Dynamic coupled heat transfer and energy conservation performance of multilayer glazing window filled with phase change material in summer day. J. Energy Storage 2022, 49, 104183. [Google Scholar] [CrossRef]
  52. Musiał, M.; Lichołai, L. The Impact of a Mobile Shading System and a Phase-Change Heat Store on the Thermal Functioning of a Transparent Building Partition. Materials 2021, 14, 2512. [Google Scholar] [CrossRef]
  53. Lee, R.; Kang, E.; Lee, H.; Yoon, J. Heat Flux and Thermal Characteristics of Electrically Heated Windows: A Case Study. Sustainability 2022, 14, 481. [Google Scholar] [CrossRef]
  54. Kaboré, M.; Michaux, G.; Le Dréau, J.; Salagnac, P.; Greffet, R. Parametric study of the thermal performance of a sin-gle-family house equipped with an airflow window integrating a heated glazing. In Proceedings of the 16th IBPSA International Conference, Rome, Italy, 2–4 September 2019. [Google Scholar] [CrossRef]
  55. Nourozi, B.; Ploskić, A.; Chen, Y.; Chiu, J.N.-W.; Wang, Q. Heat transfer model for energy-active windows—An evaluation of efficient reuse of waste heat in buildings. Renew. Energy 2020, 162, 2318–2329. [Google Scholar] [CrossRef]
  56. Elmalky, A.M.; Araji, M.T. Computational fluid dynamics using finite volume method: A numerical model for Double Skin Façades with renewable energy source in cold climates. J. Build. Eng. 2022, 60, 105231. [Google Scholar] [CrossRef]
  57. Amaral, A.R.; Rodrigues, E.; Gaspar, A.R.; Gomes, Á. A thermal performance parametric study of window type, orientation, size and shadowing effect. Sustain. Cities Soc. 2016, 26, 456–465. [Google Scholar] [CrossRef]
  58. Pavlenko, A.; Usenko, B.; Koshlak, A. Analysis of thermal peculiarities of alloying with special properties. Metall. Min. Ind. 2014, 6, 15–19. [Google Scholar]
  59. Aguilar-Santana, J.L.; Jarimi, H.; Velasco-Carrasco, M. Review on window-glazing technologies and future prospects. Int. J. Low-Carbon Technol. 2020, 15, 112–120. [Google Scholar] [CrossRef]
  60. De Giorgi, L.; Bertola, V.; Cafaro, E. Thermal convection in double glazed windows with structured gap. Energy Build. 2011, 43, 2034–2038. [Google Scholar] [CrossRef]
  61. Banionis, K.; Kumžienė, J.; Burlingis, A.; Ramanauskas, J.; Paukštys, V. The Changes in Thermal Transmittance of Window Insulating Glass Units Depending on Outdoor Temperatures in Cold Climate Countries. Energies 2021, 14, 1694. [Google Scholar] [CrossRef]
  62. Choi, H.; Kang, K.; An, Y.-E.; Lee, Y.; Kim, T. Analysis of Heat Transfer in a Slim Double Skin Façade using CFD Simulation. In Proceedings of the 16th IBPSA International Conference, Rome, Italy, 2–4 September 2019. [Google Scholar] [CrossRef]
  63. Ismail, K.A.R.; Henríquez, J.R. Two-dimensional model for the double glass naturally ventilated window. Int. J. Heat Mass Transf. 2005, 48, 461–475. [Google Scholar] [CrossRef]
  64. Ismail, K.A.; Salinas, C.T.; Henriquez, J.R. A comparative study of naturally ventilated and gas filled windows for hot climates. Energy Convers. Manage. 2009, 50, 1691–1703. [Google Scholar] [CrossRef]
  65. Cho, K.-J.; Cho, D.-W. Solar Heat Gain Coefficient Analysis of a Slim-Type Double Skin Window System: Using an Experimental and a Simulation Method. Energies 2018, 11, 115. [Google Scholar] [CrossRef]
  66. Pal, S.; Roy, B.; Neogi, S. Heat transfer modelling on windows and glazing under the exposure of solar radiation. Energy Build. 2009, 41, 654–661. [Google Scholar] [CrossRef]
  67. Demanega, I.; De Michele, G.; Avesani, S.; Pernigotto, G.; Babich, F.; Gasparella, A. CFD and ray tracing to evaluate the thermal performance of Complex Fenestration Systems. In Proceedings of the Building Simulation and Optimization 2018 Conference, Cambridge, UK, 11–12 September 2018; pp. 460–466. [Google Scholar]
  68. Bhamjee, M.; Nurick, A.; Madyira, D.M. An experimentally validated mathematical and CFD model of a supply air window: Forced and natural flow. Energy Build. 2013, 57, 289–301. [Google Scholar] [CrossRef]
  69. Najaf Khosravi, S.; Mahdavi, A. A CFD-Based Parametric Thermal Performance Analysis of Supply Air Ventilated Windows. Energies 2021, 14, 2420. [Google Scholar] [CrossRef]
  70. Chow, T.-T.; Li, C.; Lin, Z. Thermal characteristics of water-flow double-pane window. Int. J. Therm. Sci 2011, 50, 140–148. [Google Scholar] [CrossRef]
  71. Gosselin, J.R.; Chen, Q. A computational method for calculating heat transfer and airflow through a dual-airflow window. Energy Build. 2008, 40, 452–458. [Google Scholar] [CrossRef]
  72. Basok, B.I.; Davydenko, B.V.; Isaev, S.A.; Goncharuk, S.M.; Kuzhel, L.N. Numerical modeling of heat transfer through a triple-pane window. J. Eng. Phys. Thermophys. 2016, 89, 1277–1283. [Google Scholar] [CrossRef]
  73. Ismail, K.A.R.; Salinas, C.T.; Henriquez, J.G. Comparison between PCM filled glass windows and absorbing gas filled windows. Energy Build. 2008, 40, 710–719. [Google Scholar] [CrossRef]
  74. Ismail, K.A.R.; Henríquez, J.R. Simplified model for a ventilated glass window under forced air flow conditions. Appl. Therm. Eng. 2006, 26, 295–302. [Google Scholar] [CrossRef]
  75. Skaff, M.C.; Gosselin, L. Summer performance of ventilated windows with absorbing or smart glazings. Sol. Energy 2014, 105, 2–13. [Google Scholar] [CrossRef]
  76. Zeyninejad Movassag, S.; Zamzamian, K. Numerical investigation on the thermal performance of double glazing air flow window with integrated blinds. Renew. Energy 2020, 148, 852–863. [Google Scholar] [CrossRef]
  77. Lago, T.G.S.; Ismail, K.A.R.; Lino, F.A.M. Ventilated double glass window with reflective film: Modeling and assessment of performance. Sol. Energy 2019, 185, 72–88. [Google Scholar] [CrossRef]
  78. Carlos, J.S.; Corvacho, H.; Silva, P.; Gomes, J.C. Modelling and simulation of a ventilated double window. Appl. Therm. Eng. 2011, 31, 93–102. [Google Scholar] [CrossRef]
  79. Carlos, J.S.; Corvacho, H. Evaluation of the performance indices of a ventilated double window through experimental and analytical procedures: SHGC-values. Energy Build. 2015, 86, 886–897. [Google Scholar] [CrossRef]
  80. Gosselin, J.R.; Chen, Q. A Dual Airflow Window for Indoor Air Quality Improvement and Energy Conservation in Buildings. HVACR Res. 2008, 14, 359–372. [Google Scholar] [CrossRef]
  81. Thalfeldt, M.; Kurnitski, J.; Voll, H. Detailed and simplified window model and opening effects on optimal window size and heating need. Energy Build. 2016, 127, 242–251. [Google Scholar] [CrossRef]
  82. Basok, B.I.; Davydenko, B.V.; Goncharuk, S.M.; Pavlenko, A.M. Experimental and numerical studies of heat transfer from a double-glazed window with electric heating of its surface. Work. Inst. Electrodyn. Natl. Acad. Sci. Ukr. 2022, 2022, 62. [Google Scholar] [CrossRef]
  83. Han, J.; Lu, L.; Yang, H. Numerical evaluation of the mixed convective heat transfer in a double-pane window integrated with see-through a-Si PV cells with low-e coatings. Appl. Energy 2011, 87, 3431–3437. [Google Scholar] [CrossRef]
  84. Lichołai, L.; Musiał, M. Experimental Analysis of the Function of a Window with a Phase Change Heat Accumulator. Materials 2020, 13, 3647. [Google Scholar] [CrossRef]
  85. LST EN 673:2011; Glass in Building—Determination of Thermal Transmittance (U Value)—Calculation Method. European Committee for Standardization: Brussels, Belgium, 2011.
  86. ISO 15099; Thermal Performance of Windows, Doors and Shading Devices—Detailed Calculations. International Organization for Standardization: Geneva, Switzerland, 2003.
  87. Siegel, R.; Howell, J.R. Thermal Radiation Heat Transfer, 2nd ed.; Hemisphere Publishing Corporation: London, UK, 2019; 951p. [Google Scholar]
  88. Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
  89. Gan, G. Prediction of turbulent buoyant flow using an RNG k–ε model. Numer. Heat Transf. Part A Appl. 1998, 33, 169–189. [Google Scholar] [CrossRef]
  90. Basok, B.; Davydenko, B.; Novikov, V.G.; Pavlenko, A.M.; Novitska, M.P.; Sadko, K.; Goncharuk, S.M. Evaluation of heat transfer rates through transparent dividing structures. Energies 2022, 15, 4910. [Google Scholar] [CrossRef]
  91. Wright, J.L.; Jin, H.; Hollands, K.G.T.; Naylor, D. Flow visualization of natural convection in a tall, air-filled vertical cavity. Int. J. Heat Mass Transf. 2006, 49, 889–904. [Google Scholar] [CrossRef]
  92. Chow, T.; Li, V.; Lin, Z. Innovative solar windows for cooling-demand climate. Sol. Energy Mater. Sol. Cells 2010, 94, 212–220. [Google Scholar] [CrossRef]
  93. Solovjov, V.; Webb, B. A local-spectrum correlated model for radiative transfer in non-uniform gas media. J. Quant. Spectrosc. Radiat. Transf. 2002, 73, 361–373. [Google Scholar] [CrossRef]
  94. Modest, M. Radiative Heat Transfer; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
  95. Ismail, K.A.R.; Henríquez, J.R. Modeling and simulation of a simple glass window. Sol. Energy Mater. Sol. Cells 2003, 80, 355–374. [Google Scholar] [CrossRef]
  96. Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar] [CrossRef]
  97. Oliveti, G.; Arcuri, N.; Bruno, R.; De Simone, M. An accurate calculation model of solar heat gain through glazed surfaces. Energy Build. 2011, 43, 269–274. [Google Scholar] [CrossRef]
  98. Parra, J.; Guardo, A.; Egusquiza, E.; Alavedra, P. Thermal Performance of Ventilated Double Skin Façades with Venetian Blinds. Energies 2015, 8, 4882–4898. [Google Scholar] [CrossRef]
  99. Gloriant, F.; Tittelein, P.; Joulin, A.; Lassue, S. Study of the Performances of a Supply-Air Window for Air Renewal Pre-Heating. Energy Procedia 2015, 78, 525–530. [Google Scholar] [CrossRef]
  100. Ismail, K.A.R.; Salinas, C.S. Non-gray radiative convective conductive modeling of a double glass window with a cavity filled with mixtures of absorbing gases. Int. J. Heat Mass Transf. 2006, 49, 2972–2983. [Google Scholar] [CrossRef]
  101. Ismail, K.A.R.; Salinas, C.S. Gray radiative conductive 2D modeling using discrete ordinates method with multidimensional spatial scheme and non-uniform grid. Int. J. Therm. Sci. 2006, 45, 706–715. [Google Scholar] [CrossRef]
  102. Michaux, G.; Greffet, R.; Salagnac, P. Modelling of an airflow window and numerical investigation of its thermal performances by comparison to conventional double and triple-glazed windows. Appl. Energy 2019, 242, 27–45. [Google Scholar] [CrossRef]
  103. Zhang, C.; Wang, J.; Xu, X.; Zou, F.-J. Modeling and thermal performance evaluation of a switchable triple glazing exhaust air window. Appl. Therm. Eng. 2016, 92, 8–17. [Google Scholar] [CrossRef]
  104. Zhang, C.; Gang, W.; Wang, J. Numerical and experimental study on the thermal performance improvement of a triple glazed window by utilizing low-grade exhaust air. Energy 2019, 167, 1132–1143. [Google Scholar] [CrossRef]
  105. Brzezicki, M. A Systematic Review of the Most Recent Concepts in Smart Windows Technologies with a Focus on Electrochromics. Sustainability 2021, 13, 9604. [Google Scholar] [CrossRef]
  106. Heidari, N.; Eydgahi, A.; Matin, P. The Effect of Smart Colored Windows on Visual Performance of Buildings. Buildings 2022, 12, 861. [Google Scholar] [CrossRef]
  107. Aburas, M.; Soebarto, V.; Williamson, T.; Liang, R.; Ebendorff-Heidepriem, H.; Wu, Y. Thermochromic smart window technologies for building application: A review. Appl. Energy 2019, 255, 113522. [Google Scholar] [CrossRef]
  108. Sun, Y.; Liu, X.; Ming, Y.; Liu, X.; Mahon, D.; Wilson, R.; Liu, H.; Eames, P.; Wu, Y. Energy and daylight performance of a smart window: Window integrated with thermotropic parallel slat-transparent insulation material. Appl. Energy 2021, 293, 116826. [Google Scholar] [CrossRef]
  109. Zhou, Y.; Fan, F.-Y.; Zhao, S.; Xu, Q.; Wang, S.; Luo, D.; Long, Y. Unconventional smart windows: Materials, structures and designs. Nano Energy 2021, 90, 106613. [Google Scholar] [CrossRef]
  110. Feng, W.; Zou, L.; Gao, G.; Wu, G.; Shen, J.; Li, W. Gasochromic smart window: Optical and thermal properties, energy simulation and feasibility analysis. Sol. Energy Mater. Sol. Cells 2016, 144, 316–323. [Google Scholar] [CrossRef]
  111. Heiz, B.P.V.; Pan, Z.; Su, L.; Le, S.T.; Wondraczek, L. A large-area smart window with tunable shading and solar-thermal harvesting ability based on remote switching of a magneto-active liquid. Adv. Sustain. Syst 2018, 2, 1870001. [Google Scholar] [CrossRef]
  112. Hu, Y.; Heiselberg, P.K.; Guo, R. Ventilation cooling/heating performance of a PCM enhanced ventilated window—An experimental study. Energy Build. 2020, 214, 109903. [Google Scholar] [CrossRef]
  113. Rodriguez-Ake, A.; Xamán, J.; Hernández-López, I.; Sauceda, D.; Carranza-Chávez Francisco, J.; Zavala-Guillén, I. Numerical study and thermal evaluation of a triple glass window under Mexican warm climate conditions. Energy 2022, 239, 122075. [Google Scholar] [CrossRef]
  114. Yang, H.; Zhang, L.; Su, X.; Luo, Y.; Liu, Z.; Wang, X.; Qiang, S.; Pang, D. Modeling and analyzing the optical and thermal performance of window with transparent insulation slats. Energy Build. 2022, 277, 112567. [Google Scholar] [CrossRef]
  115. Rabizadeh, M.; Ehsani, M.H.; Shahidi, M.M. ZnO/metal/ZnO (metal = Ag, Pt, Au) films for energy-saving in windows application. Sci. Rep. 2022, 12, 15575. [Google Scholar] [CrossRef]
  116. Shen, C.; Li, X. Solar heat gain reduction of double glazing window with cooling pipes embedded in venetian blinds by utilizing natural cooling. Energy Build. 2016, 112, 173–183. [Google Scholar] [CrossRef]
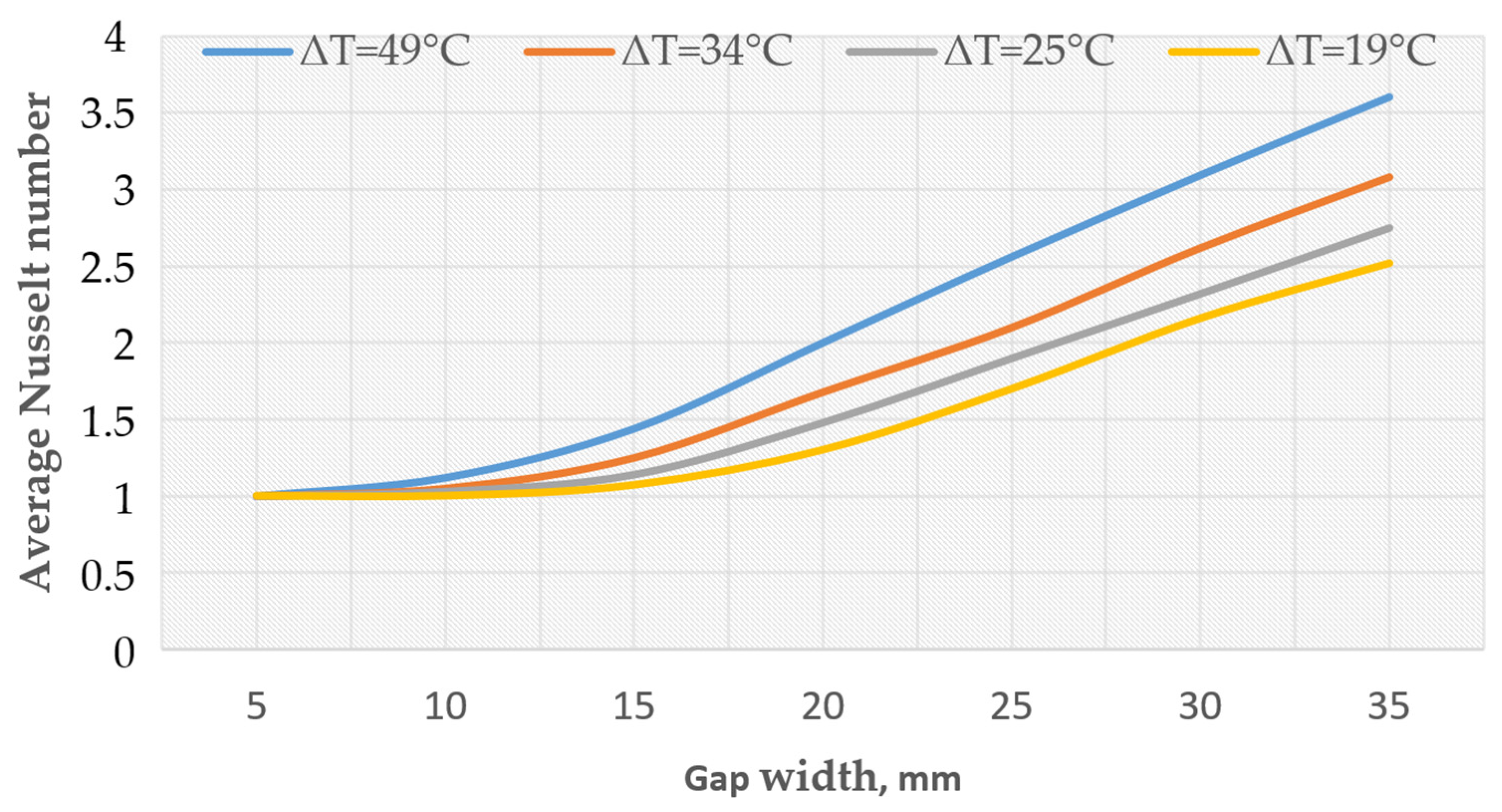
Energies 16 01425 g001 550
Figure 1. Impact of gap width on the average Nusselt number at the inner pane (summarized data from cited papers).
Figure 1. Impact of gap width on the average Nusselt number at the inner pane (summarized data from cited papers).
Energies 16 01425 g001
Energies 16 01425 g002 550
Figure 2. Variation of heat transfer coefficients depending on the number of panes (summarized data from cited papers).
Figure 2. Variation of heat transfer coefficients depending on the number of panes (summarized data from cited papers).
Energies 16 01425 g002
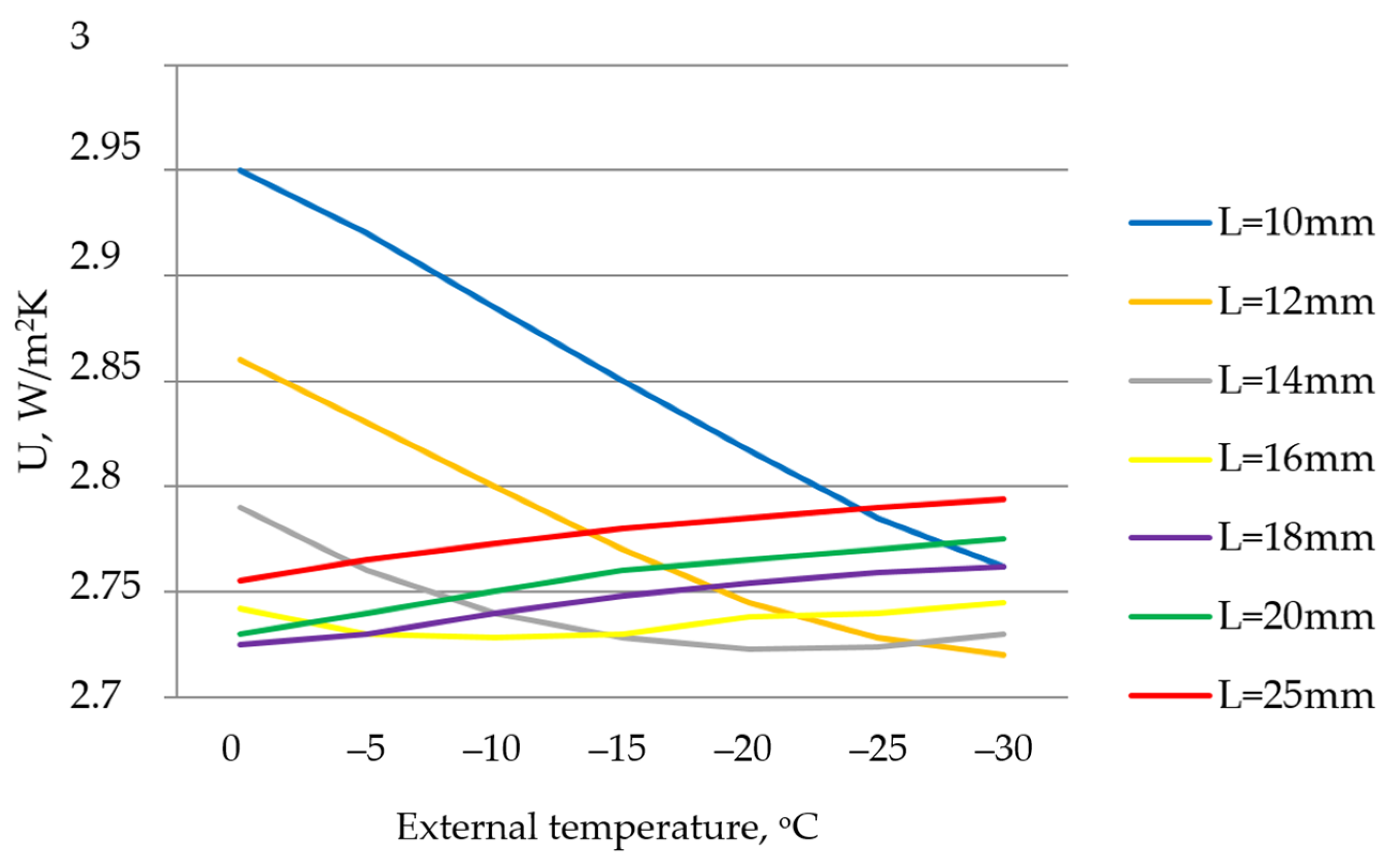
Energies 16 01425 g003 550
Figure 3. Dependence of the gap width and the outdoor temperature on the U−value of a double-pane window (ε = 0.84) (summarized data from cited papers).
Figure 3. Dependence of the gap width and the outdoor temperature on the U−value of a double-pane window (ε = 0.84) (summarized data from cited papers).
Energies 16 01425 g003
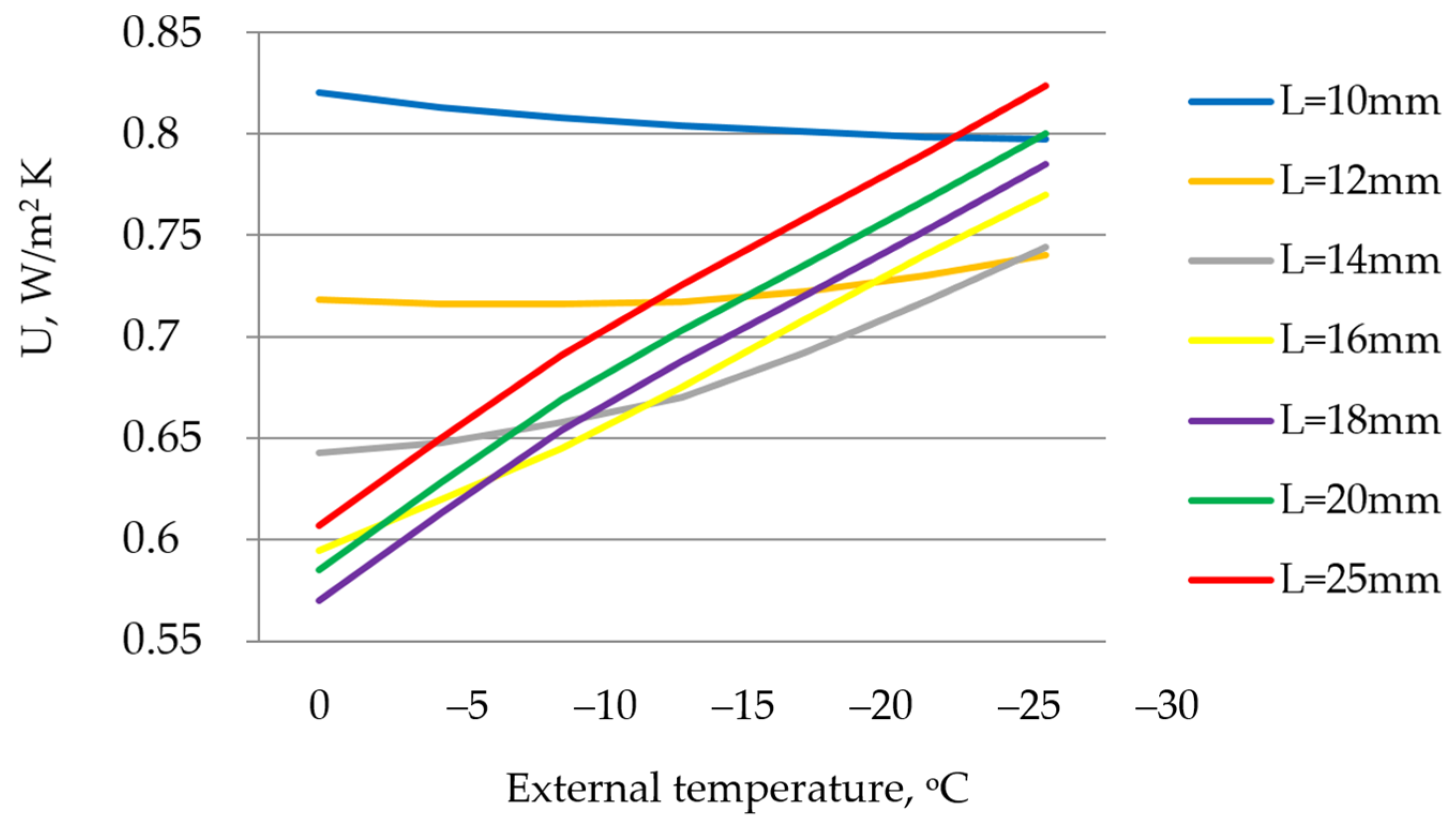
Energies 16 01425 g004 550
Figure 4. Dependence of the gap width and the outdoor temperature on the U−value of a double-pane window (ε = 0.04) (summarized data from cited papers).
Figure 4. Dependence of the gap width and the outdoor temperature on the U−value of a double-pane window (ε = 0.04) (summarized data from cited papers).
Energies 16 01425 g004
Energies 16 01425 g005 550
Figure 5. Variation of the overall heat transfer coefficient depending on the width of the gap between panes for four internal surface temperature differences (summarized data from cited papers).
Figure 5. Variation of the overall heat transfer coefficient depending on the width of the gap between panes for four internal surface temperature differences (summarized data from cited papers).
Energies 16 01425 g005
Energies 16 01425 g006 550
Figure 6. Streamlines in (a) double-, (b) triple-, and (c) quadruple-pane windows for L = 21 mm and ΔT = 15 °C [7].
Figure 6. Streamlines in (a) double-, (b) triple-, and (c) quadruple-pane windows for L = 21 mm and ΔT = 15 °C [7].
Energies 16 01425 g006
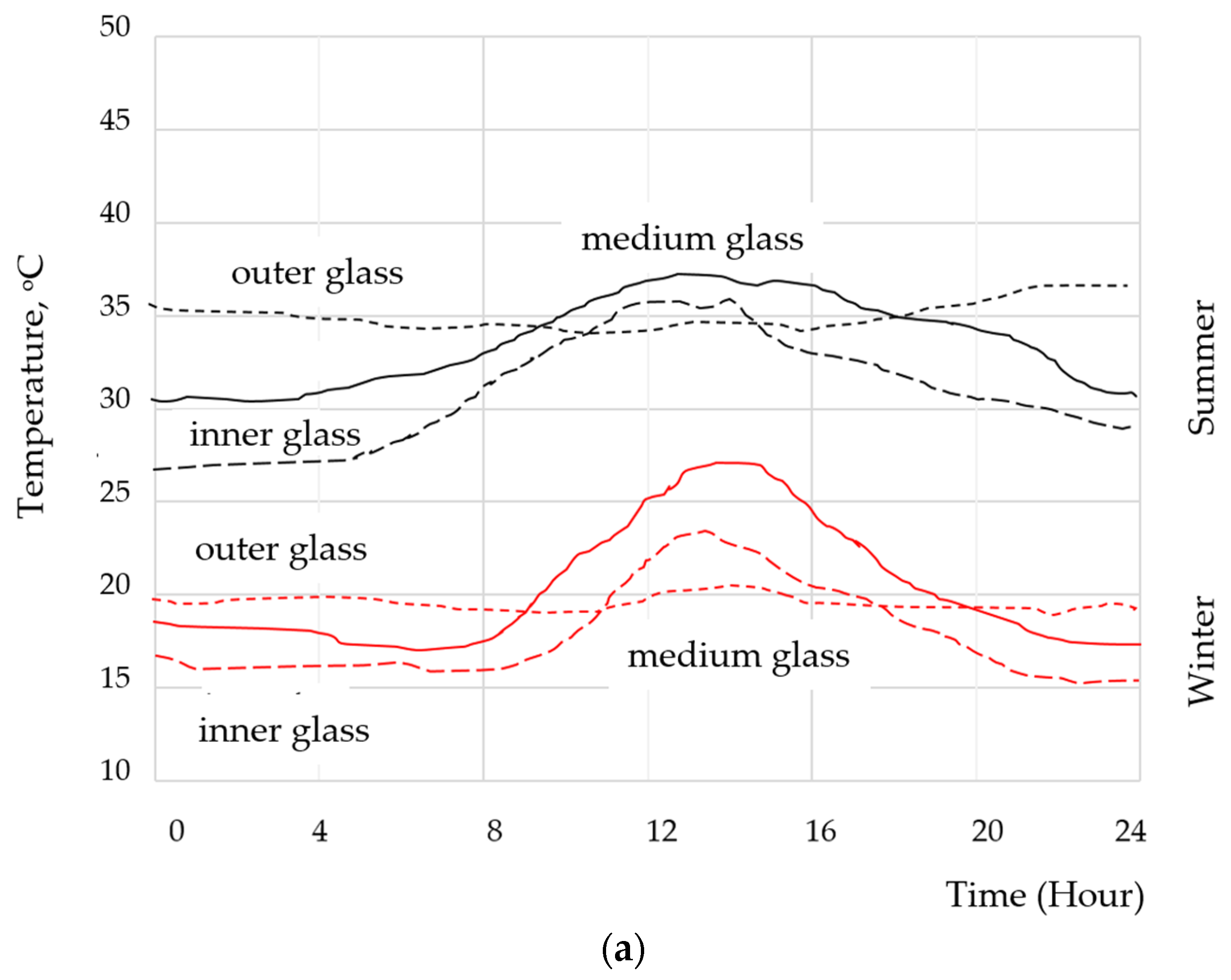
Energies 16 01425 g007a 550Energies 16 01425 g007b 550
Figure 7. (a) The temperature on the surface of window panes; (b) the solar heat gains; (c) the heat fluxes from the simulation in the summer and the winter (data obtained as a result of processing cited papers).
Figure 7. (a) The temperature on the surface of window panes; (b) the solar heat gains; (c) the heat fluxes from the simulation in the summer and the winter (data obtained as a result of processing cited papers).
Energies 16 01425 g007aEnergies 16 01425 g007b
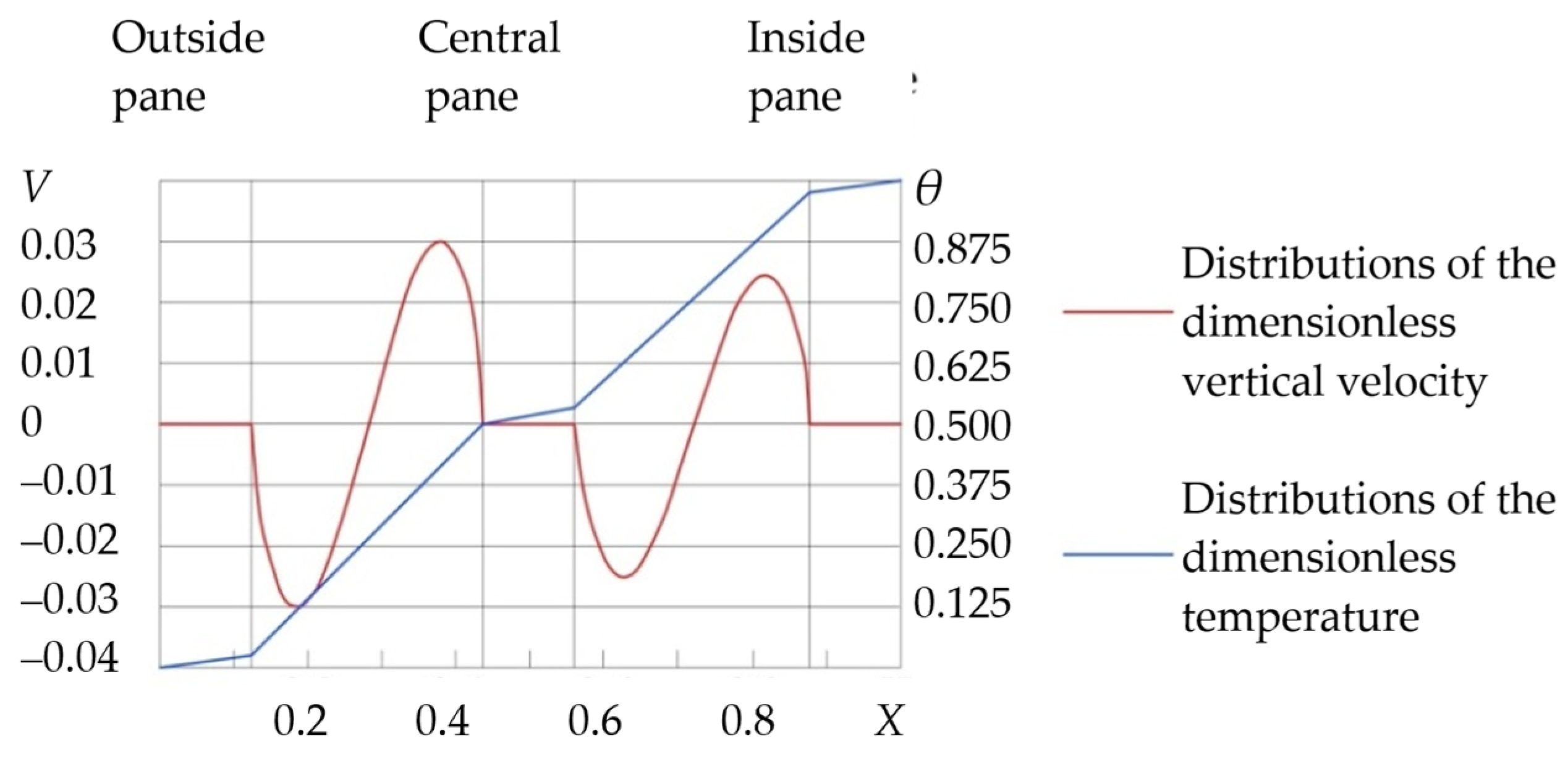
Energies 16 01425 g008 550
Figure 8. The distributions of the dimensionless vertical velocity and of the dimensionless temperature across the thickness of a triple-pane window (data obtained as a result of processing cited papers).
Figure 8. The distributions of the dimensionless vertical velocity and of the dimensionless temperature across the thickness of a triple-pane window (data obtained as a result of processing cited papers).
Energies 16 01425 g008
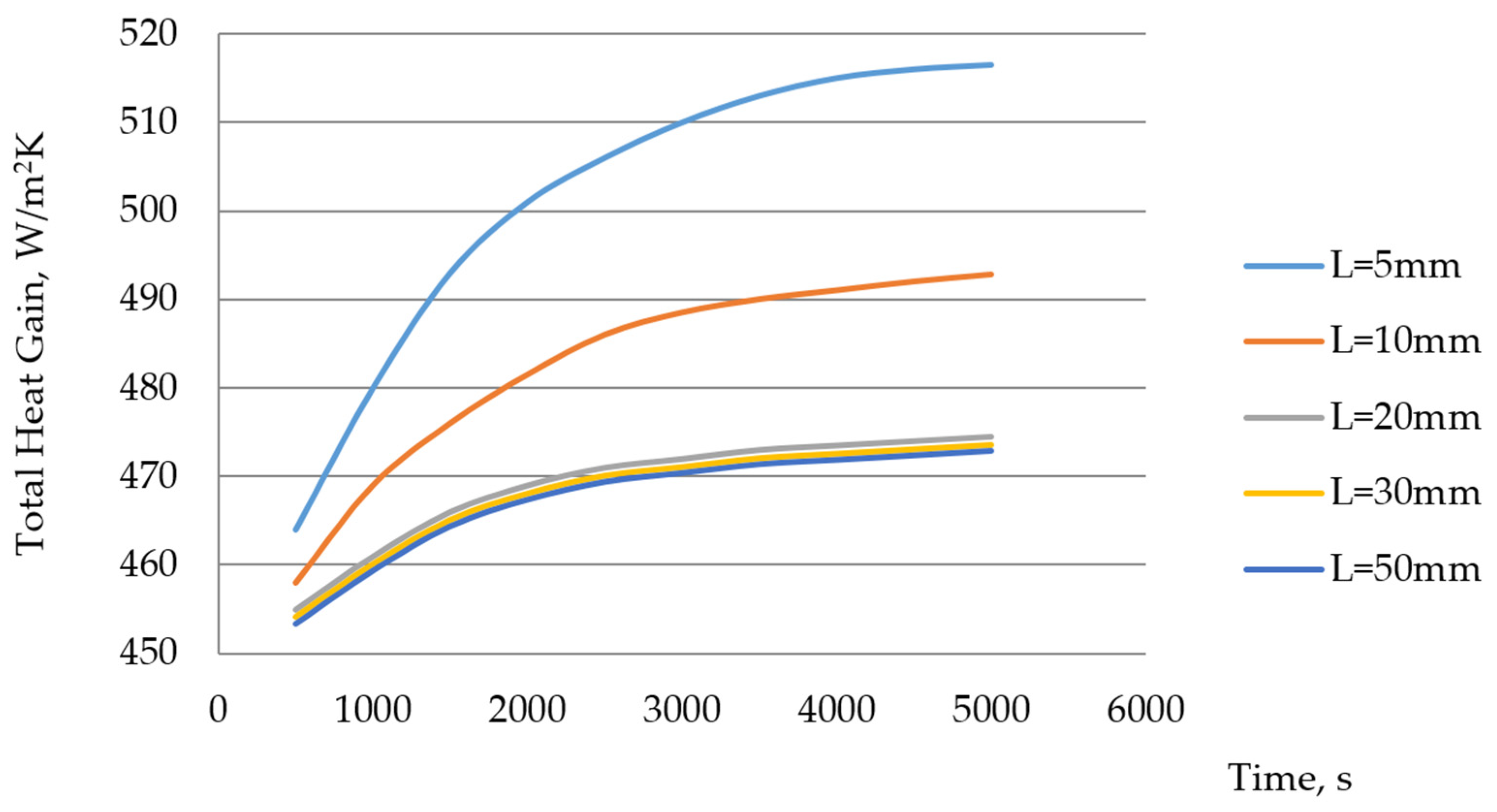
Energies 16 01425 g009 550
Figure 9. The impact of the gap width on the total heat gain of a ventilated double-pane window (data obtained as a result of processing cited papers).
Figure 9. The impact of the gap width on the total heat gain of a ventilated double-pane window (data obtained as a result of processing cited papers).
Energies 16 01425 g009
Energies 16 01425 g010 550
Figure 10. A climatic chamber at the Kielce University of Technology.
Figure 10. A climatic chamber at the Kielce University of Technology.
Energies 16 01425 g010
Energies 16 01425 g011 550
Figure 11. The studied windows installed in a climate chamber.
Figure 11. The studied windows installed in a climate chamber.
Energies 16 01425 g011
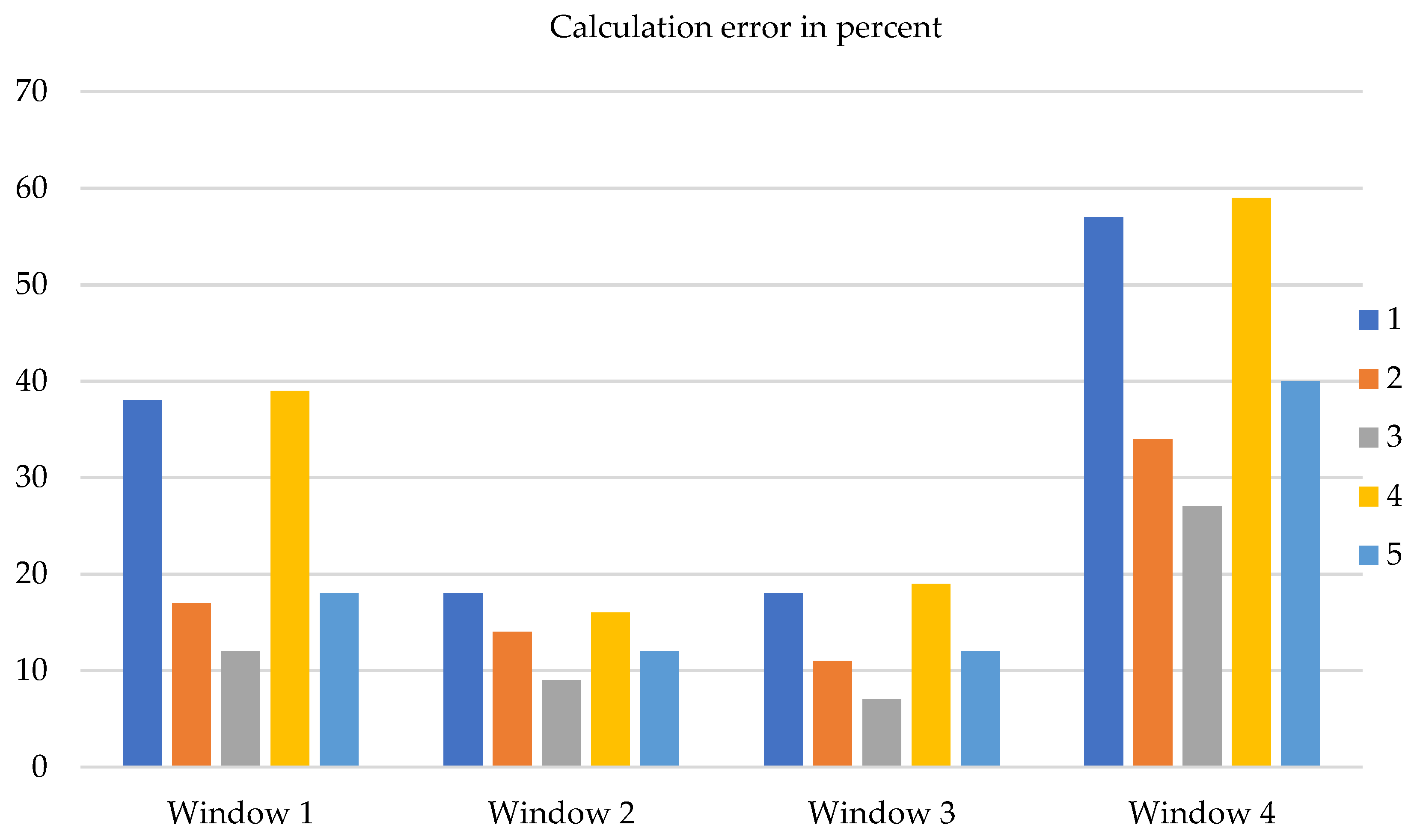
Energies 16 01425 g012 550
Figure 12. Distribution of the local values of heat flux density on the window surface: 1—upper left corner of the window; 2—lower left corner of the window; 3—in the center of the window; 4—upper right corner of the window; 5—lower right corner of window; windows: 1—standard triple-pane; 2—triple-pane filled with argon; 3—triple-pane with an interactive cover; 4—triple-pane with a heated base; The comparison of the results concerned the calculated data obtained using a standard mathematical model [90] with our experimental data.
Figure 12. Distribution of the local values of heat flux density on the window surface: 1—upper left corner of the window; 2—lower left corner of the window; 3—in the center of the window; 4—upper right corner of the window; 5—lower right corner of window; windows: 1—standard triple-pane; 2—triple-pane filled with argon; 3—triple-pane with an interactive cover; 4—triple-pane with a heated base; The comparison of the results concerned the calculated data obtained using a standard mathematical model [90] with our experimental data.
Energies 16 01425 g012
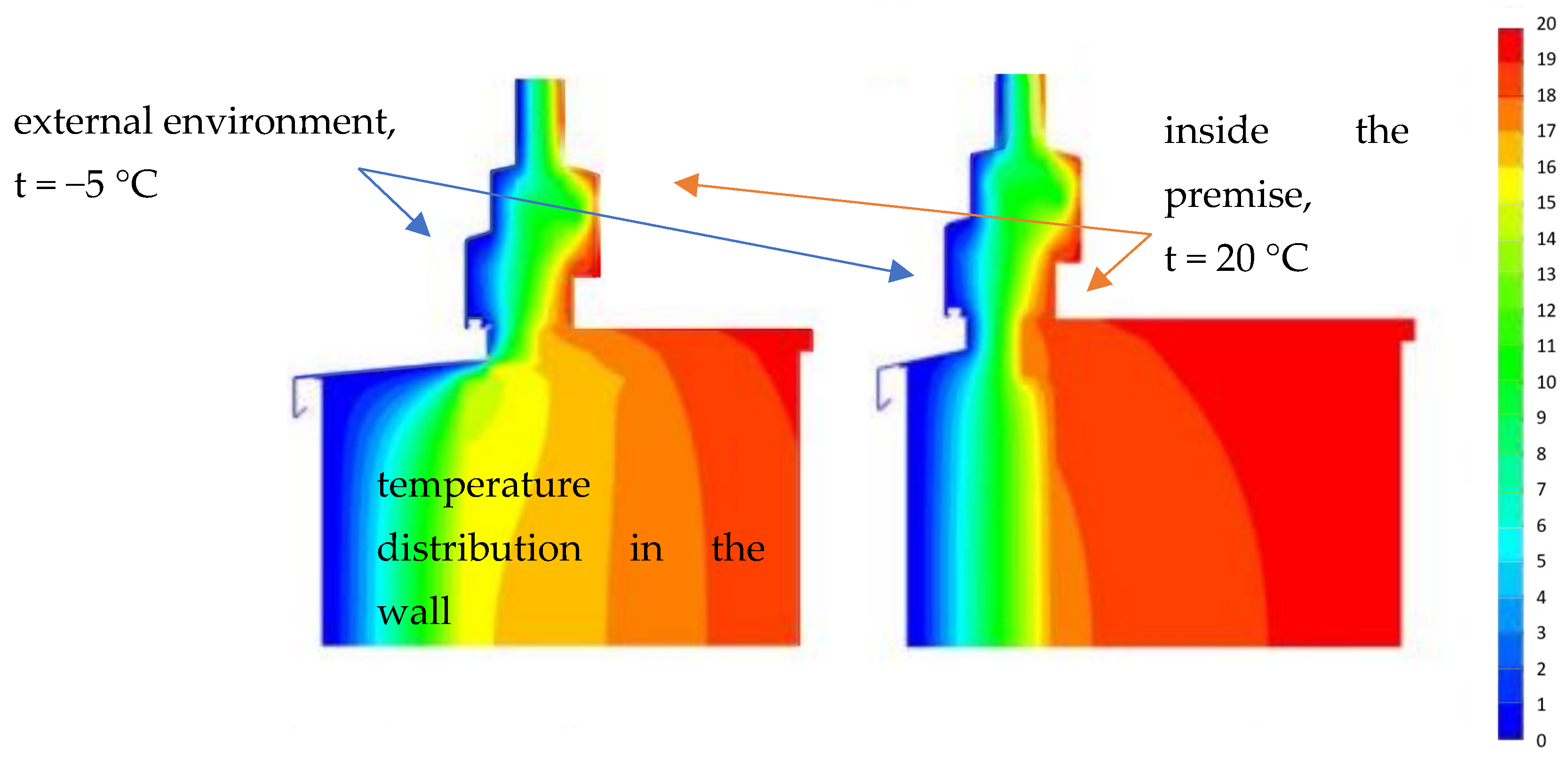
Energies 16 01425 g013 550
Figure 13. The temperature distribution in walls and windows depending on the location of the window (author data).
Figure 13. The temperature distribution in walls and windows depending on the location of the window (author data).
Energies 16 01425 g013
Table
Table 1. Overview of the topically relevant numerical investigations of heat transfer in windows.
Table 1. Overview of the topically relevant numerical investigations of heat transfer in windows.
Ref.Window Type1D/2D/3DSteady or Transient FlowAim of the StudyMathematical Formulation and Numerical MethodConside-Ring Thermal RadiationConside-Ring Solar Radiation
[6]double-, triple- and quadruple-pane windows1DsteadyDetermination of the optimal number of panes and heat transfer coefficients.Degree-day methodyesno
[7]double-, triple-, and quadruple-pane windows2DunsteadyDetermination of the air flow, the heat transfer, the overall heat transfer coefficient, and the Nusselt number depending on the number of panes, the temperature difference, and the width of the gap.CFD
Second-order upwind scheme
S2S radiation model		yesno
[10]double-pane window1DsteadyDetermination of the optimal width of the gap in double-pane windows in various climatic zones.Degree-day methodnono
[11]double-pane window2DsteadyPrediction of the thermal transmittance for varying widths of the air layer at various temperature differences through the window.CFD
Renormalization k–ε turbulence model		yesno
[12]double-pane window2DsteadyDetermination of the optimum air layer thickness for different climates.Finite difference method
ADI method		nono
[13]double-pane window2DsteadyDetermination of the optimum air layer thickness for different climates and filling, considering a conjugate heat transfer.Finite difference method
ADI method		nono
[21]double-pane window1D/2DsteadyThe impact of the Rayleigh number, the enclosure aspect ratio, and the blind geometry on the convective heat transfer.Control-volume method
Second-order upwind scheme		yesno
[30]double-, triple-, and quadruple-pane windows2DtransientDetermination of the overall heat transfer coefficient considering the number of panes, the gap width, and five different emissivity values.CFD
Second-order upwind scheme
S2S radiation model		yesno
[34]double-pane window with and without a solar control coating2Dpseudo-transientImpact of a solar control coating on the convective flux and the radiative flux.Net radiative method
Finite volume method
ACM		yesyes
[48]double-pane airflow
windows		2DsteadyEstimation of the overall forced convective heat transfer.Second-order upwind scheme
Renormalization k–ε turbulence model		yesno
[52]double- and triple-pane windows2DtransientImpact of a mobile shading system and a phase-change heat store on the thermal performance.Finite difference methodyesyes
[55]energy-active window2DsteadyComparison of an energy-active window with a conventional triple-pane one in order to calculate the U-value and select appropriate Nusselt number correlations.Finite difference methodyesyes
[60]double-pane window withtransparent
fins in the gap		3DsteadyInvestigation of reduction or suppression of the convective motion inside the gap with transparent fins for different Rayleigh numbers and aspect ratio.CFDnono
[61]double- and triple-pane windows1DsteadyDetermination of the dependence of the values of thermal transmittance on external temperatures.Standard EN 673
Standard ISO 15099		yesno
[62]slim double skin facade2DsteadyEvaluation of the impact of colored or low-emissivity pane to improve the cooling performance.Renormalization k–ε turbulence model
S2S radiation model		yesyes
[63]double-pane naturally ventilated window2DtransientDetermination of the SHGC, the shading coefficient, and the temperature field along and across the gap for different gap widths and incident radiation conditions.Finite difference method
ADI method		yesyes
[64]double-pane window2DsteadyComparison of the SHGC and the total heat gain coefficient of a double-pane window filled with an absorbing gas, a single-pane window, and a naturally ventilated double-pane window.CW number model
DO method		yesyes
single-pane window2DtransientFinite difference approximation
ADI method		yesyes
naturally ventilated double-pane window2DtransientADI methodyesyes
[65]slim-type
double skin window system		3DsteadyDetermination of the cavity air temperatures and the SHGC for the closed and open conditions of the window’s external opening.CFDyesyes
[66]single-pane
window		1DtransientDetermination of the amount of global radiation on panes and the corresponding pane surface temperature over the diurnal cycle.Finite difference methodyesyes
[67]multi-pane windows2DsteadyInvestigation of a ray-tracing method compared with the ISO 15099 standard.CFD + ray-tracing method
Standard ISO 15099		yesyes
[68]supply air ventilated window3DsteadyInvestigation of the velocity and the temperature distribution.CFD
Finite volume method
Second-order upwind scheme		yesyes
[69]supply air ventilated windows3DsteadyInvestigation of the thermal performance and the capacity to preheat ventilation air.CFDyesyes
[70]double-pane window with a controlled flow of water within the gap3DsteadyImpact of the water flow velocity, the external and internal temperatures, the incident solar radiation, and the beam angle.CFDyesyes
[71]dual-air flow window3DsteadyInvestigation a novel method for calculation of air flow through the gap and pane temperatures.Renormalization k–ε turbulence model
S2S radiation model		yesyes
[72]triple-pane window2DsteadyDetermination of the velocity, the pressure, and the temperature fields in the panes and in the gas gap.Control-volume methodyesyes
[73]double-pane window2DsteadyComparison of the thermal efficiency of windows filled with an absorbing gas and filled with a PCM.CW number model yesyes
[74]double-pane naturally ventilated window1DunsteadyImpact of the gap width and the variation of the forced mass flow rate on the total heat gain and the shading coefficient.S2S radiation modelyesyes
[75]ventilated multi-pane windows2DsteadyInvestigation of the impact of ventilation on different window setup.CFD
Finite volume method
S2S radiation model		yesyes
[76]double-pane air flow window with integrated blinds2DsteadyImpact of the tilt angle of the blinds, the gap width, and the areas of inlet and outlet vents on the thermal performance.k-ω viscous model
DO method		yesyes
[77]ventilated double-pane window2DsteadyImpact of a reflective solar control film, the gap width, and the thickness of the glass panes on the thermal performance.Finite volume methodyesyes
[78]double-pane ventilated window2DsteadyImpact of the airflow rate, the outdoor air temperature, and the solar irradiance on the temperature rise and the useful energy of the delivered air.CFD
Standard ISO 15099		yesyes
[79]double-pane ventilated window1DsteadyDetermination of the SHGC in different operating conditions and for different glass types and different glass to frame ratios.Standard ISO 15099yesyes
[80]triple-pane
dual air flow window		2DsteadyImpact of solar radiation, wind, mode of operation, airflow rate, and gap width.CFD
Renormalization k–ε turbulence model Second-order upwind scheme		yesyes
[81]triple-pane
window		2DsteadyDetermination of U-value and heat lossses for dirrenent outdoor temperature, window-to-wall ratios, glazing models and number of panes.Standard ISO 15099yesyes
[82]double-pane window with electric heating2DsteadyAnalysis of the distribution of heat flows and temperatures.Finite difference methodyesno
[83]double-pane window
integrated
with a photovoltaic system		2DsteadyDetermination of the overall heat transfer coefficient, the temperature distribution, and the flow field for different Rayleigh numbers.Finite difference methodyesyes
[84]window with a phase change heat
accumulator		2DsteadyDetermination of two complex heat transfer resistances between the external glazing and the PCM accumulator, and between the PCM accumulator and the internal glazing.Finite difference methodyesyes
Coefficients of determination were given for only a few models: [10] (R2 = 0.86), [11] (R2 = 0.99), [30] (R2 = 0.997), [52] (R2 = 0.917), [84] (R2 = 0.904)].
Table
Table 2. Smart window types and their operation mechanisms.
Table 2. Smart window types and their operation mechanisms.
Ref.Glass TypeOperation Mechanism
[105]ElectrochromicResponse to an electrical voltage or charge
[106]PhotochromicResponse to UV light
[107]ThermochromicResponse to temperature
[108]ThermotropicResponse to temperature-dependent light scattering
[109]MechanochromicResponse to optical properties
[110]GasochromicResponse to reducing or oxidizing gases
[111]MagnetochromicResponse to magnetic field intensity
Table
Table 3. Summary of the presented different approaches to mathematical modeling of the thermal transmission through windows.
Table 3. Summary of the presented different approaches to mathematical modeling of the thermal transmission through windows.
Model TypesRef.
CFD simulations were performed in many of the cited papers [7,11,21,30,60,62,65,67,68,69,70,75,78,80,113,114,115,116]
The majority of the conducted studies were focused on 2D models [7,11,12,13,21,30,34,48,52,55,62,63,64,67,72,73,75,76,77,78,80,81,82,83,84,89,99,100,101,113,115]
In many of the modeling approaches, the solar radiation was not considered [6,7,10,11,12,13,21,30]
The standard k-ε model or the RNG k-ε turbulence model were implemented for simulations of ventilated windows [48,62,71,80,98,99,103]
In some cases, heat sources were included in the energy equation [63,64,82,93,100,114]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Pavlenko, A.M.; Sadko, K. Evaluation of Numerical Methods for Predicting the Energy Performance of Windows. Energies 2023, 16, 1425. https://doi.org/10.3390/en16031425

AMA Style

Pavlenko AM, Sadko K. Evaluation of Numerical Methods for Predicting the Energy Performance of Windows. Energies. 2023; 16(3):1425. https://doi.org/10.3390/en16031425

Chicago/Turabian Style

Pavlenko, Anatoliy M., and Karolina Sadko. 2023. "Evaluation of Numerical Methods for Predicting the Energy Performance of Windows" Energies 16, no. 3: 1425. https://doi.org/10.3390/en16031425

APA Style

Pavlenko, A. M., & Sadko, K. (2023). Evaluation of Numerical Methods for Predicting the Energy Performance of Windows. Energies, 16(3), 1425. https://doi.org/10.3390/en16031425

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop