Comparison of Procedures to Combine Operating Zones of Multiple Units into Plant-Based Operating Zones
Abstract
:1. Introduction
2. Problem Formulation
3. Solution Procedures
3.1. M01: A Way to Enumerate All the Possible Combinations
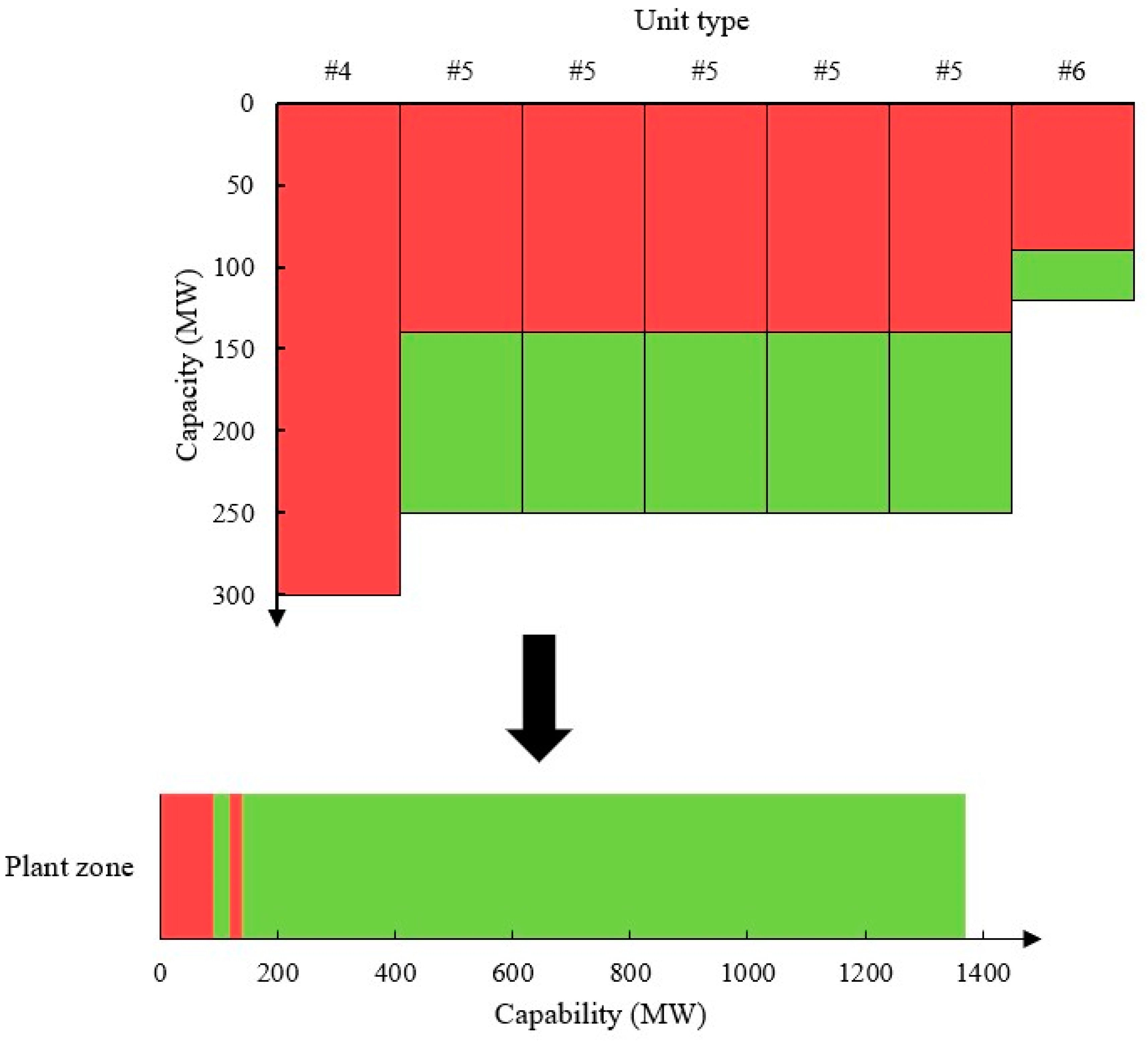
3.2. M02: A Way to Merge Zones Sequentially
3.3. M03: A Way to Use Discrete Values
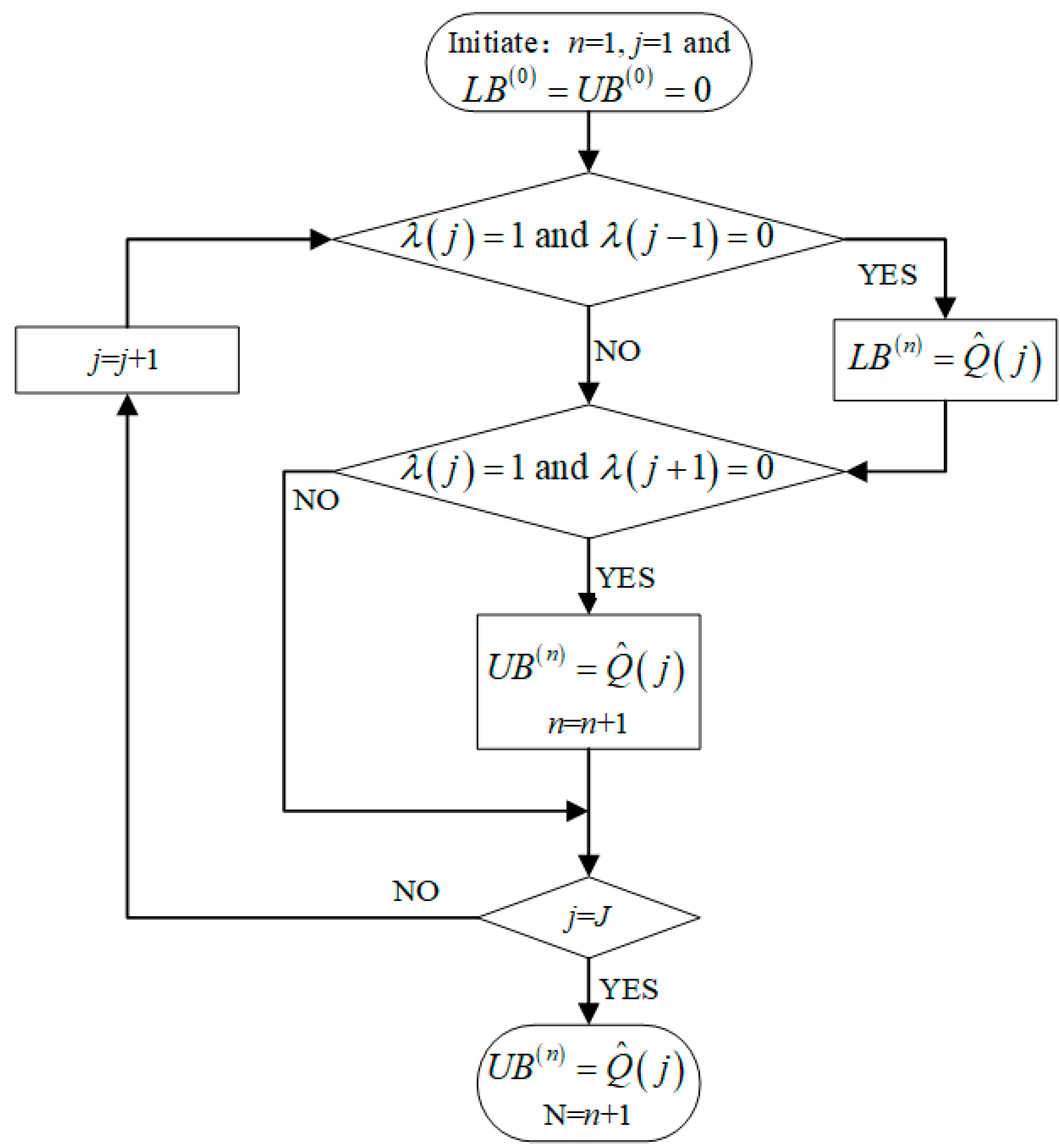
3.4. M04: A Way to Identify Zone Bounds Explicitly
4. Case Studies
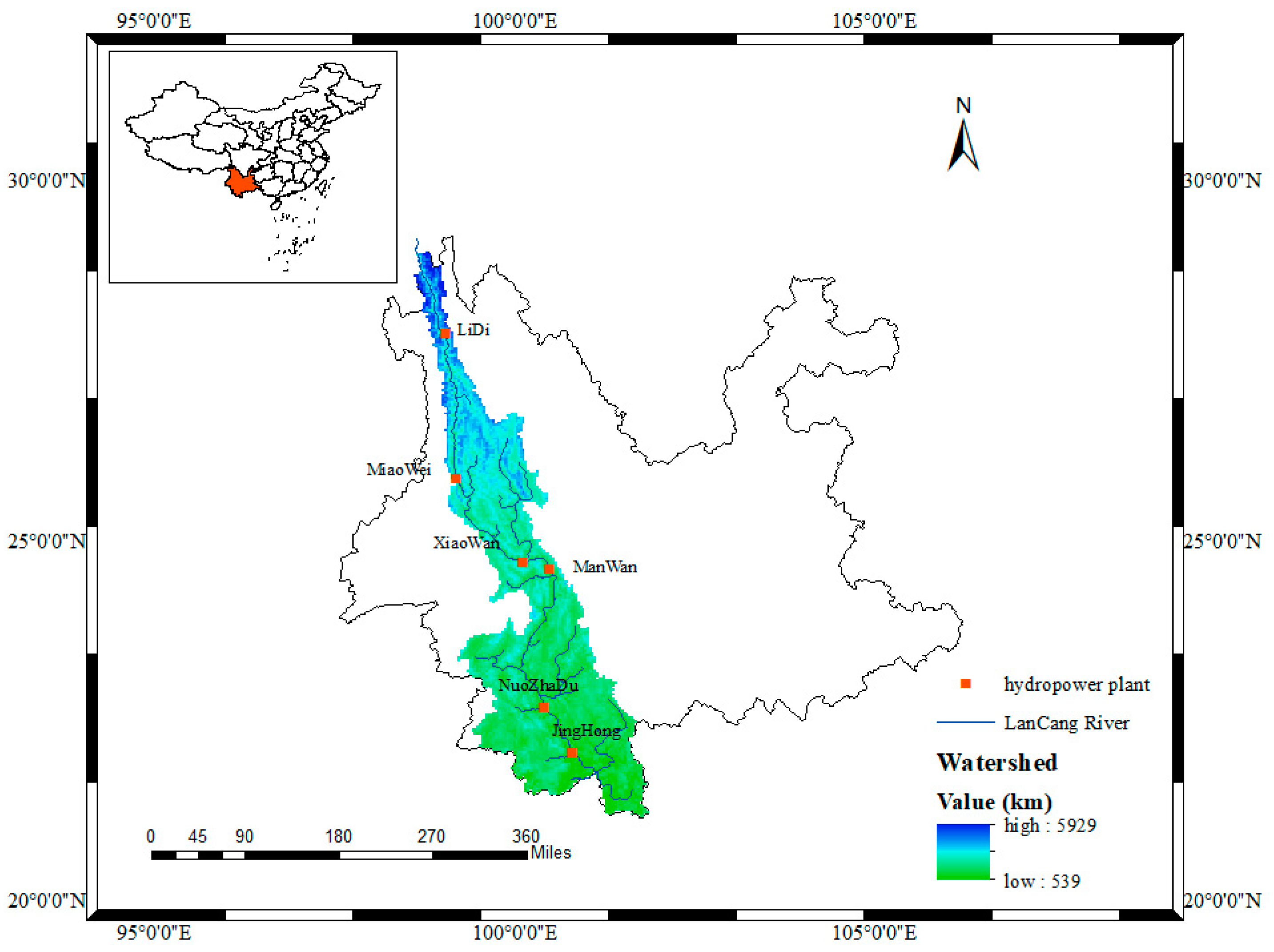
4.1. Data Preparation
4.2. Comparison of Procedures
4.3. Detailed Results
4.4. Errors from Interpolation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Ma, C.; Yang, Y.; Pang, X.L.; Liu, L.; Lian, J.J. Study on short-term optimal operation of cascade hydro-photovoltaic hybrid systems. Appl. Energy 2021, 291, 116828. [Google Scholar] [CrossRef]
- Zhang, D.H.; Wang, J.Q.; Lin, Y.G.; Si, Y.L.; Huang, C.; Yang, J.; Huang, B.; Li, W. Present situation and future prospect of renewable energy in China. Renew. Sustain. Energy Rev. 2017, 76, 865–871. [Google Scholar] [CrossRef]
- Li, J.D.; Chen, S.J.; Wu, Y.Q.; Wang, Q.H.; Liu, X.; Qi, L.J.; Lu, X.Y.; Gao, L. How to make better use of intermittent and variable energy? A review of wind and photovoltaic power consumption in China. Renew. Sustain. Energy Rev. 2021, 137, 110626. [Google Scholar] [CrossRef]
- Cheng, C.T.; Wang, J.Y.; Wu, X.Y. Hydro Unit Commitment with a Head-Sensitive Reservoir and Multiple Vibration Zones Using MILP. IEEE Trans. Power Syst. 2016, 31, 4842–4852. [Google Scholar] [CrossRef]
- Li, C.A.; Hsu, E.; Svoboda, A.J.; Tseng, C.L.; Johnson, R.B.; Hsu, E. Hydro unit commitment in hydro-thermal optimization. IEEE Trans. Power Syst. 1997, 12, 764–769. [Google Scholar] [CrossRef]
- Taktak, R.; D’Ambrosio, C. An overview on mathematical programming approaches for the deterministic unit commitment problem in hydro valleys. Energy. Syst. 2017, 8, 57–79. [Google Scholar] [CrossRef]
- Jahromi, M.Z.; Bioki, M.M.H.; Rashdinejad, M.; Fadaeinedjad, R. Solution to the unit commitment problem using an artificial neural network. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 198–212. [Google Scholar] [CrossRef]
- Postolov, B.; Iliev, A. New metaheuristic methodology for solving security constrained hydrothermal unit commitment based on adaptive genetic algorithm. Int. J. Electr. Power Energy Syst. 2022, 134, 107163. [Google Scholar] [CrossRef]
- Zhou, L.A.; Cheng, C.T.; Liao, S.L.; Wang, J. Multiobjective Scheduling Method for Short-Term Peak Shaving Operation of Cascade Hydro Plants. J. Water Resour. Plan. Manag. 2020, 146, 04020073. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, X.Y.; Liao, S.L.; Cheng, C.T. An ultra-short-term scheduling model for cascade hydropower regulated by multilevel dispatch centers suppressing wind power volatility. Int. J. Electr. Power Energy Syst. 2021, 134, 107467. [Google Scholar] [CrossRef]
- Yu, X.G.; Li, G.; Li, Y.P.; Cheng, C.T. Robust short-term scheduling based on information-gap decision theory for cascade reservoirs considering bilateral contract fulfillment and day-ahead market bidding in source systems. Environ. Res. Lett. 2021, 16, 055020. [Google Scholar] [CrossRef]
- Cheng, C.T.; Shen, J.J.; Wu, X.Y. Short-Term Scheduling for Large-Scale Cascaded Hydropower Systems with Multivibration Zones of High Head. J. Water Resour. Plan. Manag. 2012, 138, 257–267. [Google Scholar] [CrossRef]
- Wang, J.W.; Zheng, H.; Chen, C.; Liu, S.Q.; Chen, H.; Liu, R. How the Cooperation between Reservoir Operation and Unit Commitment Can Reduce Scheduled Spillages. J. Water Resour. Plan. Manag. 2022, 148, 06022002. [Google Scholar] [CrossRef]
- Zhao, Z.P.; Cheng, C.T.; Jin, X.Y.; Liu, L.J.; Yan, L.Z. A MILP model for hydro unit commitment with irregular vibration zones based on the constrained Delaunay triangulation method. Int. J. Electr. Power Energy Syst. 2020, 123, 106241. [Google Scholar] [CrossRef]
- Li, X.; Li, T.J.; Wei, J.H.; Wang, G.Q.; Yeh, W.W.G. Hydro Unit Commitment via Mixed Integer Linear Programming: A Case Study of the Three Gorges Project, China. IEEE Trans. Power Syst. 2014, 29, 1232–1241. [Google Scholar] [CrossRef]
- Cheng, X.L.; Feng, S.Z.; Zheng, H.; Wang, J.W.; Liu, S.Q. A hierarchical model in short-term hydro scheduling with unit commitment and head-dependency. Energy 2022, 251, 123908. [Google Scholar] [CrossRef]
- Cheng, X.L. A Study on the Peak-Shaving and Hierarchical Models Applied in Short-Term Optimal Scheduling of Cascaded Hydropower Reservoirs. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2021. [Google Scholar] [CrossRef]
| Unit Type | Rated Capacity (MW) | Hydropower Plant | Number of Units |
|---|---|---|---|
| 1# | 140 | Lidi | 3 |
| 2# | 350 | Miaowei | 4 |
| 3# | 700 | Xiaowan | 6 |
| 4# | 300 | Manwan | 1 |
| 5# | 250 | Manwan | 5 |
| 6# | 120 | Manwan | 1 |
| 7# | 650 | Nuozhadu | 9 |
| 8# | 350 | Jinghong | 5 |
| U09 | 650 | VH01 | 12 |
| U10 | 650 | VH02 | 15 |
| U11 | 650 | VH03 | 18 |
| Unit Type | Water Head (m) | Shutdown (MW) | Zone 1# (MW) | Zone 2# (MW) | |||
|---|---|---|---|---|---|---|---|
| LB(0) | UB(0) | LB(1) | UB(1) | LB(2) | UB(2) | ||
| 1# | 36 | 0 | 0 | 60 | 140 | -- | -- |
| 1# | 37 | 0 | 0 | 60 | 140 | -- | -- |
| 2# | 81.6 | 0 | 0 | 120 | 170 | 230 | 292.4 |
| 2# | 93 | 0 | 0 | 120 | 170 | 230 | 350 |
| 3# | 212.33 | 0 | 0 | 120 | 240 | 480 | 676 |
| 3# | 222 | 0 | 0 | 120 | 240 | 480 | 700 |
| 4# | 89 | 0 | 0 | -- | -- | -- | -- |
| 4# | 90 | 0 | 0 | 168 | 300 | -- | -- |
| 5# | 89 | 0 | 0 | 140 | 250 | -- | -- |
| 5# | 90 | 0 | 0 | 140 | 250 | -- | -- |
| 6# | 89 | 0 | 0 | 90 | 120 | -- | -- |
| 6# | 90 | 0 | 0 | 90 | 120 | -- | -- |
| 7# | 152 | 0 | 0 | 211 | 220 | 420 | 467 |
| 7# | 156 | 0 | 0 | 420 | 490 | -- | -- |
| 7# | 162 | 0 | 0 | 420 | 523 | -- | -- |
| 8# | 58 | 0 | 0 | 200 | 340 | -- | -- |
| 8# | 62 | 0 | 0 | 200 | 350 | -- | -- |
| U09 | 152 | 0 | 0 | 211 | 220 | 420 | 467 |
| U10 | 152 | 0 | 0 | 211 | 220 | 420 | 467 |
| U11 | 152 | 0 | 0 | 211 | 220 | 420 | 467 |
| Hydro Plant | Water Head (m) | Scale (Zone×Unit) | Installed Capacity (MW) | Solution Time (Milliseconds) | |||
|---|---|---|---|---|---|---|---|
| M01 | M02 | M03 | M04 | ||||
| Lidi | 36.4 | 2 × 3 | 420 | <1 | <1 | 106 | 12 |
| Miaowei | 85 | 3 × 4 | 1238 | <1 | <1 | 377 | 15 |
| Manwan | 89.4 | 1 × 1 + 2 × 5 + 2 × 1 | 1370 | <1 | <1 | 218 | 21 |
| Jinghong | 60 | 2 × 5 | 1724 | <1 | <1 | 181 | 24 |
| Xiaowan | 215 | 3 × 6 | 4095 | <1 | <1 | 528 | 66 |
| Nuozhadu | 158 | 2 × 9 | 4509 | <1 | <1 | 1624 | 73 |
| Nuozhadu | 152 | 3 × 9 | 4203 | 3 | <1 | 1558 | 120 |
| VP01 | 152 | 3 × 12 | 5604 | 73 | <1 | 1602 | 234 |
| VP02 | 152 | 3 × 15 | 7005 | 2411 | 1 | 1860 | 446 |
| VP03 | 152 | 3 × 18 | 8406 | 71,480 | 1 | 2112 | 518 |
| Hydro Plant | CPU Time Per Trial (Milliseconds) | Number of Trials | ||||||
|---|---|---|---|---|---|---|---|---|
| M01 | M02 | M03 | M04 | M01 | M02 | M03 | M04 | |
| Lidi | -- | -- | 0.03 | 4 | 8 | 8 | 4200 | 3 |
| Miaowei | -- | -- | 0.03 | 3 | 81 | 33 | 12,380 | 5 |
| Manwan | -- | -- | 0.02 | 2.33 | 64 | 30 | 13,700 | 9 |
| Jinghong | -- | -- | 0.01 | 2.18 | 32 | 22 | 17,240 | 11 |
| Xiaowan | -- | -- | 0.01 | 4.71 | 729 | 39 | 40,950 | 14 |
| Nuozhadu (158 m) | -- | -- | 0.04 | 4.29 | 512 | 82 | 45,090 | 17 |
| Nuozhadu(152 m) | -- | -- | 0.04 | 6.67 | 19,683 | 204 | 42,030 | 18 |
| VP01 | -- | -- | 0.03 | 9.75 | 312 | 303 | 56,040 | 24 |
| VP02 | -- | -- | 0.03 | 14.87 | 315 | 402 | 70,050 | 30 |
| VP03 | -- | -- | 0.03 | 14.39 | 318 | 501 | 84,060 | 36 |
| Zone # | Lidi (h = 36.4 m) | Miaowei (85 m) | Manwan (89.4 m) | Jinghong (60 m) | Xiaowan (215 m) | Nuozhadu | |
|---|---|---|---|---|---|---|---|
| (158 m) | 152 m | ||||||
| 0 | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] | [0, 0] |
| 1 | [60, 420] | [120, 170] | [90, 120] | [200, 345] | [120, 4096] | [420, 501] | [211, 220] |
| 2 | -- | [230, 340] | [140, 1370] | [400, 1725] | -- | [840, 1002] | [420, 467] |
| 3 | -- | [350, 1238] | -- | -- | -- | [1260, 1503] | [631, 687] |
| 4 | -- | -- | -- | -- | -- | [1680, 2004] | [840, 934] |
| 5 | -- | -- | -- | -- | -- | [2100, 2505] | [1051, 1154] |
| 6 | -- | -- | -- | -- | -- | [2520, 4509] | [1260, 1401] |
| 7 | -- | -- | -- | -- | -- | -- | [1471, 1621] |
| 8 | -- | -- | -- | -- | -- | -- | [1680, 1868] |
| 9 | -- | -- | -- | -- | -- | -- | [1891, 2088] |
| 10 | -- | -- | -- | -- | -- | -- | [2100, 4203] |
| Zone # | 156 m | 158 m | 162 m | ||
|---|---|---|---|---|---|
| Unit-Based | Plant-Based | Error | |||
| 0 | [0, 0] | [0, 0] | [0, 0] | 0.0 | [0, 0] |
| 1 | [420, 490] | [420, 501] | [420, 490] | [0, 11] | [420, 523] |
| 2 | [840, 980] | [840, 1002] | [840, 980] | [0, 22] | [840, 1046] |
| 3 | [1260, 1470] | [1260, 1503] | [1260, 1470] | [0, 33] | [1260, 1569] |
| 4 | [1680, 1960] | [1680, 2004] | [1680, 1960] | [0, 44] | [1680, 2092] |
| 5 | [2100, 2450] | [2100, 2505] | [2100, 2450] | [0, 55] | [2100, 4707] |
| 6 | [2520, 4410] | [2520, 4509] | [2520, 4410] | [0, 99] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Xia, W.; Wang, J.; Liu, S.; Zhou, B.; Zhao, Z.; Chen, C. Comparison of Procedures to Combine Operating Zones of Multiple Units into Plant-Based Operating Zones. Energies 2023, 16, 1435. https://doi.org/10.3390/en16031435
Wu Y, Xia W, Wang J, Liu S, Zhou B, Zhao Z, Chen C. Comparison of Procedures to Combine Operating Zones of Multiple Units into Plant-Based Operating Zones. Energies. 2023; 16(3):1435. https://doi.org/10.3390/en16031435
Chicago/Turabian StyleWu, Yang, Wang Xia, Jinwen Wang, Shuangquan Liu, Binbin Zhou, Zhenyu Zhao, and Cheng Chen. 2023. "Comparison of Procedures to Combine Operating Zones of Multiple Units into Plant-Based Operating Zones" Energies 16, no. 3: 1435. https://doi.org/10.3390/en16031435
APA StyleWu, Y., Xia, W., Wang, J., Liu, S., Zhou, B., Zhao, Z., & Chen, C. (2023). Comparison of Procedures to Combine Operating Zones of Multiple Units into Plant-Based Operating Zones. Energies, 16(3), 1435. https://doi.org/10.3390/en16031435






