Renewable Energy Potential Estimation Using Climatic-Weather-Forecasting Machine Learning Algorithms
Abstract
:1. Introduction
2. Methodology
2.1. Study Area
2.2. Data Gathering
2.3. Data Analysis
2.4. Artificial Neural Network
2.5. Feature Normalization
2.6. Learning Algorithm for Artificial Neural Network
2.6.1. Back Propagation Algorithm
2.6.2. Levenberg–Marquardt Algorithm
3. Results and Discussions
3.1. Error Analysis of the Feature-Normalized Models
- Underfitting—high validation and training error;
- Overfitting—high validation error and low training error;
- Good fit—low validation error that is slightly higher than the training error [8].
3.2. Predictions of Daily Weather Conditions by the ANN Models
3.2.1. Ambient Temperature
3.2.2. Relative Humidity
3.2.3. Pressure
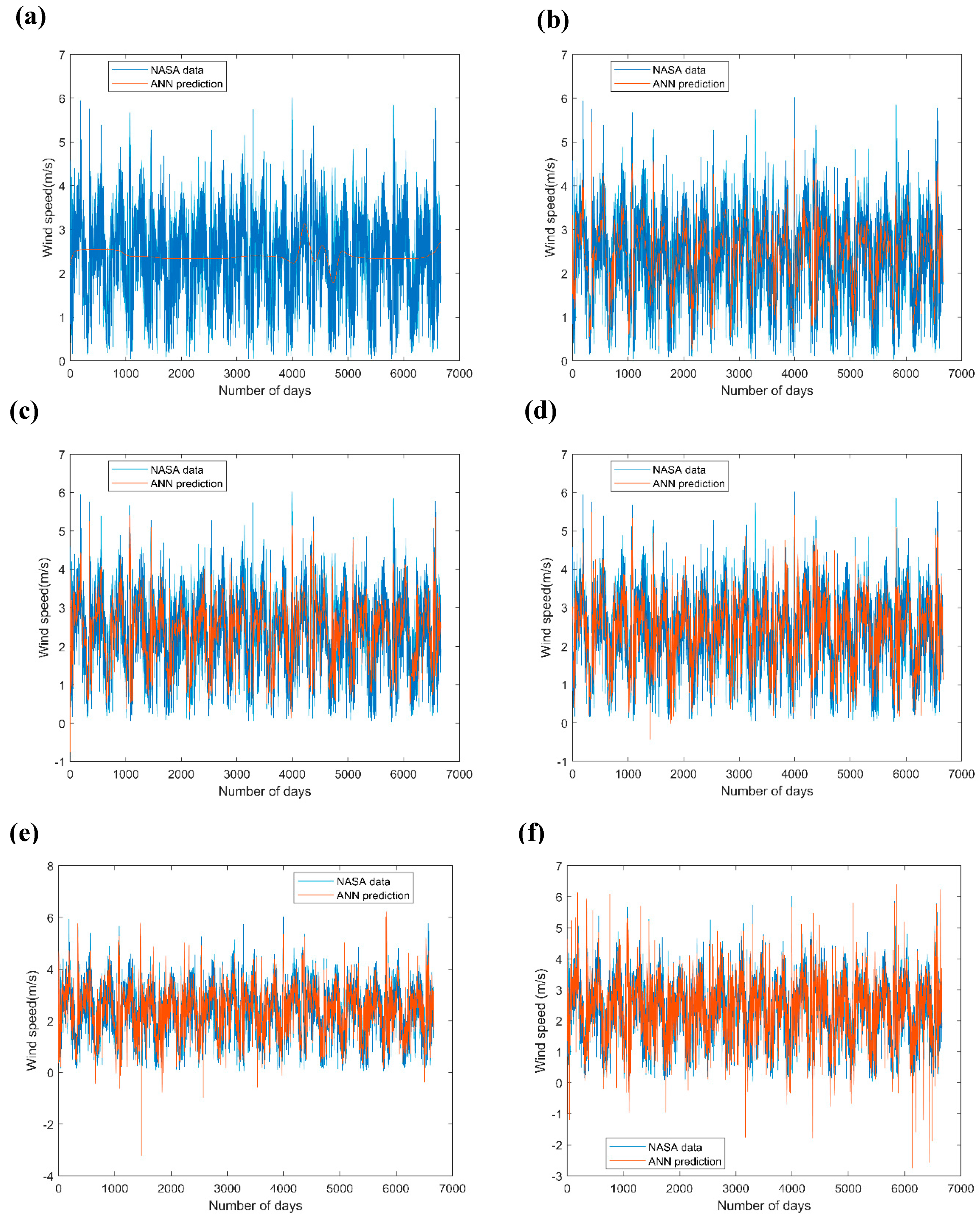
3.2.4. Wind Speed
3.2.5. Rainfall
3.2.6. Solar Irradiance
3.3. Optimum ANN Model Selection
4. Conclusions
- The third neural network with 1000 neurons in the hidden layer was the best in fitting the given dataset while avoiding overfitting. This network terminated the training process after four epochs with a minimised mean squared error of 0.007 and high regression correlations of 0.96, 0.93, 0.92, and 0.95 for the training, cross-validation, testing, and all processes, respectively.
- Increasing the number of hidden neurons beyond 1000 for a single hidden layer resulted in an overlearning of the data, leading to inaccurate predictions outside the given dataset.
- The benchmark first neural network with 10 neurons in the hidden layer provided the worst fit of the data, with a mean squared error of 0.01 and low regression correlations of 0.87 for the training, cross-validation, testing, and all processes.
- Increasing the number of neurons was beneficial for the accuracy of the network depending on the data; however, beyond a specific number of neurons, the network began to overfit while consuming massive amounts of computational time with poor performances outside the input data.
- Several avenues for further research still arise from this work. For instance, the proposed models will be extended to forecast the weather parameters of the six geopolitical zones in the country and evaluate the total climatic weather distribution in the region. Thereafter, the forecasted weather parameters could be employed in directly estimating the performance of renewable energy devices, e.g., solar panels, operating in the country and provide reasonable estimations of the devices’ performances far into the future. These parameters could be used to evaluate the potential of solar PV systems operating in the climatic zones, informing renewable energy investors on the best places to invest in these renewable energy systems.
- It is recommended that a more sophisticated network such as a deep neural network with multiple hidden layers be used in the learning of the solar irradiance and rainfall parameters. This is because the selected third neural network was not able to fully capture the trends in these datasets. This will be the emphasis of a future study. Furthermore, the use of these parameters in evaluating the performance of a solar photovoltaic cell operating in the region will be conducted in the future study. Finally, the solar cell power and efficiency will be forecasted using the proposed deep neural network while divulging the best number of hidden layers and neurons to handle the massive data generated. This approach will also be extended to cover the six geopolitical zones of Nigeria, providing a suitable substitute to the unavailable and dysfunctional meteorological stations in the developing country with massive solar potential.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ab-Belkhair, A.; Rahebi, J.; Abdulhamed Mohamed Nureddin, A. A Study of Deep Neural Network Controller-Based Power Quality Improvement of Hybrid PV/Wind Systems by Using Smart Inverter. Int. J. Photoenergy 2020, 2020, 8891469. [Google Scholar] [CrossRef]
- Osinowo, A.A.; Okogbue, E.C.; Ogungbenro, S.B.; Fashanu, O. Analysis of Global Solar Irradiance over Climatic Zones in Nigeria for Solar Energy Applications. J. Sol. Energy 2015, 2015, 819307. [Google Scholar] [CrossRef]
- Verma, S.; Mohapatra, S.; Chowdhury, S.; Dwivedi, G. Cooling Techniques of the PV Module: A Review. Mater. Today Proc. 2020, 38, 253–258. [Google Scholar] [CrossRef]
- Zaraket, J.; Aillerie, M.; Salame, C. Capacitance Evolution of PV Solar Modules under Thermal Stress. Energy Procedia 2017, 119, 702–708. [Google Scholar] [CrossRef]
- Eludoyin, O.M.; Adelekan, I.O.; Webster, R.; Eludoyin, A.O. Air Temperature, Relative Humidity, Climate Regionalization and Thermal Comfort of Nigeria. Int. J. Climatol. 2014, 34, 2000–2018. [Google Scholar] [CrossRef]
- Shiru, M.S.; Shahid, S.; Dewan, A.; Chung, E.-S.; Alias, N.; Ahmed, K.; Hassan, Q.K. Projection of Meteorological Droughts in Nigeria during Growing Seasons under Climate Change Scenarios. Sci. Rep. 2020, 10, 10107. [Google Scholar] [CrossRef]
- Adaramola, M.S. Estimating Global Solar Radiation Using Common Meteorological Data in Akure, Nigeria. Renew. Energy 2012, 47, 38–44. [Google Scholar] [CrossRef]
- Ajayi, O.O.; Ohijeagbon, O.D.; Nwadialo, C.E.; Olasope, O. New Model to Estimate Daily Global Solar Radiation over Nigeria. Sustain. Energy Technol. Assess. 2014, 5, 28–36. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate Photovoltaic Power Forecasting Models Using Deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Antonopoulos, V.Z.; Papamichail, D.M.; Aschonitis, V.G.; Antonopoulos, A.V. Solar Radiation Estimation Methods Using ANN and Empirical Models. Comput. Electron. Agric. 2019, 160, 160–167. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F.; Fung, A.S.; Raahemifar, K. Artificial Neural Network (ANN) Based Model Predictive Control (MPC) and Optimization of HVAC Systems: A State of the Art Review and Case Study of a Residential HVAC System. Energy Build. 2017, 141, 96–113. [Google Scholar] [CrossRef]
- Ozoegwu, C.G. The Solar Energy Assessment Methods for Nigeria: The Current Status, the Future Directions and a Neural Time Series Method. Renew. Sustain. Energy Rev. 2020, 92, 146–159. [Google Scholar] [CrossRef]
- Maduabuchi, C. Thermo-Mechanical Optimization of Thermoelectric Generators Using Deep Learning Artificial Intelligence Algorithms Fed with Verified Finite Element Simulation Data. Appl. Energy 2022, 315, 118943. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Global Solar Radiation Prediction by ANN Integrated with European Centre for Medium Range Weather Forecast Fields in Solar Rich Cities of Queensland Australia. J. Clean. Prod. 2019, 216, 288–310. [Google Scholar] [CrossRef]
- Garud, K.S.; Jayaraj, S.; Lee, M.Y. A Review on Modeling of Solar Photovoltaic Systems Using Artificial Neural Networks, Fuzzy Logic, Genetic Algorithm and Hybrid Models. Int. J. Energy Res. 2021, 45, 6–35. [Google Scholar] [CrossRef]
- Lo Brano, V.; Ciulla, G.; Di Falco, M. Artificial Neural Networks to Predict the Power Output of a PV Panel. Int. J. Photoenergy 2014, 2014, 193083. [Google Scholar] [CrossRef]
- Bamisile, O.; Oluwasanmi, A.; Obiora, S.; Osei-Mensah, E.; Asoronye, G.; Huang, Q. Application of Deep Learning for Solar Irradiance and Solar Photovoltaic Multi-Parameter Forecast. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 1–21. [Google Scholar] [CrossRef]
- Ali, K.; Jia, Y.; Abbas, M.; Bukhari, S.A. Environmental Effects on the Performance of Polycrystalline Silicon Solar Cells under Long-Term Outdoor Exposure in Taiyuan, China. J. Power Energy Eng. 2019, 7, 15–27. [Google Scholar] [CrossRef]
- Bhattacharya, T.; Chakraborty, A.K.; Pal, K. Effects of Ambient Temperature and Wind Speed on Performance of Monocrystalline Solar Photovoltaic Module in Tripura, India. J. Sol. Energy 2014, 2014, 817078. [Google Scholar] [CrossRef]
- Dajuma, A.; Yahaya, S.; Touré, S.; Diedhiou, A.; Adamou, R.; Konaré, A.; Sido, M.; Golba, M. Sensitivity of Solar Photovoltaic Panel Efficiency to Weather and Dust over West Africa: Comparative Experimental Study between Niamey (Niger) and Abidjan (Côte d’Ivoire). Comput. Water Energy Environ. Eng. 2016, 5, 123–147. [Google Scholar] [CrossRef] [Green Version]
- Simsek, E.; Williams, M.J.; Pilon, L. Effect of Dew and Rain on Photovoltaic Solar Cell Performances. Sol. Energy Mater. Sol. Cells 2021, 222, 110908. [Google Scholar] [CrossRef]
- Ogunrinde, A.T.; Oguntunde, P.G.; Fasinmirin, J.T.; Akinwumiju, A.S. Application of Artificial Neural Network for Forecasting Standardized Precipitation and Evapotranspiration Index: A Case Study of Nigeria. Eng. Rep. 2020, 2, e12194. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Suhail Hussain, S.M.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial Neural Networks Based Optimization Techniques: A Review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Sarker, I.H. Deep Learning: A Comprehensive Overview on Techniques, Taxonomy, Applications and Research Directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of Deep Learning: Concepts, CNN Architectures, Challenges, Applications, Future Directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Ojo, O.S.; Ogunjo, S.T. Machine Learning Models for Prediction of Rainfall over Nigeria. Sci. Afr. 2022, 16, e01246. [Google Scholar] [CrossRef]
- Ofure Eichie, J.; Oluwamayowa Agidi, E.; David Oyedum, O. Atmospheric Temperature Prediction across Nigeria Using Artificial Neural Network. In Proceedings of the ICFNDS 2021: The 5th International Conference on Future Networks & Distributed Systems, Dubai, United Arab Emirates, 15–16 December 2021; pp. 280–286. [Google Scholar] [CrossRef]
- Adams, S.; Bamanga, M. Modelling and Forecasting Seasonal Behavior of Rainfall in Abuja, Nigeria; A SARIMA Approach. Am. J. Math. Stat. 2020, 10, 10–19. [Google Scholar] [CrossRef]
- Ighile, E.H.; Shirakawa, H.; Tanikawa, H. Application of GIS and Machine Learning to Predict Flood Areas in Nigeria. Sustainability 2022, 14, 5039. [Google Scholar] [CrossRef]
- AbdulRaheem, M.; Awotunde, J.B.; Adeniyi, A.E.; Oladipo, I.D.; Adekola, S.O. Weather Prediction Performance Evaluation on Selected Machine Learning Algorithms. IAES Int. J. Artif. Intell. 2022, 11, 1535. [Google Scholar] [CrossRef]
- Danbatta, S.J.; Varol, A.; Nasab, A. Time Series Modeling and Forecasting of Expected Monthly Rainfall in Some Regions of Northern Nigeria Amid Security Challenges. In Proceedings of the 2022 3rd International Informatics and Software Engineering Conference (IISEC), Ankara, Turkey, 15–16 December 2022; pp. 1–6. [Google Scholar]
- Edwin, A.I.; Martins, O.Y. Stochastic Characteristics and Modelling of Monthly Rainfall Time Series of Ilorin, Nigeria. Open J. Mod. Hydrol. 2014, 4, 67–79. [Google Scholar] [CrossRef]
- Enete, I.; Alabi, M. Characteristics of Urban Heat Island in Enugu During Rainy Season. Ethiop. J. Environ. Stud. Manag. 2012, 5, 9–18. [Google Scholar] [CrossRef]
- Randles, C.A.; da Silva, A.M.; Buchard, V.; Colarco, P.R.; Darmenov, A.; Govindaraju, R.; Smirnov, A.; Holben, B.; Ferrare, R.; Hair, J.; et al. The MERRA-2 Aerosol Reanalysis, 1980 Onward. Part I: System Description and Data Assimilation Evaluation. J. Clim. 2017, 30, 6823–6850. [Google Scholar] [CrossRef] [PubMed]
- Schroedter-Homscheidt, M.; Arola, A.; Killius, N.; Lefèvre, M.; Saboret, L.; Wandji, W.; Wald, L.; Wey, E. The Copernicus Atmosphere Monitoring Service (CAMS) Radiation Service in a Nutshell. In Proceedings of the 22nd SolarPACES Conference 2016, Abu Dhabi, United Arab Emirates, 11–14 October 2016; pp. 1–4. [Google Scholar]
- Mbah, O.M.; Mgbemene, C.A.; Enibe, S.O.; Ozor, P.A.; Mbohwa, C. Comparison of Experimental Data and Isotropic Sky Models for Global Solar Radiation Estimation in Eastern Nigeria. In Proceedings of the World Congress on Engineering 2018, London, UK, 4–6 July 2018; Volume II, pp. 4–8. [Google Scholar]
- Does Solar Energy Work Everywhere in Nigeria? Available online: https://solyntaenergy.com/2018/01/04/does-solar-work-everywhere-in-nigeria/#:~:text=There%20is%20an%20average%20of,74.6°%20above%20the%20horizon (accessed on 5 December 2022).
- Pang, Z.; Niu, F.; O’Neill, Z. Solar Radiation Prediction Using Recurrent Neural Network and Artificial Neural Network: A Case Study with Comparisons. Renew. Energy 2020, 156, 279–289. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- Gangi Setti, S.; Rao, R.N. Artificial Neural Network Approach for Prediction of Stress–Strain Curve of near β Titanium Alloy. Rare Met. 2014, 33, 249–257. [Google Scholar] [CrossRef]
- Reynaldi, A.; Lukas, S.; Margaretha, H. Backpropagation and Levenberg-Marquardt Algorithm for Training Finite Element Neural Network. In Proceedings of the 2012 Sixth UKSim/AMSS European Symposium on Computer Modeling and Simulation, IEEE, Washington, DC, USA, 14–16 November 2012; pp. 89–94. [Google Scholar]









| Network Type | Feed-Forward Back Propagation Network |
|---|---|
| Number of neurons | 10, 500, 1000, 1500, 2000, and 2500 |
| Performance | Mean-squared error (MSE) |
| Training algorithm | Levenberg–Marquardt algorithm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maduabuchi, C.; Nsude, C.; Eneh, C.; Eke, E.; Okoli, K.; Okpara, E.; Idogho, C.; Waya, B.; Harsito, C. Renewable Energy Potential Estimation Using Climatic-Weather-Forecasting Machine Learning Algorithms. Energies 2023, 16, 1603. https://doi.org/10.3390/en16041603
Maduabuchi C, Nsude C, Eneh C, Eke E, Okoli K, Okpara E, Idogho C, Waya B, Harsito C. Renewable Energy Potential Estimation Using Climatic-Weather-Forecasting Machine Learning Algorithms. Energies. 2023; 16(4):1603. https://doi.org/10.3390/en16041603
Chicago/Turabian StyleMaduabuchi, Chika, Chinedu Nsude, Chibuoke Eneh, Emmanuel Eke, Kingsley Okoli, Emmanuel Okpara, Christian Idogho, Bryan Waya, and Catur Harsito. 2023. "Renewable Energy Potential Estimation Using Climatic-Weather-Forecasting Machine Learning Algorithms" Energies 16, no. 4: 1603. https://doi.org/10.3390/en16041603
APA StyleMaduabuchi, C., Nsude, C., Eneh, C., Eke, E., Okoli, K., Okpara, E., Idogho, C., Waya, B., & Harsito, C. (2023). Renewable Energy Potential Estimation Using Climatic-Weather-Forecasting Machine Learning Algorithms. Energies, 16(4), 1603. https://doi.org/10.3390/en16041603








