Reinforcement Learning-Based Intelligent Control Strategies for Optimal Power Management in Advanced Power Distribution Systems: A Survey

Abstract

Intelligent energy management in renewable-based power distribution applications, such as microgrids, smart grids, smart buildings, and EV systems, is becoming increasingly important in the context of the transition toward the decentralization, digitalization, and decarbonization of energy networks. Arguably, many challenges can be overcome, and benefits leveraged, in this transition by the adoption of intelligent autonomous computer-based decision-making through the introduction of smart technologies, specifically artificial intelligence. Unlike other numerical or soft computing optimization methods, the control based on artificial intelligence allows the decentralized power units to collaborate in making the best decision of fulfilling the administrator’s needs, rather than only a primitive decentralization based only on the division of tasks. Among the smart approaches, reinforcement learning stands as the most relevant and successful, particularly in power distribution management applications. The reason is it does not need an accurate model for attaining an optimized solution regarding the interaction with the environment. Accordingly, there is an ongoing need to accomplish a clear, up-to-date, vision of the development level, especially with the lack of recent comprehensive detailed reviews of this vitally important research field. Therefore, this paper fulfills the need and presents a comprehensive review of the state-of-the-art successful and distinguished intelligent control strategies-based RL in optimizing the management of power flow and distribution. Wherein extensive importance is given to the classification of the literature on emerging strategies, the proposals based on RL multiagent, and the multiagent primary secondary control of managing power flow in micro and smart grids, particularly the energy storage. As a result, 126 of the most relevant, recent, and non-incremental have been reviewed and put into relevant categories. Furthermore, salient features have been identified of the major positive and negative, of each selection.

1. Introduction

The control of renewable energy in modern power distribution applications, such as microgrids, smart grids, smart buildings, and electric vehicles (EVs) applications, is experiencing a large, fundamental transition due to several technological advances and environmental considerations. For instance, the world is gearing toward the enhancement of the introduction of renewable energy and transportation based on either EVs or alternative fuels, due to their economic, technical, and environmental advantages [1]. However, the current global electricity and alternative fuel generation is still a mixed fuel, with the supremacy of fossil fuel remaining in many regions of the world. In fact, both trends are fundamentally related since the use of renewable energy in charging EVs or generating alternative fuels such as hydrogen would significantly reduce greenhouse gas emissions [2]. Optimal power distribution control is the most prominent challenge in enhancing the penetration and sustainability of renewable energy and reducing the use of fossil fuels, due to the distributed and unpredictable nature of their power generation. This involves the optimal management of the power variables to enhance a minimized load consumption cost [3]. Where this can be accomplished, many advantages to the power system can be conferred, such as minimizing energy production and delivery cost, minimizing power losses, reducing load shedding, and maximizing system performance [4,5]. Therefore, the achievement of optimal solutions to energy management problems is the key enabler to the goals of the aforementioned concept.

In a previous work by the current authors [6], a taxonomy of control requirements for modern smart grids was elucidated, and it was established that a system-of-systems approaches (with multiple interconnected microgrids and storage systems) combined with intelligent control methods were identified as the most likely technologies and paradigms for solving the complex power management issues which will arise moving forwards in this sector. Global intelligent search methods, such as genetic algorithms (GAs) and swarm intelligence (SI), have been dealt with in the literature to solve power management problems [7,8]. Nevertheless, the methods hold three fundamental defects [9]:

• In general, they are slow and cannot be operated online, whereas online operation accomplishes more economical implementation, due to there being no need for a devoted computer of offline optimization.
• An economic issue, due to the absence of learning components. Hence, optimization iteration is mandatory at every change in the generation or load profiles.
• A separate forecasting algorithm is compulsory for the state variables prediction.

The control based on reinforcement learning (RL) of solving power management problems in advanced power distribution systems is the most convenient alternative modern choice. This is because of the following vital features [10]:

• The qualification for the offline attainment of generation and load measurements, and applicating them for any expected online generation or load.
• An accurate model is not mandatory for achieving the optimal solution of solving power management problems.
• More precise predictions can be accomplished through the application of an artificial neural network (ANN) and attain a modernized intelligent application, due to eliminating the need for a separate forecasting model.

Where the theory of introducing RL to solve power management problems refers to solving a sequential decision-making problem through the introduction of an active intelligent bio-inspired machine learning technique via agent-based modeling (ABM) [11]. Whereas ABM implies modeling an independent intelligent agent, or group of agents, to act as an independent decision-maker, learn from iterative trials and errors and maximize the total reward [12,13]. In line, the environment can be defined as a field where the agents interreact and implement their features. In more detail, the environment interacts with the agents by selecting an action for each state from a set of possible actions, and then receives feedback on the value of the actions selected [13]. While the multistage decision problem (MSDP) indicates the consideration of the complicated problem as a multistage and the practical solution is changed by raising the risks to attain the correct solution [13]. Furthermore, the development of an MSDP model for solving complicated problems should consider multiple efficiency criteria based on the interests and requirements of the decision-maker and the changes in the practical situation [14].

Given the variety of proposed recent contributions of both fundamental and applied research in this vital emerging sector, the paper intends to support the lack of recent comprehensive detailed reviews of the research field and offers great assistance for the researchers to continue and contribute. Accordingly, a detailed and comprehensive review is presented of the intelligent control strategies based on RL to solve power management problems in advanced future-facing applications, which is the aimed future vision of intelligent power distribution management. Furthermore, considered a vital enabler in reducing the use of fossil fuel and enhancing the introduction of renewable and alternate energy toward fulfilling net zero. Wherein, the focus is given to emerging advanced strategies based on the multiagent RL approach, for reasons outlined above and in our previous exposition [6]. What adds more distinguishment for this review from the previously conducted is the comprehensiveness of the research methodology from the classical and classical combined to the advanced emerging AI-based intelligent applications, especially the multiagent. Furthermore, the specialization of vital important advanced power distribution applications at present and the future image of energy distribution, and the trend in the lifestyle that the world aspires to. In this research work, existing unique research challenges are reviewed, and salient features are identified (positive and negative), with subsequent identification of further research areas. The research methodology for organizing this research work and selecting the review papers is as follows. Recent research works that demonstrate the latest unique developments of applicating control strategies were selected. Out-of-scope, incremental, similar, and repeated works were ignored. In total, 126 of the most relevant, recent, and non-incremental have been reviewed and put into relevant categories, as demonstrated in Figure 1. The remainder of this review is structured as follows. Section 2 introduces the basics of RL-based control approaches, with an emphasis on power applications. Section 3 covers classical RL-based control approaches, whereas emerging advanced RL-based strategies are demonstrated in Section 4. Finally, Section 5 is reserved for the summary and conclusions.

2. Background

2.1. Agent and Agent-Based Modeling

The agent in RL can be described as an action-maker entity qualified for doing actions and making, or collaborating in making, decisions at a level of intelligence. In particular, the agent interacts, based on software rooted in artificial intelligence (AI), to make a mandatory change in the environment continuously and autonomously on behalf of the administrator [15]. Therefore, the agent within an operation framework should hold some specifications qualifying it for the role, as demonstrated below [16]:

• Mobility: The agent is flexible to move from one location to another within a specified operational framework or environment.
• Communication: The agent can communicate with the environment, in addition to other active agents.
• Autonomy: The independence of the agent to do tasks or make actions on behalf of the administrator.
• Rationality: The agent should hold a level of intelligence to decide or collaborate of deciding regarding completing a task for the administrator.
• Reactivity: The quality of the agent to monitor the environment and respond to its changes.
• Sociality: The collaboration of the agent with the human and other active agents in accomplishing the mandatory tasks.
• Self-learning: The agent learns from the surrounding environment to make an independent improvement or adaptation in the environment.

Consequently, ABM can be offered a more detailed definition as a computational AI-based paradigm for attaining autonomy and intelligence in deciding on an action to make a mandatory change in the environment based on the task requirements or the administrator’s obligations [16]. Hence, agent-oriented programming (AOP) is an entirely advanced computer programming task to create, activate, and orient an independent agent for a specific task at a level of intelligence [17,18].

2.2. Markov Decision Process Models

Markov decision process (MDP) refers to the dynamic programming of an RL control problem to make a sequential decision of the solution under uncertainty, wherein the MDP model is typically characterized by the following [19,20,21]:

• The state space (S): The set of possible states, that holds several versions based on the level number of the states included, such as finite, denumerable, compact, etc. Where each of the states can be observed at any time point when a decision or action is being made regarding a task to make a specific change in the environment.
• The action sets (A): It refers to a set of actions and holds similar versions for the state space based on the level number of the actions involved. Wherein each action is taken depending on an observed state.
• The decision time point: It is the time interval between the decisions. Accordingly, the model is an MDP if the decision time points are constant. Otherwise, the model is semi-MDP.
• The immediate reward (R): The reward is a function of the action and the state. Where an immediate reward is earned for the given model state and action, that is inversely proportional to the cost and can be determined by the reward function in Equation (1).

  $$R :S\times A \to R$$

  (1)
• The transition probabilities $p\left(s\right)$: It implies the probabilities of the possible various next state, due to the difference between the deterministic and Markovian, environments, wherein the state transition in the Markovian environment is probabilistic. Equation (2) demonstrates the transition function for the distribution of the probability over the next coming state.

  $$T :S\times A \to p\left(S\right)$$

  (2)
• The planning horizon: The horizon of the controlled time points is planned by the suggested RL agent based on the problem solver.

The learning methodology of the Markov process is demonstrated in Figure 2, which explains the sequential decision-making behavior of the intelligent framework. Here, the agent acts at a time to affect the current state, after preserving a state and a reward from the environment. Then, this new state will be affected by the new action taken at the time after taking the state and the reward. Where this verifies the objective of the agent in an RL interaction of maximizing the expected sum of the discounted reward after a series of taken states and decided actions, as demonstrated in Equation (3), in which, the infinite summation of the discounted reward is attained for the reward received at j steps ($r_{i+j}$) multiplied by the discount factor ($0\le {\gamma }^j\le 1$) to accomplish the value of the state ($V^{\pi }\left(s\right))$ at the optimal strategy $\left(\pi \right)$ for the given policy.

$$V^{\pi }\left(S\right)={\rm E}\left[{{\displaystyle \sum }}_{j=0}^{\infty }{\gamma }^j{r}_{t+j}\right]$$

(3)

2.3. Markov Game

The MDP has been expanded to a Markov or stochastic game (MG) to accomplish environments with more than one agent involved, which is in common with the MDP in considering the state transition as a Markovian. However, the difference is that each agent has its own set of actions [22]. Therefore, for an ($n$) number of agents, the overall action space ($A$) is the result of the action state of all the interacting agents ($A1, A2, \dots$), as demonstrated in Equation (4). In accordance, the state transition equation ($T$) considers $A$, and the reward equation ($Ri$) considers the overall reward for all the agents, as explained in Equations (5) and (6). Where $S, R$ signifies the state space, and the total reward, respectively. Whereas $p\left(S\right)$ refers to the probability distribution over the next state. Akin to MDP, the agent in MG is trying to maximize its expected discounted reward under the overall policy, as shown in Equations (7) and (8) [20,23]. $r_{i,t+j}$, $V_i^{\pi }\left(S\right)$ are the received reward at j steps for the agent $i$, and the value of state, respectively.

$$A : A_1\times A_2\times \dots \times A_n$$

(4)

$$T:S\times A_1\times A_2\times \dots \times A_n \to p\left(S\right)$$

(5)

$$R_i : S\times R_1\times R_2\times \dots \times R_n \to R$$

(6)

$${\pi }_i=\left({\pi }_1, {\pi }_2, \dots , {\pi }_n\right)$$

(7)

$$V_i^{\pi }\left(S\right)={\rm E}\left[{{\displaystyle \sum }}_{j=0}^{\infty }{\gamma }^j r_{i,t+j}\right]$$

(8)

As a result, the multiagent RL system (MARL) has been introduced as the branch of the RL that refers to the interaction of multiple RL agents in a common environment [24]. Recently, the MARL system has become the appropriate selection for the immediate real-time solving of complicated problems in a variety of applications. Examples of them are robotic applications, telecommunications, economics, and energy distribution management [25]. Among the most prominent of these applications, MARL is the successful solution for solving power flow management defects in advanced power distribution applications.

2.4. Outliers of Reinforcement Learning and Detection Methods

Since RL is a subset of machine learning (ML) and AOP is an entirely advanced computer programming task. Therefore, it is vitally important to outline the identification of outliers in programming, their impact, and the sensitivity of the RL model against them through the demonstration of detection and prevention methods. Where outliers can be defined as the points that hold a significant difference from other given observations in a dataset. This can be the result of errors in data entry, errors of measurement, errors from an experiment, intentional errors, errors in processing the mandatory data, errors due to sampling, and natural outliers not resulting from an error [26,27]. The main types of outliers are:

• Global outliers: The data point is a global outlier if the value is far from the whole data of the specific set.
• Contextual outliers: The outlier is contextual if its value significantly deviates from the other data of the set.
• Collective Outliers: A group of data points represents a collective outlier if their values are close to each other, and they are, as a collection, significantly deviating from all the other data of the set.

The first action to be taken against introduced outliers is detection. Accordingly, there have been many detection methods that differ based on the application task that the model is trained for. However, two methods are considered the main classification of outlier detection, the detection using distance and density, and the highlighting of the outliers that do not meet the user threshold of a designed model [26,28].

Specifically, the methods of detecting outliers hold three main classifications [29].

• Statistical approach: The statical approach refers to the statical computation of parameters in a statical distribution, where examples of it are mean and standard deviation, wherein outliers represent the observations that cannot be classified after some iterations.
• Depth approach: It refers to the classification of the observations based on the depth, where data points are organized as convex hill layers. Accordingly, observations of the same depth are of the same class. Furthermore, observation is classified as an outlier if it lies in the utmost of these classes.
• Distance approach: In this method, the distance between the observations is the enabler of distinguishing an outlier. Where the class here represents a group of observations with a similar distance between neighbors. Accordingly, the observation is detected as an outlier if the distance from the neighbors of the class is different.

Accordingly, prevention is the enabler for raising the sensitivity against outliers with the detection. This holds crucial importance due to the negative impact of these outliers. The existence of outliers can result in a defect of the dataset, such as an affected standard deviation, increased variance errors, reduced statistical test power, decreased normality, and unwell implementation of algorithms. Consequently, there have been existing methods of preventing or reducing the chance of outlier appearance such as deleting observations, transforming values, imputation, and separate treatment. From this, it can be concluded that the sensitivity against outliers is based majorly on the employed algorithms and entirely dependent on detection and prevention [26,29].

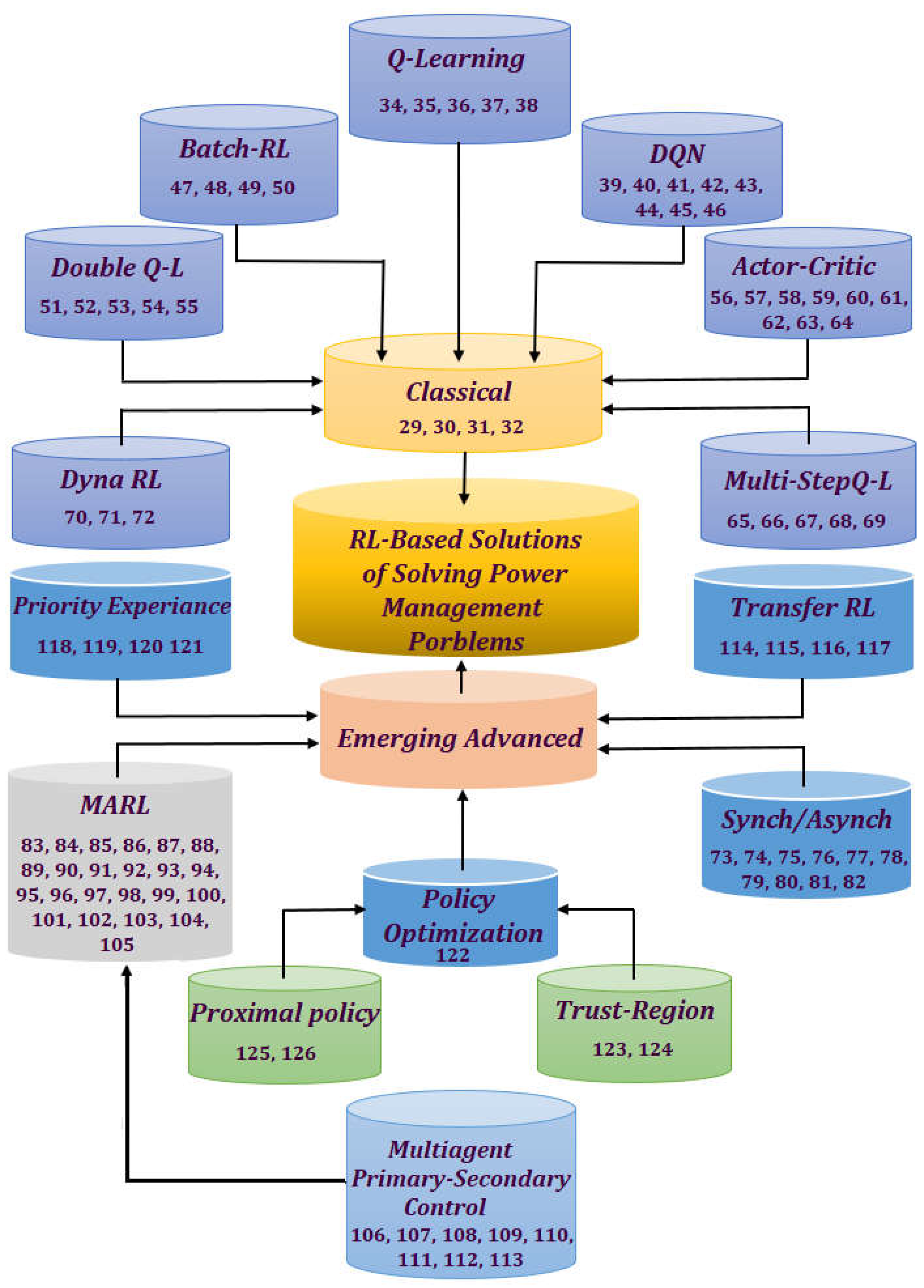
3. Classical Solutions Based on Reinforcement Learning of Power Management Problems

The solutions to power management problems through the introduction of RL have proven their success among other AI-based applications. This is because there is no need for an accurate model of accomplishing the optimized real-time solutions. Which is what suits energy applications for the changes in the system factors that are highly expected in the generation, distribution, and transmission of energy [30]. There has been remarkable progress in the development of this field. Especially in recent times, due to the urgent need for smart solutions, when pollution and the cost of fossil fuel energy became a threat. Therefore, there have been many presented proposals to develop RL-based control algorithms, which can be characterized based on their development level, and the seniority of appearance in the literature.

The availability of a model to be accessed by the administrator is mandatory in model-based algorithms to plan the best action and attain an optimal solution in some applications [31]. However, it is incompatible with some high-complexity applications, including power management, due to the following downsides [21,32]:

• The difficulty and complexity of obtaining a model of the environment.
• An error in the model is highly expected, because of the sensitive quality of the solution.
• An expected loss of computational efficiency in the case of a highly complex model and a simple application.

On the other hand, the RL-based solution is model-free if the knowledge of the model is not mandatory in the optimization. Furthermore, the RL-based solution is characterized as goal-oriented, and reliable to adapt to the changes in a variety of environment classes. Therefore, it has become a successful solution for power management applications with a complexity higher than the applications that can be solved by the module-based [33]. The model-free solution is value-based if the determination of a good state and state-action estimate pair value functions is taken as the main aim. It is policy-based if the estimate of the value functions is not compulsory in the optimization policy [33].

Classical RL solutions have been successfully introduced for solving problems in a range of applications with varying levels of complexity, especially, for solving problems of power management in advanced power distribution applications. This field has recently witnessed steps toward the development and modernization of the classical strategies’ role in solving complicated energy flow management defects, and the accomplishment of new intelligent solutions through the combination of more than one classical strategy, or the introduction of external smart technology.

3.1. Q-Learning

The Q-learning RL is the most popular classical model-free policy-based method for solving a variety of complicated problems, that is approached based on taking random actions during the interaction with the environment [34]. In more depth, the Q-learning creates an every-step updated Q-table based on the Markovian process and Boolean equation, by utilizing the attained state-action pairs environment-based learning. As a result, an outcome and reward are accomplished and update the Q-table for every action completed [5,6], as demonstrated in Equation (9).

$$Q\left(s,a\right)=Q\left(s,a\right)+\propto \left[R\left(s,a\right)+\gamma \times maxQ\left(s^{\prime },a^{\prime }\right)-Q\left(s,a\right)\right]$$

(9)

Here, an immediate updated value of Q is attained for every newly learning state-action pair and stored in the Q-table, wherein the newly action–state pair is processed through the summation of the defined reward for the new state–action pair ($R\left(s,a\right)$), and the maximum Q that can be achieved for all expected state-action pars ($maxQ(s^{\prime },a^{\prime }$)) multiplied by the discount rate ($\gamma )$, and then compared with the updated Q and multiply the overall by the learning rate $\left(\propto \right)$ to attain the immediate update $Q\left(s, a\right)$. The demonstration of the Q-learning agent in Figure 3 explains how the Q-table is updated for every new state action by the updated Q value.

The balance of exploration and exploitation aims to attain an appropriate action through exploring the status and exploiting the reward. It is of vital importance to achieve a balance between exploration and exploitation to avoid jamming during the update [5]. Accordingly, E-greedy is a highly qualified model-free Q-learning RL method to balance exploration/exploitation. Furthermore, it accomplishes immediate action during learning and provides an optimized update of the Q-table. Therefore, E-greedy can determine the involvement of the exploration and exploitation nature in the attained actions because it exploits the Q-table to maximize the reward when employed by the agent [34].

There have been recent and most recent unique attempts in the literature aimed to develop the application of the Q-learning RL in achieving optimized power management solutions. The development by B. Xu et al. [35] was planned to optimize the supervisory management system of an electric vehicle (EV) with a combined charging system of a battery and ultracapacitor, through the introduction of a Q-learning method. In accordance, a hierarchical Q-learning network was planned of two independent Q tables to assign two control layers. Furthermore, a baseline split layer was introduced to attain the power split ratio of the battery and the ultracapacitor based on the update stored in Q1. Moreover, the upper layer was developed based on the Q2 update to activate the ultracapacitor commitment. Therefore, the accomplished results have proven that the introduction of the RL was the reason for reducing the battery capacity loss by 8%. This was followed by an extended exploitation of the Q-learning by L. Bo et al. [36] through the training of the rules and parameters of an adaptive fuzzy network inference system (ANFIS) of a hybrid off-road EV (HEV). Hence, the results have verified that the proposed online Q-learning fuzzy inference system (QLFIS) was a new successful approach in off-road controlling with no prior knowledge of the driving cycle, whereas the optimization of forecasting models was not far from the interaction with Q-learning. An online forecasting model was proposed to attain an accurate wind speed prediction to enhance the integration between wind energy and the utility grid [37]. Therefore, the successful selection of an intelligent Q-learning (OMS-QL) to implement an online forecasting model pool (FMP) was the motive of an improvement in the prediction by 48% compared to the model before the development. In line, the fuel cell hybrid vehicles (FCHVs) had a most recent successful attempt to attain a new Q-learning-based energy management strategy and extend the fuel cell (FCS) lifetime [38]. Here, the designed power distribution rules were employed to pre-initialize the Q-learning table and accelerate the management process. Furthermore, the FCS power difference between adjacent moments was exploited to reduce its lifetime through the Markovian modulation of the driving cycle.

3.2. Deep Q-Network

One of the vital features offered by the RL-based solutions is the more accurate predictions with no need for a separate forecasting model through integration with an ANN. Accordingly, deep Q-learning (DQN) has been introduced as the most popular, in which, the Q-learning is integrated with an ANN, and updates solutions with higher predictions for higher complicated applications [39,40]. The superiority of the DQN over the Q-learning lies in three fundamental reasons [41]:

• An approximated action value function through the replacement of the conventional Q-learning table by an ANN.
• Improved exploration, because of the different agents involved.
• Enhanced exploitation through updating the Q-values by the best solution accomplished.

The expansion of the RL-based solutions to DQN was aimed to overcome the unstable learning of the senior Q-learning in higher-complexity applications, wherein DQN has been a collaborative development of four learning-based sub-techniques, experience replay, target network, clipping rewards, and skipping frames [41]. Furthermore, it trains the network with uncorrelated past batches to operate the target network and attain enhanced intelligence, which might be reaching the level of the human brain if organized smartly, for the benefit of solving problems that cannot be solved by the basic RL-based method. The demonstration of the DQN agent in Figure 4 illustrates the equivalization of the Q-table in the Q-learning by an ANN to approximate the action value function.

The introduction of DQN in solving complicated power management problems has been dealt with through many successful applications in the recent and most recent literature. P. Suanpang et al. [42] have recently proposed a solution to the optimization of autonomous energy management in a microgrid through the introduction of deep RL. Specifically, the collaboration of the DQN was the management of the microgrid components of, renewable resources, storages, and loads, through prioritizing the tasks based on the optimization obligations. Hence, a saving of the general energy processing cost of 13.19% was accomplished, compared to a similar strategy with no DQN. Followed by an effective attempt by Z. Zhu et al. [43] to solve the defect of sequential decision-making through the introduction of a deep deterministic policy gradient algorithm. As a result, the operation cost was reduced by 5% with enhanced generalization capabilities, whereas the inability of the conventional model-based optimization methods in regulating voltage profiles of distribution networks connected by multi-terminal soft open points (M-SOPs) was a recent concern. Voltage rise violations were diagnosed due to the high energy penetration of the distributed generators (DGs). Accordingly, P. Li et al. [44] have proposed the introduction of a deep deterministic policy gradient network (DDPG) to attain a new method of data-driven voltage control, where the problem in voltage control was taken as MDP to build the DDPG agent. Therefore, an enhanced improvement has been achieved in voltage fluctuation due to the high DG energy penetration.

The development of the hybrid electric vehicle (HEVs) was likewise successfully boosted recently by the intelligent DQN [45]. Here, the minimization of fuel consumption and the enhancement of computational speed were attained through the introduction of a DQN with long short-term memory (LSTM). Consequently, the distribution of the power between the internal combustion engine (ICE) and the electrical motor (EM) was optimized, whereas home energy management (HEM) was not in isolation from exploiting the recent DQN development. In consequence, A. Forootani et al. [46] have suggested DQN-based management to hourly schedule the controllable and time-shiftable home appliances. As a result, a reduction in the electricity cost with high consumer satisfaction has been indicated, compared to the same management system with the employment of Q-learning.

3.3. Batch Reinforcement Learning

Batch RL solutions aim to learn the best possible policy from a set of fixed priorly defined transition samples, to solve complicated applications that cannot be solved by the basic model-free Q-learning method [47]. The intelligence of batch RL learning relies on the approach followed in handling a batch of transitions and accomplishing the ultimate output. In particular, the observed transitions are stored, with a synchronous fitting on the completed batch transitions through updates. Then, the set of sample experiences is extended to incrementally improve toward a stable and efficient solution, as demonstrated in the batch learning schematic in Figure 5. This differs from the classical free-morel Q-learning that traditionally requires many iterations to attain convenient policies [5,47].

Solving optimal power management problems through the introduction of batch RL has been recently enhanced by active proposals. The optimization of energy management in buildings was a vital application. The energy consumption in buildings represents around 30% of the worldwide energy consumption, and an estimated half of it is to the heating ventilation, and air conditioning (HVAC). In accordance, the safety and optimization of the HVAC control were improved by C. Zhang et al. [48] through the introduction of batch RL. Specifically, a guided exploration was suggested through the adjustment of the introduced gaussian noise, resulting in a tradeoff between the safety and diverted dataset. The offline selection of the optimal policy was attained through the application of a rule-based model-based solver. Accordingly, an improvement of 12–35% in ramping reduction, 3–10% in 1-lead factor lessening, and 3–8% in daily peak decrease were attained compared to the classic rule-based management system before the development.

A solution to the many time steps of attaining the learning performance of HVAC under classical RL-based management was suggested by H. Liu et al. [49]. Particularly, a batch RL was introduced to improve the optimization policy through learning from the historical solutions with no interactions with the real simulators. Furthermore, a Kullback–Leibler (KL) regularization term was introduced to prevent policy deviation. Therefore, a reduction in energy consumption by 7.2% and 16.7% compared to the classic solution based on batch RL, and other state-of-the-art batch RL solutions, respectively, was achieved when applied on multi-zone and multi-floor buildings. In line, the optimization of power management in grids was likewise a recent application of batch RL. The distribution constraints in unknown grids were prevented by the introduction of batch RL [50]. Accordingly, the network-safe policy was computed from previously known controlled load aggregations. Hence, a 95% reduction in the number of rounds with a minimum of one constraint violation was accomplished. In addition, an assured safe operation for the distribution network was also accomplished.

3.4. Double Q-Learning

The overvaluation of the actions due to bias is a diagnosed defect in Q-learning, especially with higher-order applications that require a higher accurate update. Accordingly, double Q-learning has been the alternative development to overcome this defect through the boost of their update. Specifically, two Q functions are presented to generate and update unbiased actions by employing the other’s Q function within their Q function [51,52]. A comparison between the application of a conventional DQN and a double Q DQN (DDQN) in terms of the change in the average reward is in [52]. Here, the change in overall reward has earned The DDQN an outperforming because of eliminating the negative reward drops due to the incorrect actions of the agent. These drops disappeared in the DDQN in the later training stage since the agent has learned from this and avoided these wrong actions, which has proven an outpacing of DDQN over DQN in terms of learning stability and performance. Therefore, an improved algorithm’s performance was achieved via the introduction of DDQN with a total score of 271.73% in both value accuracy and policy quality.

Double Q-Learning has earned a position in solving power management problems, with an expansion to the role in the recent and most recent literature. Therefore, there have been several distinctive and successful proposals. The trend towards enhanced electricity-based transportation was one of the beneficiaries. In accordance, a proposal was suggested to enhance fuel economy in a plug-in hybrid electric vehicle (PHEV) through the development of an energy management system (EMS) [53]. Here, double Q-Learning was applied to attain an effective offline learning controller and solve the rolling optimizing process in a module predictive controller (MPC). Hence, results have proven an excellent economic fuel consumption due to the achieved optimal battery output in the predicted horizon. The enhancement of power consumption of off-highway hybrid EVs was likewise an application of the double Q-Learning. Consequently, B. Shuai et al. [54] have recently developed an active predictive double-Q in collaboration with a backup model (PDQL) to optimize the real-world driving fuel consumption of an off-highway hybrid EV. The progress of the developed PDQL over the existing standard double Q-learning (SDQL) was the enabler of achieving better efficiency by only half the iterations. Therefore, the vehicle efficiency with PDQL was improved by 1.75% higher than with SDQL. While L. Han et al. [55] have suggested an optimization of hybrid vehicle efficiency with reduced fuel consumption through the regional distribution of mechanical energy from the engine and electrical energy from the batteries. This was attained by developing the EMS through the introduction of a double Q-learning. As a result, the economic fuel consumption and the batteries’ power flow stability have been greatly improved compared to the strategy before the introduction of double Q-learning.

3.5. Actor–Critic

The learning methodology of the actor–critic refers to the setting of the possible actions from the given state and reward by the actor. The estimated value function, or critic, evaluates the actor’s actions based on the applied policy, and then updates the actor to the accomplished evaluation, which is the developed version of the model-free DQN to enhance learning performance and solve higher complicated problems. The principle and operational methodology of the actor, represented by a DQN, was modified to a continuous action domain by combining with the critic, represented by a deterministic policy gradient. In more depth, the experience relay and slow-learning target networks are employed by combining the principle of the DQN operational methodology and the deterministic policy gradient. Furthermore, further progress is achieved by exploiting the critic to manage continuous action states [39]. Accordingly, the main reason behind the superior intelligence of actor–critic solutions relies on the combination of policy and value functions, with the collaboration of both value-based and policy-based methods. Therefore, their advantages were boosted by combining the good features from both algorithms to solve higher complexity problems in a variety of advanced power distribution applications. The actor–critic is in common with the DQN regarding the use of an ANN in approximating the probabilities of all the actions, as clarified in Figure 6, which explains actor–critic interaction with a power management environment [56]. The actor takes the action based on the environment’s state and reward, in addition to the actions’ evaluation update from the critic.

There have been several active recent contributions to the introduction of the actor–critic in solving power management problems. Y. Du et al. [57] aimed to reduce energy consumption in a multizone HVAC system through the introduction of an actor–critic. Therefore, an optimized control strategy has been achieved to enhance comfort, reduce energy consumption, and comply with complex unknown environments. The description of the control process as a constrained Markov was likewise an aim [58]. The role of the actor–critic was to attain optimal control of an active distribution network under the complicated continuous and action space problems. Similarly, the activity of the actor–critic has taken its role in the development of power balance and sustainability in micro and smart grids through active recent proposals. T. Wu et al. [59] suggested the actor–critic solution to reconfigure hybrid AC-DC networks (HDNs) with a microgrid in the situation of an extreme event due to special situations, such as high penetration of the distributed generators and load mixing. In particular, the role of the actor–critic was to assist critical service restoration through the creation of isolated sections inside the HDNs and satisfy the different system states.

The random disturbance in microgrid operation due to uncertainty in renewable energy penetration of the wind and solar generations was a vital defect. Consequently, K. Han et al. [60] have suggested an adaptable composed management of lightweight actor–critic learning-based empirical mode decomposition-based networks, and an evolutionary strategy. Hence, a robust adaptable management system of the microgrid was achieved compared to the un-adapted management. The optimized coordination of the energy storage systems for the aim of reducing operational costs in microgrids was recently dealt with in [61]. Here, a multi-timescale operation method based on soft actor–critic learning was developed to coordinate the battery and supercapacitor in the microgrid through the application of a hierarchical two-stage dispatch method.

In line, the optimization of electric-based transportation was present within the recent actor–critic applications. A unique collaboration was by D. Xu et al. [62] to update the existing DRL-based management of EVs with a hybrid energy storage system (HESS) to a soft actor–critic-based system. Hence, the adoption of the extracted dynamic programming knowledge has decreased the energy loss by 8.75% compared to the strategy based on DQL. The improvement of EMS for a hybrid electric vehicle (HEV) through the introduction of actor–critic was recently dealt with to enhance energy saving. Furthermore, reduce emissions in different driving conditions [63]. Specifically, soft actor–critic (SAC) and mechanism soft actor–critic (MSAC) algorithms were employed, in addition to the application of the posturized experience replay (PER), to attain more experience sampling and optimize the EMS. Hence, an improvement was accomplished with the proposed strategy over the classic SAC of fuel consumption and robustness under various driving conditions. The reduction of the EV charging impact on the power grid has been investigated by Y. Cao et al. [64]. Accordingly, a smart charging algorithm based on SCA learning was developed to overcome uncertainties in the charging behavior of EVs through active charging scheduling. Particularly, an optimal charging learning of EV is accomplished by the SCA through a continuous charging action rather than the discrete approximation. Hence, a reduction in the expected cost by 24.03%, 21.49%, and 13.08% was gained compared to the existing strategy without the introduction of the SCA.

3.6. Multi-Step Q-Learning

The combination of two RL algorithms of attending fast learning has been dealt with in the literature. The most successful was the combination of the two abovementioned algorithms, the Q-learning, and actor–critic, that resulted in a reliable updated multi-step Q-learning [65,66]. Therefore, the updated combined solution with the combined features of both algorithms is qualified for solving problems at a level of complexity and uncertainty.

The intelligence and robustness of the multi-step Q-Learning were tracked recently to solve power management problems. L. Xi et al. [67] have integrated a deep Q-Learning and a double Q-Learning to attain a unified developed multi-step Q algorithm and overcome the overfitting defect in the management of a multiarea power grid. Consequently, the random disturbances and the frequency instability due to the over-fitting were improved in the multi-area that is covered by the interconnected grid. The regulation of the operators’ protection strategies in smart grids was investigated to attain a multistage RL-based solution of a multistage game between the attacker and the defender [68]. In accordance, the sequence of transmission line attack actions was learned for protecting a set of selected lines by the defender. Hence, more optimization was achieved in the attacking sequences under different attack aims. Likewise, the online optimization of the electrified off-highway vehicle was an implementation field of the multistep RL. Q. Zhou et al. [69] have proposed a management system based on the introduction of multi-step RL. Therefore, the new solution with the three multi-step learning strategies was the motive of optimization in energy efficiency by 44%, compared to 34% with the initial strategy before the development. Furthermore, an enhancement of prediction horizon length by 71%, in addition to a saving in energy by 7.8% in the same driving environments.

3.7. Dyna Algorithm

The combination of model-free and model-based algorithms is an effective way of enhancing learning and attaining an updated version of solving complicated problems. For example, the learning of Q-learning model-free can be boosted by the introduction of another model-based to accomplish a combined Dyna algorithm, as demonstrated in Figure 7. A model is introduced to make a prediction of the experiences. Then, the policy is updated by the estimated model predictions of state, reward, and action. [39,70]. Accordingly, the Dyna algorithm is in line with the aforesaid actor–critic on the side of the features and operational methodologies. Both are combined algorithms, to enhance the learning performance of a model-free algorithm. The Dyna algorithm aims to address shortcomings of the model-free approach, particularly Q-learning, while the actor–critic is to adapt the model-free DQN to a continuous action domain. On the other hand, Dyna differs by the accomplishment of the best action based on predictivity. The Dyna algorithm develops a transition and reward model by using the estimated predicted experience and then updates the developed model by the accomplished experience, which lastly updates the Q-learning and provides the best action. The actor–critic is accomplishing the best action based on the state and the update from the critic. The critic is evaluating the actor’s actions for the given policy to attain an updated Q for the actor [39].

Recently, the energy management of hybrid electric vehicles has benefited from the fast learning of the Dyna. G. Du et al. [70] have suggested a solution based on the Dyna algorithm to overcome the “curse of directionality” of a management system in a hybrid EV. Here, a developed DQL was applied with the collaboration of a new version of Dyna algorithm, named (Dyna-H). Furthermore, a new optimization method (AMSGard) was activated for updating the ANN weight. Hence, faster release to the training speed and lower fuel consumption were gained.

The new queue Dyna RL algorithm has taken effect to improve the performance and fuel consumption of hybrid electric vehicles (HEVs) [71]. Specifically, an updated combined Dyna of direct and indirect RL algorithms was suggested to overcome the defect of direct and indirect RL through the online construction of the model, and to deal with backward focusing and posturized sweeping. Hence, great optimized performance and reduced fuel consumption were achieved by the new queue Dyna over the direct RL, indirect RL, and conventional Dyna. Power marketing was an application field of Dyna interaction through an attempt by Q. Jia et al. [72] to suppliers bidding under a limitation of information. In accordance, an updated continuous action RL automata algorithm with the introduction of the discretization and Dyna structure was suggested to attain an improved execution in a separate game. Thus, the success of the achieved effective algorithm was verified by the simulation results.

Table 1. Summary of the classical RL-based solutions of power flow management problems.

Strategy/Application	Strengths	Weaknesses
Ref. [35] EVs	12%, and 8% Reduction of battery capacity and battery capacity loss, respectively. Extended vehicle’s range and batteries life. Qualified for different driving cycles and measurement noises. Extendable to different hybrid power systems.	More state variables consideration is mandatory. Not validated for some experimental data from externally introduced models.
Ref. [36] HEVs	Improved dynamic performance. Reduced fuel consumption and calculation time.	The attained power response performance is close to the existing DP-based strategy.
Ref. [37] Wind turbines system Integrated to grid	Optimized wind speed forecasting by 48% and 67% of two case studies in comparison with 9 previously existing methods.	Optimization is mandatory regarding the online selection of the model and the application of dynamic ensemble approaches.
Ref. [38] FCHVs	5.59%, and 13% reduction of fuel consumption and power fluctuation, respectively. 69% increase in convergence speed.	Real-time applications are mandatory.
Ref. [42] Microgrid	13.19% saved energy costs. Extendable to other industries require energy management.	Instability and sluggish convergence in real-time. Prediction of energy price is not considered.
Ref. [43] Microgrid	5% reduced operation cost. Enhanced generalization capability.	PV and load uncertainties are not included. Ignored fuel efficiency.
Ref. [44] Distribution networks	Enhanced regulation of voltage fluctuation due to the high penetration of DGs.	Further modification can be achieved of the reward function.
Ref. [45] HEVs	Efficient utilization of learned information. Enhanced computational speed. Improved fuel economy. Independence of prior knowledge in driving cycles.	Unextendible to other applications. Participation in the electricity market is not included.
Ref. [46] HEM	Reduced electricity costs. Enhanced customer satisfaction.	Participation in the electricity market is not included.
Ref. [48] Building HVAC	12%-35%, 3%-10%, and 3%-8% reduction in ramping, 1 h factor, and daily peak at deployment, respectively. Improved performance degradation compared to the existing strategy.	Still an existing performance degradation.
Ref. [49] Building HVAC	7.2%, and 16.7% reduction of energy consumption compared to the existing batch algorithm and the rule-based algorithm, respectively. Enhanced thermal comfort.	A more frequent data writing rate is mandatory.
Ref. [50] Unknown electric grids	95% reduction of the total number of rounds with at least one constraint violation.	Low setpoint tracking performance.
Ref. [53] PHEV	A superior optimization of fuel economy. Perfect adaptability to different SOC reference trajectories.	Real-time speed reduction under complex traffic conditions is not considered.
Ref. [55] HEVs	Only half of the learning iterations are needed to attain battery efficiency. 1.75%, and 5.03% improvement in vehicle energy efficiency and energy saving, respectively.	Despite an improvement achieved in energy efficiency, it is still low.
Ref. [55] HEVs	Improved fuel economy. Enhanced SOC stability.	Computational speed is not taken.
Ref. [57] Residential building HVAC	15% reduced energy consumption. 79%, and 98% reduced comfort violation compared to DQN and rule-based, respectively.	Different seasoning scenarios are not considered. Various user preferences are not included.
Ref. [58] Active distribution network	Balanced bus voltage to the allowed range. 15% reduction of system loss.	Many training episodes are required to achieve the solutions. Slow convergence.
Ref. [59] Hybrid AC-DC networks (HDNs) with microgrid	Optimized computation efficiency. Enhanced stability. Solutions can be used as an initial value to accelerate the existing traditional method. Active in various states and scales.	The accomplished optimization is similar to the existing single-agent DRL algorithm.
Ref. [60] Microgrid	Improved dynamic performance. Enhanced online learning capabilities. High control performance. Low economic costs.	The dynamic topology of the microgrid is not considered. Repeated tests in different real-life systems are essential.
Ref. [61] Microgrid	Fast convergence. Efficient addressing of exploration-exploitation defect. Improved robustness in making decisions.	Different types of energy storage systems are not considered.
Ref. [62] EV with hybrid energy storage system	8.75%, 6.09%, and 5.19% reduction of energy storage system loss compared to DQN, DDPG, and DP-based, respectively. Faster convergence compared to DDPG by 205.66% 32.24% improved energy saving.	The difficulty of tuning parameters. Tedious training time. Real-time performance is not verified.
Ref. [63] HEVs	Reduced fuel consumption. Improved robustness under different driving cycles.	Real-world validation is not attained. Platoon control is not introduced.
Ref. [64] EVs	24.03%, 21.49%, and 13.8 reduced energy costs compared to EC, OA, and AEM algorithms, respectively. 7.24% reduced charging cost compared to AEM.	5.56% increased charging cost in CALC compared to SCA. The coordination of multiple charging stations is not considered.
Ref. [67] multi-area energy system	Reduced random disturbance. Enhanced frequency stability. Fast convergence.	An increase in the time consumption for the convergence when the problem size is large.
Ref. [68] Smart grid	Optimal identification of the attack sequence under several attack objectives. Enhanced system security.	The performance of identifying vulnerable branches is required to be improved.
Ref. [69] Electrified off-highway vehicle	Optimized energy efficiency. Optimized real-time prediction. Enhanced energy saving.	The optimized energy efficiency takes long real-time learning (5 h) to be achieved.
Ref. [70] HEVs	Optimized energy management. Faster training speed. Lower fuel consumption. Adaptive to different driving cycles.	Incompatible sample selection in the planning process.
Ref. [71] HEVs	Fast learning. Satisfiable fuel consumption.	More optimized fuel consumption is needed.
Ref. [72] Power suppliers with limited information	Effective under both stationary and nonstationary environments.	Lack of reliability for virtual experience in nonstationary environments. Further validation is mandatory for scalability in more complex and variable environments.

demonstrates a summary of the reviewed classical RL-based solutions for managing power flow, with the major strengths and weaknesses of each one.

4. Emerging Advanced Reinforcement Learning-Based Solutions of Power Management Problems

Despite the progress accomplished by the classical and classical combined solutions based on RL, there remains an urgent need for more intelligent and efficient algorithms to solve complex problems that cannot be solved with classical solutions. Among these complex applications is what interests this research on highly complicated energy management problems.

4.1. Synchronous and Asynchronous RL Solutions

The asynchronous actor–critic (A3C) has been established by Google DeepMind technologies to maintain the unstable recursions of the Q-learning in the case of an introduced neural network [73], in which a group of ANN-based agents is trained with various copies of the environment to update the master agent until reaching convergence and attaining the optimal solution. The A3C has shown an advancement in learning efficiency compared to the classical DQN of solving complicated problems. However, there has been a defect in the less achieved advantage compared to its complexity. Therefore, an updated more efficient solution with less complexity and easier implementation was released in 2017 by the USA AI research company, Open AI, named synchronous actor–critic (A2C) [74]. The secret of its superiority over A3C lies in the use of the N-step return technique that guarantees improved bias-overfitting.

The A3C and A2C actor–critic solutions were involved recently in fulfilling an optimization of managing power flow and solving problems in a variety of complicated applications. A. Biwas et al. [75] have suggested an updated online energy management framework of a multimode hybrid electric powertrain through a collaborated solution of A3C based on DQN and a Markov chain model (MCM). Accordingly, the energy management policy was updated periodically by the asynchronous-based DQN, then plenty of probable future drive cycles were generated by the MCM. Therefore, the results of two training trials have demonstrated a 99% achievement in fuel economy of the global optimal and a 0.12% reduction of the deviation from the charge sustainability, in the case of unknown drive cycles generated from the same historical data. Additionally, an extra 6–10% fuel consumption than the global optimal was achieved in the case of unknown drive cycles not generated from the same historical data. The energy management system of a hybrid power train was enhanced through the introduction of the asynchronous advantage actor–critic (A3C+) to attain optimal economical operation [76]. In consequence, an enhancement of the fuel consumption optimality of 92% in charge substance and 83% in charge depletion, was achieved compared to the energy management under dynamic programming.

Likewise, the optimization of bidding in renewable energy trading has taken its position in the recent A3C applications, intending to maximize profit. Accordingly, M. Sanayha et al. [77] have proposed an adapted bidding strategy for wind energy through the introduction of the model MB-A3C. Hence, the results of the investigation in Denmark and Sweden of the “Herein conventional benchmark” that represents six wind power datasets have confirmed the success of the adapted bidding policy. Therefore, less cost was achieved compared to the previous model-free and model-based policy, followed by a reduction of the input cost of a microgrid operation through the improvement of flexible scheduling on the demand side [78]. Here, the advantage of the asynchronous memory actor–critic (M-A3C) to overcome correlation in data and instability of distribution during the training, was exploited. Therefore, enhanced convergence and optimized economic operation were achieved compared to the algorithm with no A3C. In line with the recent enhancement to the introduction of A3C, the lack of foresight in the decision-making of a demand-side management system (DSM) was improved by L. Yu et al. [79]. In accordance, an (A3C) was introduced in collaboration with a long-short-term memory (LSTM) to attain an optimized demand side management. Therefore, the learning process was speeded up with guaranteed users' privacy. Furthermore, the economy in the decision-making was confirmed. F. Sun et al. [80] have enhanced the economy of a DSM. The A3C collaborated with the LSTM to accomplish an updated pricing method for the service provider. Hence, the attainment of DSM pricing decisions under a cloud-edge environment was implemented with less mandatory historical data than in other classical methods, and Improved profit.

Similarly, the optimization of power management in grid-connected microgrids was investigated to minimize the losses of generation, transmission, and overall losses in a microgrid network [81]. The A2C was introduced as a third stage to maximize the efficiency of the microgrid and the grid. Hence, the results have shown an optimization of the prediction rapidity to 40 times than before applicating the A2C. The optimum autonomous deriving was a distinctive application of the A2C RL. This was demonstrated in a proposed strategy by W. Zhou et al. [82] to formulate a line charging decision maker of an autonomous vehicle in a highway environment of mixed traffic. Accordingly, the effective Intelligent multiagent synchronous actor–critic (MA2C) enables each autonomous vehicle of the multiagent to decide regarding the motion of both the neighboring autonomous vehicles and human-driving vehicles. Therefore, simulation results have shown progressed A2C-based strategy over several state-of-the-art strategies in overall efficiency, driving safety, and comfort during driving.

4.2. Multiagent RL Solutions

Regardless of the successful classical, combined, and advanced, single-agent-based strategies in solving complex power management problems, there is still an ongoing need to solve complicated power management problems that cannot be solved by a single-agent-based RL approach. An example of this is the accomplishment of autonomy in managing power distribution systems with multi-stage control or multiple optimization requirements, such as fulfilling the autonomy of managing micro or smart grid networks with several distributed power units of generation, distribution, storage, and demand. In accordance, multiagent RL (MARL) was the emerging solution to fill the gap and verify decentralization and independence of power management, which comprises the solution to an interacted learning of several agents to attain combined actions from the associated environment’s state and the emerged reward signals [83]. The demonstration of the agent interaction with the environment and other interacting agents in the MARL is shown in Figure 8. The transfer of mandatory information is in progress between the ($N)$ number of interacting agents and the environment.

MARL solutions are typed and classified based on the kind of the given reward. Therefore, they are cooperative if the maximization of a long-term return is a collaborative role by all the interacting agents [84]. An example of this is micro or smart grids, where the minimization of utility grid reliance is a collaborative aim of all the power agents, whether they are a resource, storage, or demand. Another is the autonomous driving systems, in which all the control units collaborate to verify the autonomous driving and avoid collisions, in line with maximizing the possibility of optimized traffic flow and reduced fuel consumption [84]. The competitive MARL aims for the return sum of all the interacting agents to be zero. Then, the third class is the cooperative–competitive, which combines the characteristics of the two above-mentioned MARL solutions and aims for the reward to be a general sum.

There are challenges influencing the transition from simple single-agent solutions to the complicated multiagent approach, as explained below:

• Stationarity: In MARL solutions, all the interacting agents can make a modification in the environment, which differs from the non-stationarity single-agent solutions, wherein the environment can be influenced by only one agent [85].
• Scalability: The algorithms for implementing the MARL need to be scalable to a high number of agents, exchanging information between them, in addition to the environment. Accordingly, most MARL approaches to attain scalability are decentralized because of the absence of a central controller and the uncertainty of communication links [86].
• Partial observability: The observability is set to be partial when correlated with a limited geographical due to the vision of the agent on only the surrounding. This can be recovered in the MARL by the similar solution that is followed in setting the DQN, which is that the first layer is replaced by a long short-term memory (LSTM) to enhance the non-observability that is occurred [87].

There has been a wide collaboration in the recent and most recent literature for the aim of improving power management optimization and intelligence of advanced power distribution systems through the introduction of MARL.

The optimization of power management in DC microgrids was rich in unique MARL attempts. Y. Mi et al. [88] were successful in managing the power flow of ESS in a DC microgrid through the enhancement of their lossy communication by the introduction of MARL. Here, the global information estimation of the lossy-communicated network was accomplished by a suggested secondary control. Furthermore, an adapted current algorithm was employed to balance the SOC of the ESS. Hence, an effective current sharing and voltage balance, and enhanced robustness to lossy information, were verified by the simulation results. A solution for the scaled consensus defect in DC microgrid with a heterogeneous multiagent system with cascaded two layers was proposed by S. Mo et al. [89]. Specifically, a two-layer controller of, a continuous feedback controller to converge with target values, and an impulsive controller to enforce the scaled consensus to the upper state component. Therefore, an appropriately scaled consensus was attained in terms of inequalities of the linear matrix achieved with the use of the Lyapunov function. Furthermore, an accomplished optionable relaxation of the distributed hybrid secondary control. In line, MARL was the motive for improving the performance of a DC-DC buck converter with constant load in a DC microgrid. In accordance, H. Sorouri et al. [90] have suggested a learning-based MPC (FCS-MPC) to address an ongoing challenge through the learning of a deep deterministic policy for the aim of an optimal coefficient design policy. Therefore, robustness was achieved against uncertainties and unknown load scenarios, in addition to, the attainment of the plug-and-play feature. The establishment of more active cyber security solutions in DC microgrid applications was one of the crucial recent needs. Therefore, a MARL algorithm was designed by A. J. Abianeh et al. [91] to fulfill the automatic discovery of the conventional detection approaches in DC microgrid applications. In addition, an enhancement sniffing feature was applied to keep the stealthy attacks under sudden connection. Hence, a more reliable performance was verified by the results.

Similarly, AC microgrids existed in the recent MARL applications. Y. Xia et al. [92] have considered time delay in optimizing the control of an AC microgrid through a proposed secondary control approach based on MARL. Specifically, each agent of the MARL was formulated by a trained DNN. Furthermore, an improved deep deterministic algorithm was applied to the secondary control to attain the optimal policy. Thus, optimal solutions under different loads and variated time delays were accomplished. Followed by another optimized secondary controller to maintain frequency in an AC microgrid by H. K. Vanashi et al. [93] through the introduction of an additional secondary controller-based MARL. Here, the secondary control parameters were tuned by particle swarm optimization (PSO) and adaptive dynamic programming (ADP) algorithms and then applied to the agents in the MARL. Therefore, improved performance was attained by oscillation results. On the trend, a proposed decentralized secondary controller-based MARL by P. Chen et al. [94] was the frequency regulator of the AC microgrid with heterogeneous BESSs. A centralized off-line learning A3C based on the MARL algorithm, with the collaboration of a conventional neural network was developed to maximize the global reward. Hence, simultaneous frequency regulation was achieved, in addition to a balanced SOC. This was followed by a successful frequency regulation-based MARL by Y. Xu et al. [95] to control the distributed frequency in AC islanded microgrid. Accordingly, each of the MARL agents provides a control action based on neighboring information with a driven deep deterministic algorithm to update the agent’s parameters. Therefore, effective regulation of frequency was accomplished with an optimized tolerance of time delay and reduced parameters. Energy management of renewable energy in an AC microgrid has benefited from the introduction of MARL. Renewable energy management was suggested by K. Deshpande et al. [96]. In accordance, the MARL agents were trained by the historic energy profile and consumption to make an optimized decision of adapting the load consumption of the microgrid. Thus, a good performance was attained in terms of the energy management balance. Furthermore, a great generalization capability, power management reliability, and resilience.

Likewise, optimization in solving power management problems of smart grids was existing within the recent MARL applications. The charge/discharge scheduling problem of plug-in electric vehicles (PEVs) in a smart grid was resolved by Y. Wan et al. [97] with consideration to the driver’s satisfaction regarding SOC and batteries degradation cost. Here, the minimization of the energy cost was taken as a Markov game of unknown probabilities, then the Markov game was solved through the development of a multiagent deep RL-based data-driven algorithm. Therefore, a lower energy cost within an unknown market was achieved, in addition to the online optimal charge/discharge. This was followed by an energy scheduling attempt by Y. Zhang et al. [98] to accomplish stabilization in the electricity market and optimization of the charging demands for EV charging stations in a smart grid. Thus, an energy distribution strategy was developed through the introduction of MARL to fulfill optimization in the energy purchasing approach and the online dispatch scheme. Therefore, optimized performance was attained with the implementation of the developed energy scheduling, which resulted in enhanced economic profit and consumer satisfaction. The complexity of implementing security situational awareness (SSA) in attaining an intelligent automated smart grid was a recently diagnosed concern by W. Lei et al. [99]. The huge heterogeneous power terminals referred to failed undelivered information. In consequence, the traditional power paradigm was addressed by the introduction of a computing edge between the cloud and power terminals, and the development of a multiagent deep deterministic policy gradient (MADDPG). Hence, faster convergence and protection in real-time were achieved with the smart grid operation.

MARL was a solution for solving recent defects in the power management of buildings. R. Shen et al. [100] have optimized the energy management of a building energy system (BES) by developing an energy management framework of a double Q network for single-agent optimization, and a value-decomposed network for multiagent cooperation. Furthermore, accelerated the convergence and enhanced the stability through the application of a feasible cation screening mechanism. Subsequently, a multi-objectives collaboration of the BES was achieved by the introduction of the MARL algorithm. Therefore, 84%, 43%, and 8% reductions in comfortability, renewable energy, and consumption cost, respectively, were attained compared to the conventional energy management approach with no introduced MARL. The reduction of the energy consumption of a heating ventilation and air conditioning (HVAC) system in an intelligent building was a point of interest for R. Z. Homod et al. [101]. Therefore, the high learning capacity of the hybrid deep clustering MARL was exploited to afford the high amount of training data sets and attain accurate weight layers. Hence, an energy saving of 32% was accomplished with enhanced thermal comfort of 21%.

Additionally, electric-based transportation was positively influenced by the recent development of MARL. In accordance, D. Qiu et al. [102] enhanced the energy resilience of EVs’ energy management system through the introduction of MARL. Specifically, both continuous and discrete actions were simultaneously computed to enhance the stability and scalability of the learning. Therefore, the resilience of the power network integrated into EVs was attained, in addition to the accomplishment of the carbon intensity service. Accelerated loss of life (LOL) of the EV charging transformers was dealt with recently by S. Li et al. [103]. Here, an updated algorithm was proposed through the collaboration of evolutionary curriculum learning (ECL) and MARL to optimize the charging transformers of LOL with the consideration of various EV charging demands. Thus, enhanced charging of too many EVs that satisfy different charging demands was accomplished. Followed by an attempt to reduce uncertainties of the autonomous mobility on demand system (AMoD) of EVs. An optimized solution was suggested by S. He et al. [104] through the development of a constrained MARL and a transition kernel uncertainty to recover charging defects. Therefore, an effective rebalancing policy was achieved in the existence of uncertainty. Furthermore, a 19.9% increase in fairness and a 75.8% decrease in rebalancing costs were accomplished. The low programming intelligence of an electric vehicle charging system (EVCS) in defending advanced mitigate persistent threats (APT) was researched in by M. Basnet et al. [105]. In consequence, a developed algorithm was suggested based on MARL in collaboration with a twin delayed deep deterministic policy gradient (TD3) to attain efficient learning of the control approach and mitigate cyberattacks. As a result, the EVCS operation was restored in the event of a threat incident by the proper correction of the legacy control generated signal. Furthermore, high accuracy was accomplished in learning nonlinear control approaches.

4.3. The Decentralized Multiagent Primary–Secondary Control

The decentralized multiagent primary–secondary control is one of the applications of MARL, which is a successful approach to decentralized power flow management in micro and smart grids, especially ESS. This is because of the qualification for providing immediate real-time information with no need for central controller or communication reliance. Furthermore, more stability and sustainability can be attained in power flow due to the several correction stages included. Moreover, the flexibility of boosting the level of intelligence through the introduction of other smart applications [106,107]. However, there has been a defect in the inaccurate synchronization of charge–discharge scenarios of the ESS agents, which has been identified as a tradeoff between the utilization of the real-time capacity and the attainment of accurate charge–discharge synchronization. This is due to the limitation of the consensus correction of fulfilling the accurate real-time balance in managing the participation of the load demand implementation, especially in the situation of a sudden high, or excessively continuous, load variation [6,108].

Accordingly, there have been attempts to improve the above-mentioned drawbacks. For instance, C. Li et al. [109] were tending toward frequency scheduling rather than droop control coefficient adaptation in fulfilling the SOC balance of energy storage systems of an AC microgrid. Here, each distributed ESS of the microgrid was considered an independent agent and responsible for scheduling an independent frequency reference. Furthermore, attaining the droop control based on the SOC of all other ESS agents. However, the plug-and-play was not attained. T. Wu et al. [110] have proposed a time-oriented SOC balancing of energy storage units in a DC microgrid, even though the speed of SOC balancing in the conventional primary–secondary consensus strategy was faster. In line, the balance of the SOC of BESS agents in a DC microgrid through the introduction of sliding mode control was suggested by T. Morstyn et al. [111]. A sliding mode controller was employed to balance the SOC of the BESS agent based on the average SOC of the neighbors’ BESS. Nevertheless, solving the overloading problem of some participating BESS agents was prioritized over the accomplishment of accurate SOC synchronization to reduce sliding mode chattering. L. Zhou et al. [112] have adopted a consensus scheme to manage the operation of BESSs in an AC-islanded microgrid and accomplish balanced SOC. Specifically, each BESS shares information with the neighbors’ BESS, then a combined approach of droop control and the proposed consensus collaborating of managing the power until reaches balanced SOC. Though, heterogeneous BESSs were not considered. A recent application was suggested in [113] to balance the SOC of energy storage units in a DC microgrid. Accordingly, a designed SOC equilibrium algorithm was proposed based on the accomplishment of accurate load sharing. Still, some instability of output voltage was existing.

The Adaptive Multiagent Primary–Secondary Control

An adaptation was recently suggested for the aforesaid defect [106], which trended towards the exploitation of the information that can be provided by multiagent communication rather than the adaptation of the droop coefficient. Specifically, each participating BESS agent shares the immediate real-time droop drop in the voltage due to the variation in the load demand and accomplishes an adapted immediate real-time reference of the local controller ($Vd\_i)$ at each participating BESS agent, which is the summation of all the neighbors’ real-time droop-regulation ($Vref\_droop\_j\_M)$, including the specific BESS droop-regulation ($Vref\_droop\_i\_M)$, and divided all by the number of neighbors plus 1 (|N| + 1), as explained in (10). This refers to the fact that any immediate real-time variation in the load participation at any of the BESS agents is collaboratively implemented by all the participating BESS agents. Thus, accurate charge/discharge synchronization can be achieved. This supports solving the circulating current between the participating BESS agents, which was due to the unsynchronized SOC because of the unbalanced implementation to the level of the participation of the load demand. The balance in the level of participation in the load demand has already been achieved by the adapted controller. Furthermore, improving the overloading defect, which was likewise due to the unbalanced SOC of the BESSs, when one or a group of BESS agents are participating in implementing the load demand, in addition to charging other BESS agents. The balance in the output voltage in the multiagent primary–secondary controller is via the collaboration of the primary and secondary control stages of the multistage decentralized controller. However, the role is arduous in the case of an excessive continuous load variation, and the deviation in the output voltage is highly expected. Accordingly, an adaptation was suggested of the real-time voltage consensus to enhance the balance of output voltage, which is that the neighbor’s voltage consensus correction $\left(VLj\_dash\right)$ is compared to the microgrid nominal voltage ($Vmg)$ before sending it to the neighbor via the multiagent. This reduces the impact of the real-time variation in the voltage due to the variation in load demand and enhances the output voltage balance against the excessive continuous load variation, as demonstrated in Equation (11).

$$Vd\_i \left(t\right)=\frac{1}{\left|N\right|+1}(({{\displaystyle \sum }}_{j=1}^{N}Vref\_droop\_j\_M \left(t\right))+Vref\_droop\_i\_M\left(t\right)$$

(10)

$$VLi\_dash \left(t\right)=VLi\left(t\right)+\frac{av}{\left|Ni\right|}{{\displaystyle \int }}_0^t\left(\frac{VLj\_dash\left(t\right)+Vmg}{2}\right)-VLi\_dash\left(t\right) dt$$

(11)

The control methodology of the proposed adapted multiagent primary–secondary control in [101] is explained in Figure 9, which is a multistage control approach, of primary control, secondary control, and secondary average consensus based on the multiagent. A consensus correction to the secondary controller is attained for both output voltage ($VLi\_dash, )$ and participation current ($ILi\_dash)$, by the real-time average consensus of both, voltage $\left(VLi+\frac{av}{\left|Ni\right|}{{\displaystyle \int }}_0^t\left(\frac{VLj\_dash+Vmg}{2}\right)-VLi\_dash dt\right)$, and current ($ILi+\frac{ai}{\left|Ni\right|}{{\displaystyle \int }}_0^t{\displaystyle \sum }_{N=1}^{j}ILj\_dash-ILi\_dash dt)$. $VLi, ILi,$ are local’s output voltage and current, and $VLj\_dash,ILj\_dash$ are neighbors’ consensus correction of voltage and current, respectively, where $av, ai, Ni$ are voltage consensus gain, current consensus gain, and the number of BESS neighbors, respectively.

Then, a secondary voltage correction reference ($Vref\_\sec \_i)$ is accomplished for the primary controller based on the attained consensus correction, which is the summation of secondary voltage correction $\left(\left(ev\_sec\times K_p^{\sec \_v}\right)+{{\displaystyle \int }}_0^t(ev\_\sec \times K_i^{\sec \_v}dt\right)$, secondary current correction $\left(\left(ei\_\sec \times K_p^{\sec \_i}\right)+{{\displaystyle \int }}_0^t(ei\_\sec \times K_i^{\sec \_i}dt\right)$, and the microgrid nominal voltage ($Vmg)$. Where $ev\_sec, ei\_sec,$ are the secondary errors of voltage and current, and $K_p^{\sec \_v}, K_i^{\sec \_i}$ are secondary voltage gain, and secondary current gain, respectively.

Followed by the attainment of droop correction ($Vref\_droop\_i\_M$) by subtracting the droop drop in the voltage due to the variation in the load participation ($ILi\ast rdi)$ from $Vref\_\sec \_i$, where $rdi$ is the droop coefficient. Next, an adapted reference of the local controller ($Vd\_i)$ is achieved from the summation of the immediate real-time drop in the voltage due to the variation in the load demand of all the neighbors divided by the number of neighbors plus 1 ($\frac{1}{\left|N\right|+1}(({\displaystyle \sum }_{j=1}^{N}Vref\_droop\_j\_M)+Vref\_droop\_i\_M).$

Subsequently, a voltage controller is employed to attain a correction current reference for both charge and discharge ($Iref\_ch\_dis\_i)$ based on the compensation of the difference between $VLi$ and $Vd\_i$. Finally, a current controller is employed to accomplish control action of the battery’s converter’s switches ($ei\_C)$ based on the different errors of $Iref\_ch\_dis\_i$ subtracted from the measured battery current ($IB\_i).$ Accordingly, the bidirectional DC-DC buck–boost converter that interfaces the 24 V battery to the 48 V microgrid DC bus is responsible for balancing the output voltage with the variation of the battery current, based on the received control action for both charge or discharge.

The flow chart demonstrated in Figure 10 explains the design methodology stages of fulfilling the proposed decentralized primary–secondary control strategy. The management of output voltage balance and real-time participation in implementing the load demand is accomplished at the local controller. The regulation of the local controller accomplishments (output voltage and the level of load participation) is the role of the droop control. Followed by the immediate real-time correction of the local controller that provides the appropriate balance to the level of participation and attains accurate charge–discharge synchronization based on the real-time multiagent information. Next, the secondary correction of the primary voltage and the participation of the load demand is achieved at the decentralized secondary controller, which is under the supervision and correction of the average consensus for both voltage and current based on the information from the neighbor BESS agents via the multiagent communication. The average voltage consensus is correcting secondary voltage reference based on the average corrections from the neighbors. The average current consensus is correcting the level of the participants provided by the secondary based on the average correction in the variation of the neighbors’ participation current. Lastly, the accomplishment of the plug-and-play feature that allows any BESS to participate and ends the participation based on operational obligations.

Additionally, multiagent communication has been formulated to accomplish an active enhanced protective plug-and-play feature. Accordingly, any BESS agent can participate if the absolute battery current is either over zero or under/equal to the battery nominal current ($0<\left|IB\_i\right|\le IB\_N)$. Otherwise, the BESS ends the participation if the battery current is either zero or over the battery nominal current ($I{B}_i=0, \left| IB\_i\right|>IB\_N$) with no impact on the stabilization of the control process and the accuracy of the charge-discharge synchronization. Then the closest BESS agent will take its position as a neighbor, as explained in the demonstration of the multiagent topology of BESSs in Figure 11.

The results of several case studies, varying based on the number of BESS agents of the microgrid, BESS agents‘ capacities, and initial SOC have confirmed that the proposed adapted strategy has outperformed the conventional strategy in attaining accurate synchronized charge–discharge scenarios and enhanced balanced output voltage under a 24 h excessive continuous load variation. This confirms that there is no circulation current between the participating BESS agents. Furthermore, no overloading on any of the participating BESS agents. The proposed plug-and-play has likewise been confirmed by the results. Accordingly, any BESS can participate or end the participation with no impact on the stabilization of the control process and the accuracy of the charge–discharge synchronization. This positively affects the optimization and stabilization of the control process, supports healthier and longer-life batteries, enhanced the batteries’ protection against high faulty currents, and improves renewable energy penetration and sustainability.

4.4. Transfer Learning Solutions

Transfer of learning refers to the use of RL knowledge that was attained to perform a task of solving a problem, in solving another RL problem not belonging to the first problem-solving task. This is to compensate for the lack of learning due to the limitation in the historical data [114]. There have been recent efforts of introducing transfer learning in solving complicated power management problems with a historical data shortage. The optimization of bidding in the electricity market was at the forefront due to the much historical information needed for attaining optimized bidding. As an application of it, J. Wu et al. [115] have proposed a bidding approach in a competitive electricity market. Specifically, the collaboration of MARL to enhance the learning of the agents interacting with varying environments, and multiagent transfer learning (MATL) to learn from other similar tasks, were exploited to attain an optimized bidding algorithm. Then, an enhancement of the accuracy and convergence in the learning speed was verified by the results. The less accurate prediction due to the insufficient historical data on microgrid power consumption was addressed by Y. Ahn et al. [116] through the introduction of transfer learning based on the collected data of a reference building. A transfer learning long-short-term memory (TL-LSTM) was developed and trained with a 24 h power consumption of an office building. Accordingly, higher accuracy was achieved by the TL-LSTM over the conventional LSTM with a 4.25% percentage variation of error. In line, transfer learning existed in the optimization of the economic operation for an integrated energy system. Here, C. Li et al. [117] have enhanced the accuracy of load forecasting through a three-stage solution. The first stage was the filter out of metrological variables by the Pearson coefficient based on the load demand and the metrological data. The second was the development of a combined model based on an ANN and the recurrent unit. Then, the third was coping with the complicated prediction environment through the adjustment to the model structure. Subsequently, a synergy was accomplished between the source and the mandatory domain data. Furthermore, an optimization of model performance was verified through the enhancement of forecasting by transfer learning.

4.5. Priority Experience Replay RL Solutions

The biased sampling of past experiences in an RL agent for accomplishing the current time learning has two major advantages, the first is optimizing stability in the classical batch and deep RL solutions, and the second is raising the learning speed [118]. RL solution-based propriety experience replay has positively influenced the resolution of power management problems in the recent literature. Accordingly, the sum rate of a multi-cell network was enhanced by A. Anzaldo et al. [119] through a proposed experience replay-based power control approach. In consequence, both historical and current knowledge were explored. Furthermore, the task degradation was reduced and learning capability was enhanced. The minimized weighted sum of time cost, and the reduced expected outage duration were recent aims of an unmanned aerial vehicle (UAV) with a cellular connection. This encouraged Y. Li et al. [120] to suggest a solution based on the collaborative introduction of deep reinforcement learning (DRL) and quantum-inspired experience replay (QiER). Here, the formulation of UAV navigation was attained through a proposed QiER to accomplish an advantageous tradeoff between the priority of sampling and diversity. Thus, the results verified the effectiveness and supremacy of the proposed strategy compared to several DRL- based strategies. In sequence, the crucial aim of optimizing fuel consumption in nuclear plants has accomplished vital advantageous achievement through the application of QiER. M.I Radaideh et al. [121] have developed a prioritized replay evolutionary and swarm algorithm (PESA), in addition to an E-greedy replay to improve PESA exploration. Accordingly, an optimized fuel was achieved with a competitive performance of PESA over the other conventional algorithms.

4.6. Policy Optimization Methods

The identification of step size for updating an RL algorithm policy is a major challenge. Large step size results in going too far in the wrong correction direction of the agent policy [122]. This is highly expected under bad gathered data or misleading experiences. In accordance, policy optimization methods have been the emerging solutions to compensate for the defect, wherein two sub-methods were included, as explained below.

4.6.1. Trust Region Policy Optimization

The optimization methodology of a surrogate in the trust region policy optimization (TRPO) is dependent upon the boundary of the updated step size. Accordingly, the avoidance of accumulated misleading experiences is restricted to a trust region [123]. Furthermore, a quadric function is employed to approximate the constraint of the policy.

TRPO has been the optimal solution for many recent modern applications. Vehicular communications were the most benefited. This can be applicated via two technical theorems, the dedicated short-range communication (DARC) and the cellular vehicle-to-everything (C-V2X) that fulfills the concept of the internet of vehicle (IoV). IoV can be defined as an emerging application of the intelligent transportation system (ITS) to attain intelligent communication between vehicles, in addition to the infrastructure, through integration with the internet of things (IoT). From the two vehicular communication technologies, the C-V2x can offer a high-performance application of IoV in terms of coverage, bandwidth, and scalability, to present it as a reliable and more convenient application of vehicular communications. Accordingly, two communication versions can be offered by C-V2X to the IoV to accomplish efficient intelligent traffic management. The first is vehicle-to-vehicle communications (V2V), and the second is vehicle-to-infrastructure communications (V2I). This supports efficient intelligent traffic management, enhanced road safety, and improved real-time information services. V2V refers to the bidirectional exchange of information between two vehicles, both holding the feature. V2I implies the bidirectional communication between the featured vehicle and the road infrastructure, to attain the mandatory knowledge regarding road management and safety, such as synchronizing with traffic light signal changes [124].

In the most recent application of TRPO, the optimization of road safety and information freshness of the “internet of vehicles” (IoV) were discussed with consideration to vehicular user pairs and cellular users during driving. Particularly, an optimization policy based on TRPO was suggested by N. Peng et al. [124] to formulate the resolution of the problem as an MDP with the adoption of TROP. In consequence, the minimization of the sum of the average age of information (AOI), and the average consumption of all users was accomplished. Hence, an optimized fast convergence speed was implemented with enhanced high stability.

4.6.2. Proximal Policy Optimization

The simpler version of TRPO is known as proximal policy optimization (PPO) and is responsible for linearizing the objective of the surrogate, in addition to linearizing the approximation of the step size. This has been verified as the most convenient for the actor–critic when dealing with multi-dimensional and continuous environments [123]. Where the activation of the demand flexibility through the residential demand response schedules was a recent beneficiary of the PPO. Accordingly, T. Peirelinck et al. [125] have overcome the shortage in data efficiency of a conventional RL-based algorithm through the introduction of PPO. Furthermore, enhanced the performance of learning through the incorporation of a demand-side response domain. Hence, the combination of PPO and transfer learning has reduced the cost by 14.51% compared to the controller with no PPO, and by 6.68% compared with a traditional controller with only PPO and no transfer learning. The tie-line power adjustment problem has earned a vital recent solution by J. Hou et al. [126] to optimize system calculations of the operation state. Specifically, the solving of the low calculation efficiency problem was formulated as a Markov process, with a designed ANN for the introduced PP. Therefore, successful validation of the optimized designed algorithm was attained by the verification via the IEEE 39-bus system.

A summary of the reviewed emerging advanced RL-based solutions to power management problems is presented in

Table 2. Summary of the emerging advanced RL-based solutions of power flow management problems.

Strategy/Application	Strengths	Weaknesses
Ref. [75] Hybrid electric powertrain	99% of the fuel economy is achieved. 0.12% Reduced deviation from charge sustainability.	Sensitivity of the DRL algorithms is not included.
Ref. [76] Hybrid powertrain	92% and 88% of fuel economy are achieved under training, and test cycles, respectively. Optimized training and running efficiency.	Reduction of fuel economy lower than 75% relative to DP EMS.
Ref. [77] Wind energy system	Reduced average per-day bidding cost. Optimized profit. Lowered uncertainties.	A very slight reduction in bidding cost compared to conventional existing A3C (nearly the same).
Ref. [78] Microgrid	Optimized performance in terms of convergence and economics.	A further enhancement is mandatory for the generalization ability of the model.
Ref. [79] Demand side management system	Faster learning process. Guaranteed users’ privacy. More economic decision-making.	Extra improvement to the decision-making is required by the separate training in each period.
Ref. [80] Demand side management system	High day-ahead achieved profit. Less required historical data.	Improvement is mandatory for real-time pricing decisions.
Ref. [81] Grid-connected hydropower plant	Optimal control policy. Maximized system efficiency.	Higher variation of the generator bus voltage. Voltage restrictions need to be improved.
Ref. [82] Autonomous vehicle	Enhanced system efficiency. Improved safety and driver comfort.	More attention is needed on fuel consumption.
Ref. [88] DC microgrid	Optimized voltage regulation and current sharing.	Requires more accurate compensation for packet loss data.
Ref. [89] DC microgrid	Improved balance of current sharing. Enhanced communication.	Communication delay. The presence of external disturbances is not considered.
Ref. [90] DC microgrid	The dependency of converter control on the operating set-point conditions is resolved. plug-and-play feature. Robust against uncertainties.	Unextendible strategy.
Ref. [91] DC microgrid	Reliable identification. Robust against communication delays and load changes.	Needs more enhancement to the identification of FDI attacks.
Ref. [92] AC microgrid	Robust under communication delays. Improved frequency/voltage restoration. Optimized active/reactive power sharing.	Unrobust against different communication topologies. A limitation due to the offline training model. A violation of privacy in communication.
Ref. [93] AC microgrid	Improved control performance. Faster reaction against disturbance.	More dependency on network configurations.
Ref. [94] AC microgrid	Optimized system performance. Better communication due to the reduction of channel congestion.	More training time compared to FCNN.
Ref. [95] AC microgrid	Greater frequency regulation. Better time-delay tolerance.	Real-time validation is not taken.
Ref. [96] AC microgrid	Good generalization capabilities. Enhanced reliability and resilience of energy management.	Limited to only three problem instances. Limited experienced energy profiles. Restricted energy management to only 5 agent components in the microgrid.
Ref. [97] Smart grid	Optimal charge/discharge. Reduced energy cost within an unknown market environment.	The randomness of PEV charging behavior.
Ref. [98] EV charging system in Smart grid	Better economic profits. Higher satisfaction ratio of EVs.	More extensive mathematical analysis is mandatory. Lack of estimation of actor and critic weights. Requires deeper analyzed multiagent energy scheduling.
Ref. [99] Smart grid	Faster convergence. Improved real-time protection.	Various grid environments are not considered.
Ref. [100] Building energy system	Optimized multi-objective management of the multiagent algorithm. 84%, 43%, and 8% reduction of uncomfortable duration, renewable energy consumption, and energy cost, respectively.	Lack of activity in indoor evaluation and control. Further control parameters of indoor comfort are essential.
Ref. [101] Intelligent building	32%, and 21% enhancement of energy saving and thermal comfort, respectively.	The multiagent approach needs to be extended to more functional agents. Reconfiguration of the RL algorithm and clustering structure is mandatory.
Ref. [102] EVs	Better system resilience. Accomplished carbon intensity service.	More enhancement of system resilience is required. Multi-energy systems are not considered.
Ref. [103] EVs	Extendable charging performance to a larger number of EVs. More satisfaction of EV owners charging demands.	No improvement in the performance compared to the existing NLopt centralized approach in terms of the test set.
Ref. [104] EVs	19.6% increase in system fairness. Robust against uncertainties.	Slight increase in rebalancing cost compared to the non-constrained MARL.
Ref. [105] EV charging station	A successful correction of the control signal.	Further analyze of the cyber security is mandatory.
Ref. [109] AC microgrid	Balanced SOC. Regulated active power.	Unrobust against communication failure. Scalability enhancement is mandatory. Plug and play is not included.
Ref. [110] DC microgrid	Balanced and fast charge/discharge. Active with different ESS capacities. Enhanced ESS protection.	The speed of SOC balance is still faster in the conventional strategy.
Ref. [111] DC microgrid	Balanced SOC. No circulating current and overloading. Activated plug and play.	Solving the overloading defect is prioritized over the accuracy of charge–discharge synchronization to reduce sliding mode chattering.
Ref. [112] AC microgrid	Balanced SOC. An enhanced balance of frequency, voltage, and reactive power sharing.	The control with heterogeneous BESSs is not considered.
Ref. [113] DC microgrid	Active under various microgrid operating conditions and weak communication. Balanced SOC under different energy storage capacities. The control is independent of line impedance.	Still existing instability of output voltage.
Ref. [115] Competitive electricity market	Better performance in terms of accuracy and convergence speed.	Game theory and Nash equilibrium are not introduced to make the entire electricity market closer to reality. More accurate results can be achieved through a more optimized load-forecasting model.
Ref. [116] Office buildings	Higher accuracy under different building locations.	Limited to office buildings. Applicable only with the availability of 24 h weather forecast data.
Ref. [117] Integrated energy systems	Satisfactory predictions can be achieved with small sample data.	Economic energy price, and demand response factors are not considered.
Ref. [119] multi-cell network	Reduced transient time. Improved long-term network performance.	Unadaptive to different network conditions.
Ref. [120] Unmanned aerial vehicle	Better learning efficiency. Extendable to other existing frameworks.	Energy saving due to the optimized navigation is not investigated.
Ref. [121] Nuclear power plant	Good, achieved scalability. Optimized nuclear fuel. Enhanced competitive performance.	Despite good scalability, still, replay memory management consumes 53% of the computing time.
Ref. [124] Internet of vehicles system	Optimized average cumulative reward. Improved convergence speed. Higher scalability.	A still decrease in the reward with the increase in the initial load. Despite it is higher than the random and the DQN.
Ref. [125] Residential demand response system	14.51%, and 6.68% reduction of the cost compared to regular hysteresis controllers and traditional PPO, respectively.	A computation drawback during the inclusion of expert knowledge in the learning pipeline.
Ref. [126] Power grid management system	Optimized policy. No reliance on the expert experience.	Imitation learning algorithm is not introduced.

, with an explanation of the major strengths and weaknesses of each strategy.

5. Conclusions and Summary

This paper has presented a detailed and comprehensive review of the state-of-the-art intelligent control strategies based on RL for advanced power distribution systems, such as microgrids, smart grids, smart buildings, and EV charging system applications. In line with the recent trend towards digitalization and decentralized power systems with heavy renewables penetration, agent-based intelligent systems for managing power flows to enhance decarbonization and integration of renewable have been focused upon with heavy interest. Therefore, it is prudent to support research and development initiatives in the field with an up-to-date exposition and reference of both the latest contributions and more established ideas. The presented research work in this study is a product of intense reviews and careful selection of 126 scientific research contributions of the most unique and recent proposals related to intelligent power management. The works have been classified, and a distinctive summary of each reviewed proposal highlights the major strengths and weaknesses that have been evaluated. Work by the current authors has also been described in a separate section, in an open and transparent way.

Recently, a variety of vital important power distribution defects has earned an intelligent solution that positively impacted their future development trend. The updates of the Q-table in the model-free Q-learning based on the Markov process and baleen education has actively raised the learning accuracy of the supervisory management for EVs, due to the highly precise response needed. The great treatment offered by the Batch RL of learning from past experiences was a brilliant enhancement of energy forecasting and bidding applications. Past experiences play a vital role in making the best energy price. The equivalent of the Q-table by an ANN in the DQN can magnificently provide the high correctness needed for an optimized fuel economy of EVs and HEVs. In line, the update to double Q-table learning has effectively treated the overvalued actions due to bias and enhanced the performance of EVs due to the capability of overcoming negative reward drops. On the same trend, the combination of the good features from both policy and value functions of the actor–critic was an intelligent method for the extreme events expected in hybrid AC-DC networks. The prediction of the best actions of Dyna was a talented solution to power management applications comprising many affecting variables and parameters.

There is still an ongoing need for stepping towards the ultimate in RL-learning intelligence. Since the technological revolution of modern power management resulted in more complicated problems. The asynchronous A3C was a qualified emerging RL solution for the unstable recursions of Q-learning and raising profits from renewable energy. However, a less advantage is achieved compared to the algorithm’s complexity. Therefore, the alternative A2C with less complexity and easier implementation emerged to solve power management problems in microgrids and reduce losses of renewable energy generation. Solutions for complicated multi-step or multi-factors power management problems have found the evolving MARL the convenient solution. A fundamental example of this is the decentralization and autonomy in power flow management of advanced power distribution systems such as microgrids, smart grids, smart buildings, and electric-based transportation approaches. Accordingly, the multiagent primary–secondary control has been a successful application of MARL to resolve a variety of complicated power distribution management problems of micro and smart grids, such as the inaccurate synchronization of charge–discharge scenarios of energy storage power flow management. The immediate real-time information, the optimized accuracy from the several correction stages, and the raising of intelligence level by introducing other smart technologies were behind the success.

Likewise, the lack of learning due to limitations in historical data was a defect in the bidding of electricity markets applications. Accordingly, transfer learning was the appropriate solution due to the use of past solutions in a current different event. The benefit of biased sampling for attaining convenient learning time in TRPO was the enabler of solving highly precise learning time settings of IoV applications. On the other hand, linearizing the objective of the surrogate can be accomplished by the simpler version of TRPO, the PPO, which reduced the energy cost of demand-side energy applications.

This research work is the second review in a series investigating distributed/decentralized power management approaches, where the first edition was successfully published last year [34]. Therefore, the sequel and forthcoming third edition in this series will specifically focus on some new developments and related testing of new control strategies based on AI-multiagent control developed by the authors, built upon previous works and the summary points drawn from this (and the previous) study.