Computational Optimization of a Loosely-Coupled Strategy for Scale-Resolving CHT CFD Simulation of Gas Turbine Combustors
Abstract
:1. Introduction
2. U-THERM3D Approach and Proposed Optimization
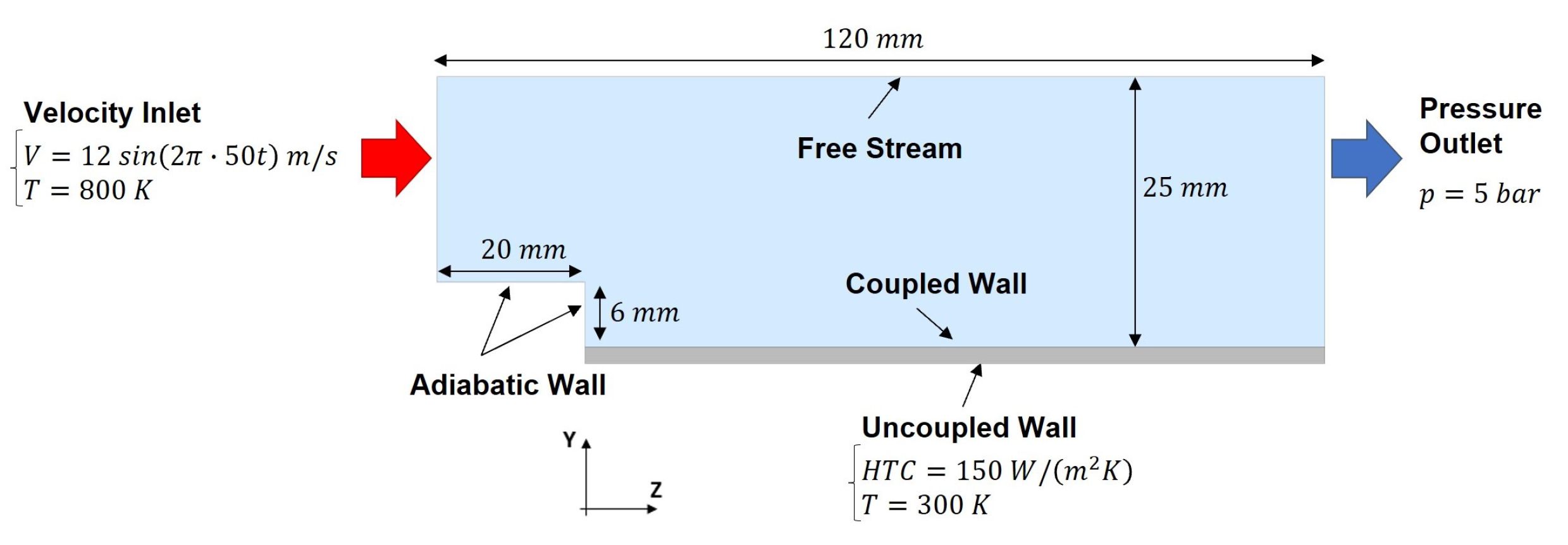
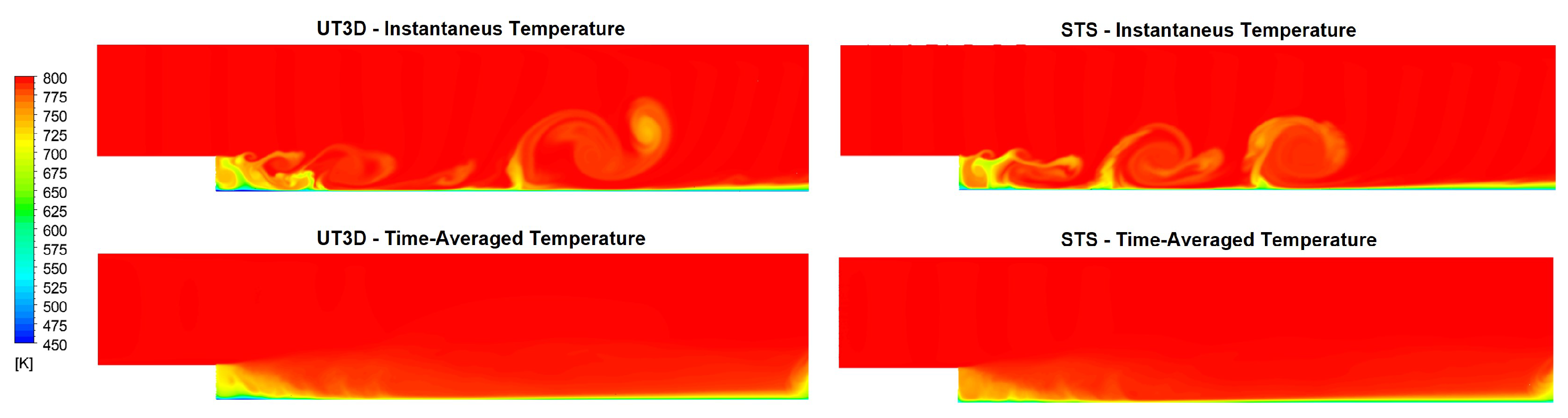
2.1. Validation of the Optimized U-THERM3D Approach
3. Experimental Test Case
4. Numerical Details
4.1. Turbulence Modeling
4.2. Combustion Modeling
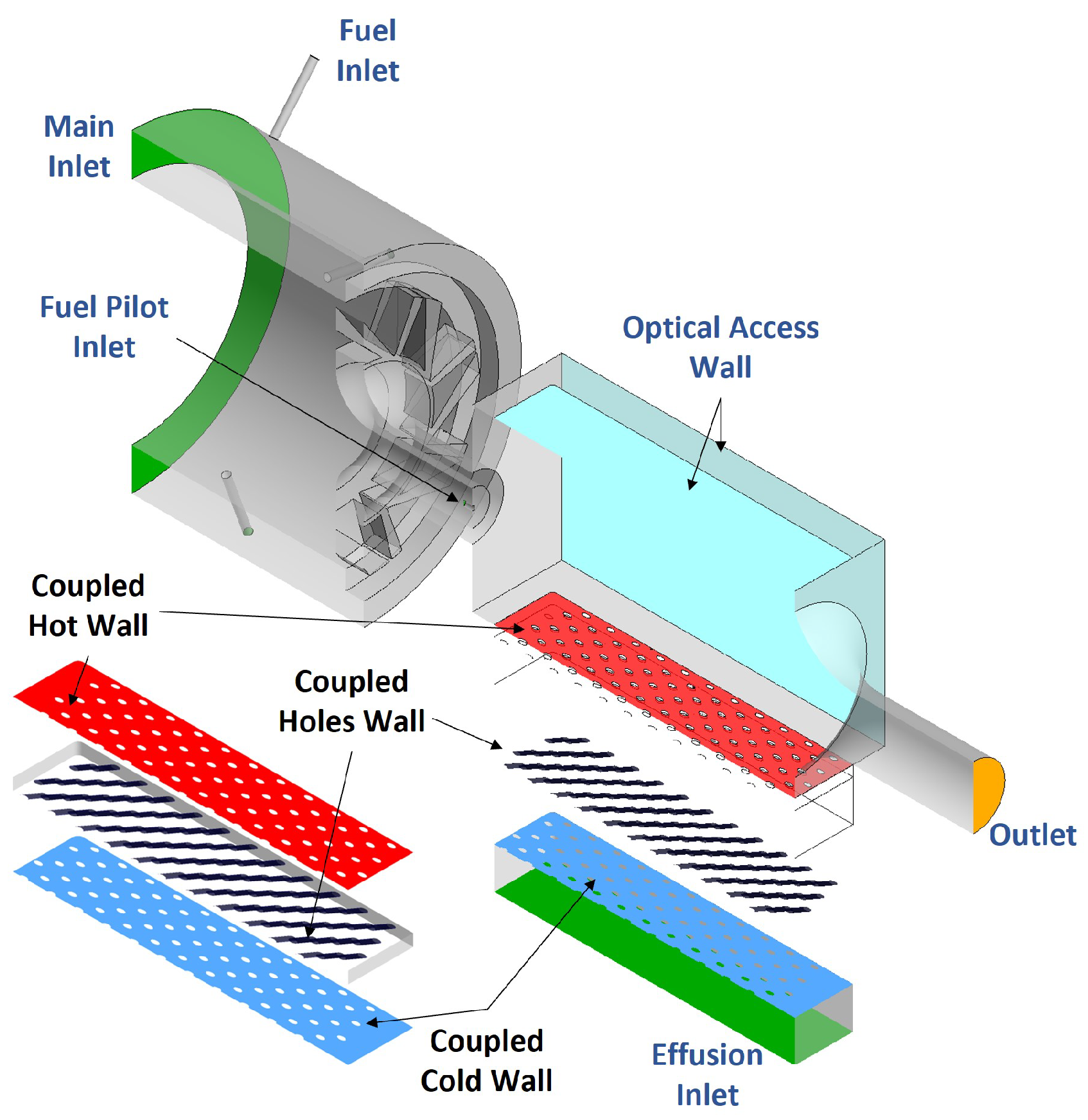
4.3. Computational Domain and Boundary Condition
4.4. Computational Grid and Numerical Setup
5. Results
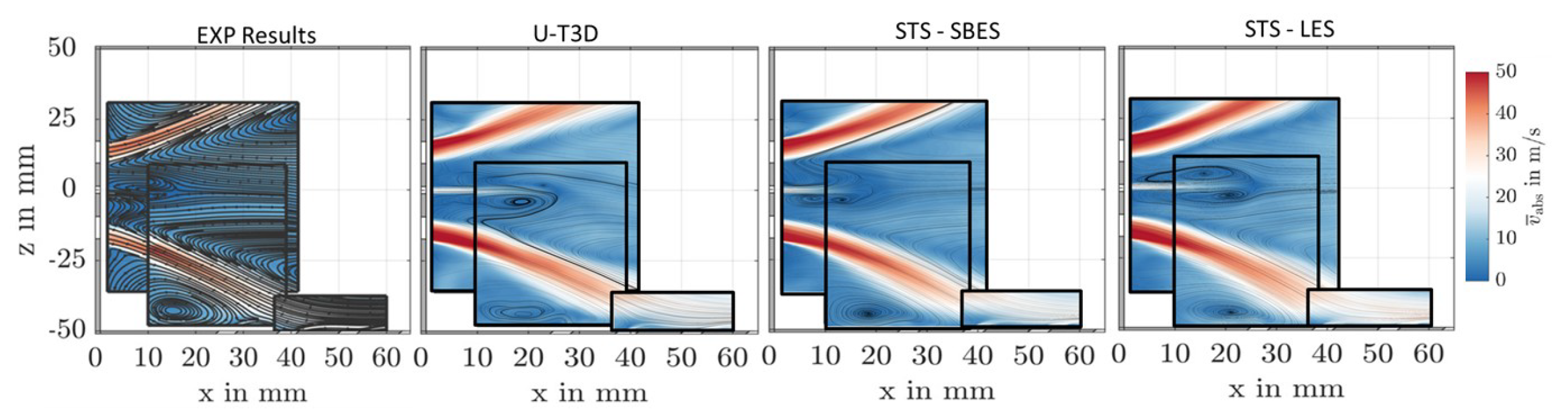
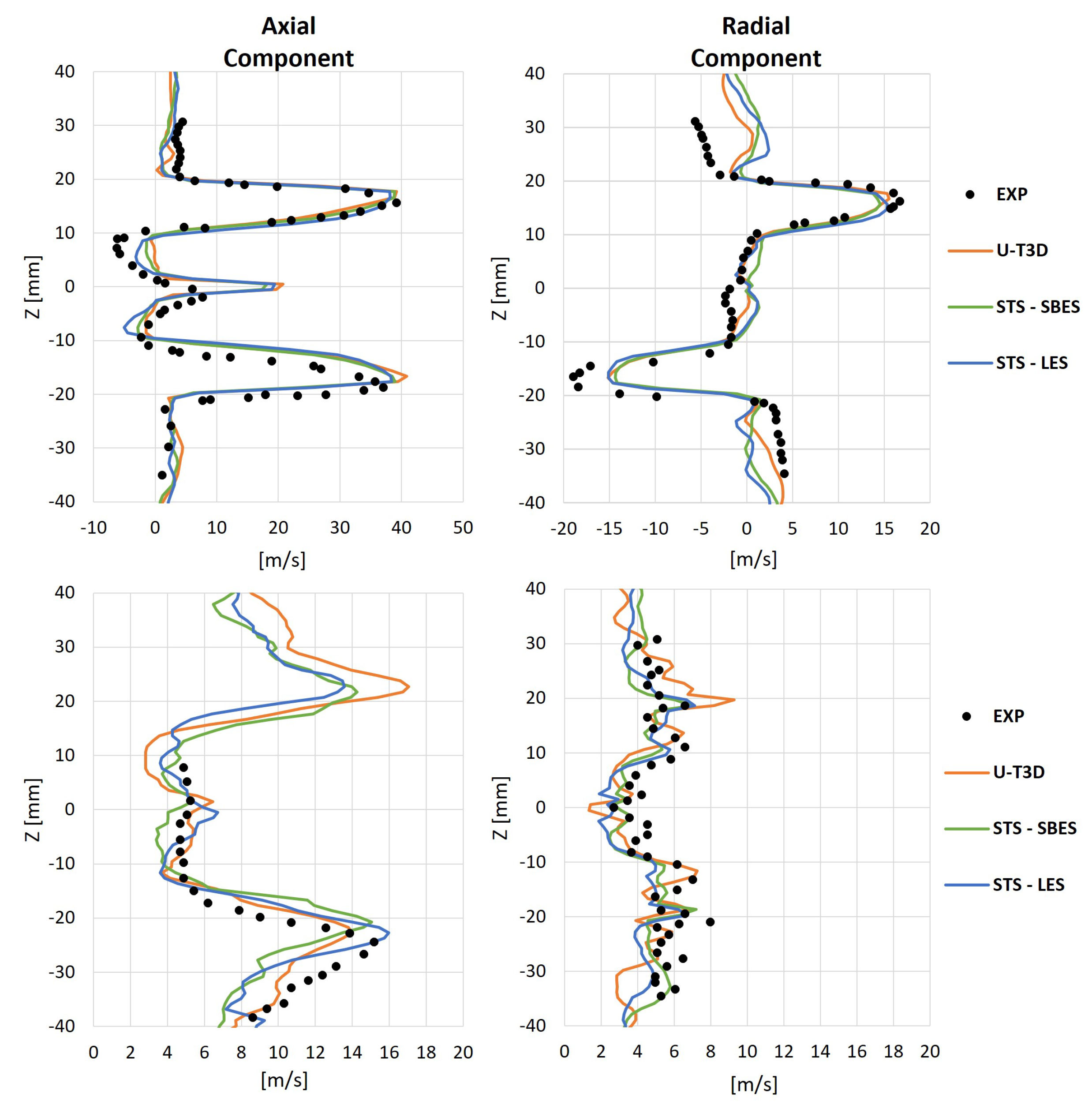
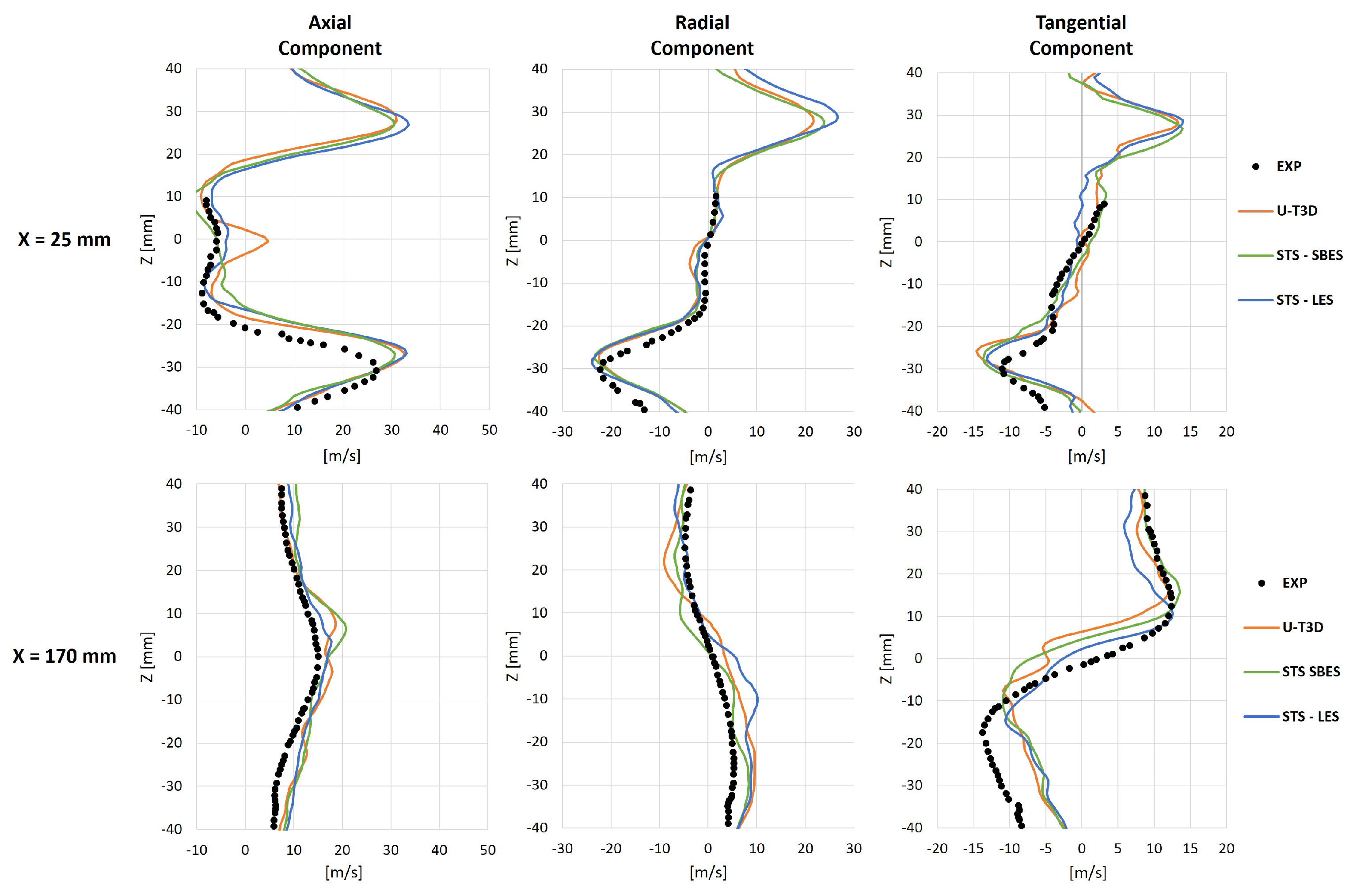
5.1. Gas Phase Velocity Fields
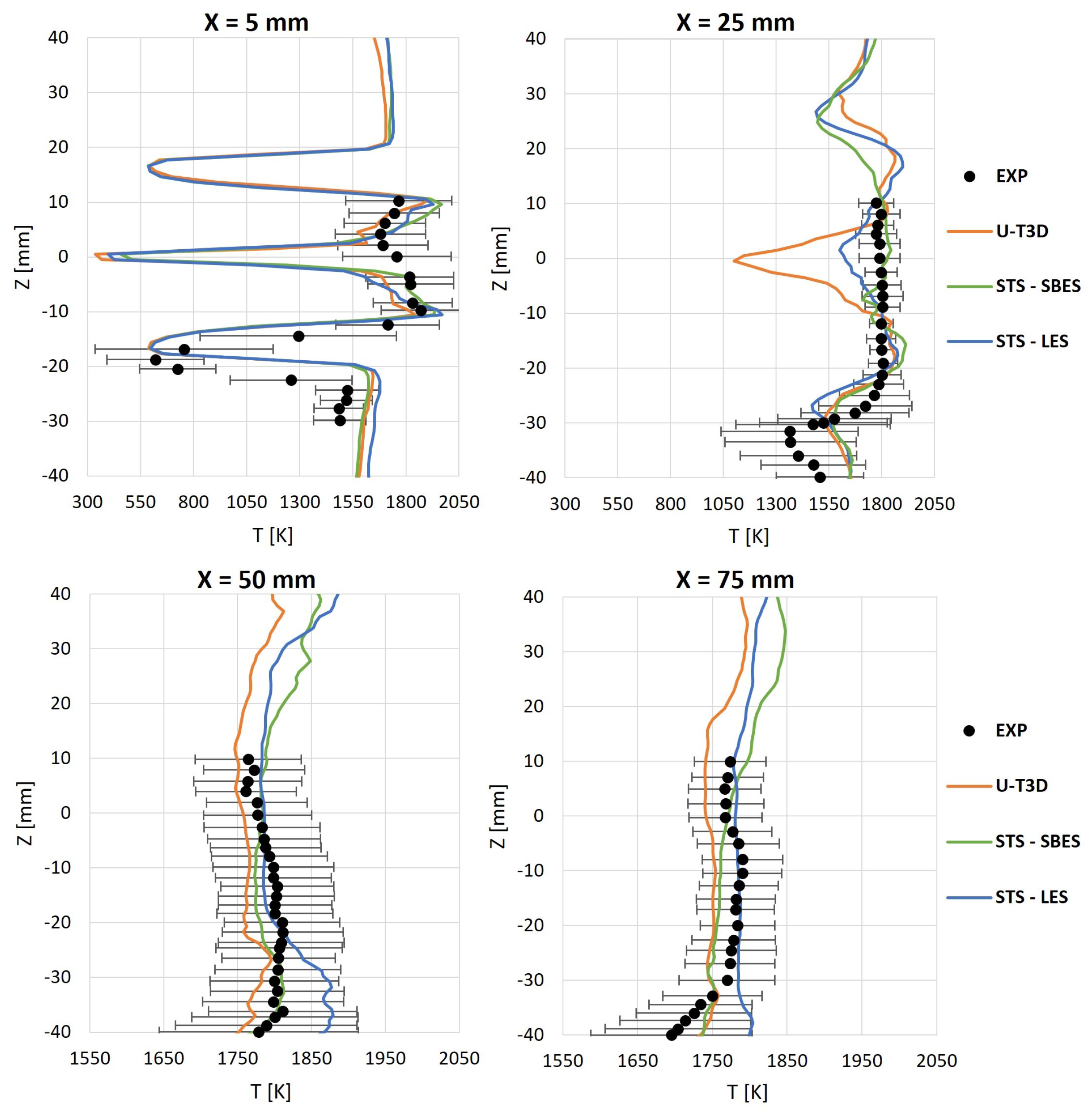
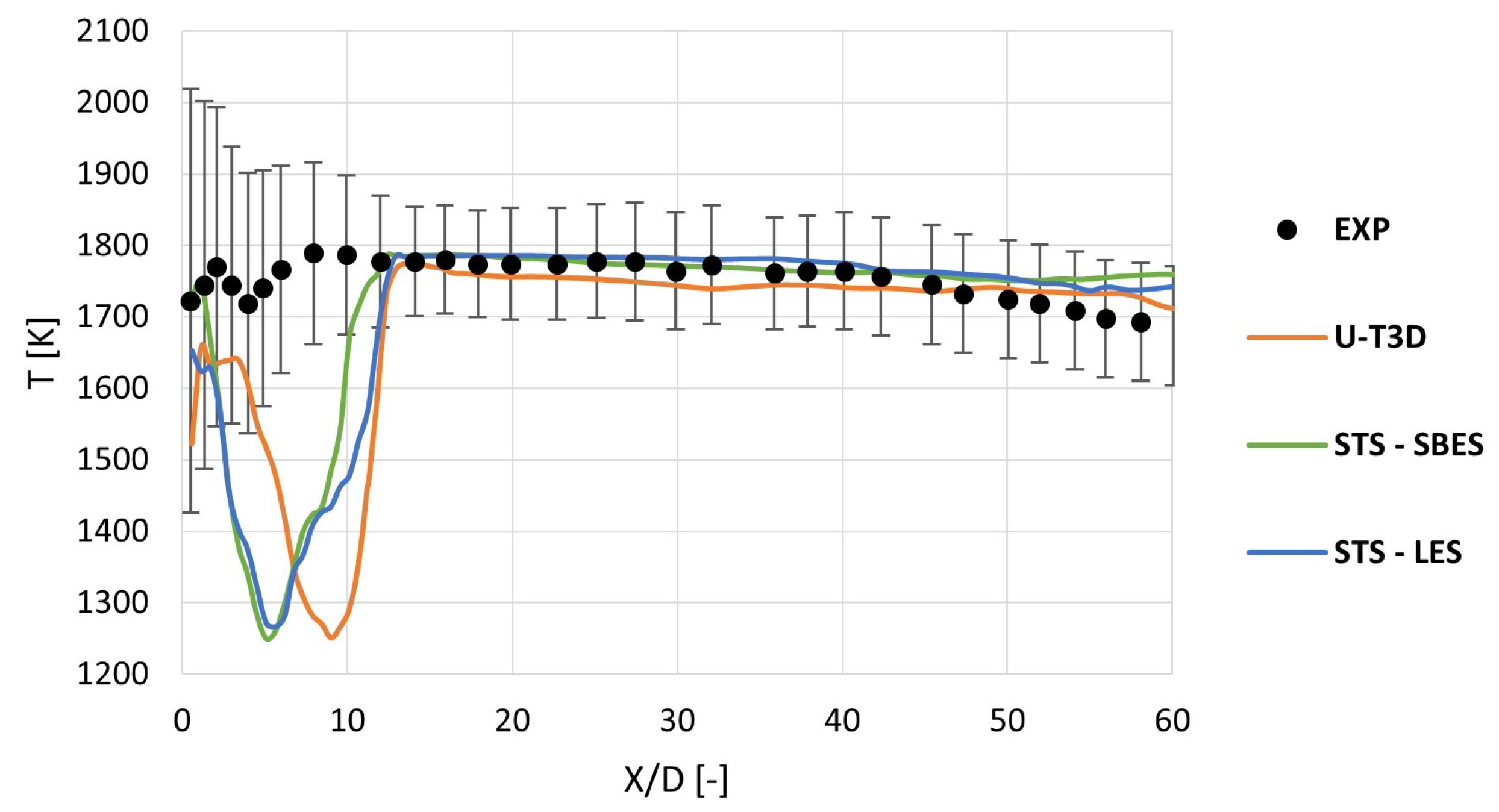
5.2. Gas Phase Temperature Fields
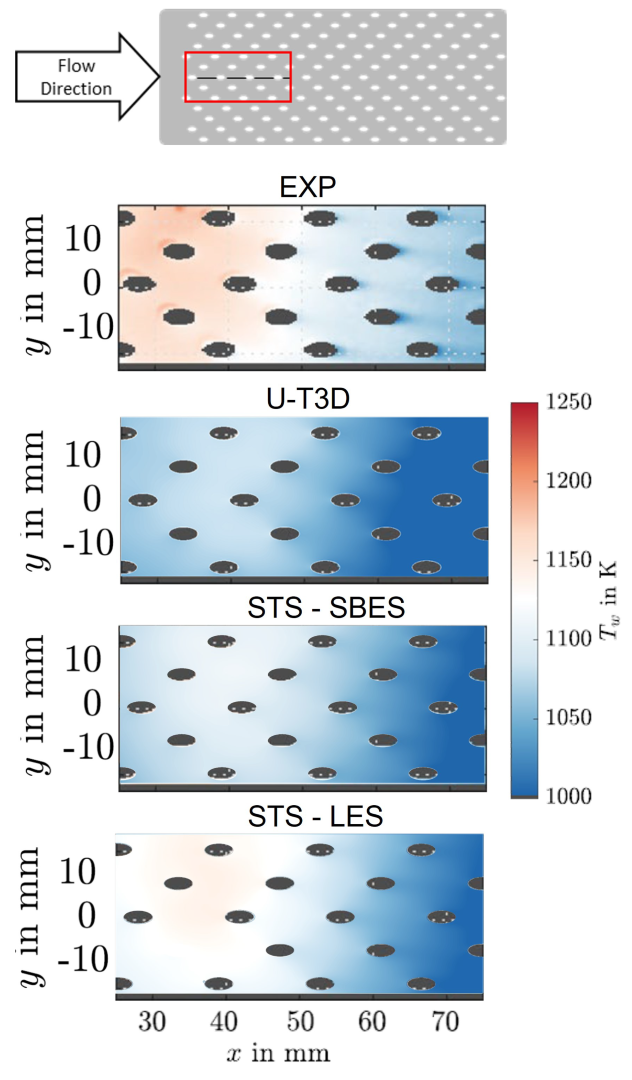
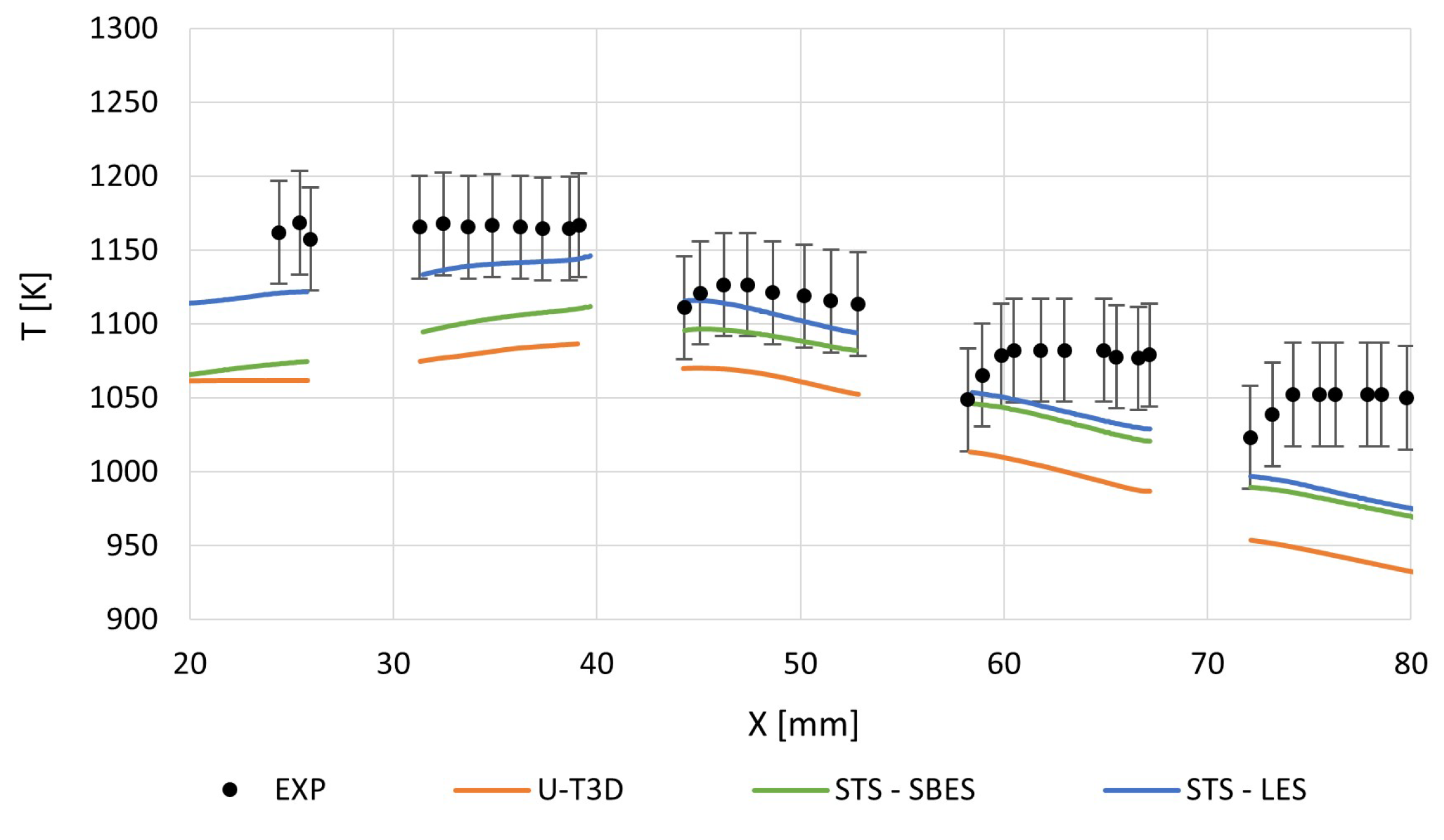
5.3. Effusion-Cooled Plate Wall Temperature
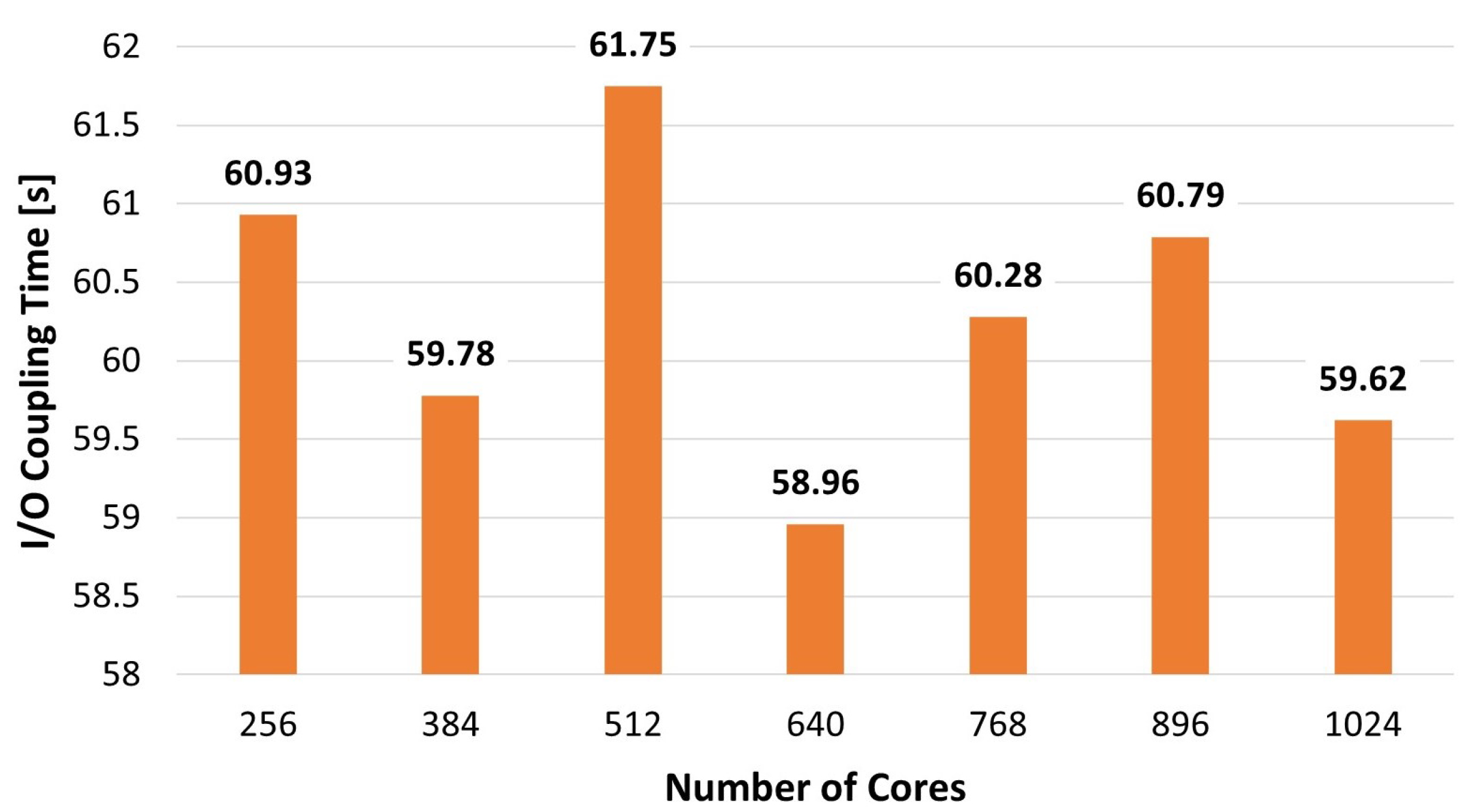
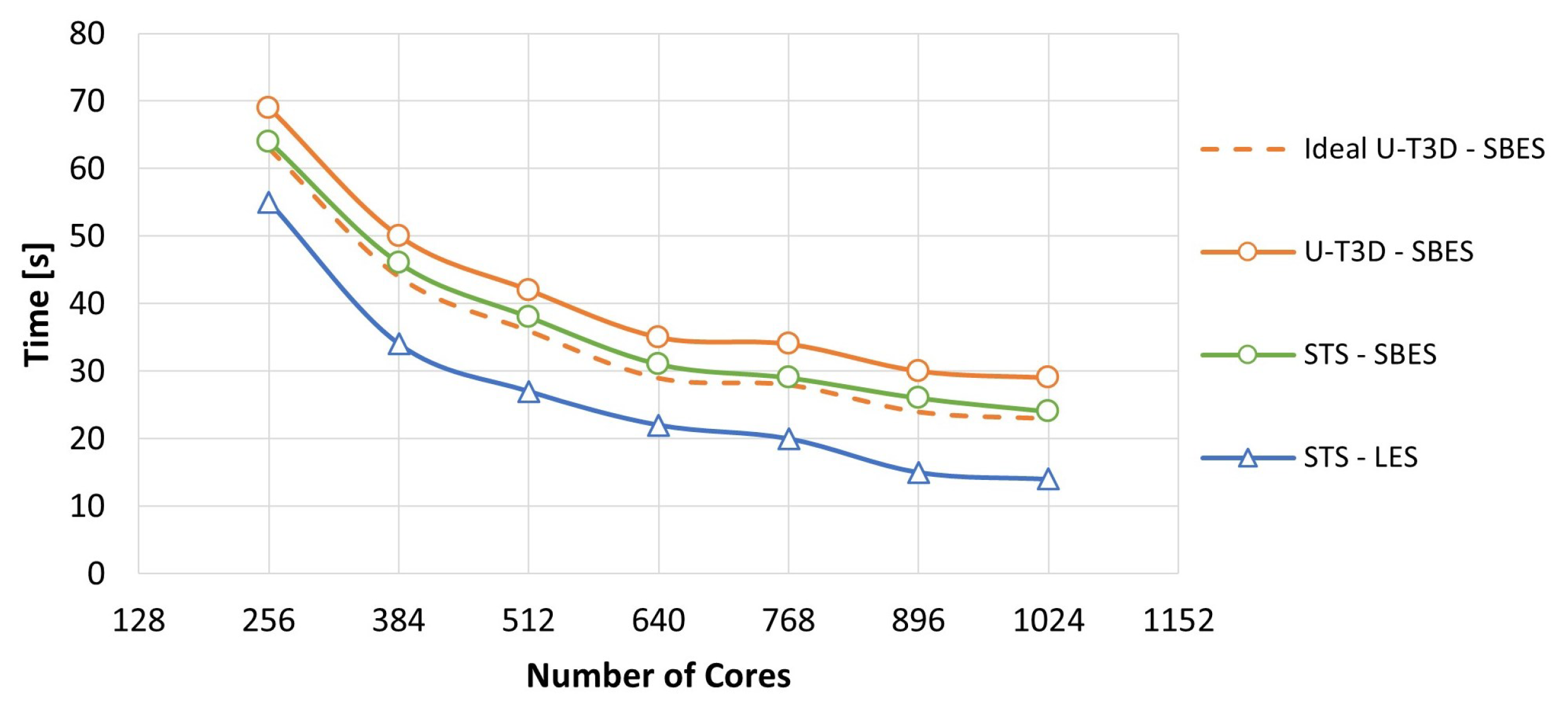
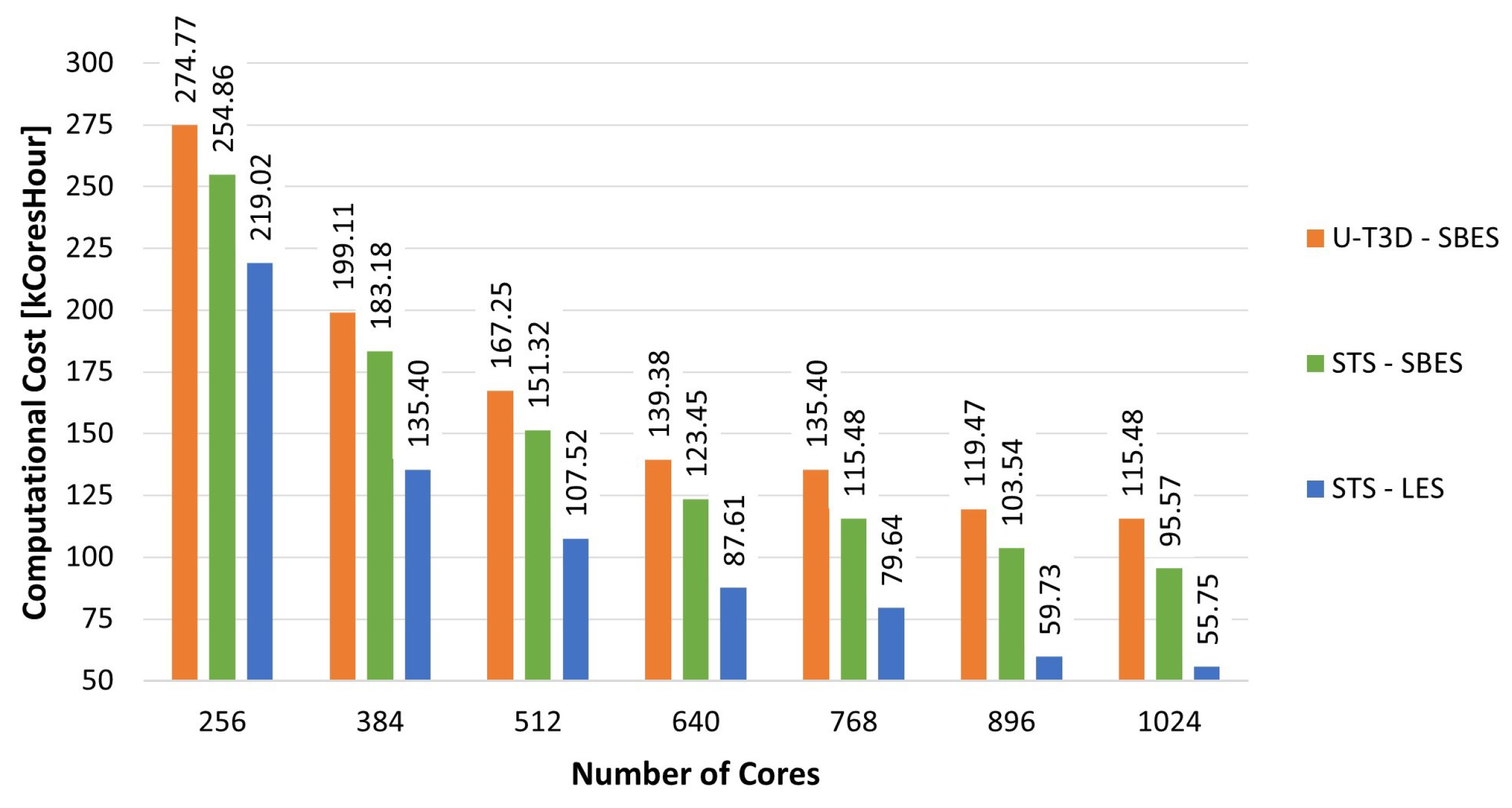
5.4. Computational Cost Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CHT | Conjugate Heat Transfer |
| DES | Detached Eddy Simulation |
| FGM | Flamelet Generated Manifold |
| GT | Gas Turbine |
| IRZ | Inner Recirculation Zone |
| LES | Large Eddy Simulations |
| OPR | Overall Pressure Ratio |
| ORZ | Outer Recirculation Zone |
| RANS | Reynolds Averaged Navier-Stokes |
| RSM | Reaktive Strömungen und Messtechnik |
| SAS | Scale-Adaptive Simulation |
| SBES | Stress-Blended Eddy Simulation |
| TIT | Turbine Inlet Temperature |
| UDF | User Defined Function |
References
- Lefebvre, A.H.; Ballal, D.R. Gas Turbine Combustion: Alternative Fuels and Emissions; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- McGuirk, J. The aerodynamic challenges of aeroengine gas-turbine combustion systems. Aeronaut. J. 2014, 118, 557–599. [Google Scholar] [CrossRef]
- Wurm, B.; Schulz, A.; Bauer, H.J.; Gerendas, M. Cooling efficiency for assessing the cooling performance of an effusion cooled combustor liner. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, San Antonio, TX, USA, 3–7 June 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013; Volume 55157, p. V03BT13A010. [Google Scholar]
- Wurm, B.; Schulz, A.; Bauer, H.J.; Gerendas, M. Impact of swirl flow on the cooling performance of an effusion cooled combustor liner. J. Eng. Gas Turbines Power 2012, 134, 121503. [Google Scholar] [CrossRef]
- Andrews, G.; Asere, A.; Gupta, M.; Mkpadi, M. Full coverage discrete hole film cooling: The influence of hole size. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Houston, TX, USA, 18–21 March 1985; American Society of Mechanical Engineers: New York, NY, USA, 1985; Volume 79405, p. V003T09A003. [Google Scholar]
- Andrews, G.; Bazdidi-Tehrani, F. Small diameter film cooling hole heat transfer: The influence of the number of holes. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Orlando, FL, USA, 3–6 June 1989; American Society of Mechanical Engineers: New York, NY, USA, 1989; Volume 79160, p. V004T08A002. [Google Scholar]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion; RT Edwards, Inc.: Dallas, TX, USA, 2005. [Google Scholar]
- Boudier, G.; Gicquel, L.; Poinsot, T. Effects of mesh resolution on large eddy simulation of reacting flows in complex geometry combustors. Combust. Flame 2008, 155, 196–214. [Google Scholar] [CrossRef]
- Oyarzun, G.; Mira, D.; Houzeaux, G. Performance assessment of CUDA and OpenACC in large scale combustion simulations. arXiv 2021, arXiv:2107.11541. [Google Scholar]
- Mira, D.; Pérez-Sánchez, E.J.; Borrell, R.; Houzeaux, G. HPC-enabling technologies for high-fidelity combustion simulations. Proc. Combust. Inst. 2022, in press. [Google Scholar] [CrossRef]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Menter, F. Stress-blended eddy simulation (SBES)—A new paradigm in hybrid RANS-LES modeling. In Proceedings of the Symposium on Hybrid RANS-LES Methods, Strasbourg, France, 26–28 September 2016; pp. 27–37. [Google Scholar]
- He, L.; Fadl, M. Multi-scale time integration for transient conjugate heat transfer. Int. J. Numer. Methods Fluids 2017, 83, 887–904. [Google Scholar] [CrossRef]
- Fadl, M.; He, L. On LES based conjugate heat transfer procedure for transient natural convection. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Charlotte, NC, USA, 26–30 June 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 50879, p. V05AT10A002. [Google Scholar]
- Berger, S.; Richard, S.; Staffelbach, G.; Duchaine, F.; Gicquel, L. Aerothermal prediction of an aeronautical combustion chamber based on the coupling of large eddy simulation, solid conduction and radiation solvers. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Montreal, QC, Canada, 15–19 June 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56710, p. V05AT10A007. [Google Scholar]
- Jaure, S.; Duchaine, F.; Staffelbach, G.; Gicquel, L. Massively parallel conjugate heat transfer methods relying on large eddy simulation applied to an aeronautical combustor. Comput. Sci. Discov. 2013, 6, 015008. [Google Scholar] [CrossRef]
- Koren, C.; Vicquelin, R.; Gicquel, O. Self-adaptive coupling frequency for unsteady coupled conjugate heat transfer simulations. Int. J. Therm. Sci. 2017, 118, 340–354. [Google Scholar] [CrossRef]
- ANSYS. Fluent 19.3 Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Mazzei, L.; Andreini, A.; Facchini, B.; Bellocci, L. A 3d Coupled Approach for the Thermal Design of Aero-Engine Combustor Liners. In Proceedings of the Fluids Engineering Division Summer Meeting, Washington, DC, USA, 10–14 July 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 49798. [Google Scholar]
- Bertini, D.; Mazzei, L.; Puggelli, S.; Andreini, A.; Facchini, B.; Bellocci, L.; Santoriello, A. Numerical and experimental investigation on an effusion-cooled lean burn aeronautical combustor: Aerothermal field and metal temperature. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Oslo, Norway, 11–15 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51104, p. V05CT17A010. [Google Scholar]
- Bertini, D.; Mazzei, L.; Andreini, A.; Facchini, B. Multiphysics numerical investigation of an aeronautical lean burn combustor. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Phoenix, AZ, USA, 17–21 June 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 58653, p. V05BT17A004. [Google Scholar]
- Bertini, D.; Mazzei, L.; Andreini, A. Prediction of Liner Metal Temperature of an Aeroengine Combustor with Multi-Physics Scale-Resolving CFD. Entropy 2021, 23, 901. [Google Scholar] [CrossRef]
- Paccati, S.; Bertini, D.; Mazzei, L.; Puggelli, S.; Andreini, A. Large-Eddy Simulation of a Model Aero-Engine Sooting Flame With a Multiphysics Approach. Flow Turbul. Combust. 2021, 106, 1329–1354. [Google Scholar] [CrossRef]
- Hermann, J.; Greifenstein, M.; Boehm, B.; Dreizler, A. Experimental investigation of global combustion characteristics in an effusion cooled single sector model gas turbine combustor. Flow Turbul. Combust. 2019, 102, 1025–1052. [Google Scholar] [CrossRef]
- Greifenstein, M.; Hermann, J.; Boehm, B.; Dreizler, A. Flame–cooling air interaction in an effusion-cooled model gas turbine combustor at elevated pressure. Exp. Fluids 2019, 60, 1–13. [Google Scholar] [CrossRef]
- Greifenstein, M.; Dreizler, A. Investigation of mixing processes of effusion cooling air and main flow in a single sector model gas turbine combustor at elevated pressure. Int. J. Heat Fluid Flow 2021, 88, 108768. [Google Scholar] [CrossRef]
- Amerini, A.; Paccati, S.; Mazzei, L.; Andreini, A. Assessment of a Conjugate Heat Transfer Method on an Effusion Cooled Combustor Operated With a Swirl Stabilized Partially Premixed Flame. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Rotterdam, The Netherlands, 13–17 June 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022; Volume 86038, p. V06AT11A001. [Google Scholar]
- Andreini, A.; Da Soghe, R.; Facchini, B.; Mazzei, L.; Colantuoni, S.; Turrini, F. Local source based CFD modeling of effusion cooling holes: Validation and application to an actual combustor test case. J. Eng. Gas Turbines Power 2014, 136, 011506. [Google Scholar] [CrossRef]
- Armaly, B.F.; Durst, F.; Pereira, J.; Schönung, B. Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 1983, 127, 473–496. [Google Scholar] [CrossRef]
- Lee, T.; Mateescu, D. Experimental and numerical investigation of 2-D backward-facing step flow. J. Fluids Struct. 1998, 12, 703–716. [Google Scholar] [CrossRef]
- Barri, M.; El Khoury, G.K.; Andersson, H.I.; Pettersen, B. DNS of backward-facing step flow with fully turbulent inflow. Int. J. Numer. Methods Fluids 2010, 64, 777–792. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, H.; Wang, X. Large eddy simulation of particle response to turbulence along its trajectory in a backward-facing step turbulent flow. Int. J. Heat Mass Transf. 2006, 49, 415–420. [Google Scholar] [CrossRef]
- Spazzini, P.G.; Iuso, G.; Onorato, M.; Zurlo, N.; Di Cicca, G. Unsteady behavior of back-facing step flow. Exp. Fluids 2001, 30, 551–561. [Google Scholar] [CrossRef]
- Velazquez, A.; Arias, J.; Mendez, B. Laminar heat transfer enhancement downstream of a backward facing step by using a pulsating flow. Int. J. Heat Mass Transf. 2008, 51, 2075–2089. [Google Scholar] [CrossRef]
- Xu, J.; Zou, S.; Inaoka, K.; Xi, G. Effect of Reynolds number on flow and heat transfer in incompressible forced convection over a 3D backward-facing step. Int. J. Refrig. 2017, 79, 164–175. [Google Scholar] [CrossRef]
- Avancha, R.V.; Pletcher, R.H. Large eddy simulation of the turbulent flow past a backward-facing step with heat transfer and property variations. Int. J. Heat Fluid Flow 2002, 23, 601–614. [Google Scholar] [CrossRef]
- Chen, L.; Asai, K.; Nonomura, T.; Xi, G.; Liu, T. A review of backward-facing step (BFS) flow mechanisms, heat transfer and control. Therm. Sci. Eng. Prog. 2018, 6, 194–216. [Google Scholar] [CrossRef]
- Menter, F. Zonal two equation kw turbulence models for aerodynamic flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; p. 2906. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Al-Abdeli, Y.M.; Masri, A.R. Review of laboratory swirl burners and experiments for model validation. Exp. Therm. Fluid Sci. 2015, 69, 178–196. [Google Scholar] [CrossRef]
- Heeger, C.; Gordon, R.; Tummers, M.; Sattelmayer, T.; Dreizler, A. Experimental analysis of flashback in lean premixed swirling flames: Upstream flame propagation. Exp. Fluids 2010, 49, 853–863. [Google Scholar] [CrossRef]
- Nassini, P.C.; Pampaloni, D.; Andreini, A. Inclusion of flame stretch and heat loss in LES combustion model. AIP Conf. Proc. 2019, 2191, 020119. [Google Scholar]
- ANSYS. Fluent 21.1 Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Meneveau, C.; Lund, T.S. The dynamic Smagorinsky model and scale-dependent coefficients in the viscous range of turbulence. Phys. Fluids 1997, 9, 3932–3934. [Google Scholar] [CrossRef]
- Pope, S.B. Small scales, many species and the manifold challenges of turbulent combustion. Proc. Combust. Inst. 2013, 34, 1–31. [Google Scholar] [CrossRef]
- Both, A.; Mira Martínez, D.; Lehmkuhl Barba, O. Assessment of tabulated chemistry models for the les of a model aero-engine combustor. In Proceedings of the Global Power and Propulsion Society (GPPS Chania22), Zurich, Switzerland, 18–20 September 2022. [Google Scholar]
- Van Oijen, J.; Donini, A.; Bastiaans, R.; ten Thije Boonkkamp, J.; De Goey, L. State-of-the-art in premixed combustion modeling using flamelet generated manifolds. Prog. Energy Combust. Sci. 2016, 57, 30–74. [Google Scholar] [CrossRef]
- Donini, A.; Bastiaans, R.J.; van Oijen, J.A.; de Goey, L.P.H. The implementation of five-dimensional FGM combustion model for the simulation of a gas turbine model combustor. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Montreal, QC, Canada, 15–19 June 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56680, p. V04AT04A007. [Google Scholar]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C.J.; et al. GRI3.0 Mechanism. Available online: https://chemistry.cerfacs.fr/en/chemical-database/mechanisms-list/gri-mech-3-0/ (accessed on 30 September 2019).
- Goodwin, D.G.; Speth, R.L.; Moffat, H.K.; Weber, B.W. Cantera: An Object-oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. Version 2.5.1. 2021. Available online: https://www.cantera.org (accessed on 30 September 2019).
- Chanson, H. Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Nassini, P.C.; Pampaloni, D.; Meloni, R.; Andreini, A. Lean blow-out prediction in an industrial gas turbine combustor through a LES-based CFD analysis. Combust. Flame 2021, 229, 111391. [Google Scholar] [CrossRef]
- Andreini, A.; Becchi, R.; Facchini, B.; Picchi, A.; Peschiulli, A. The effect of effusion holes inclination angle on the adiabatic film cooling effectiveness in a three-sector gas turbine combustor rig with a realistic swirling flow. Int. J. Therm. Sci. 2017, 121, 75–88. [Google Scholar]
- Andreini, A.; Becchi, R.; Facchini, B.; Mazzei, L.; Picchi, A.; Turrini, F. Adiabatic Effectiveness and Flow Field Measurements in a Realistic Effusion Cooled Lean Burn Combustor. J. Eng. Gas Turbines Power 2015, 138, 031506. [Google Scholar] [CrossRef]
- Lenzi, T.; Picchi, A.; Becchi, R.; Andreini, A.; Facchini, B. Swirling main flow effects on film cooling: Time resolved adiabatic effectiveness measurements in a gas turbine combustor model. Int. J. Heat Mass Transf. 2023, 200, 123554. [Google Scholar] [CrossRef]
- Li, P.; Eckels, S.J.; Zhang, N.; Mann, G.W. Effects of Parallel Processing on Large Eddy Simulations in ANSYS Fluent. In Proceedings of the Fluids Engineering Division Summer Meeting, Washington, DC, USA, 10–14 July 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 50299, p. V01BT26A004. [Google Scholar]











| Name | Symbol | Value | Unit |
|---|---|---|---|
| Density | 100 | kg/m | |
| Specific Heat | 50 | kJ/kgK | |
| Thermal Conductivity | 5 | W/mK |
| Name | Symbol | Value | Unit |
|---|---|---|---|
| Operating pressure | P | 0.25 | MPa |
| Swirl number | S | 0.7 | − |
| Oxidizer mass flow | 30 | g/s | |
| Oxidizer temperature | 623 | K | |
| Eff. cooling mass flow | 7.5 | g/s | |
| Eff. cooling temperature | 623 | K | |
| Fuel mass flow | 1.128 | g/s | |
| Pilot fuel temperature | 333 | K | |
| Staging ratio | 10% | − |
| Parameters | Specifications |
|---|---|
| Processors | 2× AMD ZEN 2 EPYC 7H12 2.6 GHz |
| Number of Cores per Compute Node | 128 |
| RAM per Compute Node | 256 GB |
| Max Memory Bandwidth | 190.7 GiB/s |
| Interconnection | Infiniband HDR 200 Gb/s |
| Coupled Interfaces | Elements Number |
|---|---|
| Hot side effusion-cooled plate | 500k |
| Effusion-cooled holes | 635k |
| Cold side effusion-cooled plate | 500k |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amerini, A.; Paccati, S.; Andreini, A. Computational Optimization of a Loosely-Coupled Strategy for Scale-Resolving CHT CFD Simulation of Gas Turbine Combustors. Energies 2023, 16, 1664. https://doi.org/10.3390/en16041664
Amerini A, Paccati S, Andreini A. Computational Optimization of a Loosely-Coupled Strategy for Scale-Resolving CHT CFD Simulation of Gas Turbine Combustors. Energies. 2023; 16(4):1664. https://doi.org/10.3390/en16041664
Chicago/Turabian StyleAmerini, Alberto, Simone Paccati, and Antonio Andreini. 2023. "Computational Optimization of a Loosely-Coupled Strategy for Scale-Resolving CHT CFD Simulation of Gas Turbine Combustors" Energies 16, no. 4: 1664. https://doi.org/10.3390/en16041664







