The evolution of variables representative of the mean profile, i.e., the wall stress and the velocity field, is explored first. This is followed by a discussion on the integral flow parameters, which includes boundary layer thickness , shape factor , and the internal layer height . A connection to the Clauser parameter is also made within this discourse to identify the fetch length at which an equilibrium emerges. An examination of the observed turbulence stresses and the budget terms of the TKE equation follows next. The analysis of the turbulence stresses and TKE budgets is buffeted by an inspection of the quadrant events and the turbulence bursting process. Finally, visualizations of fluctuations and vortical filaments are presented at the end along with an assessment of the integral length and time scales.
3.1. Frictional Velocity
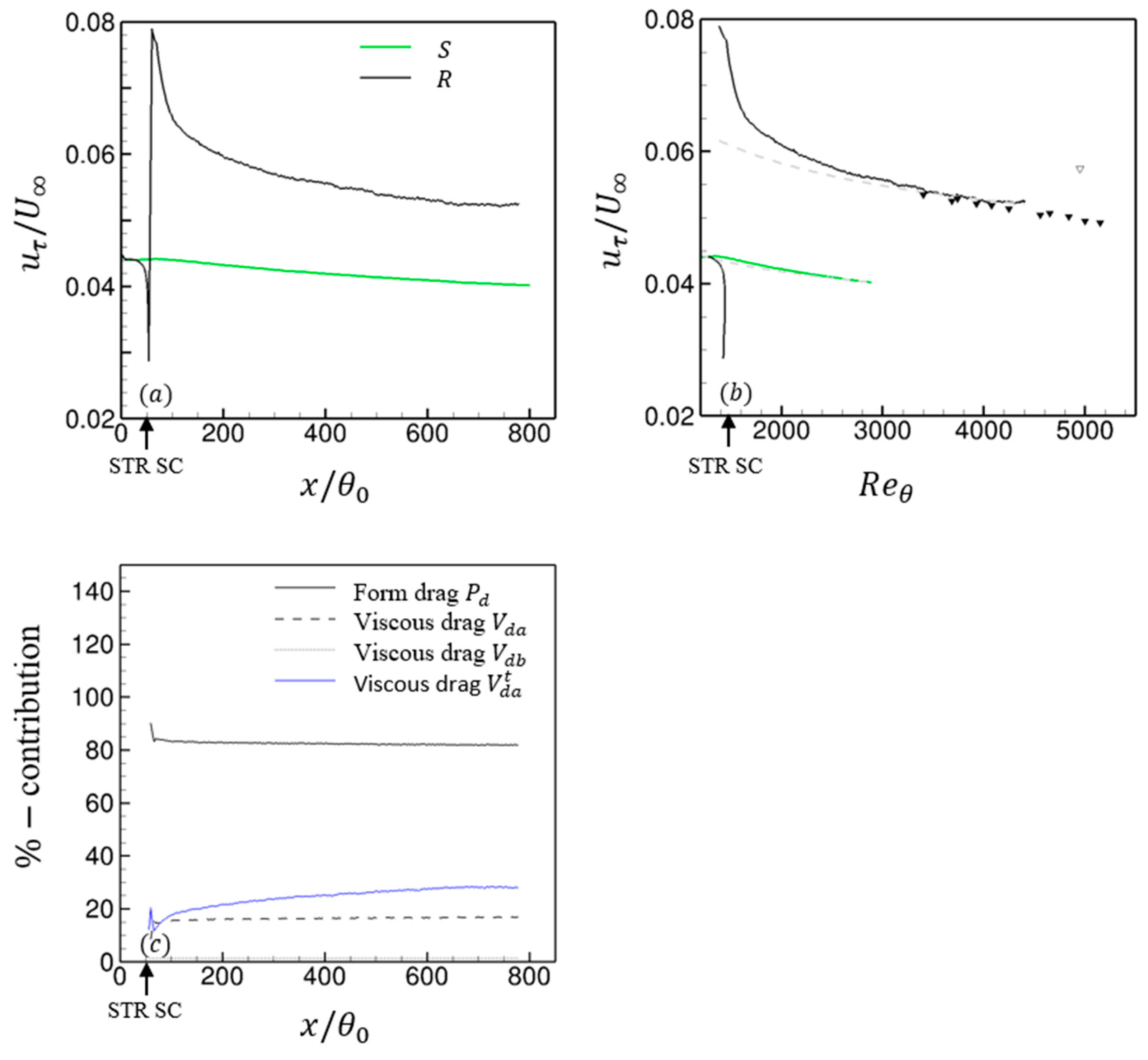
Figure 5a,b present the streamwise development of
as a function of the streamwise fetch
and
, respectively. Above rough walls, frictional velocity consists of contributions from both viscous drag
and form drag
, i.e.,
. Here, the viscous drag
can be broken down into two parts:
and
. The former comprises viscous drag from the no-slip portion of the rough wall at
and top of the roughness elements at
. The latter includes viscous drag from the
sides of these roughness elements. On the other hand,
is given by
where
is the area of the front
and back
faces of the roughness elements. Included in
Figure 5b are correlation curves of the form
[
30] with
and
for cases
and
, respectively. The
curve for case
is within
of the levels indicated by the correlation curve. Reference data from the wind-tunnel measurements by Brzek et al. [
31] and Volino, Schultz, and Flack [
32] on TBLs above rough walls are also provided in
Figure 5b.
The streamwise evolution of frictional velocity for case
overlaps the reference case curve initially before dropping off sharply upstream of the step change at
. This sharp reduction in
is due to the velocity profile becoming unstable. Momentum redistribution occurs as the TBL approaches the first set of roughness elements and induces a sharp outward ejection of fluid, which is also reflected by an abrupt rise in both
and
upstream of the step change. Downstream of the STR transition, frictional velocity increases to a magnitude above the equilibrium smooth and rough-wall levels, but then rapidly relaxes towards an asymptote as
increases. Unlike RTS boundary layers where the equilibrium frictional velocity curve after the step change is known apriori [
33], the situation is less clear in the present case. However, using the logarithmic correlation curve from the smooth TBL albeit at different
values as an estimate of recovery, we can deduce that
has relaxed to within 5% of the correlation curve with
by
. This streamwise fetch is about
downstream of the STR step change, which is notably smaller than the value of
suggested by Li et al. [
33] for the recovery of skin friction in their boundary layer experiments. Beyond
, frictional velocity for the rough surface roughly falls on the dashed correlation curve in
Figure 5b. It is therefore decaying at approximately the same rate as the reference case. Using the frictional velocity at inflow as the reference
for the upstream surface (
) and
at
for case
as a measure of the recovered frictional velocity for the downstream surface (
, the frictional velocity ratio for the two surfaces is
. This ratio is lower than the estimated value of
from the DNS by Lee [
12] but falls within the range of
–
determined from the STR experiments by Gul and Ganapathisubramani [
34]. It must be noted that Lee [
12] employed square bars as their roughness elements, while both the upstream and downstream surfaces in the STR experiments by Gul and Ganapathisubramani [
34] utilized sandgrain roughness.
The relative percentage contribution to the total skin friction
for case
from the three sources is provided in
Figure 5c. An equilibrium among
, and
is established immediately after the step change, and it shows negligible variation along the entire streamwise fetch; this equilibrium stands at
and
. Above a transitionally rough surface, on the other hand, the fractional contribution due to
would gradually decrease as
increases. While it is clear that
for the present rough wall is composed predominantly of form drag, an estimate of friction velocity relying exclusively on
will incur a 10% error. Moreover,
Figure 5c implies that as
decreases with an increasing Reynolds number, the absolute values of both
and
decrease as well.
is further decomposed into its constituents to highlight the amount of viscous stress contributed by horizontal no slip surfaces at
y = 0 and
y =
k. The blue line in
Figure 5c shows that only about 15–25% of
is from the top of the roughness elements (
.
3.2. Mean Velocity
The wall-normal variation of mean velocity using outer and defect-law scaling is presented in
Figure 6. Unsurprisingly, roughness immediately retards the entire TBL and pushes the boundary layer fluid further way from the surface, which is reflected by an increased
δ as will be discussed momentarily. Here, roughness effectively acts to make the boundary layer less stable by increasing the wake region of the velocity profile. This is indicated by the larger intercept of the logarithmic defect-layer profile.
For comparative purposes, rough surfaces under equilibrium conditions of different texture and type are characterized by ascribing them an effective sand grain roughness length scale
> 70 for fully rough surfaces). This requires equating the fitted logarithmic layer to the logarithmic profile reported by Nikuradse [
35]. Another aspect worth highlighting is the need to identify a virtual origin for the underlying undulating rough wall. A vertical shift of the rough surface by a distance
, i.e.,
, is often used to produce a logarithmic fit with an acceptable von-Karman constant
–
[
21,
36,
37]. The equation for the logarithmic fit in the overlap layer for fully rough walls can be written as
In this study,
is evaluated using the method by Jackson [
38] that uses the centroid of mean pressure forces on the roughness elements. Jackson [
38] offered a physical notion for the virtual origin
by defining it as the height at which mean pressure drag appears to act. In this work,
is determined using
The centroid of mean pressure drag lies at
, and it is independent of the streamwise fetch.
Figure 7 plots the distribution of
on the windward and leeward faces of the roughness elements at two streamwise locations:
and
. The windward face consists of two high-pressure regions: one is centered at the base and the other at the three-quarter height from the base. Their intensity
decreases with a growing fetch length. Negative pressure zones occupy the spanwise edges on the windward face. Only a single negative pressure zone, centered at
, is present on the leeward face. It is shouldered by even stronger negative pressure regions with their centers near the top of the roughness element. The intensity of the pressure distribution on the leeward side becomes progressively more negative with an increasing streamwise distance. Experimentally measuring similar pressure distribution profiles on roughness elements is a challenging task. However, the results presented here are consistent with the distributions observed on the windward and leeward faces of cuboid-shaped urban structures immersed in ABLs [
39].
With an estimate of
attained, the von-Karman constant
and the wall intercept
are the two remaining unknown parameters. A logarithmic fit at each
station was obtained by fixing
and varying
;
can then be determined by
The wall-normal variation of inner-scaled mean velocity at several discrete streamwise stations is plotted in
Figure 8. The gross effect of an increased
and modified wall layer above
is to shift the inner-scaled mean velocity downward, which is evidenced by a lower wall intercept of the logarithmic layer. An incipient logarithmic layer is first identifiable at
. This occurs significantly earlier than the corresponding observation for RTS flows at a comparable perturbation strength [
7,
9]. The logarithmic layer has an unchanging wall intercept at
. Its lower limit is defined at
70–80, which corresponds to the height at which the mean momentum transfer by viscous diffusion first becomes negligible [
36]. Initially, the upper limit of the logarithmic layer does not extend to the generally accepted height of
. However, it continuously increases as the equilibrium layer develops and has reached
by
. Note that due to a growing TBL, the upper limit of the log law (
, after complete adjustment of the inner layer, is at
at
respectively. The constancy of
along
and
–
implies that the TBL falls in the fully rough category. The strength of perturbation for a step change in the surface condition is typically expressed as
). Here,
and
are a measure of the surface length scale
for the upstream and downstream surfaces, respectively (see the equation for
given above). Using the
at inflow and
as indicators of
and
for the STR case, respectively, the estimated
. The perturbation introduced by the STR change in the present setup is weaker than the one reported by Antonia and Luxton [
4], i.e.,
, for their experiment with rib-type roughness. Our perturbation strength is comparable to the largest absolute values (
reported by Gul and Ganapathisubramani [
34] for their RTS experiments. Their
for the STR cases is comparatively smaller as these experiments involved step change from one rough surface to another. The extent of the roughness sublayer is determined as the height up until which horizontal inhomogeneity in
inside the equilibrium region is identifiable. It is about
–
, which compares favorably with the estimates found in the literature [
7,
40,
41].
The inner-scaled mean velocity profile—when written as a sum of laws of the wall and wake—can be recast into the following equation at the outer edge of the defect layer
):
In the above equation,
is the wake strength parameter. The streamwise variation of
(
Figure 8) is between 0.46 and 0.56 for the canonical smooth-wall TBL (case
), and it agrees well with the estimated values from the data by Schlatter and Örlü [
20]. Their
and
values are at
0 and
, respectively. As noted earlier, the dominant effect on the outer layer of introducing a rough surface is the enhancement of the velocity-defect-law region. Consequently, the wake strength parameter is increased above the smooth wall level. It grows from
to
between
, but the augmentation beyond
from
to 0.90 is relatively modest. These levels for the wake parameter agree favorably with
from the rough-wall TBL by Hanson and Ganapathisubramani [
6]. Among other tripping conditions, Marusic et al. [
42] studied the response of a smooth-wall ZPG boundary layer after it was perturbed using a grit sandpaper. The strong initial response for
seen here is consistent with their experiment. Additionally,
for case
is plotted only for
because a valid and complete log-law region first emerges at
. The law of the wake by Coles [
43] can be utilized to model the mean velocity in the outer layer above the rough surface by:
As shown in
Figure 9 via red lines, the outer layer velocity profile is well approximated by the above equation, where
and
is extracted from
Figure 8. The approximation faithfully models the DNS profile all the way down to
–
for
. However, it deviates from the DNS predictions in the lower part of the outer layer at the earliest rough-wall station in
Figure 9. It is important to note that Coles’ law of the wake is meant for both equilibrium and non-equilibrium turbulent-boundary-layer profiles. The results above suggests that while
across the entire TBL is in a ‘virtual’ equilibrium by
(i.e., at
), mean velocity in the inner layer adjusts much earlier (i.e., by
or in other words
). This point will be elaborated upon further in later sections.
3.3. Integral Parameters
The variation of several integral flow parameters along the fetch length is presented in
Figure 10. The boundary layer thickness at the STR step change
is
times the roughness height, and this ratio grows to
35 by
As mentioned previously, roughness pushes the boundary layer fluid away from the wall causing
to grow more quickly in comparison to the smooth wall. While the growth of displacement thickness
and momentum thickness
for the two cases overlap initially over the smooth wall portion of case
, both parameters diverged slightly upstream of the step change at
. The overlap persists much longer for
, only differing marginally for the two cases at
. This small divergence of the integral parameters upstream of STR transition is a consequence of moderately different non-local effects that the pressure field creates when surface roughness is introduced.
After the STR transition, both
and
grow more rapidly above the rough wall and are
and
times their smooth-wall counterparts at
, respectively. This forces the shape factor
to become larger than the smooth-wall level. Additionally, the increase in both
and
for the rough wall as opposed to the equilibrium smooth wall implies that the growth in the boundary layer thickness is not compensated by a corresponding increase in entrainment into the boundary layer. Both effects—the growth of
and the increase in
and
—are reflective of mean velocity profiles with a larger deficit (
Figure 6). The shape factor
initially grows rapidly to as high as
after the step change before beginning to decrease gently around
, which corresponds closely with the fetch length for near-complete recovery of
in the inner layer. Furthermore, the rate at which
decays is somewhat higher than the one seen above the smooth wall. This is consistent with the larger
for case
and its higher growth rate along the streamwise direction. The trends and values presented here regarding the influence of roughness on integral parameters of the boundary layer, i.e., the streamwise variation of
and
, agree with the experiments by Brzek et al. [
31] over a similar Reynolds number range.
To account for variation in
along
, Clauser [
44] defined a parameter
(Clauser’s shape factor) that remains unchanged under equilibrium conditions. This parameter
is a function of only
, and
[
45], and it is related to
and
by
The notation
in the above relation is used to distinguish this estimate of the skin friction from the directly computed
. The variation in
along
for the STR case is plotted in
Figure 11. Different symbol shapes and colors were used to divide the streamwise fetch into three sections:
55 <
,
200 <
, and
400 <
.
can be cast into a polynomial with
and
as its sole subjects using Coles’ law of the wake [
45]. Two different profiles of
, one with
and another with
, are also included. These values of
correspond to
and 0.95, respectively, under the assumption of Coles’ profile. Apart from the strong non-equilibrium behavior apparent in section
(black squares),
compares favorably to the equilibrium curve with a higher
at
. This agreement with the equilibrium curve at
is consistent with the predictions of
in
Figure 8b. The Clauser parameter
is also estimated using the above given relation for
and the DNS predications of
and
as inputs (inset of
Figure 11a). Except for a large variation in
present at
, it remains preserved within the narrow band between 7.9 and 8.1 once equilibrium is established. One obtains the following relation by integrating the Coles’ profile across the boundary layer,
Figure 11b shows the variation of
plotted as a function of
. Like
Figure 11a, the DNS prediction in
Figure 11b matches the equilibrium estimate from the above equation (
) at
.
An internal layer height
is generally identified for boundary layers undergoing a step change in roughness as the height above which the flow is reminiscent of the upstream equilibrium flow condition and below which it is being modulated by the downstream surface. Multiple approaches were proposed over the years to identify
as discussed in detail by Rouhi, Chung, and Hutchins [
9]. There are two common themes in general:
approaches that either employ the height at which
or the height at which
first deviates from the undisturbed velocity (hereafter referred to as
) [
46,
47];
approaches where a measure of the wall-normal variation of
is extracted [
4,
48]. We restrict ourselves to the former and identify
using two different but closely connected methods. The first method is the same as
, whereas the local
is contrasted with the upstream undisturbed profile in the second method to identify
. Due to the difficulties in separating the local velocity profile (or
) from the upstream undisturbed curve once the TBL height is approached,
is only identified until it reaches
. The streamwise variation
is plotted in a log-log format in
Figure 12. It suggests that the perturbation spreads quickly and reaches the boundary layer height within
Beyond this fetch length, the entire boundary layer is being influenced by the surface roughness.
Additionally, the variation of
along the fetch length for both methods falls very close to each other, and it is well approximated by the power law fit:
. The reference power law fits from the STR TBL by Antonia and Luxton [
4], i.e.,
, and from the STR half channel by Rouhi, Chung, and Hutchins [
9] using the approach by Elliot [
48], i.e.,
, are also included for comparison. A somewhat smaller exponent of
emerges when the internal layer height
is instead normalized by the local boundary layer thickness
, as shown in the inset of
Figure 12. Recently, Gul and Ganapathisubramani [
34] found an exponent between 0.7 and 0.8 using STR and RTS experiments of TBLs evolving from one rough surface to another, albeit at smaller
values. While the agreement of our estimate of the exponent with those found in the literature appears satisfactory, it is worth noting that different definitions could lead to quite disparate values of the exponent. Rouhi, Chung, and Hutchins [
9] showed that employing different definitions for estimating the internal layer in a half channel undergoing both RTS and STR transitions resulted in an exponent ranging between 0.34 and 0.58.
3.4. Reynolds Stresses
The wall-normal variation of turbulence stresses at different evenly spaced streamwise stations is plotted in
Figure 13. Note that like
Figure 6,
Figure 8a, and
Figure 9, the rough-wall profiles in
Figure 13 were horizontally averaged over the length of one square roughness repeating unit in addition to being time averaged and phased averaged in the spanwise direction. Above the roughness canopy, all four turbulence stresses are elevated above their smooth-wall counterparts, and this increment persists for the entire fetch length. In the outer layer, this augmentation corresponds to about
for
, nearly 50% for
and
, and around 35–40% for
. While initially the response of the rough surface on turbulent stresses is appreciable, the profiles at the last three stations indicate negligible differences among themselves. The implication is that turbulence stresses settle into a virtual equilibrium beyond
after a strong initial modulation. The rough wall is effective in rapidly suppressing the coherence of turbulence stresses. This results in both
and
being slightly amplified above the smooth-wall levels while the streamwise turbulence stress is severely depleted. One obvious question pertains to the reason behind the persistence of noticeably higher turbulence stresses in the outer layer. The prime suspect is high mean shear—or equivalently the larger velocity deficit—observed above the rough surface (
Figure 8). Its interaction with the Reynolds shear stress incites a cyclical process of turbulence energy production and diffusion, which in turn enhances the normal turbulence stresses. It is important to note that that enhancement seen above the rough surface in the equilibrium region when compared to the smooth-wall levels is not merely a Reynolds number effect. These higher magnitudes persist even when the results of the two surfaces are compared at a similar
.
A weak mean separation bubble, with length
and
in the quasi-equilibrium section, forms behind the roughness elements. As a result, the sharp mean shear at
becomes an inception cite for high turbulence stresses.
Figure 14 presents the streamwise distribution of
,
, and
(where
) inside and above the roughness canopy at
. Comparatively strong local peaks for
and
are observed at
–
after the STR step change. Their size diminishes as the TBL adjusts to an equilibrium, but the relative position of the maxima along the cavity width remains rather fixed. The streamwise inhomogeneity in both
and
persists until
, which is consistent with the previously established height of the roughness sublayer. The ratio between the turbulence and mean-straining timescales (
) relaxes to the magnitude seen above canonical smooth-wall TBLs in the outer layer, i.e.,
–
. However, it is at the crest height and near the middle of the cavity where it shows a local peak with a magnitude of
. Its position coincides with the location of the local peak for
. As it lies directly above the mean separation bubble that forms behind a roughness element, the resulting mean velocity profile is both inflectional and manifests strong mean straining (see
Figure 8a).
Further insights into the development of non-equilibrium effects on turbulence stresses can be gained by inspecting the budget terms of the TKE equation. All the budget terms in the transport equation of the TKE are first moved to the right-hand side before they are examined in
Figure 15. It must be noted that the results presented in
Figure 15 correspond to the spanwise center of the time and spanwise averaged repeating unit of the rough surface. As opposed to the outer layer, where the TKE production
is essentially balanced by the TKE dissipation
the contribution of the TKE transport terms cannot be ignored inside the canopy. Additionally, the TKE budget terms inside the canopy completely adjusted to the new surface condition by
as shown in
Figure 15a. While the dynamic balance among the multiple terms of the TKE equation is established rapidly after the STR transition, their relative magnitudes depict a small yet noticeable streamwise dependence. One noteworthy aspect of
Figure 15a is that the shape of the TKE budgets in the lower half of the canopy appears remarkably like the corresponding profiles from the near-wall region of a fully developed smooth wall. This similarity exists first in
, which shows a local peak at
, and second in the observation that the excess TKE is transported to the wall via viscous and turbulence diffusion, where
is large.
Above the canopy and after the STR step change, the gross effect of roughness is to increase both
and
in the outer layer swiftly. In congruence with the turbulence shear stress, the peak for
is sited directly above the canopy. As the boundary layer grows, the peak for
appears both to increase gradually in magnitude and shift closer to the wall. However, this is an artifact of normalization by
; in absolute terms, the location of the peak remains unchanged. When compared with its smooth-wall counterpart, higher
and
levels are present in the outer parts of the TBL even beyond
(
Figure 15b). Much stronger production and the subsequent dissipation of the TKE is not surprising given the larger wake parameter
.
The recovery of shear-stress-producing motions above the rough wall in the context of ejection and sweep events is discussed next using the quadrant splitting (QS) approach [
49]. Later, the statistical properties of high-intensity ejections and sweeps are briefly analyzed as a proxy for extreme wall events. The ratio
at several streamwise stations for the two cases is plotted in
Figure 16a.
motions, which comprise sweep events, dominate below
and
motions, which include ejection events, are dominant above this height for fully developed smooth walls. The ratio
continuously increases as one moves further out into the boundary layer. This implies a progressively smaller contribution to the turbulence shear stress by sweep events. An approximate collapse of the
ratio from all three rough-wall stations on the smooth-wall result is apparent. More precisely, the ratio at
is within 10% of the smooth-wall profile along the entirety of the outer layer. This reflects an immediate adjustment of the shear-stress-producing motions to the new surface condition and the imperviousness of such motions to the underlying surface type.
The autonomous cycle for wall turbulence involves mutual induction of streamwise vorticity and streaks. This process is connected to the intermittent yet infrequent bursting process that contributes a significant fraction of the turbulence shear stress in the near-wall region. While bursts are typically associated with a lift-up of low-speed streaks and local inflectional-type instabilities, they evade a precise description. Within the present context, we loosely follow the procedure outlined by Bourassa and Thomas [
50] to identify bursts. A burst is defined as a temporally continuous
event for which
| > 1.5. Similarly, high-intensity sweep (HIS) events (
motions) that satisfy the same threshold are also identified. Statistical properties of bursts and sweeps are evaluated using about 50,000
snapshots of
and
fluctuations; they further require an averaging operation in time and span.
The wall-normal variation of the fraction of total time occupied by bursts and HIS events at
, 650) is plotted in
Figure 16b along with a representative profile from case
. Quite expectedly, both bursts and HIS events occupy a small fraction (about
–
) of the total time for both cases. While the propensity of bursts occurring marginally increases as
increases, an opposite effect is observed for the HIS events. Apart from the region directly above the roughness canopy where HIS events transpire more frequently than those above the smooth wall at a similar
, a loose collapse across much of the outer TBL between the two surfaces is evident. Finally, despite the instant adjustment of shear-stress-producing motions to the rough surface and the structural similarity of such motions between the two surfaces,
Figure 16b further suggests that bursts last slightly longer and thus occupy a rather larger fraction of time at
and
Interestingly, this streamwise fetch length is upstream of the point where
first reaches the edge of the boundary layer.
3.5. Integral Lengthscale and Timescale
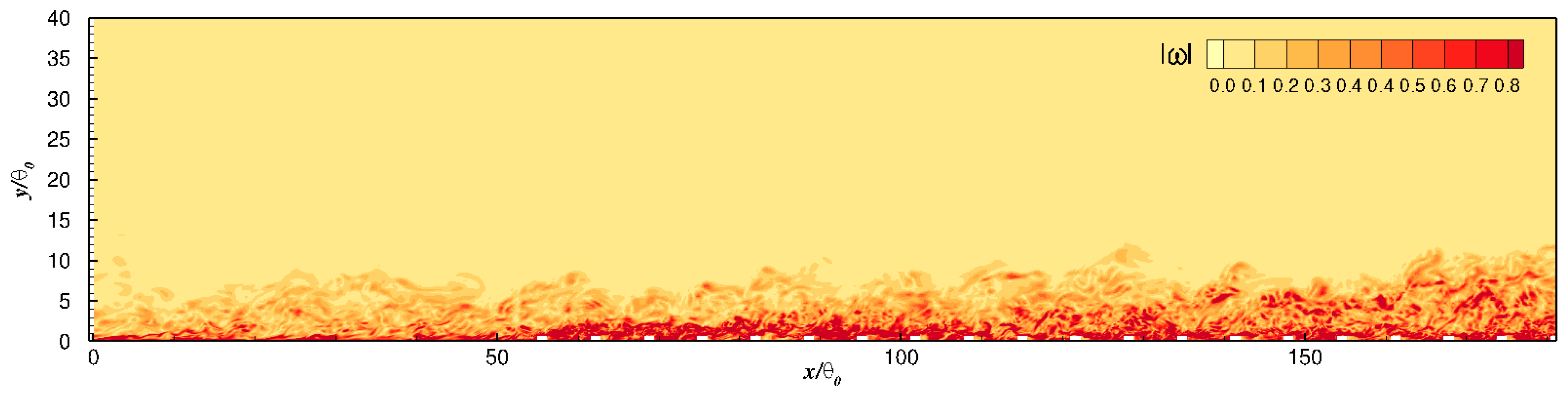
Two-point correlations of turbulent fluctuations in the spanwise direction are used to interrogate the alteration of the integral length scale
by the step change in roughness. However, before examining the statistical results, it is worthwhile to visualize the modulation effect of the step change on the instantaneous velocity fluctuations. An instantaneous
snapshot of the streamwise fluctuations inside the roughness sublayer, at
, is presented in
Figure 17; this height corresponds to
at inflow. The immediate impact of introducing rows of roughness elements is to induce numerous strong streamwise-aligned
structures of smaller
and
sizes. Despite the streak break up, the streamwise extent of these new
motions is clearly much longer than the
spacing between two roughness elements, especially in the equilibrium region. As noted by Durbin [
13], this disproportionate dampening of long streaks is effectively a result of the drag layer setup by the roughness canopy and not an imprint of the geometry. However, there appears to be a distinct streamwise modulation of the size of these new
structures in the non-equilibrium region. This is evidenced by the contrast distinguishable between the sections at
and at
. While a streamwise lengthening of these high-intensity structures coupled with a continuous reduction in their coherence is visible in the former, the latter depicts a sparse population with a negligible visible pattern of their streamwise development. It is not clear whether this streamwise modulation of
structures in the non-equilibrium zone is exclusively dictated by the developing mean shear or if the roughness morphology also plays an important role. Their higher intensity on the other hand persists across the entire fetch length, which can also be surmised from
Figure 13.
The attached turbulent motion above smooth walls consists of low-speed streaks being flanked by the legs of hairpin vortices [
51,
52]. The heads of these vortex hairpins are subsequently lifted up by induced
motion.
Figure 18 visualizes the iso-surfaces of the
–criterion [
53],
near the STR step change
and in the quasi-equilibrium section of the TBL
. A sharp increase in the population of vortical structures at this level of
is vividly apparent after the STR transition. Like
the population of vortex filaments at fixed
also gradually decreases as the TBL above the rough surface grows with increasing fetch length. While the crests of roughness elements immediately after the STR step change generate nearly horizontal hairpin vortices with a length scale
, they decay quickly and are somewhat inconsequential. In fact, shedding of roughness-induced hairpins from elements downstream of the first few rows was not observed. The vast majority of vortical filaments in
Figure 18 lie well above the roughness canopy and are due to shear-layer turbulence. These structures are lifted upon interaction with vortices originating from the shear layer downstream. They lose coherence, and their size increases as they move further away from the canopy. These roughness-layer-induced hairpins, which are connected to the newly created strong streamwise-aligned
motions (
Figure 17), instigate the vigorous momentum exchange observed above the rough surface.
The two-point correlation is estimated in a
–plane at different fetch lengths using
Here,
corresponds to one of the three components of the instantaneous velocity vector, and
refers to the spacing from the point of interest in the spanwise direction. The overbar in the above equation implies averaging over both time and span, with the temporal average covering a period of
; this period corresponds to over 50,000 instantaneous snapshots.
is determined by
In this equation,
is taken as the spanwise spacing at the which the correlation first drops below zero [
54]. The wall-normal variation of
at different streamwise stations for cases
and
is plotted in
Figure 19a. Among the three components,
and
are of approximately the same size (in fact
is slightly larger), and
is about half their size at
.
increases in relative size as one moves into the outer part of the TBL, and it is larger than the other two components at the edge of the boundary layer. This augmentation of
near
is related to the large-scale incursions of non-turbulent fluid from the free stream and the ejection of a similarly large-scale turbulent fluid into the free stream. It is further clear from
Figure 19a that above the smooth wall,
for all three velocity components first grows rapidly in the inner layer before increasing rather gradually in the outer layer. As noted by Marusic and Monty [
55], the fact that
grows with an increasing
is consistent with the implications of the attached eddy hypothesis by Townsend. A similar trend of
increasing with
is reproduced above the rough wall at
0.1, with the last two of the three streamwise stations showing a decent collapse with the smooth-wall profiles. These results suggest that a near equilibrium for the integral length scale is in place across the entire TBL by
at the most. However, non-equilibrium effects on
are apparent at the upstream location. At
, both
and
are suppressed below the equilibrium profiles immediately above the roughness canopy. This supports the conclusion drawn earlier from the instantaneous snapshot of
motions (
Figure 17). The effect on
is less severe: it approximately overlaps the equilibrium profiles up until
before quickly becoming somewhat larger at
.
Like
, an integral timescale
can be estimated by first calculating the two-point correlation of turbulent fluctuations in time
and then integrating it over the following range of temporal spacing
:
and
. The choice for
is the temporal spacing at which
first drops below
. Averaging in time and span is performed for the two-point correlation
before estimating the integral timescale. The wall-normal
) variation of
at different
stations for cases
and
is presented in
Figure 19b. There is a good agreement near the wall between the current equilibrium smooth-wall results and the data (open symbols) from the DNS of a channel at
by Quadrio and Luchini [
56]:
and
. Additionally, the ratio
at
for case
is consistent with the TBL measurements by Swamy and Gowda [
57]. The effect of roughness is to enhance the integral timescale significantly immediately above the canopy
–
, and
is still continuously increasing with growing fetch as one approaches the end of the computational domain. This increase in
is directly related to a much larger streamwise extent of turbulent structures and not merely a consequence of a higher
at the rough surface. At
,
is about three times the equilibrium smooth-wall level even though
is only
times larger. Prior evidence of large structures in the
direction above the roughness canopy can be found in the experiments by Volino, Schultz, and Flack [
32] and DNS by Ismail, Zaki, and Durbin [
14]. On the other hand,
and
(not shown)—while also being nearly tripled above the roughness canopy—display little streamwise development after
. However, the increase in the integral timescale with a growing fetch length is less sharp than the one shown by
. As a result, the outer-scaled integral timescale
decreases sluggishly as
increases for much of the outer layer after the STR step change.
As shown in
Figure 20, the profile shape of the integral timescale ratio
in the outer layer is in gross agreement with the equilibrium smooth wall result at
and
. At the former
station, the ratio is suppressed below the equilibrium level as the roughness is effective in reducing the anisotropy of the turbulence integral timescale for much of the outer layer. This effect is constricted to only the lower part of the TBL by the latter streamwise location. Consequently, a nearly excellent match with the equilibrium smooth-wall ratio for
emerges across the entire outer layer
–
.