Shock Initiation and Propagation of Detonation in ANFO
Abstract
:1. Introduction
2. Description of Numerical Models
2.1. Shock Initiation Modeling with AUTODYN
2.2. Calculation of Steady-State Detonation Applying Wood–Kirkwood Detonation Model
3. Results and Discussion
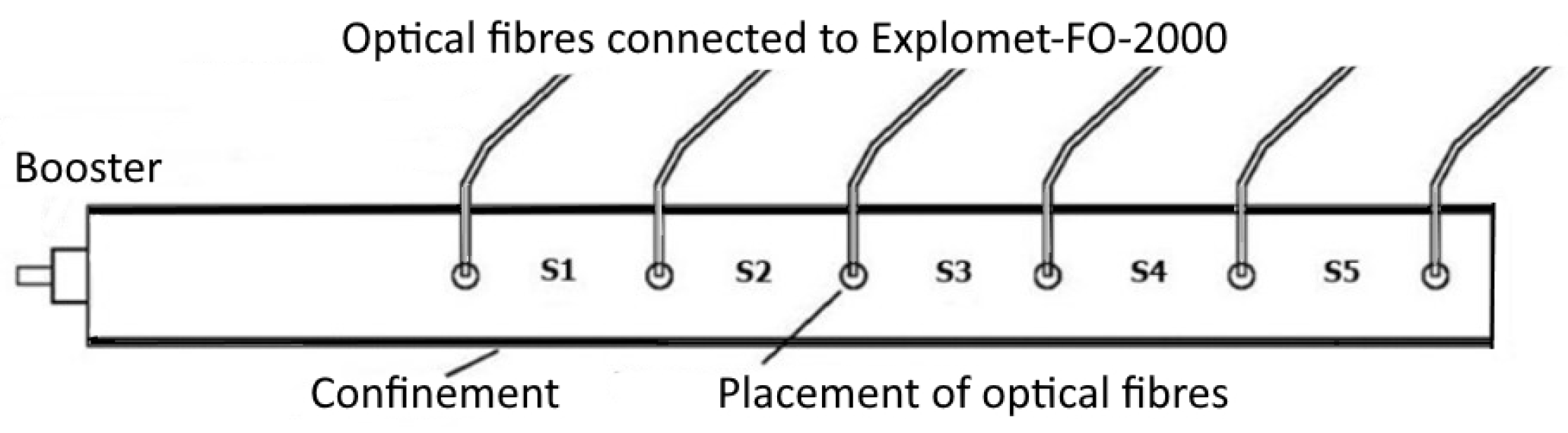
3.1. Materials and Methods
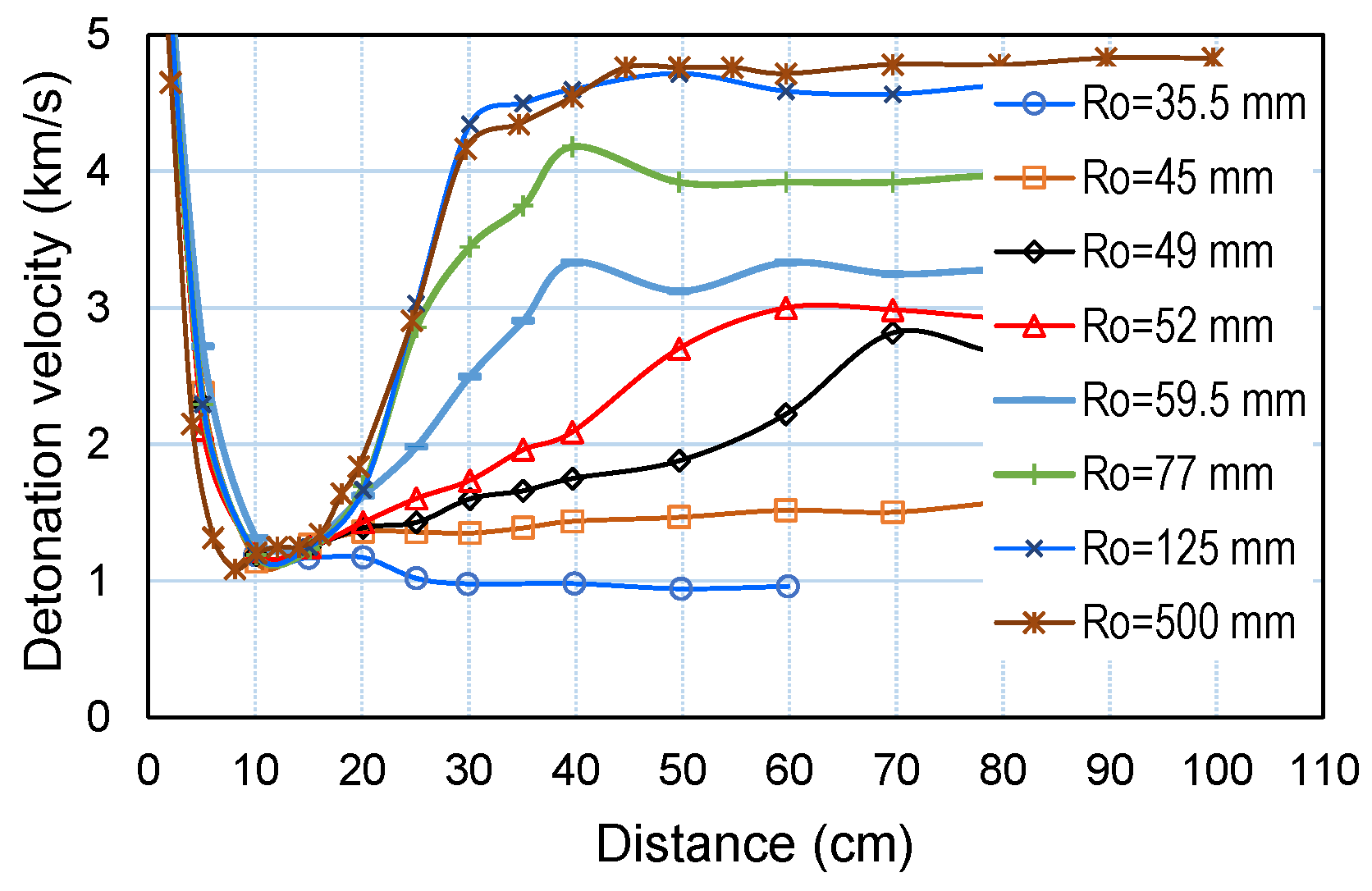
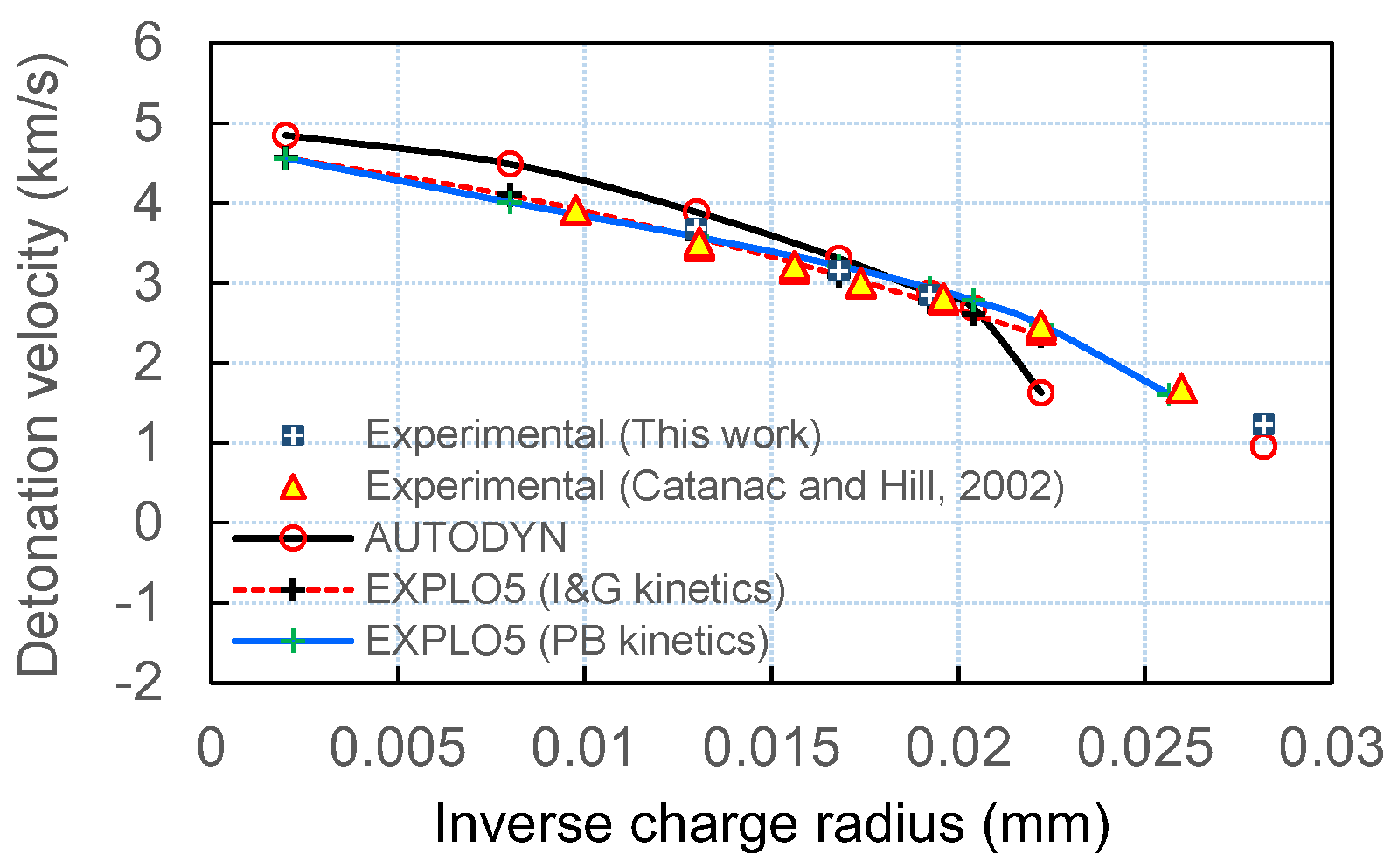
3.2. Effect of Charge Diameter on Shock Initiation Behavior
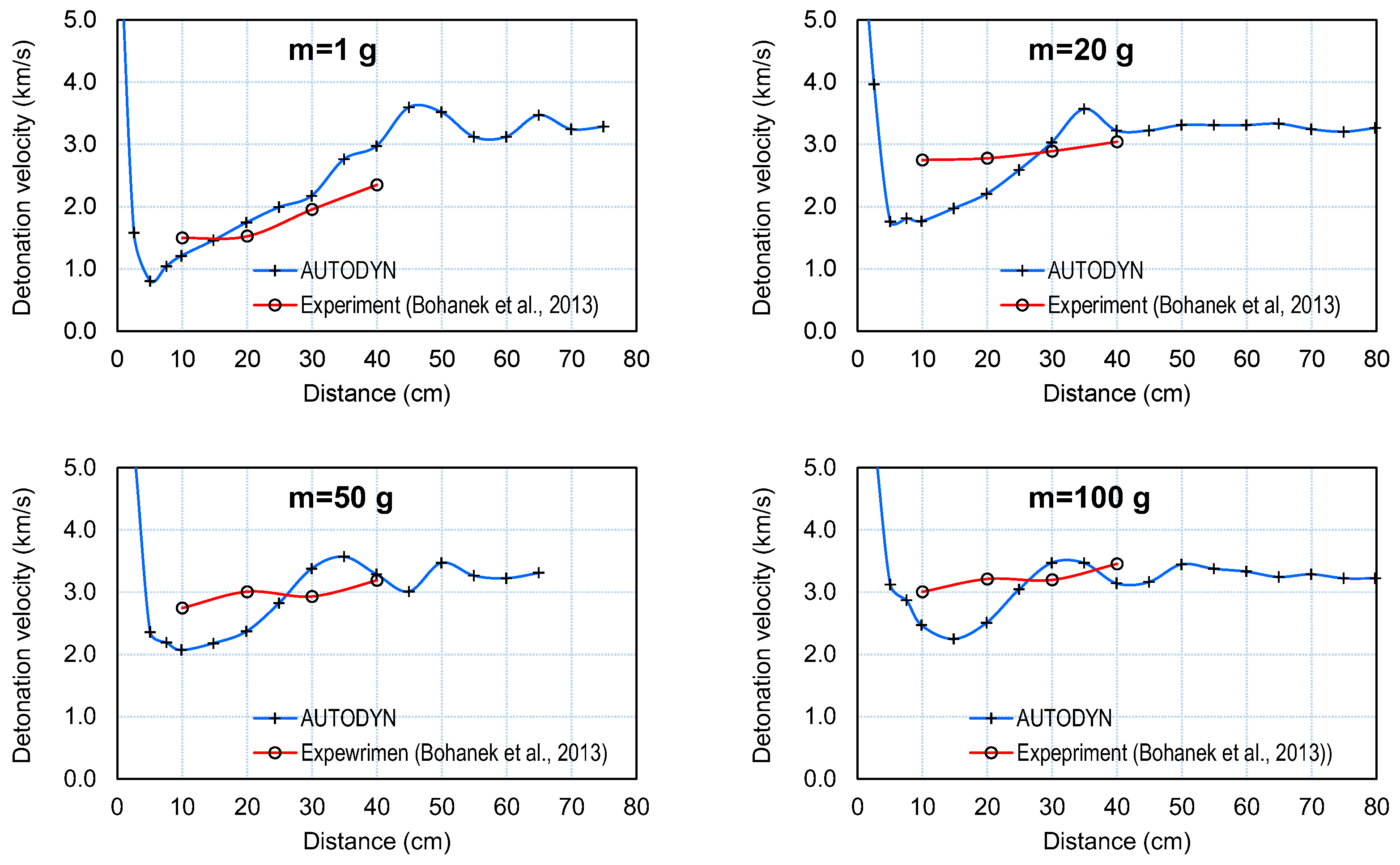
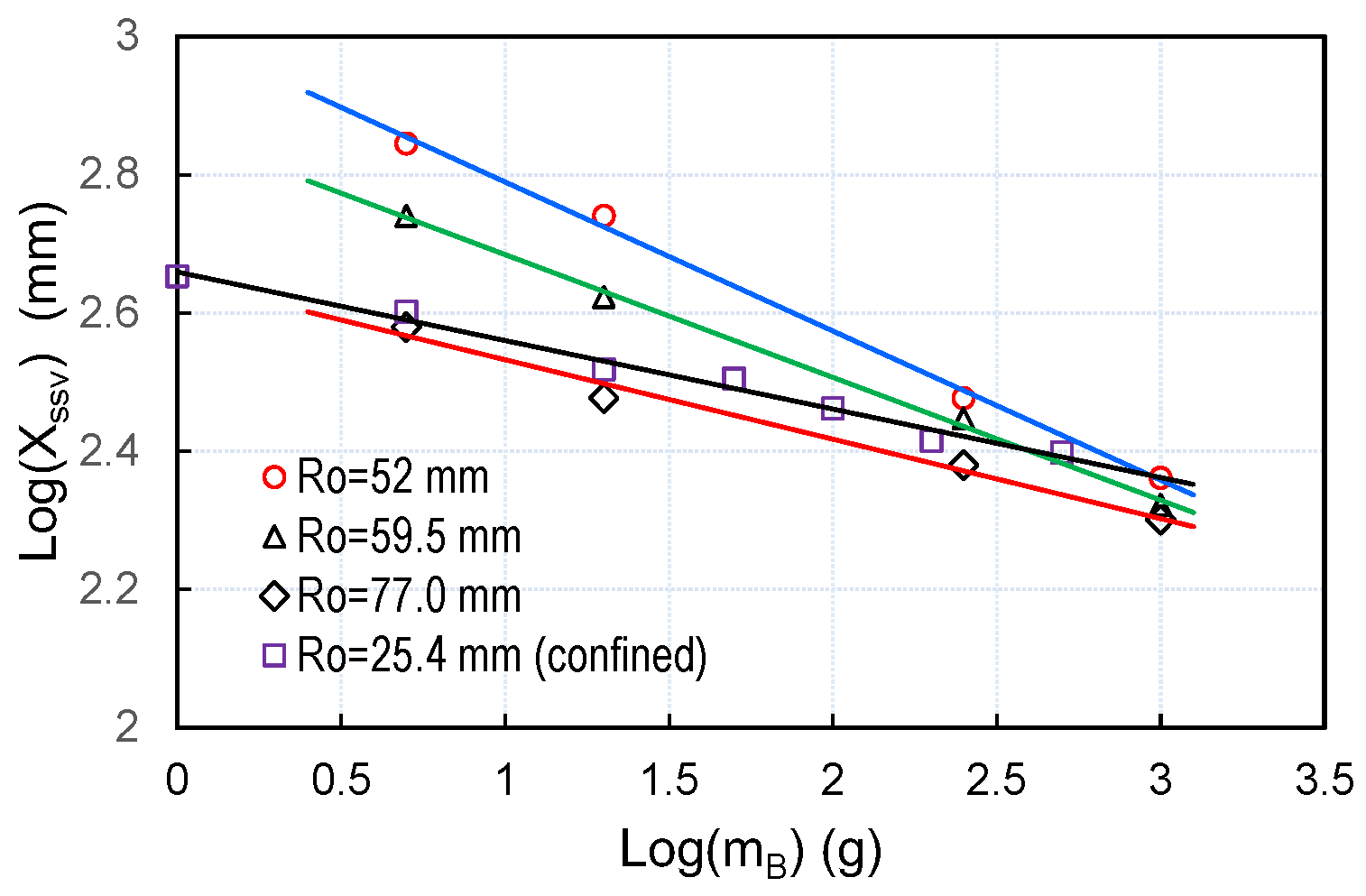
3.3. Effects of Booster Mass and Confinement on Shock Initiation Behavior
4. Conclusions
- (1)
- It was demonstrated that AUTODYN with an I&G model could qualitatively describe the initiation process and predict steady-state detonation velocity as a function of charge diameter with an error of up to 6%. The WK detonation model incorporated into EXPLO5 thermochemical code could predict accurately the steady-state detonation velocity of unconfined (i.e., lightly confined) charges with an error of up to 3.5% for R0 > 50 mm.
- (2)
- For lightly confined charges initiated by a constant mass of booster, steady-state detonation was established faster (at shorter distances) for charges of larger diameters. The initial drop in VoD and the minimum VoD reached were related to booster mass, i.e., initiating pressure impulse, and thus did not change with charge diameter. However, the shock velocity (and pressure) growth rate increased with charge diameter. This was associated with a greater expansion of products at smaller charge diameters, which resulted in stronger pressure weakening and a slower reaction rate at smaller charge diameters. Faster reaction, in turn, resulted in faster generation of additional pressure and energy that strengthened the initial shock wave, hence leading to faster growth in pressure and shock velocity and, ultimately, to a shorter distance to steady-state detonation.
- (3)
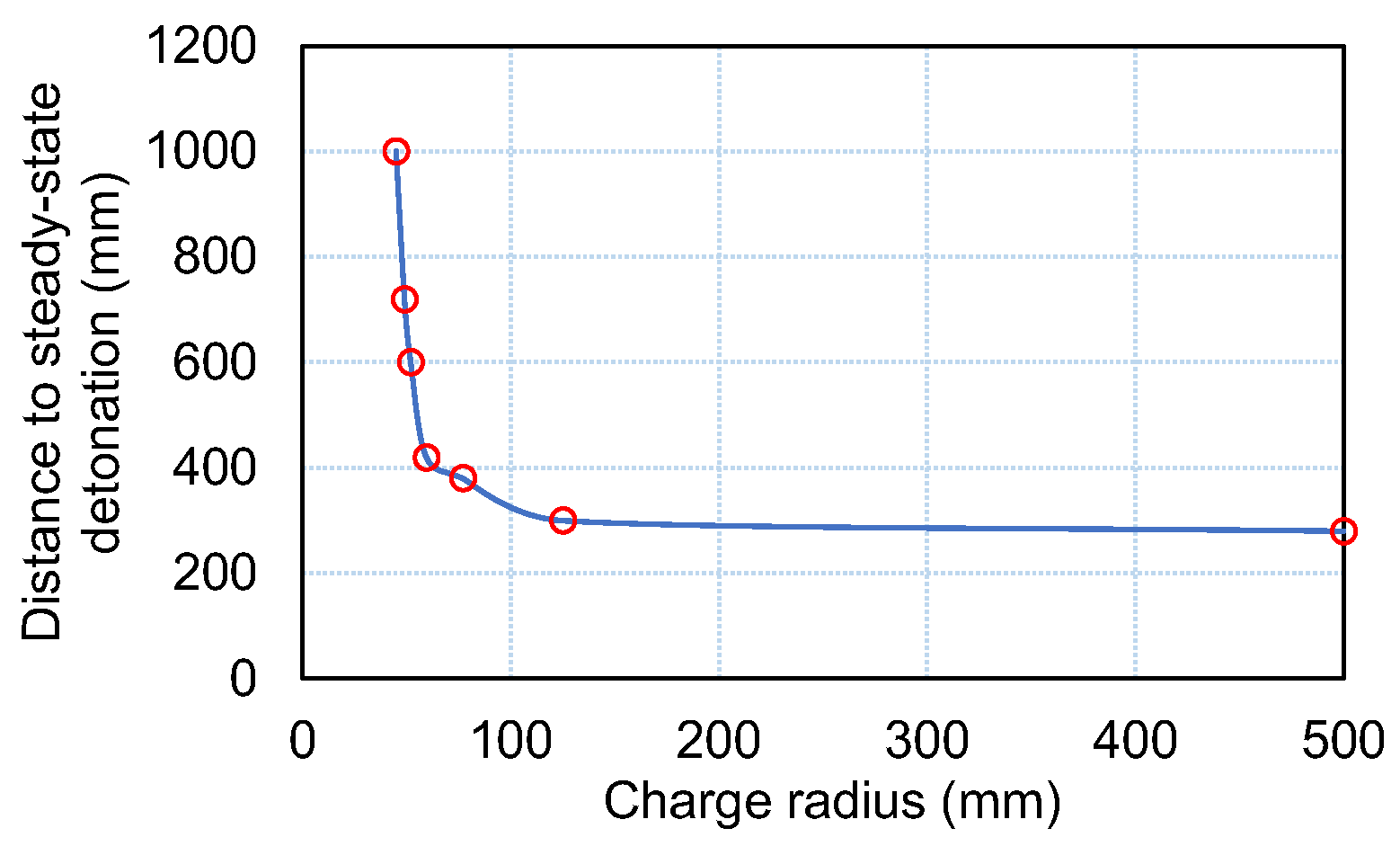
- Both the experiments and the calculations confirmed that booster mass strongly affected the resulting VoD–x profiles: the minimum VoD increased with booster mass and shifted to larger distances, the shock velocity growth rate increased, and the run-to-steady-state detonation decreased. On a log–log scale, xSDT vs. booster mass showed linear dependence analogous to a “Pop Plot”, which represents the dependence of run-to-detonation distance on initial impact pressure.
- (4)
- The log(xSDT)–log(mB) graphs for lightly confined and steel-confined charges showed that the xSDT was smaller for steel-confined charges, which supports the hypothesis that the expansion of detonation products plays an important role in the shock initiation of ANFO charges. The effect of booster mass was less pronounced for steel-confined charges.
- (5)
- Considering the wide range of parameters that could affect the shock initiation and propagation of detonation in non-ideal explosives such as ANFO, this study aimed to contribute a better understanding of the impacts of some of these factors, which is important for better tailoring the effects of ANFO for use in the mining industry.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kelso, J.R.; Choromokos, J. Ammonium Nitrate/Fuel Oil Explosives. Mil. Eng. 1973, 65, 177–180. [Google Scholar]
- Cudzilo, S.; Maranda, A.; Nowaczewski, J.; Trzciński, W.A. Shock Initiation Studies of Ammonium Nitrate Explosives. Combust. Flame 1995, 102, 64–72. [Google Scholar] [CrossRef]
- Esen, S. A Non-Ideal Detonation Model for Commercial Explosives. Ph.D. Thesis, University of Queensland, Brisbane, QLD, Australia, 2004. [Google Scholar]
- Fabin, M.; Jarosz, T. Improving ANFO: Effect of Additives and Ammonium Nitrate Morphology on Detonation Parameters. Materials 2021, 14, 5745. [Google Scholar] [CrossRef]
- Cook, M.A.; Mayfield, E.B.; Partridge, W.S. Reaction Rates of Ammonium Nitrate in Detonation. J. Phys. Chem. 1955, 59, 675–680. [Google Scholar] [CrossRef]
- King, W.A.; Bauer, A.; Heater, R.D. The Explosion Hazards of Ammonium Nitrate and Ammonium Nitrate-Based Fertilizer Composition; Report from Canadian Fertilizer Institue; Queen’s Univeristy: Kingston, ON, Canada, 1982. [Google Scholar]
- Catanach, R.A.; Hill, L.G. Diameter Effect Curve and Detonation Front Curvature Measurements for ANFO. In Proceedings of the AIP Conference, Albuquerque, NM, USA, 23–28 June 2002; Volume 620, pp. 906–909. [Google Scholar]
- Sharpe, G.J.; Braithwaite, M. Steady Non-Ideal Detonations in Cylindrical Sticks of Explosives. J. Eng. Math. 2005, 53, 39–58. [Google Scholar] [CrossRef]
- Zganec, S.; Bohanek, V.; Dobrilovic, M. Influence of a Primer on the Velocity of Detonation of ANFO and Heavy ANFO Blends. Cent. Eur. J. Energ. Mater. 2016, 13, 664–704. [Google Scholar] [CrossRef]
- Miyake, A.; Takahara, K.; Ogawa, T.; Ogata, Y.; Wada, Y.; Arai, H. Influence of Physical Properties of Ammonium Nitrate on the Detonation Behaviour of ANFO. J. Loss Prev. Process Ind. 2001, 14, 533–538. [Google Scholar] [CrossRef]
- Zygmunt, B.; Buczkowski, D. Influence of Ammonium Nitrate Prills’ Properties on Detonation Velocity of ANFO. Propellants Explos. Pyrotech. 2007, 32, 411–414. [Google Scholar] [CrossRef]
- Buczkowski, D.; Zygmunt, B. Influence of Ammonium Nitrate Prills Porosity and Dimensions on Detonation Velocity of ANFO Explosives. In Proceedings of the New Trends in Research of Energetic Materials, Pardubice, Czech Republic, 21–23 April 2003; pp. 45–51. [Google Scholar]
- Bohanek, V.; Dobrilović, M.; Škrlec, V. Influence of the Initiation Energy on the Velocity of Detonation of ANFO Explosive. Cent. Eur. J. Energ. Mater. 2013, 10, 555–568. [Google Scholar]
- Dobrilovic, M.; Bohanek, V.; Zganec, S. Influence of Explosive Charge Temperature on the Velocity of Detonation of ANFO Explosives. Cent. Eur. J. Energ. Mater. 2014, 11, 191–197. [Google Scholar]
- Zygmunt, B.; Buczkowski, D. Agriculture Grade Ammonium Nitrate as the Basic Ingredient of Massive Explosive Charges. Propellants Explos. Pyrotech. 2012, 35, 685–690. [Google Scholar] [CrossRef]
- Jackson, S.I.; Kiyanda, C.B.; Short, M. Precursor Detonation Wave Development in ANFO Due to Aluminum Confinement. In Proceedings of the 14th International Detonation Symposium, Coeur D’Alene, ID, USA, 11–16 April 2010; pp. 740–749. [Google Scholar]
- Bohanek, V.; Sućeska, M.; Dobrilović, M.; Hartlieb, P. Effect of Confinement on Detonation Velocity and Plate Dent Test Results for ANFO Explosive. Energies 2022, 15, 4404. [Google Scholar] [CrossRef]
- van der Steen, A.C.; Kodde, H.H.; Miyake, A. Detonation Velocities of the Non-Ideal Explosive Ammonium Nitrate. Propellants Explos. Pyrotech. 1990, 15, 58–61. [Google Scholar] [CrossRef]
- Suceska, M. EXPLO5 Version V6.05 Users’ Guide; OZM Research: Hrochuv Tynec, Czech Republic, 2018. [Google Scholar]
- Wood, W.W.; Kirkwood, J.G. Diameter Effect in Condensed Explosives. the Relation between Velocity and Radius of Curvature of the Detonation Wave. J. Chem. Phys. 1954, 22, 1920–1924. [Google Scholar] [CrossRef]
- Kirby, I.J.; Leiper, G.A. A Small Divergent Detonation Theory for Intermolecular Explosives. In Proceedings of the 8th International Detonation Symposium, Albuquerque, NM, USA, 15–19 July 1985; pp. 176–186. [Google Scholar]
- Lee, E.L.; Tarver, C.M. Phenomenological Model of Shock Initiation in Heterogeneous Explosives. Phys. Fluids 1980, 23, 2362–2372. [Google Scholar] [CrossRef]
- Kittell, D.E.; Cummock, N.R.; Son, S.F. Reactive Flow Modeling of Small Scale Detonation Failure Experiments for a Baseline Non-Ideal Explosive. J. Appl. Phys. 2016, 120, 064901. [Google Scholar] [CrossRef]
- Stimac, B.; Skrlec, V.; Dobrilovic, M.; Suceska, M. Numerical Modelling of Non-Ideal Detonation in ANFO Explosives Applying Wood-Kirkwood Theory Coupled with EXPLO5 Thermochemical Code. Def. Technol. 2020, 17, 1740–1752. [Google Scholar] [CrossRef]
- Fried, L.E.; Howard, W.M.; Souers, P.C.; Haselman, L. Adding Kinetics and Hydrodynamics to the CHEETAH Thermochemical Code; Report No. UCRL-ID-125794; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1997. [Google Scholar]
- Esen, S.; Souers, P.C.; Vitello, P. Prediction of the Non-Ideal Detonation Performance of Commercial Explosives Using the DeNE and JWL++codes. Int. J. Numer. Methods Eng. 2005, 64, 1889–1914. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Autodyn: User’s Manual Release 13.0; ANSYS Inc.: Canonsburg, PA, USA, 2010. [Google Scholar]
- Yi, C.; Nyberg, U.; Johansson, D. Calibration and Validation of Reactive Flow Model Parameters for an Emulsion Explosive. In Proceedings of the FragBlast 12: 12th International Symposium on Rock Fragmentation by Blasting, Lulea, Swedan, 11–13 June 2018; pp. 459–468. [Google Scholar]
- Li, Y.; Yang, X.; Wen, Y.; Xiong, S.; Li, X. Determination of Lee-Tarver Model Parameters of JO-11C Explosive. Propellants Explos. Pyrotech. 2018, 43, 1032–1040. [Google Scholar] [CrossRef]
- Fickett, W.; Davis, W.C. Detonation Theory and Experiment; Dover Publications, Inc.: Mineola, NY, USA, 2000. [Google Scholar]
- Fried, L.E.; Souers, P.C. BKWC: An Empirical BKW Parametrization Based on Cylinder Test Data. Propellants Explos. Pyrotech. 1996, 21, 215–223. [Google Scholar] [CrossRef]
- Souers, P.C.; Anderson, S.; Mercer, J.; McGuire, E.; Vitello, P. JWL++: A Simple Reactive Flow Code Package for Detonation. Propellants Explos. Pyrotech. 2000, 25, 54–58. [Google Scholar] [CrossRef]
- Braithwaite, M.; Cunningham, C.V.B.; Sharpe, G.J. Modeling and Numerical Simulation of Steady State Detonations in Highly Non-Ideal Explosives. In Proceedings of the 13th International Detonation Symposium, Norfolk, VA, USA, 23–28 July 2006. [Google Scholar]
- Suceska, M.; Stimac Tumara, B.; Dobrilovic, M.; Bohanek, V. Estimation of Detonation Front Curvature Radius by Empirical Equations. J. Energ. Mater. 2022, 1–18. [Google Scholar] [CrossRef]
- Fried, L.E.; Howard, W.M.; Souers, P.C. Cheetah 2.0 User’s Manual; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1998. [Google Scholar]
- Urtiew, P.A.; Vandersall, K.S.; Craig, M.; Garcia, F.; Forbes, J.W. Shock Initiation Experiments and Modeling of Composition B and C-4. In Proceedings of the 13th International Detonation Symposium, Norfolk, VA, USA, 23–28 July 2006; pp. 929–939. [Google Scholar]
- Souers, P.C.; Vitello, P. ANFO Calculations for Sedat Esen; Lawrence Livermore National Lab. (LLNL): Livermore, CA, USA, 2004. [Google Scholar]
- Jackson, S.I.; Short, M. Scaling of Detonation Velocity in Cylinder and Slab Geometries for Ideal, Insensitive and Non-Ideal Explosives. J. Fluid Mech. 2015, 773, 224–266. [Google Scholar] [CrossRef]


| Reacted ANFO (a) | Unreacted ANFO (b) | Lee–Tarver I&G Reaction Rate Parameters (c) |
|---|---|---|
| A = 81.6492 GPa | A = 1454.25 GPa | I = 10 1/μs |
| B = 1.7537 GPa | B = −0.347 GPa | a = 0.2 |
| R1 = 4.588863 | R1 = 21.8866 | b = 0.222 |
| R2 = 1.021101 | R2 = 0.7874 | x = 4 |
| ω = 0.32021 | ω = 3.4613 | G = 0.086 1/(μs GPa ^y) |
| D = 4.78 km/s | E0 = −0.1549 kJ/cm3 | c = 0.222 |
| pCJ = 4.61 GPa | d = 0.666 | |
| E0 = 3.4481 kJ/cm3 | y = 0.9 | |
| FIgmax = 0.3 |
| din (mm) | R0 (mm) | Detonation Velocity (km/s) | xSDT (mm) | xSDT/din | ||||
|---|---|---|---|---|---|---|---|---|
| Expt. | AUTODYN (at x > xSDT) | EXPLO5 (PB Model) | EXPLO5 (I&G Model) | Expt. | AUTODYN | |||
| 71 | 35.5 | 1.23 | 0.96 | - | - | - | - | |
| 90 | 45 | 1.63 | 2.48 | 2.34 | 1000 * | 11.11 | ||
| 98 | 49 | 2.69 | 2.78 | 2.61 | 720 | 7.35 | ||
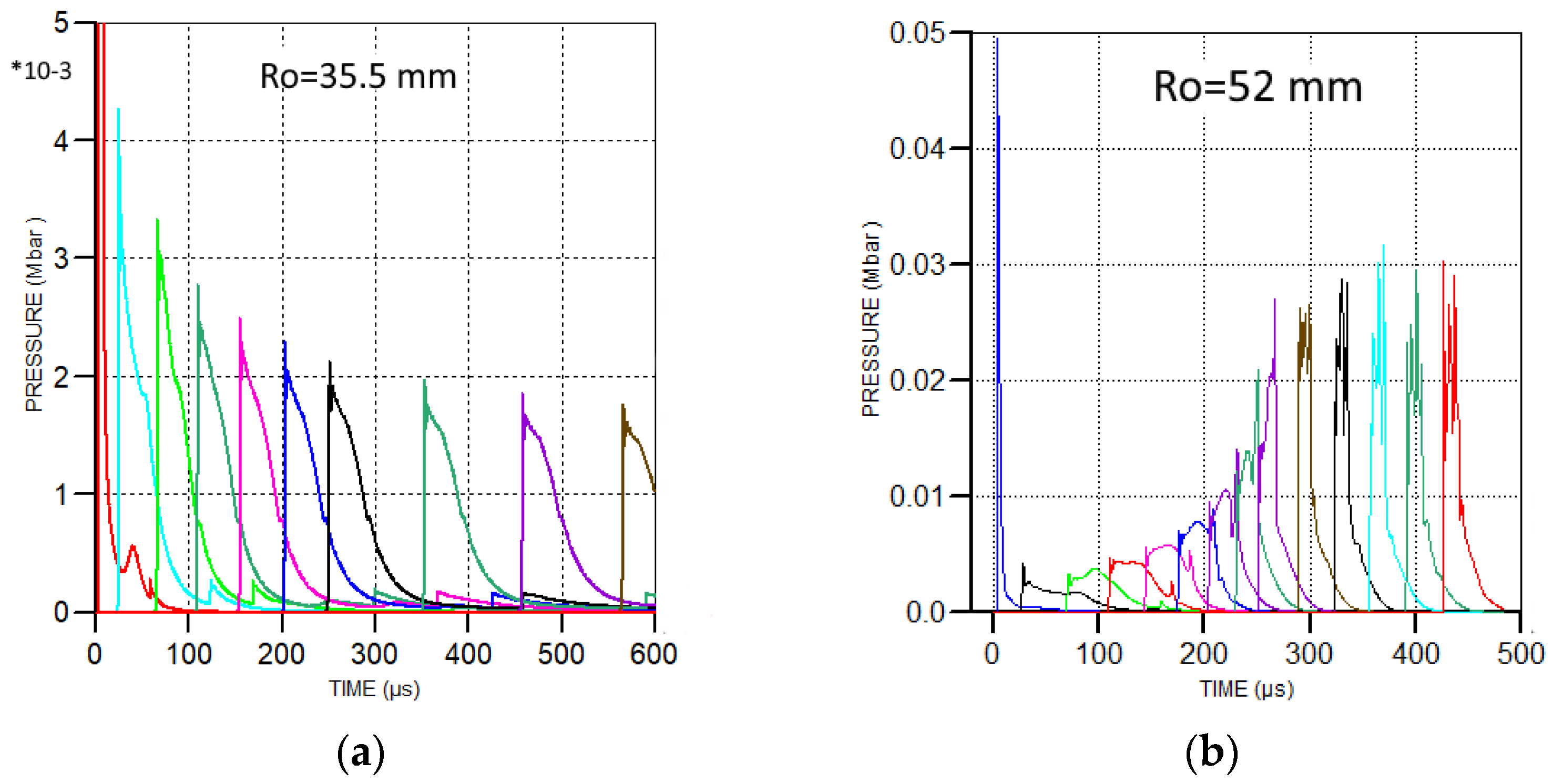
| 104 | 52 | 2.85 | 2.88 | 2.94 | 2.77 | 600 | 600 | 5.77 |
| 119 | 59.5 | 3.15 | 3.31 | 3.22 | 3.10 | 650 | 420 | 3.53 |
| 154 | 77 | 3.68 | 3.89 | 3.58 | 3.57 | 500 | 380 | 2.47 |
| 250 | 125 | 4.59 | 4.01 | 4.10 | 300 | 1.20 | ||
| 1000 | 500 | 4.85 | 4.56 | 4.57 | 280 | 0.28 | ||
| Booster (g) | Experiment | AUTODYN | ||
|---|---|---|---|---|
| VoD * (km/s) | VoD ** (km/s) | VoDmin (km/s) | xSDT (mm) | |
| 1 | 2.35 | 3.34 | 0.81 | 450 |
| 5 | 3.34 | 1.10 | 400 | |
| 20 | 3.04 | 3.28 | 1.72 | 330 |
| 50 | 3.19 | 3.31 | 2.10 | 320 |
| 100 | 3.46 | 3.33 | 2.25 | 290 |
| 200 | 3.32 | 2.45 | 260 | |
| 500 | 3.32 | 2.55 | 250 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bohanek, V.; Štimac Tumara, B.; Serene, C.H.Y.; Sućeska, M. Shock Initiation and Propagation of Detonation in ANFO. Energies 2023, 16, 1744. https://doi.org/10.3390/en16041744
Bohanek V, Štimac Tumara B, Serene CHY, Sućeska M. Shock Initiation and Propagation of Detonation in ANFO. Energies. 2023; 16(4):1744. https://doi.org/10.3390/en16041744
Chicago/Turabian StyleBohanek, Vječislav, Barbara Štimac Tumara, Chan Hay Yee Serene, and Muhamed Sućeska. 2023. "Shock Initiation and Propagation of Detonation in ANFO" Energies 16, no. 4: 1744. https://doi.org/10.3390/en16041744
APA StyleBohanek, V., Štimac Tumara, B., Serene, C. H. Y., & Sućeska, M. (2023). Shock Initiation and Propagation of Detonation in ANFO. Energies, 16(4), 1744. https://doi.org/10.3390/en16041744







