Numerical Study of Wall Heat Transfer Effects on Flow Separation in a Supersonic Overexpanded Nozzle
Abstract
:1. Introduction
2. Materials and Methods
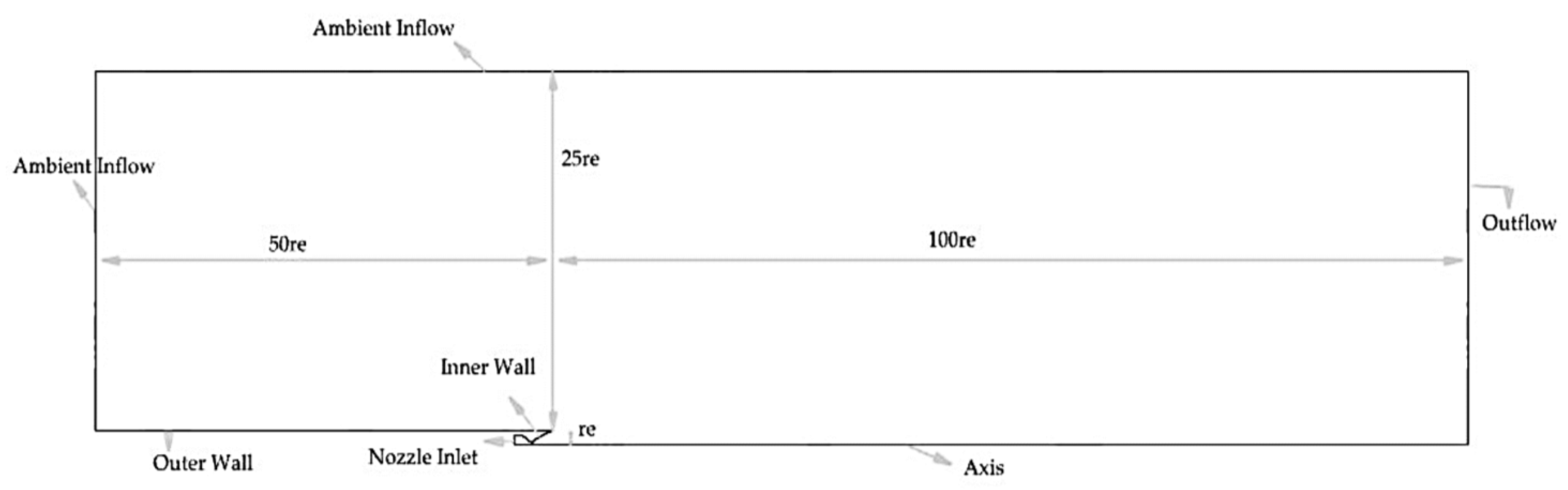
2.1. Computational Domain and Boundary Conditions
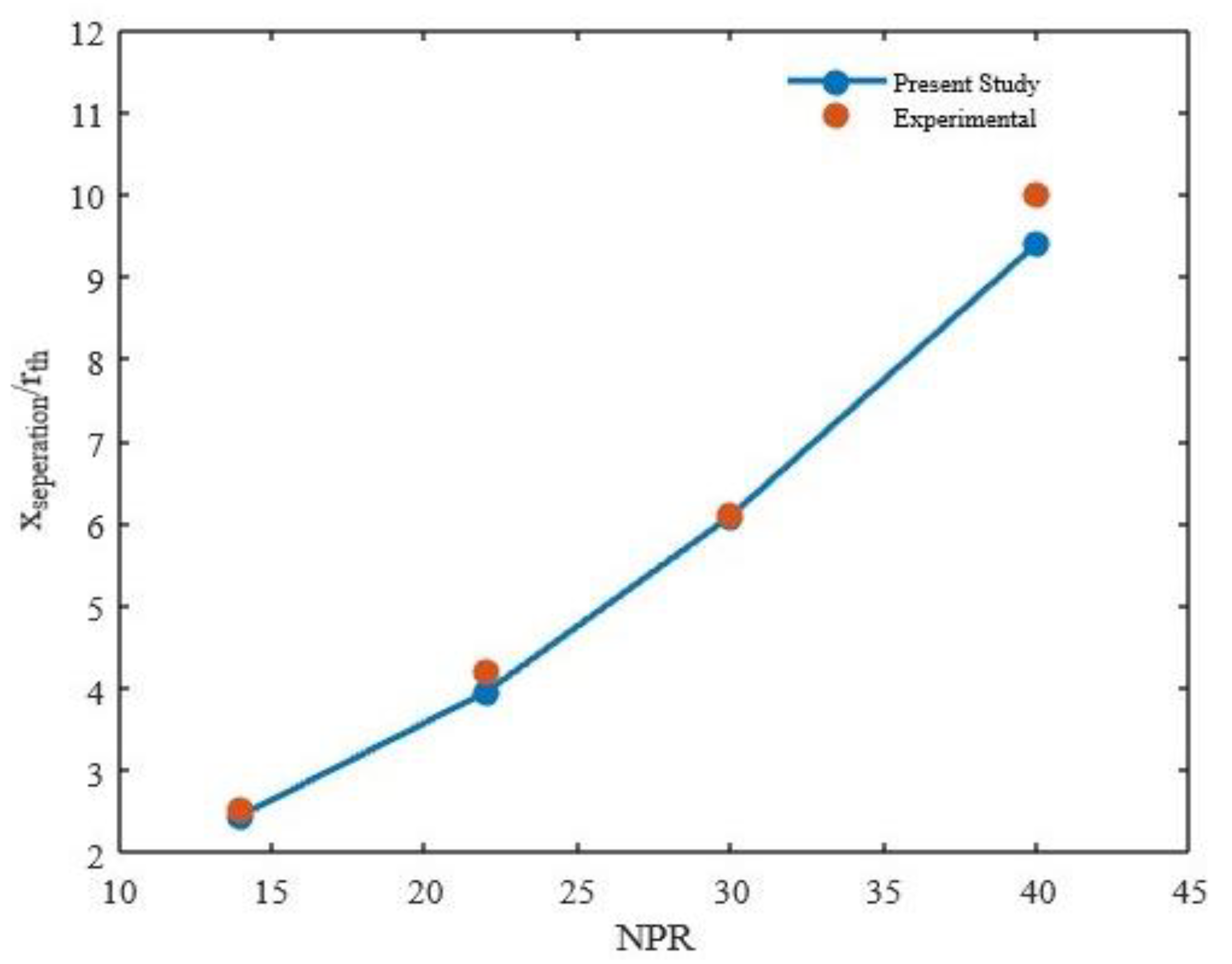
2.2. Validation
3. Results
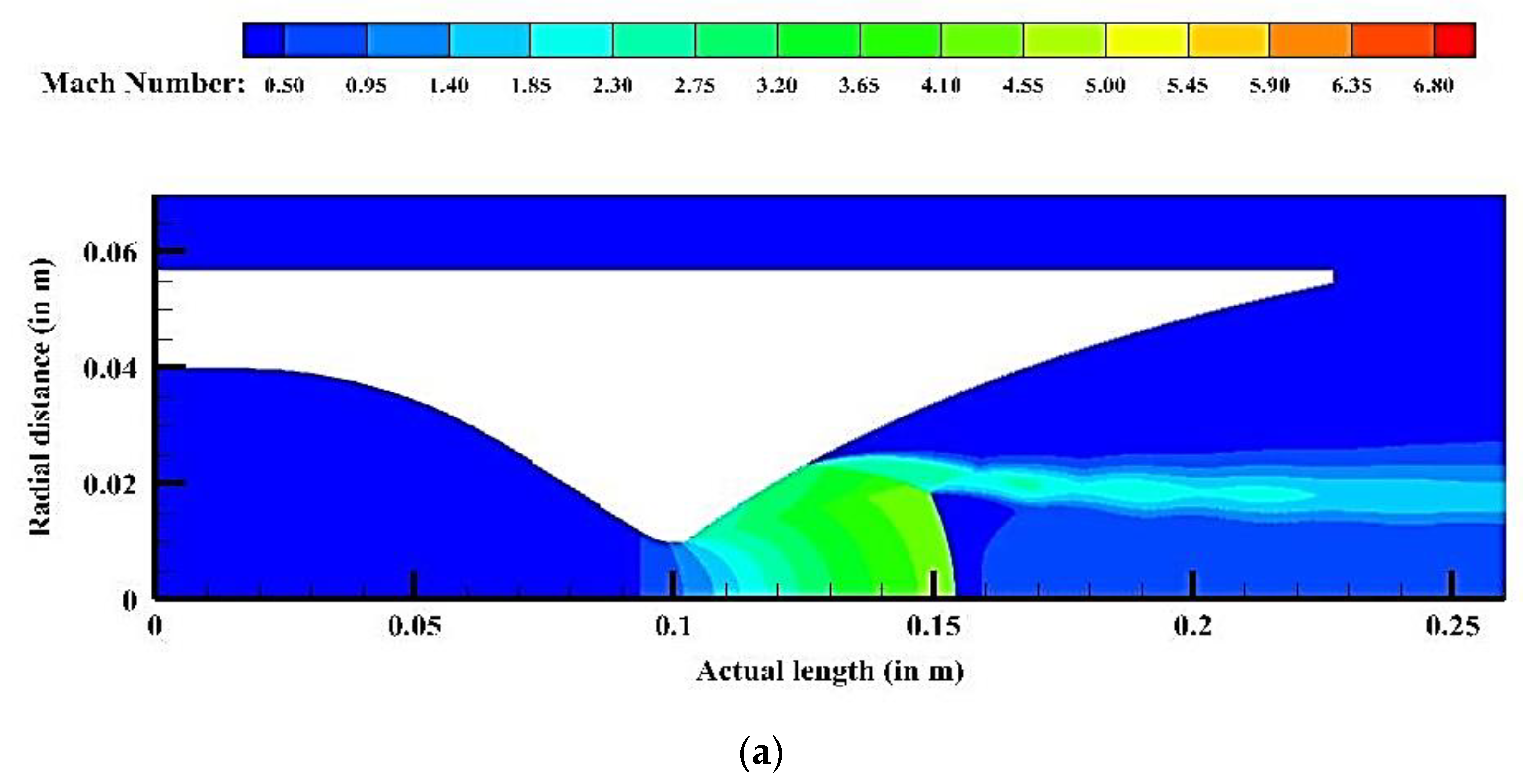
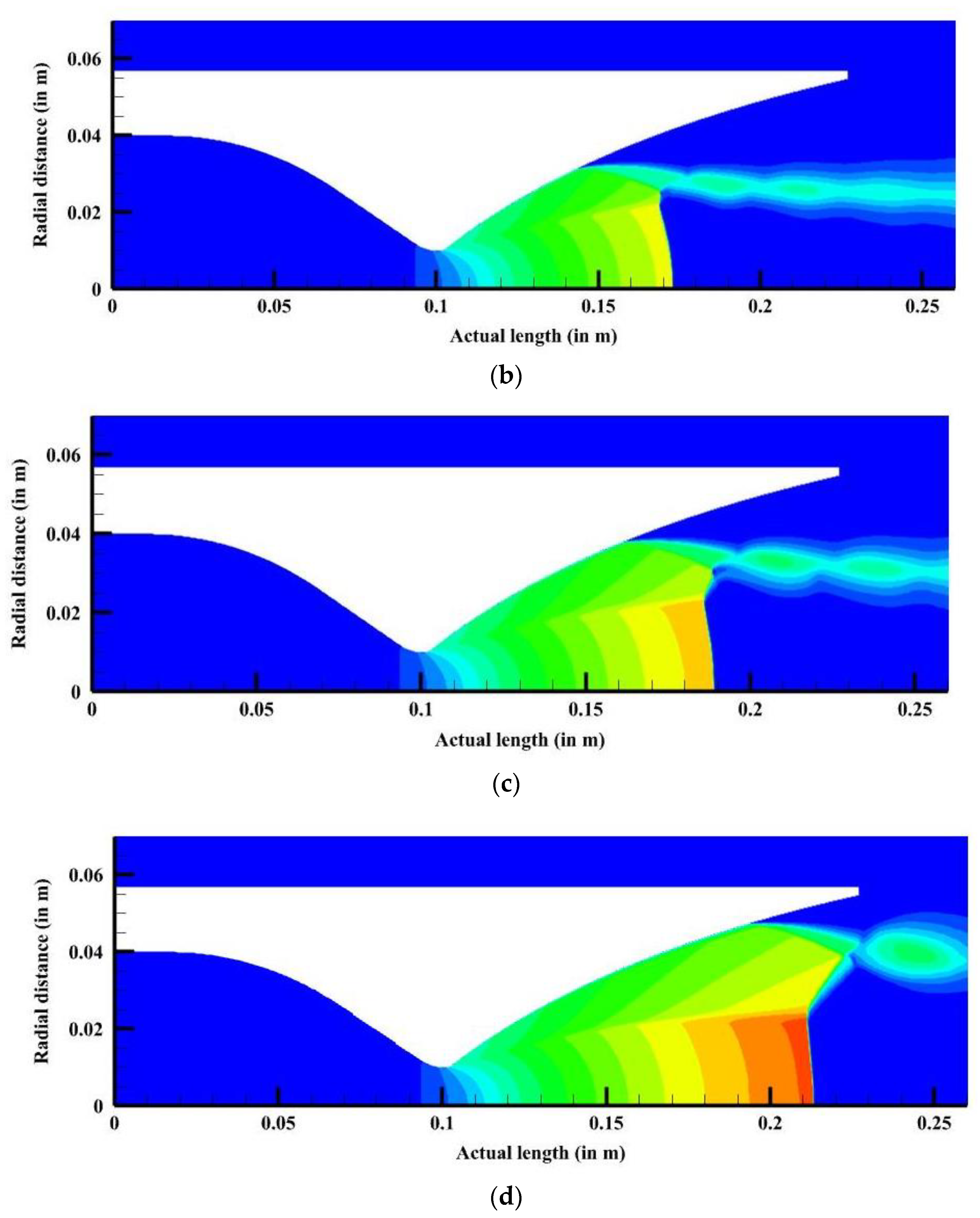
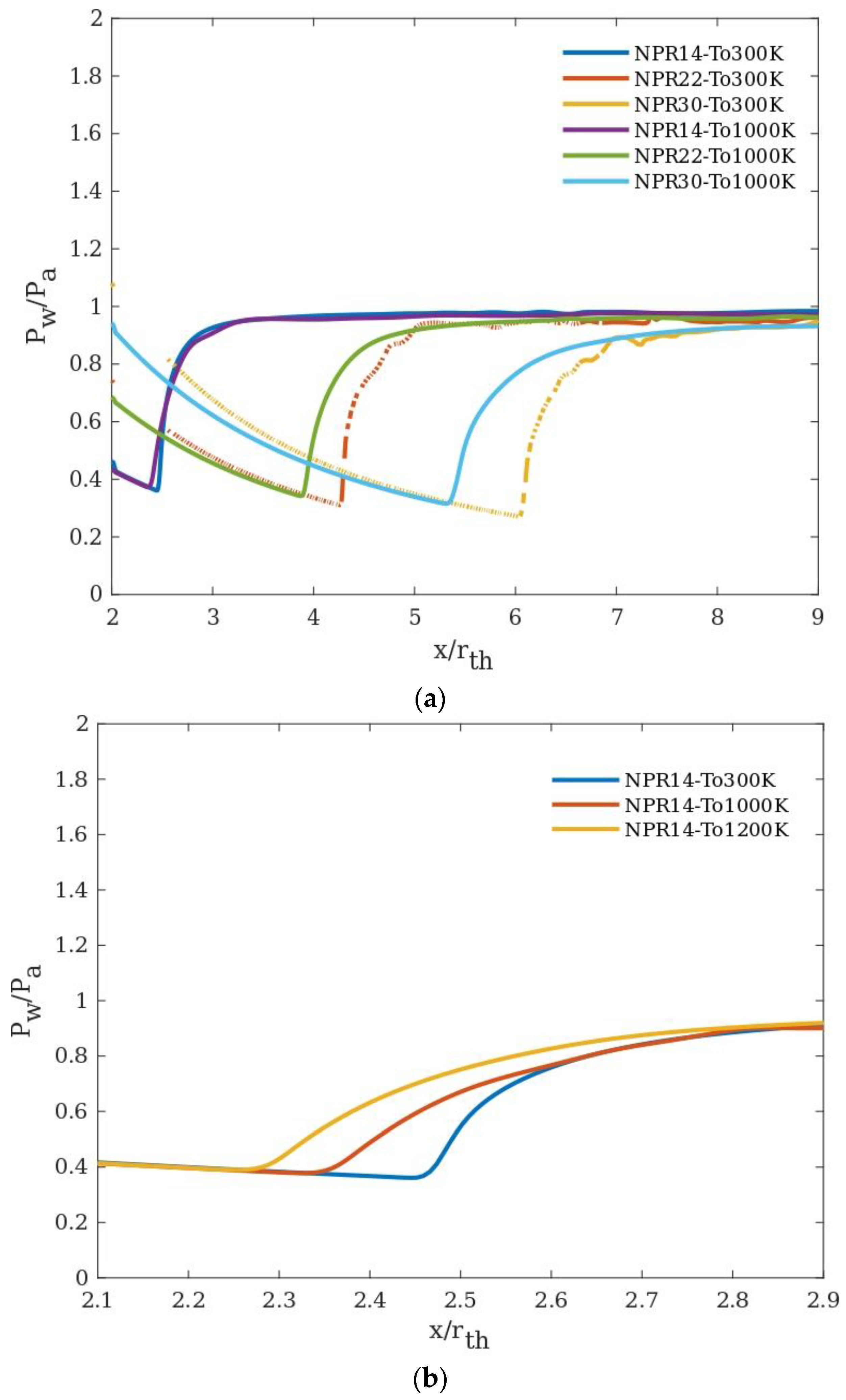
3.1. Effect of Nozzle Pressure Ratio (NPR)
3.2. Effect of Inlet Temperatures
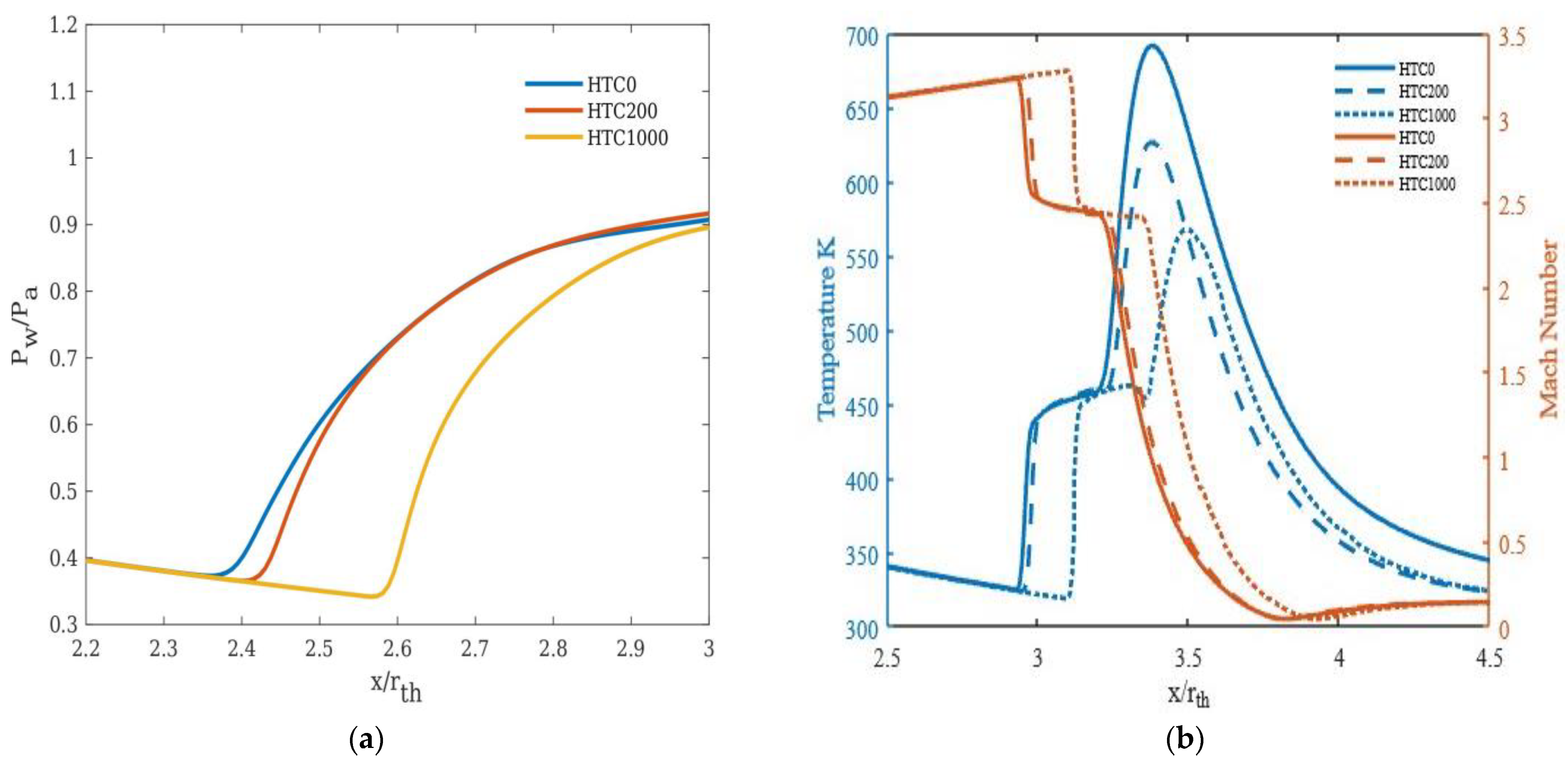
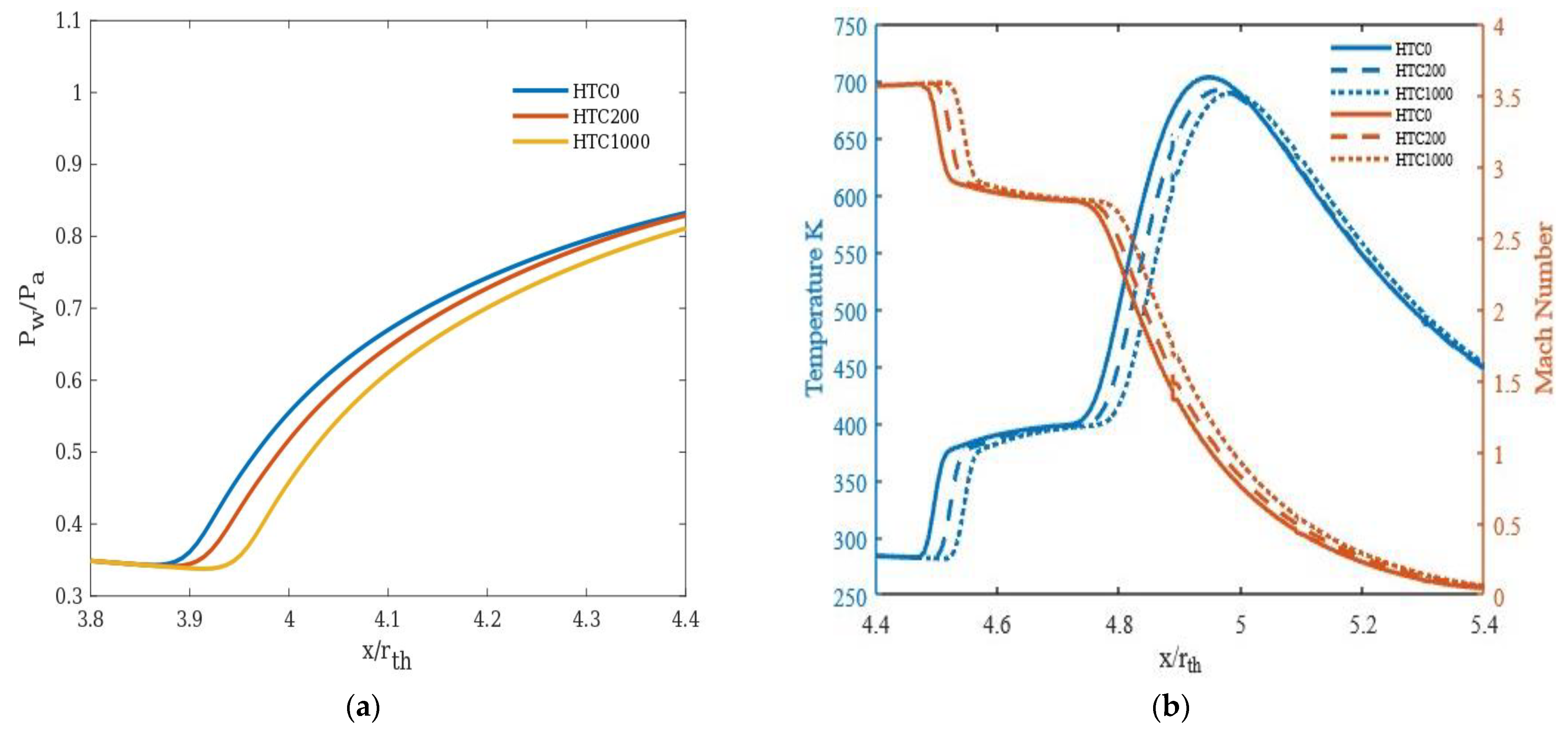
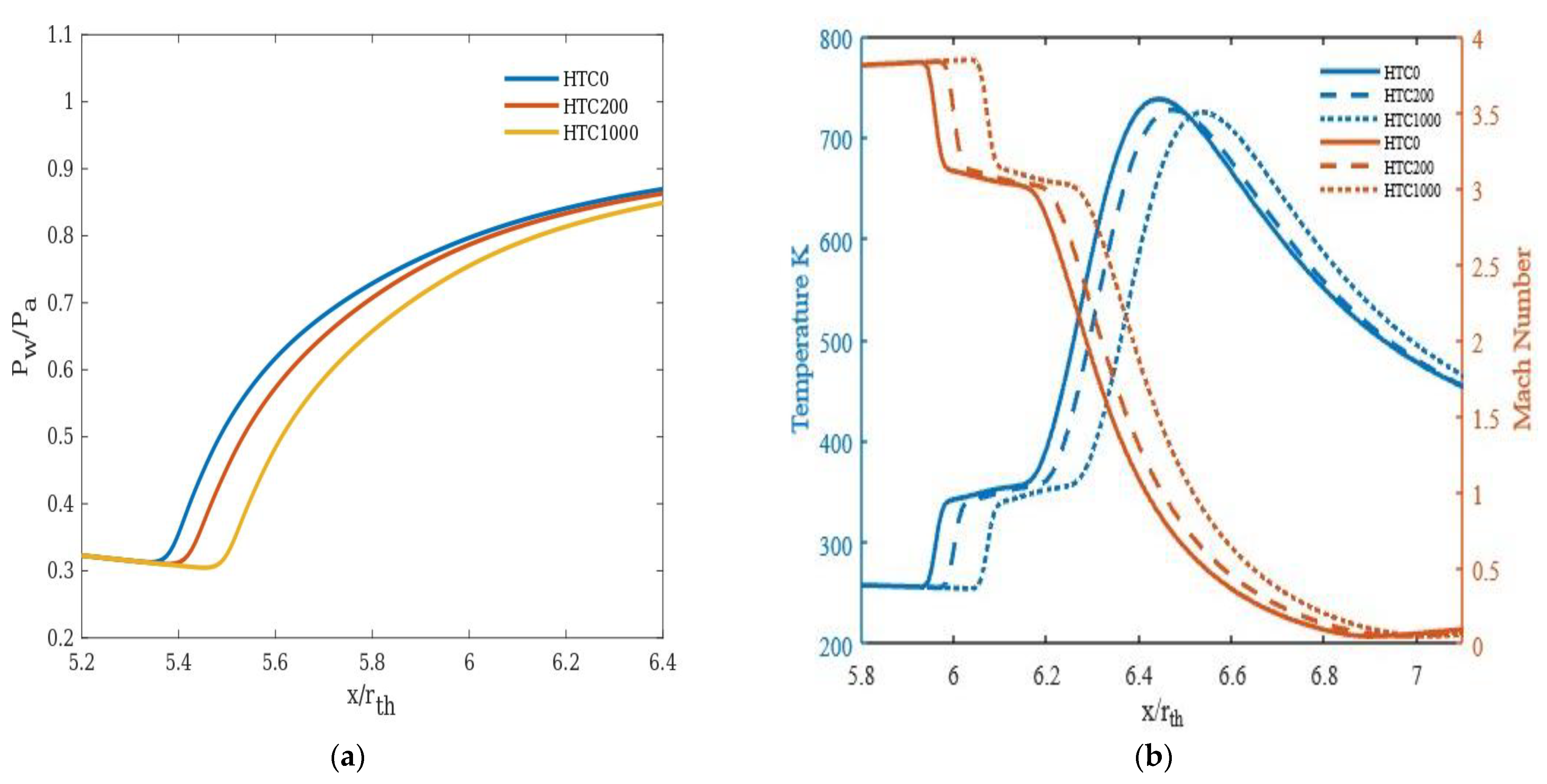
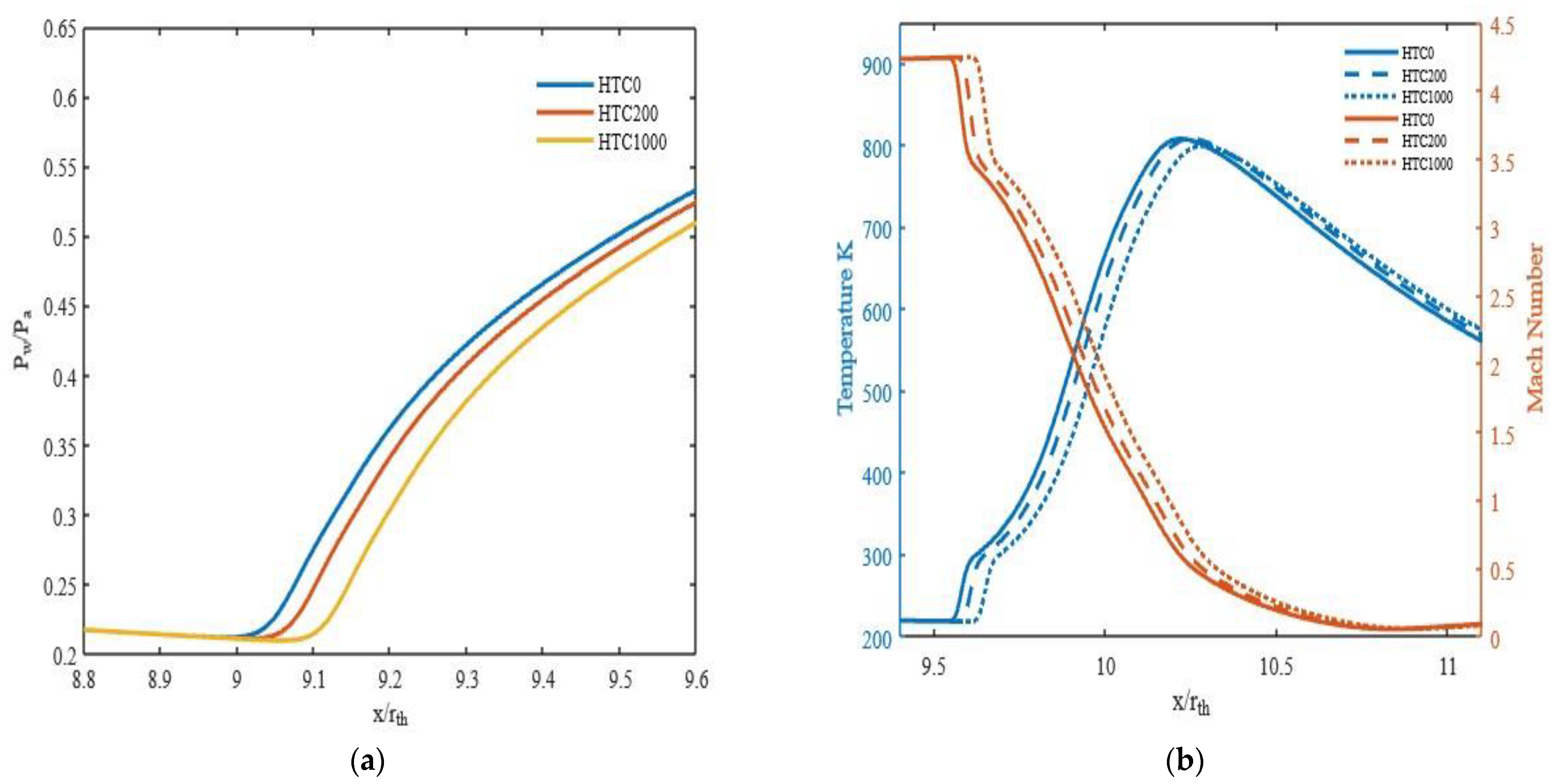
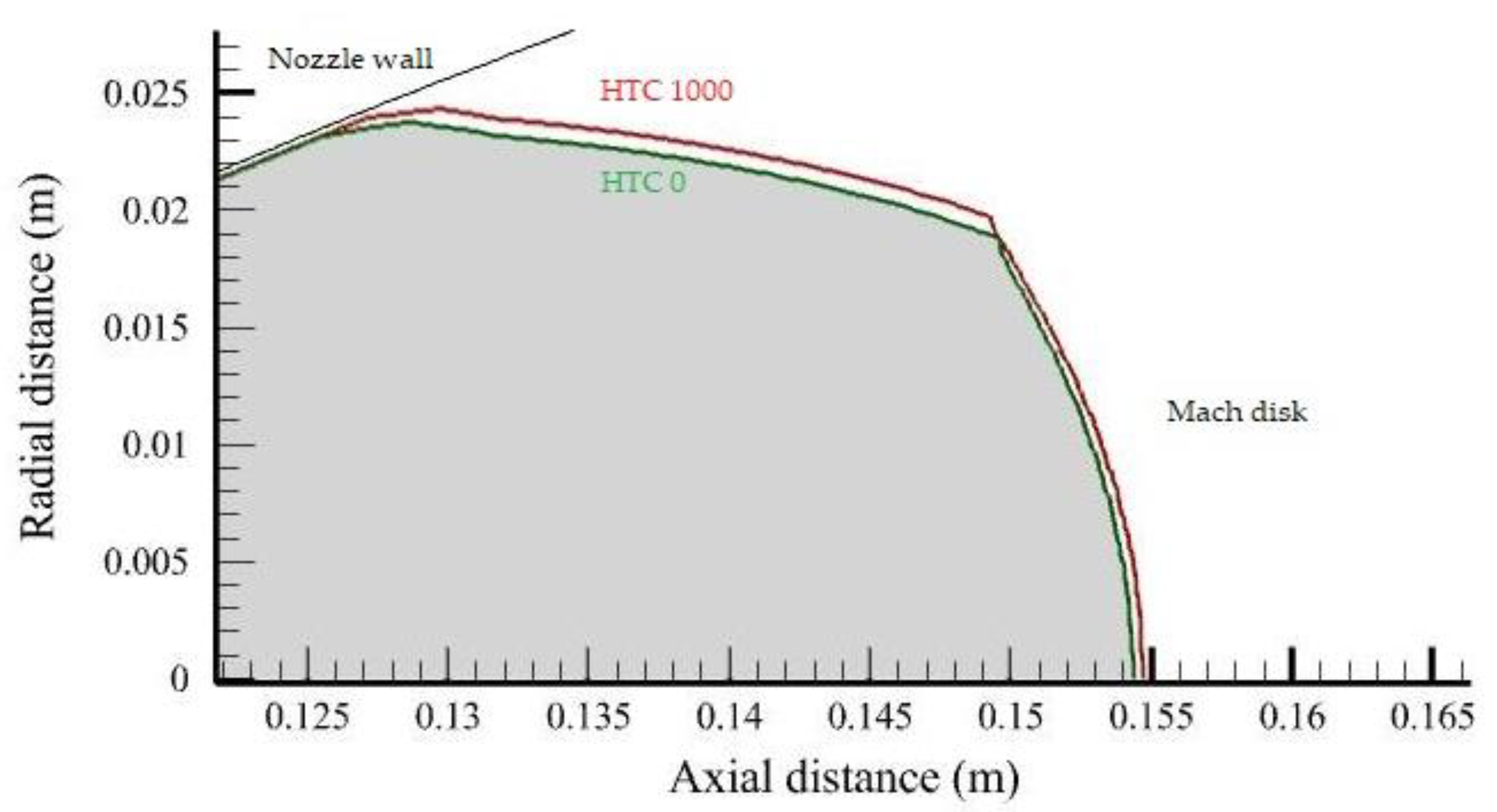
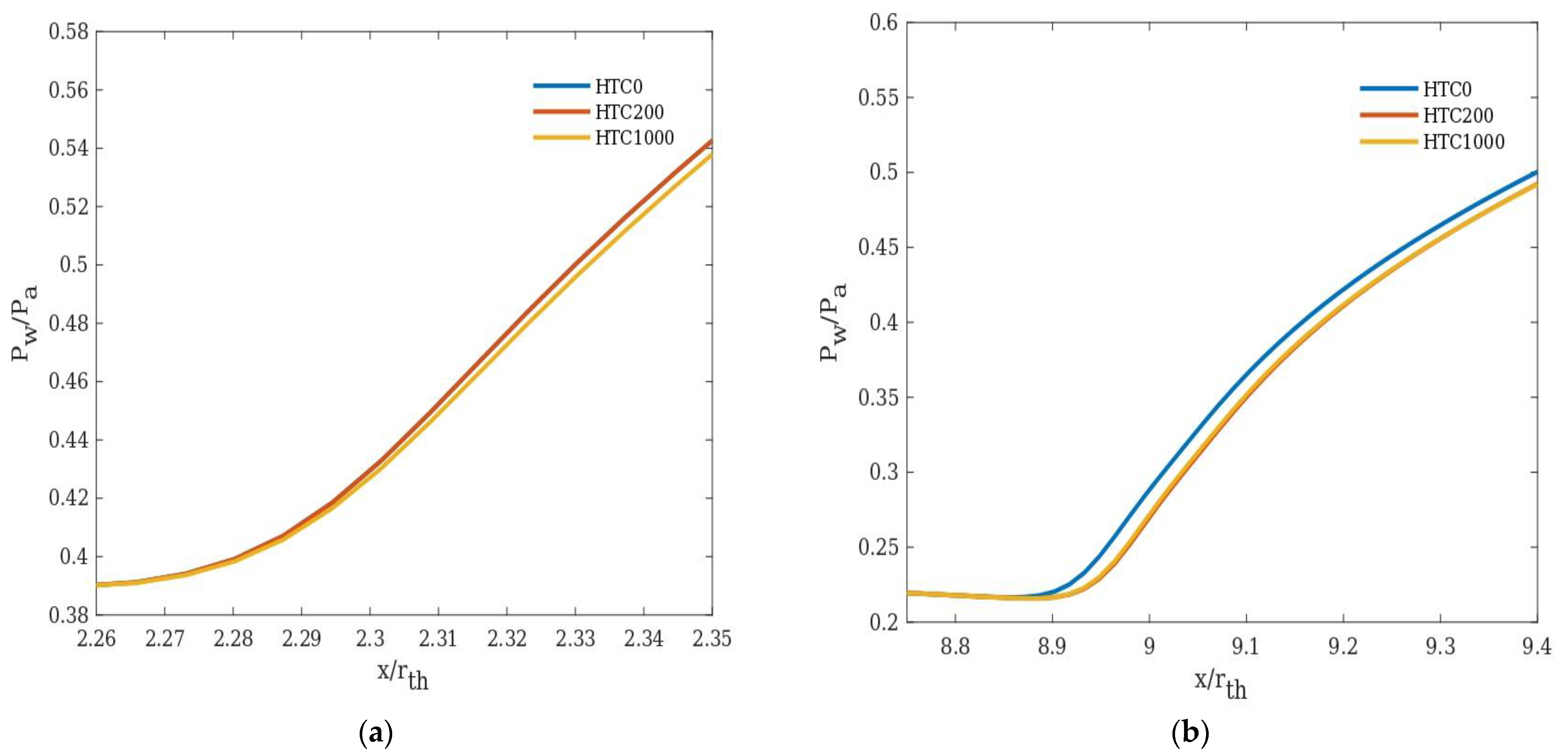
3.3. Effect of Heat Transfer Coefficients
4. Conclusions
- Increasing the inlet gas temperature results in early occurrence of separation, and for higher NPRs, the separation occurs much earlier than the lower NPRs, i.e., for NPR 14 the separation was delayed by Xft/Rth = 0.08 and the corresponding delay for NPR 30 was Xft/Rth = 0.72.
- Wall cooling (modelled in the study by way of heat transfer boundary condition) is found to delay the separation significantly under certain inlet conditions, under which the separation moves towards the nozzle exit plane further with an increase in wall heat transfer. For NPR 14 at an inlet temperature of 1000 K, the separation point moves towards the nozzle exit by 8.8% with cooling and 1.5 to 2.5% for other NPRs.
- At an inlet temperature of 1000 K, the effect of heat transfer appears to be significant for NPR 14 compared to the other NPRs considered in the study.
- With an increase in inlet temperature, the effect of heat transfer on flow separation progressively diminishes over the pressure ratios considered.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sutton, G. Rocket Propulsion Elements; John Wiley & Sons: Hoboken, NJ, USA, 1967; Volume 3. [Google Scholar]
- Östlund, J.; Damgaard, T.; Frey, M. Side-Load Phenomena in Highly Overexpanded Rocket Nozzles. J. Propuls. Power 2004, 20, 695–704. [Google Scholar] [CrossRef]
- Swan, W. The Influence of Nozzle Design on the Flight Performance of Rocket Vechicles with An Analysis of the Results of Jet Separation. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1948. [Google Scholar]
- Foster, C.R.; Cowles, F.B. Experimental Study of Gas Flow Separation in Overexpanded Exhaust Nozzles for Rocket Motors; Progress Report; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 1949. [Google Scholar]
- Summerfield, M.; Foster, C.R.; Swan, W.C. Flow separation in overexpanded supersonic exhaust nozzles. Jet Propuls. 1954, 24, 319–321. [Google Scholar]
- Nave, L.; Coffey, G. Sea level side loads in high-area-ratio rocket engines. In Proceedings of the AIAA/SAE 9th Propulsion Conference, Las Vegas, NV, USA, 5–7 November 1973. [Google Scholar] [CrossRef]
- Romine, G.L. Nozzle flow separation. AIAA J. 1998, 36, 1618–1625. [Google Scholar] [CrossRef]
- Stark, R.; Hagemann, G. Current status of numerical flow prediction for separated nozzle flows. In Proceedings of the 2nd European Conference for Aerospace Sciences (EUCASS), Brussels, Belgium, 1–6 July 2007. [Google Scholar]
- Ostlund, J.; Jaran, M. Assesment of Turbulence Models in Overexpanded Rocket Nozzle Flow Simulations. In Proceedings of the 35th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Los Angeles, CA, USA, 20–24 June 1999. [Google Scholar]
- Nebbache, A.; Pilinski, C. Pulsatory phenomenon in a thrust optimized contour nozzle. Aerosp. Sci. Technol. 2006, 10, 295–308. [Google Scholar] [CrossRef]
- Pilinski, C.; Nebbache, A. Flow separation in a truncated ideal contour nozzle. J. Turbul. 2004, 5. [Google Scholar] [CrossRef]
- Yonezawa, K.; Morimoto, T.; Tsujimoto, Y.; Watanabe, Y.; Yokota, K. A Study of an Asymmetric Flow in an Overexpanded Rocket Nozzle. J. Fluid Sci. Technol. 2007, 2, 400–409. [Google Scholar] [CrossRef]
- Allamaprabhu, Y.; Raghunandan, B.N.; Moríñigo, J.A. Numerical prediction of nozzle flow separation: Issue of turbulence modeling. Aerosp. Sci. Technol. 2016, 50, 31–43. [Google Scholar] [CrossRef]
- Lárusson, R.; Andersson, N.; Janöstlund, J. Hybrid RANS-LES Simulation of Separated Nozzle Flow. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar]
- Kamali, R.; Mousavi, S.M.; Khojasteh, D. Three-Dimensional Passive and Active Control Methods of Shock Wave Train Physics in a Duct. Int. J. Appl. Mech. 2016, 8. [Google Scholar] [CrossRef]
- Chen, C.L.; Chakravarthy, S.R.; Hung, C.M. Numerical investigation of separated nozzle flows. AIAA J. 1994, 32, 1836–1843. [Google Scholar] [CrossRef]
- Frey, M.; Hagemann, G. Status of Flow Separation Prediction in Rocket Nozzles. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998. [Google Scholar]
- Onofri, M.; Nasuti, F.; Nasutit, E. The Physical Origins of Side Loads in Rocket Nozzles. In Proceedings of the 35th AIAA/ASME/SAE/ASEE Joint Propulsion conference and Exhibit, Los Angeles, CA, USA, 20–23 June 1999. [Google Scholar]
- Thongsri, J.; Srathonghuam, K.; Boonpan, A. Gas Flow and Ablation of 122 mm Supersonic Rocket Nozzle Investigated by Conjugate Heat Transfer Analysis. Processes 2022, 10, 1823. [Google Scholar] [CrossRef]
- Haroon, M.; Rasheed, S.; Irfan, M.; Masud, M.; Munawar, M.A. Computational Investigation of the Flow Structure through an Over-Expanded Nozzle. Eng. Proc. 2022, 23, 7. [Google Scholar] [CrossRef]
- Gross, A.; Weiland, C. Numerical simulation of separated cold gas nozzle flows. J. Propuls. Power 2004, 20, 509–519. [Google Scholar] [CrossRef]
- Nasuti, F.; Onofri, M. Shock structure in separated nozzle flows. Shock. Waves 2008, 19, 229–237. [Google Scholar] [CrossRef]
- Östlund, J.; Muhammad-Klingmann, B. Supersonic flow separation with application to rocket engine nozzles. Appl. Mech. Rev. 2005, 58, 143–177. [Google Scholar] [CrossRef]
- Sreejith, K.; Dhrishit, M.; Deepu, M.; Jyachandran, T. Numerical Analysis of Flow Separation in Rocket Nozzles. In Proceedings of the 5th International and 41st National Conference on FMFP, Kanpur, India, 12–14 December 2014; Available online: http://www.springer.com/series/11236 (accessed on 21 September 2016).
- Bhide, K.; Siddappaji, K.; Abdallah, S. Influence of fluid–thermal–structural interaction on boundary layer flow in rectangular supersonic nozzles. Aerospace 2018, 5, 33. [Google Scholar] [CrossRef]
- Zmijanovic, V.; Rasuo, B.; Chpoun, A. Flow separation modes and side phenomena in an over expanded nozzle. FME Trans. 2012, 40, 111–118. [Google Scholar]
- Fouladi, N.; Farahani, M. Numerical investigation of second throat exhaust diffuser performance with thrust optimized parabolic nozzles. Aerosp. Sci. Technol. 2020, 105, 106020. [Google Scholar] [CrossRef]
- Ivanov, I.E.; Kryukov, I.A. Numerical study of ways to prevent side loads in an over–expanded rocket nozzles during the launch stage. Acta Astronaut. 2019, 163, 196–201. [Google Scholar] [CrossRef]
- Sreerag, V.N.; Mohammad, F.; Nandan, V.; Pramod, A.; Subhajayan, K.P.; Jash, S. Parametric study on a method to control flow separation in rocket nozzles. Mater. Today Proc. 2021, 46, 9950–9955. [Google Scholar] [CrossRef]
- Khobragade, N.; Wylie, J.; Gustavsson, J.; Kumar, R. Control of Flow Separation in a Rocket Nozzle Using Microjets. New Space 2019, 7, 31–42. [Google Scholar] [CrossRef]
- Hadjadj, A.; Perrot, Y.; Verma, S. Numerical study of shock/boundary layer interaction in supersonic overexpanded nozzles. Aerosp. Sci. Technol. 2015, 42, 158–168. [Google Scholar] [CrossRef]
- Verma, M.; Arya, N.; De, A. Investigation of flow characteristics inside a dual bell nozzle with and without film cooling. Aerosp. Sci. Technol. 2020, 99, 105741. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, C.; Tian, W. Study on Separation Characteristics of Nozzles with Large Expansion Ratio of Solid Rocket Motors. Aerospace 2022, 10, 4. [Google Scholar] [CrossRef]
- Shimura, K.; Asako, Y.; Lee, J.H. Numerical analysis for supersonic flows in a cooled nozzle. Numer. Heat Transfer Part A Appl. 1994, 26, 631–641. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Fluent: Theory Guide; Release 2020 R1; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Murugesan, P.; Arjun, B.; Akhil, T.K.; Shashank, P.; Girish, C.C.; Srikrishnan, A.R.; Ratna, K.V. Numerical study of characteristics of underexpanded supersonic jet. J. Aerosp. Technol. Manag. 2020, 12, 1–8. [Google Scholar] [CrossRef]
- Sudhan, K.H.; Prasad, G.K.; Kothurkar, N.K.; Srikrishnan, A.R. Studies on supersonic cold spray deposition of microparticles using a bell-type nozzle. Surf. Coat. Technol. 2019, 383, 125244. [Google Scholar] [CrossRef]
- Murugu, S.P.; Srikrishnan, A.R.; Krishnaraj, B.K.; Jayaraj, A.; Mohammad, A.; Velamati, R.K. Acoustic Modeling of Compressible Jet from Chevron Nozzle: A Comparison of URANS, LES and DES Models. Symmetry 2022, 14, 1975. [Google Scholar] [CrossRef]
- Verma, S.B. Shock unsteadiness in a thrust optimized parabolic nozzle. Shock. Waves 2008, 19, 193–212. [Google Scholar] [CrossRef]




| Authors | Turbulence Model | Nozzle Contour | Remarks on Validation |
|---|---|---|---|
| Ostlund et al. [9] | SST | TOP | over prediction for NPR 12 and 16.2 |
| Nebbache et al. [10] | SST | TOC | over prediction for NPR < 23.9 |
| Pilinski et al. [11] | SST | TIC | under prediction for NPR < 34.7 over prediction for NPR > 41.3 |
| Yonezawa et al. [12] | SST and SA | CTP (Compressed Truncated Perfect) | no differences between the two models, underpredicted |
| Stark et al. [8] | SST | TIC | Under prediction for NPR 25 |
| Authors | Nozzle Contour | Area Ratio | Nozzle Inlet Temperature (K) | Nozzle Wall Boundary Condition |
|---|---|---|---|---|
| Ostlund et al. [23] | TIC, TOP, TOC, Conical | 43.4 | 270 | Adiabatic |
| Ostlund and Jaran et al. [9] | TIC, TOP, Conical | 45, 43.4 | 270 | Adiabatic |
| Nebbache et al. [10] | TOC | 30.32 | 270 | Adiabatic |
| Pilinski et al. [11] | TIC | 13.9 | 270 | Adiabatic |
| Yonezawa et al. [12] | CTP | 49 | 290 | Adiabatic |
| Allamprabhu et al. [13] | TOP | 30 | 270 | Adiabatic |
| Laurusson et al. [14] | Parabolic nozzle | 300 | Adiabatic | |
| Onofri et al. [18] | TOP | 45 | 300 | Adiabatic |
| Gross et al. [21] | TIC, TOP, Dual bell | 13.9, 30 | 300 | Adiabatic |
| Nasuti et al. [22] | TIC, TOC, TOP | 300 | Adiabatic | |
| Sreejith et al. [24] | TIC, TOP and Conical | 13.9, 30 | 300 | Adiabatic |
| Zmijanovic et al. [26] | TOC, TOP | 30.32, 30 | 290 | Adiabatic |
| Fouladi et al. [27] | TOP | 60 | 300 | Adiabatic |
| Ivanov et al. [28] | TOC | 293 | Adiabatic | |
| Sreeraj et al. [29] | Bell nozzle | 30 | 300 | Solid wall |
| Khobragade et al. [30] | CD nozzle | 10.74 | 800 | no heat transfer |
| Hadjadj et al. [31] | TOP, TIC | 30 | 300 | Adiabatic |
| Verma et al. [32] | Dual bell | 300 and 2842 | Adiabatic | |
| Wang et al. [33] | Laval nozzle | 30.25 | Cold flow | Adiabatic |
| Shimura et al. [34] | Conical nozzle | 4.55 | 1200 | wall temperature = 300 K |
| Present study | TOP | 30 | 300, 1000, 1200 and 1500 | Adiabatic and Convective heat transfer (coefficients = 0, 200 and 1000 w/m2K) |
| No. of Elements | Separation Point (X/rth) |
|---|---|
| 198,750 | 2.62 |
| 345,834 | 2.437 |
| 928,387 | 2.434 |
| Boundary | Type | Conditions |
|---|---|---|
| Nozzle inlet | Pressure inlet | Po = NPR*Pa; To = 300 K (for cold flow), 1000, 1200 and 1500 K (for hot flow) (NPR = 14, 22, 30 and 40) |
| Ambient inflow | Pressure inlet | Po = 101,325 pa; To = 300 K |
| Inner wall | Wall | No slip; Adiabatic and convective heat transfer (HTC = 0, 200 and 1000 w/m2K) |
| Outer wall | Wall | Adiabatic |
| Outflow | Pressure outlet | Pa = 101,325 pa |
| HTC | Q_NPR14 | Q_NPR22 | Q_NPR30 | Q_NPR40 |
|---|---|---|---|---|
| 0 | - | - | - | - |
| 200 | 13.69 | 23.35 | 23.15 | 22.78 |
| 1000 | 34.55 | 116.6 | 115.76 | 113.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murugesan, P.; Srikrishnan, A.R.; Mohammad, A.; Velamati, R.K. Numerical Study of Wall Heat Transfer Effects on Flow Separation in a Supersonic Overexpanded Nozzle. Energies 2023, 16, 1762. https://doi.org/10.3390/en16041762
Murugesan P, Srikrishnan AR, Mohammad A, Velamati RK. Numerical Study of Wall Heat Transfer Effects on Flow Separation in a Supersonic Overexpanded Nozzle. Energies. 2023; 16(4):1762. https://doi.org/10.3390/en16041762
Chicago/Turabian StyleMurugesan, Priyadharshini, A. R. Srikrishnan, Akram Mohammad, and Ratna Kishore Velamati. 2023. "Numerical Study of Wall Heat Transfer Effects on Flow Separation in a Supersonic Overexpanded Nozzle" Energies 16, no. 4: 1762. https://doi.org/10.3390/en16041762
APA StyleMurugesan, P., Srikrishnan, A. R., Mohammad, A., & Velamati, R. K. (2023). Numerical Study of Wall Heat Transfer Effects on Flow Separation in a Supersonic Overexpanded Nozzle. Energies, 16(4), 1762. https://doi.org/10.3390/en16041762








