Research on the Planning of Electric Vehicle Fast Charging Stations Considering User Selection Preferences
Abstract
:1. Introduction
1.1. Problem Statement
1.2. Literature Review
1.3. Contribution to This Article
- Considering the interaction mechanism between EV user behavior and charging stations, which is missing in most current studies, a joint planning method with the objective of optimal planning of charging piles and optimal economic operation of the distribution network is constructed by quantifying EV user behavior as charging trips adding constraints.
- An improved chaotic optimized krill swarm algorithm is proposed, which introduces chaotic mapping in the initial search phase, updates the krill swarm positions, increases the randomness, optimizes the global search capability, takes into account the advantages of the robustness of the krill swarm algorithm, and improves the solution speed of the algorithm by reducing the number of algorithm parameters that need to be adjusted.
- Taking the planning area of fast charging stations and the actual distribution network in a region of Guizhou as the planning object, a case study is conducted with the characteristics of EV user demand satisfaction and the number of planned charging stations and the profitability of charging stations, etc. The results show that the joint planning and optimization method proposed in this paper, which aims at the optimal planning of charging piles and the optimal economic operation of the distribution network, effectively improves the economy and user charging efficiency when building charging stations.
2. Materials and Methods
2.1. Analysis of Electric Vehicle Parking Behavior
2.2. Joint Optimization Model for Optimal Planning of Charging Stations and Economic Operation of Distribution Networks
2.2.1. Optimization Goals
- Charging piles and other annual value investment costs
- 2.
- Annual value of grid, etc., reinforcement costs
- 3.
- Annual operation and maintenance costs of charging piles
- 4.
- Network wear and tear costs
2.2.2. Binding Conditions
- Overall balance constraint of EV charging stroke
- 2.
- Distance constraint of EV charging stroke
- 3.
- Charging pile demand constraint
- 4.
- Charging power constraint
- 5.
- Network tide equation
- 6.
- Nodal voltage magnitude constraint
- 7.
- Branch circuit current constraint
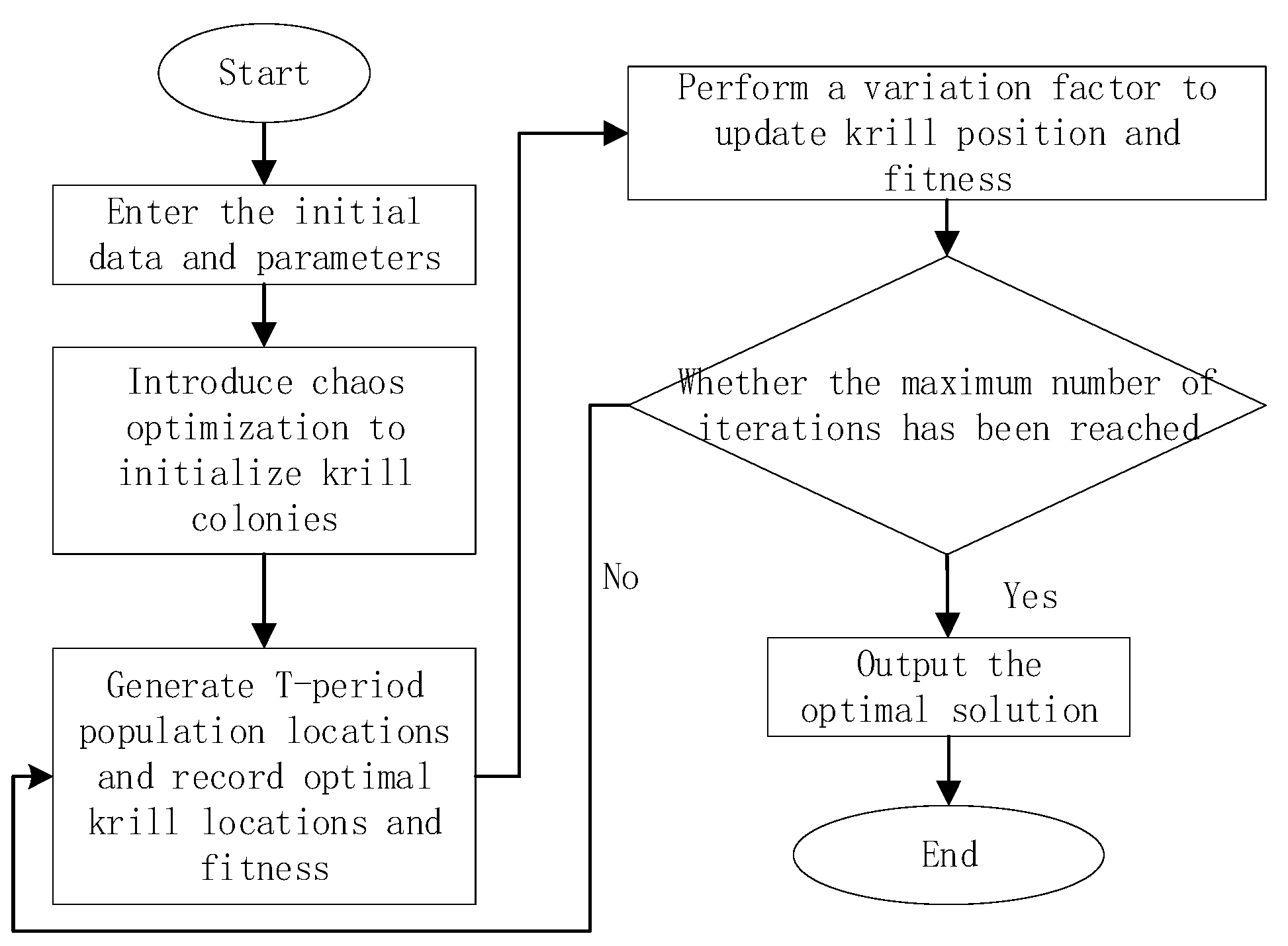
2.3. Improved Krill Swarm Algorithm
2.3.1. A Krill Swarm Algorithm Based on Chaos Optimization
2.3.2. Introduction of Variation Factors
2.3.3. Joint Planning and Optimization of Charging Stations and Distribution Networks Based on Improved Krill Swarm Algorithm
3. Results
3.1. Basic Data
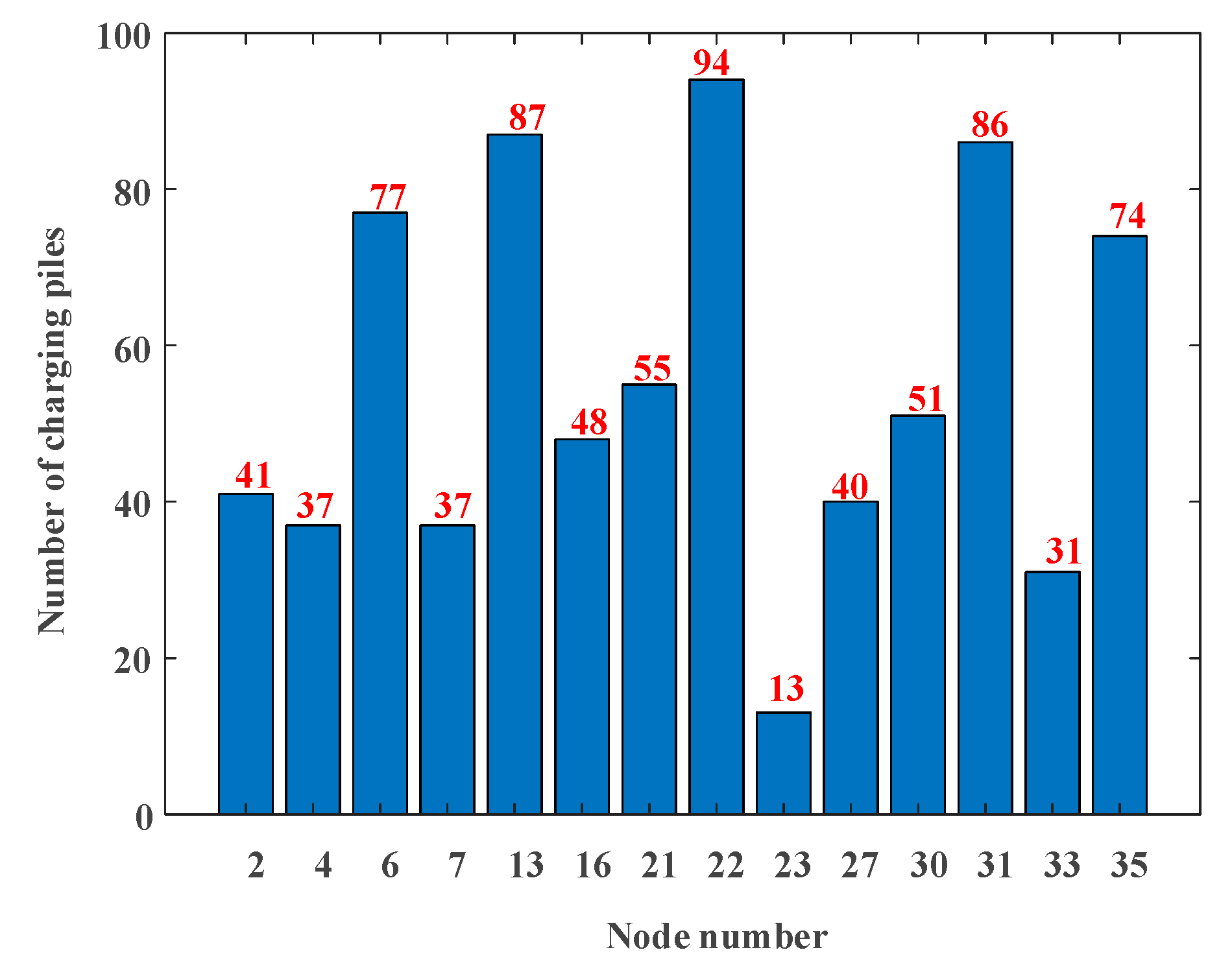
3.2. Optimal Planning Results for Charging Stations
3.3. Sensitivity Analysis
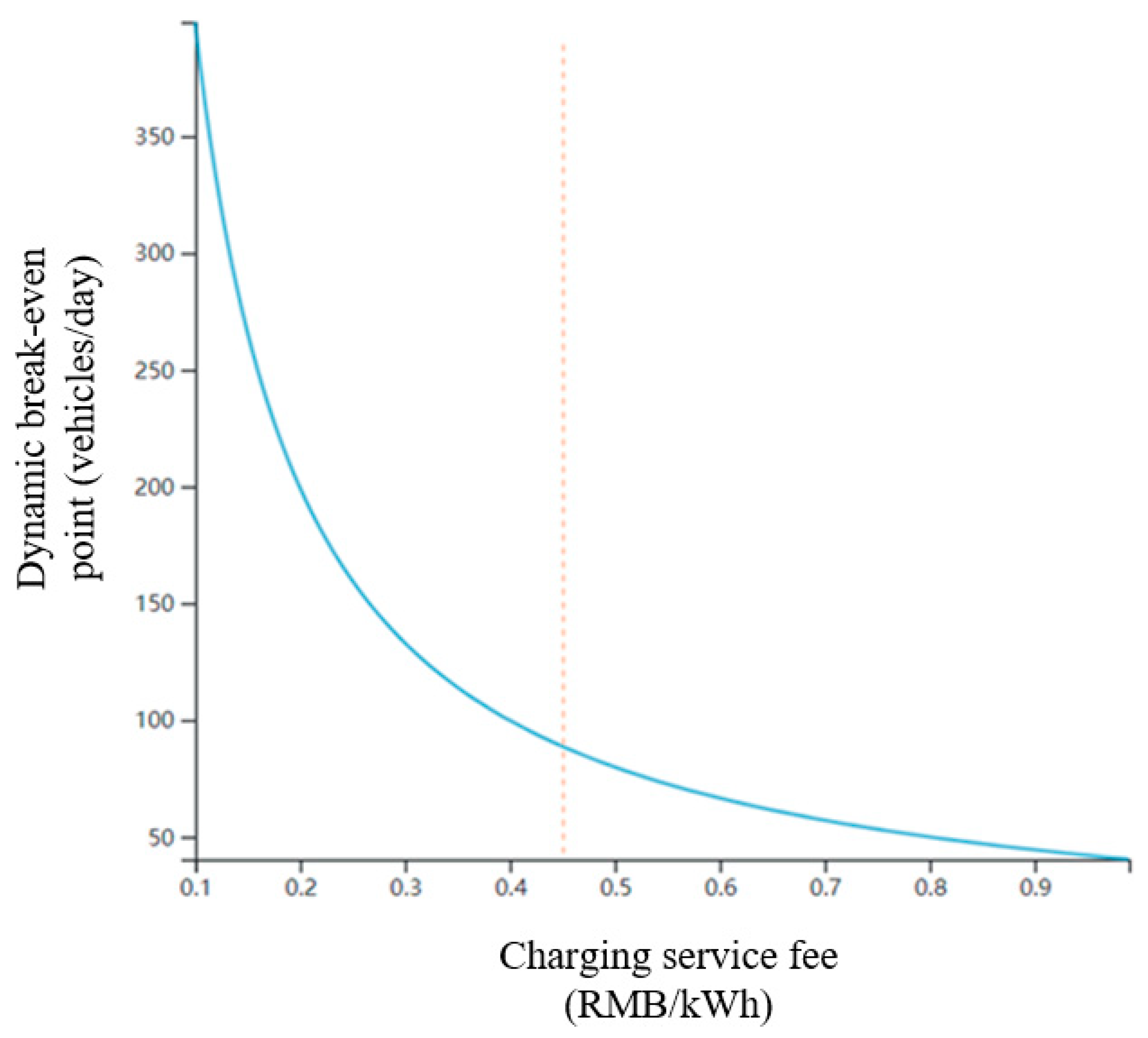
3.3.1. Difference between Electricity Purchase and Charging
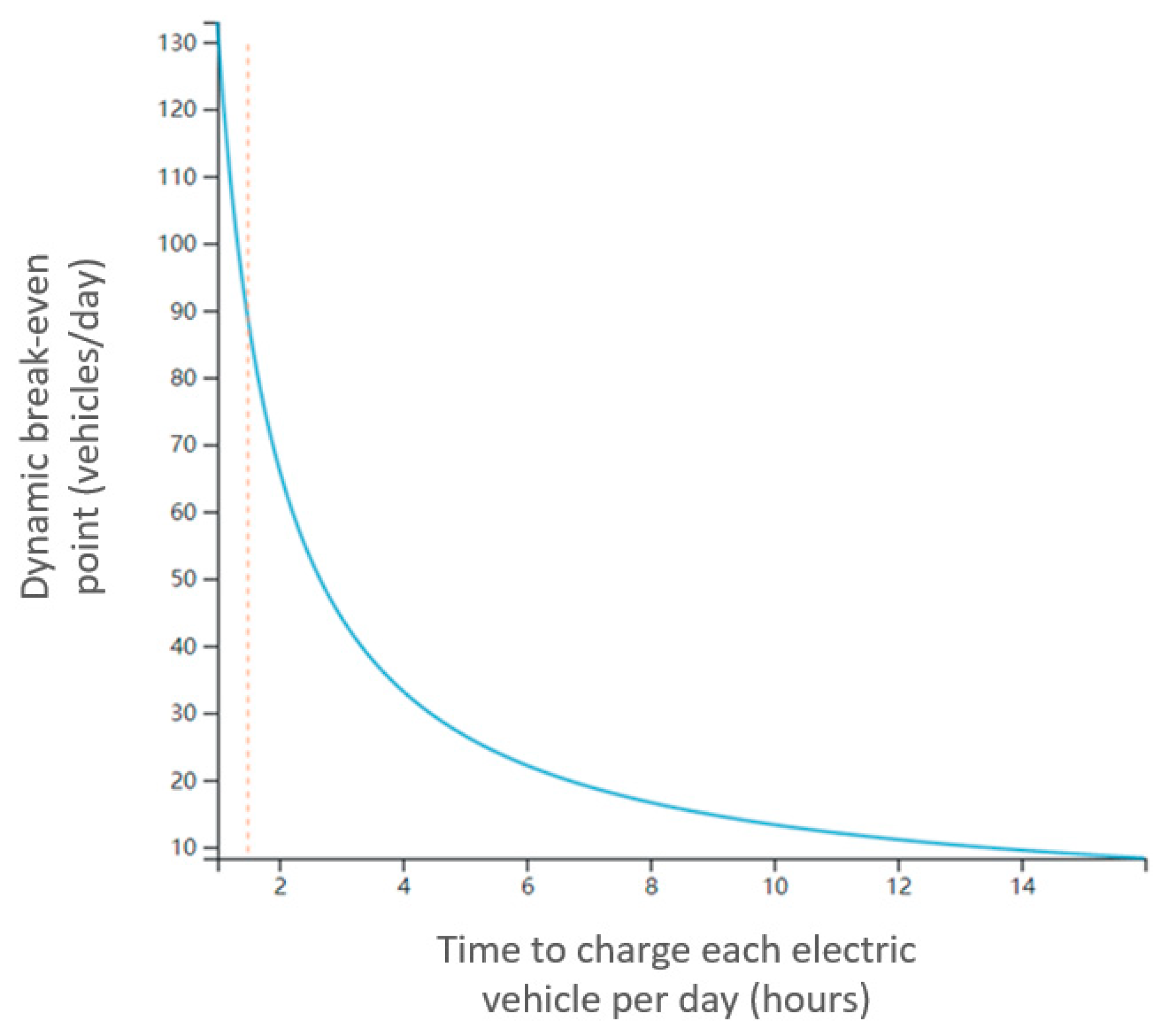
3.3.2. Charging Time and Charging Requirements
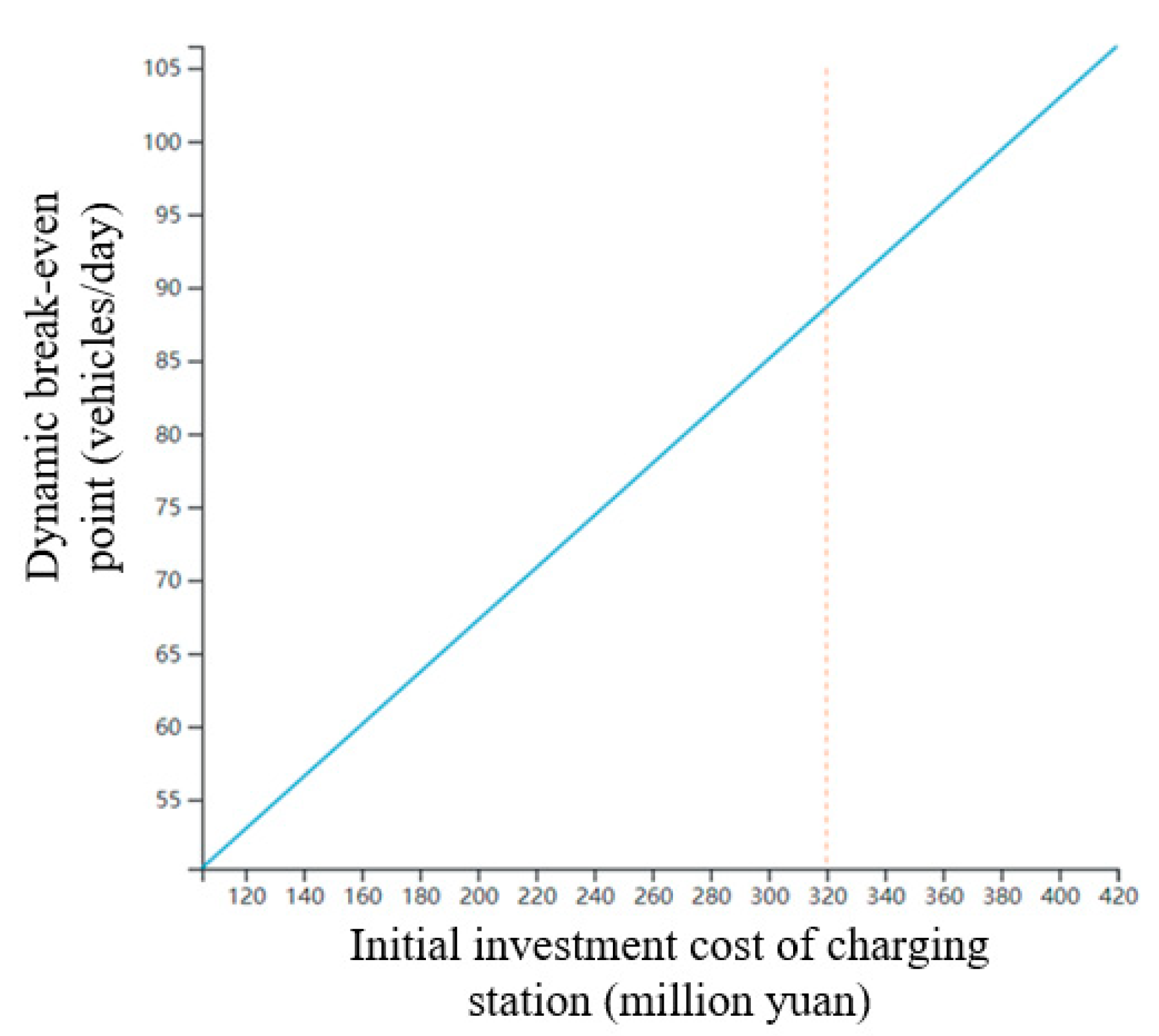
3.3.3. Initial Investment Cost of Charging Station
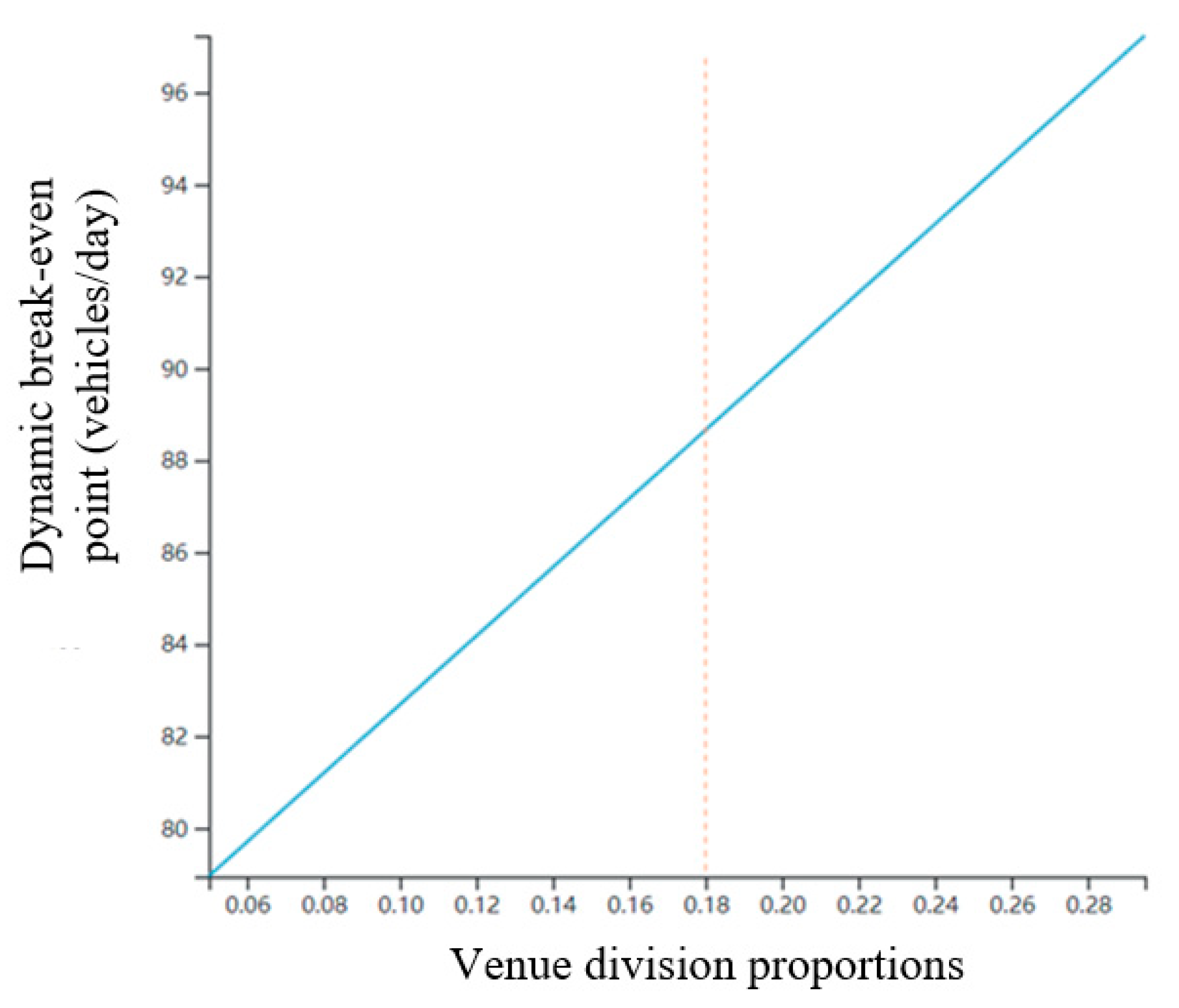
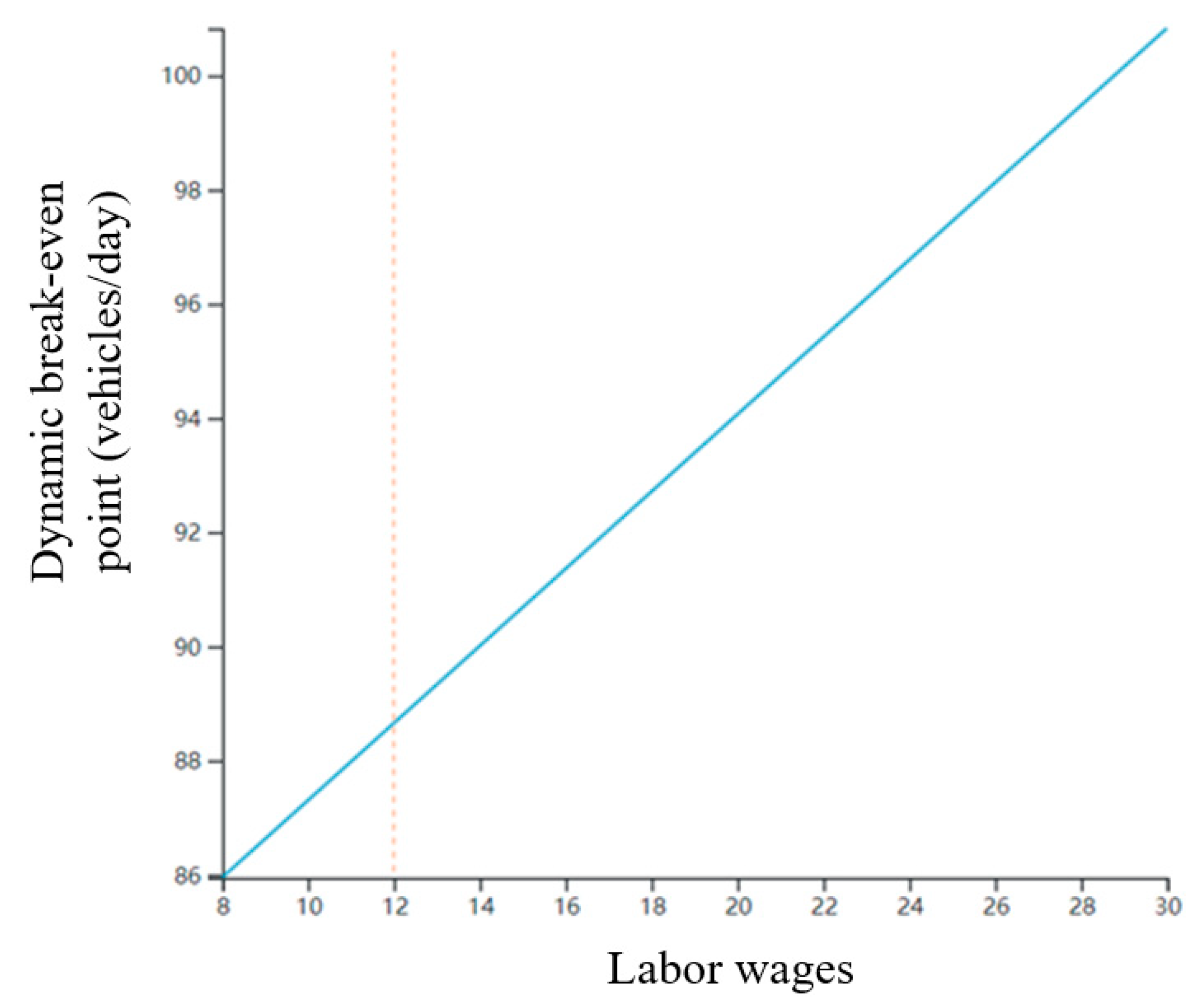
3.3.4. Labor Wages and Site Share
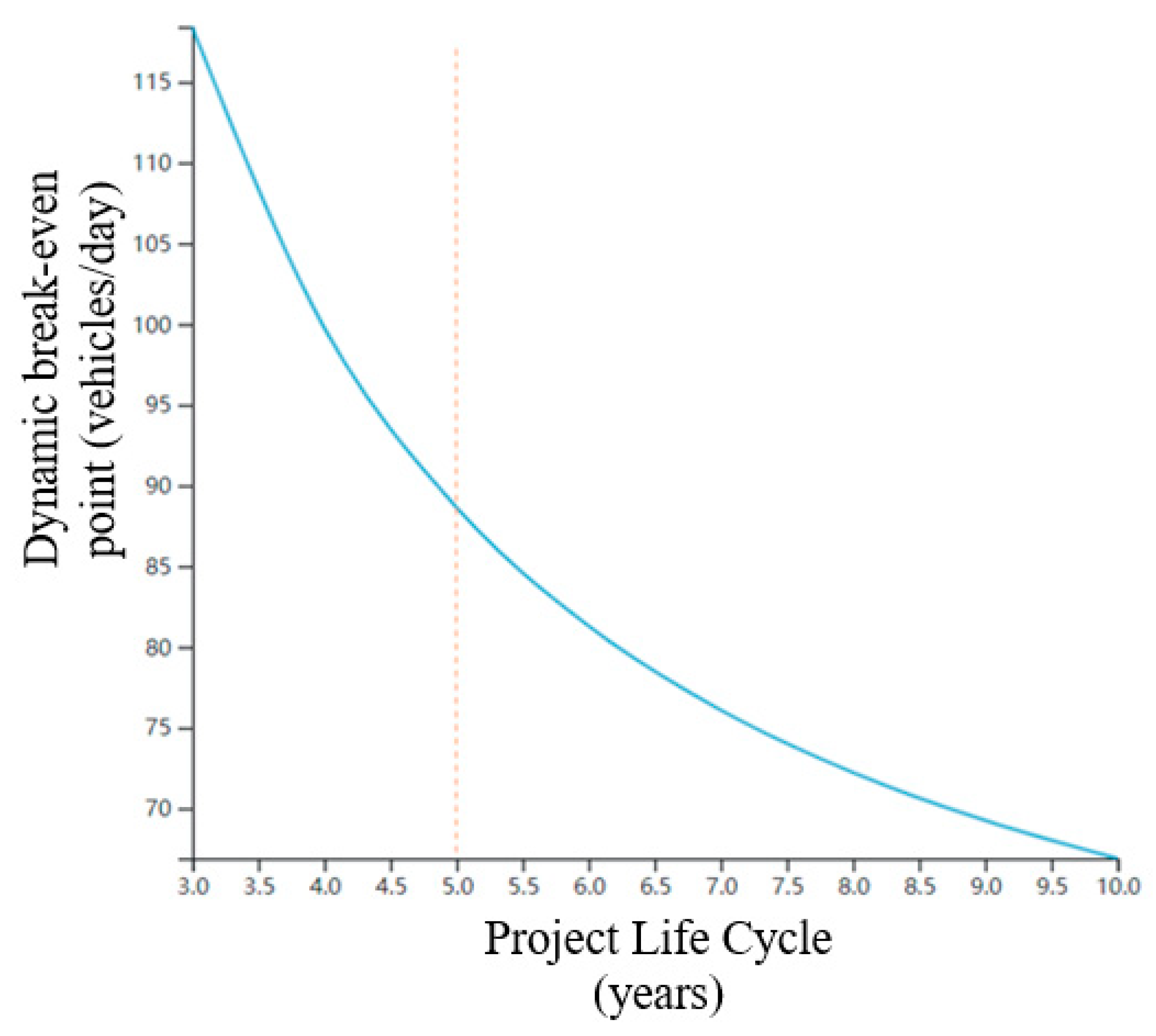
3.3.5. Project Cycle
4. Discussion
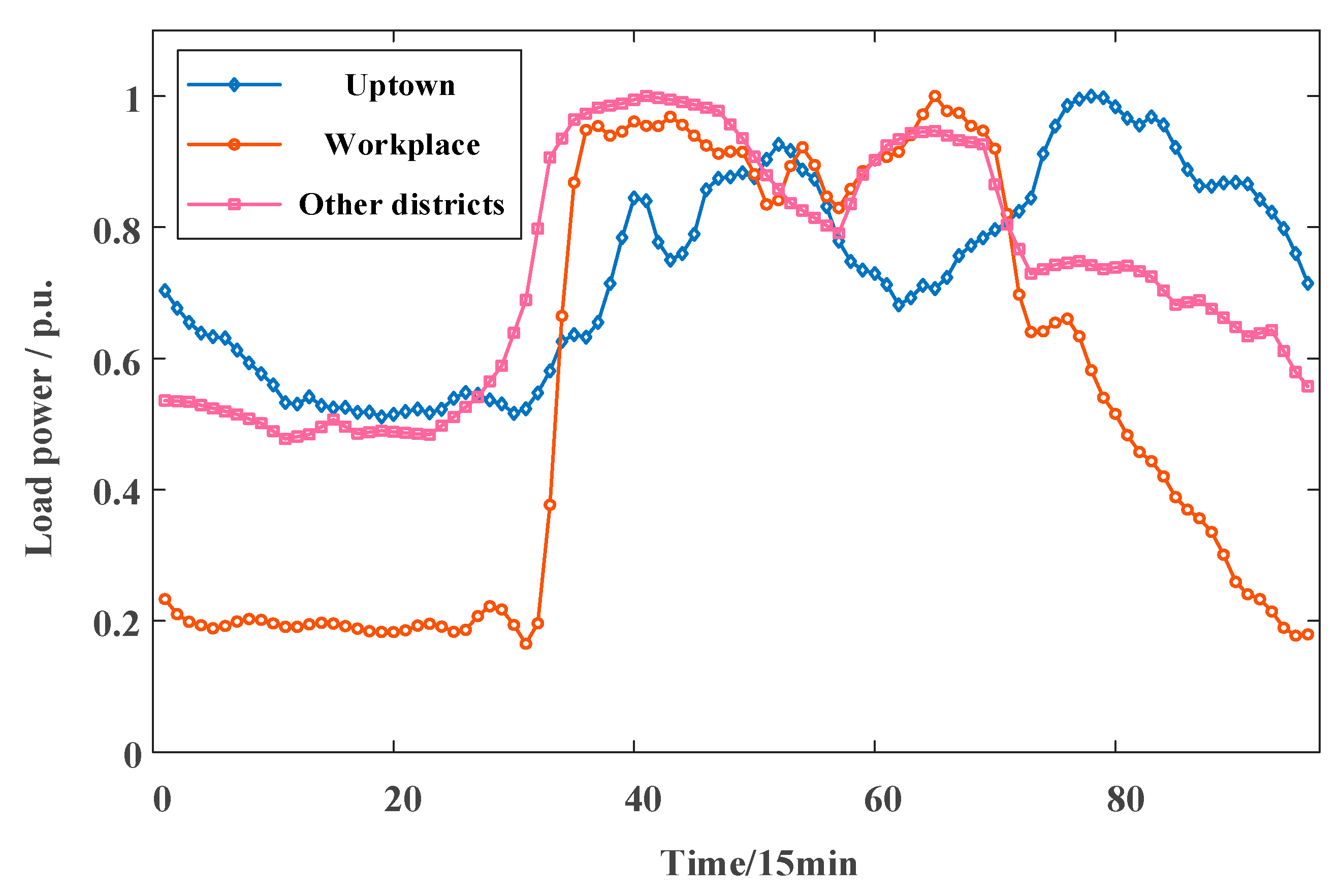
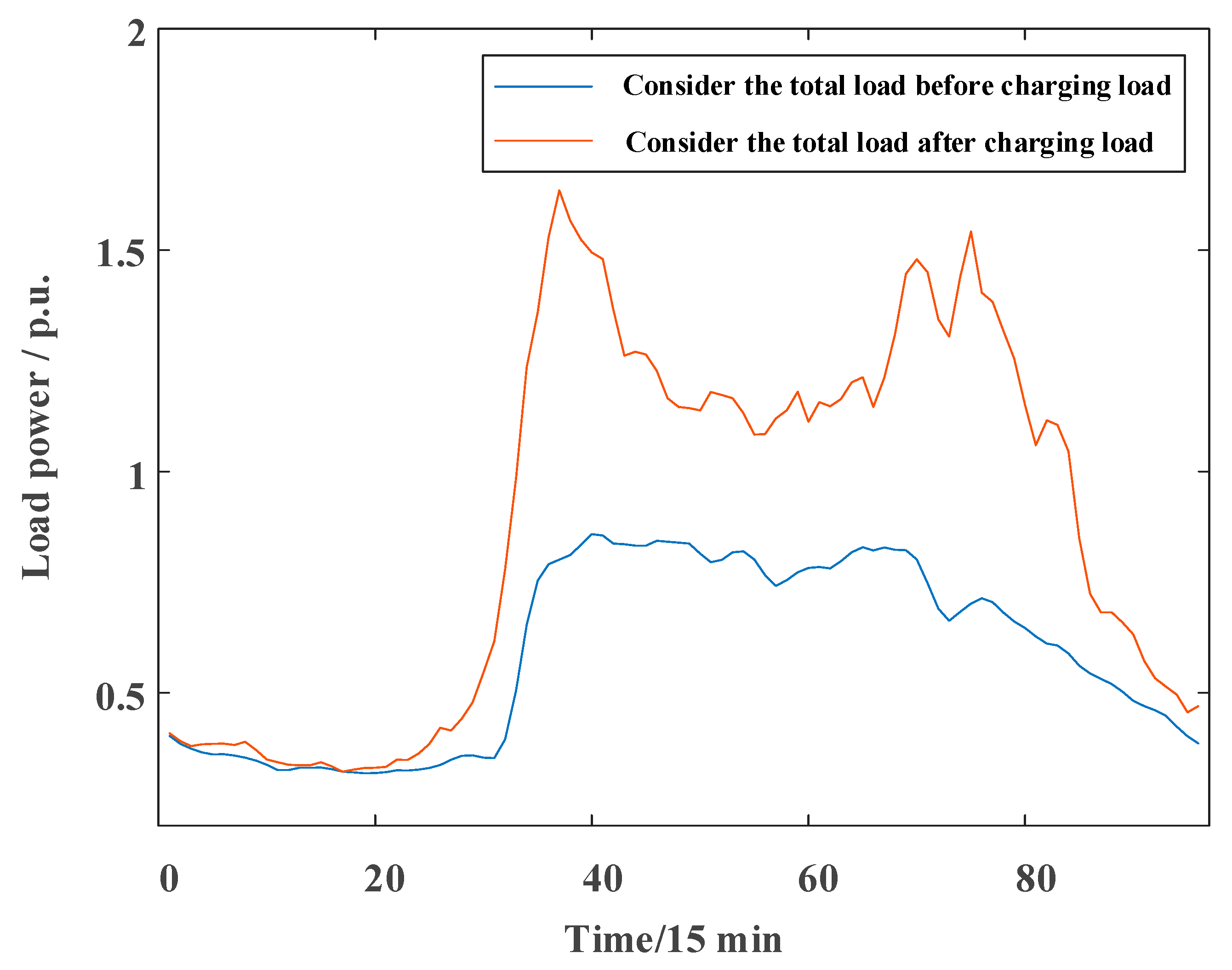
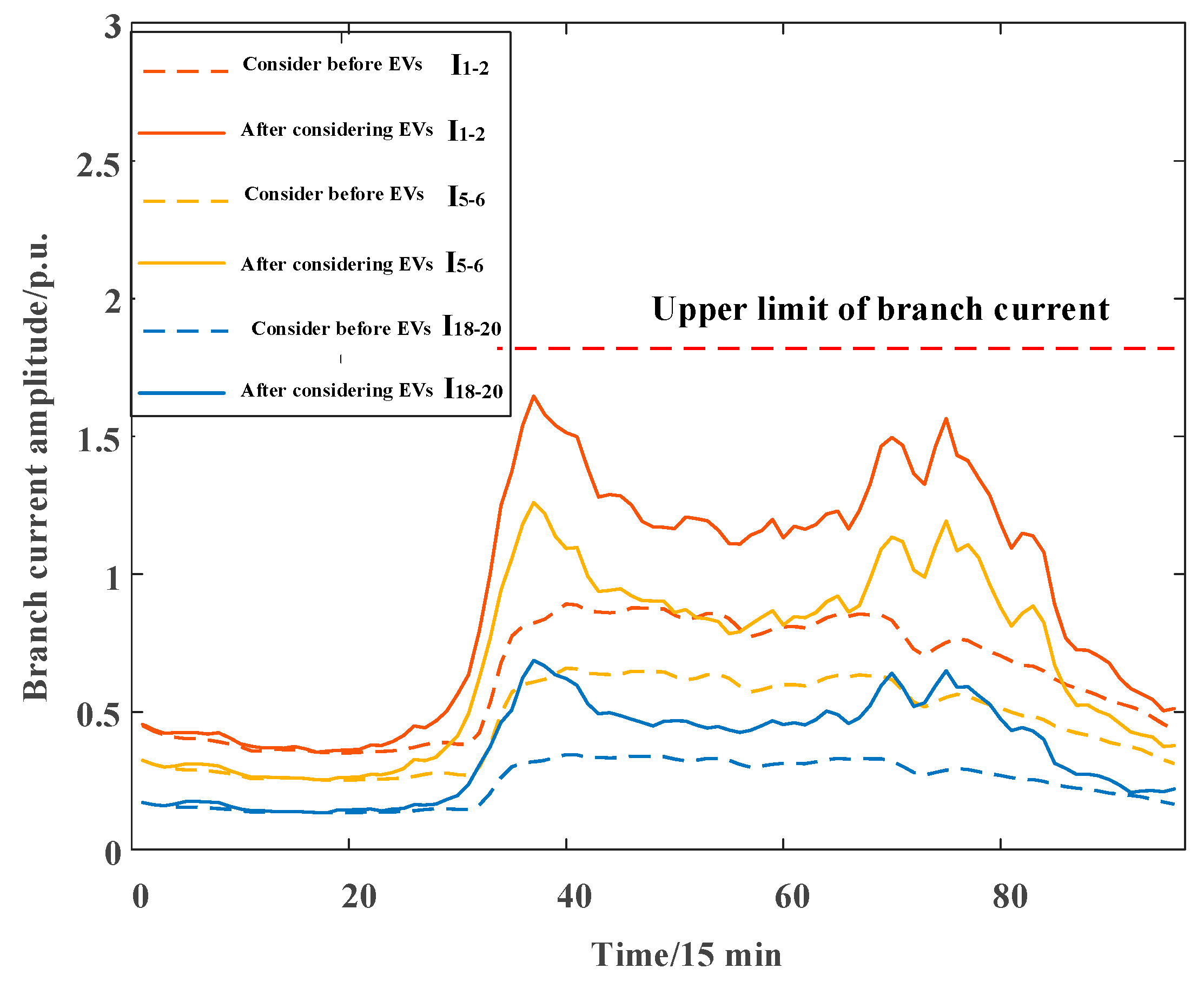
4.1. Impact on the Grid before and after EV Access
4.2. Comparative Analysis of Algorithms
5. Conclusions
- In order to meet the demand for EV trips and charging in the area, as well as the economic operation of the distribution network, the candidate nodes for each charging station were planned and the specific number of charging pile configurations for each node was obtained.
- A sensitivity analysis of the factors affecting the operation of charging stations reveals that the main factors affecting the profitability of charging stations are charging service charge (the cost difference between charging and electricity purchase), the daily charging time of electric vehicles, initial investment cost, labor wage cost and site sharing cost. The project cycle of charging stations has a relatively low impact on the profitability of charging stations.
- Through the analysis of EV access to the grid, it is found that EV load access will have a large impact on the branch currents in the network, and the grid company also needs to consider sufficient line transmission capacity in the process of building and planning charging stations.
- A krill swarm algorithm based on chaos optimization proposed in this paper demonstrated significant improvement in terms of computational time and computational accuracy. Compared with the traditional intelligent optimization algorithm, the computational time is reduced by 19.65% compared with the traditional SA algorithm, it basically does not fall into local convergence, and has higher solution efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| denotes a moment | |
| denotes the node sequence number | |
| denotes the node sequence number | |
| denotes the equivalent annual value investment cost of building charging piles | |
| denotes the grid reinforcement cost after the distribution grid is connected to the EV charging load | |
| denotes the operation and maintenance cost of charging piles | |
| denotes the network loss cost during time period | |
| denotes the construction cost of a single charging post (in dollars) | |
| denotes the number of charging piles installed at charging station candidate node of the charging station, which is an integer variable to be optimized | |
| denotes the set of charging station candidate nodes | |
| denotes the equal annual value factor | |
| denotes the depreciation rate | |
| denotes the economic lifetime of the charging post (in years). | |
| denotes the cost of grid reinforcement per unit of charging power increased (in yuan/kW) | |
| denotes the rated charging power of a single charging post (in kW) | |
| denotes the annual operation and maintenance cost of a single charging post (in dol-lars) | |
| denotes the unit cost of network losses (in $/kWh) | |
| denotes the set of lines in the network | |
| denotes the real part of the voltage vector at node | |
| denotes the imaginary part of the voltage vector at node | |
| denotes the conductance between node and node | |
| denotes the number of EVs whose destination at time is node and need to be charged | |
| denotes the number of EVs whose destination at time is node but need to be charged at charging station candidate node , an integer variable to be optimized | |
| denotes the set of all nodes | |
| denotes the distance between node and node (in km) | |
| denotes the maximum distance traveled by the EV to make additional trips | |
| denotes the regular active load at node in time period | |
| denotes the reactive load at node in time period | |
| denotes the voltage vector at node in time period | |
| denotes the upper limits of the voltage amplitude at node | |
| denotes the lower limits of the voltage amplitude at node | |
| denotes the maximum allowable line current between the node and the node | |
| denotes the sinusoidal mapping of [0, 1] | |
| denotes the upper boundaries of the position of the initial krill population | |
| denotes the lower boundaries of the position of the initial krill population | |
| denotes the location of the krill colony | |
| denotes the number of iterations | |
| denotes the variation factor | |
| denotes the fitness of krill at the th iteration |
References
- Karolemeas, C.; Tsigdinos, S.; Tzouras, P.G.; Nikitas, A.; Bakogiannis, E. Determining Electric Vehicle Charging Station Location Suitability: A Qualitative Study of Greek Stakeholders Employing Thematic Analysis and Analytical Hierarchy Process. Sustainability 2021, 13, 2298. [Google Scholar] [CrossRef]
- Li, H.; Xia, Y.; Yu, S.; Zhao, X.; Fang, D.; Feng, D.; Zhou, Y. Research on expansion planning of urban electric vehicle charging station based on user-side active charging guidance. Proc. CSEE 2023, 1–17. Available online: http://kns.cnki.net/kcms/detail/11.2107.TM.20220707.1451.012.html (accessed on 16 January 2023).
- Wang, H.; Li, Y.; Zhu, H.; Wei, Y.; Hou, C.; Dong, L. Planning of electric vehicle charging station considering distribution network load. J. Power Syst. Autom. 2022, 34, 134–141. [Google Scholar] [CrossRef]
- Castro, J.F.; Marques, D.C.; Tavares, L.; Dantas, N.K.; Fernandes, A.L.; Tuo, J.; de Medeiros, L.H.; Rosas, P. Energy and Demand Forecasting Based on Logistic Growth Method for Electric Vehicle Fast Charging Station Planning with PV Solar System. Energies 2022, 15, 6106. [Google Scholar] [CrossRef]
- Martina, C.; Giulio, M.; Benedetto, B. On sustainable positioning of electric vehicle charging stations in cities: An integrated approach for the selection of indicators. Sustain. Cities Soc. 2022, 85, 104067. [Google Scholar]
- Hou, W.; Luo, Q.; Wu, X.; Zhou, Y.; Si, G. Multiobjective Optimization of Large-Scale EVs Charging Path Planning and Charging Pricing Strategy for Charging Station. Complexity 2021, 2021, 8868617. [Google Scholar] [CrossRef]
- Strickler, A.; Castro, O., Jr.; Pozo, A.; Santana, R. An investigation of the selection strategies impact on MOEDAs: CMA-ES and UMDA. Appl. Soft Comput. 2018, 62, 963–973. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y.; Yang, Z.; He, C.; Chen, B. Research on distributed robust planning method considering the coordinated optimization of new energy and electric vehicle charging station and energy storage. Trans. Electr. Power Syst. Autom. 2023, 1. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Saha, A. Single-valued neutrosophic similarity measure-based additive ratio assessment framework for optimal site selection of electric vehicle charging station. Int. J. Intell. Syst. 2021, 36, 5573–5604. [Google Scholar] [CrossRef]
- Liang, X.; Wu, X.; Liao, H. A gained and lost dominance score II method for modelling group uncertainty: Case study of site selection of electric vehicle charging stations. J. Clean. Prod. 2020, 262, 121239. [Google Scholar] [CrossRef]
- Xia, F.; Chen, H.; Li, H.; Chen, L. Optimal planning of photovoltaic-storage fast charging station considering electric vehicle charging demand response. Energy Rep. 2022, 8, 399–412. [Google Scholar] [CrossRef]
- Li, Y.; Su, S.; Liu, B.; Yamashita, K.; Li, Y.; Du, L. Trajectory-driven planning of electric taxi charging stations based on cumulative prospect theory. Sustain. Cities Soc. 2022, 86, 104125. [Google Scholar] [CrossRef]
- Pan, H.; Yu, A.; Wang, Y.; Jin, B. Location and capacity setting of electric vehicle charging station balancing the interests of different subjects. Mod. Power 2023, 1–12. [Google Scholar] [CrossRef]
- Zuo, Y.; Li, W.; Yang, W. EV charging station planning considering the temporal and spatial distribution characteristics of charging load. Electr. Meas. Instrum. 2023, 1–10. Available online: http://kns.cnki.net/kcms/detail/23.1202.TH.20220818.1127.006.html (accessed on 16 January 2023).
- Bai, X.; Wang, Z.; Zou, L.; Liu, H.; Sun, Q.; Alsaadi, F.E. Electric vehicle charging station planning with dynamic prediction of elastic charging demand: A hybrid particle swarm optimization algorithm. Complex Intell. Syst. 2021, 8, 1035–1046. [Google Scholar] [CrossRef]
- Wang, H.; Gao, R. Research on layout optimization of fast and slow charging stations for electric vehicles based on improved particle swarm algorithm. Syst. Eng. 2023, 118, 105557. [Google Scholar]
- Ghosh, A.; Ghorui, N.; Mondal, S.P.; Kumari, S.; Mondal, B.K.; Das, A.; Gupta, M.S. Application of Hexagonal Fuzzy MCDM Methodology for Site Selection of Electric Vehicle Charging Station. Mathematics 2021, 9, 393. [Google Scholar] [CrossRef]
- Asna, M.; Shareef, H.; Muhammad, M.A.; Ismail, L.; Prasanthi, A. Multi-objective quantum atom search optimization algorithm for electric vehicle charging station planning. Int. J. Energy Res. 2022, 46, 17308–17331. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, H.; Song, Z. Integrating Transit Route Network Design and Fast Charging Station Planning for Battery Electric Buses. IEEE Access 2021, 9, 51604–51617. [Google Scholar] [CrossRef]
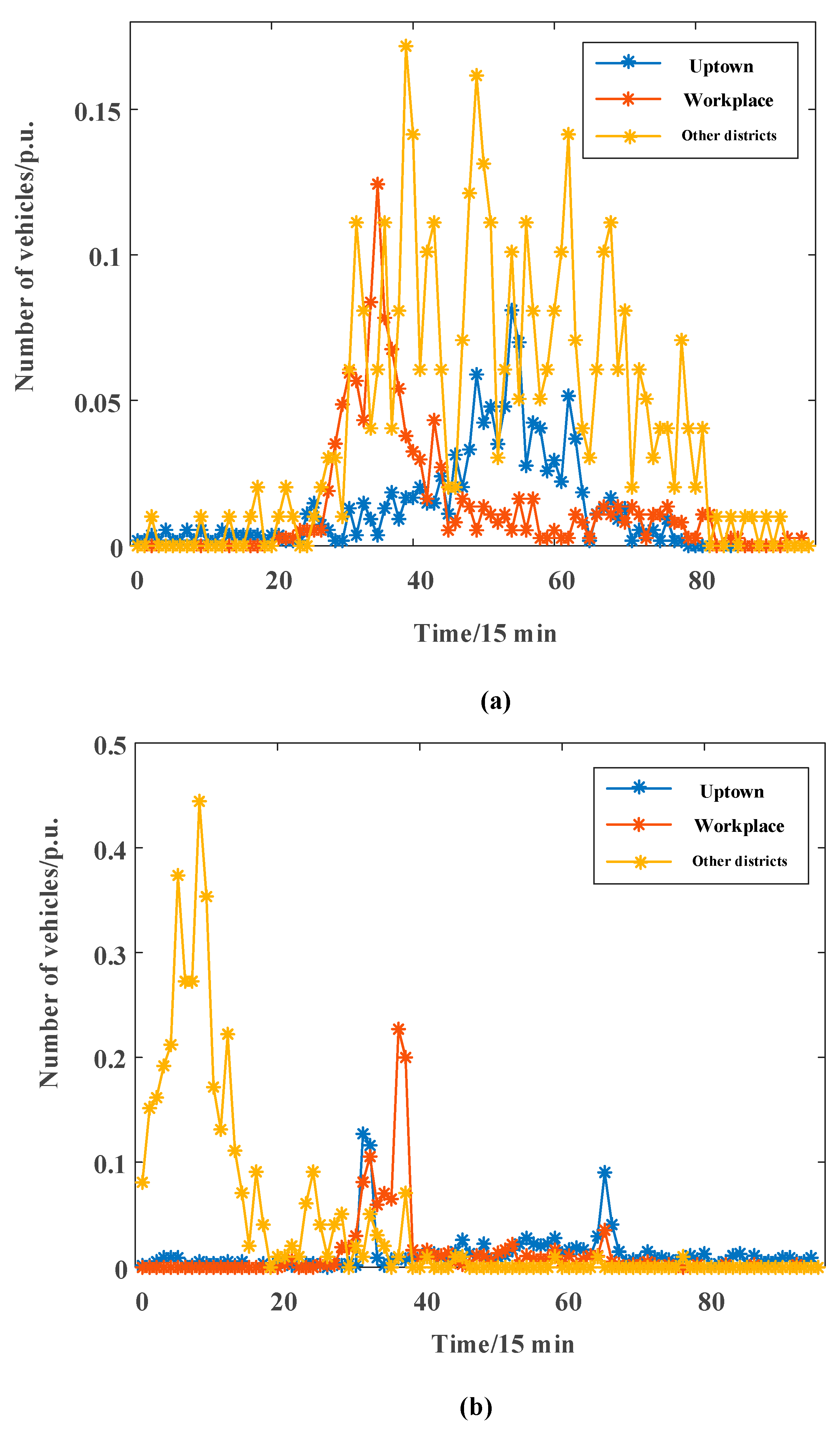
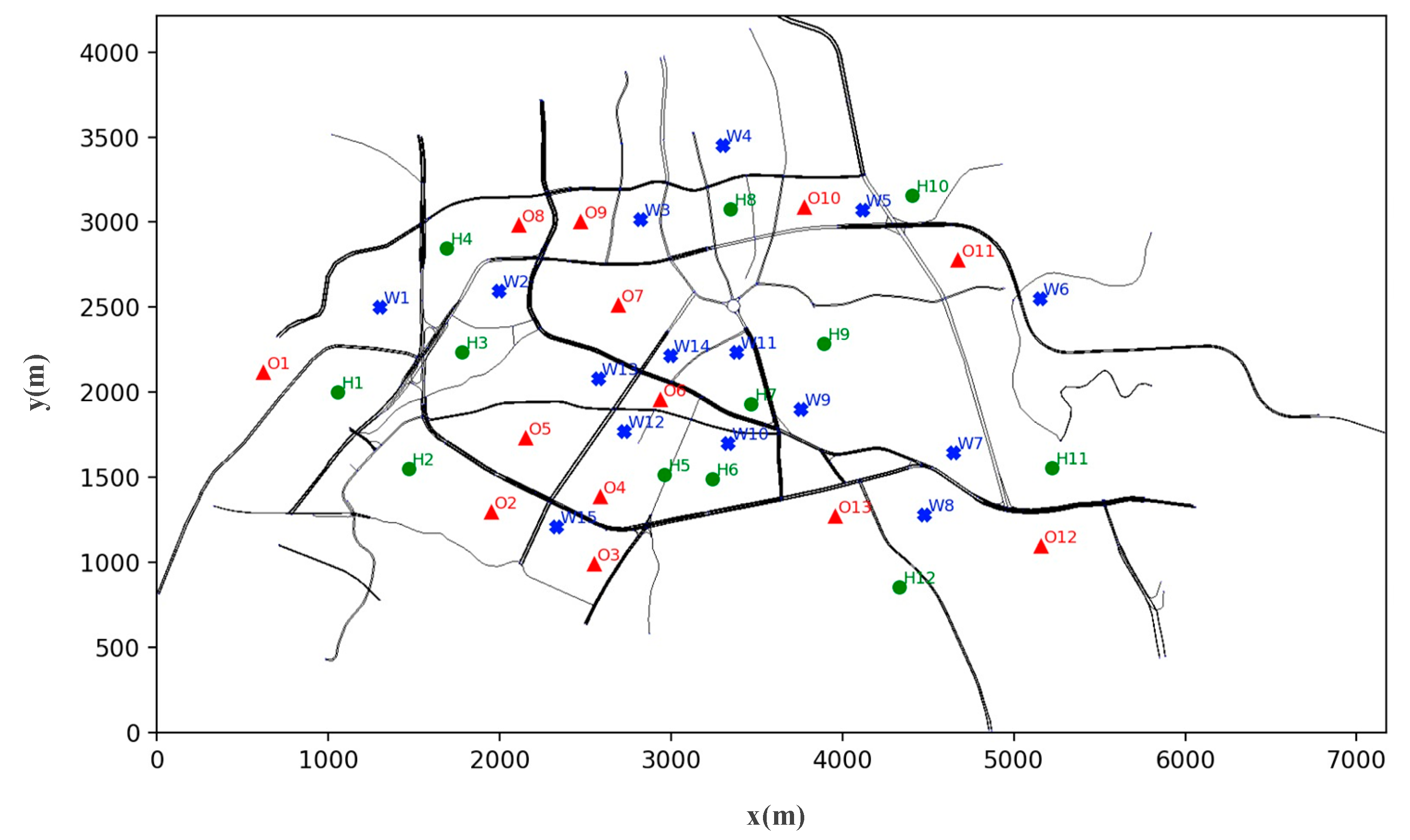

| Block | Maximum Number of Parking Spaces | Block | Maximum Number of Parking Spaces | Block | Maximum Number of Parking Spaces |
|---|---|---|---|---|---|
| H1 | 41 | W1 | 19 | O1 | 14 |
| H2 | 15 | W2 | 20 | O2 | 10 |
| H3 | 22 | W3 | 67 | O3 | 6 |
| H4 | 61 | W4 | 9 | O4 | 30 |
| H5 | 25 | W5 | 9 | O5 | 34 |
| H6 | 21 | W6 | 53 | O6 | 5 |
| H7 | 33 | W7 | 27 | O7 | 7 |
| H8 | 20 | W8 | 28 | O8 | 39 |
| H9 | 86 | W9 | 14 | O9 | 18 |
| H10 | 19 | W10 | 16 | O10 | 22 |
| H11 | 22 | W11 | 12 | O11 | 29 |
| H12 | 11 | W12 | 52 | O12 | 9 |
| W13 | 84 | O13 | 23 | ||
| W14 | 41 | ||||
| W15 | 11 |
| Parameters | Numerical Value |
|---|---|
| 0.03 | |
| 10 | |
| 60 | |
| 40,000 | |
| 750 | |
| 4000 | |
| 560 | |
| 0.6 | |
| 0.95 | |
| 1.05 | |
| 1.8187 | |
| 0.03 |
| Charging Time (h) | Total Load of Charging Stations (Vehicles/Day) | Elasticity Factor |
|---|---|---|
| 12 | 56 | / |
| 10 | 20 | 0.7 |
| 8 | 25 | 1.25 |
| 6 | 29 | 0.64 |
| 4 | 36 | 0.72 |
| 2 | 89 | 2.94 |
| Algorithm | Number of Charging Piles | Number of Iterations to Find the Optimal Solution | Number of Iterations into Local Optimum | Optimal Annual Total Cost/Billion | Solving Time/Sec |
|---|---|---|---|---|---|
| CKHA | 771 | 32 | About 2 times | 1.38 | 1.39 |
| ACO | 762 | 36 | About 15 times | 1.42 | 1.52 |
| SA | 842 | 48 | About 13 times | 1.54 | 1.73 |
| PSO | 801 | 39 | About 11 times | 1.43 | 1.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Chen, H. Research on the Planning of Electric Vehicle Fast Charging Stations Considering User Selection Preferences. Energies 2023, 16, 1794. https://doi.org/10.3390/en16041794
Chen J, Chen H. Research on the Planning of Electric Vehicle Fast Charging Stations Considering User Selection Preferences. Energies. 2023; 16(4):1794. https://doi.org/10.3390/en16041794
Chicago/Turabian StyleChen, Julong, and Haoyong Chen. 2023. "Research on the Planning of Electric Vehicle Fast Charging Stations Considering User Selection Preferences" Energies 16, no. 4: 1794. https://doi.org/10.3390/en16041794
APA StyleChen, J., & Chen, H. (2023). Research on the Planning of Electric Vehicle Fast Charging Stations Considering User Selection Preferences. Energies, 16(4), 1794. https://doi.org/10.3390/en16041794






