Analysis of Losses in Two Different Control Approaches for S-S Wireless Power Transfer Systems for Electric Vehicle
Abstract
:1. Introduction
2. Methods of Operation of SAHFWPT and DAHFWPT
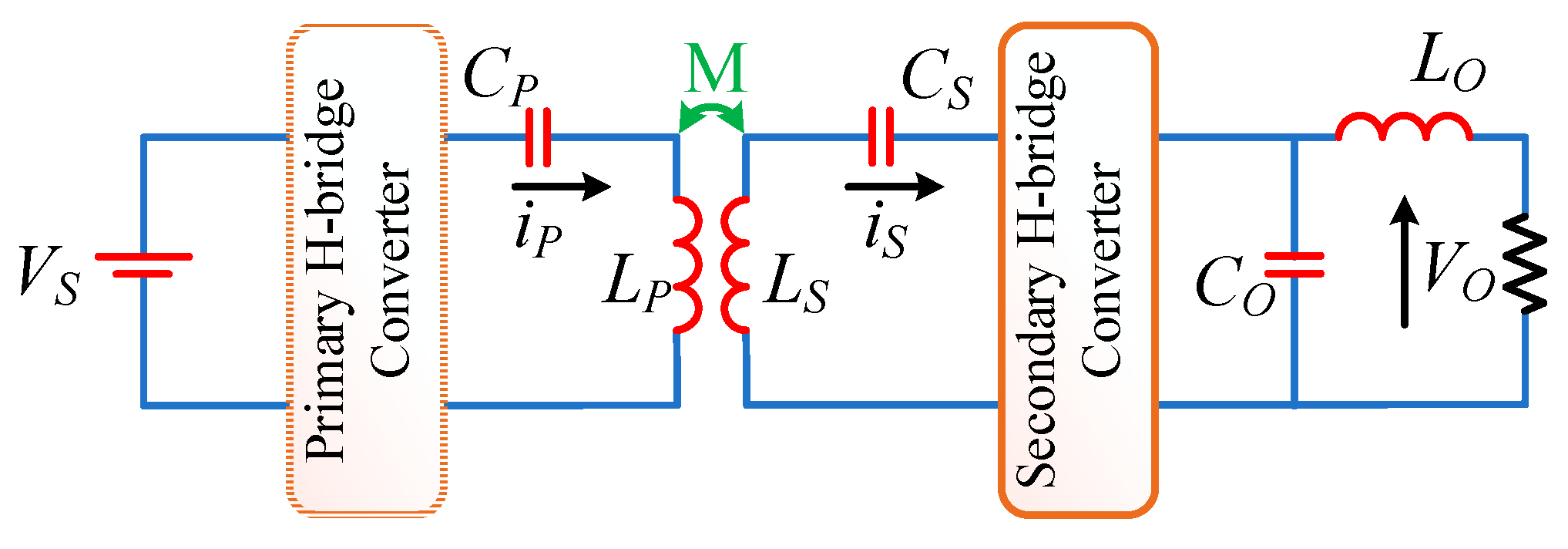
2.1. Circuit Schematic
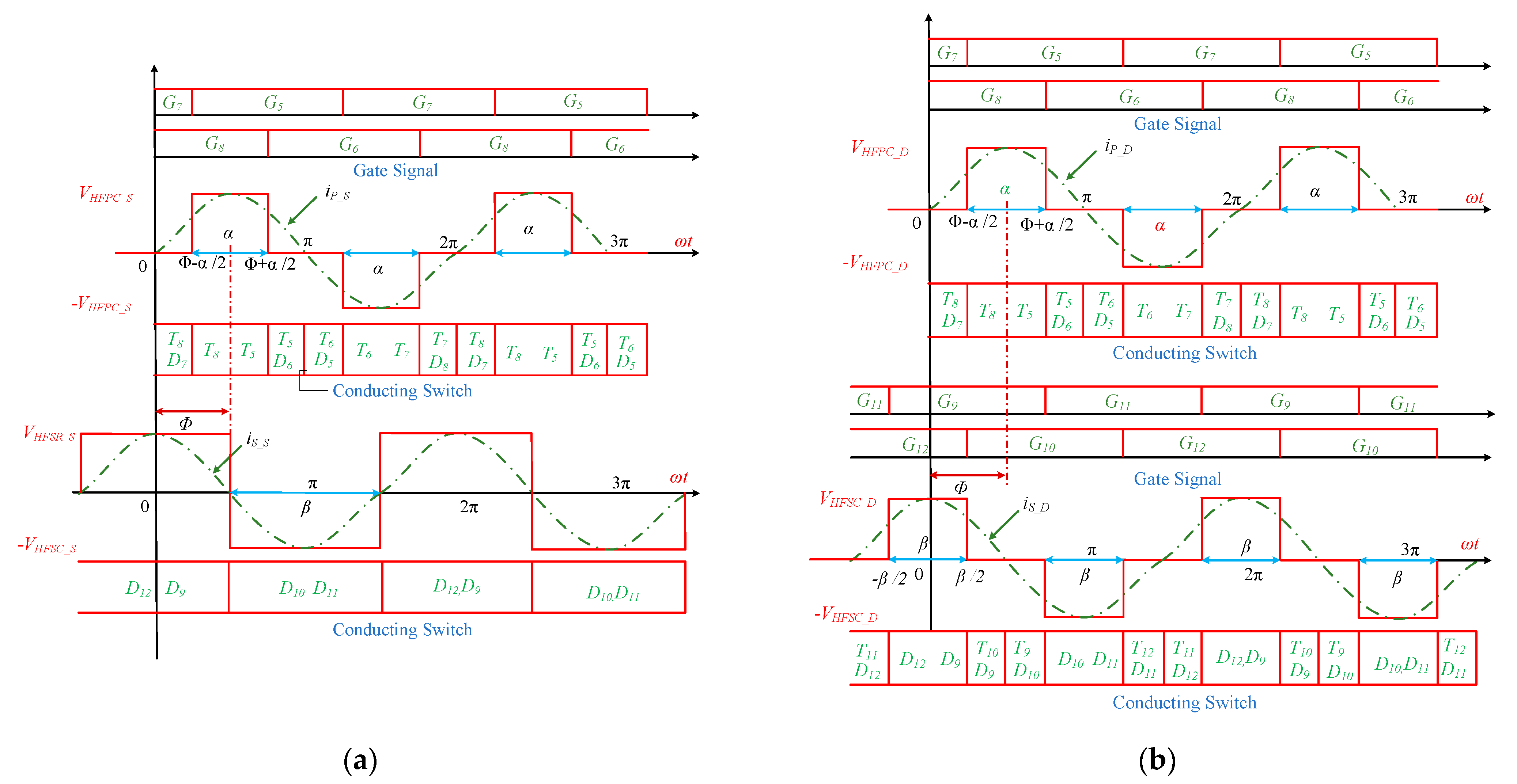
2.2. Operation and Analysis
3. Methods of Loss Analysis of SAHFWPT and DAHFWPT
3.1. S-S Coil Loss
3.2. Loss of HFSR, HFSC and HFPC
3.2.1. Conduction Loss of MOSFET and Diodes
3.2.2. Hard Turn on and off Loss
3.2.3. Other Switching Losses in the MOSFET
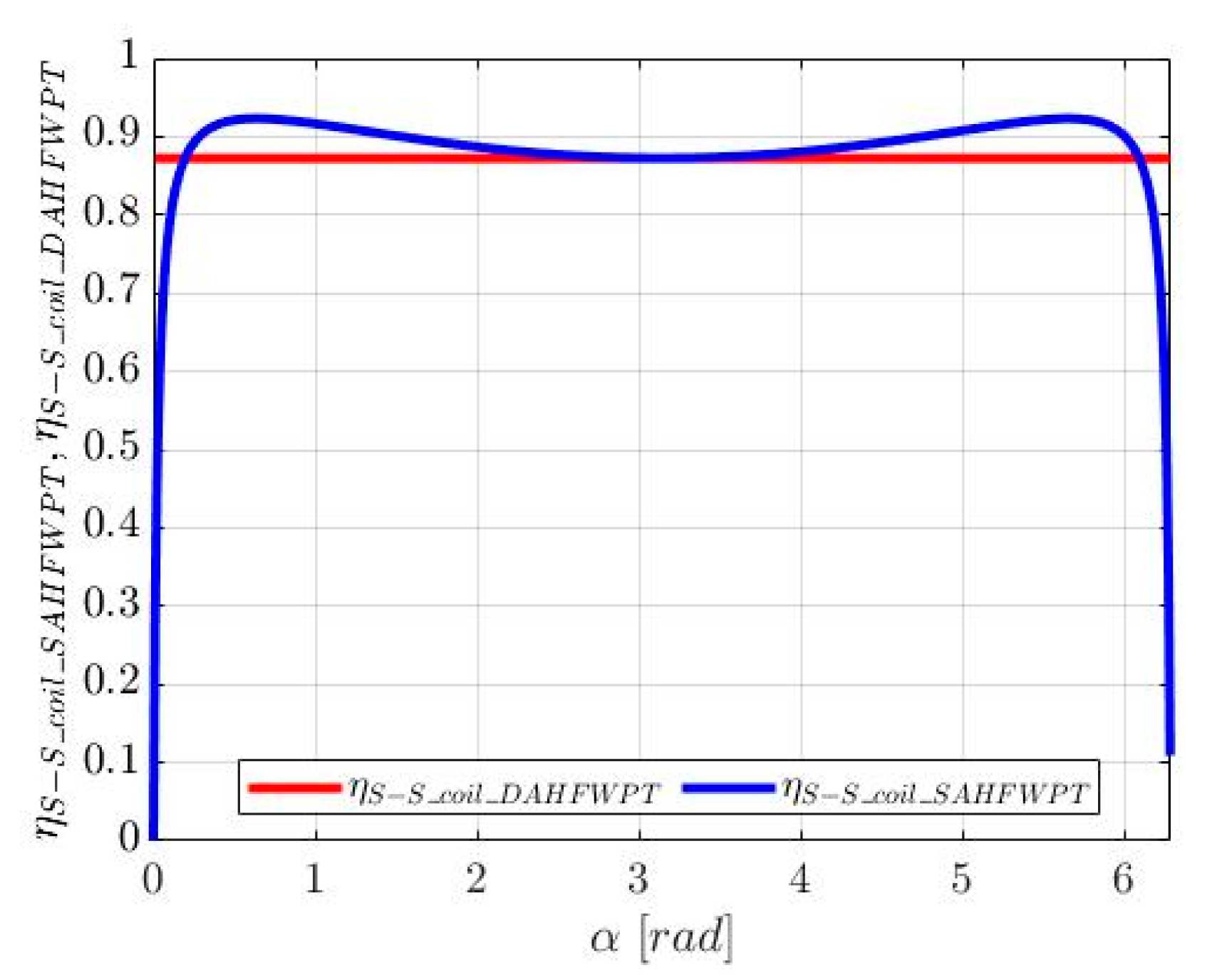
4. Efficiency of SAHFWPT and DAHFWPT
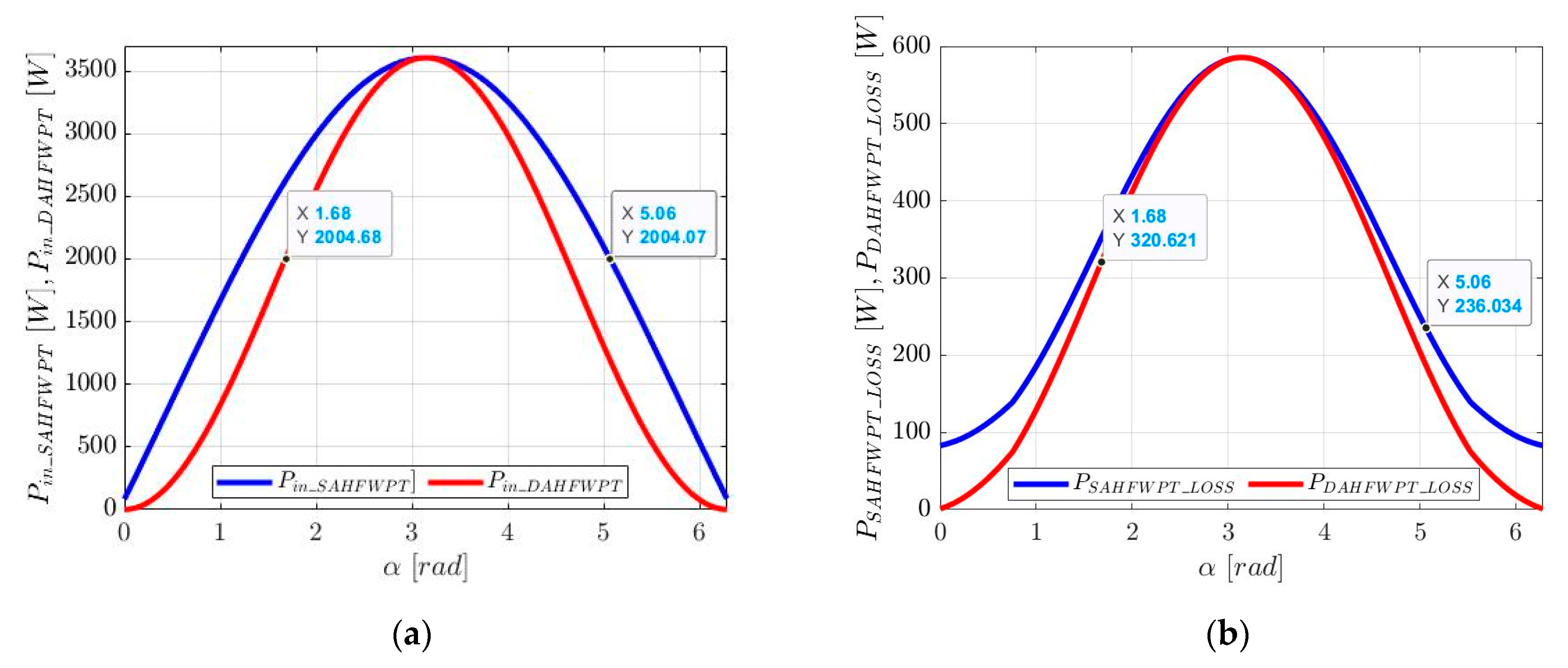
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| SAHFWPT | Single Active High-Frequency wireless power transfer |
| DAHFWPT | Dual Active High-Frequency wireless power transfer |
| SPS | Single Phase Shift |
| EPS | Extended Phase Shift |
| DPS | Dual Phase Shift |
| TPS | Triple Phase shift |
| EV | Electrical Vehicle |
| RE | Renewable Energy |
| ESS | Energy Storage System |
| SAB | Single Active Bridge |
| DAB | Dual Active Bridge |
| PSFB | Phase Shift Full Bridge |
| DC | Direct Current |
| Source Voltage | |
| Battery Equivalent Resistance | |
| Output low pass filter capacitor | |
| Output low pass filter inductor | |
| Zero Voltage Switching | |
| Zero Current Switching | |
| HFPC | High-frequency Primary Converter |
| HFSC | High-frequency Secondary Converter |
| HFSR | High-frequency Secondary Rectifier |
| DC voltage source of SAHFWPT and DAHFWPT | |
| Output voltage of HFPC of SAHFWPT and DAHFWPT | |
| Output current of HFPC of SAHFWPT and DAHFWPT | |
| Input voltage of HFSR and HFSC of SAHFWPT and DAHFWPT | |
| Input current of HFSR and HFSC of SAHFWPT and DAHFWPT | |
| Output voltage of HFSR and HFSC of SAHFWPT and DAHFWPT | |
| Resonant Frequency | |
| Φ | External Phase shift angle |
| α | Internal phase shift angle of HFPC |
| β | Internal phase shift angle of HFSC |
| Peak amplitude of output and input voltage of HFPC and HFSC of DAHFWPT | |
| Peak amplitude of input voltage of HFSR of SAHFWPT | |
| CP, CS | Primary and secondary resonant capacitor |
| LP, LS | Primary and secondary coil self-inductance |
| RP, RS | Primary and secondary coil resistance |
| , | Impedance of primary and secondary coil |
| M | Coils mutual inductance |
| Primary and secondary coil induce voltage | |
| Primary and secondary coil circulating current | |
| Average power flow from primary to secondary | |
| Fundamental Output and Input voltage of HFPC and HFSC of DAHFWPT | |
| Fundamental of Input voltage of HFSR of SAHFWPT | |
| Fundamental primary coil current of DAHFWPT and SAHFWPT | |
| Fundamental secondary coil current of DAHFWPT and SAHFWPT | |
| Secondary Power of DAHFWPT and SAHFWPT | |
| Coil Loss of DAHFWPT and SAHFWPT | |
| Efficiency of coil of DAHFWPT and SAHFWPT | |
| Conduction loss of HFPC and HFSR of SAHFWPT | |
| Conduction loss of HFPC and HFSC of DAHFWPT | |
| Switching loss of switches for HFSC | |
| Switching loss of switches for HFPC of DAHFWPT and SAHFWPT | |
| Output capacitor loss of MOSFET | |
| Body diode reverse recovery loss | |
| η | Efficiency |
| PO | Output Power |
| Input Power | |
| Power Loss | |
| Power of Battery | |
| Overall loss Power of SAHFWPT | |
| Overall loss Power of DAHFWPT | |
| Efficiency of SAHFWPT | |
| Efficiency of DAHFWPT | |
| WPT | Wireless Power Transfer |
References
- Chen, T.; Zhang, X.-P.; Wang, J.; Li, J.; Wu, C.; Hu, M.; Bian, H. A Review on Electric Vehicle Charging Infrastructure Development in the UK. J. Mod. Power Syst. Clean Energy 2020, 8, 193–205. [Google Scholar] [CrossRef]
- Far, M.F.; Paakkinen, M.; Cremers, P. A Framework for Charging Standardisation of Electric Buses in Europe. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 18 November–16 December 2020; pp. 1–4. [Google Scholar]
- Bertoluzzo, M.; Giacomuzzi, S.; Kumar, A. Design of a Bidirectional Wireless Power Transfer System for Vehicle-to-Home Applications. Vehicles 2021, 3, 406–425. [Google Scholar] [CrossRef]
- Fontana, C.; Forato, M.; Bertoluzzo, M.; Buja, G. Design characteristics of SAB and DAB converters. In Proceedings of the Intl Aegean Conference on Electrical Machines & Power Electronics (ACEMP) Intl Conference on Optimization of Electrical & Electronic Equipment (OPTIM) & Intl Symposium on Advanced Electromechanical Motion Systems (ELECTROMOTION), Side, Turkey, 2–4 September 2015; pp. 661–668. [Google Scholar]
- Jha, R.; Forato, M.; Prakash, S.; Dashora, H.; Buja, G. An Analysis-Supported Design of a Single Active Bridge (SAB) Converter. Energies 2022, 15, 666. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Sun, Y. Overview of Dual-Active-Bridge Isolated Bidirectional DC–DC Converter for High-Frequency-Link Power-Conversion System. IEEE Trans. Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Xu, F.; Wong, S.C.; Tse, C.K. Overall Loss Compensation and Optimization Control in Single-Stage Inductive Power Transfer Converter Delivering Constant Power. IEEE Trans. Power Electron. 2022, 37, 1146–1158. [Google Scholar] [CrossRef]
- Di Capua, G.; Femia, N.; Petrone, G.; Lisi, G.; Du, D.; Subramonian, R. Rajaram Subramonian. Power and efficiency analysis of high-frequency Wireless Power Transfer Systems. Int. J. Electr. Power Energy Syst. 2017, 84, 124–134. [Google Scholar] [CrossRef]
- J2954: Wireless Power Transfer for Light-Duty Plug-In/Electric Vehicles and Alignment Methodology; SAE International: Warrendale, PA, USA, 2020.
- Gonzalez-Gonzalez, J.M.; Trivino-Cabrera, A.; Aguado, J.A. Assessment of the Power Losses in a SAE J2954-Compliant Wireless Charger. IEEE Access 2022, 10, 54474–54483. [Google Scholar] [CrossRef]
- Ravikiran, V.; Keshri, R.; Rathore, A.; Chakraborty, C. Loss Analysis of Resonant Inductive Power Transfer System for Wireless Charging of e-Rickshaw. In Proceedings of the IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 2559–2564. [Google Scholar]
- Di Capua, G.; Femia, N.; Lisi, G. Impact of losses and mismatches on power and efficiency of Wireless Power Transfer Systems with controlled secondary-side rectifier. Integration 2016, 55, 384–392. [Google Scholar] [CrossRef]
- Acquaviva, A.; Rodionov, A.; Kersten, A.; Thiringer, T.; Liu, Y. Analytical Conduction Loss Calculation of a MOSFET Three-Phase Inverter Accounting for the Reverse Conduction and the Blanking Time. IEEE Trans. Ind. Electron. 2021, 68, 6682–6691. [Google Scholar] [CrossRef]
- Kalra, G.R.; Pearce, M.G.S.; Kim, S.; Thrimawithana, D.J.; Covic, G.A. A Power Loss Measurement Technique for Inductive Power Transfer Magnetic Couplers. IEEE J. Emerg. Sel. Topics Ind. Electron. 2020, 1, 113–122. [Google Scholar] [CrossRef]
- Carretero, C. Coupling Power Losses in Inductive Power Transfer Systems with Litz-Wire Coils. IEEE Trans. Ind. Electron. 2017, 64, 4474–4482. [Google Scholar] [CrossRef]
- Rossmanith, H.; Doebroenti, M.; Albach, M.; Exner, D. Measurement and Characterization of High Frequency Losses in Nonideal Litz Wires. IEEE Trans. Power Electron. 2011, 26, 3386–3394. [Google Scholar] [CrossRef]
- Ren, Y.; Xu, M.; Zhou, J.; Lee, F. Analytical loss model of power MOSFET. IEEE Trans. Power Electron. 2006, 21, 310–319. [Google Scholar]
- Huang, Z.; Lam, C.S.; Mak, P.I.; Martins, R.S.; Wong, S.C.; Tse, C.K. A Single-Stage Inductive-Power-Transfer Converter for Constant-Power and Maximum-Efficiency Battery Charging. IEEE Trans. on Power Electron. 2020, 35, 8973–8984. [Google Scholar] [CrossRef]
- Fu, M.; Tang, Z.; Liu, M.; Ma, C.; Zhu, X. Full-bridge rectifier input reactance compensation in Megahertz wireless power transfer systems. In Proceedings of the IEEE PELS Workshop on Emerging Technologies: Wireless Power, Daejeon, Republic of Korea, 5–6 June 2015; pp. 1–5. [Google Scholar]
- Enssle, A.; Parspour, N. Power Loss Shifted Design of Inductive Energy Transfer Systems. IEEE Open J. Power Electron. 2020, 1, 113–123. [Google Scholar] [CrossRef]
- Shiba, K.; Morimasa, A.; Hirano, H. Design and Development of Low-Loss Transformer for Powering Small Implantable Medical Devices. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 77–85. [Google Scholar] [CrossRef] [PubMed]
- Di Capua, G.; Sánchez, J.A.; Cabrera, A.T.; Cabrera, D.F.; Femia, N.; Petrone, G.; Spagnuolo, G. A losses-based analysis for electric vehicle wireless chargers. In Proceedings of the International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Istanbul, Turkey, 7–9 September 2015; pp. 1–4. [Google Scholar]
- Sagar, A.; Kumar, A.; Bertoluzzo, M.; Jha, R.K. Analysis and Design of a Two-winding Wireless Power Transfer System with Higher System Efficiency and Maximum Load Power. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar]
- Van Mulders, J.; Delabie, D.; Lecluyse, C.; Buyle, C.; Callebaut, G.; Van der Perre, L.; De Strycker, L. Wireless Power Transfer: Systems, Circuits, Standards, and Use Cases. Sensors 2022, 22, 5573. [Google Scholar] [CrossRef] [PubMed]
- Turzyński, M.; Bachman, S.; Jasiński, M.; Piasecki, S.; Ryłko, M.; Chiu, H.-J.; Kuo, S.-H.; Chang, Y.-C. Analytical Estimation of Power Losses in a Dual Active Bridge Converter Controlled with a Single-Phase Shift Switching Scheme. Energies 2022, 15, 8262. [Google Scholar] [CrossRef]
- Oggier, G.G.; García, G.O.; Oliva, A.R. Switching Control Strategy to Minimize Dual Active Bridge Converter Losses. IEEE Trans. Power Electron. 2009, 24, 1826–1838. [Google Scholar] [CrossRef]
- Bai, H.; Mi, C. Eliminate Reactive Power and Increase System Efficiency of Isolated Bidirectional Dual-Active-Bridge DC–DC Converters Using Novel Dual-Phase-Shift Control. IEEE Trans. Power Electron. 2008, 23, 2905–2914. [Google Scholar] [CrossRef]

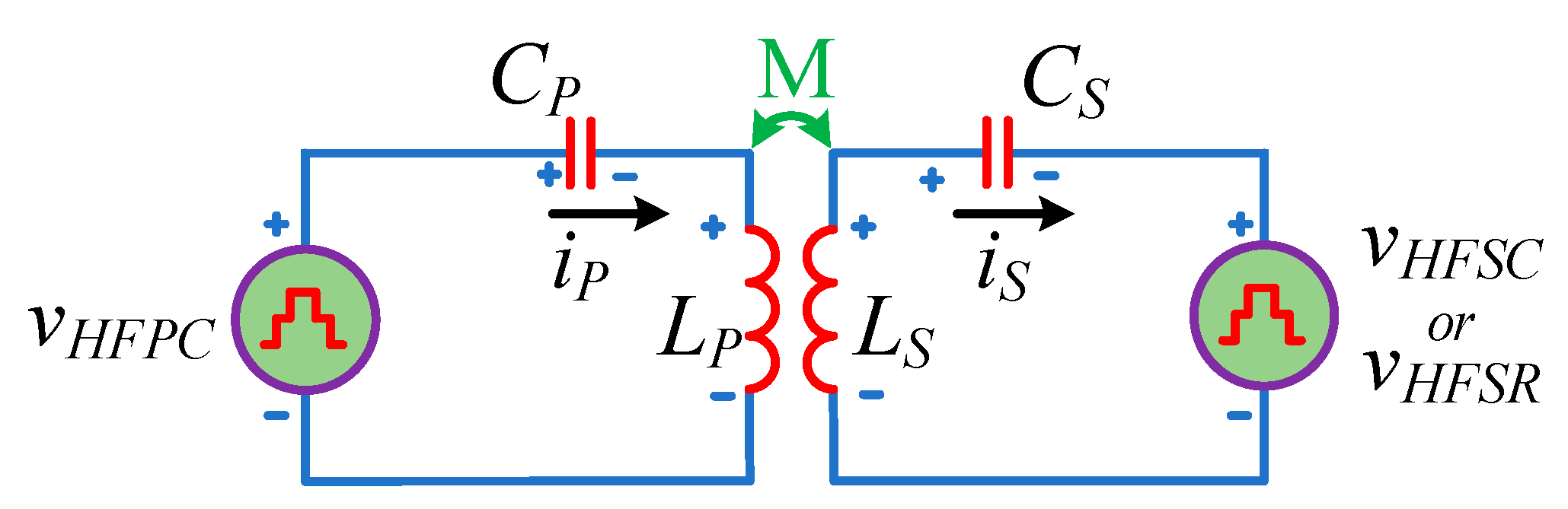



| Feature | SAHFWPT | DAHFWPT | |||||
|---|---|---|---|---|---|---|---|
| Reference | [3] | [5] | [6,7,8,9] | [3] | [5] | [6,7,8,9] | |
| Switching control | SPS | × | √ | √ | × | √ | √ |
| EPS | √ | √ | √ | × | √ | √ | |
| DPS | × | × | × | √ | √ | √ | |
| TPS | × | × | × | × | √ | √ | |
| Additional chopper | √ | √ | √ | × | × | × | |
| Hard switching of MOSFET | × | × | √ | × | × | √ | |
| Circulating current | × | × | × | × | √ | √ | |
| S-S coil loss | √ | √ | √ | √ | √ | √ | |
| Overall loss analysis | × | × | √ | × | × | √ | |
| (8) | (9) | ||
| (10) | (11) |
| (12) | (13) | ||
| (14) | (15) |
| Parameters | Symbols | Values |
|---|---|---|
| Source Rated Voltage | 384 V | |
| Battery Rated voltage | , | 120 V |
| Resonating frequency | 85 kHz | |
| MOSFETs | SiHG33N60EF | |
| Self-Inductance | 220 µH | |
| Compensation Capacitors | 15.9 nF | |
| S-S coil Resistance | 0.5 | |
| Mutual-Inductance | M | 22.5 µH |
| α | Input Power | Loss into the System | % Loss into the System | |||
|---|---|---|---|---|---|---|
| SAHFWPT | DAHFWPT | SAHFWPT | DAHFWPT | SAHFWPT | DAHFWPT | |
| 3.12 | 3605 | 3605 | 586 | 586 | 16.25 | 16.25 |
| 2.16 | 3146 | 2807 | 469 | 453 | 14.97 | 16.15 |
| 1.82 | 2795 | 2252 | 388 | 361 | 13.87 | 16.05 |
| 1.44 | 2312 | 1574 | 290 | 250 | 12.54 | 15.88 |
| 1.14 | 1881 | 1057 | 217 | 165 | 11.51 | 15.65 |
| 0.73 | 1245 | 467 | 136 | 71 | 10.94 | 15.23 |
| 0.33 | 605 | 102 | 99 | 23 | 16.34 | 22.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Bertoluzzo, M.; Jha, R.K.; Sagar, A. Analysis of Losses in Two Different Control Approaches for S-S Wireless Power Transfer Systems for Electric Vehicle. Energies 2023, 16, 1795. https://doi.org/10.3390/en16041795
Kumar A, Bertoluzzo M, Jha RK, Sagar A. Analysis of Losses in Two Different Control Approaches for S-S Wireless Power Transfer Systems for Electric Vehicle. Energies. 2023; 16(4):1795. https://doi.org/10.3390/en16041795
Chicago/Turabian StyleKumar, Abhay, Manuele Bertoluzzo, Rupesh Kumar Jha, and Amritansh Sagar. 2023. "Analysis of Losses in Two Different Control Approaches for S-S Wireless Power Transfer Systems for Electric Vehicle" Energies 16, no. 4: 1795. https://doi.org/10.3390/en16041795
APA StyleKumar, A., Bertoluzzo, M., Jha, R. K., & Sagar, A. (2023). Analysis of Losses in Two Different Control Approaches for S-S Wireless Power Transfer Systems for Electric Vehicle. Energies, 16(4), 1795. https://doi.org/10.3390/en16041795









