Abstract
The increasing demand for flexibility in hydropower systems requires pumped storage power plants to change operating modes and compensate reactive power more frequently. In this work, we demonstrate the potential of applying reinforcement learning (RL) to control the blow-out process of a hydraulic machine during pump start-up and when operating in synchronous condenser mode. Even though RL is a promising method that is currently getting much attention, safety concerns are stalling research on RL for the control of energy systems. Therefore, we present a concept that enables process control with RL through the use of a digital twin platform. This enables the safe and effective transfer of the algorithm’s learning strategy from a virtual test environment to the physical asset. The successful implementation of RL in a test environment is presented and an outlook on future research on the transfer to a model test rig is given.
1. Introduction
On the way to a sustainable future for the energy industry, the hydropower sector is confronted with two concurring developments: digitalization and the increasing share of renewable energy systems in the grid. Due to the volatile nature of wind and sunlight as energy sources, fluctuations in power grids will need to be balanced out by other energy sources and storage systems to a greater extent in the future []. Especially pumped storage power plants are expected to operate more dynamically, as they are currently the main bulk storage technology and will be so in the foreseeable future [].
Driven by emerging technologies, digitalization provides the tools to improve the operation of energy systems. Because of the specific particularities of hydropower sites, every single hydropower station is designed uniquely for its location, and digital methods for hydropower are usually developed for a specific site []. A universal and modular method that can be applied at any site is still missing. A key enabling technology that considers the required scalability of digital methods for hydropower systems is the digital twin (DT). DTs are characterized by a bidirectional data exchange between the physical component and its virtual representation, enabling transparency and expanded flexibility of assets []. On a DT platform, digital solutions are integrated to reduce energy consumption and increase economic sustainability. Examples of such digital solutions are predictive maintenance, process monitoring and analysis, and the integration of machine learning (ML) methods [].
Reinforcement learning (RL) is a type of ML where a so-called agent interacts with an environment (either real or virtual) through the trial-and-error concept, guided by a scalar reward signal. The use of RL in industrial control settings has gained much attention over the last years, as it has shown potential to outperform traditional optimal control methods []. However, safety concerns are limiting use cases to mostly simulated environments []. Recent research shows progress on the transfer from simulated to real world applications of RL for process control in the areas of robotics (e.g., [,]) and manufacturing (e.g., [,]). Especially the combination of a DT platform and the use of transfer learning (TL) seems a promising approach that allows for a reliable application of RL for process control even in large-scale industrial environments. To this date, no research on the deployment of an RL algorithm to critical infrastructure, such as hydropower systems are, is known to the authors. We therefore aim to contribute to developing a universal framework for a DT platform for hydropower systems on which RL can be used to control processes and reveal optimization potential for increased flexibility in hydropower. In this work, we make a first contribution to build such a platform by presenting a three-step learning method and demonstrate the potential of RL for flexible hydropower through a test use case.
This paper is structured as follows: First, we give an overview of the concepts of RL and DTs and introduce the three-step approach for finding a control strategy with RL on a DT platform. We then demonstrate this approach by applying it to control the blow-out process of the runner of a reversible pump turbine, which is necessary for pump start-up and operation in synchronous condenser mode. As a proof-of-concept, we apply RL in a test environment representing the virtual model of a DT. Finally, we give an outlook on future research and draw a conclusion.
2. Reinforcement Learning on a Digital Twin Platform
2.1. Reinforcement Learning
An RL agent learns an optimal decision policy by directly interacting with its environment []. Contrary to the other two forms of ML, supervised and unsupervised learning, where the ML algorithm learns to identify patterns from static data sets, RL does not need an existing data set to learn. The core of an RL algorithm is its policy, which defines how the agent behaves in a given situation []. An RL agent’s goal is to find an optimal policy through interaction with its environment []. Figure 1 shows the formalization of the agent-environment interaction. At each time step t, the RL agent decides on an action that leads to a change in the environment. The environment’s current state is then passed to the agent, together with a reward that assigns a quality measure to the state at each step and acts as feedback to the agent for learning. Based on the observation of the new state, the agent chooses the next action. By repeating this sequence, the agent learns how to optimally map states to actions, aiming to maximize the cumulative rewards received over time (called return ). After enough training episodes, this mapping ultimately yields the optimal policy , with being the probability of taking the action given the state []. The value of a state is defined by the so-called Bellman Equation (1) that calculates the expected return when starting from the state s and thereafter following the policy :
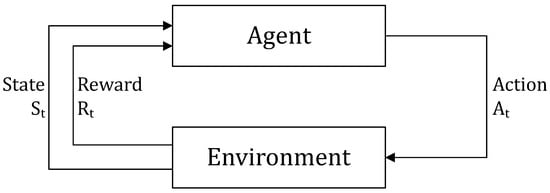
Figure 1.
Schematic agent—environment interaction within a reinforcement learning (RL) algorithm, adapted from [].
The RL agent needs to randomly explore the state space during learning to determine which actions lead to high rewards. Simultaneously, the agent has to follow strategies that have already proven to produce high rewards. This trade-off between exploration and exploitation is a core challenge for RL algorithms []. Performance improvement can be achieved only through exploiting the best of past actions. However, if exploiting is pursued too soon, the algorithm will converge to a sub-optimal policy [].
The use of RL has been gaining more and more attention over the last few years. Next to well-established applications in robotic (e.g., []) and gaming (e.g., []) problems, RL is increasingly applied in industrial settings within the area of process operations, mainly for planning and scheduling of strategic decisions []. For hydropower systems, RL has been primarily proposed and tested for optimal water reservoir operation [,,].
Research on applications of RL for process control is still in its early stage, mainly because of safety concerns for letting an intelligent algorithm interact with complex and delicate systems. Failure and destruction of components need to be avoided by following safety constraints during the exploratory phase of the RL agent []. We propose that this challenge can be tackled within the concept of a digital twin platform.
2.2. Digital Twin
The DT concept originated in the aerospace industry in the early 2000s and has since radically grown in significance in various domains []. While DT concepts in the manufacturing and automotive industries have already reached maturity, examples for implementing DTs in energy systems are still rare and limited to specific use cases []. We refer to the DT as a concept that enables the strong interconnection between a machine and its virtual representation, derived from Steindl et al. []: data from the physical and the virtual entities, together with domain knowledge, is used to implement services that help optimizing the operation of the asset.
Typical services of DTs in the energy industry are monitoring, diagnostic and prediction services that help to observe current states of the physical system and implement strategies for fault detection, predictive maintenance, or the prediction of energy consumption []. Accordingly, the application of DT methods in hydropower is currently mainly focused on predicting the plant’s performance under different operating conditions to increase the reliability and efficiency of the operation []. Further, the research on the use of DTs in the field of hydropower is still in an early stage. At the moment, the most prominent use cases for DTs in hydropower are fatigue assessment and lifetime extension [,].
Applying the DT approach for an optimal operation service is certainly challenging but also has the potential of operating hydropower plants more flexibly []. We want to use a DT platform to enable the control and optimization of processes in hydropower. The connection between the data model, the virtual and the physical entity of the DT makes it possible to develop an optimal control service using RL.
2.3. Our Approach: Three-Step Learning Process
To enable the use of RL for process control of safety-sensitive industrial equipment, such as hydropower plants, TL is combined with the DT approach. TL describes the approach of transferring knowledge and skills from previously studied to new environments []. Recent studies suggest that TL can be used to deploy an RL algorithm, which was trained in a simulation environment, onto real assets [,,] while speeding up the learning process of the RL problem []. However, simulation models used to pre-train the algorithm are mostly either not sophisticated enough to actually represent the real world unit [], or require too much computation time to ensure efficient training of the RL algorithm [].
We therefore propose a three-step learning approach that enables time efficient pre-training on a simple data model, further training on an exact, simulated replication of the real asset and the adaptation of the pre-learned strategy to the real machine unit. Implementing the RL agent on a DT platform that incorporates all three environments (historical data model, virtual replication and physical unit) makes it possible to use TL to constantly improve the RL agents strategy. Figure 2 shows our concept specifically for the augmentation of hydropower systems by combining a DT platform and RL. The DT collects historical data from the real entity, which is used as training data for the RL algorithm. After this pre-learning phase, the agent can find an optimal policy for the operation of the asset by further training of the algorithm through interaction with the environment of the virtual DT model. Then the agent is applied to the physical component, where it adapts its strategy according to the real conditions. At this point, only slight adjustments are required and the RL agent can safely interact with the machine.
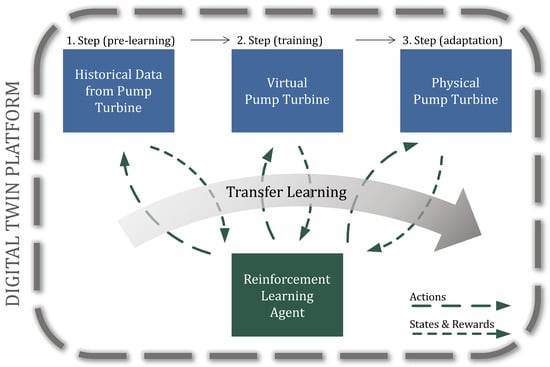
Figure 2.
Concept of the application of RL on a digital twin (DT) platform.
The proposed three-step learning process enables finding true optimal and robust results through three main advantages: First, training on the virtual model accelerates the training process compared to the direct application of RL on live operations. Second, narrowing the RL agent’s action space through pre-training significantly reduces safety concerns for learning and operating on the actual power system. And third, when operating on the actual power systems, the control strategy can be adapted to real conditions.
3. Test Case
Regarding the future role of pumped storage power plants it is expected that compensating of reactive power in the power grid as well as switching between pump and turbine mode will be required more and more frequently. Both, the operation in synchronous condenser mode and the pump start-up, require blowing out the runner []. The acceleration of the blow-out process could represent an effective tool to enable faster reaction times.
Therefore, we implemented an RL algorithm to control the blow-out process and the dewatered operation of a rotating pump turbine runner. We aim to showcase the potential of using RL to increase the flexibility of hydropower systems by training the agent to blow out the machine as fast as possible with the smallest amount of compressed air possible. As a proof-of-concept for our three-step learning approach, we apply RL to a simplified test environment and show that RL is suited for this application. Pre-training the learning agent with the strategy of a simple hysteresis controller may lead to the agent’s strategy converging faster to the optimal policy while avoiding ineffectual actions. Anticipating the transfer of the algorithm to the physical machine, TL is especially valuable since exploration on the real machine would be critical in terms of safety and take far too long.
Figure 3 shows the formalized structure of the RL model. Following the standard schematic agent—environment interaction of an RL formulation (see Figure 1), we modeled a RL problem in MATLAB/Simulink. Based on a state, which is being calculated within the simulation environment, and the according reward signal, the RL algorithm is deciding on the next action and passing it on to the environment. In Figure 3, the switch between the input action from the controller or from the RL algorithm demonstrates the option for the RL agent to observe the strategy of the hysteresis controller and pre-calculate the values for the policy function beforehand. The loop is representing the calculations during each time step of our test case. In the following paragraphs, the relevant components of the RL model are described in more detail.
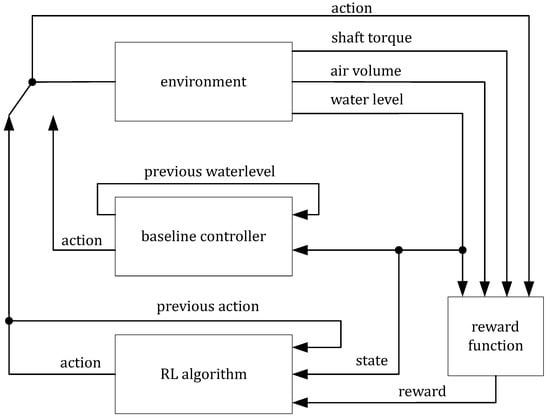
Figure 3.
Formalized agent—environment interaction loop for the blow-out process test case.
Environment As a test environment for training the RL algorithm, we employed simple relations for characterizing the blow-out process in MATLAB/Simulink. The trivial model calculates the volume of compressed air blown into the turbine draft tube , the resulting water level in the draft tube , and the corresponding shaft torque T.
Action space The possible actions for the RL agent at each decision time are whether to blow air into the draft tube or not: .
State space The environment’s state is described by the current water level . Additionally, information on the previous action a is given to the RL agent: . This tells the agent if the water level is currently rising or falling and allows it to make an informed decision about the next action.
Reward function To assess the value of an action-state pair, the reward function consists of four weighted terms. At every time step, the learning agent receives
- a reward when the shaft torque is below a certain threshold that is assigned as a criterion whether the turbine is dewatered or not,
- a penalty proportional to the torque if it is above this threshold,
- a penalty proportional to the compressed air flow into the draft tube, and
- a penalty whenever it switches the air valve to encourage more stable operation.
Termination criterion The learning episode is terminated after a simulation time of 600 s. Furthermore, the total volume of compressed air that was blown into the draft tube is monitored. If it exceeds a certain threshold (indicating that the compressor’s limit is reached), the RL agent receives a high penalty, and the episode is aborted.
RL algorithm To control the blow-out process, a SARSA agent from the MATLAB Reinforcement Learning Toolbox (https://de.mathworks.com/help/reinforcement-learning/ug/sarsa-agents.html, accessed on 11 January 2023) was used. The SARSA algorithm is a value-based RL method that selects an action according to the exploration probability . With probability , a random action is selected to enable exploration, and with probability , the action with the greatest expected return is selected. After observing the reward and the next state from the environment, the value is updated in a table that stores the calculated values for each state-action pair. When training is finished, the agent’s optimal policy can be derived from this table.
Training options The SARSA agent was trained for 2000 episodes with an exploration probability of . After each training episode, was updated following a decay function until the minimum value was reached. The initial water level inside the draft tube was randomized for each training episode. This helps the agent to visit all possible states, which ensures obtaining a complete and reliable final policy.
Baseline controller To evaluate the RL agent’s strategy, a simple hysteresis control with two limit switches for an upper and lower water level in the draft tube was implemented.
Transfer learning TL was implemented by presenting the agent with the baseline controller’s strategy. In this way, the agent could observe the environment’s behavior without selecting actions by itself and preliminarily calculate the values for the state-action table. Subsequently, the agent’s actual training was picked up from the pre-learned strategy. When TL is used, the initial exploration probability can be lowered considerably, which enables faster convergence.
4. Results and Discussion
The RL algorithm was trained to control the blow-out process within the test environment, as documented in Section 3. The algorithm was trained for 2000 episodes, with each episode lasting a maximum of 600 time steps, with one time step corresponding to one second in the simulation. The goal was for the algorithm to manage to balance between rapidly reaching and remaining in blown-out operation mode while minimizing the amount of dissipated compressed air. In the first training run, the RL agent did not receive any prior information on the state-action values from the baseline controller (i.e., TL was not applied). The control strategy of the trained RL agent was then compared to the strategy of the hysteresis controller. Subsequently, we presented the agent with the hysteresis controller’s strategy to implement TL. We then compared the training processes of the agents for training with and without TL.
The RL agent successfully learned to control the blow-out process within our test simulation environment. Figure 4 shows the control strategy of the SARSA agent over its training history, as well as the control strategy of the baseline controller. At the beginning of training, the agent fails to blow out the runner rapidly because it explores random action sequences. However, once the blown-out condition is reached, the agent manages to hold the water level below the dewatering threshold of 0.2 m most of the time. After 2000 training episodes, the policy of the learning algorithm is stable and can be interpreted as a repeating sequence of three phases. At the beginning of the episode, when the runner is filled with water, the strategy for operating the blow-out process is to blow air into the draft tube () until the water level has reached a minimum height. Then, blowing air is stopped () and the water level rises again, indicating that air is dissipating. When the threshold for the shaft torque, up until which the operation mode is considered blown-out, is reached, air is again blown into the draft tube ().
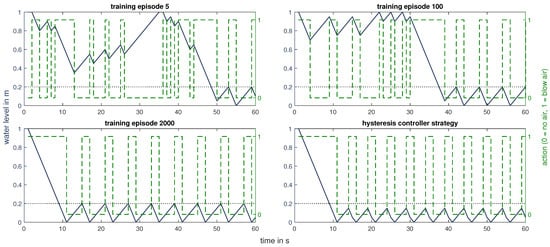
Figure 4.
Control strategies for the blow-out process of different training stages of the RL agent as well as the strategy of the baseline controller. Water level in draft tube in m and control action over the first 60 s of an episode. The dotted horizontal line indicates the water level under which the runner is considered blown out.
This cycle is repeated until simulation time has ended. It can be seen in Figure 4 that the RL algorithm reaches a very similar policy as the two-point controller without knowing the values for the limit switches beforehand. Entirely through effective reward shaping, we succeeded in training the SARSA agent even to outperform the hysteresis controller. While both strategies successfully manage to reach the blown-out condition equally fast, following the self-learning strategy of the RL agent minimizes the number of switches between actions by exhausting the water level limits for blown-out condition. This results in a higher cumulative reward for the agent than for the baseline controller.
In this simple test-case the same result could have been achieved by adjusting the limit values of the hysteresis controller. Though, our RL on a DT platform approach can be extended to much more complex control tasks, where adjusting control parameters manually is not feasible.
The benefit of applying TL to train RL algorithms is illustrated in Figure 5. For training with TL, the agent observes the baseline controller’s strategy before the actual training starts. The cumulative reward for the final and optimal strategy is 188. Both training curves show that the optimal control strategy is found after 25 training episodes, when the training curves converge to an average reward of 175. However, the training without TL starts with suboptimal action trajectories, indicated by the low average return of −11.3 in the beginning of the training. This behavior could imply unwanted machine conditions when transferred to actual machine units. Possibly harmful conditions can be prevented by instructing the RL agent to pre-learn from established operating strategies. Through observing the controller’s strategy preliminarily, the agent instantly achieves a high return of 73.7. After 15 episodes, the pre-trained agent adapts its strategy from the hysteresis controller’s logic to the optimal strategy for the blow-out process within the test environment, which can be seen in Figure 5 through the lift of the average cumulative reward curve from the visible plateau.
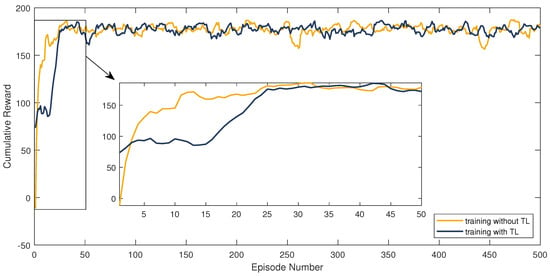
Figure 5.
Comparison of the SARSA agent’s learning progress over 500 training episodes for training with and without pre-learning with the hysteresis controller’s strategy.
In this simple test case, the agent converges to the optimal policy equally fast whether TL is applied or not. However, when advancing to more complex controlling objectives and environments, we do not expect the RL agent to find the optimal policy as quickly. During future research, pre-learning from historic data is presumed to significantly accelerate the training process and make it more robust.
5. Outlook
The full potential of increasing the flexibility of hydropower with RL on a DT platform will unfold once we apply the concept to a real machine. For these tests, we have a radial model pump turbine located at the test facilities of the Institute of Energy Systems and Thermodynamics (IET) (see Figure 6). Before the algorithm’s strategy can be transferred from the simulation to the model machine, several things need to be implemented.

Figure 6.
Test rig with scale reduced model of a radial pump turbine at the hydraulic lab of the Institute of Energy Systems and Thermodynamics, TU Wien.
The agent will be trained to control more complex use cases within the virtual environment. Therefore, a highly sophisticated model of the lab-scale model machine is being created. Further, an RL agent using deep neural networks instead of simple tabular algorithms to optimize its policy will be deployed to handle the continuous control of the operation in synchronous condenser mode. The coupling of the physical entity with the virtual space of the DT platform will be realized via a SCADA system. Through a message broker, the optimal control service incorporating the RL algorithm will be able to communicate with the model machine. Though, before TL is applied and the learning agent interacts autonomously with the physical unit, reliability and safety measures will have to be taken. Further research is already on the way to address these requirements.
6. Conclusions
In this paper, we demonstrated a concept for enabling the application of RL for hydropower systems. RL can be an effective tool to optimize highly complex and unstable industrial processes. By autonomously interacting with the environment, the RL algorithm finds an optimal policy without the need for exact mathematical models. To tackle technical safety barriers that are stalling research on applying RL for process control in hydropower systems, we propose a concept to apply a three-step learning approach. Implementing a DT platform makes it possible to pre-train the learning algorithm within a virtual environment and transfer the optimal control strategy to the machine. To evaluate this concept, we applied RL to a test environment representing the virtual model of our test rig. We showed that RL is suitable for controlling the blow-out process for synchronous condenser mode in this first proof-of-concept. Further, we demonstrated that TL enhances the performance of the RL algorithm and prevents non-optimal operating conditions.
The next step is to transfer these results to the test rig in the laboratory. Before letting the pre-learned RL agent interact with the test rig, additional safety constraints must be integrated to limit the agent’s possible action space. We will then apply the RL algorithm to the model machine in the lab and control the blow-out process with the autonomously learned optimal strategy. Following this example use case, future research will focus on a universal method that enables increased flexibility in hydropower through RL on a DT platform.
Author Contributions
Conceptualization, C.T., F.B., A.M. and R.H.; methodology, C.T., F.B. and A.M.; validation, F.B. and A.M.; formal analysis, C.T. and F.B.; writing—original draft preparation, C.T.; writing—review and editing, C.T., F.B., A.M. and R.H.; visualization, C.T.; supervision, R.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors thank Christian Bauer, for his guidance and advice. The authors acknowledge the support of this work through the women’s promotion program of the Faculty of Mechanical and Industrial Engineering (MWBF) at TU Wien. The authors further acknowledge TU Wien Bibliothek for financial support through its Open Access Funding Programme.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DT | Digital twin |
| ML | Machine learning |
| RL | Reinforcement learning |
| TL | Transfer learning |
References
- Gimeno-Gutiérrez, M.; Lacal-Arántegui, R. Assessment of the European potential for pumped hydropower energy storage based on two existing reservoirs. Renew. Energy 2015, 75, 856–868. [Google Scholar] [CrossRef]
- Sayer, M.; Haas, R.; Ajanovic, A. Current State And Perspectives Of Pumped Hydro Storage In The Electricity System. In Proceedings of the 1st IAEE Online Conference Energy, Covid and Climate Change, Online, 7–9 June 2021. [Google Scholar]
- Kougias, I.; Aggidis, G.; Avellan, F.; Deniz, S.; Lundin, U.; Moro, A.; Muntean, S.; Novara, D.; Pérez-Díaz, J.I.; Quaranta, E.; et al. Analysis of emerging technologies in the hydropower sector. Renew. Sustain. Energy Rev. 2019, 113, 109257. [Google Scholar] [CrossRef]
- Steindl, G.; Stagl, M.; Kasper, L.; Kastner, W.; Hofmann, R. Generic Digital Twin Architecture for Industrial Energy Systems. Appl. Sci. 2020, 10, 8903. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, H.; Liu, A.; Nee, A.Y.C. Digital Twin in Industry: State-of-the-Art. IEEE Trans. Ind. Inform. 2019, 15, 2405–2415. [Google Scholar] [CrossRef]
- Shin, J.; Badgwell, T.A.; Liu, K.H.; Lee, J.H. Reinforcement Learning—Overview of recent progress and implications for process control. Comput. Chem. Eng. 2019, 127, 282–294. [Google Scholar] [CrossRef]
- Nian, R.; Liu, J.; Huang, B. A review On reinforcement learning: Introduction and applications in industrial process control. Comput. Chem. Eng. 2020, 139, 106886. [Google Scholar] [CrossRef]
- Ju, H.; Juan, R.; Gomez, R.; Nakamura, K.; Li, G. Transferring policy of deep reinforcement learning from simulation to reality for robotics. Nat. Mach. Intell. 2022, 4, 1077–1087. [Google Scholar] [CrossRef]
- Salvato, E.; Fenu, G.; Medvet, E.; Pellegrino, F.A. Crossing the Reality Gap: A Survey on Sim-to-Real Transferability of Robot Controllers in Reinforcement Learning. IEEE Access 2021, 9, 153171–153187. [Google Scholar] [CrossRef]
- Li, J.; Pang, D.; Zheng, Y.; Le, X. Digital Twin Enhanced Assembly Based on Deep Reinforcement Learning. In Proceedings of the 2021 11th International Conference on Information Science and Technology (ICIST), Chengdu, China, 21–23 May 2021; pp. 432–437. [Google Scholar] [CrossRef]
- Maschler, B.; Braun, D.; Jazdi, N.; Weyrich, M. Transfer learning as an enabler of the intelligent digital twin. Procedia CIRP 2021, 100, 127–132. [Google Scholar] [CrossRef]
- Lee, J.H.; Shin, J.; Realff, M.J. Machine learning: Overview of the recent progresses and implications for the process systems engineering field. Comput. Chem. Eng. 2018, 114, 111–121. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A. Reinforcement Learning: An Introduction, 2nd ed.; Adaptive Computation and Machine Learning; The MIT Press: Cambridge, MA, USA; London, UK, 2018. [Google Scholar]
- Langford, J. Efficient Exploration in Reinforcement Learning. In Encyclopedia of Machine Learning and Data Mining, 2nd ed.; Sammut, C., Webb, G.I., Eds.; Springer Reference; Springer: New York, NY, USA, 2017; pp. 389–392. [Google Scholar] [CrossRef]
- Kober, J.; Bagnell, J.A.; Peters, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2022, 32, 1238–1274. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Castelletti, A.; Galelli, S.; Restelli, M.; Soncini-Sessa, R. Tree-based reinforcement learning for optimal water reservoir operation. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Lee, J.H.; Labadie, J.W. Stochastic optimization of multireservoir systems via reinforcement learning. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, X.; Peng, A.; Liang, Y. Deep Reinforcement Learning for Cascaded Hydropower Reservoirs Considering Inflow Forecasts. Water Resour. Manag. 2020, 34, 3003–3018. [Google Scholar] [CrossRef]
- Singh, M.; Fuenmayor, E.; Hinchy, E.P.; Qiao, Y.; Murray, N.; Devine, D. Digital Twin: Origin to Future. Appl. Syst. Innov. 2021, 4, 36. [Google Scholar] [CrossRef]
- Kasper, L.; Birkelbach, F.; Schwarzmayr, P.; Steindl, G.; Ramsauer, D.; Hofmann, R. Toward a Practical Digital Twin Platform Tailored to the Requirements of Industrial Energy Systems. Appl. Sci. 2022, 12, 6981. [Google Scholar] [CrossRef]
- Ristić, B.; Bozic, I. Digital technologies emergence in the contemporary hydropower plants operation. In Proceedings of the International Conference Power Plants, Belgrade, Serbia, 16–17 December 2021. [Google Scholar]
- Dreyer, M.; Nicolet, C.; Gaspoz, A.; Gonçalves, N.; Rey-Mermet, S.; Boulicaut, B. Monitoring 4.0 of penstocks: Digital twin for fatigue assessment. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012009. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Matulis, M.; Harvey, C. A robot arm digital twin utilising reinforcement learning. Comput. Graph. 2021, 95, 106–114. [Google Scholar] [CrossRef]
- Taylor, M.E.; Stone, P. Transfer Learning for Reinforcement Learning Domains: A Survey. J. Mach. Learn. Res. 2009, 10, 1633–1685. [Google Scholar]
- Maly, A.; Bauer, C. Experimental investigation of a free surface oscillation in a model pump-turbine. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012068. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).