Research on Aerodynamic Design of an End Wall Based on a Quasi-3D Optimization Method
Abstract
:1. Introduction
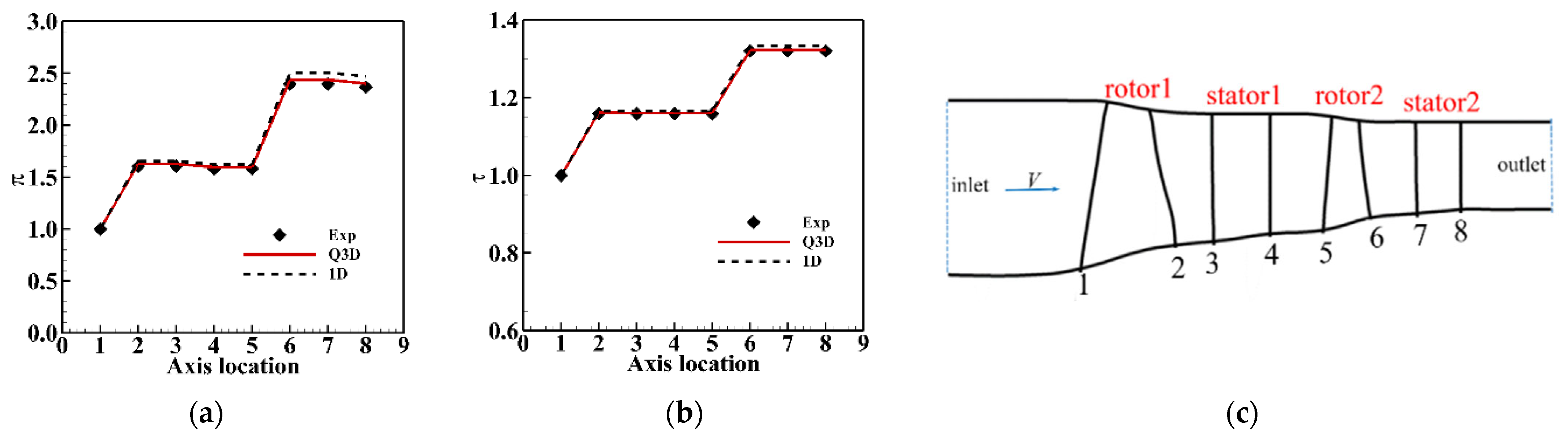
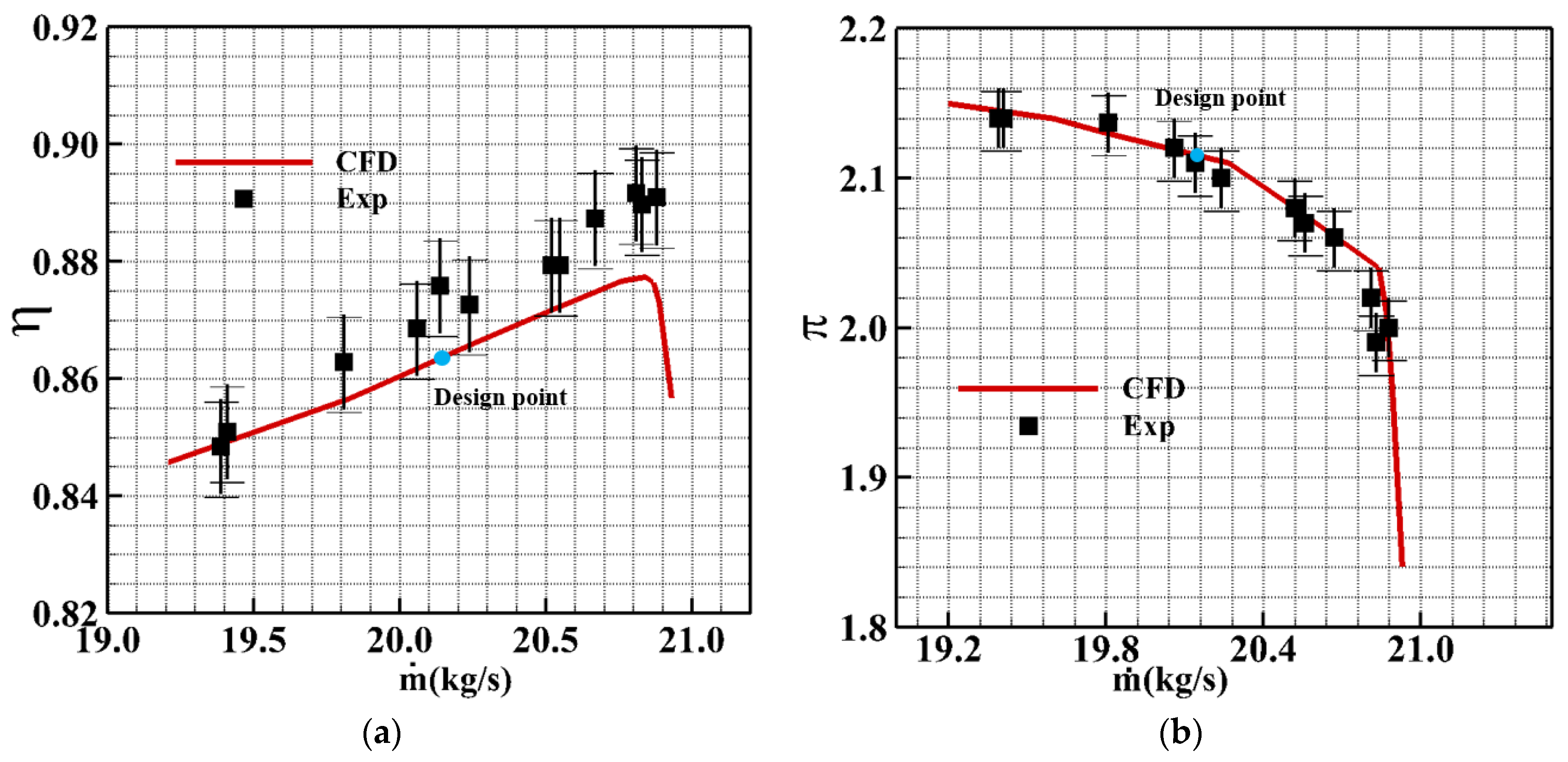
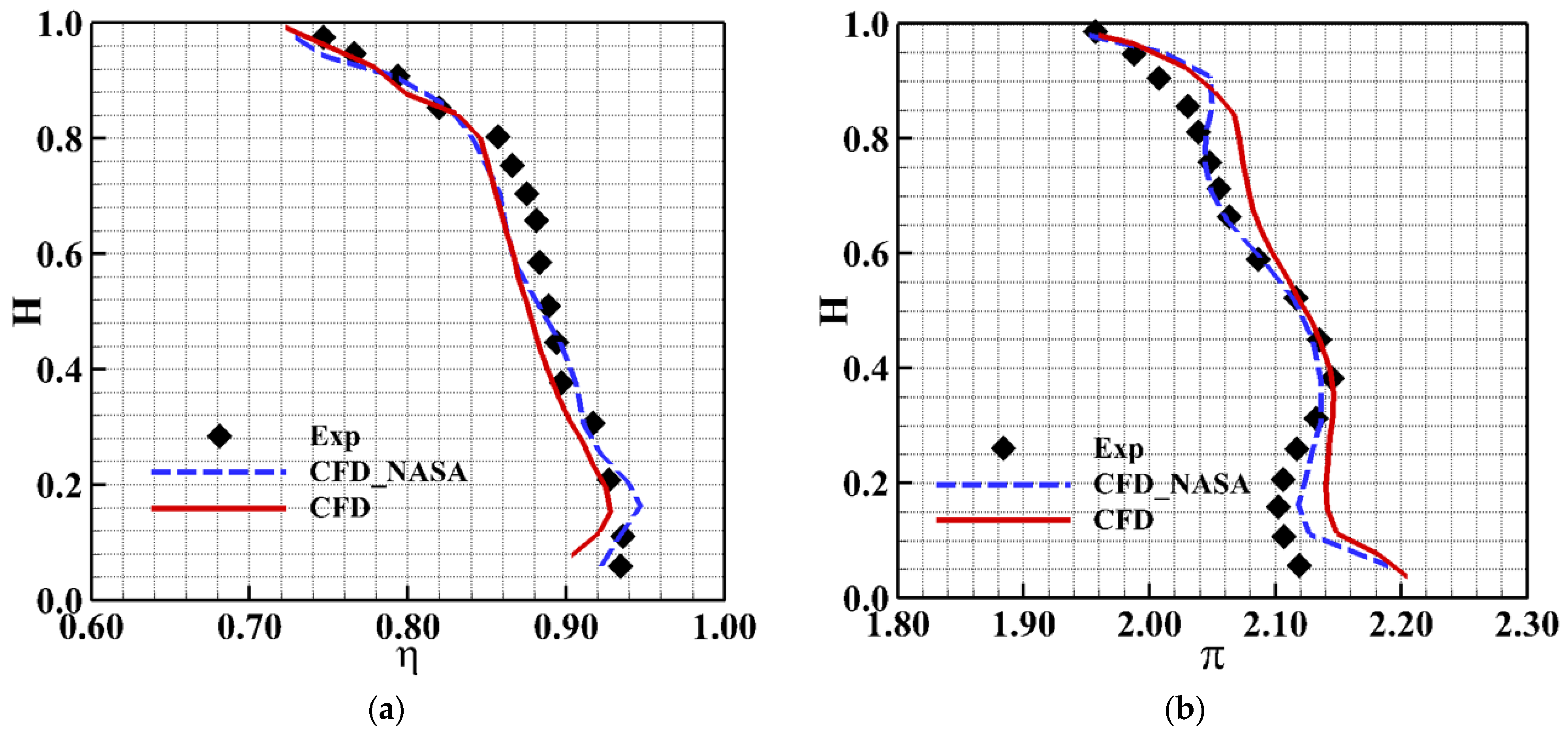
2. Research Object and Numerical Simulation Method Validation
2.1. D and Quasi-3D Aerodynamic Design
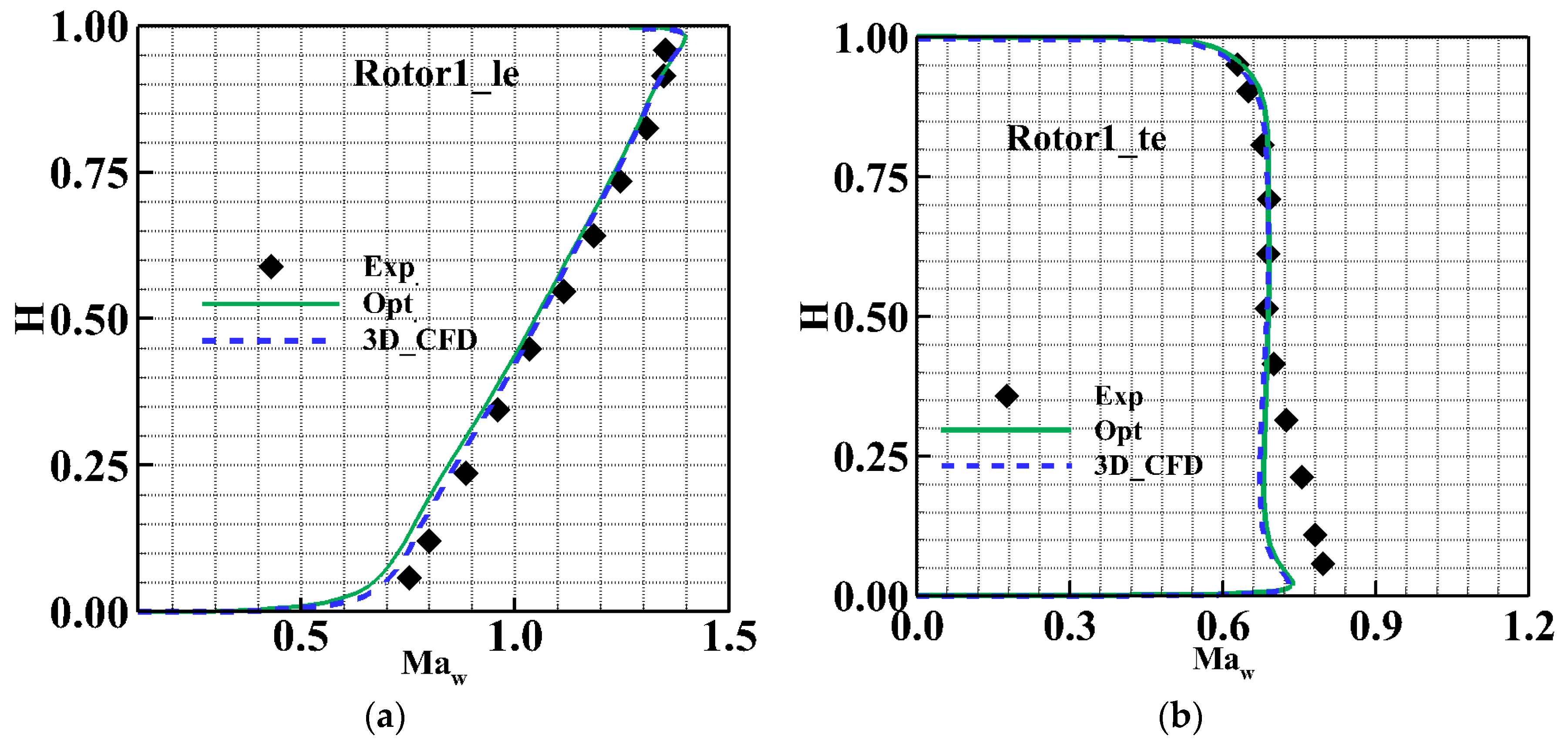
2.2. Independence Verification
3. Quasi-3D End Wall Optimization Method
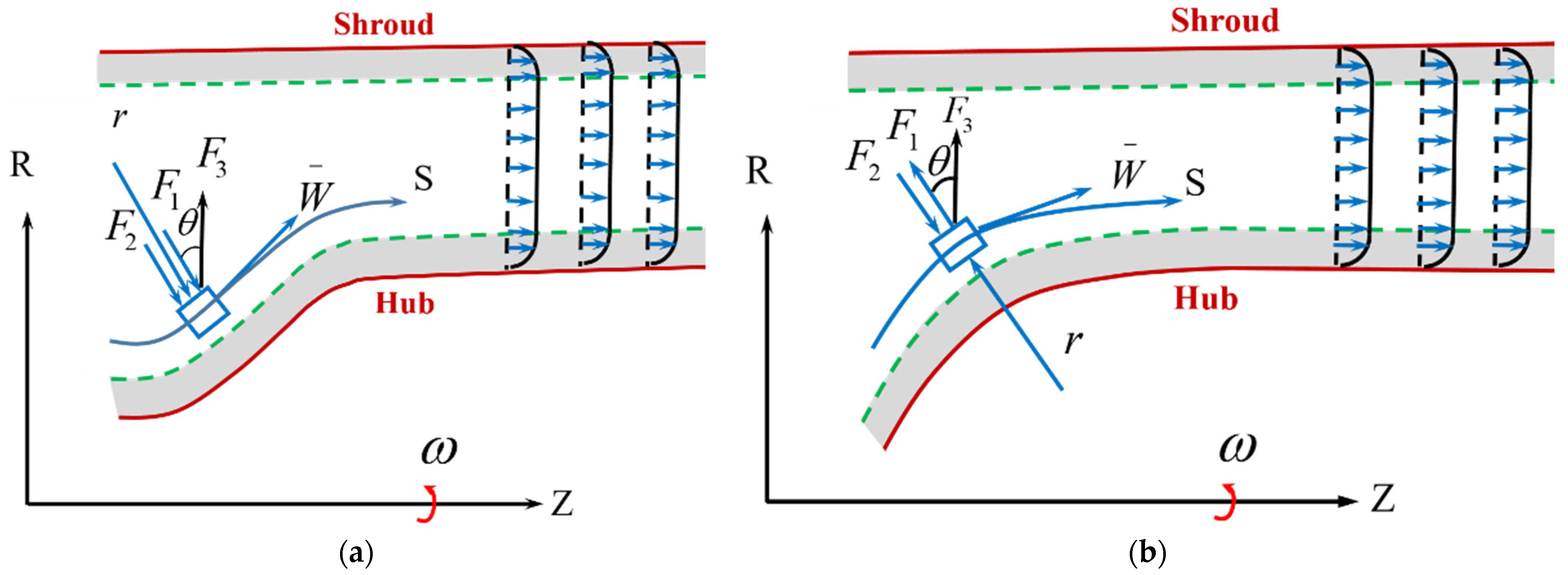
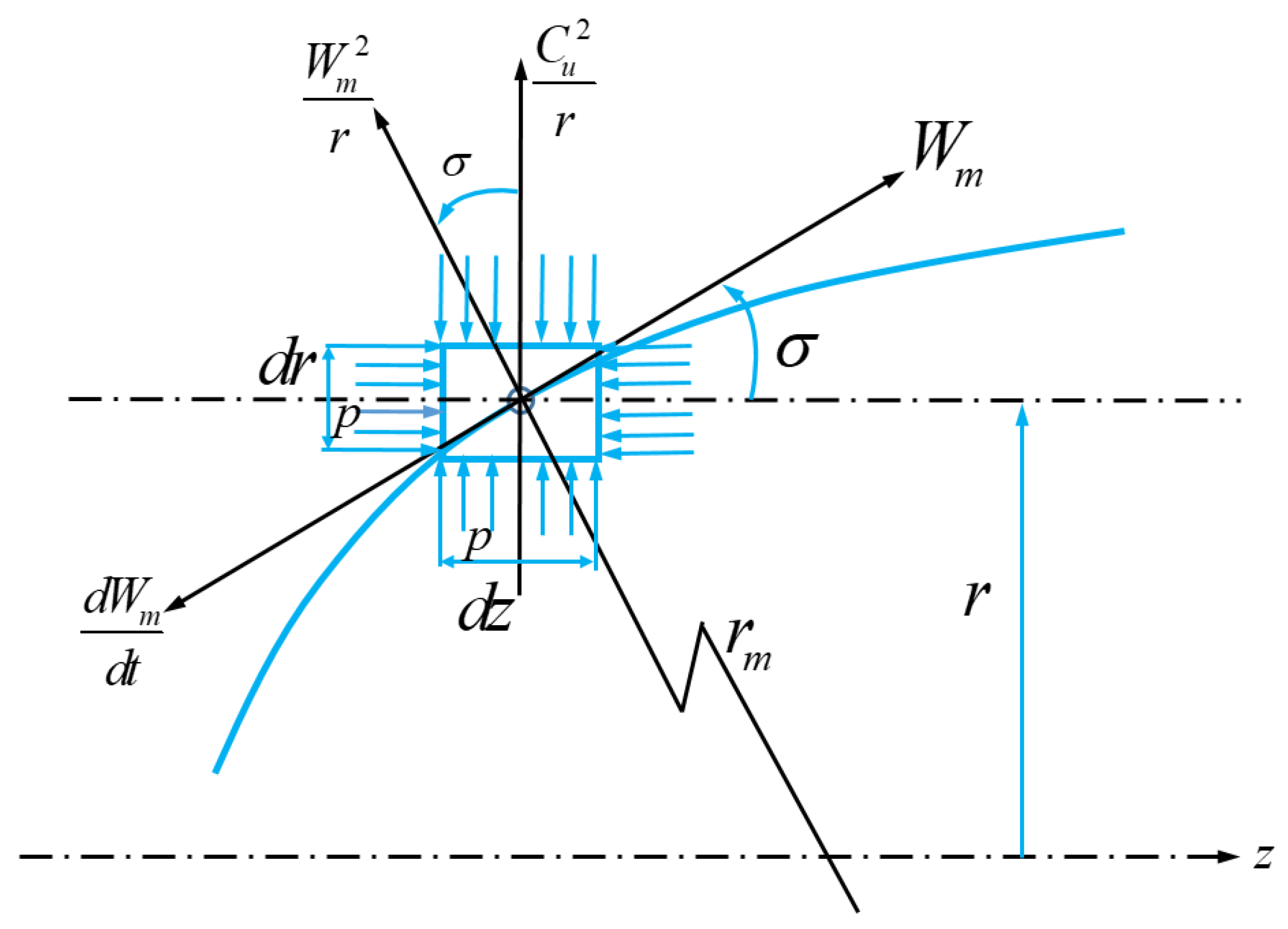
3.1. Aerodynamic Optimization Theory of the End Wall
- (1)
- The centripetal acceleration caused by the circumference velocity Cu2/r;
- (2)
- The radial component of the centripetal acceleration Wm2/rm in the meridional plane due to the curve motion;
- (3)
- The radial component of the meridional acceleration dWm/dt;
- (4)
- The radial component of the F is caused by the uneven static pressure in the circumference.
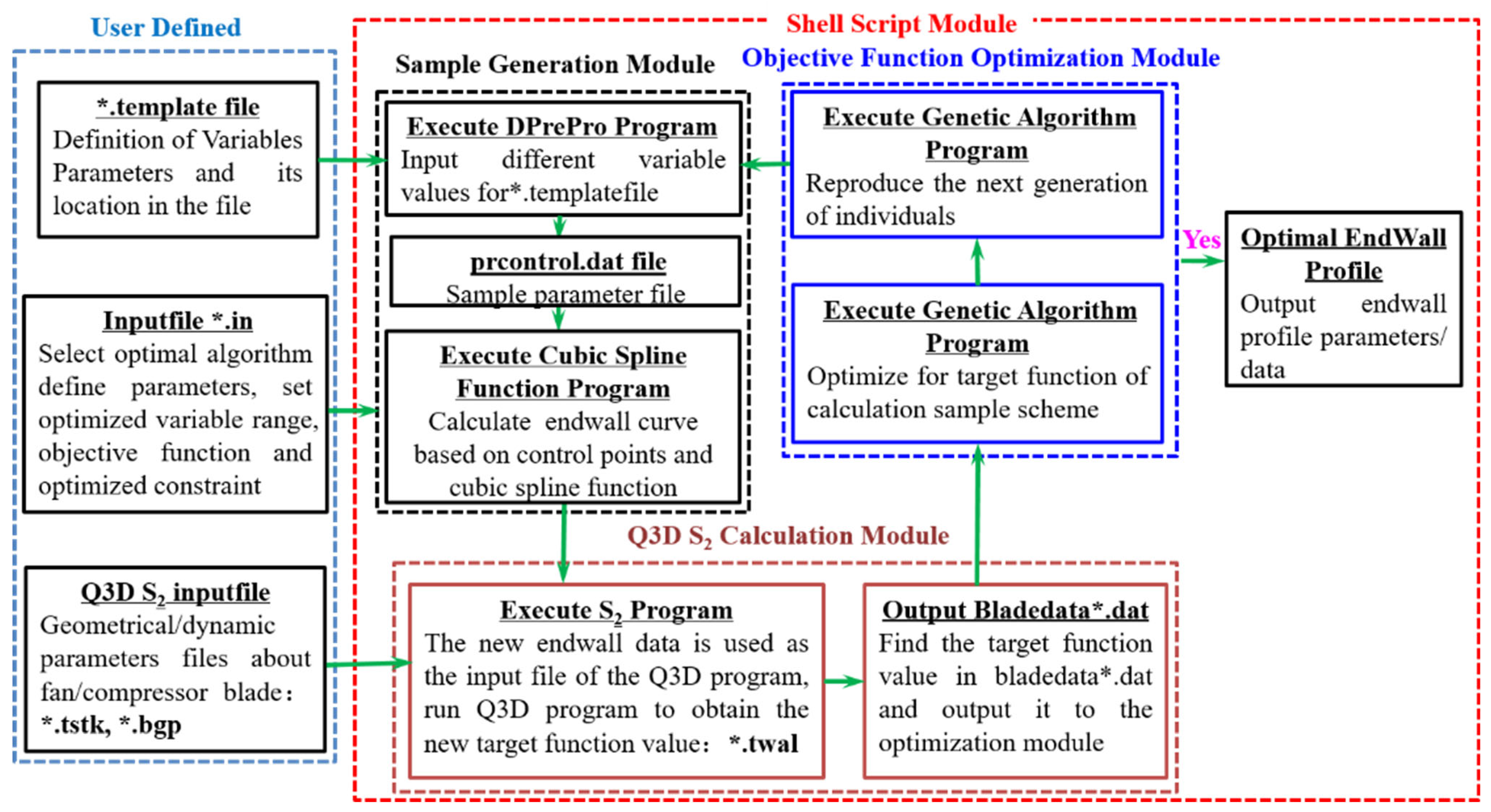
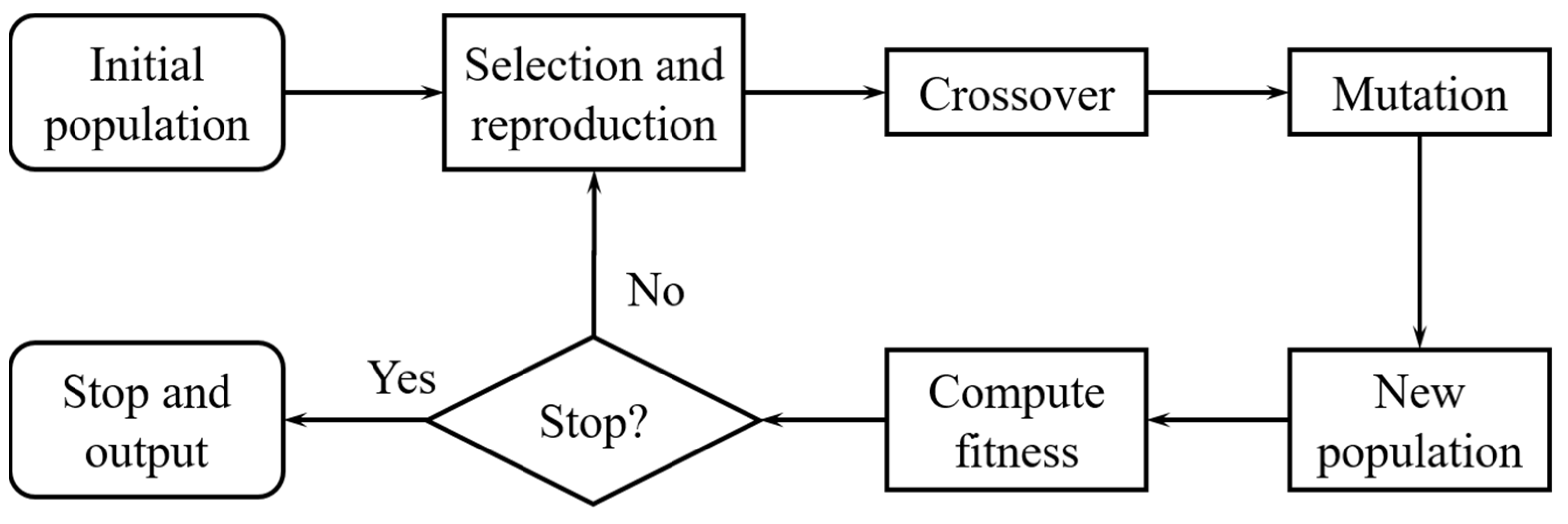
3.2. Aerodynamic Optimization Method and Platform of the End Wall
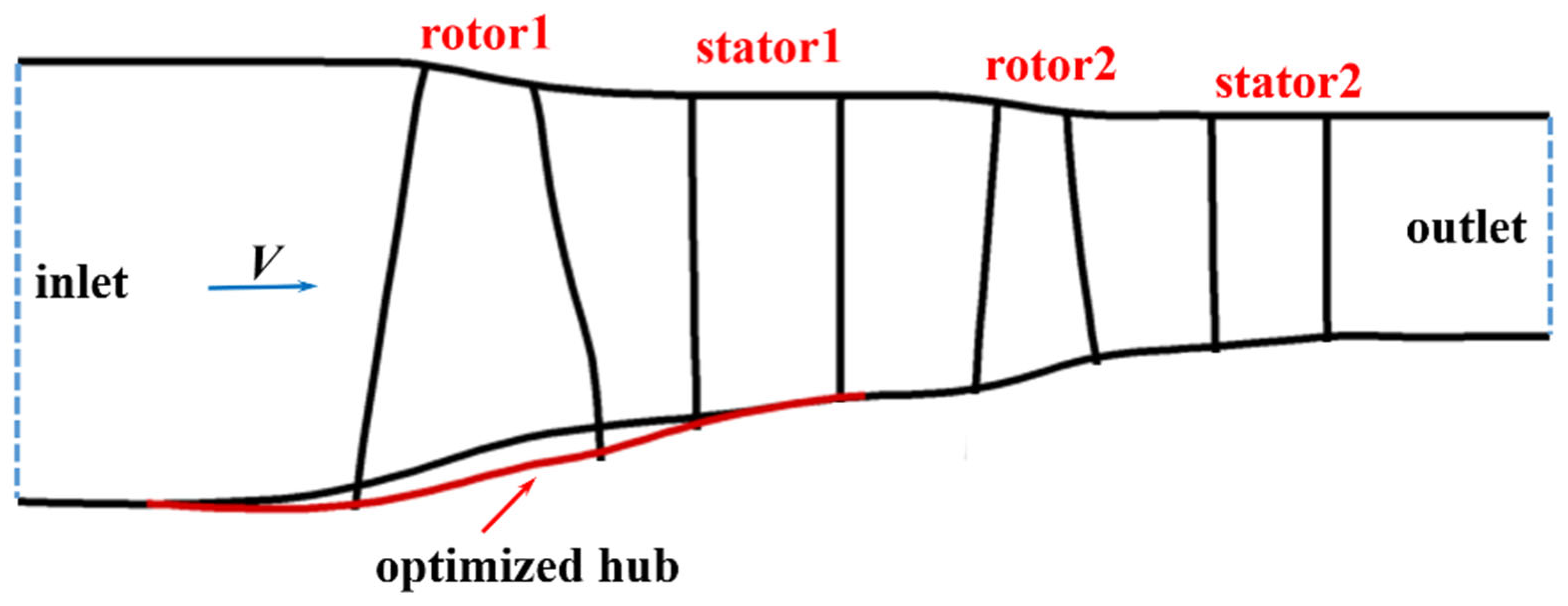
4. The Analysis of the Optimized-Hub Results for a Two-Stage Fan
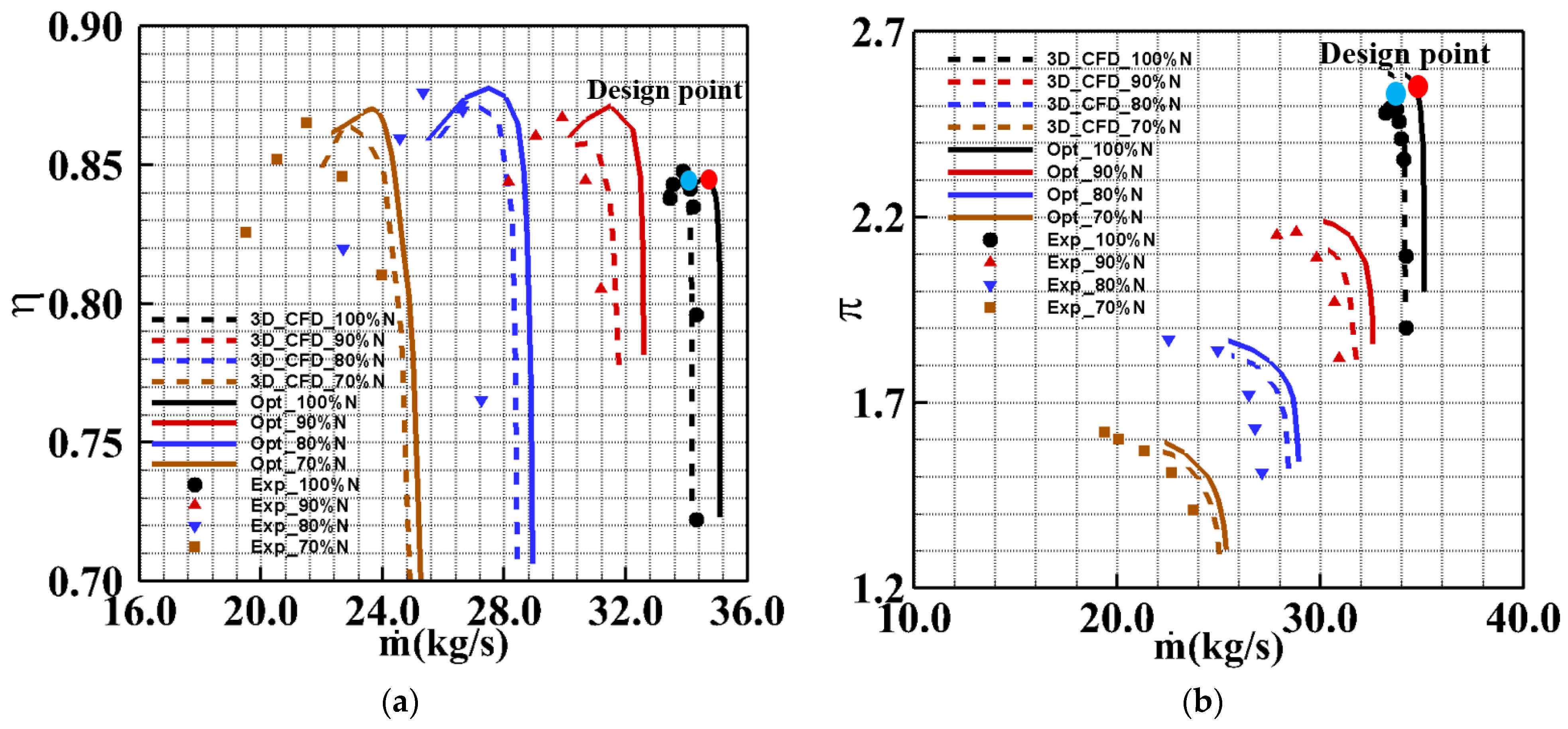
4.1. Aerodynamic Performance Analysis
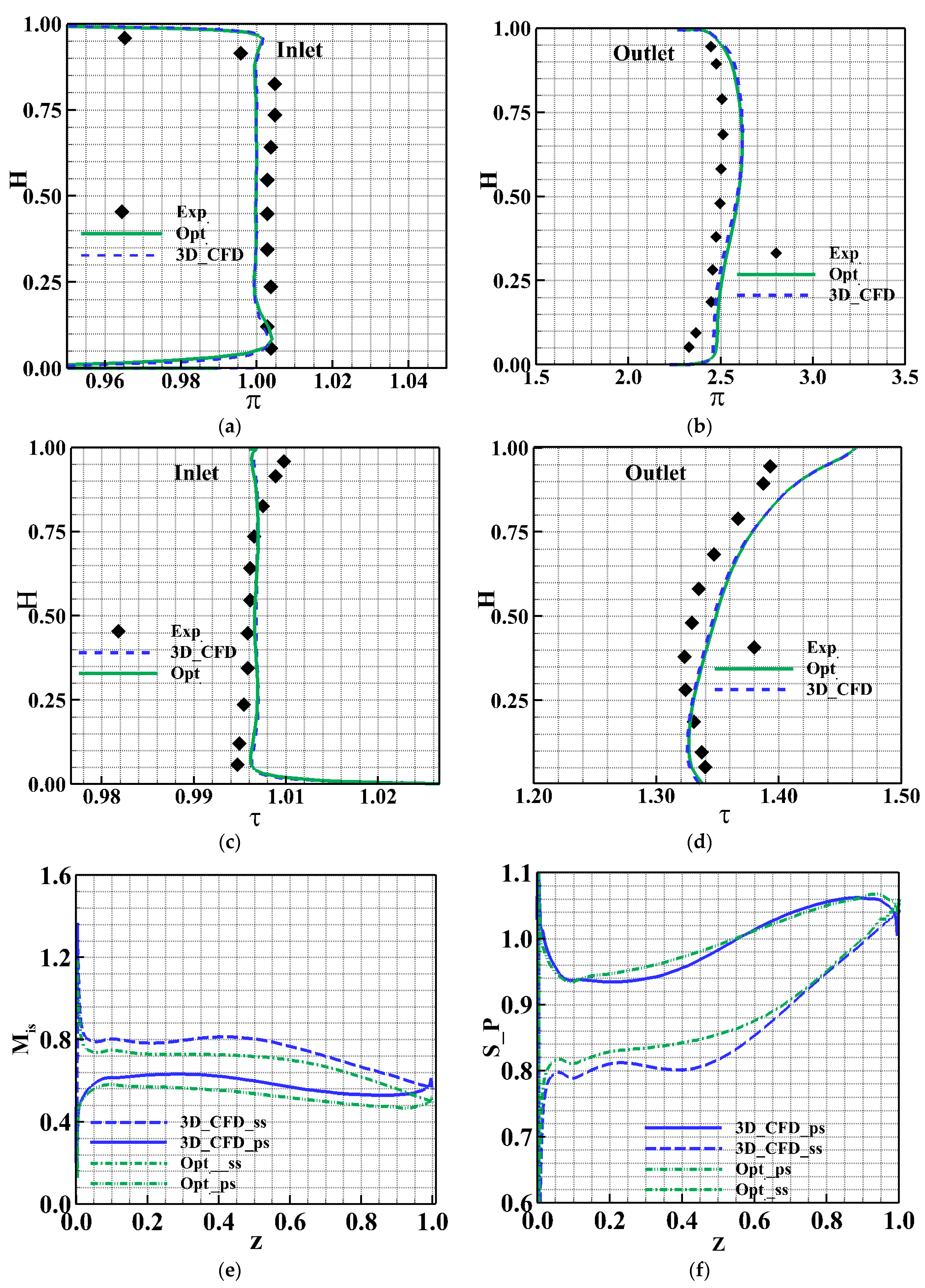
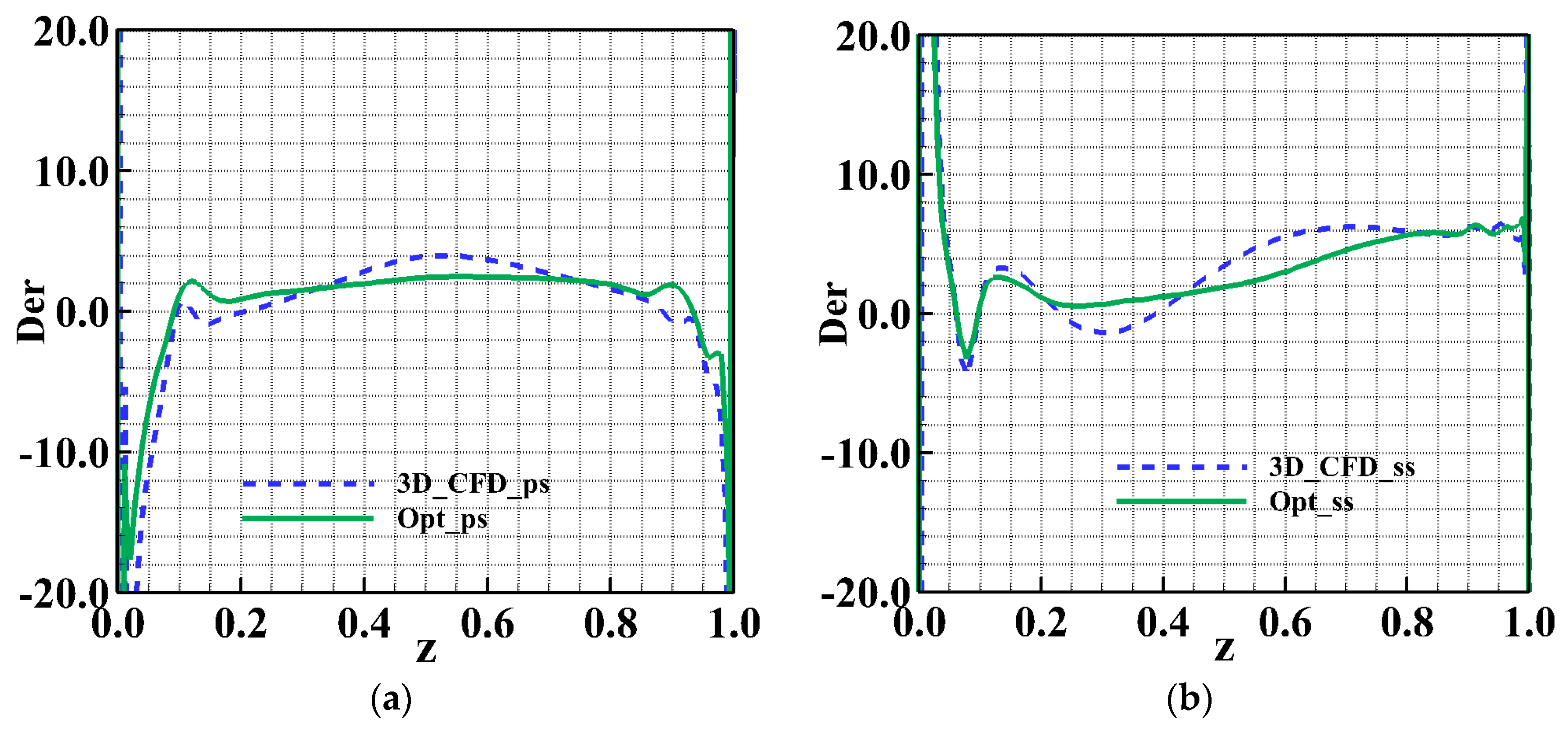
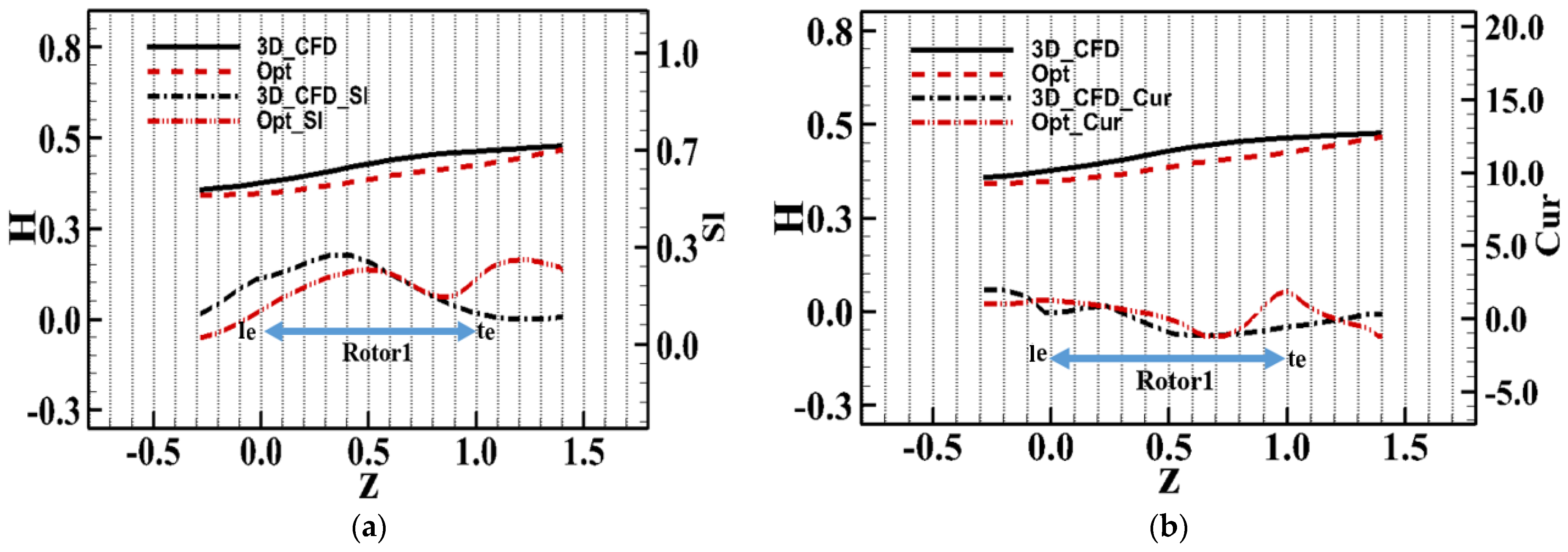
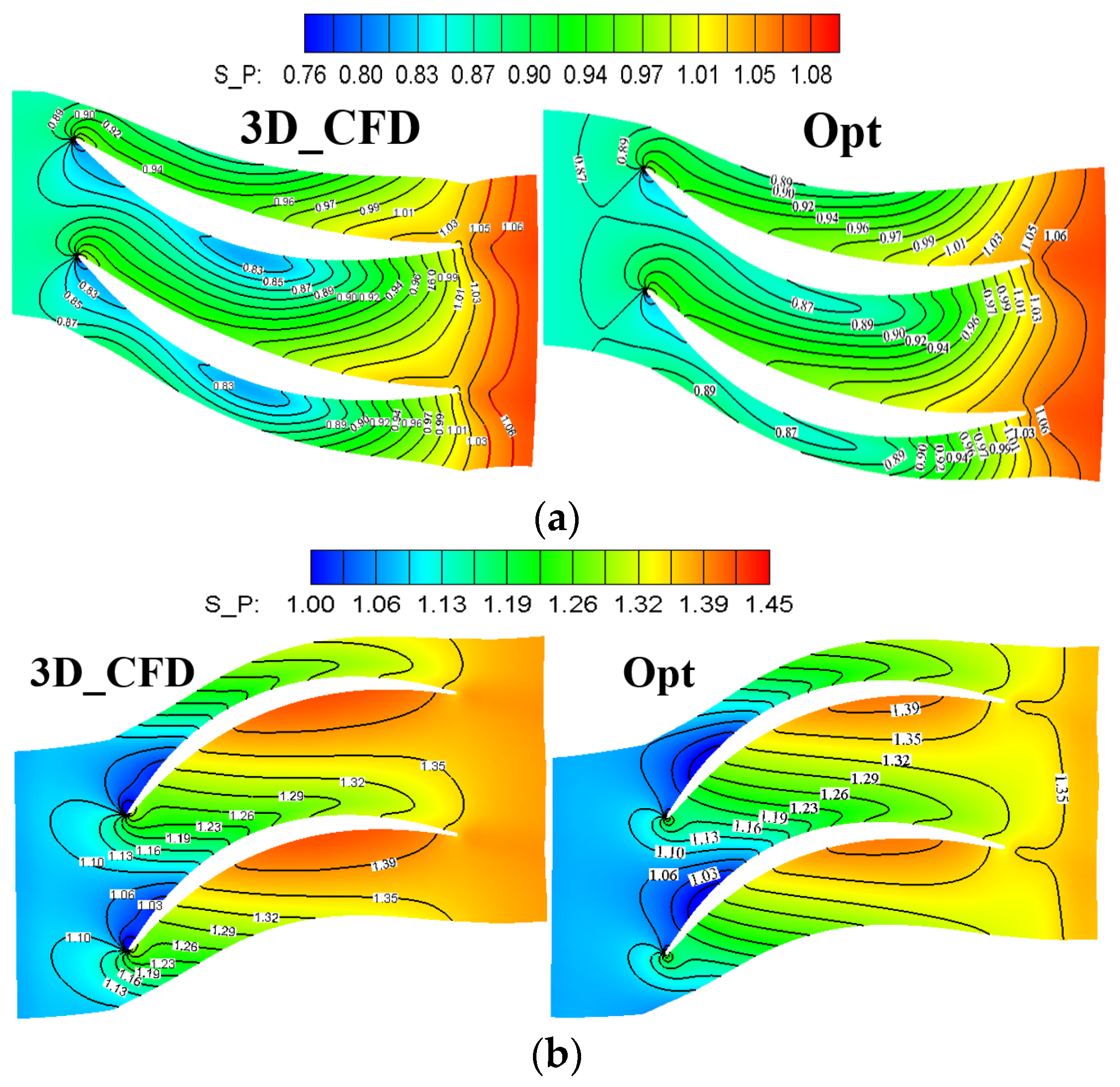
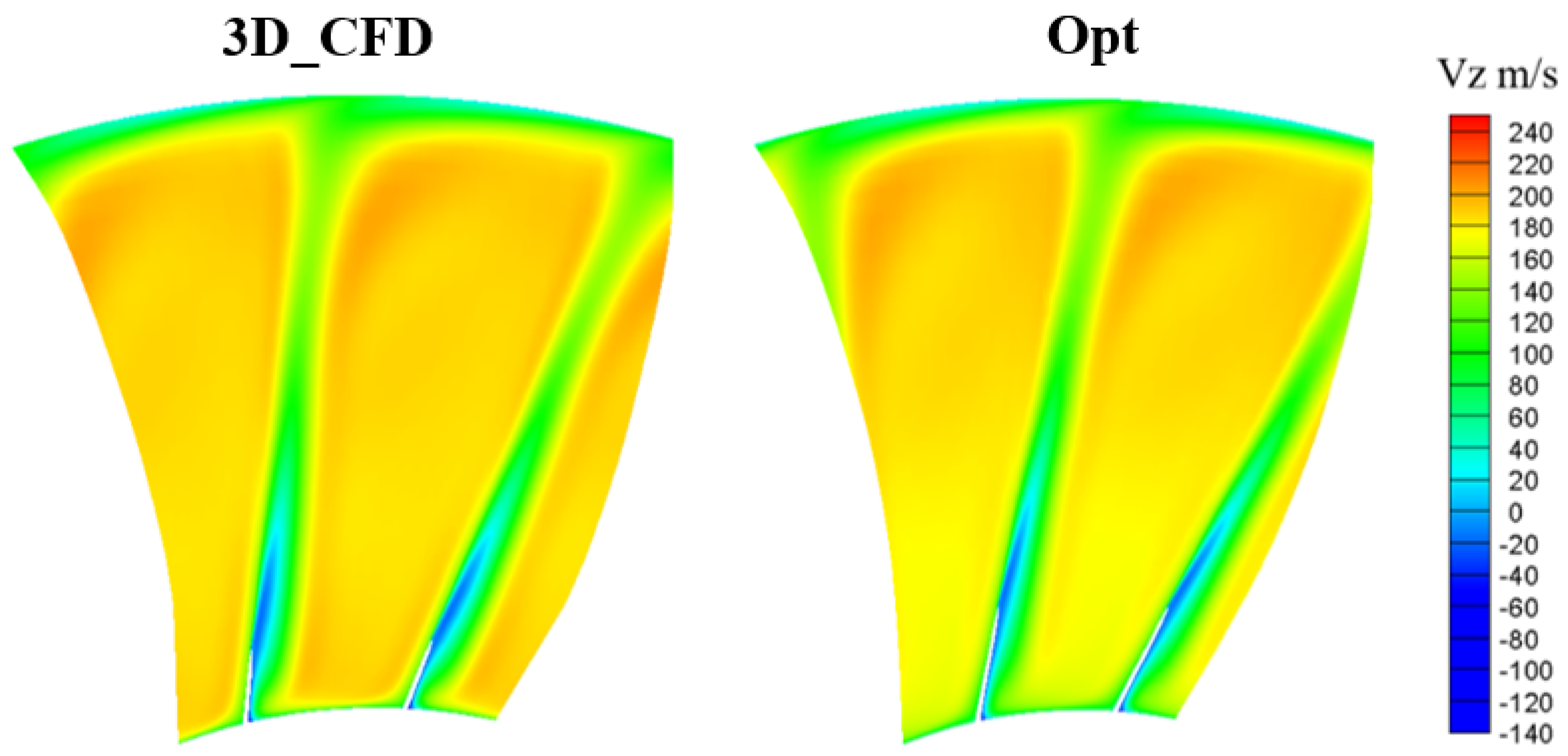
4.2. Comparison and Analysis of Flow Detail
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Variables | |
| Mass flow rate (kg/s) | |
| N | Rotational speed (rpm) |
| T* | Total temperature (K) |
| P* | Total pressure (pa) |
| MaW | Relative Mach number |
| U | Tangential velocity (m/s) |
| n | Hub ratio |
| r | Rotor or radius |
| s | Stator |
| F | Force |
| S | Streamline |
| W | The tangential direction of the streamline |
| Z | The axial direction |
| P | Static pressure (pa) |
| C | Absolute velocity (m/s) |
| CP | Control points |
| V | Flow speed (m/s) |
| H | The spanwise direction |
| A | Area or zone (m2) |
| VZ | Axial velocity (m/s) |
| NS | Navier-Stokes |
| Greek | |
| η | Adiabatic efficiency |
| π | Total pressure ratio |
| α | Absolute flow angle (°) |
| Δ | Tip clearance (mm) |
| ϕ | Flow mass coefficient |
| ω | Angular speed (rad/s) |
| σ | Angle (°) |
| θ | Angle (°) |
| τ | Total temperature ratio |
| Subscripts/Superscripts | |
| * | Total condition |
| in | Inlet conditions |
| out | Outlet conditions |
| u | Tangential component |
| h | Hub |
| s | Shroud |
| is | The isentropic term |
| w | The relative term |
| Abbreviations | |
| 1D | One dimensional |
| Q3D | Quasi-three dimensional |
| 3D | Three dimensional |
| S_P | Static pressure/Total pressure at the inlet |
| Der | The first derivative of static pressure |
| le | Leading edge |
| te | Trailing edge |
| Sl | Slope |
| Cur | Curvature |
References
- Otter, J.J.; Goulos, I.; Christie, R. Design and analysis of non-axisymmetric installed aero-engine exhaust systems. Aerosp. Sci. Technol. 2020, 106, 106210. [Google Scholar] [CrossRef]
- Jaron, R.; Moreau, A.; Guerin, S. Multidisciplinary Design Optimization of a Low-Noise and Efficient Next-Generation Aero-Engine Fan. J. Turbomach. 2022, 144, 011004. [Google Scholar]
- Luo, D.; Sun, X.; Huang, D. Design of 1+ 1/2 counter rotating centrifugal turbine and performance comparison with two-stage centrifugal turbine. Energy 2020, 211, 118628. [Google Scholar] [CrossRef]
- Wu, C.H. A general theory of three-dimensional flow in subsonic and supersonic turbomachines of axial, radial, and mixed-flow types. J. Fluids Eng. 1952, 74, 1363–1380. [Google Scholar] [CrossRef]
- Novak, R.A.; Hearsey, R.M. A nearly three-dimensional intrablade computing system for turbomachinery. J. Fluids Eng. 1977, 99, 154–166. [Google Scholar] [CrossRef]
- Marsh, H. A Digital Computer Program for the Through-Flow Fluid Mechanics in an Arbitrary Turbomachine Using a Matrix Method; Aeronautical Research Council R & M: London, UK, 1968; No. 3509. [Google Scholar]
- Shang, E.; Wang, Z.; Su, J.X. IGTC-13 A Perspective and Effective Way to Improve the Compressor Cascade Performance; Gas Turbine Society of Japan: Tokyo, Japan, 1991. [Google Scholar]
- Deich, M.E.; Gubalev, A.B.; Filippov, G.A. A new method of profiling the guide blade cascades of turbine stages with small diameter-span ratio. Teploenergetika 1962, 8, 42–46. [Google Scholar]
- Ding, X.; Jin, D.; Gui, X. Effect of load distribution at the roots among stages on performance of a high bypass-ratio fan/booster. J. Phys. Conf. Ser. 2018, 1064, 012052. [Google Scholar] [CrossRef]
- Wang, Z.; Su, J.; Zhong, J. The effect of the pressure distribution in a three-dimensional flow field of a cascade on the type of curved blade. In Proceedings of the ASME International Gas Turbine & Aeroengine Congress & Exposition, The Hague, The Netherlands, 13–16 June 1994. [Google Scholar]
- Mahmood, S.; Turner, M.G.; Siddappaji, K. Flow characteristics of an optimized axial compressor rotor using smooth design parameters. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016. 2C Turbomachinery. [Google Scholar]
- Nemnem, A.F.; Turner, M.G.; Siddappaji, K. A smooth curvature-defined meanline section option for a general turbomachinery geometry generator. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. 2B Turbomachinery. [Google Scholar]
- Corral, R.; Gisbert, F. Profiled end-wall design using an adjoint navier-stokes solver. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; Volume 6, pp. 1363–1372, Turbomachinery, Parts A and B. [Google Scholar]
- Hartland, J.; Gregory-Smith, G.; Harvey, W. Nonaxisymmetric turbine end wall design: Part II—Experimental validation. J. Turbomach. 2000, 122, V001T03A050. [Google Scholar] [CrossRef]
- Jin, D.H.; Liu, X.W. Optimization of Endwall Contouring in Axial Compressor S-shaped Ducts. Chin. J. Aeronaut. 2015, 28, 1076–1086. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, H. End-wall boundary layers and blockages of multistage axial compressors under different conditions. J. Propuls. Power 2017, 33, 908–916. [Google Scholar] [CrossRef]
- Hu, S.; Lu, X. Numerical investigation of a high-subsonic axial-flow compressor rotor with non-axisymmetric hub endwall. J. Therm. Sci. 2010, 19, 14–20. [Google Scholar] [CrossRef]
- Giacomo, M. Secondary Flow Mitigation in Vanes through Endwall Fence Shape Optimization; Delft University of Technology: Delft, The Netherlands, 2018. [Google Scholar]
- Zhang, H.; Chen, S.; Meng, Q. Flow Separation Control Using Unsteady Pulsed Suction Through Endwall Bleeding Holes in a Highly Loaded Compressor Cascade. Aerosp. Sci. Technol. 2018, 72, 455–464. [Google Scholar] [CrossRef]
- Donald, C.U.; William, T.G.; Walter, S.C. Performance of Two-Stage Fan Having Low-Aspect-Ratio, First-Stage Rotor Blading; NASA Report; NASA: Washington, DC, USA, 1979; pp. 49–78. [Google Scholar]
- Ru-Gen, W.; Jia, H.U.; Chao, Y.U. Research on swecondary flow vortex structure in transonic compressor rotor. J. Propuls. Technol. 2015, 4, 504–512. [Google Scholar]
- Dalbert, P.; Wiss, D.H. Numerical transonic flow field predictions for NASA compressor rotor 37. In Proceedings of the ASME International Gas Turbine & Aeroengine Congress & Exposition, Houston, TX, USA, 5–8 June 1995; p. V001T01A090. [Google Scholar]
- Bruna, D.; Turner, M.G. Isothermal Boundary Condition at Casing Applied to the Rotor 37 Transonic Axial Flow Compressor. J. Turbomach. 2013, 135, 420–431. [Google Scholar] [CrossRef]





| Design Parameters | Values |
|---|---|
| Stage number | 2 |
| Design flow rate (kg/s) | 33.248 |
| Corrected design angular velocity N (rpm) | 16,042.8 |
| Inlet total temperature T * (K) | 288.15 |
| Inlet total pressure P * (Pa) | 101,325.0 |
| Outlet absolute flow angle αout (deg) | 0.0 |
| Outlet absolute Mach number M | 0.442 |
| Tangential speed at L. E. of the rotor tip U (m/s) | 428.9 |
| Relative velocity at L. E. of the rotor tip W (m/s) | 458.4 |
| Clearance at Rotor1 tip Δ (mm) | 0.4 |
| Tip flow coefficient of rotor ϕ | 0.491 |
| Hub/tip ratio at the inlet of the first rotor ν | 0.705 |
| The number of blades (r1, s1, r2, s2) | (22, 34, 38, 42) |
| Case | Total Grid Cell Number | Performance Parameters | ||
|---|---|---|---|---|
| Efficiency η | Total Pressure Ratio π | |||
| 1 | 1,943,740 | 0.8415 | 2.510 | 33.42 |
| 2 | 2,098,428 | 0.8435 | 2.521 | 33.66 |
| 3 | 2,252,788 | 0.8451 | 2.544 | 33.82 |
| 4 | 2,450,448 | 0.8453 | 2.550 | 33.86 |
| 5 | 2,581,896 | 0.8453 | 2.548 | 33.85 |
| Case | Total Grid Cell Number | Performance Parameters | ||
|---|---|---|---|---|
| Efficiency η | Total Pressure Ratio π | |||
| 1 | 1,943,740 | 0.7253 | 1.760 | 33.79 |
| 2 | 2,098,428 | 0.7271 | 1.769 | 34.00 |
| 3 | 2,252,788 | 0.7292 | 1.792 | 34.18 |
| 4 | 2,450,448 | 0.7294 | 1.793 | 34.20 |
| 5 | 2,581,896 | 0.7293 | 1.793 | 34.21 |
| Different Programs | 3D_CFD Results | Opt Results | Values Differences | Percentage Differences | |
|---|---|---|---|---|---|
| Different Parameters | |||||
| Design point | Adiabatic efficiency η | 84.51% | 84.55% | 0.04% | 0.04% |
| Total pressure ratio π | 2.54 | 2.56 | 0.02 | 0.79% | |
| Mass flow rate (kg/s) | 33.82 | 34.72 | 0.90 | 2.66% | |
| Choking mass flow rate (kg/s) | 34.18 | 35.11 | 0.93 | 2.72% | |
| Stall mass flow rate (kg/s) | 33.41 | 34.01 | 0.6 | 1.80% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, T.; Chen, H.; Wu, Z.; Liu, Y.; Yan, P. Research on Aerodynamic Design of an End Wall Based on a Quasi-3D Optimization Method. Energies 2023, 16, 1859. https://doi.org/10.3390/en16041859
Yan T, Chen H, Wu Z, Liu Y, Yan P. Research on Aerodynamic Design of an End Wall Based on a Quasi-3D Optimization Method. Energies. 2023; 16(4):1859. https://doi.org/10.3390/en16041859
Chicago/Turabian StyleYan, Tingsong, Huanlong Chen, Zhiqian Wu, Yang Liu, and Peigang Yan. 2023. "Research on Aerodynamic Design of an End Wall Based on a Quasi-3D Optimization Method" Energies 16, no. 4: 1859. https://doi.org/10.3390/en16041859
APA StyleYan, T., Chen, H., Wu, Z., Liu, Y., & Yan, P. (2023). Research on Aerodynamic Design of an End Wall Based on a Quasi-3D Optimization Method. Energies, 16(4), 1859. https://doi.org/10.3390/en16041859





