A Model-Based Approach for Setting the Initial Angle of the Drive Axles in a 4 × 4 High Mobility Wheeled Vehicle
Abstract
:1. Introduction
2. The Characteristics of the Research Object
2.1. The Vehicle Tire Characteristics
2.2. The Characteristics of Spring Elements in the Vehicle Suspension
2.3. The Characteristics of the Vehicle Axle Suspension and Driveline
3. The Characteristics of the Cooperation of Selected Vehicle Components
3.1. The Model of Cooperation between the Propeller Shaft, Transfer Case, and Main Gear
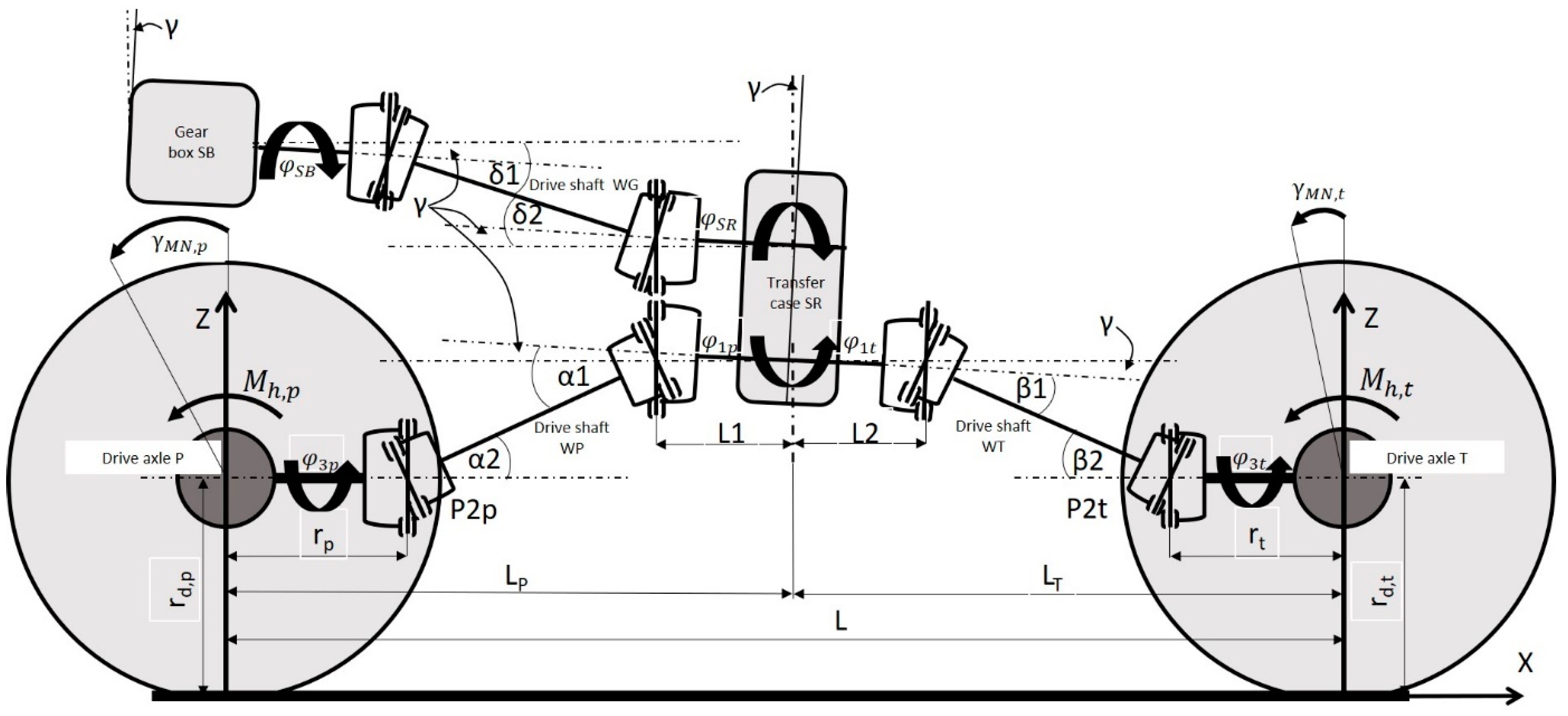
3.2. The Identification of the Values of Inclination Angles of the Drive Shafts
4. An Analysis of Kinematic Incompatibility in the Driveline
| ΔiWPmax = 1.10% | γMN,p0 = −2 | γMN,t0= −2 | ||
|---|---|---|---|---|
| ΔiWTmax = 3.19% | α1 [°] | α2 [°] | β1 [°] | β2 [°] |
| Vehicle without load, static conditions | 9.0 | 9.0 | 3.0 | 3.0 |
| Vehicle with load, static conditions | 8.2 | 8.2 | −0.6 | 3.4 |
| Vehicle without load, braking | 6.7 | 3.0 | 5.1 | 10.9 |
| Vehicle with load, braking | 4.2 | −0.8 | 2.4 | 10.5 |

| ΔiWPmax = 1.10% | γMN,p0 = −2 | γMN,t0= 0.8 or (2) | ||
|---|---|---|---|---|
| ΔiWTmax = 1.63% for 0.8 or 1.22 for (2) | α1 [°] | α2 [°] | β1 [°] | β2 [°] |
| Vehicle without load, static conditions | 9.0 | 9.0 | 3.0 | 5.8 (7.0) |
| Vehicle with load, static conditions | 8.2 | 8.2 | −0.6 | 0.6 (−0.6) |
| Vehicle without load, braking | 6.7 | 3.0 | 5.1 | 8.1 (6.9) |
| Vehicle with load, braking | 4.2 | −0.8 | 2.4 | 7.7 (6.5) |
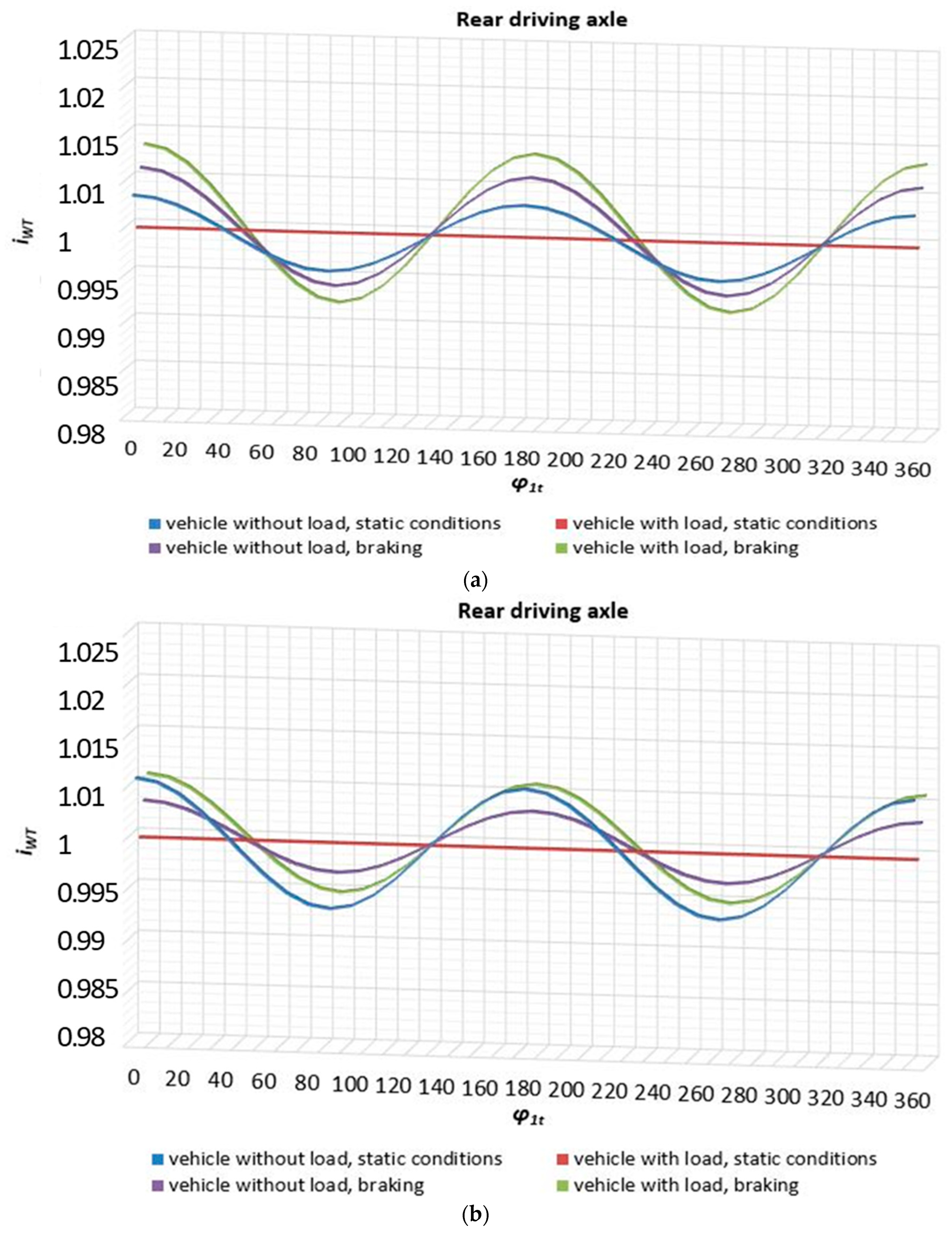
| ΔiWPmax = 2.47% | γMN,p0 = −5.7 | γMN,t0= 38 | ||
|---|---|---|---|---|
| ΔiWTmax = 2.09% | α1 [°] | α2 [°] | β1 [°] | β2 [°] |
| Vehicle without load, static conditions | 9 | 12.7 | 3 | 8.8 |
| Vehicle with load, static conditions | 8.2 | 11.9 | −0.6 | −2.4 |
| Vehicle without load, braking | 6.7 | 6.7 | 5.1 | 5.1 |
| Vehicle with load, braking | 4.2 | 2.9 | 2.4 | 4.7 |
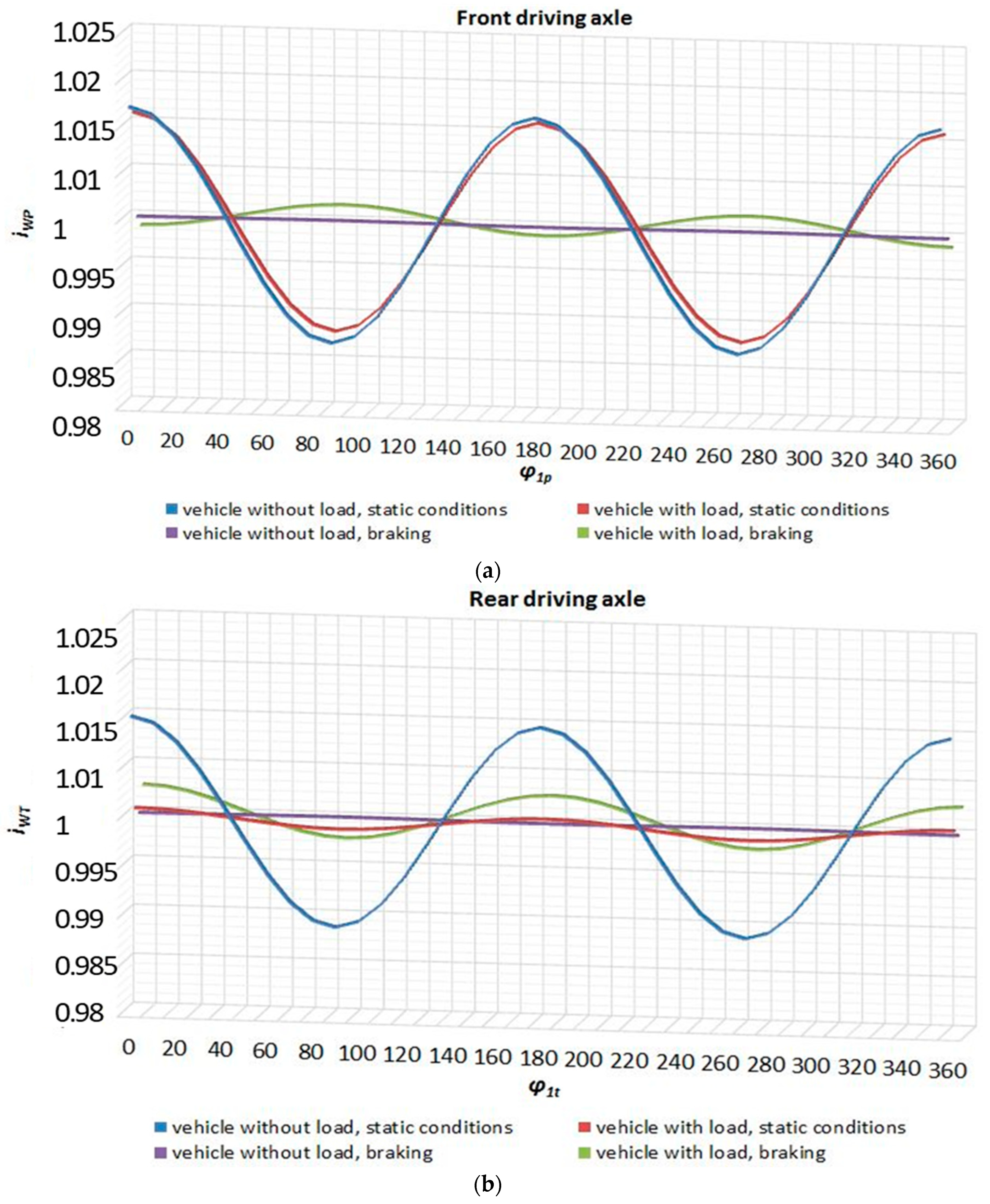
| ΔiWPmax = 1.52% for (1.4) or 3.55 for (−7) | γMN,p0 = 1.4 (−7) | γMN,t0= 6.1 | ||
|---|---|---|---|---|
| ΔiWTmax = 3.50% | α1 [°] | α2 [°] | β1 [°] | β2 [°] |
| Vehicle without load, static conditions | 9 | 5.6 (14) | 3 | 11.1 |
| Vehicle with load, static conditions | 8.2 | 4.8 (13.2) | −0.6 | −4.7 |
| Vehicle without load, braking | 6.7 | −0.4 (8.0) | 5.1 | 2.8 |
| Vegicle with load, braking | 4.2 | −4.2 (4.2) | 2.4 | 2.4 |
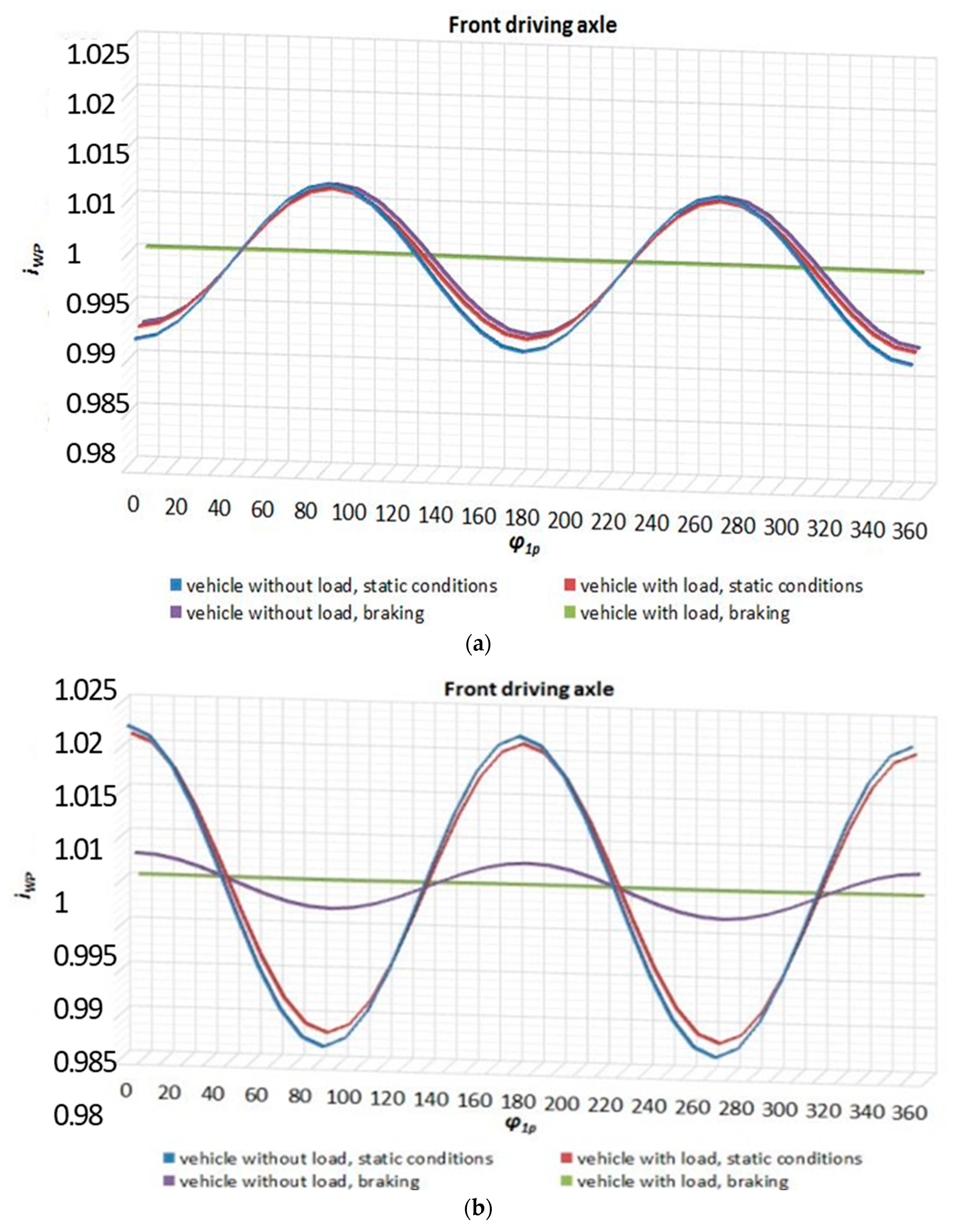

5. Summary

Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ministry of Defence. Structure of the Car Fleet of the Polish Armed Forces; Ministry of Defence: Warszawa, Poland, 1999. (In Polish)
- Regulation of the Minister of Transport. Construction and Maritime Economy on the Approval of Motor Vehicles and Trailers and Their Equipment Objects or Parts (Dz.U z 25.09.2015, poz. 1475); Ministry of Transport: Warszawa, Poland, 2015. (In Polish)
- Reimpel, J.; Betzler, J. Automotive Chassis. Fundamentals of Construction; WKiŁ: Warszawa, Poland, 2008. (In Polish) [Google Scholar]
- Wong, J. Terramechanics and Off-Road Vehicle Engineering. Terrain Behaviour, Off-Road Vehicle Performance and Design; Butterworth-Heinemann: Amsterdam, The Netherland, 2010. [Google Scholar]
- Prochowski, L.; Żuchowski, A. Trucks and Buses; WKiŁ: Warszawa, Poland, 2016. (In Polish) [Google Scholar]
- Kosobudzki, M. Speed distribution on road test sections for the need of profile ground testing of special wheeled vehicles. In Proceedings of the XI International Conference on Structural Dynamics, Athens, Greece, 23–26 November 2020; pp. 669–675. [Google Scholar] [CrossRef]
- Browne, M.; Palazzolo, A. Super harmonic nonlinear lateral vibrations of a segmented driveline incorporating a tuned damper excited by a non-constant velicity joints. J. Sound Vib. 2009, 232, 334–351. [Google Scholar] [CrossRef] [Green Version]
- Parszewski, Z. Theory of Machines and Mechanisms; WKiŁ: Warszawa, Poland, 1978. (In Polish) [Google Scholar]
- Kosobudzki, M.; Smolnicki, T. Generalized vehicle durability index for different trafic conditions. AIP Conf. Proc. 2019, 2078, 020017. [Google Scholar]
- MIL-STD-810H; Environmental Engineering Considerations and Laboratory Tests. Department of Defence: Washington, VA, USA, 2019.
- Jamroziak, K.; Kwaśniowski, S.; Kosobudzki, M.; Zajac, P. Analysis of heat exchange in the powertrain of a road vehicle with a retarder. Eksploat. Niezawodn. Maint. Reliab. 2019, 21, 577–584. [Google Scholar] [CrossRef]
- Road Traffic Regulations. Dz.U. 1997, nr 98, poz. 602; Ministry of Transport: Warszawa, Poland, 1997. (In Polish)
- Michelin. Technical Characteristics of Tire 14.00R20XZL+TL164/160J MI. 2014. Available online: https://www.heuver.com/product/b01400020migxzl54/14-00r20-michelin-xzl-complete-on-wheel-164-160g-tl (accessed on 10 February 2023).
- Kulikowski, K.; Szpica, D. Determination of directional stiffenesses of vehicles’ tires under a static load operation. Eksploat. Niezawodn. Maint. Reliab. 2014, 16, 66–72. [Google Scholar]
- Luty, W.; Simiński, P. Analysis of elasticity of radial tyres14.00R20 with Run-Flat insert. Czas. Tech. 2008, 6, 131–138. (In Polish) [Google Scholar]
- Mazzei, A.; Scott, R. Principal parametric resonance zones of a rotating rigid shaft driven through a universal joint. J. Sound Vib. 2001, 244, 555–562. [Google Scholar] [CrossRef] [Green Version]
- Kosobudzki, M.; Stańco, M. Problems in assessing the durability of a selected vehicle component based on the accelearted proving groud test. Eksploat. Niezawodn. Maint. Reliab. 2019, 21, 592–598. [Google Scholar] [CrossRef]
- Operation Manual of Truck Jelcz 442.32; Jelcz Sp. z o.o.: Jelcz Laskowice, Poland, 2016. (In Polish)
- SAE. Spring Design Manual; SAE: Pittsburg, PA, USA, 1990. [Google Scholar]
- Porat, I. Moment transmission by a universal joint. Mech. Mach. Theory 1980, 15, 245–254. [Google Scholar] [CrossRef]

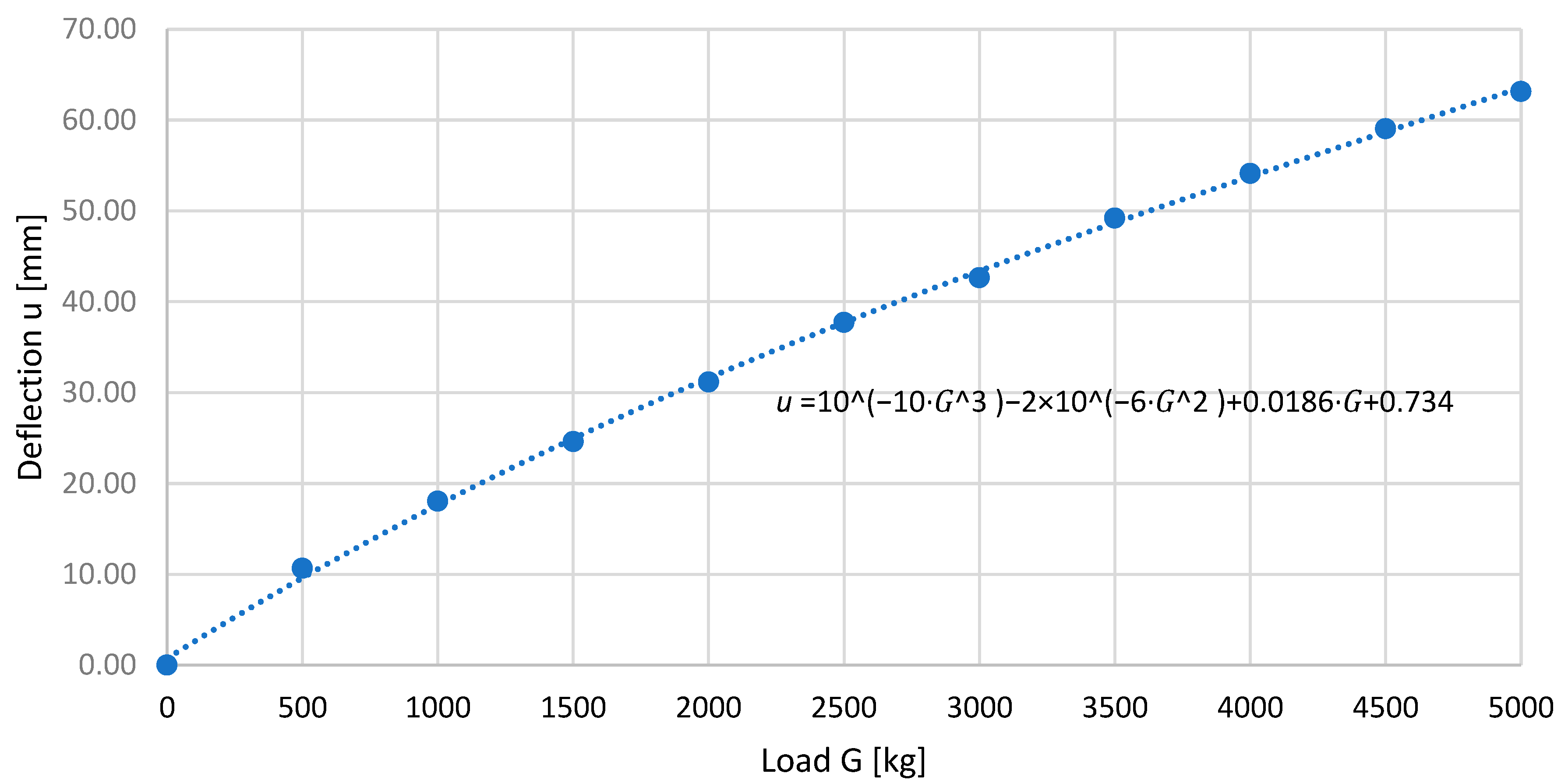
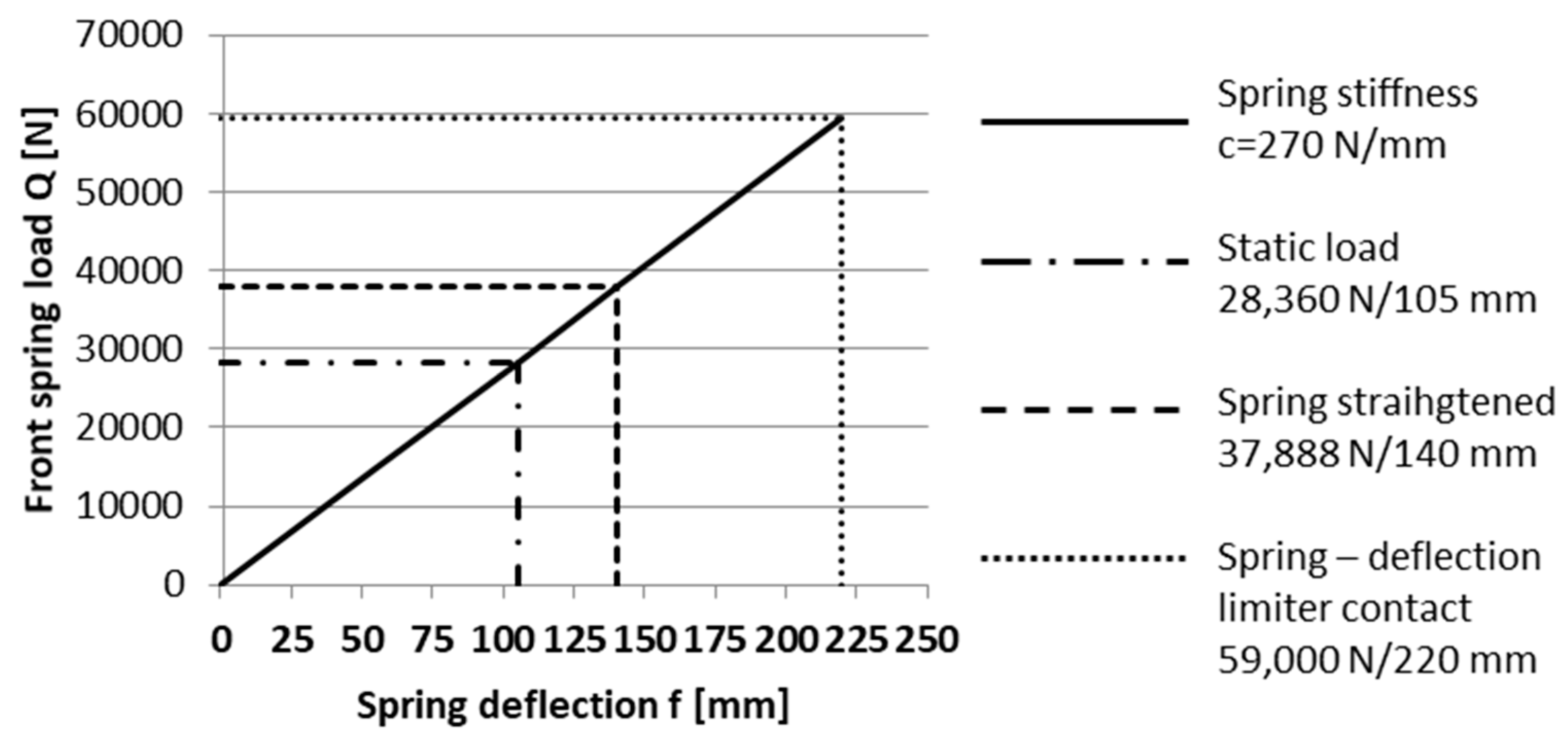
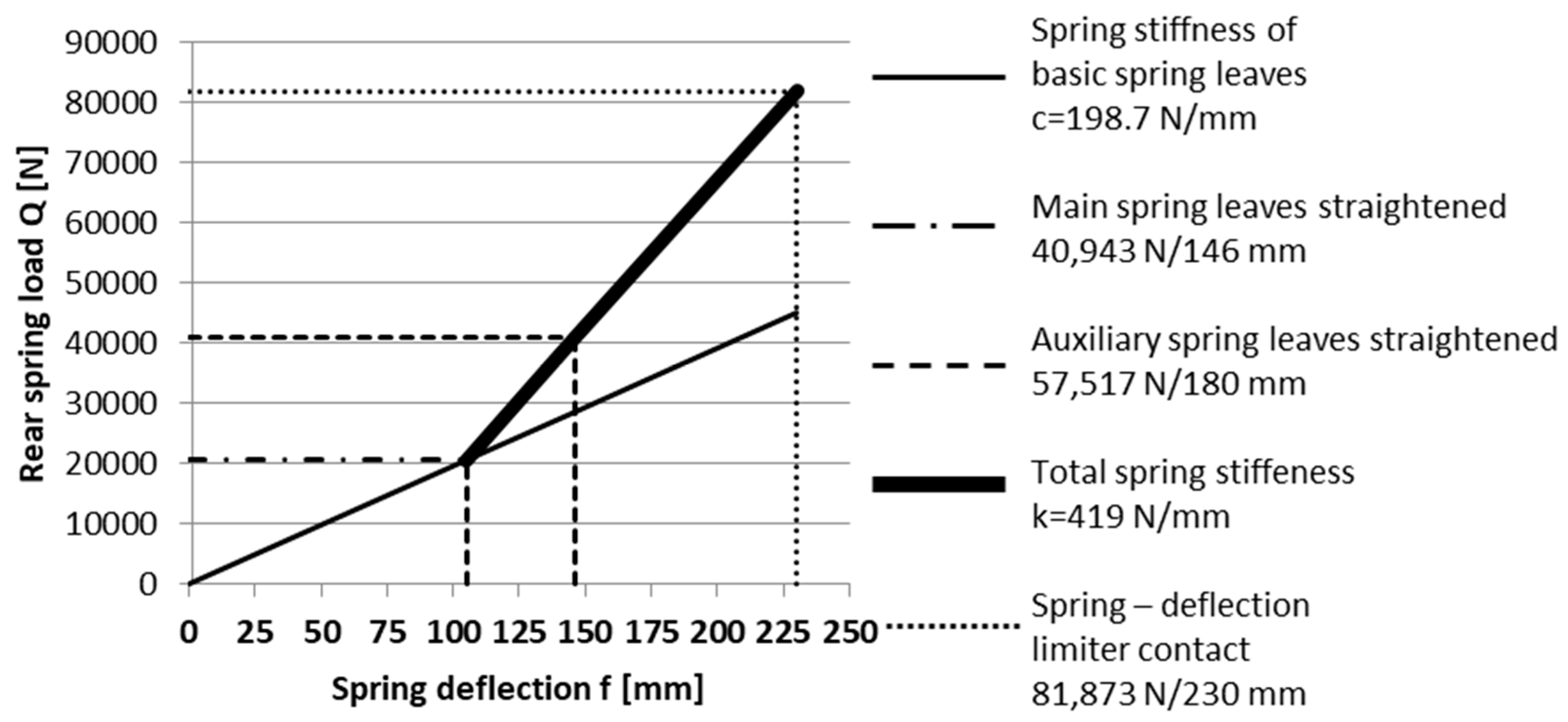

| Front Axle Stabilizer | Rear Axle Stabilizer | |
|---|---|---|
| Length of the element subject to torsion | 730 mm | 820 mm |
| Length of stabilizer arm | 520 mm | 340 mm |
| Diameter of the element subject to torsion | 40 mm | 50 mm |
| Max. Engine Torque: | Nominal Engine Power: | Tire: | 14.00R20 164/160J (rdyn,nom = 0.582 m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1300 [Nm] | 1200 ÷ 1600 [1/min] | 240 [kW] | 2200 [1/min] | Correction of Cross-Country Speed [km/h] Depending on Deflection of Tire: | ||||||||
| Road Speed [km/h] (iSR = 1) | Cross-Country Speed [km/h] (iSR = 2) | U = 0.86 (Nominal Deflection) | U = 0.8 | U = 0.7 | U = 0.6 | U = 0.5 | ||||||
| Gear | ic | V (n = 1700 [1/min]) | ΔV (Δn = ±500 [1/min]) | Gear | ic | V (n = 1700 [1/min]) | ΔV (Δn = ±500 [1/min]) | ΔV0.86 | ΔV0.8 | ΔV0.7 | ΔV0.6 | ΔV0.5 |
| C | 56.88 | 6.9 | 2.0 | C | 113.76 | 3.4 | 1 | 0.0 | −0.1 | −0.2 | −0.3 | −0.4 |
| 1 | 39.48 | 9.9 | 2.9 | 1 | 78.96 | 4.9 | 1.5 | 0.0 | −0.1 | −0.3 | −0.4 | −0.4 |
| 2 | 28.08 | 13.9 | 4.1 | 2 | 56.16 | 6.9 | 2 | 0.0 | −0.2 | −0.4 | −0.4 | −0.8 |
| 3 | 20.88 | 18.7 | 5.5 | 3 | 41.76 | 9.3 | 2.7 | 0.0 | −0.3 | −0.5 | −0.8 | −1.1 |
| 4 | 15.72 | 24.8 | 7.3 | 4 | 31.44 | 12.4 | 3.6 | 0.0 | −0.4 | −0.7 | −1.1 | −1.5 |
| 5 | 11.34 | 34.4 | 10.2 | 5 | 22.68 | 17.2 | 5.1 | 0.0 | −0.5 | −1.0 | −1.6 | −2.1 |
| 6 | 8.1 | 48.2 | 14.2 | 6 | 16.3 | 24.1 | 7.1 | 0.0 | −0.7 | −1.4 | −2.2 | −2.9 |
| 7 | 6 | 65 | 19.1 | 7 | 12 | 32.5 | 9.6 | 0.0 | −0.9 | −1.9 | −2.9 | −3.9 |
| 8 | 4.5 | 86.7 | 25.5 | 8 | 9 | 43.4 | 12.8 | 0.0 | −1.2 | −2.6 | −3.9 | −5.3 |
| R | 53.82 | 7.2 | 2.1 | R | 107.64 | 3.6 | 1.1 | 0.0 | −0.1 | −0.2 | −0.3 | −0.4 |
| L, [mm] | 4100 | length of center part WP, [mm] | 1340 |
| LP, [mm] | 2150 | length of center part WT, [mm] | 1302 |
| LT, [mm] | 1950 | rd, [mm] | 430 |
| L1, [mm] | 385 | rd,t, [mm] | 430 |
| L2, [mm] | 220 | γ, [°] | 2 |
| X (Behind Rear Axle) [mm] | Z [mm] | |
|---|---|---|
| Vehicle unladen | 1460 | 1230 |
| Vehicle laden 6000 kg | 2230 | 1430 |
| Front Axle | Rear Axle | |
|---|---|---|
| Unladen vehicle (μ = 0.7) | ||
| One spring deflection during braking, mm | 26.5 | −36 |
| Axle rotation angle due to braking torque, ° | 3.7 | 1.8 |
| Displacement in the Z axis of joint P2p due to rotation of the driving axle, mm | 28 | |
| Displacement in the Z axis of joint P2t due to rotation of the driving axle, mm | −13.3 | |
| Total displacement in the Z axis of joint P2p, mm | 26.5 + 28 = 54.5 | |
| Total displacement in the Z axis of joint P2t, mm | −36 − 13.3 = −49.2 | |
| Vehicles laden 6000 [kg] (μ = 0.7) | ||
| One spring deflection due to the load (static), mm | 18.1 | 81 |
| One spring deflection during braking, mm | 57.4 | −37 |
| Axle rotation angle due to braking, ° | 5 | 4.1 |
| Displacement in the Z axis of joint P2p due to rotation of the driving axle, mm | 37.2 | |
| Displacement in the Z axis of joint P2t due to rotation of the driving axle, mm | −30.6 | |
| Total displacement in the Z axis of joint P2p | 18.1 + 57.4 + 37.2 = 112.7 | |
| Total displacement in the Z axis of joint P2t | 81 − 37 − 30.6 = 13.5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosobudzki, M.; Zajac, P.; Gardyński, L. A Model-Based Approach for Setting the Initial Angle of the Drive Axles in a 4 × 4 High Mobility Wheeled Vehicle. Energies 2023, 16, 1938. https://doi.org/10.3390/en16041938
Kosobudzki M, Zajac P, Gardyński L. A Model-Based Approach for Setting the Initial Angle of the Drive Axles in a 4 × 4 High Mobility Wheeled Vehicle. Energies. 2023; 16(4):1938. https://doi.org/10.3390/en16041938
Chicago/Turabian StyleKosobudzki, Mariusz, Pawel Zajac, and Leszek Gardyński. 2023. "A Model-Based Approach for Setting the Initial Angle of the Drive Axles in a 4 × 4 High Mobility Wheeled Vehicle" Energies 16, no. 4: 1938. https://doi.org/10.3390/en16041938
APA StyleKosobudzki, M., Zajac, P., & Gardyński, L. (2023). A Model-Based Approach for Setting the Initial Angle of the Drive Axles in a 4 × 4 High Mobility Wheeled Vehicle. Energies, 16(4), 1938. https://doi.org/10.3390/en16041938







