Open-Circuit Fault Detection and Location in AC-DC-AC Converters Based on Entropy Analysis
Abstract
:1. Introduction
2. Entropy Methods
- and : approximate entropy was proposed by Pincus in 1991. The objective of is to determine how often different patterns of data are found in the dataset. According to [30], the bias of means that the results suggest more regularity than there is in reality. This bias is obviously more important for samples with a small length of the series. Eliminating this bias by preventing each vector from being counted with itself would make unstable in many situations, leaving it undetermined if each vector does not find at least one match. To avoid those two problems, Richman [30] defined , a statistic which does not have self-counting. For a time series with a given embedding dimension m, tolerance r and time lag , the Algorithm 1 for determining the of a sequence is as follows:
| Algorithm 1: Approximation Entropy |
|
- : certain information provided by times series can only be extracted by analyzing the dynamical characteristics. The conventional entropy gives information about the number of states available for the dynamical system in phase space. Therefore, it does not provide any information on how the system evolves. On the contrary, the [31] takes into account how often these states are visited by a trajectory, i.e., it provides information about the dynamic evolution of the system.The initial time series can be divided into a finite partition , according to , where is the time delay parameter. The Shannon entropy of such a partition is given as:The Kolmogorov entropy [31] is then defined byThe difference is the average information needed to predict which partition will be visited.
- : Porta [32] reports the conditional entropy () to distinguish the entropy variation over short data sequences. A time series is reduced to a process with zero mean and unitary variance by means of the normalisationwhere and are the mean and standard deviation of the series. From the normalised series, a reconstructed L dimensional phase space [32] is obtained by considering vectors , for a pattern of L consecutive samples. The can be obtained as the variation in the Shannon entropy ofSmall Shannon entropy values are obtained when a length L pattern appears several times. Small values are obtained when a length L pattern can be predicted by a length pattern. quantifies the variation in information necessary to specify a new state in a one-dimensional incremented phase space.
- : cosine similarity entropy is amplitude-independent and robust to spikes and short time series, two key problems that occur with the . The algorithm [33] replicates the computational steps in the approach with the following modifications: the angle between two embedding vectors is evaluated instead of the Chebyshev distance; then the estimated entropy is based on the global probability of occurrences of similar patterns using the local probability of occurrences of similar patterns . For a time series , with a given embedding dimension m, tolerance r and time lag , the Algorithm 2 for determining the of a sequence is as follows:
| Algorithm 2: Cosine Similarity Entropy |
|
- : fuzzy entropy introduces the concept of uncertainty reasoning to solve the drawback of sample entropy , which adopts a hard threshold as a discriminant criterion, which may result in unstable results. Several fuzzy membership functions, including triangular, trapezoidal, Z-shaped, bell-shaped, Gaussian, constant-Gaussian, and exponential functions, have been employed in . In [34], it was found that has a stronger relative consistency and less dependence on data length.introduces two modifications to the algorithm: (1) reconstructing the embedding vectors in , they are centred using their own means in order to become zero-mean. (2) The calculates the fuzzy similarity obtained from a fuzzy membership function [35], where is the order of the Gaussian function.For a time series , the steps of the approach are summarized in the third Algorithm 3 [33] as follows:
| Algorithm 3: Fuzzy Entropy |
|
- [36] consists of two steps. First, the Shannon entropy is used to characterize the state of a system within a time window, which represents the information contained in the time period. The one-dimensional discrete time series of length N is divided into consecutive non-overlapping windows. Secondly, the Shannon entropy is used instead of the sample entropy, to characterize the degree of change in the states. As the Shannon entropy is computed twice, this algorithm is called entropy of entropy.
- , , : the analysis of time series at different temporal scales is also frequent. The multiple time scales are constructed from the original time series by averaging the data points within non-overlapping windows of increasing length. [37,38,39,40,41], that represents the system dynamics on different scales, relies on the computation of the sample entropy over a range of scales. The algorithm is composed of two steps:
- (i)
- A coarse-graining procedure. To represent the time-series dynamics on different time scales, a coarse-graining procedure is used to derive a set of time series. For a discrete signal of length N, the coarse-grained time series is computed asThe length of the coarse-grained time series for a scale factor s is . Figure 1 presents the coarse-grained time series for a scale 4.
- (ii)
- Sample entropy computation. Sample entropy is a conditional probability measure that a sequence of m consecutive data points will also match the other sequence when one more point is added to each sequence [30]. Sample entropy is determined aswhere is the probability that two sequences will match for points and is the probability that two sequences will match for m points (self-matches are excluded). They are computed as described in [40]. From Equation (6), can be written aswhere and are calculated from the coarse-grained time series at the scale factor s.
3. System Description
4. Datasets
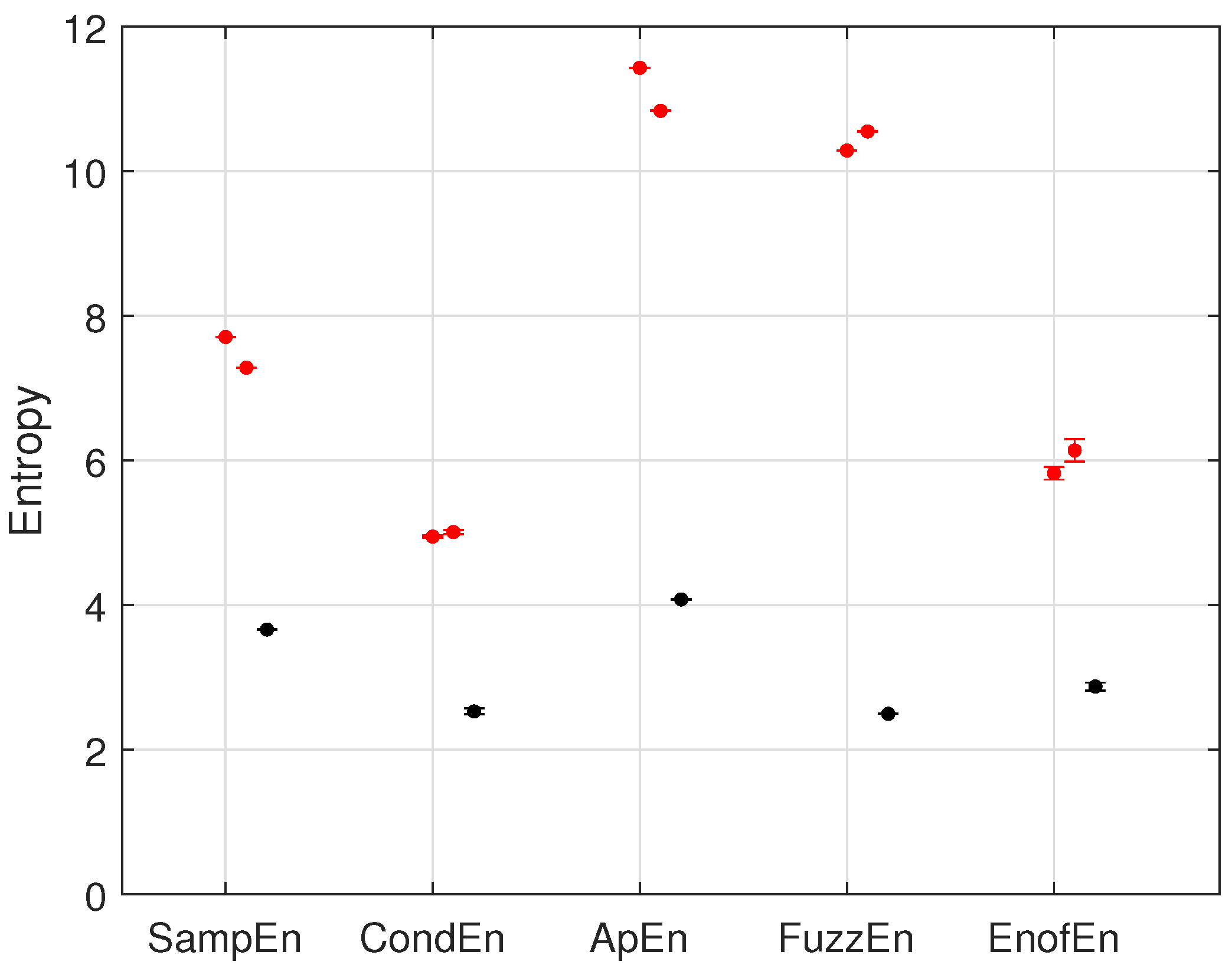
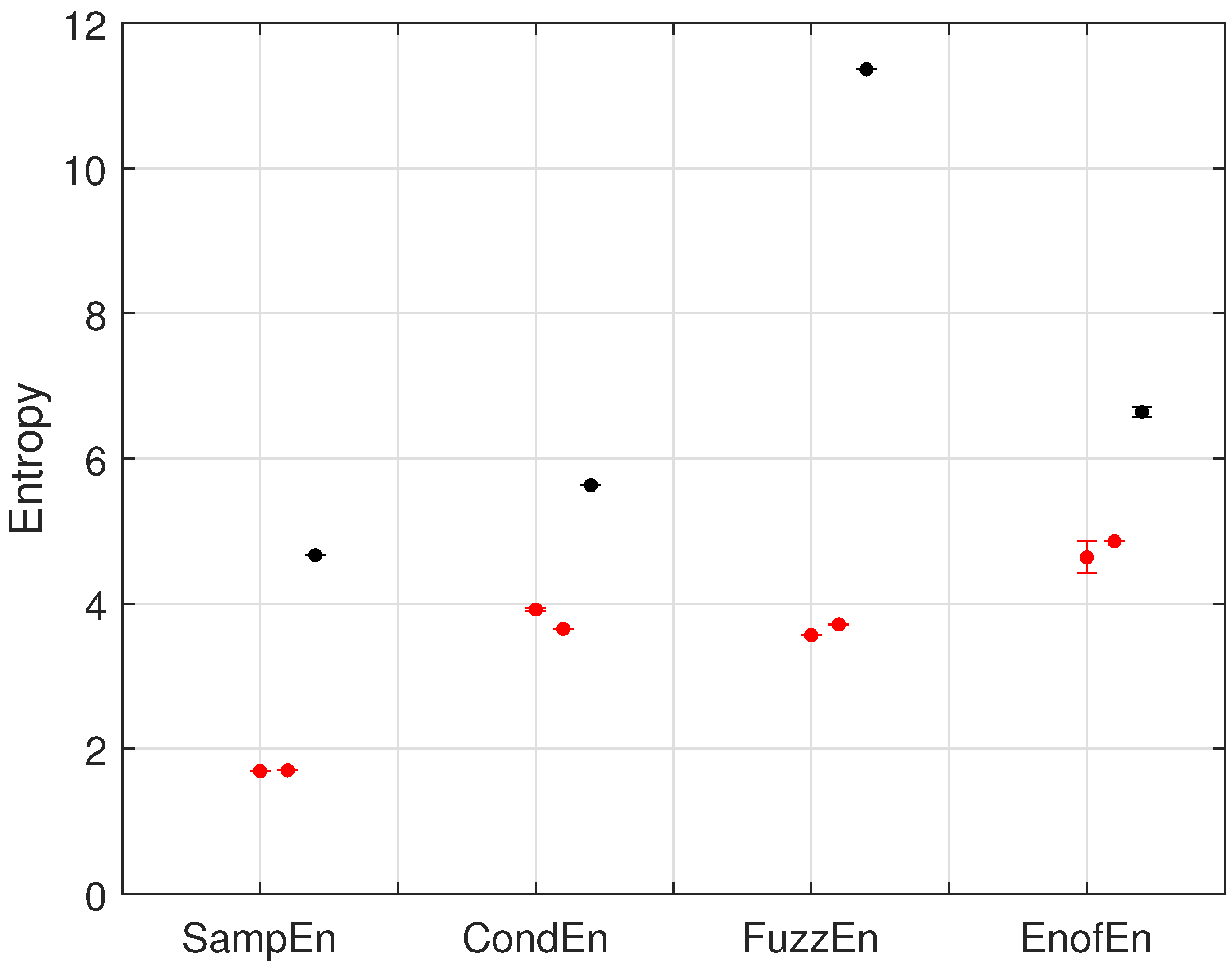
5. Results and Discussion
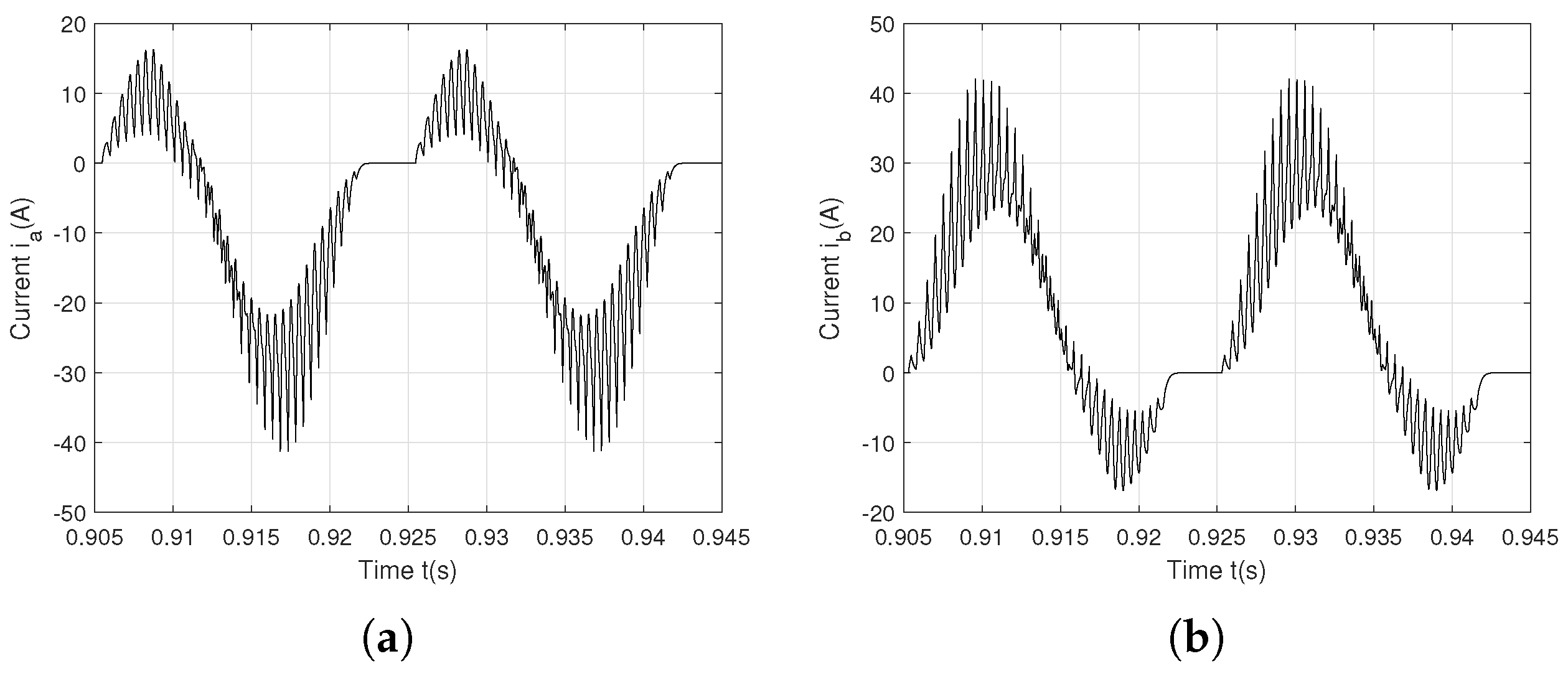
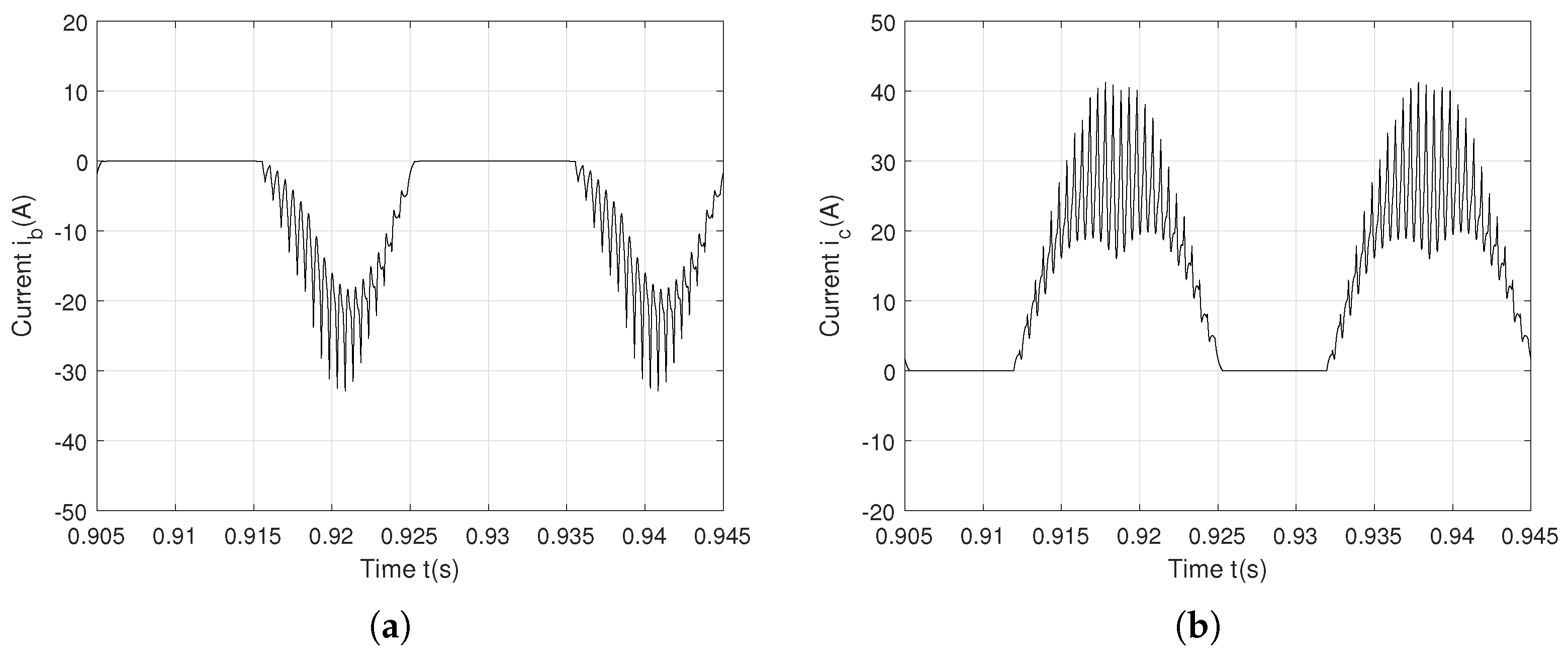
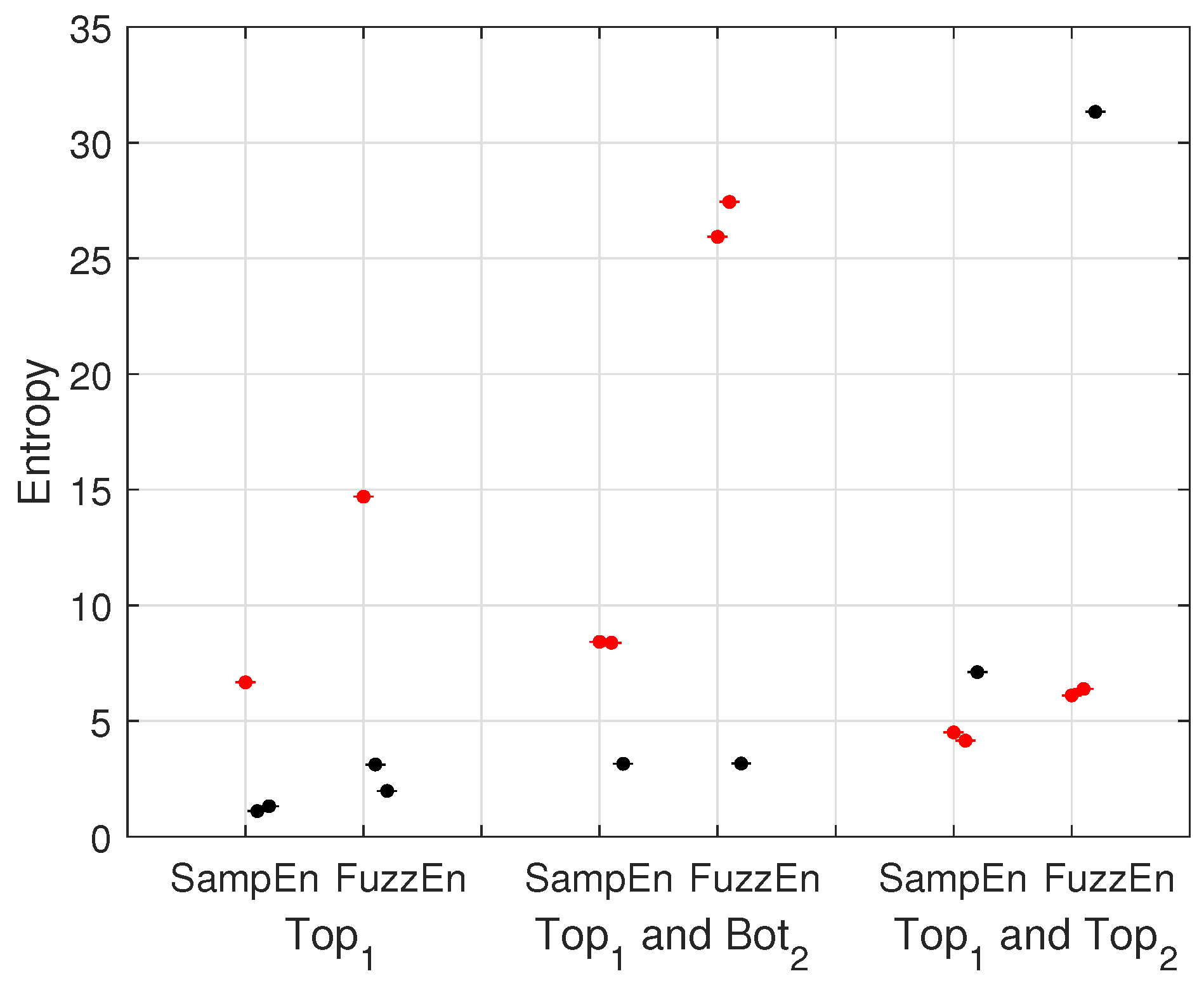
5.1. One Open-Circuit Fault on on the Phase a
5.2. Two Open-Circuit Faults on —Phase a and on —Phase b
5.3. Two Open-Circuit Faults on —Phase a and —Phase b
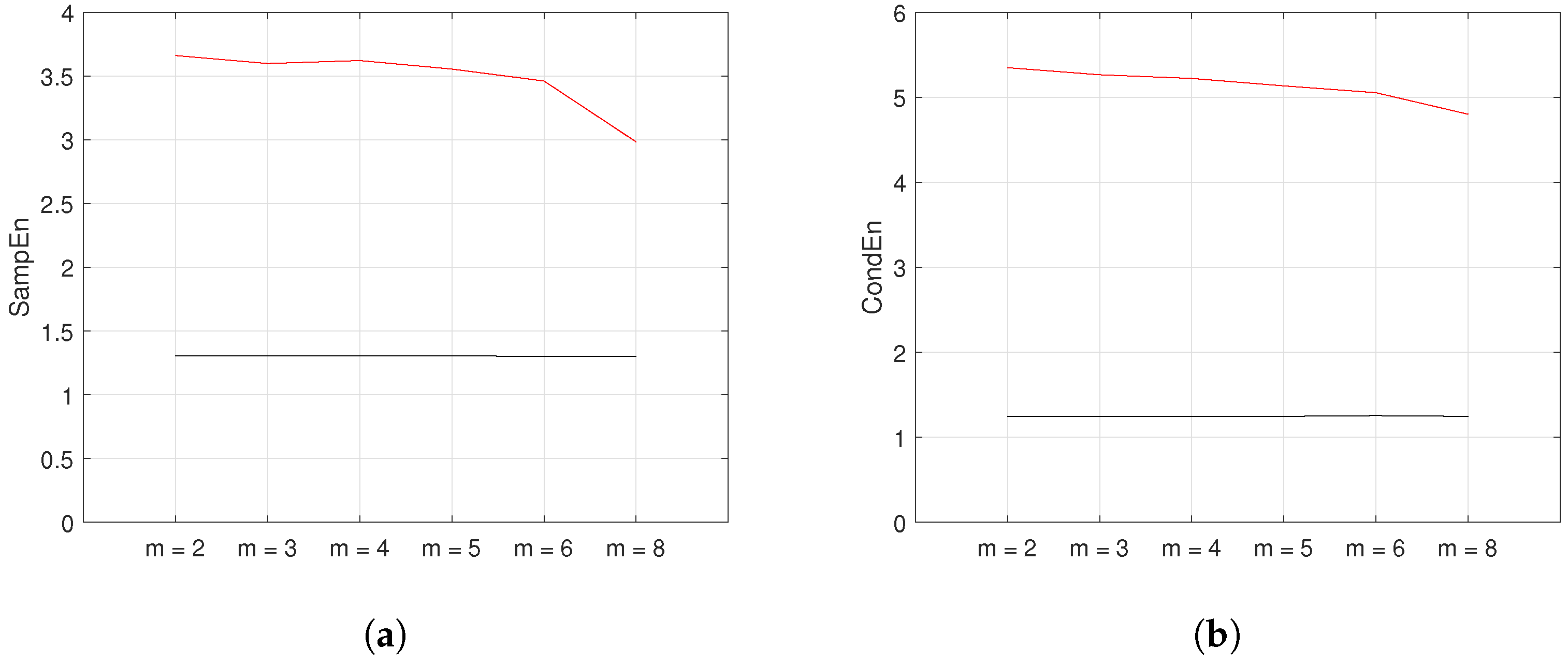
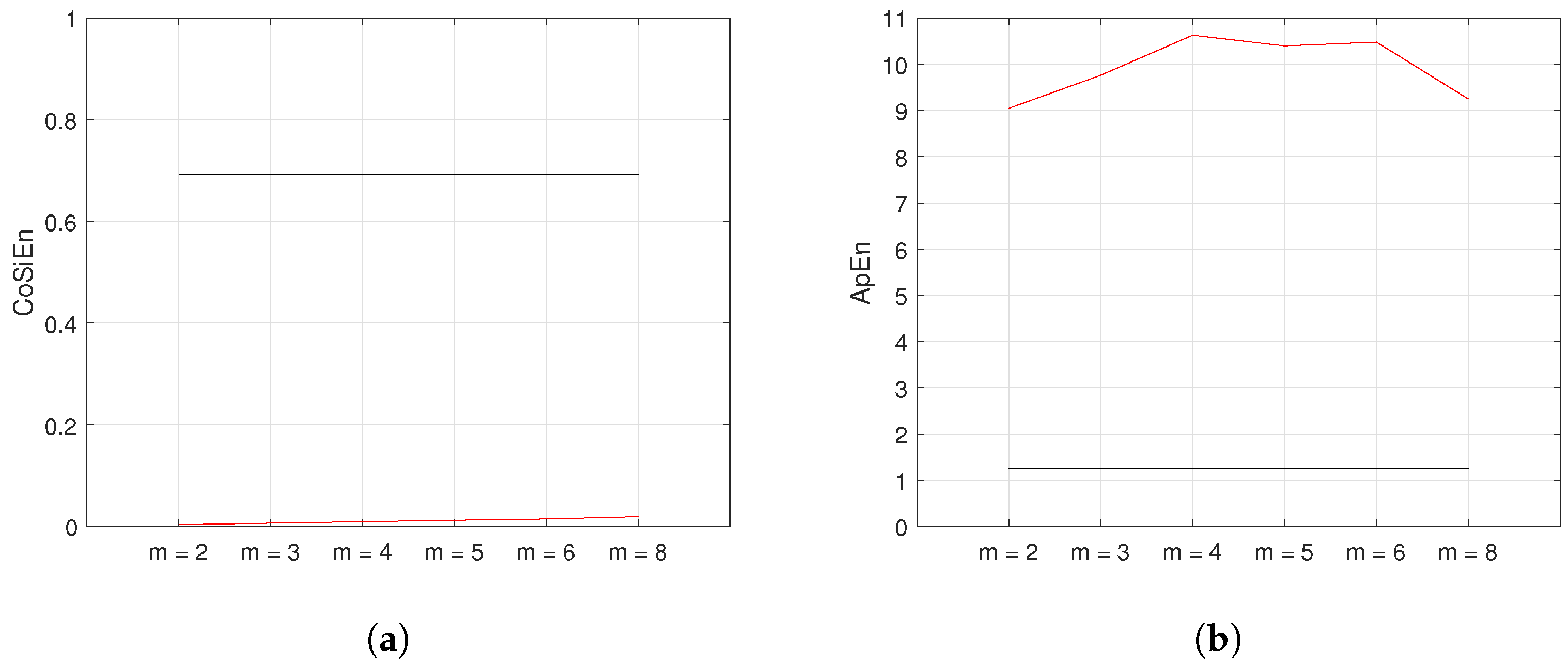
5.4. Varied Embedding Dimension (m)
5.5. Varied Data Length (N)
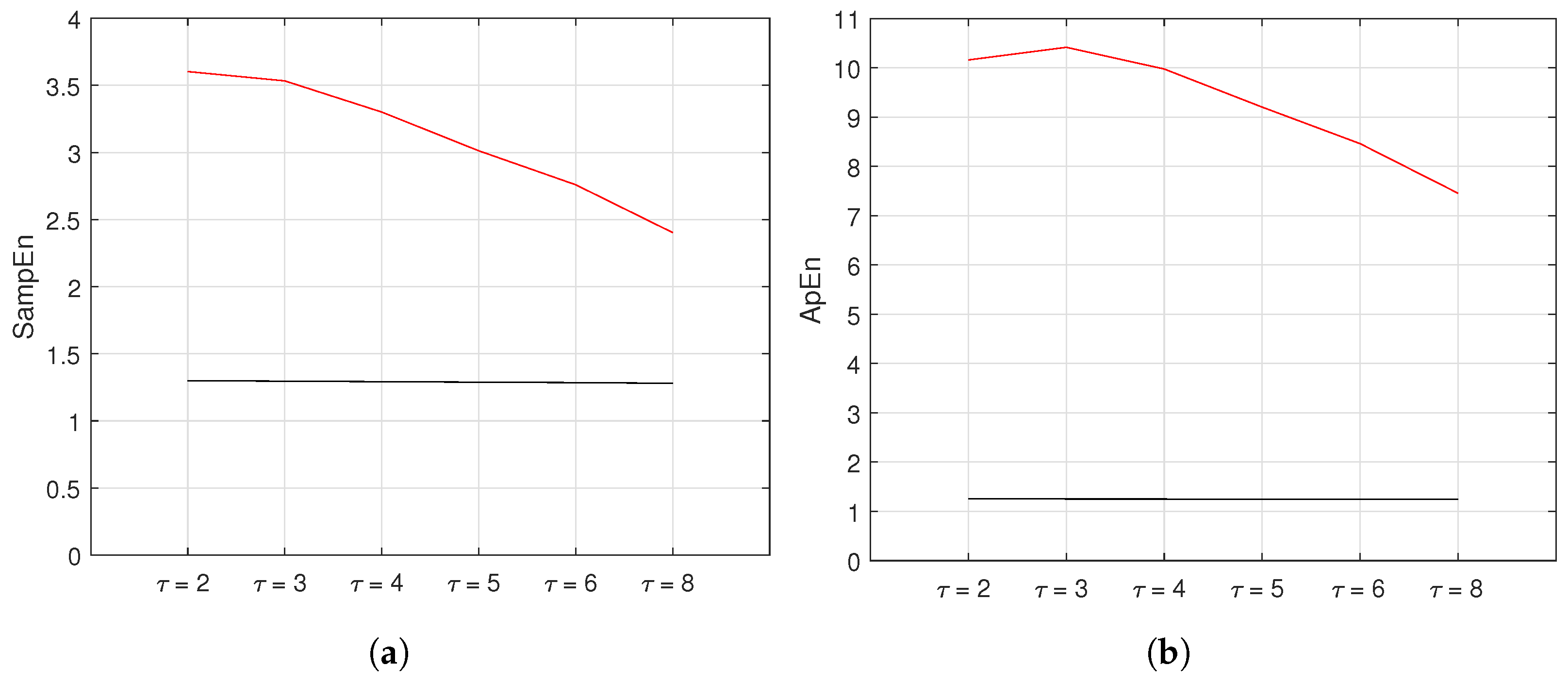
5.6. Varied Time Lag ()
5.7. Varied Tolerance (r)
5.8. New Parameters Setting
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, P.; Jiang, D.; Zhou, Y.; Liang, Y.; Guo, J.; Lin, Z. Energy-balancing control strategy for modular multilevel converters under SM fault conditions. IEEE Trans. Power Electron. 2014, 29, 5021–5030. [Google Scholar] [CrossRef]
- Yang, S.; Tang, Y.; Wang, P. Open-circuit fault diagnosis of switching devices in a modular multilevel converter with distributed control. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 November 2017; pp. 4208–4214. [Google Scholar]
- Perez, M.A.; Bernet, S.; Rodriguez, J.; Kouro, S.; Lizana, R. Circuit topologies, modeling, control schemes, and applications of modular multilevel converters. IEEE Trans. Power Electon. 2015, 30, 4–17. [Google Scholar] [CrossRef]
- Rong, F.; Gong, X.; Huang, S. A Novel Grid-Connected PV System Based on MMC to Get the Maximum Power Under Partial Shading Conditions. IEEE Trans. Power Electron. 2015, 32, 4320–4333. [Google Scholar] [CrossRef]
- Estima, J.; Cordoso, A.J.M. A new approach for real-time multiple open-circuit fault diagnosis in volt-age-source inverters. IEEE Trans. Ind. Appl. 2011, 47, 2487–2494. [Google Scholar] [CrossRef]
- Li, B.; Zhou, S.; Xu, D.; Yang, R.; Xu, D.; Buccella, C.; Cecati, C. An improved circulating current injection method for modular multilevel converters in variable-speed drives. IEEE Trans. Ind. Electron. 2016, 63, 7215–7225. [Google Scholar] [CrossRef]
- Huo, Z.; Miguel Martínez-García, M.; Zhang, Y.; Yan, R.; Shu, L. Entropy Measures in Machine Fault Diagnosis: Insights and Applications. IEEE Trans. Instrum. Meas. 2020, 69, 2607–2620. [Google Scholar] [CrossRef]
- Ahmadi, S.; Poure, P.; Saadate, S.; Khaburi, D.A. A Real-Time Fault Diagnosis for Neutral-Point-Clamped Inverters Based on Failure-Mode Algorithm. IEEE Trans. Ind. Inform. 2021, 17, 1100–1110. [Google Scholar] [CrossRef]
- Caseiro, L.M.A.; Mendes, A.M.S. Real-time IGBT open-circuit fault diagnosis in three-level neutral-point-clamped voltage-source rectifiers based on instant voltage error. IEEE Trans. Ind. Electron. 2015, 62, 1669–1678. [Google Scholar] [CrossRef]
- Nsaif, Y.; Lipu, M.S.H.; Hussain, A.; Ayob, A.; Yusof, Y.; Zainuri, M.A. A New Voltage Based Fault Detection Technique for Distribution Network Connected to Photovoltaic Sources Using Variational Mode Decomposition Integrated Ensemble Bagged Trees Approach. Energies 2022, 15, 7762. [Google Scholar] [CrossRef]
- Lee, J.S.; Lee, K.B.; Blaabjerg, F. Open-switch fault detection method of a back-to-back converter using NPC topology for wind turbine systems. IEEE Trans. Ind. Appl. 2014, 51, 325–335. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, Y.; Huang, W.; Teffah, K. A fast-acting diagnostic algorithm of insulated gate bipolar transistor open circuit faults for power inverters in electric vehicles. Energies 2017, 10, 552. [Google Scholar] [CrossRef] [Green Version]
- Park, B.G.; Lee, K.J.; Kim, R.Y.; Kim, T.S.; Ryu, J.S.; Hyun, D.S. Simple fault diagnosis based on operating characteristic of brushless direct-current motor drives. IEEE Trans. Ind. Electron. 2011, 58, 1586–1593. [Google Scholar] [CrossRef]
- Faraz, G.; Majid, A.; Khan, B.; Saleem, J.; Rehman, N. An Integral Sliding Mode Observer Based Fault Diagnosis Approach for Modular Multilevel Converter. In Proceedings of the 2019 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Swat, Pakistan, 24–25 July 2019; pp. 1–6. [Google Scholar]
- Song, B.; Qi, G.; Xu, L. A new approach to open-circuit fault diagnosis of MMC sub-module. Syst. Sci. Control Eng. 2020, 8, 119–127. [Google Scholar] [CrossRef] [Green Version]
- Deng, F.; Chen, Z.; Khan, M.; Zhu, R. Fault Detection and Localization Method for Modular Multilevel Converters. IEEE Trans. Power Electron. 2015, 30, 2721–2732. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, H.; Liu, Z. Concurrent fault diagnosis of a modular multi-level converter with kalman filter and optimized support vector machine. Syst. Sci. Control Eng. 2019, 7, 43–53. [Google Scholar] [CrossRef] [Green Version]
- Volonescu, C. Fault Detection and Diagnosis; IntechOpen: London, UK, 2018; ISBN 13 978-1789844368. [Google Scholar]
- Estima, J.O.; Freire, N.M.A.; Cardoso, A.J.M. Recent advances in fault diagnosis by Park’s vector approach. IEEE Workshop Electr. Mach. Des. Control Diagn. 2013, 2, 279–288. [Google Scholar]
- Wang, C.; Lizana, F.; Li, Z. Submodule short-circuit fault diagnosis based on wavelet transform and support vector machines for a modular multi-level converter with series and parallel connectivity. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 3239–3244. [Google Scholar]
- Xing, W. An open-circuit fault detection and location strategy for MMC with feature extraction and random forest. In Proceedings of the 2021 IEEE Applied Power Electronics Conference and Exposition (APEC), Phoenix, AZ, USA, 14–17 June 2021; pp. 1111–1116. [Google Scholar]
- Wang, Q.; Yu, Y.; Hoa, A. Fault detection and classification in MMC-HVDC systems using learning methods. Sensors 2020, 20, 4438. [Google Scholar] [CrossRef]
- Morel, C.; Akrad, A.; Sehab, R.; Azib, T.; Larouci, C. IGBT Open-Circuit Fault-Tolerant Strategy for Interleaved Boost Converters via Filippov Method. Energies 2022, 15, 352. [Google Scholar] [CrossRef]
- Li, T.; Zhao, C.; Li, L.; Zhang, F.; Zhai, X. Sub-module fault diagnosis and local protection scheme for MMC-HVDC system. Proc. CSEE 2014, 34, 1641–1649. [Google Scholar]
- Mendes, A.; Cardoso, A.; Saraiva, E.S. Voltage source inverter fault diagnosis in variable speed AC drives, by the average current Park’s vector approach. In Proceedings of the IEEE International Electric Machines and Drives Conference, Seattle, WA, USA, 9–12 May 1999; pp. 704–706. [Google Scholar]
- Ke, L.; Liu, Z.; Zhang, Y. Fault Diagnosis of Modular Multilevel Converter Based on Optimized Support Vector Machine. In Proceedings of the 2020 39th Chinese Control Conference, Shenyang, China, 27–29 July 2020; pp. 4204–4209. [Google Scholar]
- Geng, Z.; Wang, Q.; Han, Y.; Chen, K.; Xie, F.; Wang, Y. Fault Diagnosis of Modular Multilevel Converter Based on RNN and Wavelet Analysis. In Proceedings of the 2020 Chinese Automation Congress, Shanghai, China, 6–8 November 2020; pp. 1097–1101. [Google Scholar]
- Wang, S.; Bi, T.; Jia, K. Wavelet entropy based single pole grounding fault detection approach for MMC-HVDC overhead lines. Power Syst. Technol. 2016, 40, 2179–2185. [Google Scholar]
- Shen, Y.; Wang, T.; Amirat, Y.; Chen, G. IGBT Open-Circuit Fault Diagnosis for MMC Submodules Based on Weighted-Amplitude Permutation Entropy and DS Evidence Fusion Theory. Machines 2021, 9, 317. [Google Scholar] [CrossRef]
- Richman, J.; Randall Moorman, J. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar] [CrossRef] [Green Version]
- Unakafova, V.; Unakafov, A.; Keller, K. An approach to comparing Kolmogorov-Sinai and permutation entropy. Eur. Phys. J. 2013, 222, 353–361. [Google Scholar] [CrossRef] [Green Version]
- Porta, A.; Baselli, G.; Liberati, D.; Montano, N.; Cogliati, C.; Gnecchi-Ruscone, T.; Malliani, A.; Cerutti, S. Measuring regularity by means of a corrected conditional entropy in sympathetic outflow. Biol. Cybern. 1998, 78, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Theerasak, C.; Mandic, D. Cosine Similarity Entropy: Self-Correlation-Based Complexity Analysis of Dynamical Systems. Entropy 2017, 19, 652. [Google Scholar]
- Azami, H.; Li, P.; Arnold, S.; Escuder, J.; Humeau-Heurtier, A. Fuzzy Entropy Metrics for the Analysis of Biomedical Signals: Assessment and Comparison. IEEE Access 2016, 4, 1–16. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy, Neural Systems and Rehabilitation Engineering. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Chang, F.; Sung-Yang, W.; Huang, H.P.; Hsu, L.; Chi, S.; Peng, C.K. Entropy of Entropy: Measurement of Dynamical Complexity for Biological Systems. Entropy 2017, 19, 550. [Google Scholar]
- Costa, M.; Goldberger, A.; Peng, C. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [Green Version]
- Costa, M.; Goldberger, A.; Peng, C. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Cui, L.; Zhang, J.; Zhang, C. Research on fault diagnosis of planetary gearbox based on Variable Multi-Scale Morphological Filtering and improved Symbol Dynamic Entropy. Int. J. Adv. Manuf. Technol. 2023, 124, 3947–3961. [Google Scholar] [CrossRef]
- Silva, L.; Duque, J.; Felipe, J.; Murta, L.; Humeau-Heurtier, A. Twodimensional multiscale entropy analysis: Applications to image texture evaluation. Signal Process. 2018, 147, 224–232. [Google Scholar] [CrossRef]
- Morel, C.; Humeau-Heurtier, A. Multiscale permutation entropy for two-dimensional patterns. Pattern Recognit. Lett. 2021, 150, 139–146. [Google Scholar] [CrossRef]
- Valencia, J.; Porta, A.; Vallverdu, M.; Claria, F.; Baranovski, R.; Orlowska-Baranovska, E.; Caminal, P. Refined multiscale entropy: Application to 24-h Holter records of heart period variability in hearthy and aortic stenosis subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Wu, C.; Lin, S.; Lee, K.; Peng, C. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Wu, S.; Wu, C.; Lin, S.; Wang, C.; Lee, K. Time series analysis using composite multiscale entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef] [Green Version]
- Humeau-Heurtier, A. The Multiscale Entropy Algorithm and Its Variants: A Review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef] [Green Version]
- Dai, M.; Marwali, M.N.; Jung, J.-W.; Keyhani, A. A Three-Phase Four-Wire Inverter Control Technique for a Single Distributed Generation Unit in Island Mode. IEEE Trans. Power Electron. 2008, 23, 322–331. [Google Scholar] [CrossRef]
- Raja, N.; Mathewb, J.; Ga, J.; George, S. Open-Transistor Fault Detection and Diagnosis Based on Current Trajectory in a Two-level Voltage Source Inverter. Procedia Technol. 2016, 25, 669–675. [Google Scholar] [CrossRef] [Green Version]

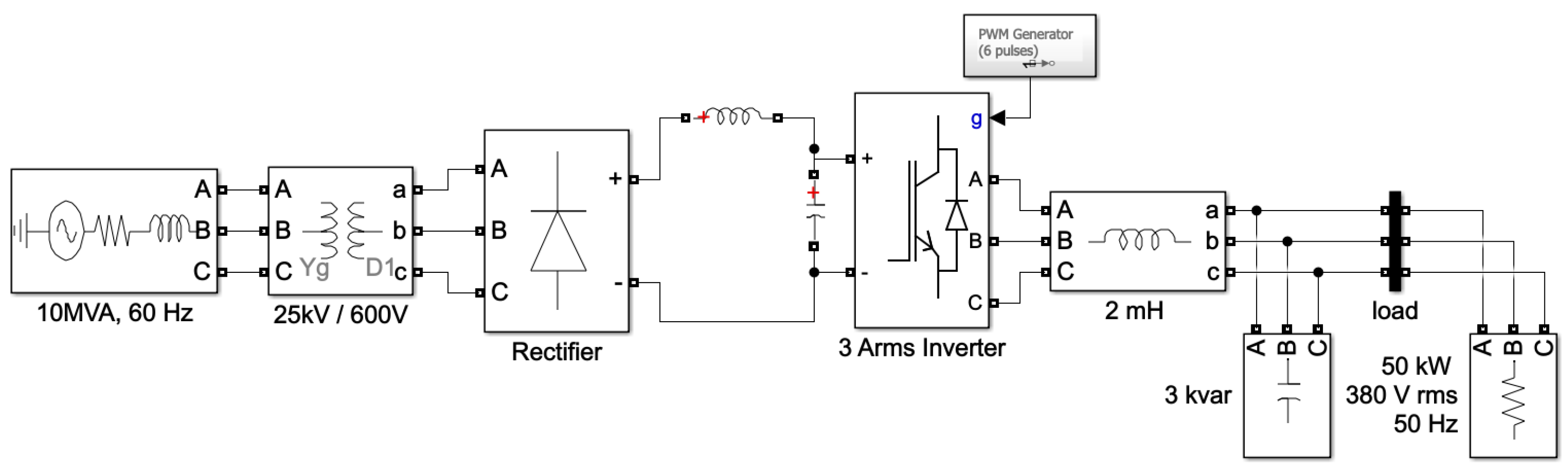










| Especification | Parameter | Value |
|---|---|---|
| Input voltage | Input phase-to-phase voltage | 25 kV |
| Input power | 10 MVA | |
| Grid frequency | 60 Hz | |
| Three-phase transformer Winding 1 | Phase-to-phase voltage | 25 kV |
| Resistance | 0.004 | |
| Inductance | 0.02 H | |
| Three-phase transformer Winding 2 | Phase-to-phase voltage | 600 V |
| Resistance | 0.004 | |
| Inductance | 0.02 H | |
| Rectifier | Snubber resistance | 100 |
| Snubber capacitance | 0.1 F | |
| Ron | 0.001 | |
| Foward voltage | 0.8 V | |
| Filtre DC | Inductance | 200 H |
| Capacitance | 5 mF | |
| Inverter | Switching frequency | 50 Hz |
| Output filtre | Inductance | 2 mH |
| Capacitive reactive power | 3 kVAR | |
| Load | Phase-to-phase voltage | 380 V |
| Output power | 50 kW | |
| Frequency | 50 Hz |
| Mean | |||
|---|---|---|---|
| No fault | −0.0034 | −0.0034 | −0.0034 |
| Open circuit— | −9.2848 | 4.7236 | 4.5612 |
| Open circuit— and | −6.8013 | 6.9350 | −0.1337 |
| Open circuit— and | −6.2230 | −6.2388 | 12.4618 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morel, C.; Akrad, A. Open-Circuit Fault Detection and Location in AC-DC-AC Converters Based on Entropy Analysis. Energies 2023, 16, 1959. https://doi.org/10.3390/en16041959
Morel C, Akrad A. Open-Circuit Fault Detection and Location in AC-DC-AC Converters Based on Entropy Analysis. Energies. 2023; 16(4):1959. https://doi.org/10.3390/en16041959
Chicago/Turabian StyleMorel, Cristina, and Ahmad Akrad. 2023. "Open-Circuit Fault Detection and Location in AC-DC-AC Converters Based on Entropy Analysis" Energies 16, no. 4: 1959. https://doi.org/10.3390/en16041959
APA StyleMorel, C., & Akrad, A. (2023). Open-Circuit Fault Detection and Location in AC-DC-AC Converters Based on Entropy Analysis. Energies, 16(4), 1959. https://doi.org/10.3390/en16041959






