1. Introduction
As the cost of power generation using wind power has decreased over the past decade, wind power generation is attracting attention as an efficient power generation source to achieve carbon neutrality [
1,
2]. As of the end of 2021, the cumulative installed capacity of wind power generation facilities worldwide was about 837 GW, and 93.6 GW of new wind power generation facilities were installed in 2021 alone [
3]. Although large wind power is leading the growth of the wind power generation equipment market, small wind turbines are also showing steady growth especially for small loads and stand-alone systems [
4,
5].
According to IEC 61400-2, the international design standard for small wind turbines, a small wind turbine is defined as a wind turbine with a rotor swept area of 200 m
2 or less and generating electricity at a voltage less than 1000 VAC or 1500 VDC [
6]. Various shapes of small wind turbines in addition to the common horizontal-axis lift-type wind turbines with three blades are commercially available including vertical-axis machines [
7,
8] and horizontal-axis machines with spiral blades [
9]. However, such wind turbines of various shapes other than horizontal axis lift type ones are mainly applied to hybrid solar–wind powered streetlights with a rated capacity of 1 kW or less. In the case of grid-connected small wind turbines with a capacity of 10 kW or more, horizontal-axis lift-type wind turbines with three blades are mainly used, similar to general MW-class large wind turbines.
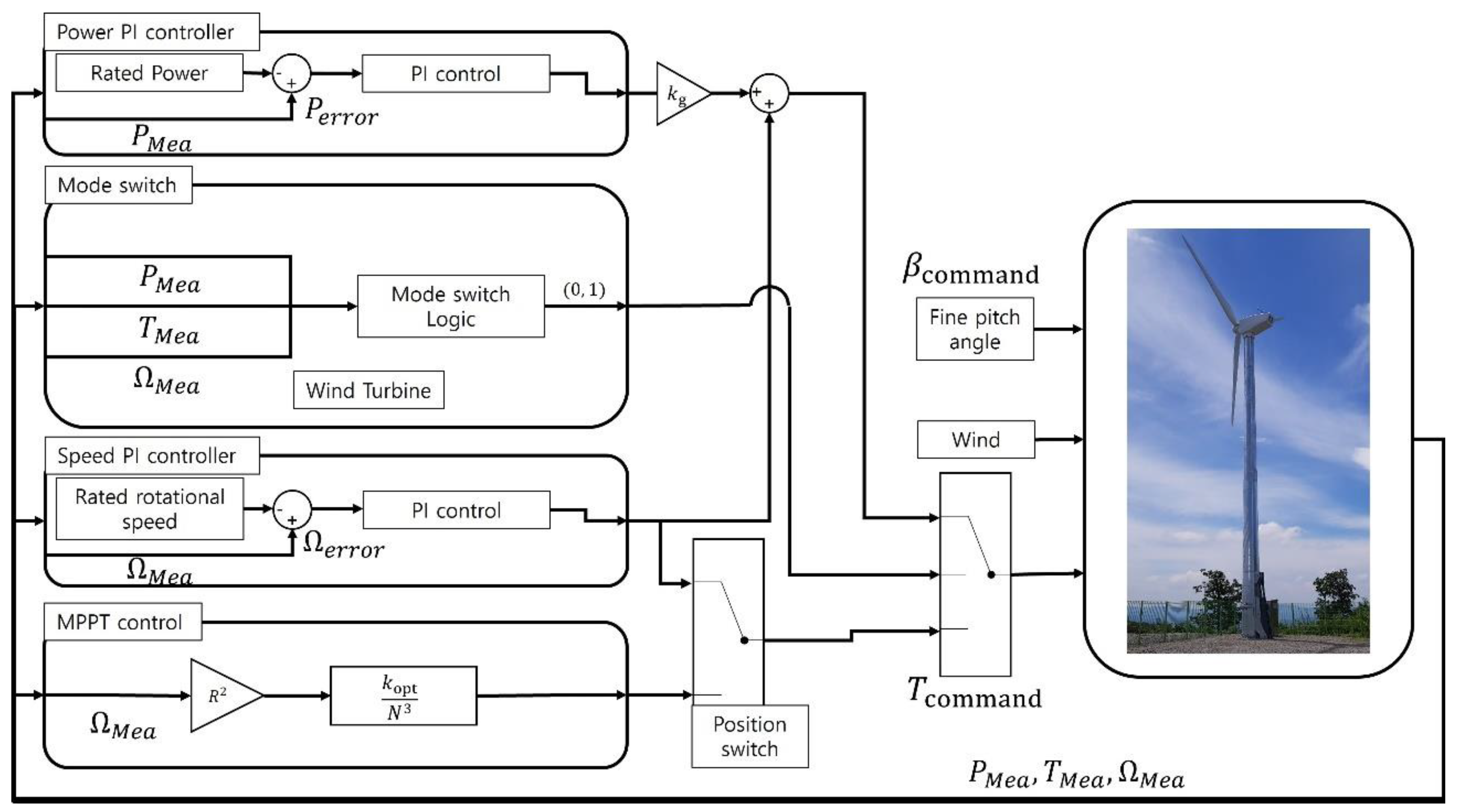
The MW class large-scale wind turbine is a variable speed variable pitch system. Variable speed is required to maximize energy harvesting with varying wind speeds, and variable pitch (of blade) is used to effectively regulate the electrical power not to exceed the rated value. For control of variable-speed variable-pitch wind turbines, in the wind speed lower than the rated wind speed, the blade pitch angle is fixed to the fine pitch angle, and the rotational speed of the wind turbine blades is varied through the generator reaction torque control to achieve the maximum power coefficient. In addition, above the rated wind speed, the rated rotational speed of the generator is maintained by adjusting the blade pitch angle according to the change in wind speed as a strategy for maintaining the rated power using the blade pitch actuator installed in the hub.
Such active pitch control technology is a standard power control method for MW-class wind turbines in the rated power region [
10,
11], and is gradually being applied to hundreds of kW-class medium-sized wind turbines [
12,
13] or tens of kW-class grid-connected small wind power. However, in general, small wind turbines with a rated capacity of 20 kW or less mainly adopt fixed pitch systems rather than variable pitch systems for economic reasons and size limitations. The control mechanism for variable-speed variable-pitch wind turbines at a wind speed lower than the rated wind speed are commonly applied to the small variable-speed fixed-pitch wind turbines because no blade pitching is used. It is implemented by measuring the rotational speed of the generator, multiplying the optimal mode gain, and issuing the generator torque command through the open loop controller to achieve the maximum power coefficient [
14].
The control mechanism at a wind speed higher than the rated wind speed of the fixed pitch system may be largely divided into a method with side furling and a method with stall control. The control using side furling is a method of implementing a mechanical mechanism so that the rotor and the nacelle parts are folded sideways in a high wind speed and the rotor deviates from the wind direction. However, in order to implement Side Furling so that it does not exceed the desired rated power, some Furling occurs even when the power is lower than the rated power, so the power is degraded, and it needs a relatively high rotational speed above the rated wind speed [
15].
Stall control above the rated wind speed of the fixed pitch system is a method of generating an aerodynamic stall phenomenon by increasing the inflow angle of attack of the blade above the stall threshold angle in the high wind speed region without a pitch system. If a stall occurs in the blade, the lift coefficient decreases significantly and the drag coefficient increases significantly, resulting in a decrease in the power of the wind turbine.
Most of the papers on power control of fixed pitch systems are limited to control to maintain maximum efficiency in areas below rated wind speed, and the literature on stall control in areas above rated wind speed is very limited. Muljadi et al. proposed a method, ‘soft stall’ to maximize the power coefficient below the rated wind speed and limit the rotor speed above the rated wind speed through the generator torque control [
16]. The result of verifying the controller through ADAMS simulation for wind turbines having a nominal rated power of 275 kW showed that the rotor speed was limited to 62 rpm and the power was limited to 385 kW at high wind speeds. However, as the proposed control strategy was not an active control but used a generator torque schedule to control the generator speed, it could constrain the power in a certain limit but could not control the power to track the rated power in a stalled condition at high wind speeds.
Pierce and Migliore proposed a new control method, ‘active stall’, for a variable-speed fixed-pitch wind turbine, which is similar to ‘soft stall’ but different in that it has a longer range of maximum power coefficient operation, and a different method of limiting rotor speed at high wind speeds [
17]. Strategies to maximize the power coefficient, to keep the generator rotational speed constant, and to keep the power constant were applied for different speed regions from low to high wind speeds. They used a closed loop PI control to regulate the rotor speed and did experimental validation in the field with a 275 kW wind turbine. In the validation, they showed good rotor speed regulation performance and energy capture but no demonstration of the maximum power tracking at high wind speeds was possible due to insufficient field data obtained.
Chen et al. proposed a control algorithm that can be applied to the entire below and above the rated wind speed regions similar to previous studies [
16,
17] as a new control strategy. Adaptive Fuzzy Logic Controller was applied for the current command of the DC-DC converter to minimize the error of the generator-rectification voltage corresponding to the generator rotational speed in each strategy [
18]. They validated the proposed algorithm with a 1.2 kW virtual micro wind turbine model using matlab/simulink and a laboratory-scale motor-generator simulator. However, no detailed validation of the proposed controller at turbulent wind using an aeroelastic code such as Bladed and Fast was performed. Although they showed some dynamic results from the motor-generator simulator for 100 s, no clear information of the turbulent wind was provided, and the power tracking performance of the controller at high winds was not analyzed quantitatively for verification.
In another study, Chen et al. proposed an algorithm similar to the previous method for a VSVP wind turbine, but PID controllers with an aerodynamic power observer were applied instead of Adaptive Fuzzy Logic Controller [
19]. However, like the previous study, no detailed dynamic performance validation of the proposed controller at turbulent winds was done with any aeroelastic code. They did some experimental validation using a lab scale motor-generator simulator representing a 1.2 kW micro wind turbine and showed some power curves obtained, but no quantitative analysis of the experiments was provided to show the dynamic performance of the controller.
Currently, the validation of the wind turbine controller using aeroelastic codes such as Bladed and Fast at three-dimensional turbulent winds is almost a standard procedure before the algorithm is actually applied to a commercial wind turbine [
12,
13,
20,
21,
22]. The dynamic simulation results from those codes are considered to be accurate by international certification companies of wind turbines and known to be close to actual results in the field. Although several algorithms have previously been proposed as a power control algorithm for VSFP wind turbines, the algorithms verified with such accurate codes for actual application to a commercial wind turbine are very rare in the literature, and no quantitative analysis of power performance and load analysis was done with the proposed control algorithms.
Therefore, in this study, the power control algorithm for a VSFP wind turbine is revisited and newly proposed like in previous studies but different from those in that it is made to be applicable to a commercial small wind turbine. For this, a 20 kW commercial VSFP wind turbine was targeted, and a new control algorithm which resembles the control algorithm designed and applied to a commercial medium wind turbine was proposed [
12]. The proposed algorithm covers the entire wind turbine operating regions similar to previous studies including Maximum Power Coefficient Region (Region II), Transition Region (Region II-1/2), and Rated Power Region (Region III) [
23]. The aeroelastic code Bladed was chosen for this study, and a detailed modeling of the target wind turbine was performed by data both provided by the wind turbine manufacturer and obtained by a 3D laser scanning process. The proposed control algorithm was validated in turbulent winds using Bladed, and dynamic performances were analyzed. The dynamic performance of the proposed control algorithm was also compared with the performance of the same wind turbine with a conventional VSVP algorithm.
In this study, a power controller was designed and verified for a 20 kW horizontal axis lift-type wind turbine using dynamic simulation in turbulent wind. The blade shape was acquired through 3D laser scanning, and the wind turbine parts were modeled using the Bladed program with the target turbine data. The proposed algorithm consists of a pitch controller and a stall controller, both of which utilize components such as pitch PI control, torque schedule, speed PI control, mode switch, and position switch. The pitch controller aims to set the blade pitch angle to a fixed fine pitch angle for maximum power point tracking (MPPT) control and transition control, while the stall controller aims to maintain the generator torque and speed. The power control algorithm was verified through simulation and compared to a variable-speed variable-pitch wind turbine power controller. The results showed that the proposed controller performed similarly to the variable-speed variable-pitch controller for regions below the rated wind speed but had better rated power tracking performance in Region III. The stall control also demonstrated relatively high stability in rotor speed in high turbulence gusts. However, the average load of the fixed-pitch wind turbine was found to be greater than that of the variable-pitch wind turbine, with a lower fatigue load due to its lack of a pitch system. The study provides insight into the control performance and features of various wind turbine types, but its results may not be applicable to larger wind turbines.
2. Wind Turbine Model
The target wind turbine used in this study is a commercial 20 kW horizontal axis lift type wind turbine. The target wind turbine was modeled for simulations using DNV’s Bladed program, which is an aeroelastic code for wind turbines widely used for dynamic simulations and validation of control algorithms [
15]. Detailed specifications and the photo of the target wind turbine are presented in
Table 1 and
Figure 1, respectively.
For modeling of the target wind turbine blade, blade shape data were obtained through a 3D scanning process. In addition, the shape data of the acquired blade was applied to a 3D CAD program and used to extract the airfoil shape [
24]. As shown in
Figure 2, airfoil information for a total of 20 sections was obtained in the spanwise direction of the blade, and aerodynamic analysis was performed using Qblade [
25].
Figure 3 shows the process of blade modeling.
With the information of the airfoils, aerodynamic analysis was performed using Qblade and Xfoil. The target wind turbine is a small wind turbine with a capacity of 20 kW and operates in Reynolds numbers much lower than a large wind turbine; therefore, the aerodynamic performance of the blade is affected relatively significantly by the Reynolds number changes compared to a large wind turbine. Therefore, the lift and drag coefficients were obtained for airfoils along the blade span with Reynolds number ranges that will occur in actual operation to be used for the bladed simulation [
26]. Equation (5) represents the Reynolds number required for aerodynamic analysis.
is the Reynolds number,
is the air density,
is the chord length, and
is the coefficient of viscosity.
Figure 3 shows the changes in power and thrust coefficient depending on the tip speed ratio change, which is the result of the Qblade simulation of the target wind turbine rotor. In the figure, the power coefficient represents the efficiency of converting the wind power to the mechanical power of the rotor, and the thrust coefficient represents the ratio of the thrust received from the wind divided by the dynamic force of the wind. The power coefficient and thrust coefficient are mathematically defined by Equations (2) and (3), respectively.
is the output power,
is the thrust force of wind turbine,
is the air density,
is the rotational area, and
is the wind speed [
27].
In addition, the tip speed ratio is the ratio of the tangential speed of the blade tip to the wind speed, which can be expressed by Equation (4).
is the tip speed ratio,
is the rotor radius,
is the rotational speed of the rotor, and
is the wind speed.
4. Validation of Control Algorithm
To verify the performance of the proposed variable-speed fixed-pitch wind turbine control algorithm, a dynamic simulation using turbulent wind was carried out. In addition, the same wind turbine was assumed to be variable-speed variable-pitch, and a control algorithm was designed and applied to enable blade pitch control, and the results were compared and analyzed with the case of applying the variable-speed fixed-pitch control algorithm.
The simulation was performed for 600 s under three-dimensional turbulent wind field using Bladed. The turbulence intensity based on the normal turbulence model specified in IEC-61400-2 was used for different wind speeds. In the case of the low wind speed region (Region II) simulation, the average wind speed and the turbulent wind speed were 10 m/s and 21%, respectively. In the high wind speed region (Region III), the average wind speed was 16 m/s and a turbulence intensity of 17% was applied.
Figure 11a shows the simulation result with an average wind speed of 10 m/s. Basically, in the case of the region below the rated wind speed, the variable-pitch control and the fixed-pitch control show similar results, and it can be seen that the two controllers show a difference in the region above the rated wind speed between 80 and 150 s. Looking at the figure, it can be seen that the pitch control between 80 and 150 s adjusts the blade pitch angle when the electrical power exceeds the rated, maintains the rotor speed close to the rated value, and operates at the rated power through the rated torque output.
On the other hand, in the stall control in the same time range, as the generator torque increases, the rotor speed becomes lower than the rated value. In the case of the section above the rated power, it can be seen that the blade pitch control has better rated power tracking performance than the stall control.
Figure 11b shows the simulation results to which the average wind speed of 16 m/s is applied. It can be seen that the maximum wind speed of the simulation reaches about 25 m/s due to the influence of 17% turbulence intensity. Unlike the 10 m/s simulation, it can be seen that the wind turbine is controlled by the rated power because most of the areas correspond to the rated wind speed or higher.
Looking at
Figure 11b, it can be seen that in the case of pitch control, the rotor speed is maintained closely to the rated value and the power is controlled to the rated power, while the blade pitch angles become larger than those in the case of 10 m/s. In the case of stall control, it can be confirmed that the rotation speed becomes lower than in the case of 10 m/s due to the increased wind speed and the power is maintained at the rated power. Comparing the performances of the stall controller in
Figure 11a,b, as the wind speed increases, the generator torque increases and the rotor speed decreases while driving. Therefore, it can be confirmed that the wind turbine with a fixed pitch controller is controlled by following line F-G in
Figure 7 above the rated wind speed.
Table 2 and
Table 3 show the dynamic simulation results of
Figure 11 quantitatively. It can be seen in the table that the output power of both controllers is about 2 kW lower than the rated power of 20 kW, and the average value decreases due to sudden power fluctuations in both pitch control and stall control due to mode conversion in the transition region (region II-1/2). The table also shows that the generator torque with the stall control becomes slightly larger than that with the pitch control because it is the only way to reduce the generator speed without blade pitching.
In order to compare the difference in load according to the two control methods of the same wind turbine, it is possible to quantitatively evaluate the degree of fatigue damage using the mean load (ML) of the wind turbine and the damage equivalent load (DEL) based on rain-flow counting method. These are shown in
Table 4 and
Table 5 for two different wind speeds, 10 m/s and 16 m/s.
Comparing the simulation loads in
Table 4 and
Table 5, it can be seen that the mean load in each wind speed region increases in all parts of the stall control compared to the pitch control, especially up to 242% larger in Blade My (out of plane bending moment at blade root). However, it was confirmed that DEL decreased in all parts except for Blade Mx (in-plane bending moment at blade root), especially in Tower Mx (side-side direction bending moment at Tower bottom). Blade My shows that the mean load of the stall control increases up to 242% based on the pitch control value at 16 m/s, but decreases by 39% in DEL and 59% in Tower Mx DEL.
Figure 12 shows the load fluctuations of Blade My of the pitch control and stall control in the simulation at 16 m/s. Compared to the pitch control, the stall control increased the average load, but the peak-to-peak amplitude of the load fluctuation decreased. The reason why the average load and DEL are different is that the DEL is derived from the rain-flow counting method, which is calculated by applying the maximum and minimum values of vibration to the equation, not the size of the DC component load [
30,
31].
6. Conclusions
A power controller was designed and verified for a 20 kW horizontal axis lift-type wind turbine through dynamic simulation in turbulent wind. The blade shape was acquired through 3D laser scanning. The wind turbine parts were modeled using the target turbine data with the Bladed program.
The pitch controller was constructed with pitch PI control, torque schedule, speed PI control, position switch, and mode switch. The torque schedule is an open-loop control that uses generator speed to maximize the power coefficient. The position switch combines maximum power coefficient control and speed PI control, with the mode switch determining the control mode based on generator speed, electrical power, and blade pitch angle. The mode switch can either set the blade pitch angle to a fixed fine pitch angle for MPPT control and transition control or fix the generator reaction torque to the rated torque for blade pitch control in Region III.
The stall controller was constructed with power PI control, generator speed PI control, torque schedule, mode switch, and position switch. The torque schedule is used to maximize the power coefficient, while the mode switch determines the operating modes based on the generator torque, electrical power, and generator speed. The generator speed is maintained by the speed PI control in Region II-1/2, and the torque command is determined by the sum of the power and speed PI controllers in Region III above the rated wind speed. The PI gains for the power PI controller were obtained through the Ziegler–Nichols method and the speed PI control gain was selected to have the same value as the pitch control.
The proposed algorithm uses a generator torque command obtained by combining the outputs of the power and speed PI controllers above the rated wind speed. The output performance was improved by adjusting the gain value of the power PI control loop. Simulations were performed with various gains (0.1, 0.5, 1 (base), and 1.5) and the results showed that the power tracking performance varies with the magnitude of the gain. Larger gains lead to lower rotational speeds and electrical power, with the mean electrical power approaching the rated power.
To verify the power control algorithm of the target wind turbine proposed in this research, a dynamic simulation was conducted in turbulent wind, and two cases were conducted at an average wind speed of 10 m/s and 16 m/s. In addition, in order to compare and analyze the performance of the proposed controller compared to the variable-speed variable-pitch wind turbine power controller, the target turbine was assumed to be a pitch controllable wind turbine, and the power controller was designed and simulated.
Based on the simulation results, the controller proposed in this study showed the same controller performance as the variable-speed variable-pitch controller for Region II and Region II-1/2 below rated wind speed. Although the standard deviation of the electrical power was found to be higher than that of the variable-speed variable-pitch controller, the variable- speed fixed-pitch controller showed well-rated power tracking performance in Region III. In addition, simulation results showed that the stall control has relatively high stability in rotor speed in high turbulence gusts due to SWT’s small rotational inertia because the rotor speed is maintained to a lower value than the rated value in Region III. In addition, it was confirmed that the mean load with the stall control was higher than that with the pitch control, but the fatigue load was smaller with the stall control.
This study analyzed the control performance and features of various VSVP and VSFP wind turbines. Specifically, the optimization process was carried out using a power-weighted gain value for a VSVP wind turbine, and the stable power performance was established. Furthermore, it was found that the average load of the VSFP wind turbine is greater than that of the VSVP wind turbine, but its fatigue load, calculated using the rain-flow counting method, is lower due to its lack of a pitch system. However, in the case of large wind turbines, the impact of the load is significant, thus limiting the applicability of this study.