An All-Vanadium Redox Flow Battery: A Comprehensive Equivalent Circuit Model

Abstract

In this paper, we propose a sophisticated battery model for vanadium redox flow batteries (VRFBs), which are a promising energy storage technology due to their design flexibility, low manufacturing costs on a large scale, indefinite lifetime, and recyclable electrolytes. Primarily, fluid distribution is analysed using computational fluid dynamics (CFD) considering only half-cells. Based on the analysis results, a novel model is developed in the MATLAB Simulink environment which is capable of identifying both the steady-state and dynamic characteristics of VRFBs. Unlike the majority of published studies, the inherent characteristics of the flow battery, such as shunt current, ion diffusion, and pumping energy consumption, are considered. Furthermore, simplified charge transfer resistance (CTR) is taken into account based on electrochemical impedance spectroscopy (EIS) measurement results. The accuracy of the model was determined by comparing the simulation results generated by the equivalent circuit battery model developed in this study with real datasets. The obtained results indicate that the developed model has an accuracy of 3% under the sample operating conditions selected. This study can also be used to fill the gap left by the absence of the VRFB battery model in commonly used programs for renewable energy systems, such as TRNSYS.

1. Introduction

Several important factors contribute to the decline of fossil fuels as an attractive energy source. The limited availability of these resources and the negative environmental impact associated with their extraction, transportation, and use have prompted increased awareness and concern regarding their continued utilization. In addition, the cost of renewable energy sources such as wind and solar power has become more competitive, and government policies aimed at reducing the use of fossil fuels and promoting the use of renewable energy sources have further diminished the appeal of fossil fuels.

As the demand for a sustainable energy economy increases, electric networks and their supporting infrastructure must become more adaptable. Energy storage systems (ESS) offer a variety of applications that improve the stability, dependability, and efficiency of electric grids, and play a crucial role in this transition. ESS can be used to integrate renewable energy sources into the grid, level loads, reduce peaks, and regulate frequency and area, among other applications [1]. Invented at NASA (National Aeronautics and Space Administration) by Thaller [2], flow batteries are a promising option for energy storage in grid systems. Depending on local requirements, these batteries provide a highly efficient, scalable, and environmentally friendly solution for energy storage that can significantly improve the robustness and dependability of electrical distribution networks in both urban and rural areas. Flow batteries are a safer option for grid integration because their design parameters are flexible and their electrolytes are non-inflammable [3]. Incorporating flow batteries into grid systems provides a number of advantages that support the transition to a more sustainable energy economy.

However, in order to build effective power systems using ESS and perform accurate calculations, realistic battery models are required. Due to the fact that flow batteries have more dynamic parameters than conventional batteries, the process of generating equivalent circuits is slightly more complicated. The following studies have been conducted in the literature on this subject. The flow battery’s Nernst equation is presented as a function of the cell’s standard electrode potential, temperature, and state of charge (SOC) [4]. The Rint model is the basic and simplest model for batteries. In a study [5], parallel-connected polarization resistor and capacitor units are added to the Rint model, which simulates the dynamic characteristics of the battery during the generation and elimination of the polarization phenomenon. However, other factors such as the shunt current generated by the potential gradient across the stacks, which drives the ions through the common manifolds, should be taken into account in the equivalent battery model [6]. Additionally, pump power is a factor that must be considered in the model as a parasitic loss [7]. In the study [8], the overall battery efficiency is calculated for variable and constant flowrate operation by including both pumping and shunt current losses. In all-vanadium redox flow batteries (VRFBs), it is crucial to consider the effects of electroless chemical aging on porous carbon felt electrodes. This phenomenon can have a significant impact on the performance and durability of VRFBs; therefore, it must be thoroughly investigated to ensure the dependable operation of these ESSs. Electrochemical impedance spectroscopy (EIS) and ex situ X-ray photoelectron spectroscopy (XPS) were used to figure out how the charge transfer resistance (CTR) changed due to chemical aging [9]. Due to these features, it has been various authors have used the equivalent circuit model (ECM) to achieve more accurate results, mainly for the estimation of the state of charge (SOC) [10,11,12,13]. This model was also applied to PV/ESS systems [14] and PV field-wind/ESS turbine energy generation systems (SWEG) [15]. Essentially, the first basic ECM for VRFB were derived from those utilized in lithium-ion batteries [16]. Particularly, researchers have contributed various advanced control algorithms to address the overcharging and safety risks in Li-ion batteries [17]. Furthermore, researchers considered some particular phenomena of the VRFB, such as vanadium crossover causing self-discharging [18,19]. Later, electrochemical and thermal dynamics are coupled in [20], and the relationship between the state of charge and the flow rate is provided in [21]. On the other hand, for fuel cells (which are a concept very similar to VRFBs), an automated machine learning structure–composition property relationship of perovskite materials is provided in [22], paving the way for the discovery of advanced energy materials.

Currently, the study of VRFB models is concentrated in three primary areas: fluid-dynamic optimization, automatic control, and model-based condition monitoring. A powerful tool, Computational Fluid Dynamics (CFD) analysis, can be employed to construct a mathematical model of VRFB. This enables the development of feasible numerical models aimed at improving the performance and lifetime of VRFBs [23]. Here, priority is placed on achieving uniform electrolyte distribution and minimizing the influence of pressure drop in order to achieve the lowest overpotential and highest efficiency in stack configuration. Numerous dynamic models, control strategies, and observers have been developed in the field of automatic control. These studies present more complex and realistic models that take into account factors such as corrosion, degradation, and unexpected reactions, resulting in lower research and development costs [24]. In the field of model-based condition monitoring, studies have simulated the dynamics of the VRFB using a first-order resistor-capacitance (RC) model. A recursive total least squares (RTLS) method has been employed to reduce the impact of external disturbances and accurately track real-time changes in model parameters. Experiments were conducted to validate the proposed method, which demonstrated an ability to accurately track changes in model parameters under the influence of noise disturbances, with a SOC estimation error bound under 3% [25].

In addition to these studies in the literature, there is a need for an accurate and advanced battery model to address the shortage of advanced VRFB battery models in libraries of commonly utilized exergy analysis programs such as TRNSYS. As demonstrated in [19], this model should provide rapid results through the use of a single RC structure. Therefore, it will be appropriate for co-simulation. Consequently, in this study, a battery model is being developed that will combine the features of many existing studies in the literature and be suitable for use in co-simulations.

The main contribution of this study is the proposal of a novel, comprehensive equivalent circuit model for flow batteries wherein the missing aspects of the equivalent battery circuit studies in the literature are combined. The dynamic characteristics of the flow battery, shunt currents, pump power, and charge transfer resistance are considered in the development of the battery model, which is created in the MATLAB Simulink environment. A preliminary version of the presented information was previously presented as a short paper at the 17th Conference on Sustainable Development of Energy Water and Environmental Systems, held in Paphos [26].

This paper is organized as follows: In Section 2, a comprehensive equivalent circuit model for VRFB is discussed. The vanadium redox flow battery system structure is described, and an ECM parameter is identified. In addition, fluid distribution and analysis results are given. In Section 3, simulation results for self-discharging, shunt currents, porous electrode aging, and battery response are presented. In Section 4, the proposed model is verified with experimental data. Finally, Section 5 presents the discussion.

2. Comprehensive Equivalent Circuit Model for VRFB

The equivalent circuit model (ECM) employs a circuit component to create a specific circuit network that is used to characterize the circuit’s operational characteristics. This model establishes a relationship between the external characteristics of the operating battery and the battery’s internal state.

2.1. Vanadium Redox Flow Battery System Structure

Vanadium redox flow batteries generally consist of at least one stack, which can be considered as the combination of negative and positive half-cells, two electrolyte tanks, two circulating pumps, and other components. The proposed model is based on a 1 kW/1 kWh VRFB system described in [27].

On the electrochemical side, vanadium redox batteries work based on the oxidation and reduction of vanadium species, whose chemical reactions are given as follows.

The general reaction equation:

$$V{O}^{2+}+H_{2}O+V^{3+}discharge \leftrightharpoons charge V{O}_2^{+}+V^{2+}+2H^{+}$$

(1)

The positive electrode (catholyte):

$$V^{4+}-e^{-}discharge \leftrightharpoons charge V^{5+}$$

(2)

The negative electrode (anolyte):

$$V^{3+}+e^{-}discharge \leftrightharpoons charge V^{2+}$$

(3)

For instance, during the discharging state, vanadium (II) releases an electron and transforms into vanadium (III), whereas on the catholyte side (positive half-cell), vanadium (V) captures an electron emitted by the load and transforms into vanadium (IV). The potential difference between the electrodes is approximately 1.26 volts [28].

2.2. Equivalent Circuit Model for VRFB

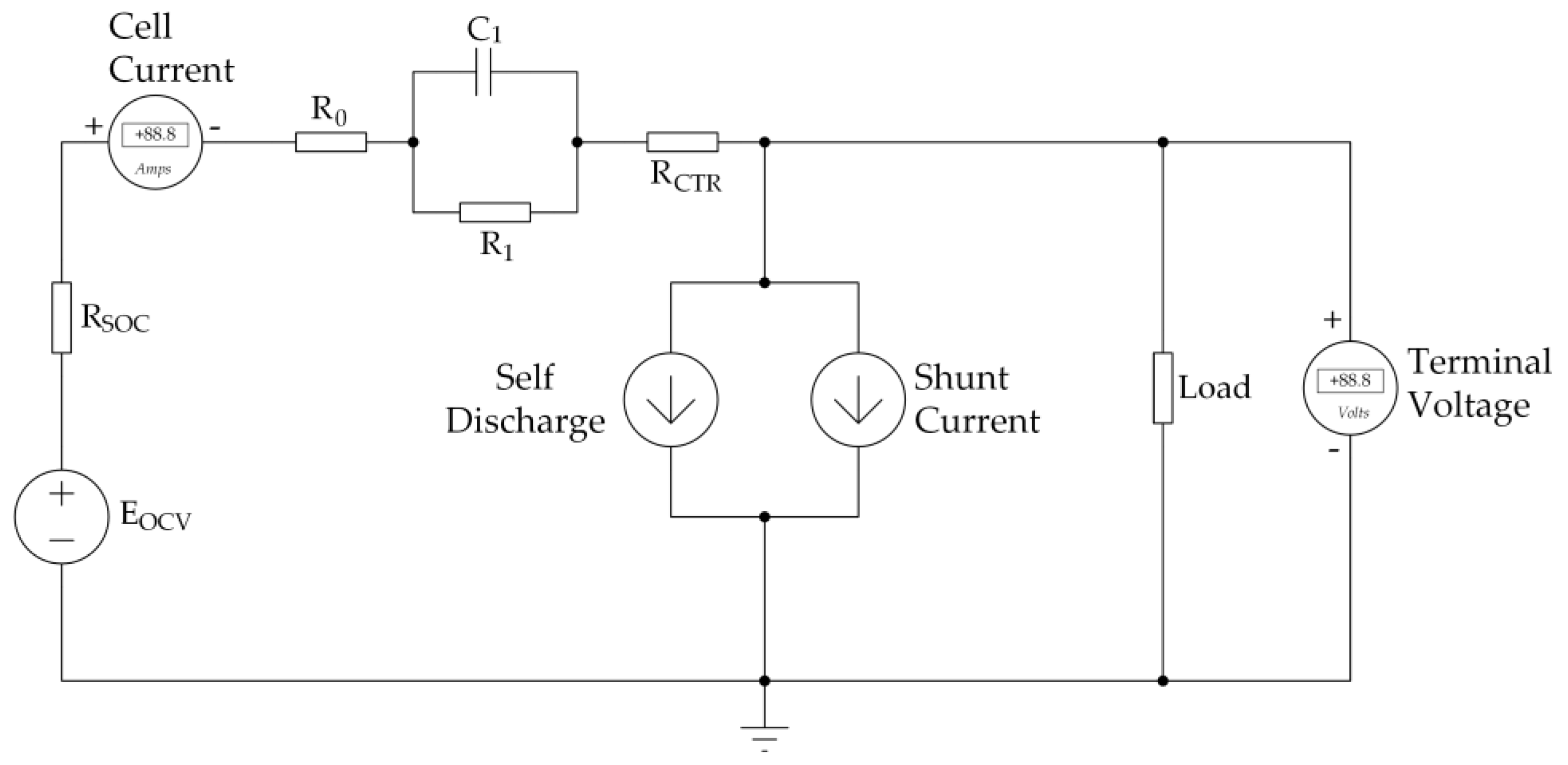
An ECM consists of a SOC-dependent controlled voltage source in series with resistor–capacitor networks. In this paper, the ECM is constructed by resembling the Li-ion and NiMH battery models [29]. However, the way VRFB ions move causes self-discharge from one half cell to the next. Polar connections caused shunt currents, and chemical reactions caused the porous electrodes to wear out over time. Therefore, the promised model includes all of these characteristics, as shown in Figure 1.

2.2.1. Nernst Equation and SOC

The E_OCV represents the open-circuit voltage of the battery in its ideal state, which is dependent on the vanadium species concentration. This voltage is calculated using the Nernst equation [30].

$$E_{ocv}=E_0+\frac{2RT}{F} ln\left(\frac{SO{C}_{cell}}{1-SO{C}_{cell}}\right)$$

(4)

where E₀ is the standard potential, which is 1.39 V [8,11], R is the gas constant, which is 8.314 [Joule/Kelvin × mol], T is the temperature in kelvin and F is the Faraday constant 96,485 [Ampere × Second/mol]. $SO{C}_{cell}$ is the cell state of charge.

$SO{C}_{cell}$ is required in order to determine the E_OCV potential. Since SOC is not uniformly distributed in the cell, $SO{C}_{cell}$ represents the mean value and is related to the cell current ($I_{cell}$), the electrolyte flow volume rate ($Q_{vrb})$, inlet SOC and the number of cells ($n_{cell}$). This may be obtained by Equation (5):

$$SO{C}_{cell}\left(t\right)=SO{C}_{tank}\left(t\right)+\frac{n_{cell}{I}_{cell}}{2F{Q}_{vrb}{C}_v}$$

(5)

where $C_v$ is the concentration of vanadium ions [mol/m³].

Finally, the $SO{C}_{tank}\left(t\right)$ value is determined by using Equation (6):

$$SO{C}_{tank}\left(t\right)=SO{C}_{tank}\left(0\right)+\frac{n_{cell}}{F{V}_{tank}{C}_v}{\int }_0^t{I}_{cell}d\tau$$

(6)

Therefore, the terminal voltage is determined by the following Equation (7):

$$V_t=n_{cell}[E_0+\frac{2RT}{F} ln\left(\frac{SO{C}_{cell}}{1-SO{C}_{cell}}\right)]+I_{ter}{R}_{int}$$

(7)

2.2.2. ECM Parameter Identification

Identification of ECM parameters is crucial for the development of a VRFB model, as it helps to accurately represent the physical behaviour of the VRFB system. The ECM model is composed of electrical circuit components that represent the various electrical processes occurring within the VRFB.

If the input current and its voltage response are known, the components of the ECM can be identified using the least square technique based on Kirchhoff voltage law, as previously demonstrated by Y. Zhang [18]. The obtained parameters are given in

Table 1. ECM parameters under different current densities and flow volume rates.

${\mathit{i}}_{\mathit{t}\mathit{e}\mathit{r}}\left[\raisebox{1ex}{$\mathit{m}\mathit{A}$}\!\left/ \!\raisebox{-1ex}{$\mathit{c}{\mathit{m}}^2$}\right.\right]$	${\mathit{Q}}_{\mathit{v}\mathit{r}\mathit{b}} \left[\raisebox{1ex}{$\mathit{L}$}\!\left/ \!\raisebox{-1ex}{$\mathit{m}\mathit{i}\mathit{n}$}\right.\right]$	$\mathit{a}$	${\mathit{R}}_{\mathit{i}\mathit{n}\mathit{t} }\left[\mathbf{\Omega }\right]$	${\mathit{R}}_{0 }\left[\mathbf{\Omega }\right]$	${\mathit{R}}_1 \left[\mathbf{\Omega }\right]$	${\mathit{C}}_1 \left[\mathit{F}\right]$
160	2	1.6999	0.0294	0.0209	0.0085	1.16 × 103
160	4	1.4537	0.0248	0.0217	0.0031	1.90 × 103
160	6	1.3364	0.0231	0.0218	0.0013	4.48 × 103
80	2	1.3203	0.0320	0.0222	0.0098	1.34 × 103
80	4	1.2534	0.0291	0.0247	0.0044	3.77 × 103
80	6	1.2176	0.0271	0.0252	0.0019	6.57 × 103
−80	2	1.3461	0.0222	0.007	0.0152	1.77 × 103
−80	4	1.2738	0.0191	0.0102	0.0089	2.84 × 103
−80	6	1.2471	0.0168	0.0103	0.0065	4.42 × 103
−160	2	1.5531	0.0244	0.0107	0.0137	1.61 × 103
−160	4	1.3921	0.0201	0.0104	0.0097	1.11 × 103
−160	6	1.3491	0.0186	0.0102	0.0084	1.65 × 103

.

As mentioned above, during battery operation, the chemical reactions on the half-cells prompt decays on the structure of the porous electrodes, which causes an increase in resistance to electron flow over time. This aging effect is investigated and demonstrated by I. Derr [9]. Therefore, in this paper, the aging effect is considered a result of serial charge transfer resistance, as given in

Table 2. Charge transfer resistance by the number of days.

Days	${\mathit{R}}_{\mathit{C}\mathit{T}\mathit{R}} \left[\mathit{m}\mathbf{\Omega } \mathit{g}\right]$
1	16.6
2	23.1
3	28
4	32.1
5	34.5
6	33.1
7	36.3
8	36.6

.

2.3. Fluid Distribution Analysis

The VRFB system involves the flow of two distinct vanadium-based electrolyte solutions through a series of flow channels and electrodes, and the uniformity of fluid distribution is crucial for ensuring consistent and optimal performance.

If the liquid in the battery cells is not distributed uniformly, the flow through the pores will differ from what was theorized. When developing the battery model, this circumstance must be taken into account. For this reason, computational fluid dynamics (CFD) analysis was performed to examine this situation.

A short explanation of the CFD analysis methodology follows. It is begun by creating a 3D CAD model of the fluid field or domain, and continues with the meshing process to be able to solve the momentum and energy equations for each small enough element simultaneously via numerical iteration solving. In this study, all CFD analyses were carried out using the ANSYS simulation environment.

The CFD analysis results for a half-cell only, showing that the fluid is uniformly distributed by a porous electrode inside the half-cell. Figure 2a,b show the velocity distribution, and Figure 2c,d show the vectors without an electrode to compare with those shown in Figure 2b,d when an electrode is used.

According to CFD analysis, the porous electrode concept provides uniform velocity distribution inside the cell. While inspecting Figure 2a,c the vortex and near-zero velocity zones occur in the field, which could cause a significant efficiency reduction on the chemical side of the battery.

CFD results were obtained under maximum 0.842 skewness, and an average 1.22 aspect ratio. An average 4.5 cell density [$Number of cells/m{m}^3$] was present, and there were around 200 k cells in total, evenly distributed. The main target of the CFD analysis is to be able to see the zero velocity fields and the uniform velocity profile inside the half-cell. At this point, the porosity parameters, such as the pore size and the pore size distribution, which are neglected in the CFD analysis instead of working with a complex model, play an important role. For simplicity, the existing permeability parameters (viscous resistance) are used.

3. Simulation

In this study, the proposed novel VRFB model is implemented in the MATLAB/Simulink environment. Based on the density of the current, the model uses numerical methods to estimate the terminal voltage. The model is developed utilizing the 1 kWh/1 kW VRFB system data shown in

Table 3. Parameters of VRFB system.

Parameters of VRFB System	Value	Unit
$\mathrm{Number} \mathrm{of} \mathrm{cells}, n_{cell}$	15
Active area	780	$[{\mathrm{cm}}^2$]
$\mathrm{Tank} \mathrm{volume}, V_{tank}$	0.03	$[{\mathrm{m}}^3$]
$\mathrm{Electrolyte} \mathrm{density}, \rho$	1400	$[\mathrm{kg}/{\mathrm{m}}^3$]
$\mathrm{The} \mathrm{concentration} \mathrm{of} \mathrm{V} \mathrm{ion}, c_v$	2	$[\mathrm{mol}/{\mathrm{m}}^3$]
$\mathrm{Operating} \mathrm{temperature} \mathrm{of} \mathrm{VRFB}, T$	42.5	$[\mathrm{Celcius}$]

[27].

3.1. Self-Discharging

Self-discharging in a VRFB refers to the gradual loss of stored energy caused by internal chemical reactions. This can happen when the vanadium ions in the electrolyte solutions are not completely balanced, causing an electrochemical gradient between the anode and cathode compartments. Because of this gradient, vanadium ions can slowly move from one compartment to another, causing energy to be lost. When there is a vanadium ion concentration difference across the membrane, self-discharge and side reactions will occur and significantly reduce the capacity of the battery in the long term. Zhang’s [18] work is utilized to model the self-discharging mechanism. The model response is given in Figure 3.

3.2. Shunt Currents

The potential gradient across the cell stack moves the ions through electrolyte guide channels, which cause efficiency loss for the battery system. In a VRFB, shunt currents are the electrical currents that flow through the bypass circuit instead of the main circuit. These shunt currents can be caused by a variety of factors, such as poor cell design, electrolyte management, and cell imbalance. Shunt currents can decrease the battery’s overall efficiency and increase heat production, which is undesirable and can be detrimental to the battery. In the charging state, shunt currents make the cell current go down, but in the discharging state, they make the cell current go up. This means that there is a loss in both charging and discharging. For large-scale VRFB systems, shunt currents can be more substantial, and in the model, shunt current losses are considered based on the work of Y. Zhang [18] illustrated in Figure 4.

3.3. Porous Electrode Aging

Porous electrode aging refers to the degradation of the porous electrodes in a VRFB over time. The electrodes of a VRFB are usually made of carbon materials, such as carbon felt or carbon paper. They hold vanadium ions while the battery is being charged and discharged. Porous electrodes can wear down over time due to factors such as mechanical wear and tear, exposure to high temperatures and humidity, and exposure to corrosive electrolyte solutions. As the electrodes wear down, the VRFB’s performance can be affected. This can lead to a drop in the battery’s overall efficiency, a rise in self-discharge, and a shorter overall life.

According to the work of I. Derr [13], the effect of aging is approximated by a CTR that varies with simulation time or, in the real world, with battery usage time. Figure 5 illustrates the results of the CTR simulation.

The model uses eight days of experimental data. After day 8, it is assumed that the CTR will increase linearly. Future efforts should implement long-term data for more realistic CTR simulations.

3.4. Battery Response

The battery response of a vanadium redox flow battery (VRFB) is its ability to respond to changes in charging and discharging conditions. This includes factors such as the rate at which the battery is charged or discharged, the operating temperature, and the battery’s state of charge.

Utilizing the battery model, it is possible to analyze the voltage and charge value of a battery under varying charge–discharge currents. Figure 6 shows how the battery reacts (voltage and SOC) when the flow rate is 4 L/min and certain current steps are used.

4. Model Verification

To thoroughly evaluate the accuracy of the proposed model, it is necessary to compare the results of experimental studies with the results provided by the proposed model. This comparison will tell us a lot about how well the model can predict the outcomes we want, and it will be a key metric for judging the proposed model.

A review of the literature revealed an experimental study that is comparable to the battery system presented in the study [27], and the developed model was compared with the experimental data as shown in Figure 6.

In order to thoroughly evaluate the accuracy of the proposed model, a comparison between the results of experimental studies and the results provided by the model play a key role. This comparison will provide valuable insights into the model’s ability to accurately predict the desired outcomes. A comprehensive literature review revealed an experimental study that is comparable to the proposed battery system model presented in this article [27]. The developed model was compared with the experimental data, as shown in Figure 7.

The proposed model is primarily designed to work with the TRNSYS software; as a result, it is significantly more linear than the reference models and has larger timestep intervals. Additionally, the aging factor is included in the proposed model, which prompts a reduction in the state of charge. In Figure 6, the model output is compared with the experimental data under a 4 L/min flow rate and 80 mA/cm² and 160 mA/cm² terminal current density conditions. The results were obtained by setting the initial state of charge at 0.15 for the charging state and 0.85 for the discharging state.

In terms of errors between the model and the experimental data, the highest error percentage is close to −2% at the 160 mA/cm² current density, and −3% at the 80 mA/cm² current density, which are in the dynamic zone due to initial values of the SOC for both charging and discharging. When we reach the stationary zone, the error fluctuates between −1% and 1%, which meets our needs. The number of RC pairs utilized has been identified as the source of the error. Increasing the number of RC pairs improves resolution. In order to achieve optimal simulation time, which is deemed essential in the TRNSYS/MATLAB co-simulation environment, this study chooses to utilize only a single RC pair.

Alternatively, in the Exergy calculations, our battery model will be used predominantly in the stationary zone, so the expected error will be smaller and will be acceptable when we consider a year of simulations.

On the other hand, a comparison with the model in reference [23] revealed that our proposed model exhibits a lower state of charge and correspondingly lower voltage due to its aging and linear behaviour. While this may result in reduced simulation time on the TRANSYS side, it is acceptable for long-term scenarios. Figure 8 illustrates the differences in terminal voltage and state of charge between the models.

On the other hand, our model shows a lower SOC and terminal voltage compared to the model in reference [24]. This is due to its aging and linear behaviour. However, this is acceptable in long-term scenarios because it reduces simulation time, particularly for co-simulations with software such as TRANSYS. Figure 8 illustrates the differences in terminal voltage and SOC between the models.

5. Discussion

VRFBs and other types of batteries have been the focus of numerous studies in the past. A major challenge in this field is the estimation of the state of charge (SOC) due to the inherent chemical instability of battery systems. The capacity and chemical form of electrolytes may change during charging and discharging, leading to a loss of efficiency. While previous models have provided accurate SOC estimates for available batteries on the market, they do not consider the aging effect, leading to diminishing accuracy over time. In contrast, vanadium-based redox flow batteries have a long, but not indefinite, lifespan. The primary goal of this study is to address the issue of SOC estimation by considering the overall effects, including the impact of aging, on the porous electrode. Future research should investigate the underlying cause of aging in VRFBs and develop solutions to mitigate or eliminate this effect, potentially leading to the development of VRFBs with unlimited lifespans.

The design of the equivalent circuit model for the vanadium flow battery took into account the potential non-uniformity of the proton-exchange membrane (PEM), a crucial component for the battery’s operation. The researchers utilized CFD techniques to analyze and simulate the flow of fluids within the battery system in order to verify the uniformity of the membrane. Through this analysis, it was determined that the PEM had a uniform structure, enabling an accurate model of the battery’s behaviour. These data were then incorporated into the development of the equivalent circuit model, ensuring its precision and reliability in predicting the performance of the vanadium flow battery. According to the simulation results, there are no vortexes and near-zero velocity zones in the flow field inside the cell.

To obtain more realistic results, this model takes into account a number of parameters that have previously been overlooked in the modelling of these systems. These parameters include shunt current, which refers to the unintended current that bypasses the main current path in the battery; ion diffusions, which describe the movement of ions within the battery; and charge transfer resistance, which represents the resistance to the transfer of charge within the battery. By including these previously disregarded parameters, the proposed model offers a more comprehensive and accurate representation of the behaviour of all-vanadium flow redox batteries.

In terms of comparison of the proposed model with the experimental results, the terminal voltage error is within the ±3% band on the dynamic zone, ±1% on the stationary zone. The effectiveness of the battery model developed depends on the accuracy of the experimentally determined model (ECM) parameters [9]. The results indicate that the developed model’s precision corresponds to the values re-ported in relevant case studies in the literature. The accuracy is depending between the mean error 1% and 7% on the similar studies [9,31]

On the basis of experimental data from a 1 kW/1 kWh VRFB system, the model depicting transient and long-term battery reactions is successfully implemented in the MATLAB/Simulink environment. The development phases of the battery model are detailed and a case study of the battery’s response to a terminal current is presented.

By incorporating the aging effect on the porous electrode, the proposed model makes a significant contribution to the existing literature, thereby paving the way for long-term exergy analysis and investigation of vanadium-based flow type batteries.

As a next step in exploring the full capabilities of the model, conduction of a co-simulation using the TRNSYS software in an upcoming study has been proposed. This co-simulation will investigate the interactions between the battery model and renewable energy sources in order to gain valuable insights into the behaviour of integrated energy systems. In addition, this will provide a platform for demonstrating the practicability and efficacy of the battery model in real-world applications.