Statistical Image Analysis on Liquid-Liquid Mixing Uniformity of Micro-Scale Pipeline with Chaotic Structure
Abstract
:1. Introduction
2. Experiments and Methods
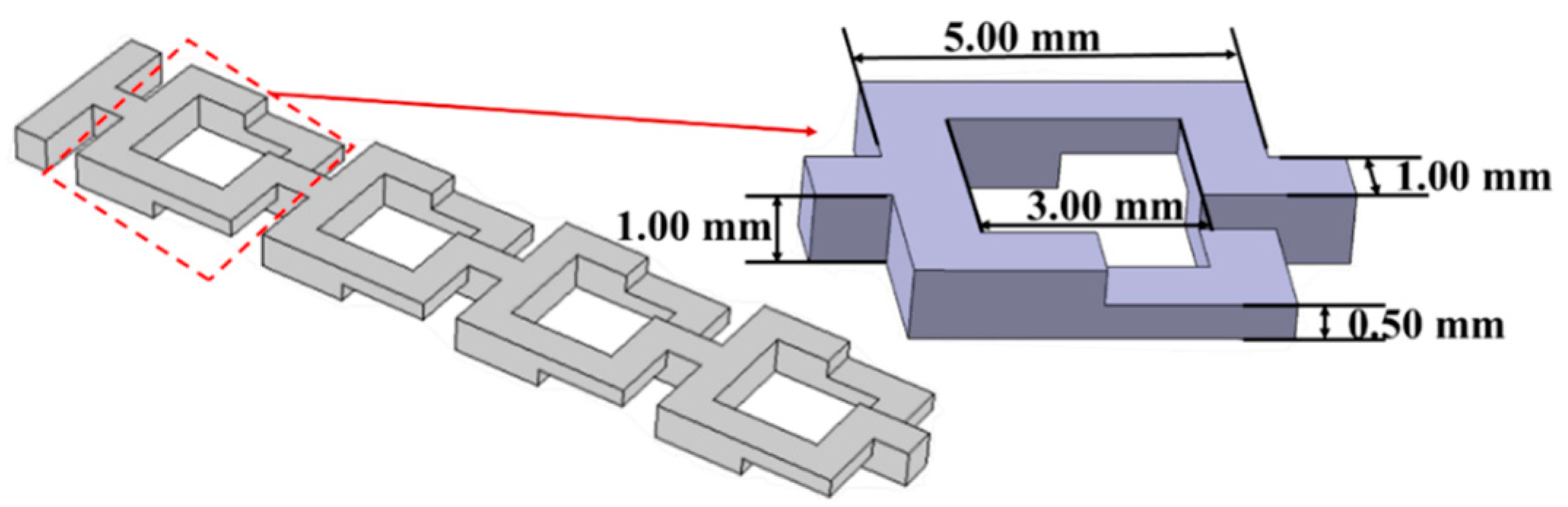
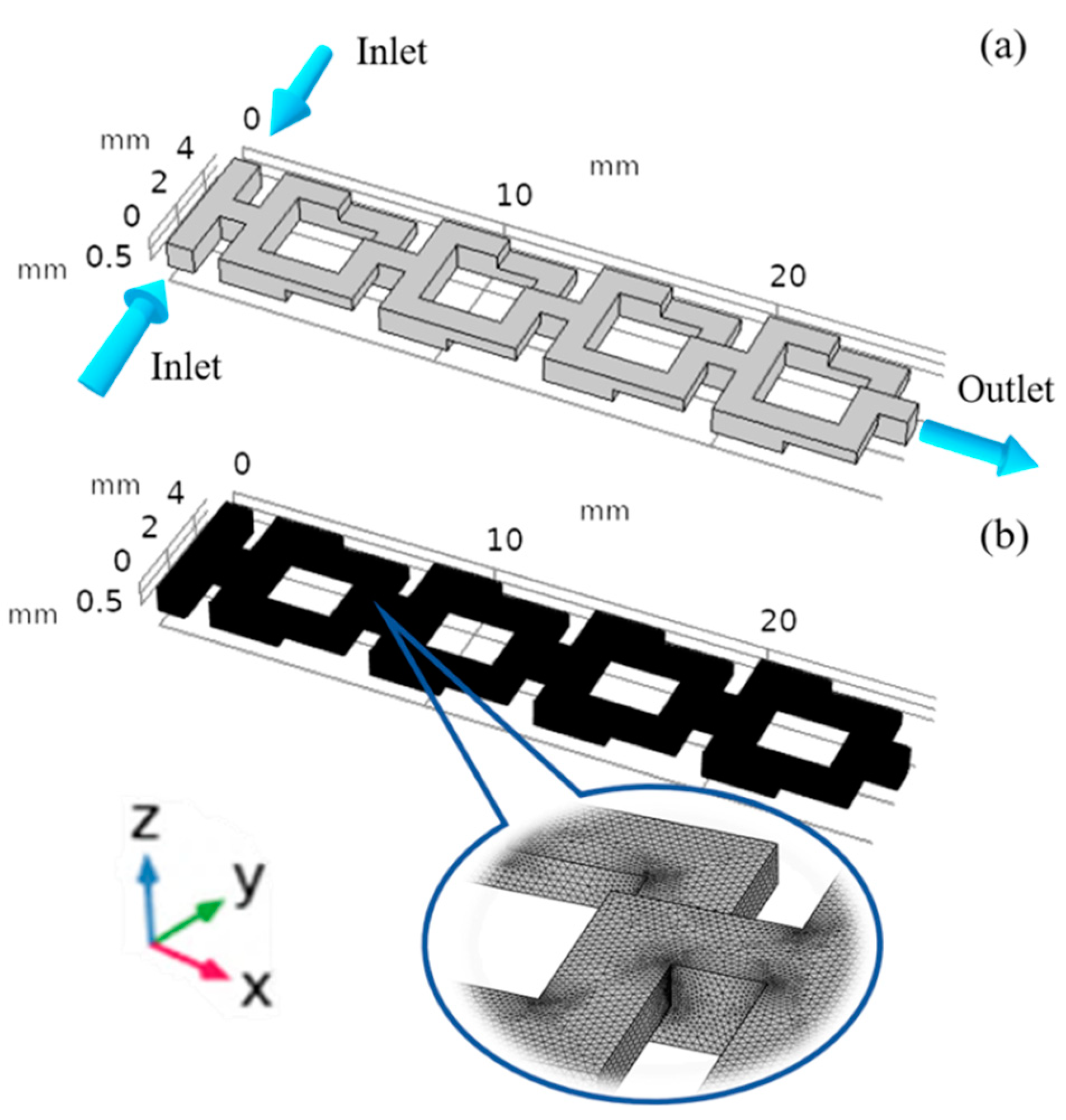
2.1. Fundamentals of Micromixer
2.2. Numerical Simulations
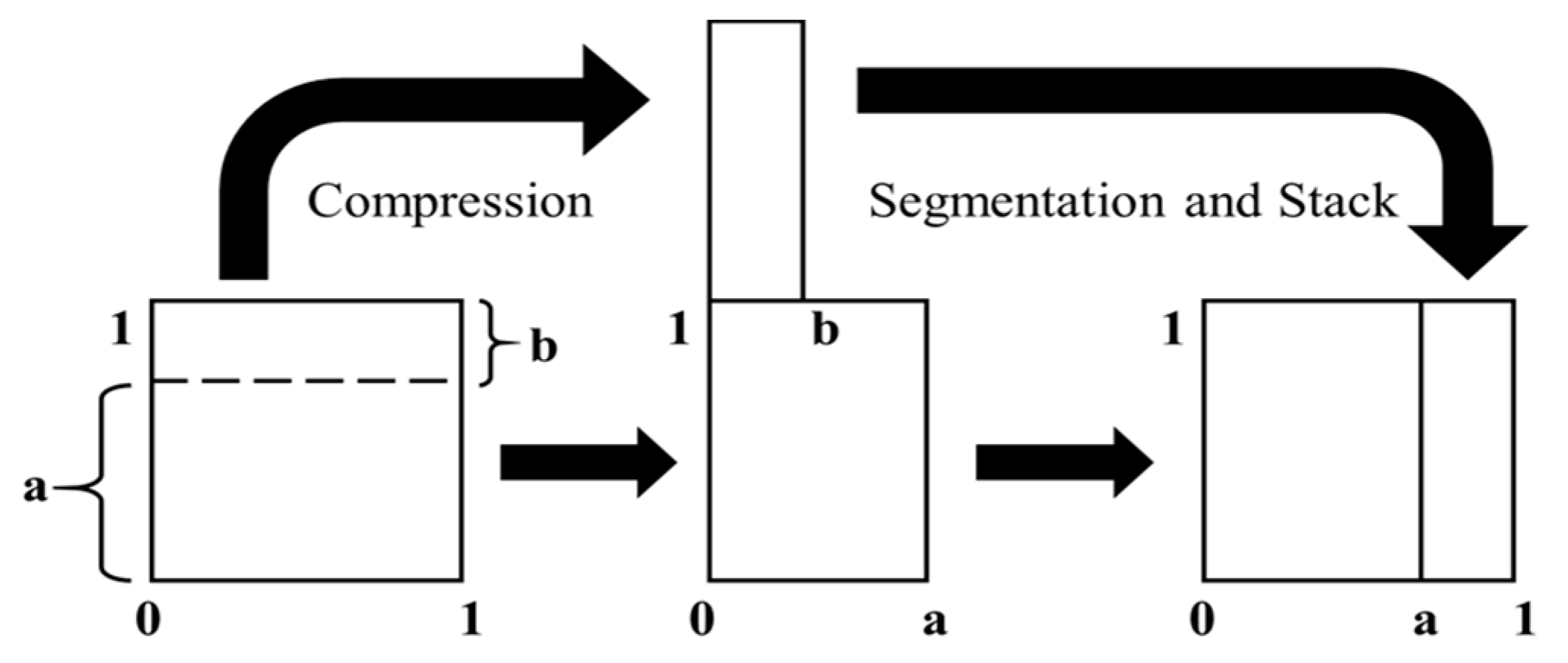
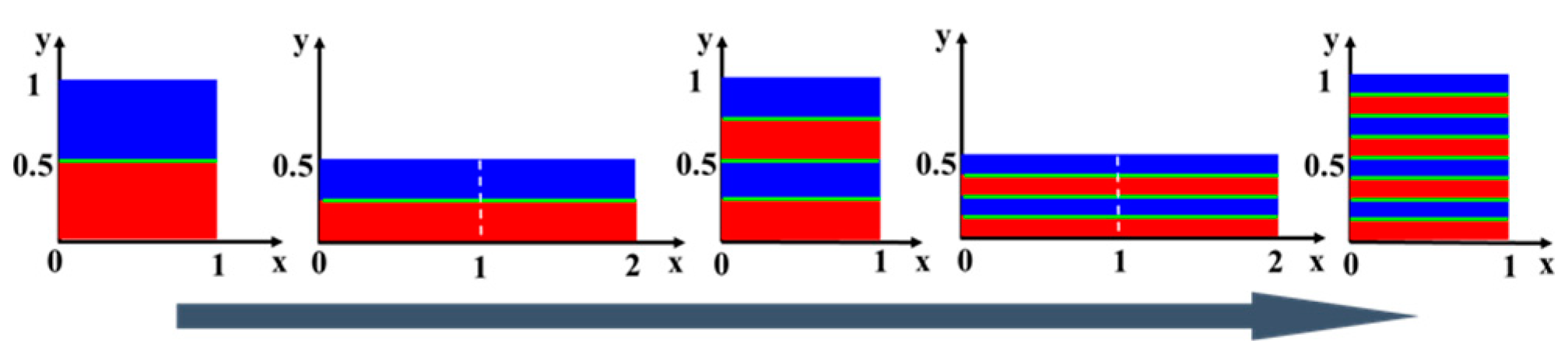
2.3. Proposed Method
3. Results and Discussion
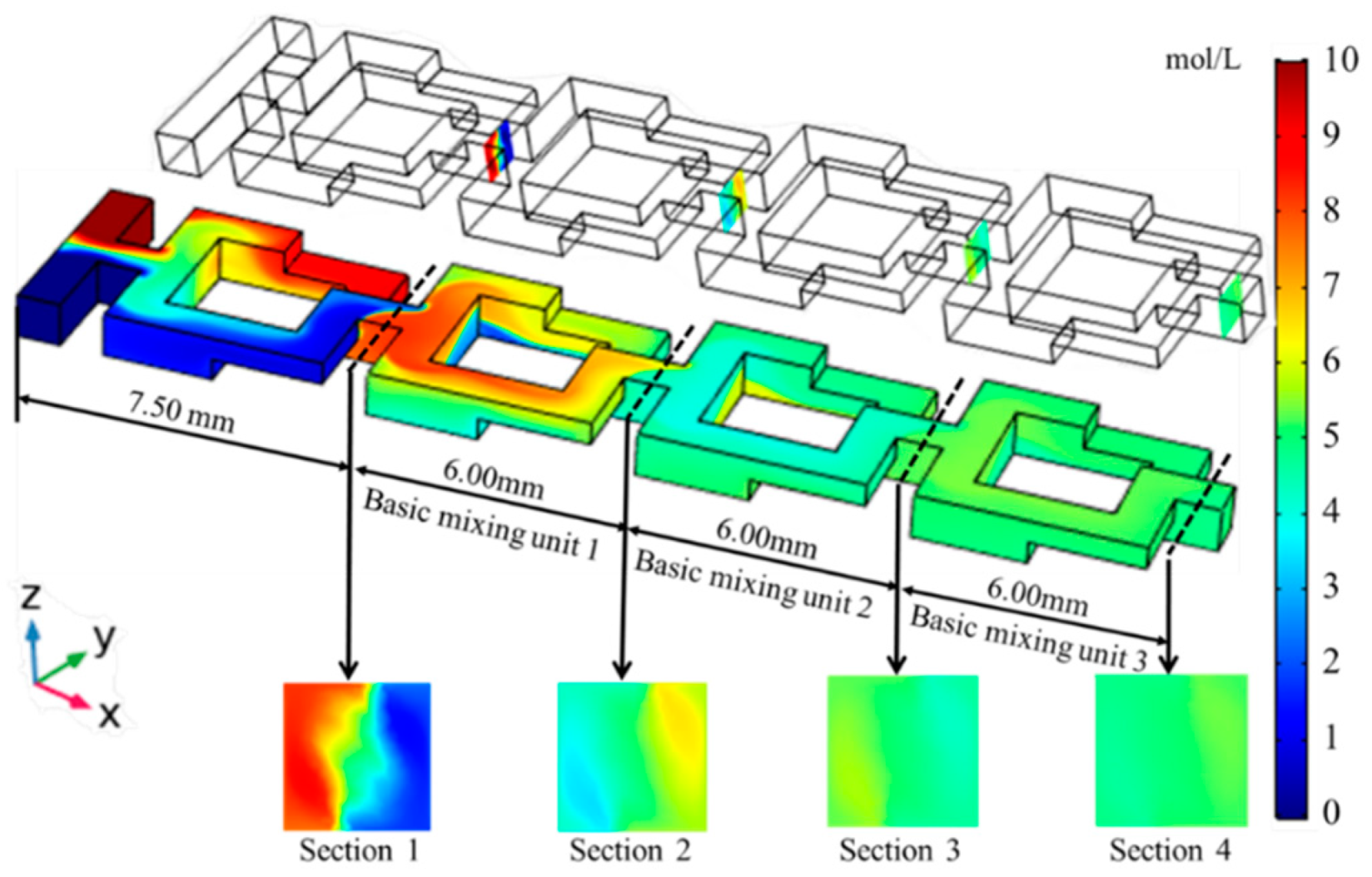
3.1. Mixing Performance of Basic Mixing Unit
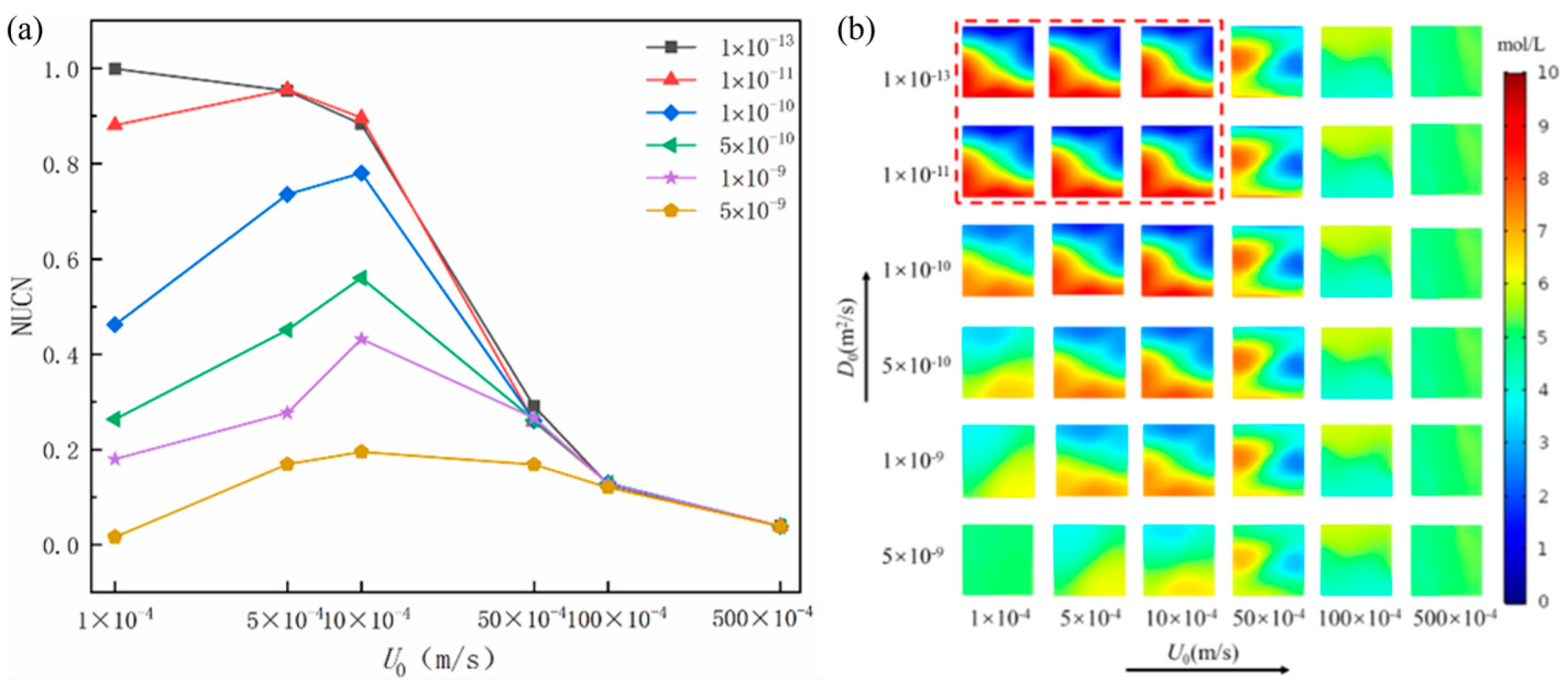
3.2. Effect of Diffusion Coefficient on Uniformity Coefficient
3.3. Effect of Initial Velocity on Uniformity Coefficient
4. Conclusions
- (1)
- The contribution of the basic mixing unit of the chaotic Baker pipeline to the whole fluid mixing process is studied by using the non-uniformity coefficient (NUC) method under various conditions (thirty-six cases in this study). The experimental results show that the optimal contribution ratio of the basic mixing unit is about 6:3:1 (calculated in turn along the fluid flow direction), which can provide theoretical guidance for the structural design of the millimeter mixer.
- (2)
- The effects of two parameters (initial velocity and diffusion coefficient) on the quality of the mixing state in the mixing process of liquid-liquid flow are investigated thoroughly, and the uniformity of the fluid concentration field under different experimental conditions is calculated. It is found that the highest mixing uniformity can be achieved when the initial velocity U0 = 0.05 m/s, and the diffusion coefficient D0 = 5 × 10−9 m2/s.
- (3)
- Based on image processing technology, under thirty-six different working conditions, it is analyzed from three dimensions: the contribution of the basic mixing unit of the chaotic Baker pipeline, the diffusion coefficient, and the influence of initial velocity on fluid mixing in the chaotic Baker pipeline. The experimental results show that the non-uniformity coefficient method can evaluate the characteristics of the macro mixing process and provide a method for directly measuring the uniformity of the macro mixing process. The statistical image analysis technique based on uniform design theory is illustrated to be reliable and effective in yielding accurate concentration field information of the simulated chaotic mixer. Meanwhile, it is also found that the quantification of the non-uniformity coefficient method can also amplify the difference.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Valdés, J.P.; Kahouadji, L.; Matar, O.K. Current advances in liquid-liquid mixing in static mixers: A review. Chem. Eng. Res. Des. 2022, 177, 694–731. [Google Scholar] [CrossRef]
- Chen, X.; Li, T. A novel passive micromixer designed by applying an optimization algorithm to the zigzag microchannel. Chem. Eng. J. 2017, 313, 1406–1414. [Google Scholar] [CrossRef]
- Li, X.; Jiang, F.; Ravindra, A.V.; Zhou, J.; Zhou, A.; Le, T.; Peng, J.; Ju, S. Mixing processes in a 3D printed large-flow microstructured reactor: Finite element simulations and experimental study. Chem. Eng. J. 2019, 370, 295–304. [Google Scholar] [CrossRef]
- Le The, H.; Le Thanh, H.; Dong, T.; Ta, B.Q.; Tran-Minh, N.; Karlsen, F. An effective passive micromixer with shifted trapezoidal blades using wide Reynolds number range. Chem. Eng. Res. Des. 2015, 93, 1–11. [Google Scholar] [CrossRef]
- Ruijin, W.; Beiqi, L.; Dongdong, S.; Zefei, Z. Investigation on the splitting-merging passive micromixer based on Baker’s transformation. Sens. Actuators B 2017, 249, 395–404. [Google Scholar] [CrossRef]
- Glatzel, T.; Litterst, C.; Cupelli, C.; Lindemann, T.; Moosmann, C.; Niekrawietz, R.; Streule, W.; Zengerle, R.; Koltay, P. Computational fluid dynamics (CFD) software tools for microfluidic applications—A case study. Comput. Fluids 2008, 37, 218–235. [Google Scholar] [CrossRef]
- Kim, D.S.; Lee, S.W.; Kwon, T.H.; Lee, S.S. A barrier embedded chaotic micromixer. J. Micromech. Microeng. 2004, 14, 798–805. [Google Scholar] [CrossRef]
- Han, Q.; Liu, Z.; Li, W. Enhanced thermal performance by spatial chaotic mixing in a saw-like microchannel. Int. J. Therm. Sci. 2023, 186, 108148. [Google Scholar] [CrossRef]
- Verma, R.K.; Ghosh, S. Two-phase flow in miniature geometries: Comparison of gas-liquid and liquid-liquid flows. ChemBioEng Rev. 2019, 6, 5–16. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Cheng, Y.; Zhang, W.; Li, K.; Wang, P.; Zhao, W. Mixing performance analysis of the novel passive micromixer designed by applying fuzzy grey relational analysis. Int. J. Heat Mass Transfer 2021, 178, 121638. [Google Scholar] [CrossRef]
- Okuducu, M.B.; Aral, M.M. Novel 3-D T-shaped passive micromixer design with helicoidal flows. Processes 2019, 7, 637. [Google Scholar] [CrossRef] [Green Version]
- Hossain, S.; Ansari, M.A.; Kim, K.Y. Evaluation of the mixing performance of three passive micromixers. Chem. Eng. J. 2009, 150, 492–501. [Google Scholar] [CrossRef]
- Mondal, B.; Mehta, K.S.; Patowari, K.P.; Pati, S. Numerical study of mixing in wavy micromixers: Comparison between raccoon and serpentine mixer. Chem. Eng. Process. 2019, 136, 44–61. [Google Scholar] [CrossRef]
- Zhang, J.; Dong, X.; Ma, H.; Li, X.; Feng, Y. Chaotic analysis of the concentration field in a submerged impinging stream mixer. Chem. Eng. Technol. 2015, 38, 1530–1536. [Google Scholar] [CrossRef]
- Yang, K.; Liu, J.; Wang, M.; Wang, H.; Xiao, Q. Identifying flow patterns in a narrow channel via feature extraction of conductivity measurements with a support vector machine. Sensors 2023, 23, 1907. [Google Scholar] [CrossRef]
- Ding, S.L.; Song, E.Z.; Yang, L.P.; Litak, G.; Wang, Y.Y.; Yao, C.; Ma, X.Z. Analysis of chaos in the combustion process of premixed natural gas engine. Appl. Therm. Eng. 2017, 121, 768–778. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, K.; Li, M.; Xiao, Q.; Wang, H. Enhancement of solid-liquid mixing state quality in a stirred tank by cascade chaotic rotating speed of main shaft. Powder Technol. 2022, 397, 117020. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, K.; Li, M.; Xiao, Q.; Wang, H. Experimental investigation on the uniformity optimization and chaos characterization of gas-liquid two-phase mixing process using statistical image analysis. Adv. Powder Technol. 2021, 32, 1627–1640. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, K.; Li, M.; Xiao, Q.; Wang, H. Chaotic characterization of macromixing effect in a gas-liquid stirring system using modified 0-1 test. Can. J. Chem. Eng. 2022, 100, 261–275. [Google Scholar] [CrossRef]
- Yuan, S.; Zhou, M.; Peng, T.; Peng, T.; Li, Q.; Jiang, F. An investigation of chaotic mixing behavior in a planar microfluidic mixer. Phys. Fluids 2022, 34, 032007. [Google Scholar] [CrossRef]
- Zhang, K.; Guo, S.; Zhao, L.; Zhao, X.; Chan, H.L.; Wang, Y. Realization of planar mixing by chaotic velocity in microfluidics. Microelectron. Eng. 2011, 88, 959–963. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chang, C.L.; Wang, Y.N.; Fu, L.M. Microfluidic mixing: A review. Int. J. Mol. Sci. 2011, 12, 3263–3287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, D.; Zhang, S. A contraction-expansion helical mixer in the laminar regime. Chin. J. Chem. Eng. 2014, 22, 261–266. [Google Scholar] [CrossRef]
- Adam, T.; Hashim, U. Design and fabrication of micro-mixer with short turns angles for self-generated turbulent structures. Microsyst. Technol. 2016, 22, 433–440. [Google Scholar] [CrossRef]
- Yang, J.; Breault, R.W.; Rowan, S.L. Applying image processing methods to study hydrodynamic characteristics in a rectangular spouted bed. Chem. Eng. Sci. 2018, 188, 238–251. [Google Scholar] [CrossRef]
- Rivera, F.F.; Hidalgo, P.E.; Castañeda-Záldivar, F.; Terol-Villalobos, I.R.; Orozco, G. Phenomenological behavior coupling hydrodynamics and electrode kinetics in a flow electrochemical reactor. Numerical analysis and experimental validation. Chem. Eng. J. 2019, 355, 457–469. [Google Scholar] [CrossRef]
- Li, J.; Agarwal, R.K.; Zhou, L.; Yang, B. Investigation of a bubbling fluidized bed methanation reactor by using CFD-DEM and approximate image processing method. Chem. Eng. Sci. 2019, 207, 1107–1120. [Google Scholar] [CrossRef]
- Bai, W.; Chu, D.; He, Y. Bubble characteristic of carbon nanotubes growth process in a tapered fluidized bed reactor without a distributor. Chem. Eng. J. 2021, 407, 126792. [Google Scholar] [CrossRef]
- Soleimanian, N.; Akhtarpour, A. A new method for estimating pollutant concentration in unsaturated soil using digital image processing technique. J. Phys. Conf. Ser. 2021, 1973, 012204. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, X.; Li, M.; Xiao, Q.; Wang, H. Measurement of mixing time in a gas-liquid mixing system stirred by top-blown air using ECT and image analysis. Flow Meas. Instrum. 2022, 84, 102143. [Google Scholar] [CrossRef]
- Han, B.; Sun, Z.; Zhu, J.; Fu, Z.; Kong, X.; Barghi, S. Bubble dynamics in 2-D gas-solid fluidized bed with Geldart A or Geldart B particles by image processing method. Can. J. Chem. Eng. 2022, 100, 3588–3599. [Google Scholar] [CrossRef]
- Mouza, A.A.; Patsa, C.M.; Schönfeld, F. Mixing performance of a chaotic micro-mixer. Chem. Eng. Res. Des. 2008, 86, 1128–1134. [Google Scholar] [CrossRef]
- Sui, Y.; Teo, C.J.; Lee, P.S. Direct numerical simulation of fluid flow and heat transfer in periodic wavy channels with rectangular cross-sections. Int. J. Heat Mass Transfer 2012, 55, 73–88. [Google Scholar] [CrossRef]
- Zhang, H.N.; Li, F.C.; Cao, Y.; Tomoaki, K.; Yu, B. Direct numerical simulation of elastic turbulence and its mixing-enhancement effect in a straight channel flow. Chin. Phys. B 2013, 22, 024703. [Google Scholar] [CrossRef]
- Cai, W.H.; Li, Y.Y.; Zhang, H.N.; Li, Y.K.; Cheng, J.P.; Li, X.B.; Li, F.C. An efficient micro-mixer by elastic instabilities of viscoelastic fluids: Mixing performance and mechanistic analysis. Int. J. Heat Fluid Flow 2018, 74, 130–143. [Google Scholar] [CrossRef]
- Jost AM, D.; Glockner, S.; Erriguible, A. Direct numerical simulations of fluids mixing above mixture critical point. J. Supercrit. Fluids 2020, 165, 104939. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhai, Y.; Lv, Z.; Xu, J.; Pan, J.; Wang, H. Non-uniformity quantification of temperature and concentration fields by statistical measure and image analysis. Appl. Therm. Eng. 2017, 124, 1134–1141. [Google Scholar] [CrossRef] [Green Version]
- Ju, Y.; Wu, L.; Li, M.; Xiao, Q.; Wang, H. A novel hybrid model for flow image segmentation and bubble pattern extraction. Measurement 2022, 192, 110861. [Google Scholar] [CrossRef]
- Yang, K.; Wang, Y.; Li, M.; Li, X.; Wang, H.; Xiao, Q. Modeling topological nature of gas–liquid mixing process inside rectangular channel using RBF-NN combined with CEEMDAN-VMD. Chem. Eng. Sci. 2023, 267, 118353. [Google Scholar] [CrossRef]
- Wang, R.; Lin, J.; Li, H. Chaotic mixing on a micromixer with barriers embedded. Chaos Solitons Fractals 2007, 33, 1362–1366. [Google Scholar] [CrossRef]
- Pishkoo, A.; Darus, M. Using fractal calculus to solve fractal Navier–Stokes equations, and simulation of laminar static mixing in COMSOL multiphysics. Fractal Fract. 2021, 5, 16. [Google Scholar] [CrossRef]
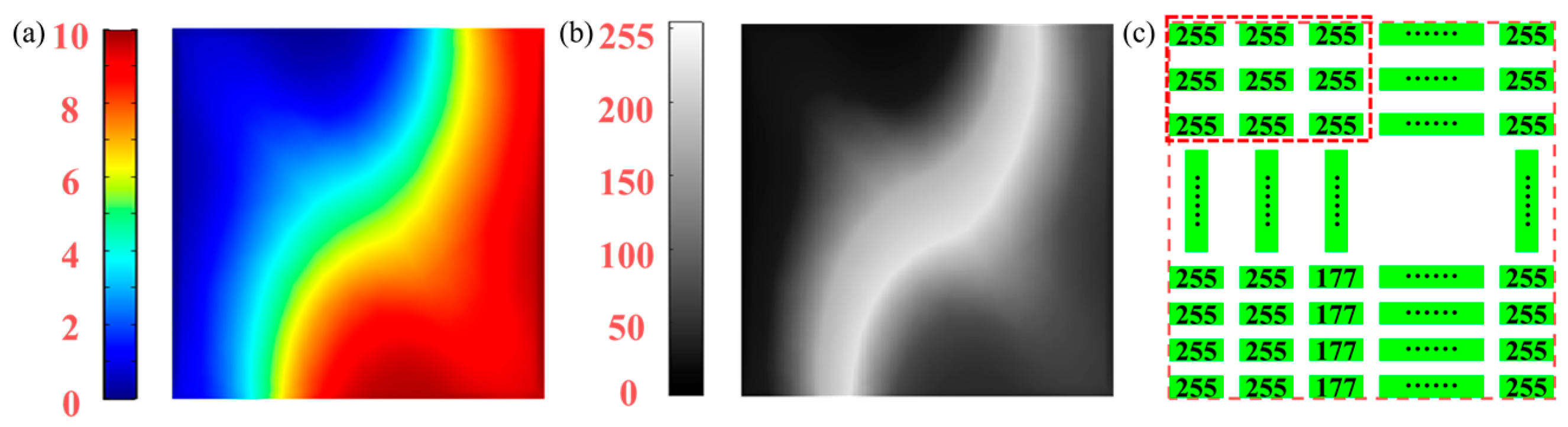
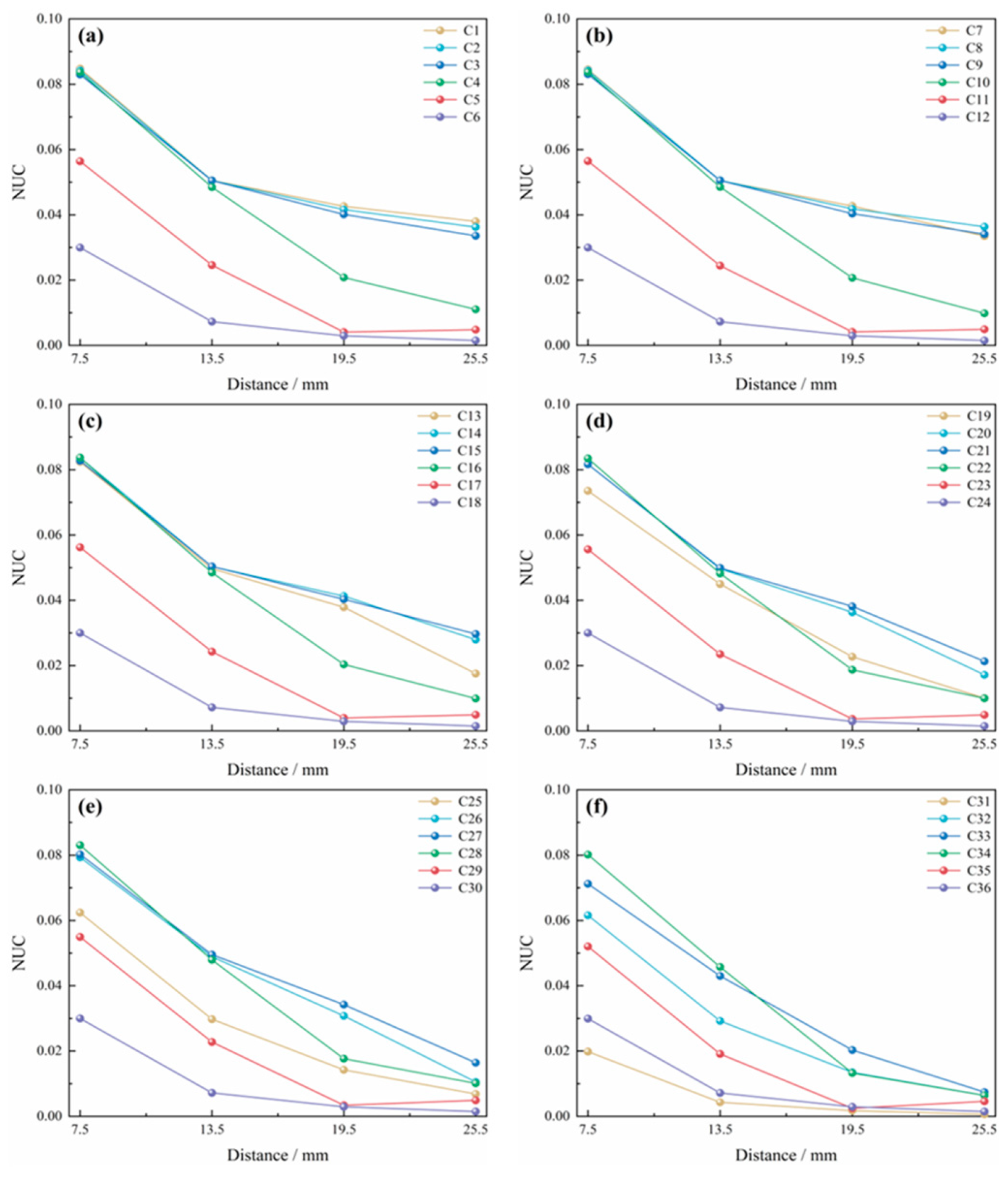

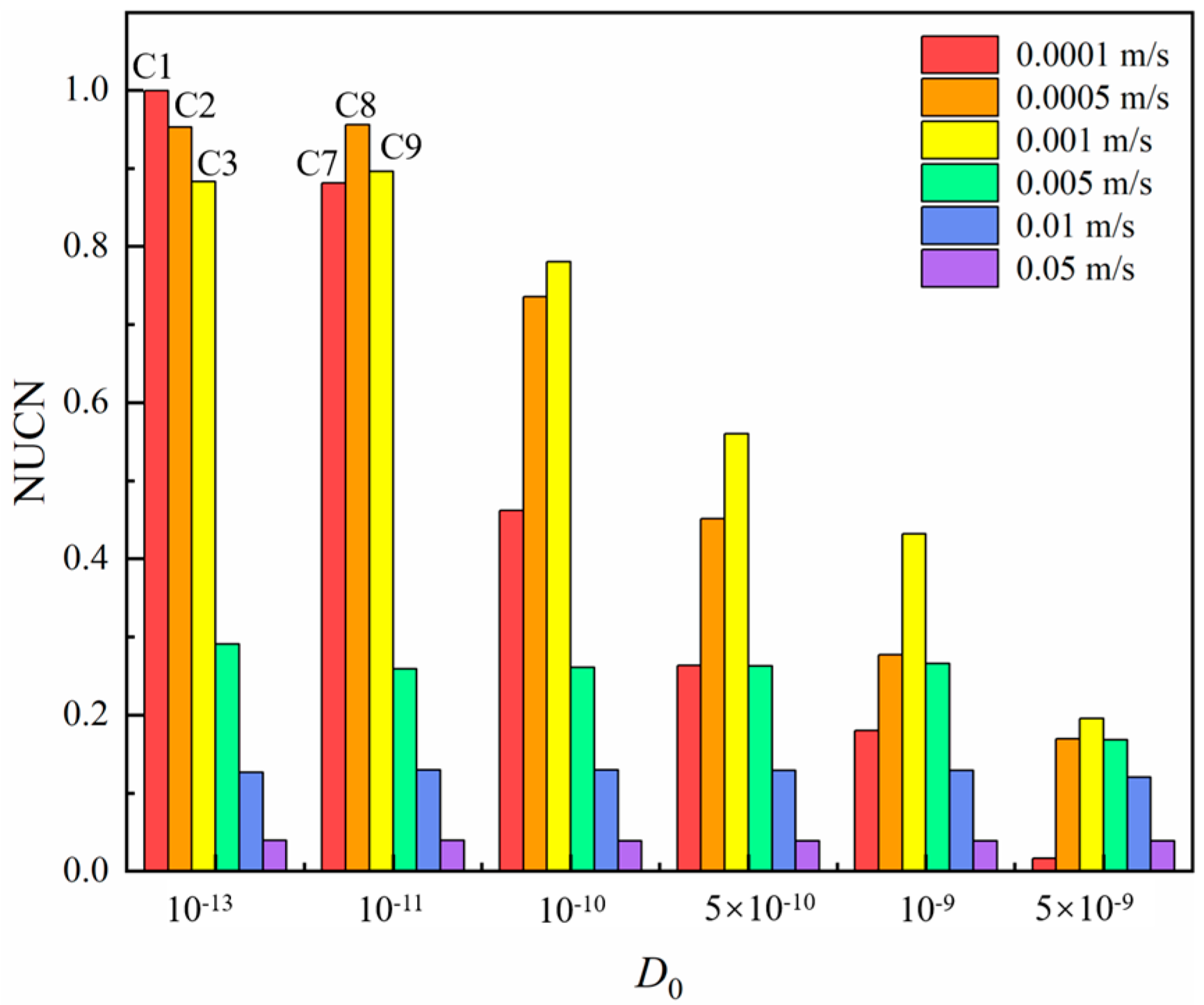
| D0 (m2/s) | 10−13 | 10−11 | 10−10 | 5 × 10−10 | 10−9 | 5 × 10−9 | |
|---|---|---|---|---|---|---|---|
| U0 (m/s) | |||||||
| 0.0001 | C1 | C7 | C13 | C19 | C25 | C31 | |
| 0.0005 | C2 | C8 | C14 | C20 | C26 | C32 | |
| 0.001 | C3 | C9 | C15 | C21 | C27 | C33 | |
| 0.005 | C4 | C10 | C16 | C22 | C28 | C34 | |
| 0.01 | C5 | C11 | C17 | C23 | C29 | C35 | |
| 0.05 | C6 | C12 | C18 | C24 | C30 | C36 | |
| D0 (m2/s) | 10−13 | 10−11 | 10−10 | 5 × 10−10 | 10−9 | 5 × 10−9 | |
|---|---|---|---|---|---|---|---|
| U0 (m/s) | |||||||
| 0.0001 | 0.037971 | 0.033478 | 0.017556 | 0.010015 | 0.006837 | 0.000621 | |
| 0.0005 | 0.03621 | 0.036321 | 0.027941 | 0.017137 | 0.010518 | 0.006425 | |
| 0.001 | 0.033552 | 0.034063 | 0.029661 | 0.021283 | 0.016404 | 0.007419 | |
| 0.005 | 0.011038 | 0.009832 | 0.009909 | 0.009972 | 0.010109 | 0.00639 | |
| 0.01 | 0.004801 | 0.004916 | 0.004928 | 0.004904 | 0.004889 | 0.00457 | |
| 0.05 | 0.00149 | 0.001486 | 0.001474 | 0.001473 | 0.001472 | 0.001464 | |
| D0 (m2/s) | 10−13 | 10−11 | 10−10 | 5 × 10−10 | 10−9 | 5 × 10−9 | |
|---|---|---|---|---|---|---|---|
| U0 (m/s) | |||||||
| 0.0001 | 0.999242 | 0.881013 | 0.461991 | 0.263553 | 0.179908 | 0.016349 | |
| 0.0005 | 0.952899 | 0.955803 | 0.735291 | 0.450962 | 0.276799 | 0.16908 | |
| 0.001 | 0.88296 | 0.896383 | 0.780565 | 0.560092 | 0.431693 | 0.195229 | |
| 0.005 | 0.290462 | 0.258744 | 0.260774 | 0.262412 | 0.26603 | 0.168155 | |
| 0.01 | 0.126348 | 0.129364 | 0.129679 | 0.129055 | 0.128658 | 0.120262 | |
| 0.05 | 0.039211 | 0.039103 | 0.039792 | 0.038756 | 0.038727 | 0.038516 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Yang, K.; Wang, H.; Wu, J.; Xiao, Q. Statistical Image Analysis on Liquid-Liquid Mixing Uniformity of Micro-Scale Pipeline with Chaotic Structure. Energies 2023, 16, 2045. https://doi.org/10.3390/en16042045
Wang H, Yang K, Wang H, Wu J, Xiao Q. Statistical Image Analysis on Liquid-Liquid Mixing Uniformity of Micro-Scale Pipeline with Chaotic Structure. Energies. 2023; 16(4):2045. https://doi.org/10.3390/en16042045
Chicago/Turabian StyleWang, Haotian, Kai Yang, Hua Wang, Jingyuan Wu, and Qingtai Xiao. 2023. "Statistical Image Analysis on Liquid-Liquid Mixing Uniformity of Micro-Scale Pipeline with Chaotic Structure" Energies 16, no. 4: 2045. https://doi.org/10.3390/en16042045
APA StyleWang, H., Yang, K., Wang, H., Wu, J., & Xiao, Q. (2023). Statistical Image Analysis on Liquid-Liquid Mixing Uniformity of Micro-Scale Pipeline with Chaotic Structure. Energies, 16(4), 2045. https://doi.org/10.3390/en16042045







