Pore Structure Evolution in Sandstone of Underground Gas Storage during Cyclic Injection and Production Based on Nuclear Magnetic Resonance Technology
Abstract
:1. Introduction
2. NMR-Based Pore Structure Analytical Method and Classification of Clastic Reservoir
2.1. NMR-Based Pore Structure Analytical Method
2.2. Classification of Clastic Reservoirs Based on Pore Throat Characteristics
3. Physical and Mechanical Properties of Specimen
3.1. Mineralogy and Micro-Structure Characteristics
3.2. Stress Sensitivity of Permeability in Medium Porosity Sandstone
4. Experimental Set-Up
4.1. NMR Experimental System and Rock Preparation
4.2. Experimental Conditions
5. Results and Discussion
5.1. Pore Size Distribution Based on High-Pressure Mercury Tests
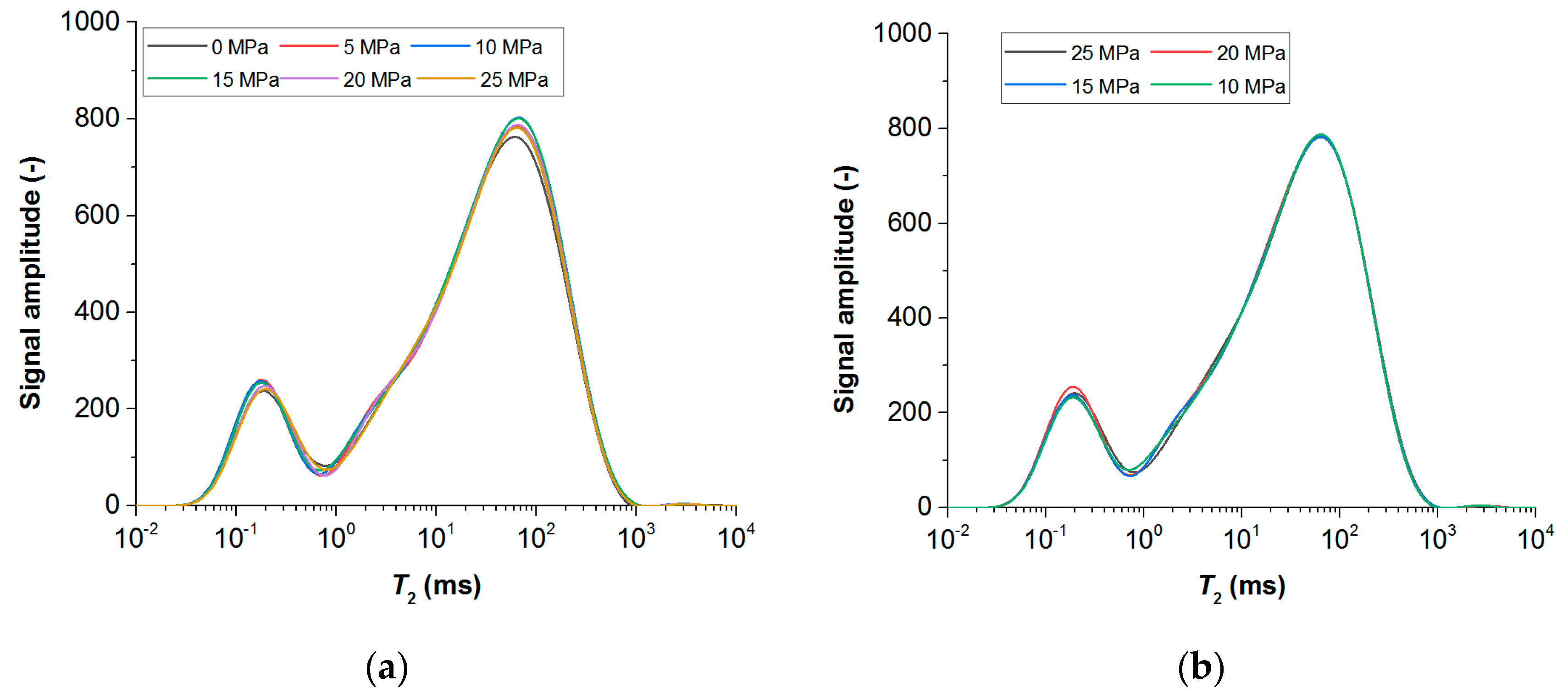
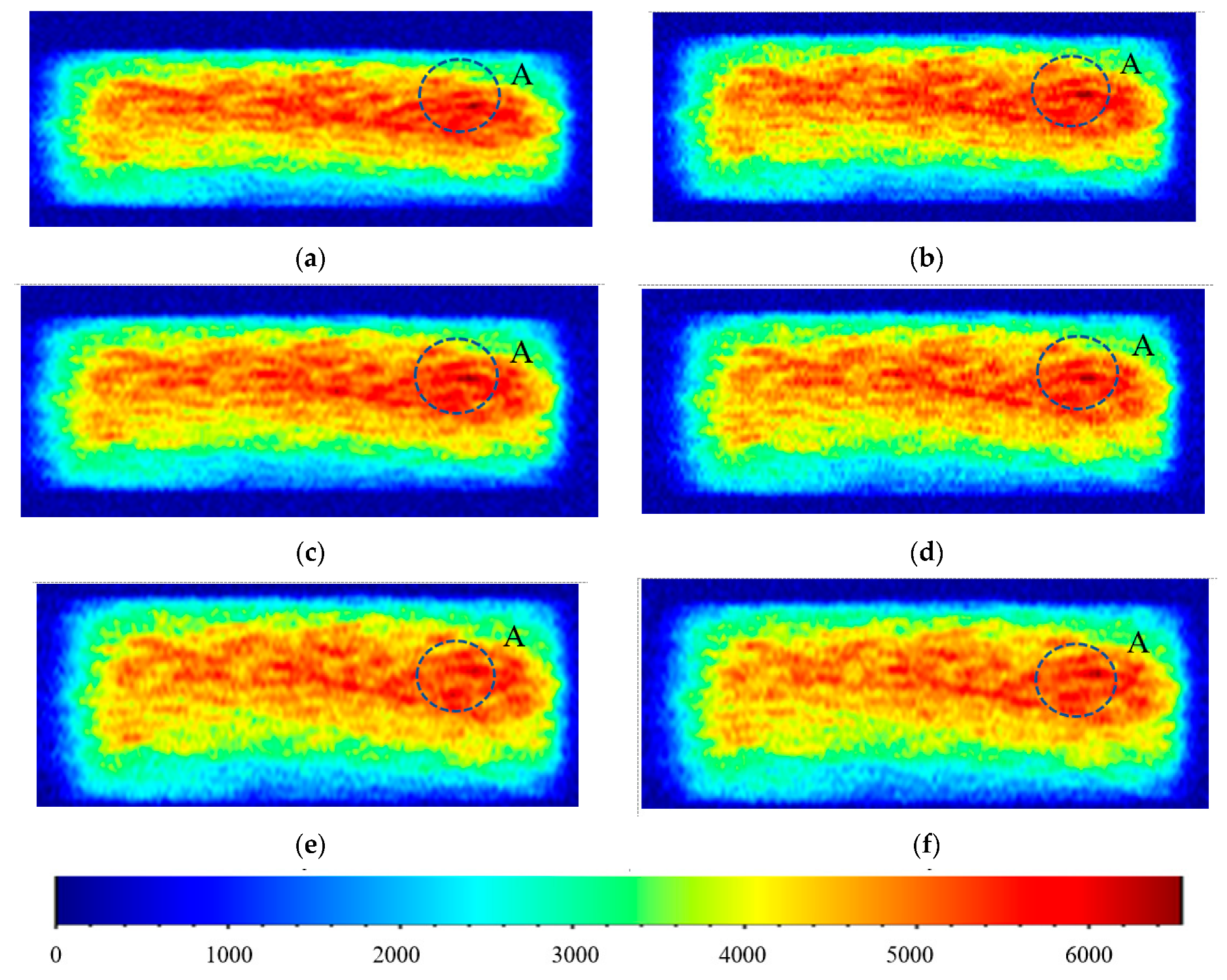
5.2. Peak Area and T2 Spectrum Variation in NMR Data
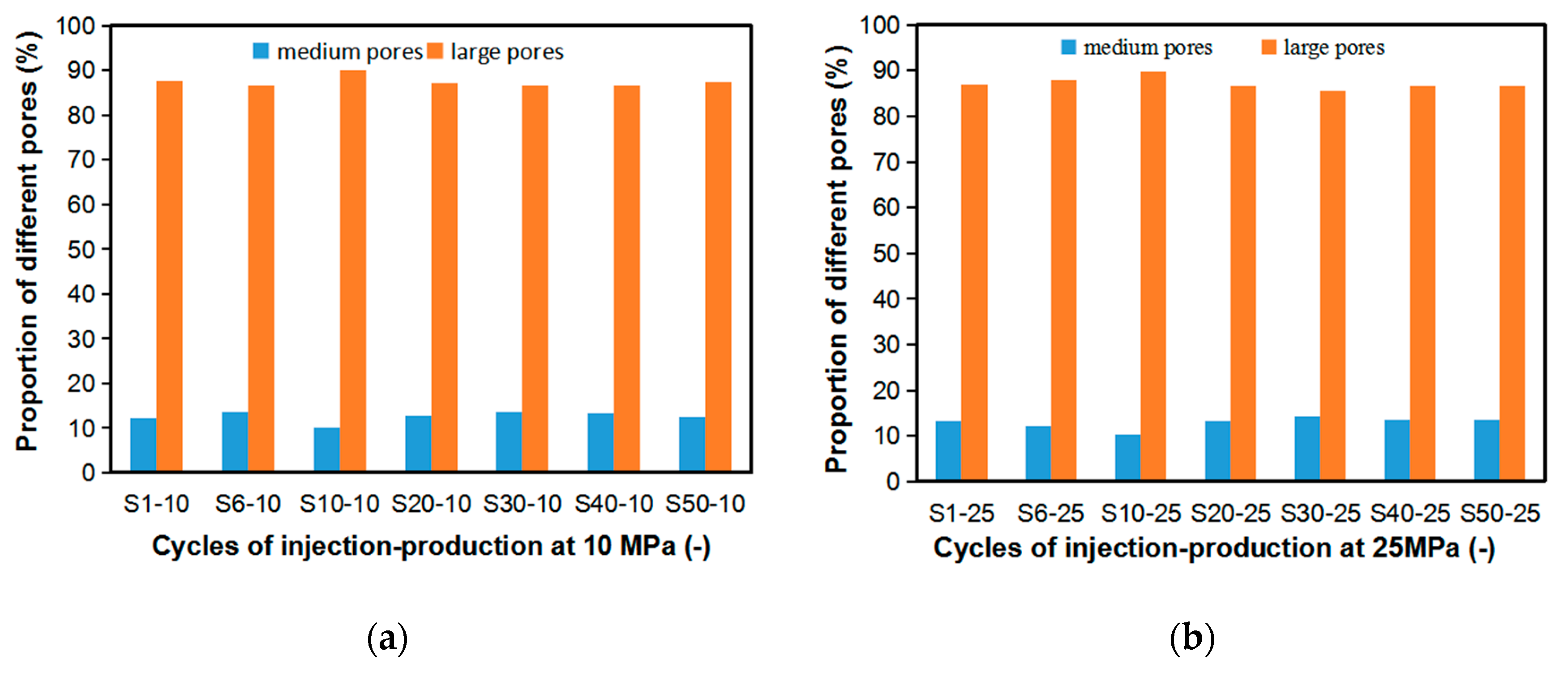
5.3. Proportion of Different Types of Pores under Different Cycles of Injection and Production
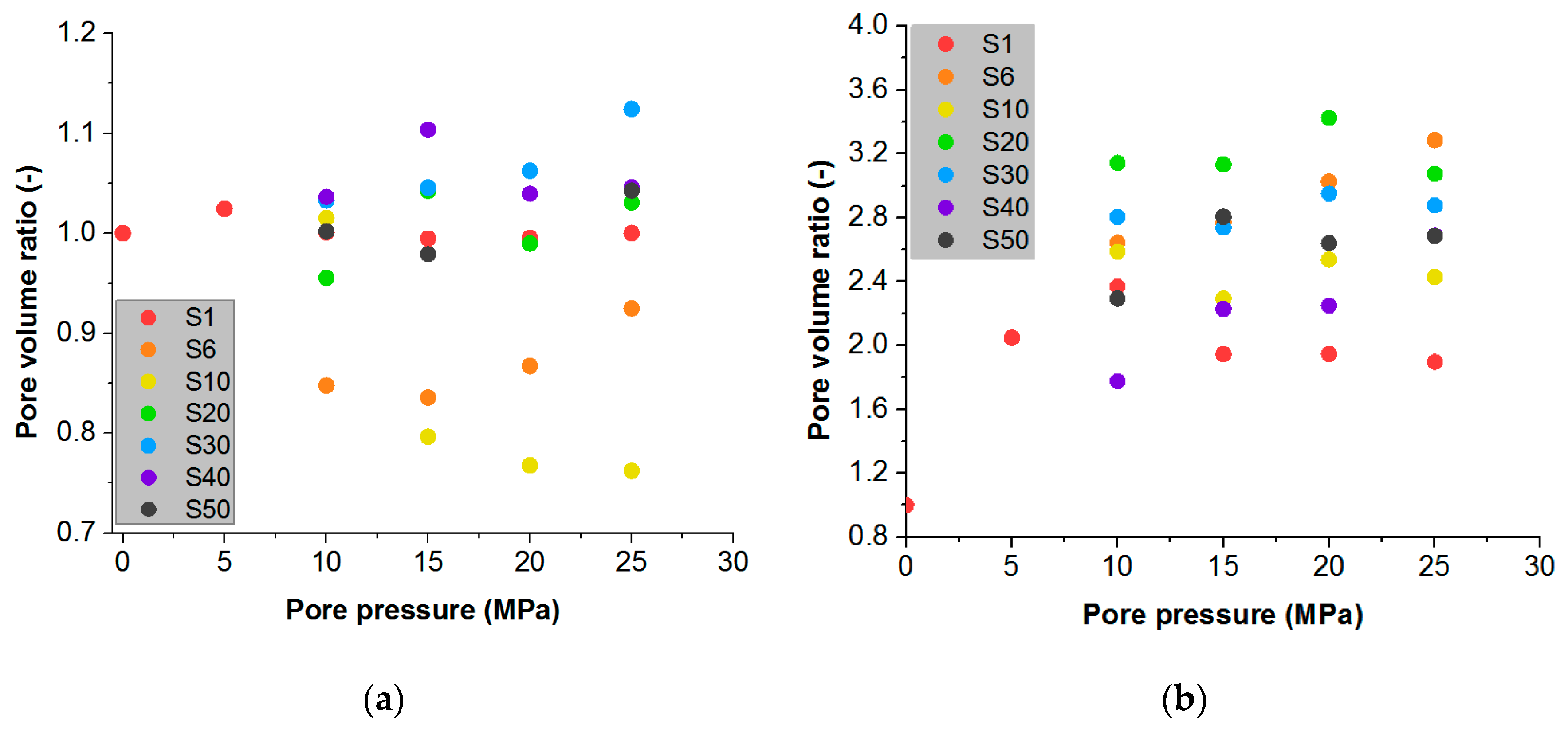
5.4. Rock Damage Evaluation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Losson, L. Underground gas storage in the world-2022 status. CEDIGAZ Rep. 2022, 45. Available online: https://www.cedigaz.org/wp-content/uploads (accessed on 19 February 2023).
- Wang, C.; Liu, X.; Wang, H.; Li, Y. Research on sealing performance of special thread of tubing under complex load. J. Phys. Conf. Ser. 2022, 2230, 012034. [Google Scholar] [CrossRef]
- Shao, J.; You, L.; Kang, Y.; Gao, X.; Chen, M.; Meng, S.; Zhang, N. Experimental study on stress sensitivity of underground gas storage. J Petrol. Sci. Eng. 2020, 195, 107577. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, X. Sealing capability evaluation and study of operation optimization of one natural gas storage in North China. In Proceedings of the International Petroleum and Petrochemical Technology Conference, Beijing, China, 27–29 March 2019; pp. 343–350. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Xu, S.; Li, C.; Wang, J.; He, R.; Wang, S.; Liu, J.; Xie, J.; Zhang, J. Change mechanism of pore structure and filling efficiency during injection production of sandstone underground gas storage. J. Nat. Gas Sci. Eng. 2022, 97, 104366. [Google Scholar] [CrossRef]
- Francus, P. An image-analysis technique to measure grain-size variation in thin sections of soft clastic sediments. Sediment. Geol. 1998, 121, 289–298. [Google Scholar] [CrossRef]
- Welch, N.; Gray, F.; Butcher, A.; Boek, E.; Crawshaw, J. High-resolution 3D FIB-SEM image analysis and validation of numerical simulations of nanometre scale porous ceramic with comparisons to experimental results. Transp. Porous Media 2017, 118, 373–392. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Shi, Y.; Fang, Z.; Liu, J.; Zhang, L.; Tong, R. Seepage characteristics of thermally and chemically treated Mesozoic granite from geothermal region of Liaodong Peninsula. Envion. Earth Sci. 2021, 80, 599. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Y.; Wang, J.; Zeng, Q. Pore structure damages in cement-based materials by mercury intrusion: A non-destructive assessment by X-ray computed tomography. Materials 2019, 12, 2220. [Google Scholar] [CrossRef] [Green Version]
- Faisal, T.F.; Awedalkarim, A.; Chevalier, S.; Jouini, M.S.; Sassi, M. Direct scale comparison of numerical linear elastic moduli with acoustic experiments for carbonate rock X-ray CT scanned at multi-resolutions. J. Petrol. Sci. Eng. 2017, 152, 653–663. [Google Scholar] [CrossRef]
- Xu, L.; Li, Q.; Myers, M.; Chen, Q.; Li, X. Application of nuclear magnetic resonance technology to carbon capture, utilization and storage: A review. J. Rock Mech. Geotech. 2019, 11, 892–908. [Google Scholar] [CrossRef]
- Gane, P.A.C.; Ridgway, C.J.; Lehtinen, E. Comparison of NMR cryoporometry, mercury intrusion porosimetry, and DSC thermoporosimetry in characterizing pore size distributions of compressed finely ground calcium carbonate structures. Ind. Eng. Chem. Res. 2004, 43, 7920–7927. [Google Scholar] [CrossRef]
- Coates, G.R.; Xiao, L.; Prammer, M.G. NMR Logging Principles and Applications; Gulf Professional Publishing: Houston, TX, USA, 1999. [Google Scholar]
- Mitchell, J.; Gladden, L.F.; Chandrasekera, T.C. Low-field permanent magnets for industrial process and quality control. Prog. Nucl. Magn. Reson. Spectrosc. 2014, 76, 1–60. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Liu, D. Comparison of low-field NMR and mercury intrusion porosimetry in characterizing pore size distributions of coals. Fuel 2012, 95, 152–158. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, H.; Weng, L.; Liu, Q.; Shen, J. Investigations on the seepage characteristics of fractured sandstone based on NMR real-time imaging. Ch. J. Rock Mech. Eng. 2021, 40, 263–275. [Google Scholar] [CrossRef]
- Kenyon, W.; Day, P.; Straley, C.; Willemsen, J. A three-part study of NMR longitudinal relaxation properties of water-saturated sandstones. SPE Form. Eval. 1988, 3, 622–636. [Google Scholar] [CrossRef]
- Bu, T.; Cao, T. Study of pore structure and seepage characteristics of Shaximiao formation reservoir in ZJ gas field. J. Mineral. Petrol. 2018, 38, 104–112. [Google Scholar] [CrossRef]
- Bencsik, M.; Ramanathan, C. Direct measurement of porous media local hydrodynamical permeability using gas MRI. Magn. Reson. Imaging 2001, 19, 379–383. [Google Scholar] [CrossRef]
- Baldwin, B.A.; Yamanashi, W.S. Detecting fluid movement and isolation in reservoir core with medical NMR imaging techniques. SPE Reserv. Eng. 1989, 4, 207–212. [Google Scholar] [CrossRef]
- Bai, S.; Cheng, D.; Wan, J.; Yang, L.; Peng, H.; Guo, X.; Zeng, J. Quantitative characterization of sandstone NMR T2 spectrum. Acta Petrol. Sin. 2016, 37, 382–391, 414. (In Chinese) [Google Scholar] [CrossRef]
- Wang, S. The Evolution of Sandstone Pore Size under Different Pressures Based on NMR. Master’s Thesis, China University of Mining and Technology, Beijing, China, 2020. (In Chinese). [Google Scholar] [CrossRef]
- Almenningen, S.; Roy, S.; Hussain, A.; Seland, J.G.; Ersland, G. Effect of mineral composition on transverse relaxation time distributions and MR imaging of tight rocks from offshore Ireland. Minerals 2020, 10, 232. [Google Scholar] [CrossRef] [Green Version]
- Ge, X.; Myers, M.T.; Liu, J.; Fan, Y.; Zahid, M.; Zhao, J.; Hathon, L. Determing the transverse surface relaxivity of reservoir rocks: A critical review and perspective. Mar. Petrol. Geol. 2021, 126, 104934. [Google Scholar] [CrossRef]
- Keating, K.; Knight, R. A laboratory study to determine the effect of iron oxides on proton NMR measurements. Geophysics 2007, 72, 27–32. [Google Scholar] [CrossRef]
- Jaeger, F.; Bowe, S.; Van As, H.; Schaumann, G.E. Evaluation of 1H NMR relaxometry for the assessment of pore-size distribution in soil samples. Eur. J. Soil Sci. 2009, 60, 1052–1064. [Google Scholar] [CrossRef]
- Stingaciu, L.; Weihermüller, L.; Haber-Pohlmeier, S.; Stapf, S.; Vereecken, H.; Pohlmeier, A. Determination of pore size distribution and hydraulic properties using nuclear magnetic resonance relaxometry: A comparative study of laboratory methods. Water Resour. Res. 2010, 46, W11510. [Google Scholar] [CrossRef] [Green Version]
- Kleinberg, R.L.; Horsfield, M.A. Transverse relaxation processes in porous sedimentary rock. J. Mang. Reson. 1990, 88, 9–19. [Google Scholar] [CrossRef]
- Rouquerol, J.; Avnir, D.; Fairbridge, C.W.; Everett, D.H.; Haynes, J.H.; Pernicone, N.; Ramsay, J.D.F.; Sing, K.S.W.; Unger, K. Recommendations for the characterization of porous solids, International Union of pure and applied chemistry. Pure Appl. Chem. 1994, 68, 1739–1758. [Google Scholar] [CrossRef]
- Chalmers, G.R.L.; Bustin, R.M.; Power, I. Characterization of gas shale pore systems by porosimetry, pycnometry, surface area, and field emission scanning electron microscopy/transmission electron microscopy image analyses: Examples from the Barnett, Woodford, Haynesville, Marcellus, and Doig units. AAPG Bull. 2012, 96, 1099–1119. [Google Scholar] [CrossRef]
- Chalmers, G.R.L.; Bustin, R.M. Porosity and pore size distribution of deeply-buried fine-grained rocks: Influence of diagenetic and metamorphic processes on shale reservoir quality and exploration. J. Unconv. Oil Gas Resour. 2015, 12, 134–142. [Google Scholar] [CrossRef]
- Li, J.; Kaunda, R.; Zhou, K. Experimental investigations on the effects of ambient freeze-thaw cycling on dynamic properties and rock pore structure deterioration of sandstone. Cold Regions Sci. Technol. 2018, 154, 133–141. [Google Scholar] [CrossRef]
- Wang, J.; Shi, L.; Zhang, Y.; Zhang, K.; Li, C.; Chen, X.; Sun, J.; Qiu, X. Simulation of petroleum phase behavior in injection and production process of underground gas storage in a gas reservoir. Petrol. Explor. D 2022, 49, 1386–1397. [Google Scholar] [CrossRef]
- Li, J.; Meng, L.; Fu, X.; Jin, Y.; Jiang, M.; Liu, C. Analysis of efficient operation conditions of the Shuang 6 gas storage in Shuangtaizi oilfield, Liaohe Basin. China. Arab. J. Geosci. 2022, 15, 1486. [Google Scholar] [CrossRef]
- Ni, X.; Chen, Z.; Wang, P.; Wu, J.; Wu, Y.; Gong, P. Experimental investigation of the influence of differential stress, confining pressure and strain on aquifer sandstone permeability. Eur. J. Environ. Civ. Eng. 2020, 24, 915–930. [Google Scholar] [CrossRef]
- Hoseini, M.; Bindiganavile, V.; Banthia, N. The effect of mechanical stress on permeability of concrete: A review. Cem. Concr. Compos. 2009, 31, 213–220. [Google Scholar] [CrossRef]
- Zhou, J.P.; Deng, G.R.; Tian, S.F.; Xian, X.F.; Yang, K.; Zhang, C.P.; Dong, Z.Q. Experimental study on the permeability variation of sandstone at cyclic stress: Implication for underground gas storage. J. Energy Storage 2023, 60, 106677. [Google Scholar] [CrossRef]









| Class I | Class II | Class III | Class IV | |
|---|---|---|---|---|
| Types of pores | Dissolution pores dominated, few cement and clay minerals | Micropores dominated, followed by intergranular and intragranular pores | Micropores dominated | Micropores dominated |
| Porosity | >20% | 13–20% | 4–13% | <4% |
| Permeability | >100 mD | 10–100 mD | 1–10 mD | <1 mD |
| Pore throat characteristics | Good pore connectivity, the maximum connecting pore throat is >1.2 µm | The pore throat radius is not large, with the maximum value of 1.13–1.2 µm | The maximum connecting pore throat is 1.1–1.13 µm | The maximum connecting pore throat is <1.1 µm |
| Reservoir type | High porosity and medium permeability reservoir | Medium porosity and medium permeability | Medium–low porosity and low permeability | Low porosity and low permeability |
| Argillaceous Siltstone | Medium-Grained Sandstone | Fine-Grained Sandstone | Siltstone | |
|---|---|---|---|---|
| Illite | 19.75% | 6.10% | 4.51% | 8.26% |
| Kaolinite | 8.12% | 2.02% | 4.47% | 7.45% |
| Quartz | 25.65% | 29.81% | 11.95% | 20.33% |
| Microcline | 16.29% | 26.92% | 49.46% | 26.78% |
| Albite | 27.82% | 29.09% | 29.61% | 28.92% |
| Calcite | 1.04% | 6.05% | - | - |
| Ankerite | - | - | - | 8.26% |
| Gypsum | 1.33% | - | - | - |
| No. | Lithology | Density (kg/m3) | Pore Volume (cm3) | Porosity(-) | Permeability (mD) |
|---|---|---|---|---|---|
| 8-8 | Siltstone | 2310 | 3.244 | 13.32 | 2.133 |
| 10-21 | Argillaceous siltstone | 2200 | 2.607 | 10.71 | 0.565 |
| 12-22-1 | Siltstone | 2360 | 2.133 | 8.76 | 0.619 |
| 12-22-2 | Siltstone | 2350 | 2.032 | 8.35 | 0.586 |
| 12-8 | Fine-grained sandstone | 2100 | 0.901 | 3.7 | 9.553 |
| 10-27 | Medium-grained sandstone | 2020 | 5.326 | 21.87 | 50.12 |
| 11-5 | Medium-grained sandstone | 2150 | 3.911 | 16.19 | 65.14 |
| 13-26 | Conglomerate | 2140 | 4.282 | 17.59 | 235.4 |
| Cycles | Total Spectral Area | Spectral Peak Area 1 (SPA1) | Variation Ratio of SPA1 | Spectral Peak Area 2 (SPA2) | Variation Ratio of SPA2 |
|---|---|---|---|---|---|
| S1-0 | 38,628.547 | 3597.306 | - | 35,031.24 | - |
| S1-5 | 38,428.711 | 3727.497 | 3.62% | 34,701.214 | −0.94% |
| S1-25 | 38,543.095 | 3494.961 | −0.03% | 35,048.133 | 0.05% |
| S6-25 | 38,235.224 | 4015.571 | 11.63% | 34,219.653 | −2.32% |
| S10-25 | 38,702.333 | 3563.353 | −0.94% | 35,138.98 | 0.31% |
| S20-25 | 38,243.937 | 3481.076 | −3.23% | 34,762.862 | −0.77% |
| S30-25 | 38,709.475 | 3830.756 | 6.49% | 34,871.83 | −0.46% |
| S40-25 | 38,796.919 | 3807.142 | 5.83% | 34,979.926 | −0.15% |
| S50-25 | 38,165.064 | 3949.906 | 9.80% | 34,215.157 | −2.33% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, X.; Liu, H.; Liu, M.; Mao, H.; Wang, D.; Ying, Q.; Ban, S. Pore Structure Evolution in Sandstone of Underground Gas Storage during Cyclic Injection and Production Based on Nuclear Magnetic Resonance Technology. Energies 2023, 16, 2096. https://doi.org/10.3390/en16052096
Qiu X, Liu H, Liu M, Mao H, Wang D, Ying Q, Ban S. Pore Structure Evolution in Sandstone of Underground Gas Storage during Cyclic Injection and Production Based on Nuclear Magnetic Resonance Technology. Energies. 2023; 16(5):2096. https://doi.org/10.3390/en16052096
Chicago/Turabian StyleQiu, Xiaosong, Hejuan Liu, Mancang Liu, Haijun Mao, Duocai Wang, Qiqi Ying, and Shengnan Ban. 2023. "Pore Structure Evolution in Sandstone of Underground Gas Storage during Cyclic Injection and Production Based on Nuclear Magnetic Resonance Technology" Energies 16, no. 5: 2096. https://doi.org/10.3390/en16052096





