FRT Capability Enhancement of Offshore Wind Farm by DC Chopper
Abstract
:1. Introduction
2. Materials and Methods
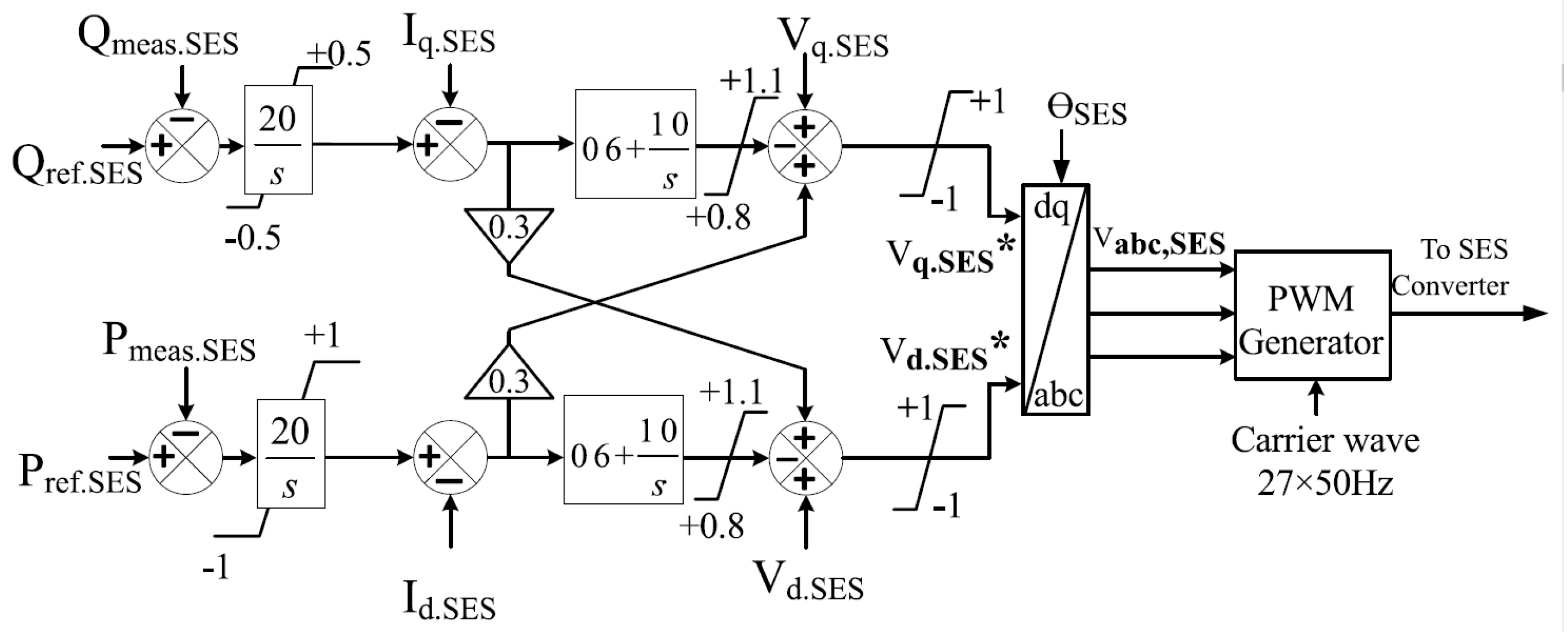
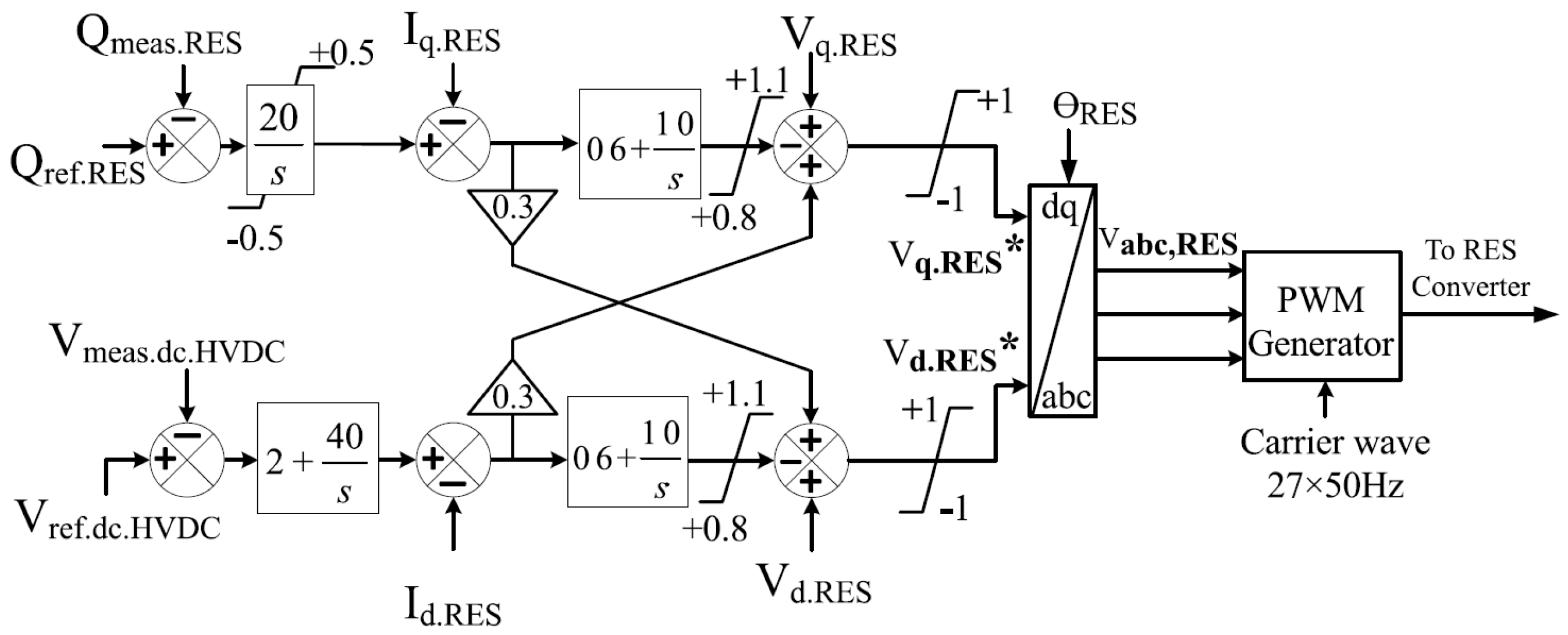
2.1. Description of the Power System Model
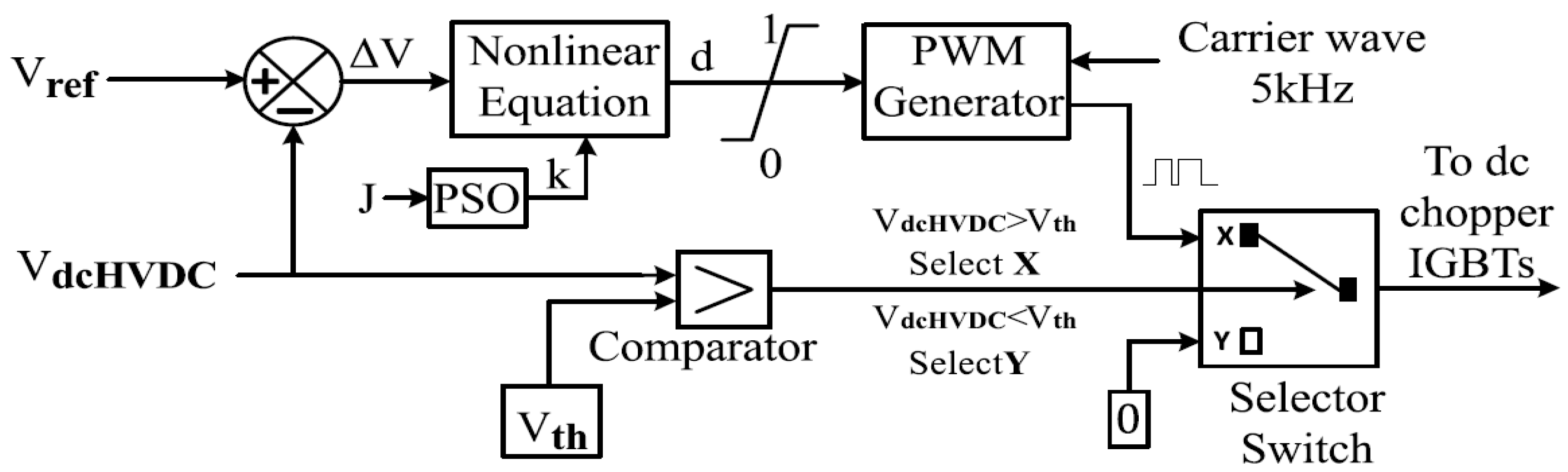
2.2. PSO Controller-Based DC Chopper
2.2.1. DC Chopper
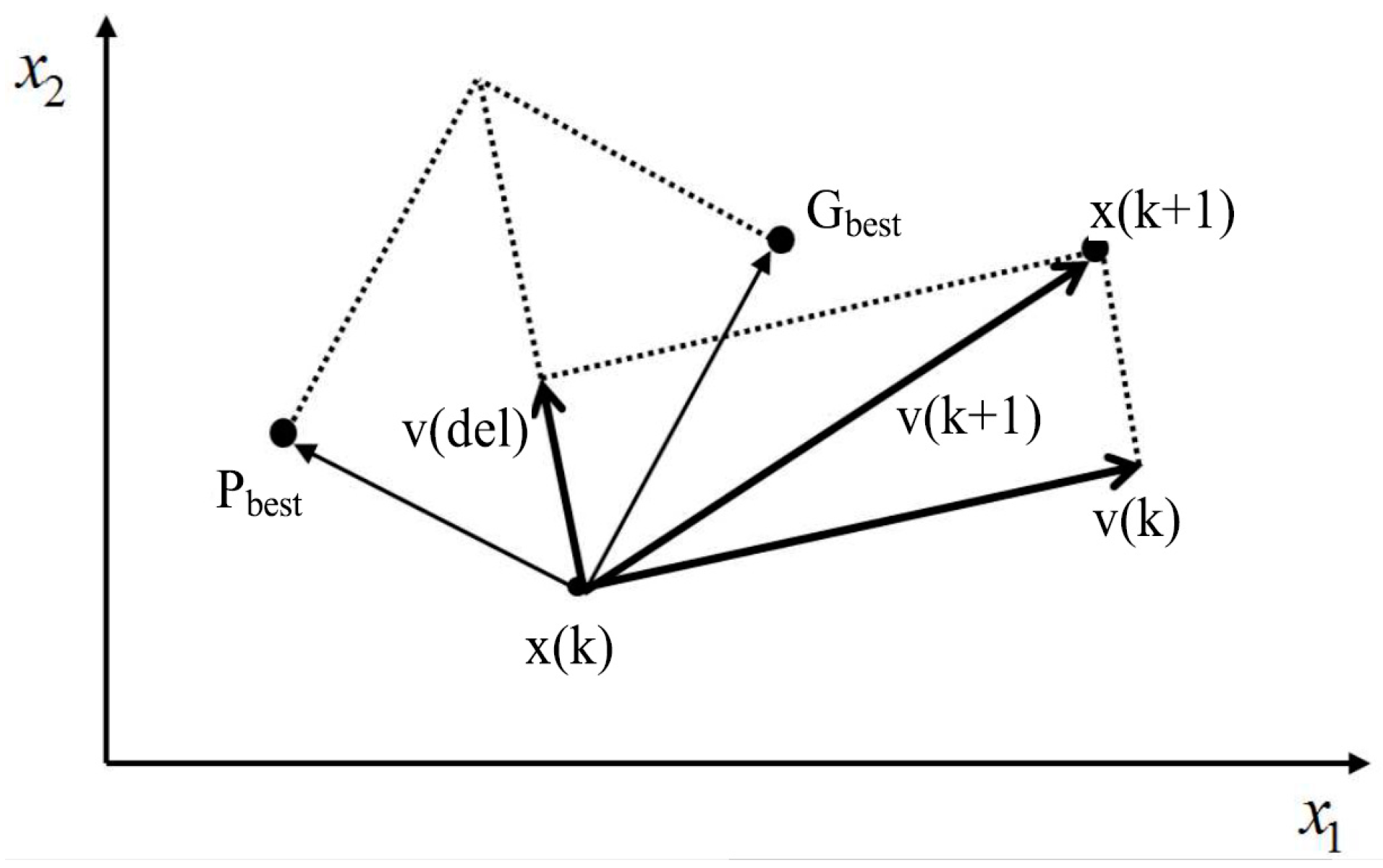
2.2.2. PSO Overview
- No gradient information is required;
- Simple implementation;
- The optimization time is less compared to other methods;
- Ease of use in online optimization schemes;
- Accuracy is high compared to the complexity involved;
- Objective function is used to search in the solution range or area;
- Only the numerical value of the objective function can be used;
- From the initial search point, the optimized solution is guaranteed.
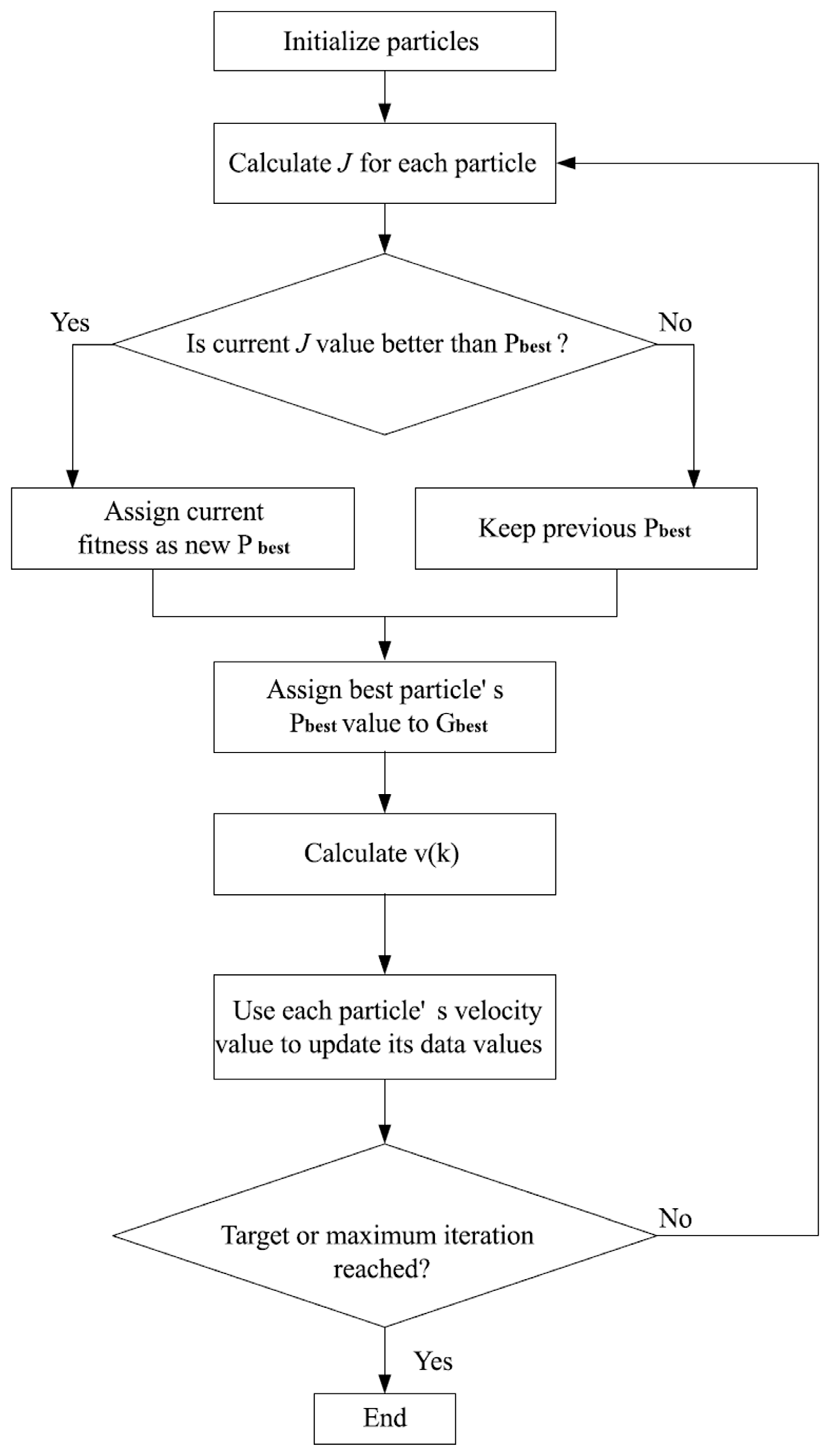
2.2.3. PSO Algorithm
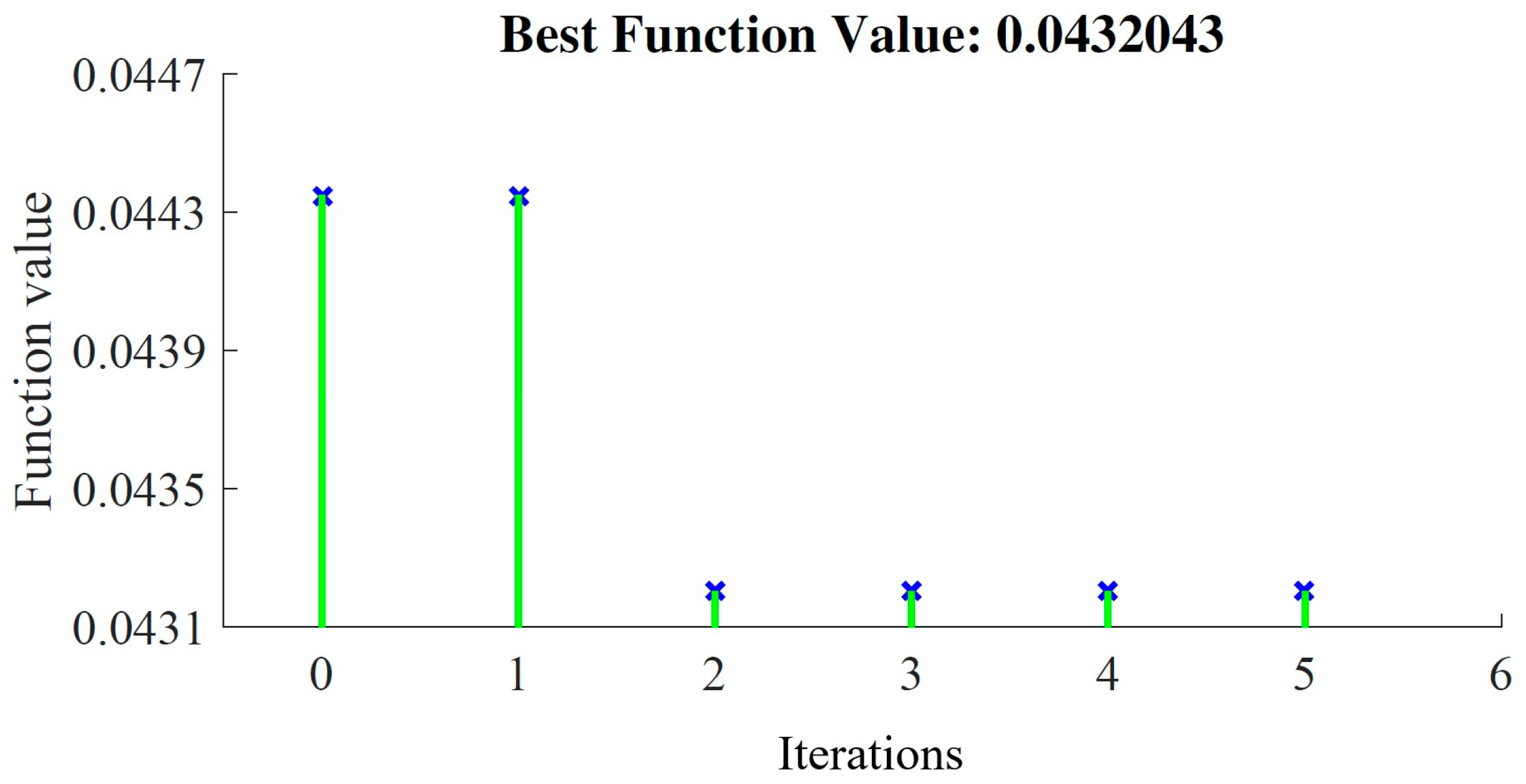
2.2.4. PSO for DC Chopper Optimization
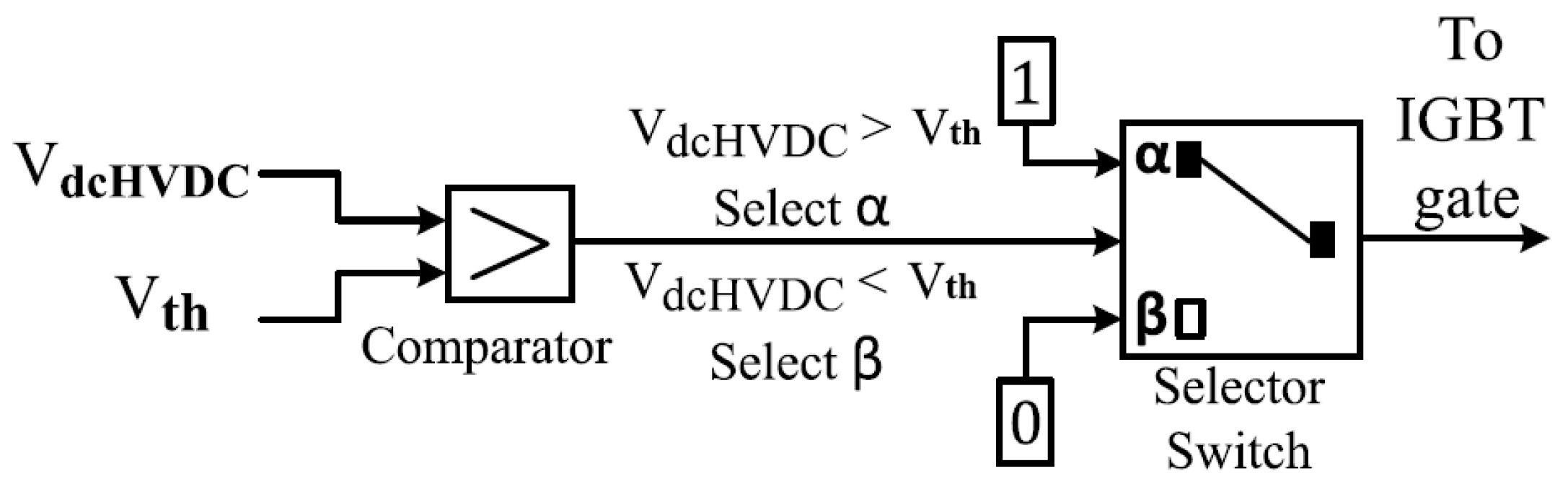
2.2.5. Conventionally Controlled DC Chopper
3. Results and Discussion
3.1. Simulation Considerations
- (1)
- Scenario A: with no controller;
- (2)
- Scenario B: with conventional DC chopper;
- (3)
- Scenario C: with PSO DC chopper.
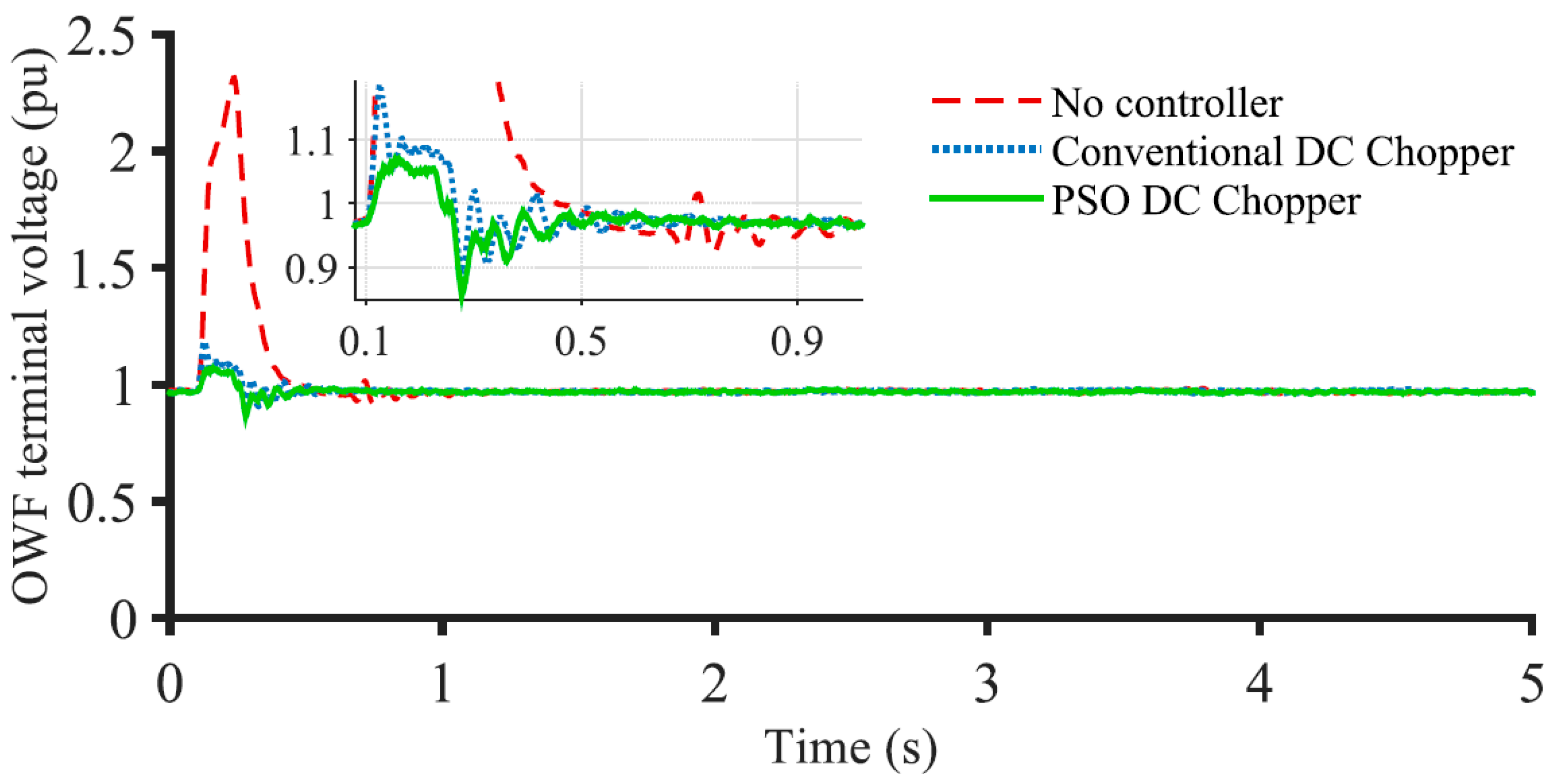
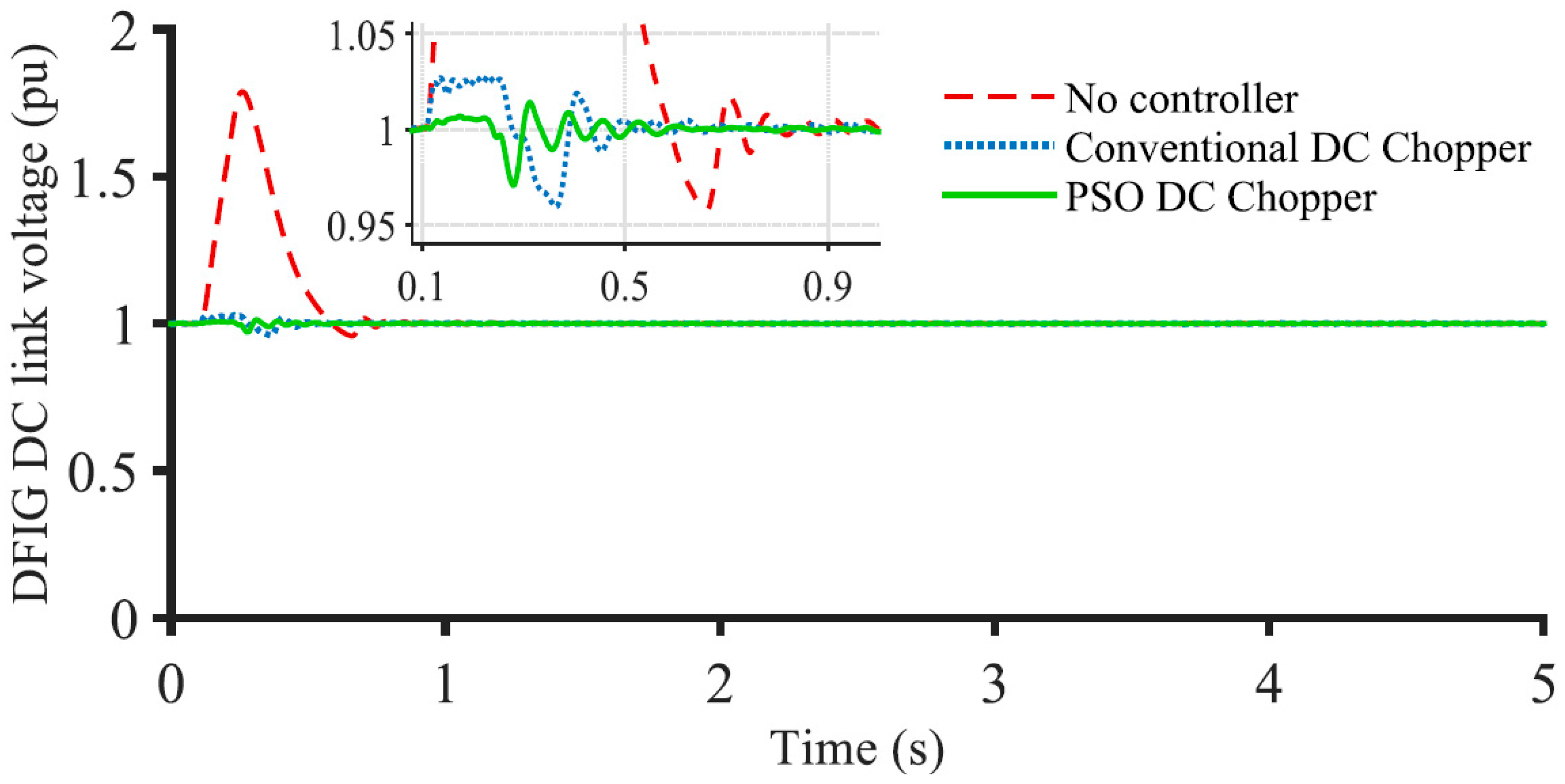
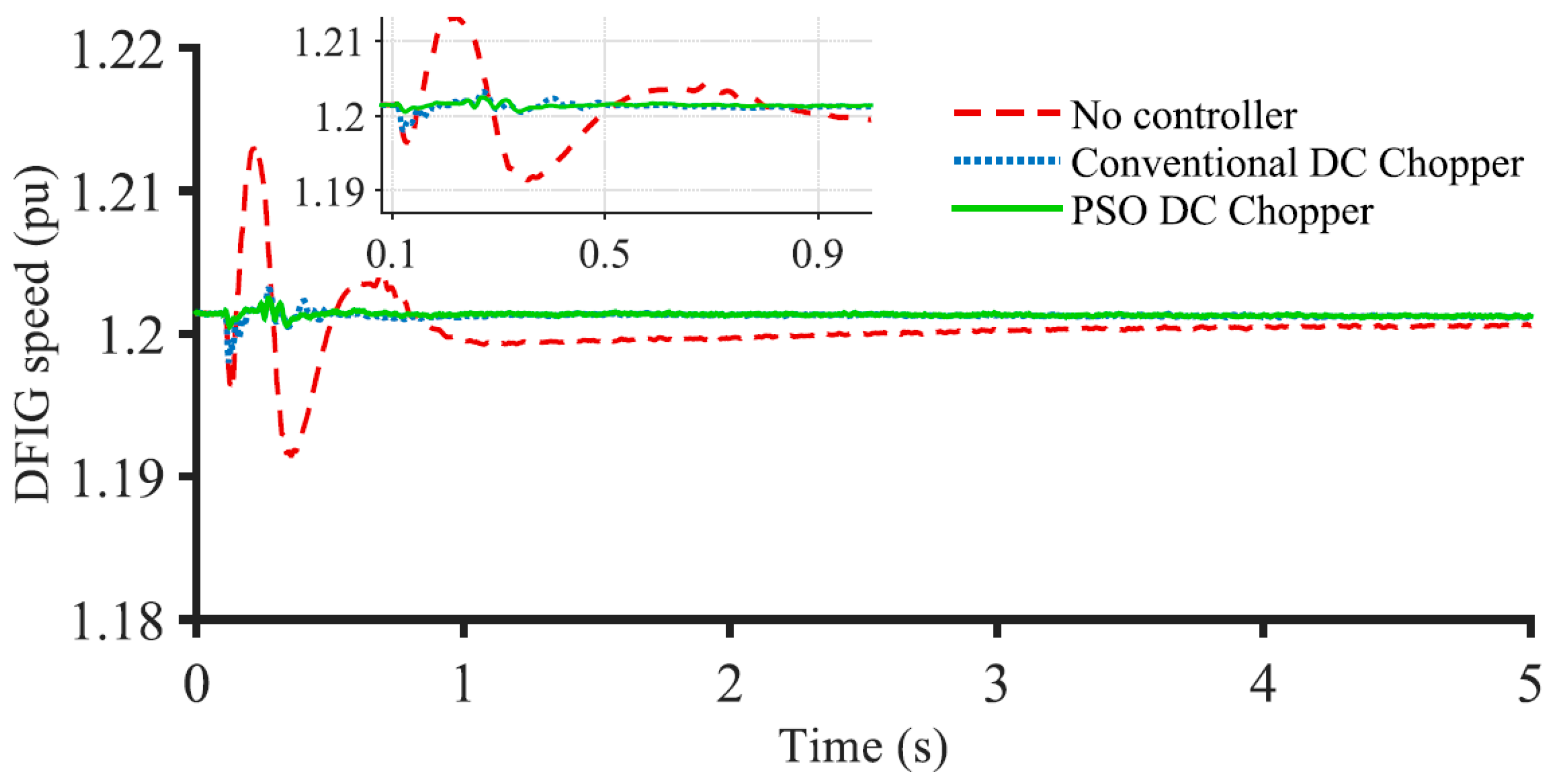
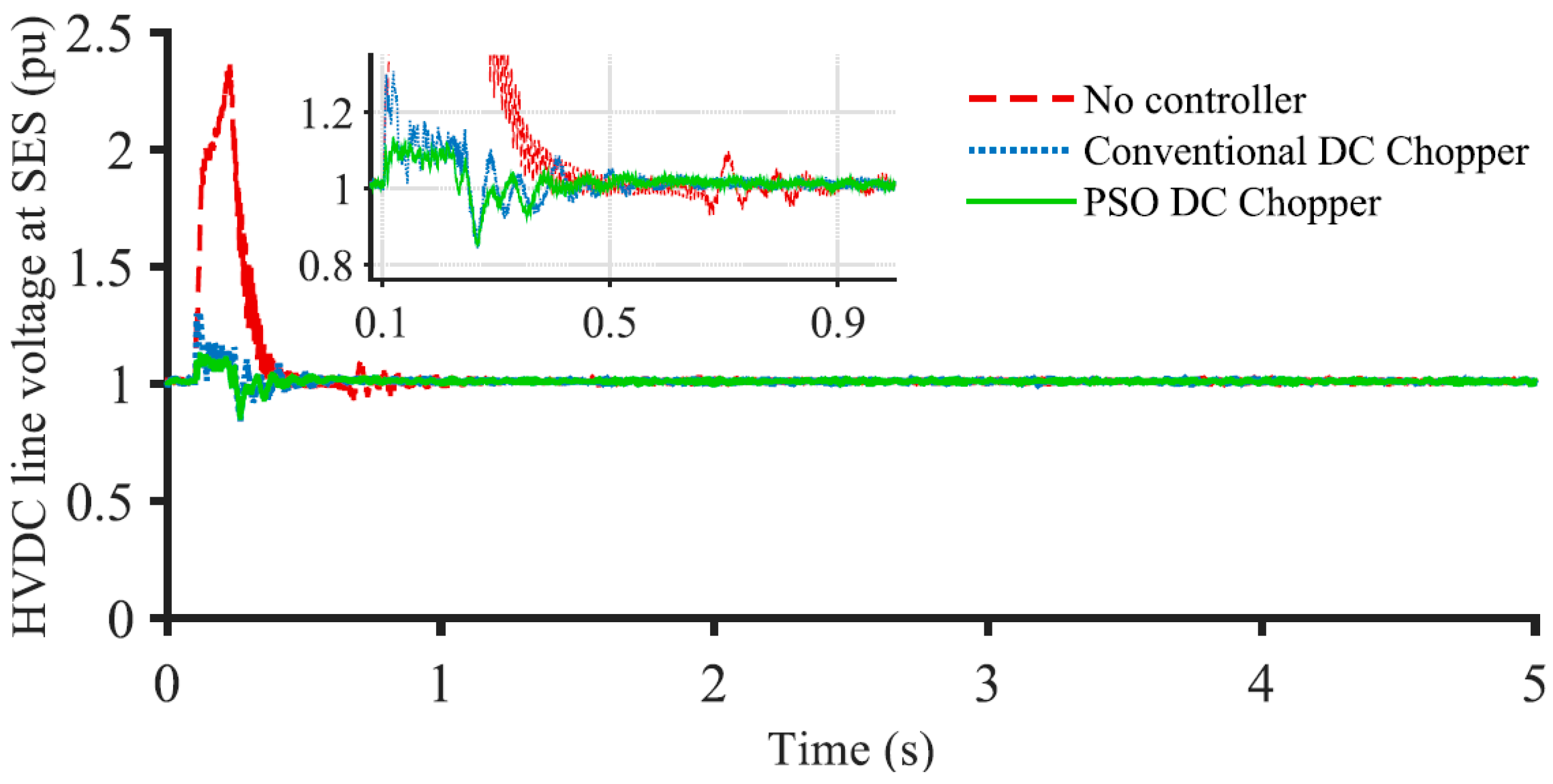
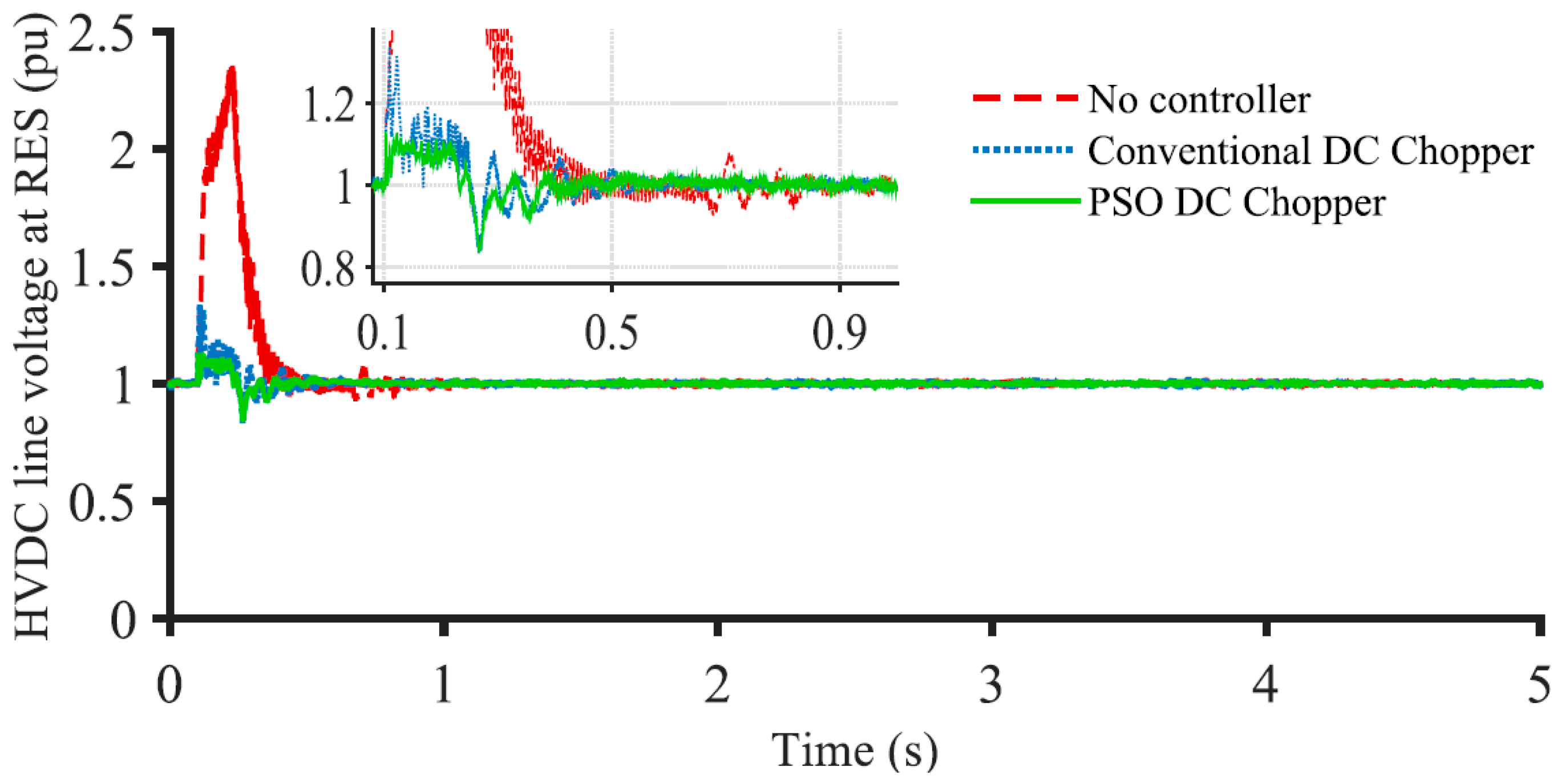
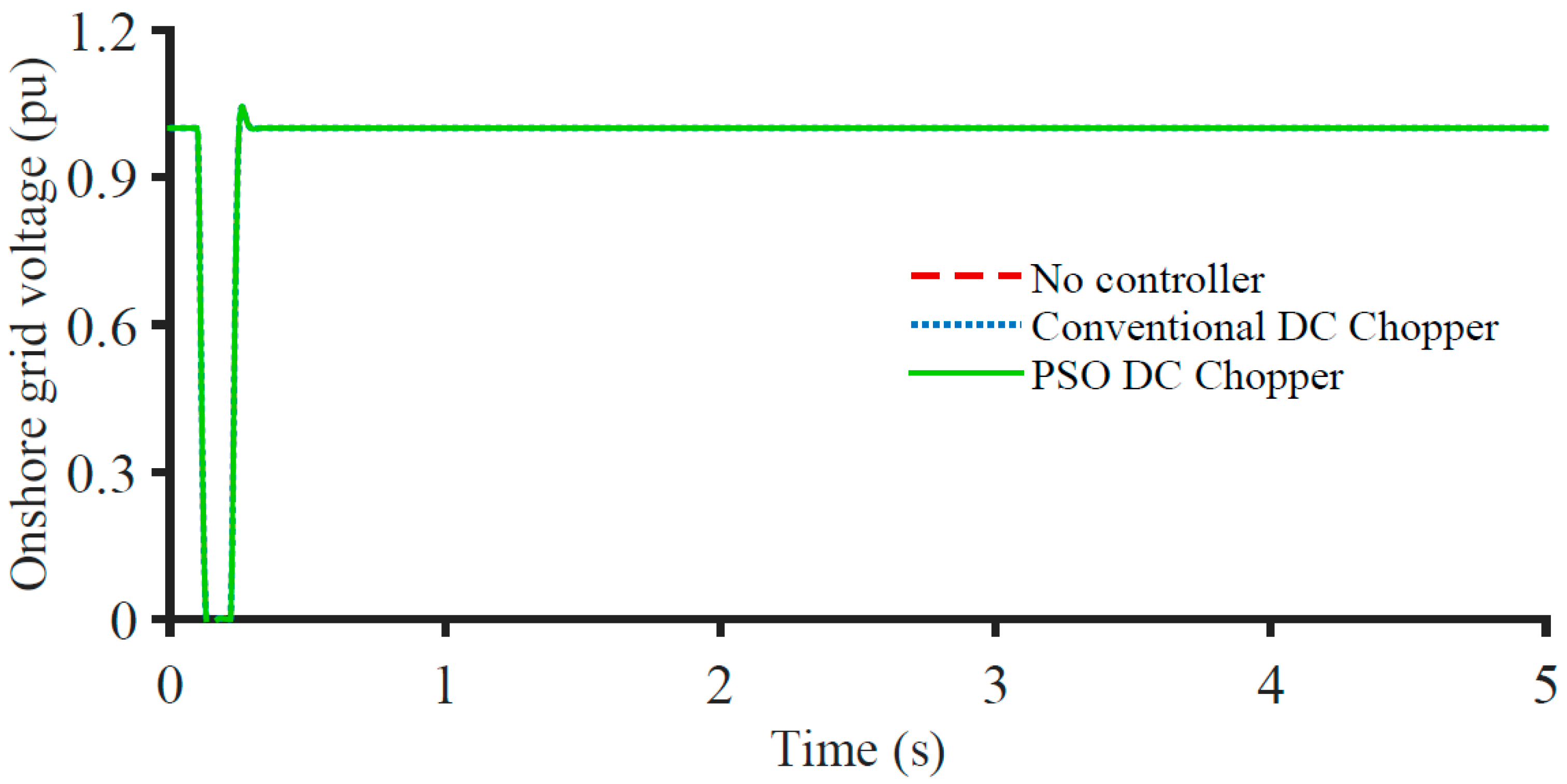
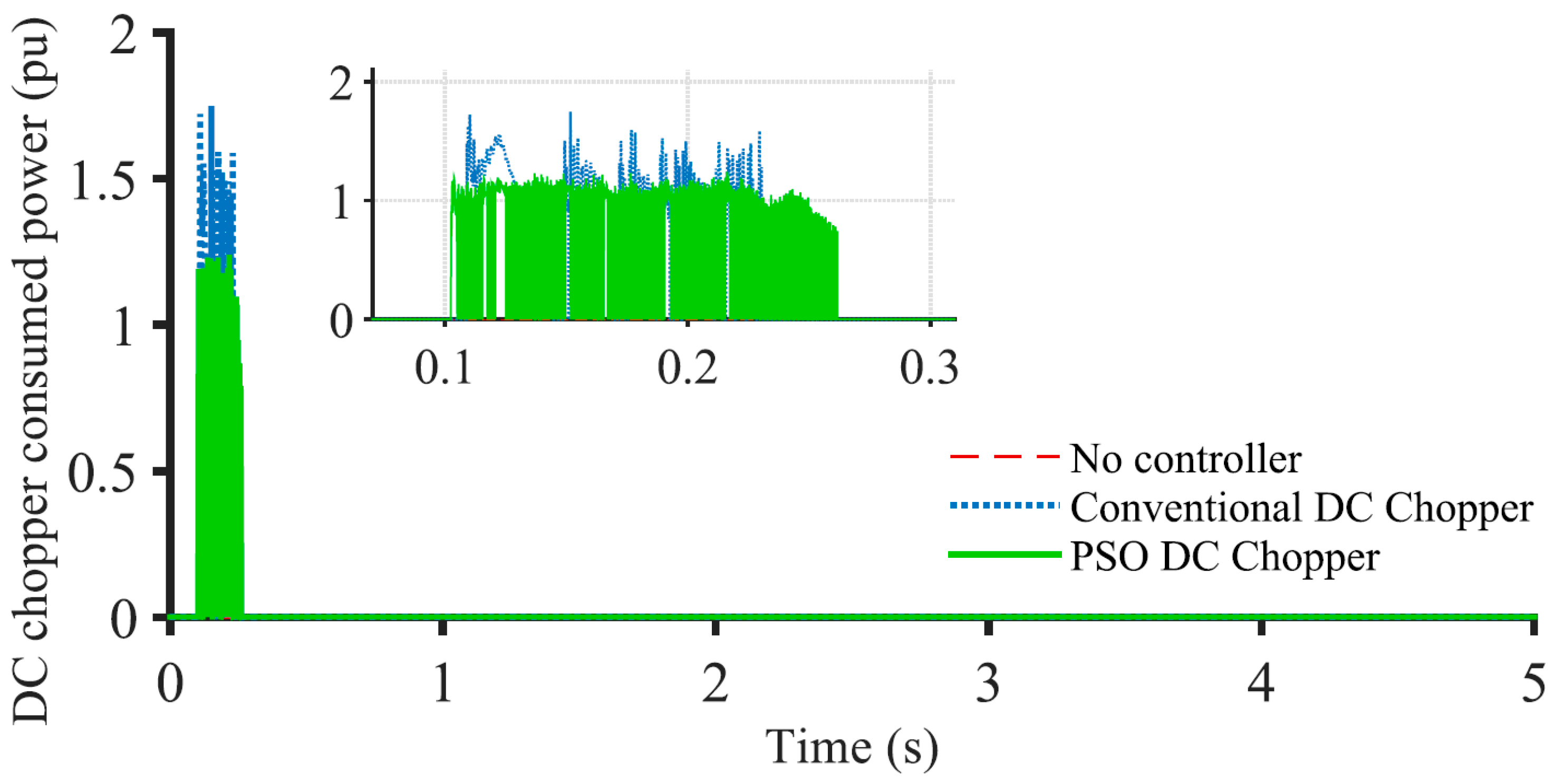
3.2. FRT Performance for Onshore Grid 3LG Fault
3.3. Index-Based Comparison
3.4. Limitations
4. Conclusions
- (i)
- The FRT capability of a DFIG-based offshore wind farms can be enhanced noticeably using the proposed PSO-optimized DC chopper for onshore grid faults;
- (ii)
- The wind farm can continue more stable operation with the proposed PSO-optimized DC chopper;
- (iii)
- The PSO-optimized DC chopper exhibits much better performance than the conventional DC chopper;
- (iv)
- The voltage, speed, and active power profile of the system is improved from 25% to 35% at fault by using the PSO-based DC chopper over the conventionally controlled DC chopper.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deveci, K.; Barutçu, B.; Alpman, E.; Taşcıkaraoğlu, A.; Erdinç, O. On the importance of wind turbine wake boundary to wind energy and environmental impact. Energy Convers. Manag. 2023, 277, 116664. [Google Scholar] [CrossRef]
- US Office of Energy Efficiency & Renewable Energy: Offshore Wind Market Report. Available online: https://www.energy.gov/eere/wind/articles/offshore-wind-market-report-2022-edition (accessed on 5 February 2023).
- Changizian, M.; Mizani, A.; Shoulaie, A. Proposed a new voltage rebalancing method for pole-to-ground fault in bipolar two-level VSC-HVDC. IEEE Trans. Ind. Electron. 2022, 69, 2157–2165. [Google Scholar] [CrossRef]
- Rashid, G.; Ali, M.H. Nonlinear control-based modified BFCL for LVRT capacity enhancement of DFIG based wind farm. IEEE Trans. Energy Convers. 2017, 32, 284–295. [Google Scholar] [CrossRef]
- Rashid, G.; Ali, M.H. Fault ride through capability improvement of DFIG based wind farm by fuzzy logic controlled parallel resonance fault current limiter. J. Electr. Power Syst. Res. 2017, 146, 1–8. [Google Scholar] [CrossRef]
- Rashid, G.; Ali, M.H. Transient stability enhancement of doubly fed induction machine-based wind generator by bridge-type fault current limiter. IEEE Trans. Energy Convers. 2015, 30, 939–947. [Google Scholar] [CrossRef]
- Nanou, S.I.; Papathanassiou, S.A. Grid Code Compatibility of VSC-HVDC connected offshore wind turbines employing power synchronization control. IEEE Trans. Power Syst. 2016, 31, 5042–5050. [Google Scholar] [CrossRef]
- Erlich, I.; Feltes, C.; Shewarega, F. Enhanced voltage drop control by VSC–HVDC systems for improving wind farm fault ride through capability. IEEE Trans. Power Deliv. 2014, 29, 378–385. [Google Scholar] [CrossRef]
- Ali, S.W.; Sadiq, M.; Terriche, Y.; Naqvi, S.A.R.; Mutarraf, M.U.; Hassan, M.A.; Guerrero, J.M. Offshore wind farm-grid integration: A review on infrastructure, challenges, and grid solutions. IEEE Access 2021, 9, 102811–102827. [Google Scholar] [CrossRef]
- Farrar, N.; Ali, M.H.; Dasgupta, D. Artificial intelligence and machine learning in grid connected wind turbine control systems: A comprehensive review. Energies 2023, 16, 1530. [Google Scholar] [CrossRef]
- Ramtharan, G.; Arulampalam, A.; Ekanayake, J.B.; Hughes, F.; Jenkins, N. Fault ride through of fully rated converter wind turbines with AC and DC transmission. IET Renew. Power Gener. 2009, 3, 426–438. [Google Scholar] [CrossRef]
- Harnefors, L.; Jiang-Hafner, Y.; Hyttinen, M.; Jonsson, T. Ride-through methods for wind farms connected to the grid via a VSC- HVDC transmission. In Proceedings of the Nordic Wind Power Conference, Roskilde, Denmark, 1–2 November 2007. [Google Scholar]
- Mohammadi, L.; Avendano-Mora, M.; Barnes, M.; Chan, J. A study on Fault Ride-Through of VSC-connected offshore wind farms. In Proceedings of the IEEE Power and Energy Society, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Xu, L.; Yao, L. DC voltage control and power dispatch of a multi-terminal HVDC system for integrating large offshore wind farms. IET Renew. Power Gener. 2011, 5, 223–233. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Z. Contribution of VSC-HVDC to frequency regulation of power systems with offshore wind generation. IEEE Trans. Energy Convers. 2015, 30, 918–926. [Google Scholar] [CrossRef]
- Martinez Sanz, I.; Chaudhuri, B.; Strbac, G. Inertial response from offshore wind farms connected through DC grids. IEEE Trans. Power Syst. 2015, 30, 1518–1527. [Google Scholar] [CrossRef] [Green Version]
- Silva, B.; Moreira, C.; Seca, L.; Phulpin, Y.; Lopes, J. Provision of inertial and primary frequency control services using offshore multiterminal HVDC networks. IEEE Trans. Sustain. Energy 2012, 3, 800–808. [Google Scholar] [CrossRef]
- Zhu, J.; Booth, C.D.; Adam, G.P.; Roscoe, A.J.; Bright, C.G. Inertia emulation control strategy for VSC-HVDC transmission systems. IEEE Trans. Power Syst. 2013, 28, 1277–1287. [Google Scholar] [CrossRef] [Green Version]
- Junyent-Ferré, A.; Pipelzadeh, Y.; Green, T.C. Blending HVDC-link energy storage and offshore wind turbine inertia for fast frequency response. IEEE Trans. Sustain. Energy 2015, 6, 1059–1066. [Google Scholar] [CrossRef] [Green Version]
- Mitra, P.; Zhang, L.; Harnefors, L. Offshore wind integration to a weak grid by VSC-HVDC links using power-synchronization control: A case study. IEEE Trans. Power Deliv. 2014, 29, 453–461. [Google Scholar] [CrossRef]
- Nam, T.; Shim, J.W.; Hur, K. The beneficial role of SMES coil in DC lines as an energy buffer for integrating large scale wind power. IEEE Trans. Appl. Supercond. 2012, 22, 5701404. [Google Scholar] [CrossRef]
- Daoud, M.I.; Massoud, A.M.; Abdel-Khalik, A.S.; Elserougi, A.; Ahmed, S. A flywheel energy storage system for fault ride through support of grid-connected VSC HVDC-based offshore wind farms. IEEE Trans. Power Syst. 2016, 31, 1671–1680. [Google Scholar] [CrossRef]
- Ahmed, K.; Abdel-Khalik, A.; Elserougi, A.; Massoud, A.; Ahmed, S. Fault ride-through capability enhancement based on flywheel energy storage system for wind farms connected via VSC high voltage DC transmission. In Proceedings of the 10th IET International Conference on AC and DC Power Transmission (ACDC 2012), Birmingham, UK, 4–5 December 2012; pp. 1–6. [Google Scholar]
- Chaudhary, S.K.; Teodorescu, R.; Rodriguez, P.; Kjar, P. Chopper controlled resistors in VSC HVDC transmission for WPP with full-scale converters. In Proceedings of the IEEE PES/IAS Conference on Sustainable Alternative Energy (SAE), Valencia, Spain, 28–30 September 2009; pp. 1–8. [Google Scholar]
- Muisyo, I.; Muriithi, C.; Kamau, S. Enhancing low voltage ride through capability of grid connected DFIG based WECS using WCA-PSO tuned STATCOM controller. Heliyon 2022, 30, e09999. [Google Scholar] [CrossRef]
- Kumeshan, R.; Saha, A.K. A review of swarm-based metaheuristic optimization techniques and their application to doubly fed induction generator. Heliyon 2022, 8, e10956. [Google Scholar]
- Zhu, K.; Chen, Z.; Zong, L.; Metwally, A.S.; Ali, S.; Mohammed, A.H.; Jaszczur, M. Implementation of modified multi-objective particle swarm optimization to multi-machine power system stability. J. Clean. Prod. 2022, 10, 132664. [Google Scholar] [CrossRef]
- Mohammadpour, H.A.; Santi, E. Modeling and control of gate-controlled series capacitor interfaced with a DFIG-based wind farm. IEEE Trans. Ind. Electr. 2015, 62, 1022–1033. [Google Scholar] [CrossRef]
- Rashid, G.; Ali, M.H. Application of parallel resonance fault current limiter for fault ride through capability augmentation of DFIG based wind farm. In Proceedings of the IEEE PES Transmission & Distribution (T&D) Conference & Exposition, Dallas, TX, USA, 3–5 May 2016; pp. 1–5, paper ID:TD0149. [Google Scholar]
- Rashid, G.; Ali, M.H. Asymmetrical fault ride through capacity augmentation of DFIG based wind farms by parallel resonance fault current limiter. In Proceedings of the IEEE Power Energy Society, Boston, MA, USA, 17–21 July 2016; pp. 1–5, paper ID:16PESGM0946. [Google Scholar]
- Lindberg, A. PWM and Control of Two and Three Level High Power Voltage Source Converters. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 1995. [Google Scholar]
- Matlab, VSC-Based HVDC Link. Available online: http://www.mathworks.com/help/physmod/sps/powersys/ug/vsc-based-hvdc-link.html#bqsqow_ (accessed on 5 February 2023).
- Bianchi, L.; Dorigo, M.; Gambardella, L.M.; Gutjahr, W.J. A survey on metaheuristics for stochastic combinatorial optimization. Nat. Comput. 2009, 8, 239–287. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Western Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, New York, NY, USA, 4–6 October 1995; Volume 1, pp. 39–43. [Google Scholar]
- Chen, P.-H.; Kuo, C.-C.; Chen, F.-H.; Chen, C.-C. Refined binary particle swarm optimization and application in power system. WSEAS Trans. Syst. 2009, 8, 169–178. [Google Scholar]
- Engelbrecht, A.P. Fundamentals of Computational Swarm Intelligence; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Kennedy, J.R.; Eberhart, R.C.; Shi, Y. Swarm Intelligence; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2001. [Google Scholar]
- Dorigo, M.; Thomas, S. Ant Colony Optimization; The MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Kim, J.-Y.; Kim, H.-M.; Kim, S.-K.; Jeon, J.-H.; Choi, H.-K. Designing an energy storage system fuzzy PID controller for microgrid islanded operation. Energies 2011, 4, 1443–1460. [Google Scholar] [CrossRef] [Green Version]


| Characteristics | Value |
|---|---|
| Nominal power | 1.67 MVA |
| Rated voltage (V) | 690 V |
| Stator to rotor turns ratio | 0.3 |
| System frequency | 50 Hz |
| Stator resistance (Rs) | 0.012 pu |
| Stator inductance (Ls) | 0.15 pu (referred to stator) |
| Rotor resistance (Rr) | 0.012 pu |
| Rotor reactance (Lr) | 0.15 pu (referred to stator) |
| Mutual inductance (Lm) | 4 pu |
| DFIG inertia Constant (H) | 0.0685 pu |
| DC link rated voltage (Edc) | 1200 V |
| Turbine inertia constant | 4.32 s |
| Shaft spring constant | 1.11 pu |
| Shaft mutual damping | 1.5 pu |
| Index Parameters (%) | Values of Indices | ||
|---|---|---|---|
| No Auxiliary Controller | Conventional DC Chopper | PSO-Based DC Chopper | |
| VOWF (pu·s) | 14.85 | 3.96 | 3.19 |
| ωDFIG (pu·s) | 0.74 | 0.11 | 0.08 |
| POWF (pu·s) | 23.51 | 5.12 | 3.80 |
| VdcHVDC (pu·s) | 22.56 | 5.39 | 4.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, G.; Ali, M.H. FRT Capability Enhancement of Offshore Wind Farm by DC Chopper. Energies 2023, 16, 2129. https://doi.org/10.3390/en16052129
Rashid G, Ali MH. FRT Capability Enhancement of Offshore Wind Farm by DC Chopper. Energies. 2023; 16(5):2129. https://doi.org/10.3390/en16052129
Chicago/Turabian StyleRashid, Gilmanur, and Mohd Hasan Ali. 2023. "FRT Capability Enhancement of Offshore Wind Farm by DC Chopper" Energies 16, no. 5: 2129. https://doi.org/10.3390/en16052129
APA StyleRashid, G., & Ali, M. H. (2023). FRT Capability Enhancement of Offshore Wind Farm by DC Chopper. Energies, 16(5), 2129. https://doi.org/10.3390/en16052129







